Abstract
DNA A-tracts have been defined as four or more consecutive A·T base pairs without a TpA step. When inserted in phase with the DNA helical repeat, bending is manifested macroscopically as anomalous migration on polyacrylamide gels, first observed >20 years ago. An unsolved conundrum is why DNA containing in-phase A-tract repeats of A4T4 are bent, whereas T4A4 is straight. We have determined the solution structures of the DNA duplexes formed by d(GCAAAATTTTGC) [A4T4] and d(CGTTTTAAAACG) [T4A4] with 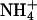 counterions by using NMR spectroscopy, including refinement with residual dipolar couplings. Analysis of the structures shows that the ApT step has a large negative roll, resulting in a local bend toward the minor groove, whereas the TpA step has a positive roll and locally bends toward the major groove. For A4T4, this bend is nearly in phase with bends at the two A-tract junctions, resulting in an overall bend toward the minor groove of the A-tract, whereas for T4A4, the bends oppose each other, resulting in a relatively straight helix. NMR-based structural modeling of d(CAAAATTTTG)15 and d(GTTTTAAAAC)15 reveals that the former forms a left-handed superhelix with a diameter of ≈110 Å and pitch of 80 Å, similar to DNA in the nucleosome, whereas the latter has a gentle writhe with a pitch of >250 Å and diameter of ≈50 Å. Results of gel electrophoretic mobility studies are consistent with the higher-order structure of the DNA and furthermore depend on the nature of the monovalent cation present in the running buffer.
counterions by using NMR spectroscopy, including refinement with residual dipolar couplings. Analysis of the structures shows that the ApT step has a large negative roll, resulting in a local bend toward the minor groove, whereas the TpA step has a positive roll and locally bends toward the major groove. For A4T4, this bend is nearly in phase with bends at the two A-tract junctions, resulting in an overall bend toward the minor groove of the A-tract, whereas for T4A4, the bends oppose each other, resulting in a relatively straight helix. NMR-based structural modeling of d(CAAAATTTTG)15 and d(GTTTTAAAAC)15 reveals that the former forms a left-handed superhelix with a diameter of ≈110 Å and pitch of 80 Å, similar to DNA in the nucleosome, whereas the latter has a gentle writhe with a pitch of >250 Å and diameter of ≈50 Å. Results of gel electrophoretic mobility studies are consistent with the higher-order structure of the DNA and furthermore depend on the nature of the monovalent cation present in the running buffer.
Sequence-directed bending of DNA was first observed >20 years ago as an anomalously slow gel electrophoretic mobility of DNA fragments isolated from the kinetoplast body of Leishmania tarentolae (1). The sequences giving rise to the bending were identified as repeating runs of consecutive (four to six) A·T base pairs (A-tract) in phase with the 10-bp helical repeat (2). The idea that conserved DNA sequences could have an intrinsic sequence-directed curvature immediately suggested a functional role for DNA bending in control of cellular processes and led to extensive efforts to understand the structural origin of the so-called A-tract bending (reviewed in refs. 3 and 4). Two major models emerged, the wedge model (5–8), which attributes bending to cumulative local bends between base-pair steps, usually in the A-tract; and the junction model (9, 10), which assumes a discontinuity between helical trajectories at the junction between the A- and non-A-tract DNA. Although these two models have long been debated, they are in fact not mutually exclusive and to a certain extent depend on how and where the helical axis is defined (11). Recent analyses of DNA bending have considered this and have proposed a delocalized bend model that incorporates aspects of both wedge and junction models (4).
The bend angle for a single helical turn of DNA containing an A-tract has been estimated by various studies to be 11–28° (4). A large number of biochemical studies of A-tract bending have used DNA oligonucleotides containing a single (or two) helical repeats of a sequence containing a single phased (or two or three phased) A-tract ligated together to make a polymer with n repeats, so that the small bends in a single A-tract added in phase give rise to a macroscopically observable bending as assayed by gel electrophoresis, circularization assays, or electron microscopy (4). Concurrently, both x-ray crystallography and NMR spectroscopy have been used to determine the structures of DNA oligonucleotides containing single A-tracts in an attempt to understand DNA bending on a dinucleotide level (reviewed in refs. 4 and 12). Certain characteristics of A-tracts have emerged, i.e., narrow minor groove, generally high propeller twist, and hydration and/or ions in the minor groove, which may be associated with A-tract bending. However, x-ray crystallography has not resolved the issue of the structural origin of bending, because crystal packing, lattice forces, and crystallization agents strongly influence the bending (13–16). The A-tracts in crystal structures are straight (17), inconsistent with wedge models, and therefore it has been proposed that bending must occur at the junctions of A-tract (17, 18). High-resolution structure determination of DNA by NMR has been limited both by the relatively low number of short-range restraints that determine the local dinucleotide structure and, until recently, by lack of long-range (>7 Å) restraints for the accurate determination of the global bend. The application of residual dipolar couplings (RDCs) (19) has in principle made it possible to get accurate long-range angular information for DNA helices, and several recent studies have used them (20–22). Both x-ray and solution structural analysis of A-tract bending have also been limited by the short DNA length (usually only one helical turn) and end effects.
A-tracts have been variously described as homopolymeric runs of four to six A·T base pairs (23) (sometimes this is extended to eight) or, because an ApT step does not abolish macroscopically observed bending, four to eight A·T base pairs without a TpA step (3, 12). The defining experiments for the latter definition were the gel electrophoretic mobility studies of Hagerman, which showed that polynucleotides containing repeating runs of A3T3 or A4T4 at 10-bp intervals were significantly bent (24), whereas those with T4A4 were straight (25). It has proven difficult to reconcile these results with any of the models for DNA A-tract bending. The polarity of A-tracts separated by a helical repeat does not significantly affect bending (9). The vast majority of biochemical as well as structural studies have considered only homopolymeric A-tracts. Here, we present the solution structures of d(GCAAAATTTTGC) [A4T4] and d(CGTTTTAAAACG) [T4A4] duplexes with 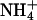 counterions by NMR spectroscopy, including refinement with RDCs. The two DNA dodecamers have significantly different global bends due in large part to differences at the TpA vs. ApT steps. For T4A4, the bend at the TpA step opposes the two bends at the junctions with non-A-tract DNA, resulting in a relatively straight molecule, whereas for A4T4, all bends are nearly in phase, resulting in a global bend toward the minor groove of the A-tract. In both cases, the junctions of the two A4 blocks cause an abrupt change in helical parameters. Thus, the two A4 blocks are best considered as separate A-tracts. The helical parameters determined for the central 10 base pairs of the duplexes were used to construct models of d(CA4T4G)15 and d(GT4A4C)15. Surprisingly, d(CA4T4G)15 forms a left-handed superhelix with a diameter of ≈110 Å and a pitch of 80 Å, similar to the DNA superhelix in nucleosome core particles (26), whereas d(GT4A4C)15 has a gentle writhe with a pitch of >250 Å and diameter of ≈50 Å. Results of gel electrophoretic mobility studies are consistent with the higher-order structures of these molecules. Furthermore, the magnitude of the gel electrophoretic mobility anomaly depends on the nature of the monovalent cation present in the running buffer.
counterions by NMR spectroscopy, including refinement with RDCs. The two DNA dodecamers have significantly different global bends due in large part to differences at the TpA vs. ApT steps. For T4A4, the bend at the TpA step opposes the two bends at the junctions with non-A-tract DNA, resulting in a relatively straight molecule, whereas for A4T4, all bends are nearly in phase, resulting in a global bend toward the minor groove of the A-tract. In both cases, the junctions of the two A4 blocks cause an abrupt change in helical parameters. Thus, the two A4 blocks are best considered as separate A-tracts. The helical parameters determined for the central 10 base pairs of the duplexes were used to construct models of d(CA4T4G)15 and d(GT4A4C)15. Surprisingly, d(CA4T4G)15 forms a left-handed superhelix with a diameter of ≈110 Å and a pitch of 80 Å, similar to the DNA superhelix in nucleosome core particles (26), whereas d(GT4A4C)15 has a gentle writhe with a pitch of >250 Å and diameter of ≈50 Å. Results of gel electrophoretic mobility studies are consistent with the higher-order structures of these molecules. Furthermore, the magnitude of the gel electrophoretic mobility anomaly depends on the nature of the monovalent cation present in the running buffer.
Materials and Methods
Sample Preparation. The DNA dodecamers, A4T4, d(GCA4T4GC) and T4A4, d(CGT4A4CG), were chemically synthesized on an ABI 381 (Applied Biosystems) synthesizer by using standard phosphoramidite chemistry and purified on 20% denaturing polyacrylamide gels. 13C,15N-labeled DNA was enzymatically synthesized and purified as described (27) by using 13C,15N-labeled dNTPs. NMR samples were 1 and 2 mM in duplex for unlabeled and uniformly 13C,15N-labeled samples, respectively, in 25 mM NH4Cl, pH 6.0 (adjusted with ammonium hydroxide) in either 2H2O or 90% 1H2O/10% 2H2O.
NMR Spectroscopy. All NMR spectra were recorded on Bruker (Billerica, MA) DRX 500- and 600-MHz spectrometers at 15°C unless otherwise specified. 2D NOESY (τm = 300 ms) and 1H-13C heteronuclear sequential quantum correlation (HSQC) spectra acquired on unlabeled 2H2O samples and 3D 1H-13C NOESY-heteronuclear multiple quantum correlation (HMQC) spectra acquired on 13C,15N-labeled samples were used to assign the nonexchangeable resonances. Exchangeable resonances were assigned from  echo NOESY at 1°C on unlabeled H2O samples. For nuclear Overhauser effect (NOE) build-up curves, a series of 2D 2H2O NOESY spectra were acquired with mixing times of 50, 80, 120, and 180 ms. Distance restraints were derived from the spectra by fitting the NOE volumes at different mixing times to binomial curves, by using the derivatives at time 0 to calculate relative distances with the cytosine H5–H6 distances as a standard. The upper and lower limits were imposed at ±20% of the calculated distances. NOE restraints derived from 3D 1H-13C NOESY-HMQC, and 2D
echo NOESY at 1°C on unlabeled H2O samples. For nuclear Overhauser effect (NOE) build-up curves, a series of 2D 2H2O NOESY spectra were acquired with mixing times of 50, 80, 120, and 180 ms. Distance restraints were derived from the spectra by fitting the NOE volumes at different mixing times to binomial curves, by using the derivatives at time 0 to calculate relative distances with the cytosine H5–H6 distances as a standard. The upper and lower limits were imposed at ±20% of the calculated distances. NOE restraints derived from 3D 1H-13C NOESY-HMQC, and 2D 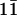 -echo NOESY experiments were incorporated into structure calculations as qualitative restraints of 1.8–5.5 Å. 3J(H1′,H2′) scalar coupling constants were obtained from analysis of double-quantum-filtered COSY spectra. A range of 8.5–11 Hz was observed, which was used to constrain the sugar conformations to the C2′ endo and C1′ exo regions of the pseudorotation phase angle. ε and β dihedral angles were measured by using 31P spin-echo difference CT-HSQC and spin-echo difference CH-HCCH correlation experiments (28, 29). χ angles were determined as described (30). Error bounds of ±30° for all experimentally determined torsion angles were used in structural calculations.
-echo NOESY experiments were incorporated into structure calculations as qualitative restraints of 1.8–5.5 Å. 3J(H1′,H2′) scalar coupling constants were obtained from analysis of double-quantum-filtered COSY spectra. A range of 8.5–11 Hz was observed, which was used to constrain the sugar conformations to the C2′ endo and C1′ exo regions of the pseudorotation phase angle. ε and β dihedral angles were measured by using 31P spin-echo difference CT-HSQC and spin-echo difference CH-HCCH correlation experiments (28, 29). χ angles were determined as described (30). Error bounds of ±30° for all experimentally determined torsion angles were used in structural calculations.
Determination of RDCs. Pf1 phage was prepared, and spectra for measurement of one-bond H–C RDCs were acquired as described (31). The stock of Pf1 phage (50–60 mg/ml) was dialyzed extensively into the NMR buffer before being mixed with the unlabeled DNA samples to a final concentration of 15 mg/ml. 2D 1H-13C heteronuclear sequential quantum correlation spectra were acquired on unlabeled DNA samples with or without Pf1 phage in 2H2O. One-bond H–C RDCs were calculated from the differences of peak splitting in the direct (1H) dimension of the anisotropic and isotropic spectra.
Structure Calculations. Structures were calculated in vacuo by using amber 7.0 software (32) with the Cornell et al. force field (33) with a refinement protocol as described (34). Test calculations using the generalized-Born solvation model (35) resulted in only negligible changes in the structures. Square-well penalty functions with error bounds as indicated above and in Table 1 were used for all experimental restraints. Refinements were performed in two steps. In the first step, refinement with NOEs and torsion angles was done starting from completely randomized structures. In the second step, the RDCs were used in addition to NOE and torsion angle restraints. Initial estimates of the alignment tensors were obtained from the preliminary structures resulting from the first refinement step, as described (36). To impose better convergence of the ensembles, some artificial torsion angle restraints were used for α (270–330°), γ (30–90°), and ξ (240–300°) (20); these restraints cover the B-DNA range and do not exert any force on the final structures. To prevent high violations of local geometries while accommodating the RDC restraints, additional angle restraints to maintain proper local geometries were used (36). The family of best structures (9 of 30 calculated for A4T4 and T4A4 molecules) was selected on the basis of lowest energy and lowest violation. Structural statistics of the final A4T4 and T4A4 ensembles along with NMR restraints used are summarized in Table 1. Helical parameters (Table 2, which is published as supporting information on the PNAS web site) were calculated with 3dna software (37) by using the mean base-pair reference frame (38). The madbend program was used for the calculation of overall DNA curvature (39). The reference frame was put to the center of A4T4 and T4A4, and the terminal base pairs were neglected due to end effects. Average values of tilt, roll, and twist from the ensemble of nine best structures were used for the bend calculations.
Table 1. Structural statistics for the ensemble of nine best structures.
| A4T4 | T4A4 | |
|---|---|---|
| Experimental data | ||
| NOEs | 586 | 549 |
| WC hydrogen bonds | 28 | 28 |
| Torsion angles | 160 | 160 |
| PPA | 24 | 24 |
| RDCs | 72 | 72 |
| Violations of experimental restraints | ||
| Distance restraints | ||
| No. of violations >0.2 Å | 2 | 0 |
| Maximum violation, Å | 0.26 | 0.19 |
| Residual dipolar couplings | ||
| Average violation, Hz | -0.03 | 0.05 |
| Maximum violation, Hz | -2.5 | 2.8 |
| rms deviation from ideal geometry | ||
| Bonds, Å | 0.0084 ± 0.0004 | 0.0098 ± 0.0006 |
| Angles, ° | 2.21 ± 0.02 | 2.55 ± 0.021 |
| Average atomic pairwise rms deviation of all atoms, Å | 0.57 ± 0.11 | 0.51 ± 0.11 |
Final force constants used for square-well penalty functions of individual types of restraints were 32 kcal·mol-1·Å-2 for NOEs and WC hydrogen bonds, 200 kcal·mol-1·rad-2 for torsion angles and PPA, and 0.3 kcal·mol-1·Hz-2 for RDCs. The force constants were ramped up during the simulated annealing protocol as described (34). Error bounds of ± 1.5 Hz were used for all residual dipolar coupling restraints.
Structural Models of d(CAAAATTTTG)15 and d(GTTTTAAAAC)15. The local helical parameters from the central 10 base pairs of the A4T4 and T4A4 structures were extracted by using 3dna (37) and used to generate DNA helices of d(CA4T4G)15 and d(GT4A4C)15. Similar calculations were performed for the published d(GGCA6CGG)·d(CCGT6GCCC) structure (PDB ID code 1FZX). Because only the central 10 base pairs were used, errors due to end effects are largely eliminated.
Gel Electrophoretic-Mobility Assays. DNA oligonucleotides d(CA4T4G), d(GT4A4C), d(GCA6CG), d(CGT6GC), d(GGCA4GCC), and d(GGCT4GCC) were ligated and 32P labeled as described (9). One times TBE solution was made with 89 mM Tris-borate/2.5 mM EDTA, pH 8.14/25 mM NH4Cl, KCl, or NaCl. 8% nondenaturing polyacrylamide gels (mono/bis acrylamide, ratio 29:1) were prepared with 25 mM corresponding counterions. The gels were run at 7 V/cm for 12 h in the cold room (5–8°C) before autoradiography. Ten- and 25-bp DNA ladders (Invitrogen) were 5′-labeled with [γ-32P]ATP and electrophoresed adjacent to ligated products as molecular weight markers.
Results and Discussion
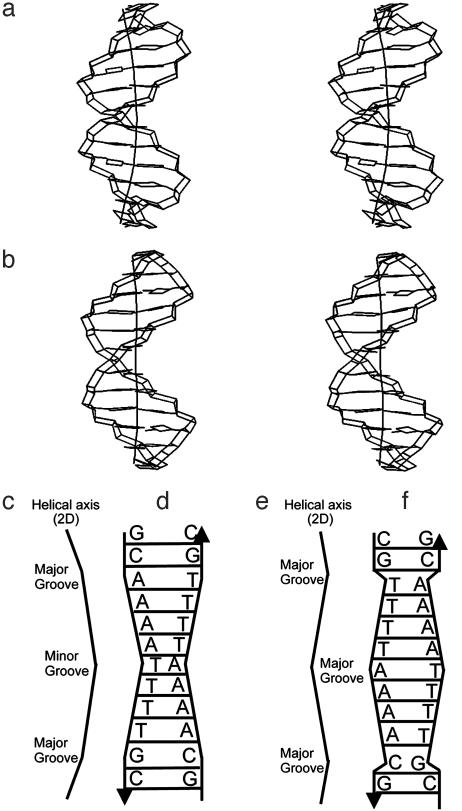
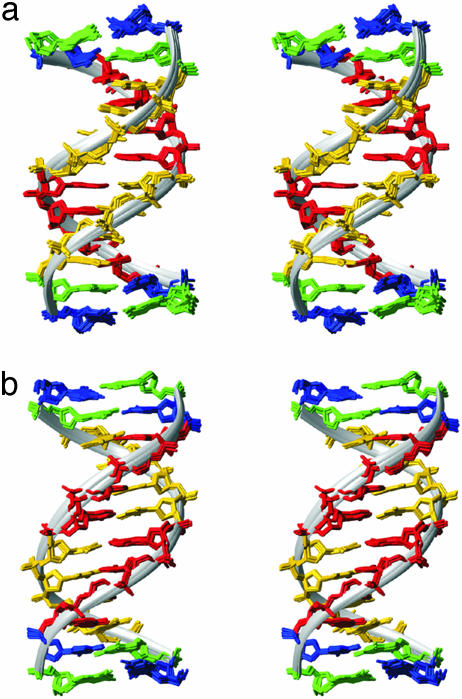
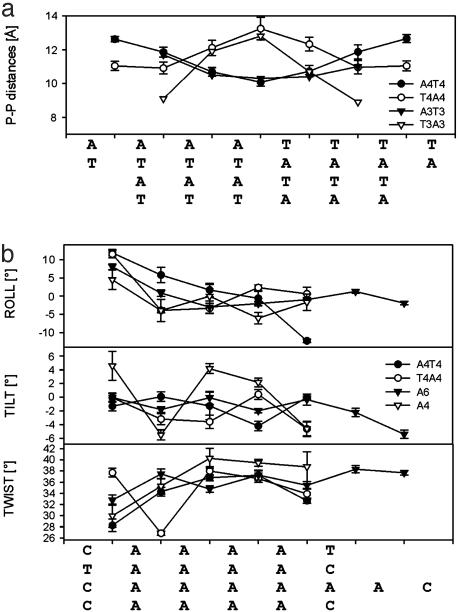
Solution Structures of [d(GCAAAATTTTGC)]2 and [d(CGTTTTAAAACG)]2. From the definition of an A-tract as four or more consecutive A·T base pairs without a TpA step (3, 12, 40), the A4T4 sequence consists of a single A-tract element, whereas the T4A4 sequence consists of two consecutive A-tract elements disrupted by a TpA step. Instead of using this A-tract definition, we describe A4T4 and T4A4 as molecular architectures consisting of two A4-blocks each, where the A4-blocks are connected at the 3′ ends of the A-strands (tail-to-tail) and at the 5′ ends (head-to-head), respectively (see Fig. 2). Both A4T4 and T4A4 form well-determined right-handed B-DNA double helices (Fig. 1 and Table 1). The most remarkable difference between the molecules is the minor groove profile. The A4T4 structure displays a symmetrical and progressive narrowing of the minor groove, reaching a minimal width of ≈10 Å (closest P–P distances) at the central ApT step. The T4A4 structure shows the inverse trend. Its minor groove is symmetrically widened toward the central TpA step where the maximal minor groove width ≈13 Å is found (Figs. 1, 2, and 3a). Narrowing of the minor grooves of A-blocks in the 5′→3′ direction of the A-strand has been previously observed with techniques including hydroxyl radical footprinting, x-ray crystallography, and NMR, and proposed to be a general feature of A-tracts (4, 12). The opposite orientations of the A-blocks in the two duplexes result in an entirely different environment for the base-stacking interactions at the ApT and TpA steps and is a key factor for A4T4 being so different from T4A4 in terms of global bending. Most importantly, there is an opposite direction of the local bend at these steps. The ApT step has high negative roll (–12°), providing a local bend toward the minor groove, whereas the TpA step displays high positive roll (11°), resulting in a local bend toward the major groove (Figs. 2 and 3b). This trend has also been observed in crystal structures of DNA duplexes containing A-tracts (41), albeit of smaller magnitude (as a result of external crystal packing) and in DNA–protein and DNA–drug complexes (42). These two opposite local bends contribute significantly to the different global bends in A4T4 and T4A4, as can be seen in Fig. 2 and as is discussed below. Both A4T4 and T4A4 have two additional bends, which occur at the junctions of the A-blocks with the C·G base pairs. Basically, there are two types of these bends. At the 5′ end of A-blocks where the minor groove is wide (the case of A4T4), the bends occur almost exclusively via positive roll (≈+12°) toward the major grooves (Figs. 2 and 3). These bends are very similar to the one at the TpA step. At the 3′ end of A-blocks where the minor groove is narrow (the case of T4A4), the bends take place via a combination of roll and tilt, providing local bends toward the major grooves, and tend to be distributed to the flanking GC-rich sequence as well.
Fig. 2.
Schematic representations of the structures of A4T4 (a, c, and d) and T4A4 (b, e, and f), illustrating the minor groove narrowing and widening and helical axis bending. (a and b) Structures and 3D helical axis calculated by curves 5.3 (56). (c and e) Simplified helical axes in 2D space, with direction of local bends indicated. (d and f) Schematics illustrating relative groove widths.
Fig. 1.
Superpositions of the nine best structures of A4T4 (a) and T4A4 (b). The minor groove of the A-tracts is shown in front, and a ribbon is fitted to the phosphate atoms to highlight the differences in minor groove widths. Nucleotides are colored blue (G), green (C), red (A), and orange (T). Only nonhydrogen atoms are depicted.
Fig. 3.
(a) Comparison of minor groove widths among different juxtaposed A-blocks (AnTn and TnAn). Closest P–P distances of A4T4 (black circles), T4A4 (white circles), and crystal structures of d(CGCA3T3GCG)2 [A3T3] (black inverted triangles) (57) and d(CCT3A3GG)2 [T3A3] (white inverted triangles) (41) are shown. The method of closest P–P distances was used to describe minor groove profile (as implemented in x3dna (37). (b) Comparison of helical parameters of A-blocks from the following solution structures refined with residual dipolar couplings: A4T4 (black circles), T4A4 (white circles), d(GGCA6CGG)2 [A6] (black inverted triangles) (21), and d(GGCA4CGG)2 [A4] (white inverted triangles) (22).
Because there are three local bends (junction type), the global bend depends critically on how they are phased relative to each other along the helix. In the case of A4T4 (Fig. 2), the bend at the central ApT step is almost entirely “in phase,” i.e., on the same face of the helix, with the other two bends present in the molecule at the 5′ ends of both A-blocks. Thus, the three local bends are additive and globally bend the molecule toward the minor groove by ≈23°. In the case of T4A4 (Fig. 2), the bend at the central T-A step is out of phase with the other two bends in the molecule, which again occur at the 5′ ends of both A4-blocks. In other words, the local bend at the TpA step opposes the local bends at the A-block junctions. Although the major contribution for bending comes from the junctions of A-blocks, there is also a smaller contribution coming from within the A-blocks, which are not entirely straight. These “wedges” provide a small contribution to the overall bend toward the minor groove of the A-tracts via a combination of nonzero roll and tilt (Fig. 3). Overall, the bends at the junctions and within the A-blocks support the delocalized model first proposed by Crothers and Shakked (4). One important feature of the global bend in these dodecamers, which can be seen in the 3D view (Fig. 2 a and b), is that their helical axes do not lie in a plane. For example, for A4T4, the two-junction bends toward the major groove point into and out of the plane of the paper, respectively.
Reliability of the Structures. The low proton density of nucleotides compared to peptides results in only a limited number of NOEs in nucleic acids for determination of local and global structure; thus, many of the structural features depend on only a few restraints. If these are not both correct and sufficiently precise, an error within the local structure (e.g., sequence-specific base-stacking interactions) can be propagated along the length of the double helix and, for example, have a large impact on the accuracy of helix axis bending. Inclusion of RDCs (restraints containing long-range angular information) can remove, to some extent, the inaccuracies imposed by lack of long-range distance restraints in DNA. However, in the absence of a highly overdetermined set of RDCs (20, 34, 43), they cannot remove errors or increase the precision and accuracy of the local structure. This is illustrated in the following tests we performed with our data: we removed/changed a few critical NOEs during the first refinement step and checked to see whether, on inclusion of RDCs, we got the original structure back. The outcome was that the test structures had the same overall global bend but different local helical parameters around the site where experimental NOE data were removed or changed. This means that even with a limited set of RDCs, the overall bend is reproduced albeit distributed via different local structures that depend on the NOE data. Thus we are confident in the accuracy of the determination of the overall bend direction, magnitude, and angle but are more cautious in interpreting the fine local geometries of the solved structures.
Comparison to Related Solution and Crystal Structures. Before we compare A4T4 and T4A4 with related DNA A-tract-containing structures, it should be highlighted that A4T4 and T4A4 are rather special cases of A-tracts molecules, because there are two symmetrical A-blocks (for each molecule) connected in head-to-head and tail-to-tail manner. Indeed, we observe deviations from standard A-tract characteristics, mostly at the unique central ApT and TpA for A4T4 and T4A4, respectively. It should be noted that these steps do not represent the average ApT and TpA features from a random sequence. They have a unique geometry, because they occur at a junction where two A-blocks meet each other with opposite polarity (Fig. 2). The importance of flanking sequence on the conformation of ApT and TpA steps was previously demonstrated by Dickerson and coworkers (41). In A4T4 and T4A4, the ApT and TpA steps are located where the minor groove is narrowest and widest, respectively (Figs. 2 and 3a). The crystal structures of d(CCT3A3GG) [T3A3] and d(CGCA3T3GCG) [A3T3] show similar trends in minor groove widths (Fig. 3a). For both A4T4 and T4A4, the juxtaposition of the two A-blocks with opposite propeller twists creates structural stress at the junction between them that we propose leads to a local bend. The high positive or negative rolls of the TpA and ApT steps (discussed above), respectively, probably suppress the propeller twist around the central (TpA or ApT) steps relative to the outer parts of A-blocks (≈–16° for A4T4 and –17° for T4A4) (Table 2). High propeller twists in A-tracts have been observed in all crystal structures and also in an NMR structure solved with RDCs (21), resulting in A-tract bifurcated hydrogen bonds in the major groove, and have been associated with the compression of the minor groove (13, 14, 17, 21). However, in a recently published A-tract structure determined by NMR with RDCs (22), neither A-tract minor groove compression nor bending was found to structurally depend on high propeller twisting. A-tract bending has also been found to be independent of bifurcated hydrogen bonds by Diekmann et al. (44).
We analyzed the two other DNA A-tracts d(GGCAAAACGG) [A4] (22) and d(GGCAAAAAACGG) [A6] (21), which were solved by using NMR with RDCs and compared them with A4T4 and T4A4 structures in terms of helical parameters (calculated by using 3DNA) (Fig. 3b). The solution structures of these A-tracts were determined at different temperatures and salt conditions, which may affect bending (refs. 45 and 46, and see below). Nevertheless, when these molecules are aligned along the A-tracts (Fig. 3b), general trends are clear; bending occurs via positive rolling at the 5′ end of A-tract, and from negative tilt with only a small contribution from roll at the 3′ end. Within all of the A-tract sequences there is a nonzero tilt and roll that results in small “wedges” that contribute to the overall bend. Taken together, the structural results support the delocalized bend model (4, 22).
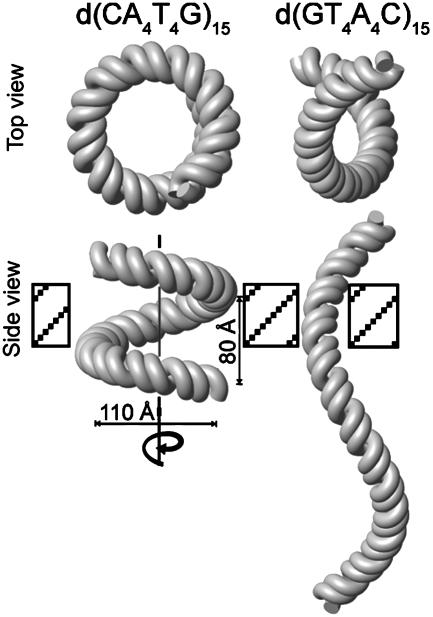
Global Bend of d(CAAAATTTTG)n and d(GTTTTAAAAC)n. The small local bends in A-tract sequences give rise to macroscopically observable bending when these sequences are repeated multiple times in phase with the helical repeat. To visualize this, we used the helical parameters determined for A4T4 and T4A4 to make models of DNA polymers containing 15 repeats of the central 10 base pairs of the dodecamers (see Materials and Methods). Because the local bends for A4T4 are not perfectly aligned along one face of the helix, i.e., the helix trajectory for one helical turn is not in a plane, d(CA4T4G)15 also does not bend in a plane but rather forms a left-handed superhelix with a diameter of ≈110 Å and a helical pitch of ≈80 Å (Fig. 4). One full turn of the superhelix is ≈120 bp. Surprisingly, this molecular architecture resembles the conformation of DNA in the nucleosome core particle (26). d(GT4A4C)15 also forms a left-handed superhelix but with a narrower diameter and a much greater helical pitch of >250 Å. Thus, along the long axis of the DNA helix, it has an elongated S-shape.
Fig. 4.
Structure-based models of d(CAAAATTTTG)15 (Left) and d(GTTTTAAAAC)15 (Right) showing views parallel with (Upper) and perpendicular to (Lower) the superhelical axis.
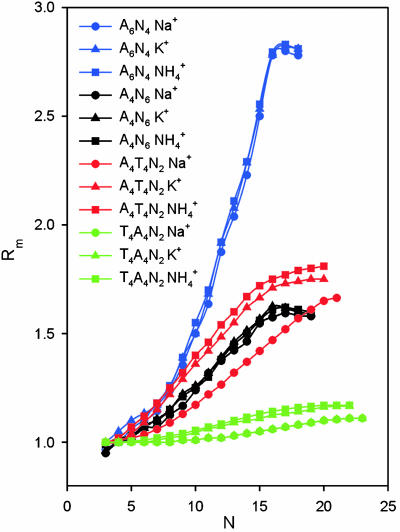
The difference in the superhelical structures of d(CA4T4G)15 and d(GT4A4C)15 is also consistent with the results of the early gel electrophoretic mobility studies of Hagerman (25) that were done with standard TBE, which has a total [Na+]of ≈8 mM. To compare the DNA bending results from our structural study directly to gel retardation results, we repeated these experiments for our sequences in polyacrylamide gels containing the same total salt used in our NMR samples, 25 mM NH4Cl, in the running buffer (Fig. 5). As observed in the earlier study, d(CA4T4G)n [A4T4N2] shows a large gel migration anomaly indicative of DNA bending, whereas d(CT4A4G)n [T4A4N2] migrates almost like a straight helix. The superhelical structure of A4T4N2 would be expected to retard migration through the gel, because the diameter of the superhelix is larger than the gel pores, forcing it to move through the gel with a corkscrew motion. Because T4A4N2 forms a supercoil with a very gentle writhe, it can worm its way through the gel more easily and thus has only a small electrophoretic mobility anomaly that does not begin to be apparent until there are >60 bp.
Fig. 5.
Plot of the relative gel electrophoretic mobilities of d(A4T4N2)n (red), d(T4A4N2)n (green), d(A6N4)n (blue), and d(A4N6)n (black) in 25 mM NH4Cl (squares), KCl (triangles), or NaCl (circles) as a function of n. Rm is ratio of apparent multimer size vs. actual chain length.
It has previously been recognized that A-tract repeats that are not in phase with the helical repeat will give rise to left- or right-handed supercoils (47, 48), which will affect their mobility in polyacrylamide gels. However, these previous analyses of gel electrophoretic mobility of A-tract DNA have assumed that the global bend within a single helical repeat is planar. For A4T4 and T4A4, this is clearly not the case. Therefore, even if the central 10 base pairs form a perfect helical repeat, the polymers would still be supercoiled. The actual helical repeat of d(CAAAATTTTG) is 10.3 base pairs per turn. Test calculations in which the twist of the last C·G base pairs was adjusted to give a total of 360° per 10 base pairs gave superhelical parameters that deviated only slightly from those obtained here.
The extent of the gel migration anomaly for different A-tract sequences has been used to determine relative global bends, with the slowest migration indicating the largest bend. However, if the A-tract bending results in the polymers forming superhelices, then different rates of migration cannot be directly correlated with degree of bending. This appears to be the case when we compare the results for d(GCA6CG)n [A6N4] to A4T4N2. Although the global bend of a single repeat of A6N4 (≈16°) is less than that of A4T4N2 (≈23°), this sequence shows the largest migration anomaly. Furthermore, the shapes of the gel migration curves are very different. We modeled d(GCA6CG)n based on the published helical parameters from the NMR structure (21) and found that it forms a nearly planar circle as reported with a diameter of ≈200 Å. This large circle would be expected to be more strongly retarded on migrating through the gel than the smaller-diameter A4T4N2 superhelix, which could more rapidly corkscrew (48) through the gel. We were unable to model d(GGCA4CGG)n [A4N6], which has a bend angle of ≈9°, because the solved NMR structure was only a decamer (22).
Monovalent Cation Dependence of A-Tract Bending. X-ray crystallography (49, 50), molecular dynamics (51), capillary electrophoresis (52), and NMR (53) studies of DNA have shown that, in addition to waters, monovalent cations can bind specifically in the minor groove of A-tracts, although the relative occupancies remain unresolved (54). In our previous NMR studies of A4T4 and T4A4, 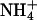 were found to localize in the narrowest parts of the minor grooves, resulting in a very different distribution of cation localization for the two molecules that was proposed to contribute to A-tract bending (53).
were found to localize in the narrowest parts of the minor grooves, resulting in a very different distribution of cation localization for the two molecules that was proposed to contribute to A-tract bending (53). 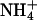 has a van der Waals radius about the same as K+, and both are larger than Na+. Based on a simple electrostatic model for interaction and on size considerations,
has a van der Waals radius about the same as K+, and both are larger than Na+. Based on a simple electrostatic model for interaction and on size considerations, 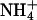 and K+ would be expected to fit in the same sites and bind with similar affinities. To test for the effect of monovalent cations on DNA bending, the electrophoretic mobilities of A4T4N2, T4A4N2, A6N4, and A4N6 repeats in 25 mM NH4Cl, NaCl, and KCl were compared (Fig. 5). The A4T4N2 polymers show a clear cation dependence for DNA bending, with
and K+ would be expected to fit in the same sites and bind with similar affinities. To test for the effect of monovalent cations on DNA bending, the electrophoretic mobilities of A4T4N2, T4A4N2, A6N4, and A4N6 repeats in 25 mM NH4Cl, NaCl, and KCl were compared (Fig. 5). The A4T4N2 polymers show a clear cation dependence for DNA bending, with 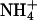 resulting in the largest migration anomaly, followed closely by K+, whereas the migration anomaly with Na+ is much smaller. A similar but smaller monovalent cation dependence on gel migration is observed for T4A4N2. For the A6N4 and A4N6 polymers, gel migration anomaly, and therefore bending, appears to be largely independent of the species of monovalent cation present in the running buffer, although in both cases the curves for the oligomers in Na+ are very slightly below those for
resulting in the largest migration anomaly, followed closely by K+, whereas the migration anomaly with Na+ is much smaller. A similar but smaller monovalent cation dependence on gel migration is observed for T4A4N2. For the A6N4 and A4N6 polymers, gel migration anomaly, and therefore bending, appears to be largely independent of the species of monovalent cation present in the running buffer, although in both cases the curves for the oligomers in Na+ are very slightly below those for 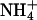 and K+. This is, to our knowledge, the first evidence for a specific monovalent cation dependence on a DNA structure. The magnitude of the effect is consistent with previous experimental results on the extent and location of
and K+. This is, to our knowledge, the first evidence for a specific monovalent cation dependence on a DNA structure. The magnitude of the effect is consistent with previous experimental results on the extent and location of 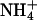 binding to A4T4, T4A4, and GCA5CG (53). The ApT step represents a unique and species-dependent tight binding site for monovalent cations, which can coordinate to the two opposing T carbonyls (41, 49–53, 55). We propose that the specific minor groove width-dependent binding of monovalent cations at the ApT step contributes to the global bend observed for A4T4. Furthermore, the monovalent cation dependence on gel migration observed for T4A4N2 is consistent with previous experimental results, showing that
binding to A4T4, T4A4, and GCA5CG (53). The ApT step represents a unique and species-dependent tight binding site for monovalent cations, which can coordinate to the two opposing T carbonyls (41, 49–53, 55). We propose that the specific minor groove width-dependent binding of monovalent cations at the ApT step contributes to the global bend observed for A4T4. Furthermore, the monovalent cation dependence on gel migration observed for T4A4N2 is consistent with previous experimental results, showing that 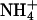 localizes at two ends of the A-blocks, where the minor groove is narrowest, but interacts more weakly with these sites than it does with A4T4. It is also consistent with the results on GCA5CG, which binds
localizes at two ends of the A-blocks, where the minor groove is narrowest, but interacts more weakly with these sites than it does with A4T4. It is also consistent with the results on GCA5CG, which binds 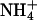 at only one site in the narrowest part of the A-tract minor groove and more weakly than A4T4. That the type of monovalent cations does not significantly affect the macroscopically observed bending in homopolymeric A-tracts but does affect A4T4 and to a lesser extent T4A4 provides further support for our conclusion that A4T4 and T4A4 are best considered as special cases of two juxtaposed A-tracts, which differ in behavior due to the ApT vs. TpA step. Furthermore, that different monovalent cations can differentially affect bending provides evidence that they play a fundamental role in DNA A-tract bending.
at only one site in the narrowest part of the A-tract minor groove and more weakly than A4T4. That the type of monovalent cations does not significantly affect the macroscopically observed bending in homopolymeric A-tracts but does affect A4T4 and to a lesser extent T4A4 provides further support for our conclusion that A4T4 and T4A4 are best considered as special cases of two juxtaposed A-tracts, which differ in behavior due to the ApT vs. TpA step. Furthermore, that different monovalent cations can differentially affect bending provides evidence that they play a fundamental role in DNA A-tract bending.
Supplementary Material
Acknowledgments
We thank Dr. David Case for implementation of the flat-bottom potential for RDCs in amber 7. This work was supported by National Institutes of Health Grant GM48123 (to J.F.), European Molecular Biology Organization and Human Frontier Science Program Organization postdoctoral fellowships (to R.S.), and Ministerstvo Školství, Mládeže a Tělovýchovy Grant LN00A016 (to V.S.).
Abbreviations: RDC, residual dipolar couplings; NOE, nuclear Overhauser effect.
Data deposition: The atomic coordinates of d(GCAAAATTTTGC) and d(CGTTTTAAAACG) have been deposited in the Protein Data Bank, www.rcsb.org (PDB ID codes 1RVH and 1RVI, respectively).
References
- 1.Marini, J. C., Levene, S. D., Crothers, D. M. & Englund, P. T. (1982) Proc. Natl. Acad. Sci. USA 79, 7664–7668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wu, H.-M. & Crothers, D. M. (1984) Nature 308, 509–513. [DOI] [PubMed] [Google Scholar]
- 3.Hagerman, P. J. (1990) Annu. Rev. Biochem. 59, 755–781. [DOI] [PubMed] [Google Scholar]
- 4.Crothers, D. M. & Shakked, Z. (1999) in Oxford Handbook of Nucleic Acid Structure, ed. Neidle, S. (Oxford Univ. Press, Oxford), pp. 455–470.
- 5.Trifonov, E. N. & Sussman, J. L. (1980) Proc. Natl. Acad. Sci. USA 77, 3816–3820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ulanovsky, L. E. & Trifonov, E. N. (1987) Nature 326, 720–722. [DOI] [PubMed] [Google Scholar]
- 7.Bolshoy, A., McNamara, P., Harrington, R. E. & Trifonov, E. N. (1991) Proc. Natl. Acad. Sci. USA 88, 2312–2316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.De Santis, P., Palleschi, A., Savino, M. & Scipioni, A. (1990) Biochemistry 29, 9269–9273. [DOI] [PubMed] [Google Scholar]
- 9.Koo, H.-S., Wu, H.-M. & Crothers, D. M. (1986) Nature 320, 501–506. [DOI] [PubMed] [Google Scholar]
- 10.Koo, H. S. & Crothers, D. M. (1988) Proc. Natl. Acad. Sci. USA 85, 1763–1767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Haran, T. E., Hahn, J. D. & Crothers, D. M. (1994) J. Mol. Biol. 244, 135–143. [DOI] [PubMed] [Google Scholar]
- 12.Hud, N. V. & Plavec, J. (2003) Biopolymers 69, 144–158. [DOI] [PubMed] [Google Scholar]
- 13.DiGabriele, A. D. & Steitz, T. A. (1993) J. Mol. Biol. 231, 1024–1039. [DOI] [PubMed] [Google Scholar]
- 14.DiGabriele, A. D., Sanderson, M. R. & Steitz, T. A. (1989) Proc. Natl. Acad. Sci. USA 86, 1816–1820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Dickerson, R. E., Goodsell, D. S. & Neidle, S. (1994) Proc. Natl. Acad. Sci. USA 91, 3579–3583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Dlakic, M., Park, K., Griffith, J. D., Harvey, S. C. & Harrington, R. E. (1996) J. Biol. Chem. 271, 17911–17919. [DOI] [PubMed] [Google Scholar]
- 17.Nelson, H. C., Finch, J. T., Luisi, B. F. & Klug, A. (1987) Nature 330, 221–226. [DOI] [PubMed] [Google Scholar]
- 18.Dickerson, R. E., Goodsell, D. & Kopka, M. L. (1996) J. Mol. Biol. 256, 108–125. [DOI] [PubMed] [Google Scholar]
- 19.Tjandra, N. & Bax, A. (1997) Science 278, 1111–1114. [DOI] [PubMed] [Google Scholar]
- 20.Tjandra, N., Tate, S., Ono, A., Kainosho, M. & Bax, A. (2000) J. Am. Chem. Soc. 122, 6190–6200. [Google Scholar]
- 21.MacDonald, D., Herbert, K., Zhang, X. L., Polgruto, T. & Lu, P. (2001) J. Mol. Biol. 306, 1081–1098. [DOI] [PubMed] [Google Scholar]
- 22.Barbic, A., Zimmer, D. P. & Crothers, D. M. (2003) Proc. Natl. Acad. Sci. USA 100, 2369–2373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Crothers, D. M. (1994) Science 266, 1819–1820. [DOI] [PubMed] [Google Scholar]
- 24.Hagerman, P. J. (1988) in Unusual DNA Structures, eds. Wells, R. D. & Harvey, S. C. (Springer, New York), pp. 225–236.
- 25.Hagerman, P. J. (1986) Nature 321, 449–450. [DOI] [PubMed] [Google Scholar]
- 26.Richmond, T. J. & Davey, C. A. (2003) Nature 423, 145–150. [DOI] [PubMed] [Google Scholar]
- 27.Masse, J., Bortmann, P., Dieckmann, T. & Feigon, J. (1998) Nucleic Acids Res. 26, 2618–2624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kolk, M. H., Wijmenga, S. S., Heus, H. A. & Hilbers, C. W. (1998) J. Biomol. NMR 12, 423–433. [Google Scholar]
- 29.Legault, P., Jucker, F. M. & Pardi, A. (1995) FEBS Lett. 362, 156–160. [DOI] [PubMed] [Google Scholar]
- 30.Trantirek, L., Stefl, R., Masse, J. E., Feigon, J. & Sklenář, V. (2002) J. Biolmol. NMR 23, 1–12. [DOI] [PubMed] [Google Scholar]
- 31.Hansen, M. R., Mueller, L. & Pardi, A. (1998) Nat. Struct. Biol. 5, 1065–1074. [DOI] [PubMed] [Google Scholar]
- 32.Case, D. A., Pearlman, D. A., Caldwell, J. W., Cheatham, T. E. I., Wang, J., Ross, W. S., Simmerling, C. L., Darden, T. A., Merz, K. M., Stanton, R. V., et al. (2002) amber 7 (University of California, San Francisco).
- 33.Cornell, W. D., Cieplak, P., Bayly, C. I., Gould, I. R., Merz, K. M. J., Ferguson, D. M., Spellmeyer, D. C., Fox, T., Caldwell, J. W. & Kollman, P. A. (1995) J. Am. Chem. Soc. 117, 5179–5197. [Google Scholar]
- 34.Padrta, P., Stefl, R., Králík, L., Zídek, L. & Sklenář, V. (2002) J. Biomol. NMR 24, 1–14. [DOI] [PubMed] [Google Scholar]
- 35.Bashford, D. & Case, D. A. (2000) Annu. Rev. Phys. Chem. 51, 129–152. [DOI] [PubMed] [Google Scholar]
- 36.Tsui, V., Zhu, L., Huang, T.-H., Wright, P. E. & Case, D. A. (2000) J. Biomol. NMR 16, 9–21. [DOI] [PubMed] [Google Scholar]
- 37.Lu, X. J., Shakked, Z. & Olson, W. K. (2000) J. Mol. Biol. 300, 819–840. [DOI] [PubMed] [Google Scholar]
- 38.Olson, W. K., Bansal, M., Burley, S. K., Dickerson, R. E., Gerstein, M., Harvey, S. C., Heinemann, U., Lu, X. J., Neidle, S., Shakked, Z., et al. (2001) J. Mol. Biol. 313, 229–237. [DOI] [PubMed] [Google Scholar]
- 39.Strahs, D. & Schlick, T. (2000) J. Mol. Biol. 301, 643–663. [DOI] [PubMed] [Google Scholar]
- 40.Hud, N. V., Schultze, P. & Feigon, J. (1998) J. Am. Chem. Soc. 120, 6403–6404. [Google Scholar]
- 41.Mack, D. R., Chiu, T. K. & Dickerson, R. E. (2001) J. Mol. Biol. 312, 1037–1049. [DOI] [PubMed] [Google Scholar]
- 42.Young, M. A., Ravishanker, G., Beveridge, D. L. & Berman, H. M. (1995) Biophys. J. 68, 2454–2468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Boisbouvier, J., Delaglio, F. & Bax, A. (2003) Proc. Natl. Acad. Sci. USA 100, 11333–11338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Diekmann, S., Mazzarelli, J. M., McLaughlin, L. W., von Kitzing, E. & Travers, A. A. (1992) J. Mol. Biol. 225, 729–738. [DOI] [PubMed] [Google Scholar]
- 45.Jerkovic, B. & Bolton, P. H. (2000) Biochemistry 39, 12121–12127. [DOI] [PubMed] [Google Scholar]
- 46.Diekmann, S. (1987) Nucleic Acids Res. 15, 247–265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Drew, H. R. & Dickerson, R. E. (1981) J. Mol. Biol. 151, 535–556. [DOI] [PubMed] [Google Scholar]
- 48.Drak, J. & Crothers, D. M. (1991) Proc. Natl. Acad. Sci. USA 88, 3074–3078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Tereshko, V., Minasov, G. & Egli, M. (1999) J. Am. Chem. Soc. 121, 3590–3595. [Google Scholar]
- 50.Woods, K. K., McFail-Isom, L., Sines, C. C., Howerton, S. B., Stephens, R. K. & Williams, L. D. (2000) J. Am. Chem. Soc. 122, 1546–1547. [Google Scholar]
- 51.Young, M. A., Jayaram, B. & Beveridge, D. L. (1997) J. Am. Chem. Soc. 119, 59–69. [Google Scholar]
- 52.Stellwagen, N. C., Magnusdottir, S., Gelfi, C. & Righetti, P. G. (2001) J. Mol. Biol. 305, 1025–1033. [DOI] [PubMed] [Google Scholar]
- 53.Hud, N. V., Sklenář, V. & Feigon, J. (1999) J. Mol. Biol. 286, 651–659. [DOI] [PubMed] [Google Scholar]
- 54.Denisov, V. P. & Halle, B. (2000) Proc. Natl. Acad. Sci. USA 97, 629–633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Stefl, R. & Koca, J. (2000) J. Am. Chem. Soc. 122, 5025–5033. [Google Scholar]
- 56.Lavery, R. & Sklenář, H. (1988) J. Biomol. Struct. Dyn. 6, 63–91. [DOI] [PubMed] [Google Scholar]
- 57.Edwards, K. J., Brown, D. G., Spink, N., Skelly, J. V. & Neidle, S. (1992) J. Mol. Biol. 226, 1161–1173. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.