Sensitivity to Tumor Microvasculature Without Contrast Agents in High Spectral and Spatial Resolution MR Images

Abstract

Contrast-enhanced (CE)-MRI is sensitive to cancers but can produce adverse reactions and suffers from insufficient specificity and morphological detail. This research investigated whether high spectral and spatial resolution (HiSS) MRI detects tumor vasculature without contrast agents, based on the sensitivity of the water resonance line shape to tumor blood vessels. HiSS data from AT6.1 tumors inoculated in the hind legs of rats (N = 8) were collected pre- and post– blood pool contrast agent (iron-oxide particles) injection. The waterline in small voxels was significantly more asymmetric at the tumor rim compared to the tumor center and normal muscle (P < 0.003). Composite images were synthesized, with the intensity in each voxel determined by the Fourier component (FC) of the water resonance having the greatest relative image contrast at that position. We tested whether regions with high contrast in FC images (FCIs) contain vasculature by comparing FCIs with CE-MRI as the “gold standard” of vascular density. The FCIs had 75% ± 13% sensitivity, 74% ± 10% specificity, and 91% ± 4% positive predictive value (PPV) for vasculature detection at the tumor rim. These results suggest that tumor microvasculature can be detected using HiSS imaging without the use of contrast agents.

Contrast-enhanced magnetic resonance imaging (CE-MRI) is currently the most sensitive method for detecting early stage breast cancer, when it can be most easily treated. However, the use of contrast agents has some drawbacks that suggest a need for alternative and/or supplementary methods. When contrast agents are used in a large number of women, as suggested by recent changes in American Cancer Society (ACS) guidelines (1), concerns about toxicity become significant (2). (Note that similar concerns may apply to prostate cancer if advances in MRI of the prostate continue (3,4)). In addition, optimal detection of cancer with the low-molecular-weight contrast agents that are used clinically requires high temporal resolution imaging (5) which necessitates a relatively low spatial resolution and signal-to-noise ratio (SNR). Finally, the use of contrast agents can obscure the native morphology of tumors due to “blooming artifacts” caused by susceptibility gradients, motion, limited spatial resolution, or some combination of these factors (6 – 8). Therefore, we are investigating the use of high spectral and spatial resolution (HiSS) MRI to image tumor vasculature without the use of contrast agents.

We propose to do this by detecting the effects of deoxygenated tumor blood vessels on the line shape of the water proton resonance. Blood deoxyhemoglobin produces local variations in magnetic susceptibility and is an important source of inhomogeneous broadening of the water resonance in small image voxels (9 –11). (In the following, the term “inhomogeneous broadening” is used to indicate that the water spectrum is composed of different populations of water molecules with different resonance frequencies, and that there is very slow or nonexistent exchange among these different populations.) This blood dependent local variation in magnetic susceptibility is the basis for blood oxygenation level-dependent (BOLD) MRI (12,13) and has been used in this laboratory and by other investigators to image the changes in tumor oxygenation during therapy (14 –19). Related methods have been used for venography in the brain (20,21) using susceptibility-weighted imaging (SWI), which is sensitive to the magnetic field gradients produced by venous blood.

Blood vessels in tumors often contain high levels of deoxyhemoglobin due to the imbalance between oxygen delivery and oxygen consumption, an effect that may be very large in aggressive cancers (22,23). The inhomogeneous distribution of deoxygenated blood vessels commonly found in tumors introduces local magnetic susceptibility gradients, and these are likely to produce asymmetric features of the water spectrum. Deoxyhemoglobin affects $T_2^{\ast }(R_2^{\ast })$, and this can be measured using multi-gradient-echo (multi-GRE) imaging (24). However, water resonances from small voxels in tumors frequently have complicated non-Lorentzian line shapes (11) due to the highly heterogeneous microenvironment, and therefore local magnetic susceptibility effects are most accurately and conveniently evaluated in the spectral domain (10). Therefore, we propose that detailed analysis of the water spectral line shape can detect the effects of tumor vasculature on local magnetic susceptibility. Here we test the hypothesis that shoulders and/or partially resolved components of the water resonance are reliable markers for tumor blood vessels, particularly when those vessels contain high levels of deoxyhemoglobin.

Local variations in the magnetic field were detected using HiSS MRI. This can be performed with reasonable run times using echo-planar spectroscopic imaging (EPSI) (29). In contrast to conventional MRI, HiSS MRI acquires a high-resolution spectrum of the water and fat resonances in each voxel at the spatial resolution of conventional anatomic MRI or higher. This spectral information serves as a source of information that cannot be attained by conventional imaging. HiSS MRI of water and fat has been demonstrated to provide images of human breast lesions with more detailed morphology than conventional imaging techniques (10,27) and with improved fat suppression (28). Examination of the water lines collected in HiSS data sets demonstrates that they are often inhomogeneously broadened (11,14,30). Spectral inhomogeneity typically produces a partially resolved peak or shoulder at frequencies either above or below that of the main water peak, i.e., the position of maximum signal intensity. Spectral inhomogeneities can be localized by examining the 2D spatial array at each frequency along the water resonance. We refer to these arrays as Fourier component images (FCIs). Images of individual FCs of the water line provide a novel source of contrast and are sensitive to local variations in magnetic susceptibility (31). In the present work, FCIs are tested as markers for deoxygenated tumor vasculature.

Copenhagen rats bearing AT6.1 prostatic tumors inoculated in the hind leg were imaged at 4.7 T. These tumors are very aggressive and highly angiogenic (32,33). Dense vasculature is produced in and around the tumor, particularly at the tumor rim, where the rate of proliferation is greatest (34,35). We developed several different measures of spectral asymmetry in HiSS data sets of this tumor model as potential markers for tumor vasculature, as follows:

1. We compared the integral of the low-frequency half of the water resonance (below the main water peak) to the integral of the high-frequency half of the water resonance (above the main water peak). Asymmetric water resonances produced a significant difference between these two integrals. Images were produced in which the intensity in each pixel was proportional to the asymmetry of the water resonance integral. This is a very high-SNR measure of asymmetry, but has limited sensitivity to subtle spectral features.

2. As a means of increasing sensitivity to subtle spectral features, we compared the amplitudes of individual FCs that were symmetric about the main peak. For example, the amplitude of the water resonance at 6 Hz below the peak was compared with the amplitude at 6 Hz above the peak. Images were produced with intensity proportional to the difference between symmetric FCs.

3. Images were produced that were sensitive to the local relative contrast in off-peak FCIs (i.e., images of the FCs of the water resonance at various frequency offsets from the peak of the water resonance). A frequency-specific shoulder/partially-resolved component of the water resonance in a small cluster of voxels produces a sharp change in signal intensity at the cluster position of the FCI of that frequency. An efficient way to detect these spectrally-specific spatial features is to measure the contrast in FCIs. A small region with high contrast in an FCI is usually caused by a local change in water resonance line shape. To maximize sensitivity to small groups of pixels that have sharp contrast relative to their surroundings, we synthesized images in which intensity at each pixel was determined by the FCI with the greatest image contrast at those spatial coordinates. These images can be thought of as maximum intensity projection (MIP) images along the spectral direction (referred to in the following as FCI-MIPs). FCI-MIPs are another means of detecting variations in magnetic susceptibility within each voxel that may be due to blood vessels.

Changes in GRE image intensity following injection of a blood pool contrast agent (800 –900 μm diameter iron-oxide particles; Bangs Laboratories) were used as the “gold standard” for identification of vasculature. Blood pool CE GRE images were used in this context because they are commonly used to show tumor microvasculature with high SNR (36). This gold standard was used to calculate the sensitivity, specificity, and positive predictive value (PPV) of precontrast FCI-MIP images for detection of tumor vasculature.

MATERIALS AND METHODS

Data Collection

All data were collected with a small, specialized, in-house-built, low-pass birdcage coil (eight-leg, cylindrical design with length and diameter of 3.2 cm each) designed for rodent imaging at 4.7 T using a Bruker BioSpec 33-cm horizontal bore scanner (Billerica, MA, USA) with 20-cm bore self-shielded gradient coils (maximum gradient strength = 100 mT/m). Experiments (N = 8) were performed using Copenhagen rats bearing highly metastatic anaplastic tumor 6.1 (AT6.1) rodent prostatic tumors inoculated in the hind leg. Tumor localization was performed using multislice spin-echo (SE) (TR/TE = 4100/56 ms, array size = 256 × 256, field of view [FOV] = 40 –50 mm, in-plane resolution = 156 –195 μm, slice thickness = 0.6 mm, number of averages [NEX] = 2), and GRE (TR/TE = 750/15 ms, array size = 256 × 256, FOV = 40 mm, in-plane resolution = 156 μm, slice thickness = 0.6 mm, flip angle = 30°, NEX = 2) images.

FastMap (37) was performed on a cubic voxel centered within the leg encompassing the tumor, the tumor rim, and the normal muscle extending beyond the muscle/tumor interface to improve localized shimming to the second order. The voxel was oriented such that the image plane was oriented parallel to the cube face. The residual macroscopic B₀ gradient that remained following shimming was well approximated as a linear gradient with a typical variation of 63 Hz/cm across the FOV, or approximately 0.4 ± 0.3 Hz per pixel (averaged over all experiments). This residual gradient was much smaller than the average water line width in each voxel (12.9 ± 6.1 Hz) and nearly a factor of 10 less than the spectral resolution of HiSS data sets (3.1 Hz). Such a B₀ gradient was not sufficient to produce shoulders or partially resolved components of the water resonance in each voxel.

Four slices were selected for subsequent HiSS imaging using EPSI with the same spatial resolution and slice thickness as the GRE and SE images. Imaging was respiratory-gated to minimize motion artifacts associated with breathing. Because of this, the minimum TR was determined by the respiration rate; this was typically ~1200 ms (TE = 175 ms, array size = 256 × 256 × 64, flip angle = 30°, NEX = 2, spectral resolution = 3.1 Hz, scan time = ~9 min). These imaging parameters were used both pre-and post-injection of contrast. Contrast (300 μl Fe0₂ particles in 1.4 ml saline) was injected via a catheter inserted in the tail vein, and two-slice EPSI scans were acquired ~30 and 40 min postinjection (for a total of four post-contrast slices). GRE images used for all analyses were constructed from the fourth echo of both the pre- and postcontrast HiSS data sets (TE = ~10 ms). This ensured that variations between HiSS data sets and GRE images due to motion and changes in tumor blood oxygenation were minimized.

All procedures performed on animals followed protocols approved by the Institutional Animal Care and Use Committee and were in compliance with the Animal Welfare Act and NIH Guide for the Care and Use of Laboratory Animals. Rats were immobilized on a Plexiglas board with vet wrap and tape, and anesthetized with 1.5–2% isoflurane gas mixed with medical air (2 liters/min) delivered through a mask. Temperature, ECG, and respiration rate were continuously monitored throughout each experiment (SA Instruments, Stony Brook, NY, USA). Temperature was maintained using a warm air blower fed into the bore of the magnet.

Data Analysis

Data were processed and analyzed using IDL (RSI, Boulder, CO, USA). HiSS data were collected using EPSI, utilizing conventional excitation (in this study a single 30° pulse) followed by an oscillating, multilobed readout gradient train (38). This allows for detection of signal decay as a function of time for each point in k-space. For HiSS data, each slice of complex raw data was reformatted into a three-dimensional (3D) array (k_x × k_y × time). 3D arrays were Fourier transformed in all three dimensions to produce two spatial dimensions and one spectral dimension (x × y × ν). A modulus water spectrum was produced for each image voxel. Spectral ghosting was removed by correcting the error in phase between the even and odd echoes (39) of the GRE train, improved estimates of the frequency of the water peak were obtained with a frequency-shifting method (40), and the spectral intensity baseline for each spectrum was determined and subtracted (11). These spectrally-corrected HiSS data sets were used throughout all subsequent analyses. Water peak height (PH) images were constructed from HiSS data sets such that signal intensity at each pixel in the 2D array was proportional to the maximum signal intensity in the corresponding voxels’ water resonance.

Voxels with signal intensity below 10 times the noise (as determined by the standard deviation [SD] of background signal outside of the leg/tumor in the PH image) were detected in the PH image and thresholded. The thresholded voxels in the PH image were propagated to all FCs of the HiSS data set. This prevented noise amplification in subsequent analysis. Note that because of the high-SNR voxels that remained after thresholding, all subsequent analyses of modulus spectra were performed on approximately Gaussian distributed noise (41).

Regions of interest (ROIs) were manually selected to include the tumor rim, tumor center, and normal muscle. These specific ROIs were selected because they represent very different vascular architectures and blood oxygenation concentrations. The tumor rim tends to have increased microvascular density relative to the tumor center (34,35). Further, tumor blood, especially on the venous side, tends to have a much lower concentration of deoxyhemoglobin than that of normal tissue (22,23). The tumor rim was identified in PH images and defined as a 10-pixel-thick band at the manually outlined perimeter of the tumor rim. The tumor center was manually defined within the tumor with the specific requirement that it not intersect the tumor rim. Normal muscle was manually selected from muscle outside of the tumor, at least 10 pixels from the tumor rim/muscle interface.

Spectral asymmetry, Asym(x,y), was measured for each voxel of each HiSS data set as the difference between the integrals of the high-frequency and low-frequency halves of the water spectrum about the main water peak, normalized by the integral of the total water spectrum. The absolute value of the normalized difference was calculated:

$$\mathit{Asym}(x,y)=\left|\frac{\underset{v_{\mathit{min}}}{\overset{v_{\mathit{peak}}}{\int }}s(x,y,v^{\prime })d{v}^{\prime }-\underset{v_{\mathit{peak}}}{\overset{v_{\mathit{max}}}{\int }}s(x,y,v^{\prime })d{v}^{\prime }}{\underset{v_{\mathit{min}}}{\overset{v_{\mathit{max}}}{\int }}s(x,y,v^{\prime })d{v}^{\prime }}\right|,$$ [1]

where the positions of ν_min and ν_max along each spectrum, s(x,y,*), were defined as one-quarter of the spectral window (~48.8 Hz) above and below the main water peak, ν_peak. These cutoff values ensured that the range of integration was large enough that all off-peak components were included in the integrals. A large value indicates asymmetry, whereas a small value indicates a more Lorentzian-shaped waterline. The noise in the spectral data was propagated through Eq. [1] to produce an asymmetry image noise distribution. The SD of this distribution was used as the propagated noise value. Asymmetry values greater than eight times the propagated noise value were considered significant. Noise propagation was performed on a voxel-by-voxel basis to ensure unbiased thresholding due to the variable normalization constant in Eq. [1]. This conservative thresholding criterion was used to isolate only the regions of greatest asymmetry.

To maximize sensitivity to shoulders or partially resolved components of the water resonance, the amplitudes of pairs of FCs that were symmetrical about the peak of the water resonance were compared. Waterlines were normalized by the area under the entire spectrum as described in the asymmetry analysis, and the absolute difference between normalized symmetric components was computed. By this metric, symmetric components produce small values. For example, the FC at 6 Hz above the peak of the water resonance would have the same amplitude as the FC 6 Hz below the peak in a purely Lorentzian modulus spectrum. The difference between these two components would increase with increased spectral asymmetry. Differences between symmetrical FCs were considered significant above eight times the propagated noise level. Because of the normalization procedure, the symmetry is in units of percent of the total waterline. In fact, the sum of the symmetric components over an entire waterline is the asymmetry value defined in Eq. [1].

Abrupt changes in contrast in FCIs are generally due to the presence of a shoulder or partially resolved component of the water resonance. These spectral features are the consequence of local variations in magnetic susceptibility (i.e., on a scale smaller than a single image voxel). Therefore, these contrast changes may reflect the presence of small tumor blood vessels. To identify variations in contrast in FCIs from −30 Hz to +30 Hz about the peak of the water resonance, the contrast in each FCI was locally normalized using a modification of the procedure described by Foracchia et al. (42). Specifically, the signal intensity in each pixel of each FCI_ν, f′(x,y,ν), was normalized by the mean signal in an array of 11 × 11 pixel with the pixel of interest at the center as follows:

$$f(x,y,v)=\frac{f^{\prime }(x,y,v)}{\frac{1}{(2i+1)\times (2j+1)}{\displaystyle \sum _{-i}^i}{\displaystyle \sum _{-j}^j}{f}^{\prime }(x+i,y+j,v)},$$ [2]

where f(x,y,ν) is a pixel in the locally normalized FCI, f′(x,y,ν) is the corresponding pixel in the precontrast-normalized FCI, and i and j are indices determined by the array size (in this case 11 × 11 pixels, where i and j are equal to 5). The resulting images are referred to here as locally normalized FCIs. For each voxel of the 3D, locally normalized HiSS data set, the FC of the water resonance with the greatest contrast relative to surrounding voxels was identified. This is an efficient way of identifying shoulders/partially-resolved components in the water resonance for a given voxel, or cluster of voxels. A composite image was produced based on the largest locally normalized FC for each voxel. This can be thought of as a MIP along the spectral dimension of the locally normalized HiSS data set (referred to in the following as an FCI-MIP), which emphasizes shoulders or partially-resolved peaks of the water resonance. Each FCI-MIP was normalized by the mean signal intensity in normal muscle to facilitate comparison between experiments. The FCI-MIPs were then thresholded by 3.75 times the mean muscle signal (a value determined by receiver operating characteristic [ROC] analysis, as described below).

We tested the hypothesis that areas of high intensity in the FCI-MIPs that remained following thresholding showed regions of high vascular density. These regions were correlated with blood pool contrast agent-enhanced images. To accomplish this, post-contrast GRE images were subtracted from pre-contrast GRE images. Subtraction images were thresholded by eight times the propagated noise value to ensure that differences were real and not due to random fluctuations in signal intensity. These images were used as gold standards for vasculature localization. Thresholded FCI-MIP images were correlated with these gold standard images. Individual high-intensity voxels of FCI-MIPs were allowed ~400 μm tolerance for co-registration. This allowed for small variations due to motion as well as extended field distortions caused by high local concentrations of the iron-oxide contrast agent.

A ROC curve was calculated (43) to test the reliability of the co-registration between the FCI-MIP and the thresholded GRE difference image. Points of the ROC curve were generated by computing the sensitivity and specificity of the FCI-MIP at various threshold values; the previously reported threshold value of 3.75 produced the best compromise between sensitivity and specificity. The ROC curve was fit and the area under the curve (Az) was determined.

Unless otherwise noted, all statistical analyses were performed by means of a one-way analysis of variance (ANOVA) to determine the level of significance (SPSS Inc., Chicago, IL, USA) between different means. A level of P < 0.05 was considered significant.

RESULTS

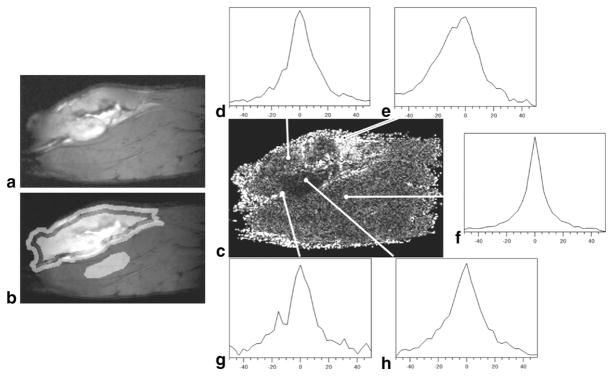
ROIs in the tumor rim, tumor center, and normal muscle were manually defined for each slice of each experiment. The percentage of voxels with significant asymmetry was calculated over all pooled pre-contrast HiSS data for each ROI. Significant spectral asymmetry occurred in 82% ± 6% of voxels at the tumor rims, 91% ± 2% of voxels in the tumor centers, and 59% ± 3% of voxels in normal muscle. The high degree of asymmetry in the tumor rim and center compared with that of the normal muscle is clearly seen in the asymmetry image shown in Fig. 1b. The mean asymmetry of those voxels that remained after thresholding was 19% ± 4% at the tumor rim, 8.0% ± 1.5% at the tumor center, and 4.8% ± 0.6% in muscle (asymmetry is reported as a percentage of the integral of the water resonance). The asymmetry at the tumor rim was significantly higher than in the other two ROIs (P < 0.003). Typical water line shapes in selected ROIs are shown in Fig. 1c– e. While a greater percentage of voxels in the tumor center were asymmetric, the mean asymmetry in the tumor rim was much greater. This indicates that there are voxels with very large asymmetry at the tumor rim.

FIG. 1.

a: Water PH image of a tumor-bearing rat leg. b: Water PH image with tumor rim, tumor center, and normal muscle ROIs highlighted. c: Corresponding absolute asymmetry image. Typical spectra observed the (e, g) tumor rim, (d, h) tumor center, and (f) normal muscle. Spectra in the tumor rim are visually more asymmetrically broadened.

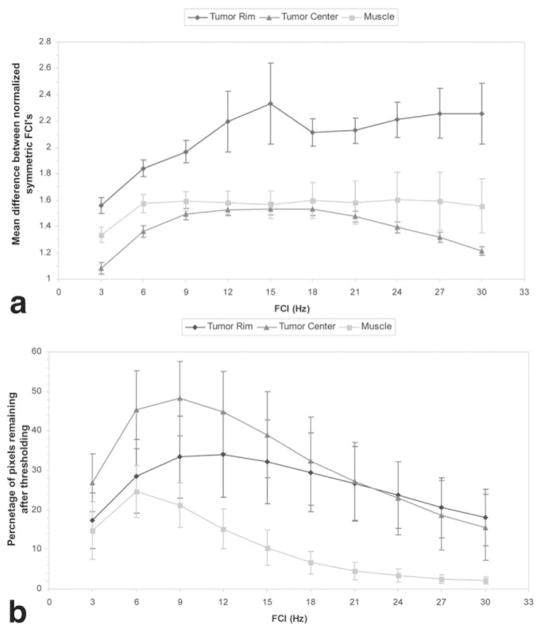
The greatest significant differences between symmetrical FCs of the water spectrum over all pooled data occurred at the tumor rim. These differences were most prominent at ±15 Hz from the main water peak (Fig. 2a). Highly significant differences between FCI₋₁₅ and FCI₁₅ were found in 32% ± 10% of voxels at the tumor rim, 39% ± 10% of voxels at the tumor center, and 10% ± 4% of voxels in the normal muscle (Fig. 2b). The average difference in symmetric components was significantly larger (P < 0.04, Student’s t-test) at the tumor rim (2.3% ± 0.3%) compared to the tumor center (1.5% ± 0.05%). Note that these percentages for individual FCs are given relative to the total integral of the water resonance in each voxel. Although these values are small, since they are a percentage of the entire waterline, these values are large relative to the individual components themselves.

FIG. 2.

Plots show (a) the difference (mean ± SD) between FCs of the water resonance that are symmetrical about the main water peak, and (b) the percentage of pixels (mean ± SD) in each ROI with significant differences between symmetrical FCs. Note that while fewer pixels in the tumor rim have differences between symmetric components that are above the threshold, the mean difference at each frequency is much greater at the tumor rim than in other ROIs.

Comparison of precontrast FCI-MIPs with GRE difference images demonstrated significant correlation. Figure 3a– d show a typical example of a water PH image, vasculature identified in CE images, vasculature identified in FCI-MIPs, and the correlation between the two. Changes in signal intensity in GRE images post-contrast occur throughout the tumor and normal muscle (Fig. 3b), but the largest changes occur at or near the tumor rim (light blue regions). The vasculature identified by FCI-MIPs (Fig. 3c) and the greatest agreement between FCI-MIPs and CE GRE images (green regions in Fig. 3d) occur at the tumor rim as well. The sensitivity averaged over all experiments of the FCI-MIPs at the tumor rim (based on CE images as the gold standard) was 75% ± 13%. This is significantly larger (P < 0.0004) than that at the tumor center or normal muscle (Table 1). The sensitivity and PPVs were 74% ± 10% and 91% ± 4% at the tumor rim, respectively. ROC analysis of data for the tumor rim produced an Az value of 0.82.

FIG. 3.

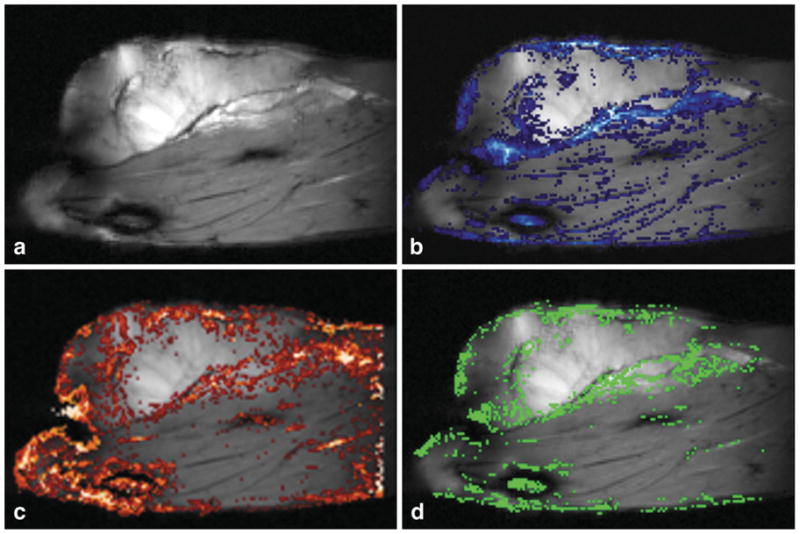
a: Water PH image. b: Water PH image with GRE differences overlaid (blue scale: dark to light blue is a high signal in difference images). c: Water PH image with thresholded FCI-MIP overlaid (red scale: dark to light red indicates lower to higher signal intensities). d: The water PH image with pixels where GRE difference images and HiSS data agree superimposed in green. The greatest concentrations of correlated pixels are in the tumor rim, which is the typical anatomical location of tumor microvasculature.

Table 1.

Results of FCI-MIP comparison with blood-pool CE GRE^*

ROI	Sensitivity	Specificity	PPV
Tumor rim	75 ± 13	74 ± 10	91 ± 4
Tumor center	45 ± 17	95 ± 4	96 ± 2
Normal muscle	3 ± 8	99 ± 1	58 ± 16

^*Sensitivity to tumor vasculature is greatest in the tumor rim (P < 0.0004) compared with that of the tumor center of normal muscle. Specificity is less in the tumor rim than in the other two ROIs, but this value indicates the inherent compromise between sensitivity and specificity. Greater sensitivity or specificity could be achieved, but at the expense of the other. Positive predictive value in both tumor ROIs are high. This suggests that when vasculature is present in either the tumor rim or center, HiSS is capable at detecting it.

DISCUSSION

The results indicate that HiSS data sets are sensitive to regions of dense tumor microvasculature. This suggests that inhomogeneous broadening of the waterline is due, at least in part, to the presence of deoxygenated hemoglobin in tumor blood vessels, which produces magnetic susceptibility gradients that alter the water resonance line shape. Deoxyhemoglobin concentration is high in tumor vasculature due to an imbalance between oxygen supply and delivery. With enough microvasculature present in a voxel, sufficient water protons experience the change in the local B-field and inhomogeneous broadening is observed.

The tumor rim has the greatest degree of asymmetric spectral broadening compared to the tumor center and normal muscle, and this result is highly statistically significant. The increased prevalence of larger asymmetry values at the tumor rim compared to the tumor center and normal muscle can be explained by tumor vascular anatomy. The tumor rim typically has dense vasculature, whereas the tumor center has relatively few functional vessels. Other anatomic features in tumors, such as calcifications, could contribute to asymmetric broadening of the water resonance. However, the strong correlation between asymmetry and contrast enhancement suggests that blood vessels have the most significant effect on the water line shape. The increased asymmetry in the tumor compared to normal muscle could be due to the disproportionate concentrations of deoxyhemoglobin in tumor microvasculature.

As seen in Fig. 3c, not all regions of increased signal intensity in FCI-MIPs correspond with regions of dense tumor microvasculature. Specifically, the region about the femur and regions in the normal muscle have increased signal intensity in the FCI-MIP. Off-peak spectral features in these regions may be due to large veins containing deoxygenated blood, but could also be due to other sources of magnetic susceptibility variation. Some of these include bone/tissue interfaces (or other interfaces between different tissue types), calcium deposits, and iron deposits. However, within the tumors themselves, the strong correlation with contrast media uptake suggests that tumor vasculature is the source of increased signal intensity in FCI-MIPs.

It is possible for a water line to be inhomogeneously broadened and still be relatively symmetrical. For example, a water resonance may be composed of different populations of water molecules that are not in rapid exchange but whose resonance frequencies follow a normal distribution. In this case, the asymmetry metric would be small while this waterline is inhomogeneously broadened. However, spatially inhomogeneous distributions and orientations of tumor blood vessels are likely to produce asymmetric local water spectra with distinct shoulders or partially resolved components. Because of the inhomogeneous orientation of these blood vessels, water spectra can be asymmetrically broadened to either side of the main water peak. Therefore, the comparison of symmetric components of the water line by use of the normalized difference described here is a valid approach to detect the local magnetic susceptibility gradients produced by blood vessels, independently of vasculature orientation.

The greatest differences between symmetric components occur in the tumor rim. Shoulders or partially resolved components are detected at a range of frequency offsets from the peak of the water resonance. This is consistent with the experimental phantom study results of Chu et al. (44), demonstrating that the shift in resonance frequency due to localized small changes in bulk magnetic susceptibility depends on orientation of blood vessels with respect to B₀. Tumor vasculature is highly unorganized and follows very tortuous paths compared to vasculature in normal tissue. Instead of producing clearly resolved secondary peaks, as with the results of Chu et al., (44) this is likely to produce asymmetric water spectra due to the varied distributions of vessel orientations in a voxel, which can serve markers for dense tumor vasculature.

Asymmetry at the tissue/air interface of Fig. 1 represents a potential source of error in our analyses. However, the effect of this magnetic susceptibility mismatch extends only a few pixels beyond the edge of the tissue. The high degree of asymmetry at the tumor rim extends far beyond the influence of the tissue/air interface. Further, asymmetry along the tissue/air interface varies dramatically, suggesting that even in this region, the magnetic susceptibility mismatch between air and tissue is not the only source of non-Lorentzian broadening. Nevertheless, to avoid this potential source of error in the future, we are currently investigating the use of susceptibility matching materials along the surface of the leg to minimize this effect.

The sensitivity, specificity, and PPVs of the FCI-MIPs support the results of the asymmetry analysis, and indicate that tumor microvasculature can be detected using HiSS imaging without contrast agents. Our hypothesis is that regions of dense vasculature appear in individual FCIs as small groups of pixels that have sharp contrast relative to surrounding pixels. These groups of pixels likely vary from FCI by FCI due to shifts in resonance associated with variations in local magnetic susceptibility. By producing FCI-MIPs, we are able to locate these regions and condense them into a single composite image so that they are easily visualized. The large Az value determined from ROC analysis indicates that this test is reliable. While the accuracy of the method achieved here is modest, it is likely that increased sensitivity, specificity, and PPV can be achieved with further improvements in HiSS image acquisition and analysis.

The ability to detect tumor vasculature without contrast agents could have important clinical applications, including the following:

1. HiSS without contrast media could be used for cancer detection in patients who are at risk for adverse reactions to contrast agents.

2. HiSS could provide improved visualization of tumor vascular morphology before contrast agent is injected. This would avoid blooming artifacts and blurring caused by contrast agents (6 – 8). Information from pre-contrast HiSS scans combined with conventional MRI could increase diagnostic accuracy.

3. Accurate delineation of tumor vasculature before contrast media is injected would allow prescription of subsequent dynamic CE-MRI scans to achieve maximum temporal and spatial resolution in areas where there is suspicious vascular density, with more modest spatial and temporal resolution elsewhere. This could improve the effectiveness of dynamic CE-MRI and increase diagnostic accuracy.

CONCLUSIONS

This work demonstrates that HiSS imaging is sensitive to tumor microvasculature without the use of an exogenous contrast agent. Spectral asymmetry analyses indicate that inhomogeneous broadening of the water line is more prevalent at the tumor rim than either the tumor center or normal muscle. Comparisons of FCI-MIPs with CE images demonstrate that these images have moderate sensitivity and specificity and high PPV to tumor microvasculature. ROC analysis indicates that the methods used for these measurements are reliable. These findings are potentially clinically relevant as the detection of tumor vasculature is an important marker for the detection and diagnosis of tumors, and could guide treatment planning. HiSS imaging could be used clinically for tumor microvasculature localization.