Inhibition of kinesin motility by ADP and phosphate supports a hand-over-hand mechanism

Abstract

The motor protein kinesin couples a temporally periodic chemical cycle (the hydrolysis of ATP) to a spatially periodic mechanical cycle (movement along a microtubule). To distinguish between different models of such chemical-to-mechanical coupling, we measured the speed of movement of conventional kinesin along microtubules in in vitro motility assays over a wide range of substrate (ATP) and product (ADP and inorganic phosphate) concentrations. In the presence and absence of products, the dependence of speed on [ATP] was well described by the Michaelis–Menten equation. In the absence of products, the K_M (the [ATP] required for half-maximal speed) was 28 ± 1 μM, and the maximum speed was 904 nm/s. P_i behaved as a competitive inhibitor with K_I = 9 ± 1 mM. ADP behaved approximately as a competitive inhibitor with K_I = 35 ± 2 μM. The data were compared to four-state kinetic models in which changes in nucleotide state are coupled to chemical and/or mechanical changes. We found that the deviation from competitive inhibition by ADP was inconsistent with models in which P_i is released before ADP. This is surprising because all known ATPases (and GTPases) with high structural similarity to the motor domains of kinesin release P_i before ADP (or GDP). Our result is therefore inconsistent with models, such as one-headed and inchworm mechanisms, in which the hydrolysis cycle takes place on one head only. However, it is simply explained by hand-over-hand models in which ADP release from one head precedes P_i release from the other.

Kinesin is a motor protein that couples the free energy derived from the hydrolysis of ATP into mechanical work used to drive cellular motility. Two properties of kinesin are essential for its function. First, kinesin undergoes directed motion. It moves toward the plus- or fast-growing end of a microtubule as it transports membrane-bounded organelles toward the periphery of neurons and other cells (1) where the plus ends of microtubules are usually located (2). And second, kinesin is processive. An individual kinesin molecule can move up to several microns along a microtubule without dissociating (3). Processivity ensures that even a small vesicle with just one or two motors on its surface will spend a large fraction of its time attached to and moving along a microtubule (as opposed to diffusing in the cytoplasm).

The directed and processive motion of kinesin is tightly coupled to the hydrolysis of ATP. High-precision tracking of kinesin-coated beads reveals that kinesin takes 8-nm steps (4) from one tubulin dimer to the next along a path that is parallel to the axis of the microtubule (5). Direct measurement of the ATPase rate and its correlation to the speed of movement indicates that in standard motility assays where the load is low, kinesin hydrolyses only one ATP per 8-nm step (6). A stoichiometry of 1 step per ATP implies that each cycle of ATP hydrolysis [the binding of ATP to kinesin's nucleotide-binding pocket, its hydrolysis to ADP and inorganic phosphate (P_i), and the subsequent release of these products] has a high probability of generating an 8-nm step [>90% (6)]. At the same time, the high degree of processivity implies that there is a low probability of detaching during each step [<1% (3)]. Hence, the probability that kinesin takes a misstep (a backwards movement or a dissociation) is very low.

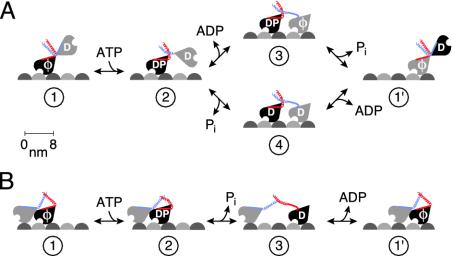
How does kinesin couple, so precisely, molecular motion to the hydrolysis of ATP? Several models have been proposed. In “hand-over-hand” models (3, 7), kinesin's two motor domains (8), called “heads,” alternate their binding to the microtubule such that one head leads and then the other (Fig. 1A). This provides a simple explanation for processivity if one head remains attached until the other head attaches (9), analogous to bipedal walking. Directionality follows if the probability that the trailing head moves to the front position (toward the plus end of the microtubule) is much greater than the probability of the leading head moving to the trailing position.

Fig. 1.

Hand-over-hand and inchworm models. (A) Hand-over-hand models. The ADP-released-first model corresponds to the upper path (1 → 2 → 3 → 1′). The P_i-released-first model corresponds to the lower path (1 → 2 → 4 → 1′). In the random-release model, either path can be taken. (B) In the inchworm model, P_i is thought to be released first (see text). D, ADP; P, P_i;ϕ, empty nucleotide-binding site.

There are a number of alternatives to the hand-over-hand models. In the “inchworm” model (Fig. 1B), the heads alternate their attachment to the microtubule but maintain their order along the microtubule, with one head always leading and the other always trailing (10). To satisfy the condition that there is only one ATP hydrolyzed per 8-nm step, the inchworm model must have ATP hydrolysis occurring in only one head. From a chemical point of view, the inchworm model is therefore a one-headed mechanism, with the second head providing a crutch or passive attachment to the microtubule and the second nucleotide-binding site perhaps playing a regulatory role.

An important characteristic of the various models is the order in which the products are released. In this paper, we present product inhibition experiments designed to determine which of the products, P_i or ADP, is released first. Our data are best fit by an ordered mechanism in which ADP is released before P_i. This result is surprising, because kinesin's nucleotide-binding pocket is expected to release P_i before ADP (see Discussion). Thus, our results are not readily accounted for by one-headed or inchworm models. However, they are simply explained by hand-over-hand models in which the release of ADP from one head precedes the release of P_i from the other. We discuss how such a mechanism can account quantitatively for the precision of kinesin's motion.

Materials and Methods

Proteins and Reagents. Native kinesin and tubulin were purified from bovine brain (11). Full-length Drosophila conventional kinesin was expressed in bacteria and purified as described (6). Both kinesin and tubulin were stored at –80°C in a solution containing 100 μM ATP. ATP and ADP were purchased from Boehringer Mannheim and stock solutions contained equimolar magnesium (from MgCl₂). The level of ATP contamination in the ADP stock was measured to be <0.2% (12). Anhydrous inorganic phosphate (K₂HPO₄) was purchased from Fisher and adjusted to pH 7.0 with HCl. All other reagents were bought from Sigma. Casein (C-7078, Sigma) was passed through a buffer exchange column (G25, Pharmacia) to remove contaminating P_i; a 1 mg/ml casein solution contained 100 ± 4 μMP_i (n = 8), estimated by using a colorimetric assay (6), and this was reduced ≈1,000-fold by the column.

A mixture of 25% rhodamine-labeled tubulin (13) and 75% unlabeled tubulin (total tubulin concentration 32 μM) was polymerized for 15 min at 37°C in BRB80 (80 mM Pipes/1 mM EGTA/1 mM MgCl₂, pH 6.9 with KOH), supplemented with 1 mM GTP, 4 mM Mg²⁺, and 5% DMSO, and diluted 100-fold into BRB80 augmented with 10 μM taxol to stabilize the microtubules.

Gliding Assay. Flow cells were constructed as described (3) except that double-sided sticky tape (thickness 80 μm) was used as a spacer. Cell volumes were ≈4 μl (18 × 3 × 0.08 mm). The temperatures of the flow cell and the room were usually maintained at 25 ± 1°C. In some cases, experiments were performed at temperatures as low as 22°C; in those cases, a temperature correction of 7%/°C was applied to the speeds (14). Motility assays at various [ATP], [ADP], and [P_i] were set up by using the following procedure. (i) One volume of BRB80 augmented with 1 mg/ml casein was infused into the flow cell and allowed to sit for 5 min. (ii) For high-density assays, one volume of bovine kinesin (at a final concentration of 10–100 nM after dilution into BRB80 plus 0.2 mg/ml casein) was flowed in and allowed to sit for 5 min. The average kinesin density on the surfaces of the flow cell was calculated to be 200–2,000 μm^–2, assuming that all of the protein adsorbs. For low-density assays, the concentration was 0.05–0.5 nM corresponding to a density of 1–10 μm^–2. (iii) To remove nucleotides introduced in the kinesin-containing solution as well as to accurately set the nucleotide concentrations, the flow cell was washed three times with 20 μl of BRB80 plus 0.2 mg/ml casein and the appropriate [ATP], [ADP], and [P_i]. There was a 30-s wait between washes. (iv) The flow cell was infused with 20 μl of motility solution {BRB80 containing 0.2 mg/ml casein, 32 nM polymerized tubulin, 10 μM taxol, an oxygen-scavenging system (9), and the appropriate [ATP], [ADP] and [P_i]}. Microtubules (mean length 5 μm) were visualized by fluorescence microscopy, representative fields were videotaped, and the speed was measured off-line as described (9). The speeds of 5–30 microtubules from various parts of the flow cell were measured within 15 min of adding motility solution. Over this time there was no systematic change of the speed, indicating that neither the depletion or synthesis of ATP nor the liberation of products was influencing the results.

Nonlinear least-squares curve fitting was performed in igor (WaveMetrics, Lake Oswego, OR). Unless stated otherwise, the errors are standard errors of the mean. Systematic errors of 3% in the speed and 5% in the [ATP], [ADP], and [P_i] were assumed. The differential equations associated with the kinetic diagrams (e.g., Fig. 6) can be found in ref. 15.

Fig. 6.

ADP-released-first model for kinesin motility. In this four-state model, the following chemical and structural transitions occur. (1) The attached head binds ATP and hydrolyses it (forward and reverse rate constants k₁ and k_–1). (2) The forward head attaches to the microtubule and releases its ADP (forward and reverse rate constants k₂ and k_–2). (3) The rear head detaches from the microtubule and releases its P_i (forward and reverse rate constants k₃ and k_–3). The top transition denotes the binding of ADP that competes for ATP binding (inhibitory constant ). The bracketed structures denote hypothetical transition states. T, ATP; D, ADP; P, P_i; ϕ, empty nucleotide-binding site.

Results

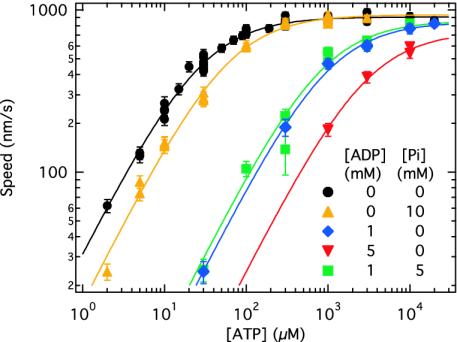
To distinguish among the possible kinetic mechanisms for kinesin, the speeds of microtubules moving across surfaces coated with kinesin at high density were measured over a wide range of [ATP], [ADP], and [P_i]. Under all conditions used in the present work, the dependence of the speed on the [ATP] (Fig. 1) was well described by

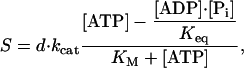[1]

where d is the step size of kinesin (d = 8 nm), k_cat is the maximum steady-state hydrolysis rate (which depends on the [ADP] and [P_i]), and K_M is the [ATP] required to attain the half-maximum speed (which also depends on the [ADP] and [P_i]). The equilibrium constant for the hydrolysis reaction, K_eq = 4.9 × 10¹¹ μM measured in a standard solution {[Mg²⁺]_free = 1 mM, pH = 7, ionic strength = 250 mM, 25°C (16)} similar to that used in these experiments, is so large that the second term in the numerator is negligible under all conditions used in this study. Thus, Eq. 1 reduces to the Michaelis–Menten equation and K_M is the Michaelis constant.

In the absence of products (Fig. 2, black curve), the speed versus [ATP] was well fit by the Michaelis–Menten equation with 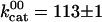s^–1 and 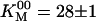μM. In accordance with previous measurements on bovine kinesin (3, 17), there was no evidence that the binding of ATP to the two heads is cooperative: the Hill coefficient (15, 18) was not significantly different from 1. Note that the lack of cooperativity does not rule out interaction between the two nucleotide binding sites.

Fig. 2.

Speed versus [ATP] at various [ADP] and [P_i]. Solid lines are global fits to the ADP-first mechanism with dead-end inhibition by ADP.

The speed versus [ATP] was also well described by the Michaelis–Menten equation in the presence of products (Fig. 2). The inhibition by ADP and P_i were described empirically by using the inhibition constants (15, 18) that are collected in Table 1 and that are defined by

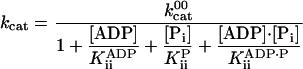[2]

and

[3]

In Eqs. 2 and 3, and 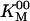are the values of k_cat and K_M, respectively, at zero ADP and zero P_i. We use the following terminology: a “competitive” inhibitor affects K_M and not k_cat, a “noncompetitive” inhibitor affects k_cat not K_M, a “mixed” inhibitor affects both k_cat and K_M, and a “dead-end” inhibitor traps the molecule in a state off the main cycle (15, 18).

Table 1. Measured parameters.

Parameter	Meaning	Value, mean ± SE
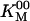	Maximum ATPase rate*	113.2 ± 1.1 s-1
	Michaelis constant*	28.1 ± 0.9 μM
	Pi competitive†	9 ± 1 mM
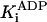	Pi noncompetitive†	≥200 mM‡
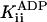	ADP competitive†	34.6 ± 2.6 μM
	ADP noncompetitive†	23 ± 8 mM
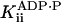	Joint competitive†	≥95 mM2§
	Joint noncompetitive†	≥30 mM2‡

^*In the absence of products.

^†Inhibition constant.

^‡95% confidence lower bound.

^§90% confidence lower bound.

Inhibition by Phosphate. Phosphate acted as a competitive inhibitor for ATP: as [P_i] was increased, K_M increased but k_cat was unchanged (Fig. 2, yellow curve). For example, fits of the Michaelis–Menten equation to individual data sets showed that addition of 5 and 10 mM P_i increased the K_M from 28 ± 1 μM to 44 ± 3 μM and 59 ± 3 μM, respectively, but did not significantly change k_cat, which was 113 ± 1 s^–1 in the absence of P and 116 ± 2 s^–1 and 117 ± 2 s^–1 i in the presence of 5 and 10 mM P_i, respectively (Figs. 3 A and B, blue curves). A graph of the speed versus [P_i] at fixed [ATP] (Fig. 4A) illustrates the competitive nature of the inhibition: P_i reduces the speed at low [ATP] but has little effect at high [ATP]. The inhibition constant, , was 9 ± 1 mM when using the data in Fig. 3B. This means that when [P_i] = 9 mM, twice as much ATP was required to reach the same speed as in the absence of P_i. The competitive inhibition by P_i cannot be explained as an effect of the increased ionic strength of the high-[P_i] solutions. For example, addition of 10 mM P_i (at pH 7) increased the ionic strength by 25 mM; yet, addition of 30 mM KCl (that increased the ionic strength by 30 mM) actually increased, rather than decreased, the speed, although the effect was very slight (1.6%).

Fig. 3.

Effect of products on k_cat and K_M. (A) The maximum ATPase rate (the maximum speed divided by the step size of 8 nm) decreases with the [ADP] (red squares), inconsistent with purely competitive inhibition. The maximum ATPase rate, k_cat, is unaffected by P_i (blue squares), consistent with purely competitive inhibition. The solid curves are fits to Eqs. 1 and 2. The dashed lines correspond to 95% confidence intervals. (B) The [ATP] for half-maximal speed, K_M, increases with the [ADP] (red triangles), consistent with competitive inhibition. The increase in K_M with the [P_i] (blue triangles) is also consistent with competitive inhibition. The solid curves are fits to Eqs. 1 and 3.

Fig. 4.

Effect of products on speed. (A)P_i slows the motor at low [ATP] but has no effect at high [ATP], consistent with competitive inhibition. Solid lines are global fits to the ADP-first mechanism with dead-end inhibition by ADP. (B) ADP slows the motor at moderate [ATP]. This effect is reduced but not eliminated at higher [ATP], suggesting a combination of competitive and noncompetitive inhibition. Solid lines are global fits to the ADP-first mechanism with dead-end inhibition by ADP.

We can place a limit on any noncompetitive effect of P_i. If we correct the k_cat vs. [P_i] data in Fig. 3A for the small effect of ionic strength (see above), we find that 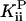≥ 200 mM at the 95% confidence level.

Inhibition by ADP. The inhibition by ADP was mixed. The primary effect of ADP was as a competitive inhibitor (Fig. 2, blue and red curves). The K_M rose from 28 μM in the absence of ADP to 1,000 ± 110 μM and 2,900 ± 550 μM at 1 and 5 mM ADP, respectively (Fig. 3B, red curve). The competitive nature of the inhibition is also seen in Fig. 4B: ADP inhibits strongly at low [ATP] but only weakly at high [ATP]. The inhibition constant, , was 35 ± 3 μM when using the data in Fig. 3B.

The inhibition by ADP was not purely competitive: ADP also decreased k_cat. This is seen in Fig. 2, which shows that k_cat decreased from 113 ± 1 s^–1 in the absence of ADP to 105 ± 4 s^–1 and 92 ± 8s^–1 at 1 and 5 mM ADP, respectively. The inhibition constant for this noncompetitive component, 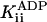, was 23 ± 8 mM. A Student's t test showed the probability that 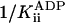is different from zero to be 0.95. Control experiments showed that the deviation from purely competitive inhibition cannot be due to the increased ionic strength contributed by the added ADP: the increased ionic strength is expected to (slightly) increase rather than decrease k_cat.

Inhibition by ADP and Phosphate. The joint inhibitory effect of ADP and P_i was modeled according to Eqs. 2 and 3 as terms proportional to the product of the [ADP] and [P_i]. Higher-order terms were neglected. For both k_cat and K_M, the joint effect was small. Comparison of the values of k_cat measured at 1 mM ADP and 0 mM P_i, 1 mM ADP and 5 mM P_i, and 0 mM ADP and 5 mM P_i indicated that 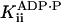≥ 30 mM² (at the 95% confidence level). Comparison of the speed dependence on ADP at 30 μM ATP with and without 10 mM P_i (Fig. 5) indicated that ≥ 95 mM² (at the 90% confidence level; experimental uncertainties prevent higher confidence).

Fig. 5.

Joint effect of products on reciprocal speed. In the presence of 10 mM P_i (red circles), the speed is lower than in the absence of P_i (black circles) but the slope is unchanged. Note that the ordinate is the inverse of speed. Solid lines are global fits to the ADP-first mechanism with dead-end inhibition by ADP.

Single-Molecule Assays. All of the experiments reported above were done at relatively high densities of motors to facilitate the collection of a large set of data. Under these conditions, we estimate that between 10 and 100 motors are moving each microtubule. To justify the interpretation of our results in terms of the hydrolysis cycle of an individual molecule (e.g., Fig. 1), we repeated several key experiments at low motor densities at which several lines of evidence suggest that the motility was due to single molecules (3).

The single-motor speed at high [ATP] in the absence of products was indistinguishable from the multimotor speed, as previously observed (3, 9, 19). At 1 and 10 mM ATP, the single-motor speeds were 901 ± 53 nm/s (n = 4) and 867 ± 46 nm/s (n = 52), respectively, consistent with the values of 880 ± 39 and 891 ± 43 nm/s measured at high densities (Fig. 2).

The effects of ADP at high [ATP] were the same in single- and multiple-motor assays. At 1 mM ATP, 1 mM ADP reduced the single-motor speed by 49% to 457 ± 54 nm/s (n = 24), similar to the reduction of 47% observed at high densities (Fig. 4B). At 10 mM ATP, 1 mM ADP significantly reduced the single-motor speed to 757 ± 45 nm/s(n = 60), corresponding to a reduction of 14%. This is similar to the reduction of 13% observed at high densities (Fig. 4B) and is consistent with there being a noncompetitive component of inhibition by ADP in single-motor assays. ADP had no significant effect on the processivity: the run length at 10 mM ATP was 5.2 ± 2.0 μm(n = 21 runs) in the absence of ADP and 3.4 ± 1.3 μm(n = 22) in the presence of 1 mM ADP. The small reduction in run length of 35% by addition of ADP is similar to that seen by Yajima et al. (20).

The inhibition by P_i was similar in single- and multiple-motor assays. At low ATP (5 μM), 10 mM P_i decreased the single-motor speed by 49%, from 179 ± 20 nm/s (n = 40) to 91 ± 9 nm/s (n = 40). This is similar to the reduction of 37%, from 128 ± 5 to 81 ± 8 nm/s, observed at high densities (Fig. 4A). P_i had no significant effect on processivity: the run length at 5 μM ATP was 3.3 ± 1.0 μm(n = 29 runs) in the absence of P_i and 1.51 ± 0.44 μm(n = 24) in the presence of 10 mM P_i.

As observed in earlier work, the speed at low [ATP] (without P_i) was higher in single-motor assays than in multimotor assays. This means that our value of 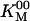obtained from the multimotor assays (28 ± 1 μM) is an overestimate of the single-motor value, but the error is small, and the present data are consistent with the value of 30 μM obtained from the earlier single-motor assays (3). All of the single-motor experiments were repeated with a full-length recombinant conventional kinesin from Drosophila (6), and the results (Table 5, which is published as supporting information on the PNAS web site) were similar to those obtained with bovine kinesin.

Discussion

We have measured the inhibition of the speed of kinesin motility by the products of hydrolysis, ADP and P_i. We found that P_i acted like a purely competitive inhibitor, meaning that the inhibition could be overcome by adding high enough ATP. This result is new, although inhibition by vanadate (21, 22) and phosphate analogues (23) have been reported in less detail. We also found that ADP acted as a mixed inhibitor, with an effect that was largely competitive but also included a small noncompetitive component. The finding of a noncompetitive component of ADP inhibition is new. Competitive inhibition of kinesin speed by ADP was previously observed by Cohn et al. (21).

Kinetic Mechanisms. We now consider which kinetic mechanisms are consistent with the data that are summarized in Table 1. To do this, we rely on earlier work, summarized in the Introduction, showing that there is tight coupling between ATP hydrolysis and motility. This means that the speed is proportional to the ATPase rate and so the chemical rates can be inferred from the motility data. However, there is a potential caveat in that most of our data were obtained by using high-density gliding assays where several kinesin molecules drive the microtubules, and it is possible that interactions between motors alter the relationship between the speed and the ATPase rate. We do not believe that this is a problem because several earlier studies have found only a weak dependence of speed on motor number (3, 9, 19) and, furthermore, we have confirmed several key findings by using single-molecule assays.

We considered the three simplest kinetic mechanisms with one substrate and two products: ordered product release with ADP released first, ordered with P_i released first, and random order of release (Table 2). Mechanisms that invoke cooperativity in ATP binding were not considered because no cooperativity was detected. However, we did consider more complex mechanisms in which ATP, ADP, or P_i binding to either head causes dead-end inhibition.

Table 2. Kinetic mechanisms for kinesin and their inhibition patterns.

Order of product release	Kinetic mechanism*	Inhibition pattern†
ADP first	K ↔ K·D·P ↔ K·P ↔ K	M, C
Pi first	K ↔ K·D·P ↔ K·D ↔ K	C, M
	K ↔ K·D·P ↔ K·D
Random	↕ ↕	M, M
	K·P ↔ K

K, kinesin-microtubule complex; D, ADP; P, P_i; C, competitive inhibition; M, mixed competitive and noncompetitive inhibition.

^*The unimolecular reaction K·T ↔ K·D·P has no effect on the pattern of inhibition.

^†The effect of ADP is listed first. See refs. 15 and 18 for details of the steady-state solutions to these schemes.

Of the simplest mechanisms, only one, in which ADP is released before P_i, predicts that ADP will be a mixed inhibitor and P_i will be a competitive inhibitor, as observed (Table 2). The reason is that only in this mechanism do P_i and ATP bind exclusively to the same state (so that P_i inhibition is purely competitive) and ADP binds to a different state (so that ADP inhibition has a noncompetitive component). The other ordered mechanism, with P_i released first, can be ruled out at the 95% confidence level because it fails to account for the reduction in maximum speed by ADP (i.e., the noncompetitive inhibition). The random mechanism is difficult to exclude because it contains a large number of free parameters, and judicial choice of these parameters could lead to a nonzero but not detectable noncompetitive inhibition by P_i. Because it is more complex, and we have no positive evidence for it, we will no longer consider the random mechanism.

In its simplest form, the ADP-released-first mechanism cannot account for the data quantitatively because it predicts too weak a competitive inhibition by ADP. To fit the data, we have to allow ADP to bind to the nucleotide-free state and act as a “dead-end” inhibitor (i.e., ADP has to unbind from the dead-end state before the reaction can proceed). As described below, there is considerable evidence for ADP binding to the nucleotide-free state from other experiments (12, 24). We have tested all 12 extensions of the ADP- and P_i-first mechanisms that include ADP or P_i dead-end binding to either head (i.e., accounting for binding to the passive head in inchworm models), and only the ADP-first mechanism with ADP binding to the nucleotide-free state can quantitatively account for the data.

Hand-over-Hand vs. Inchworm Models. The ADP-released-first model with ADP binding to the nucleotide-free state has been incorporated into the hand-over-hand model shown in Fig. 6. This model is a condensed version of the six-state model proposed by Hancock and Howard (12) and W.R.S. and J.H. (25). In this model, there is very strict coordination (i.e., interaction) between the two heads. To account for this coordination, we postulate that the release of ADP from the forward head creates intramolecular strain within the two-heads-bound state (state 3 of Fig. 6) and that this leads to the detachment of the rear head and release of its P_i.

Several other versions of the hand-over-hand model are consistent with release of ADP before P_i (12, 20, 25–29). Less specific models that allow for ADP-first, P_i-first, or random release (24, 30–32) will now have to be refined in light of our data. Hand-over-hand models requiring ATP-binding to the forward head of the two-heads-bound state [state 3 in Fig. 6 (31, 27)] are unlikely to be correct for the following reasons: (i) at limiting low [ATP], these models are untenable because rear-head detachment and P_i release (state 3 → state 1 in Fig. 6) will occur before ATP can bind to the forward head; (ii) at high [ATP] such models either lead to substrate inhibition if the ATP is not hydrolyzed (i.e., the speed decreases at high [ATP], which is not observed) or to P_i being released before ADP, in contradiction to our results.

The inchworm (10) and other one-headed (17, 33) models are probably not consistent with our data. The reason is that one-headed kinesin likely has an ordered mechanism in which P_i is released before ADP. This is based on the following evidence. First, both monomeric and dimeric kinesin release P_i before ADP in the absence of microtubules (34–36). And second, the myosin motor domain, which has high structural similarity to the kinesin motor domain (37), releases P_i before ADP in both the presence and absence of actin (38). Similarly, G proteins, which also have high structural similarity to the motor domain of kinesin (39), release P_i before GDP (40). Thus, the finding that the release of ADP precedes that of P_i is not readily accounted for by one-headed models. Furthermore, our data are not consistent with inchworm models in which ADP or P_i binding to the passive head inhibits the active head. On the other hand, our data are simply explained by hand-over-hand models in which the release of ADP from one head precedes the release of P_i from the other.

If, in a hand-over-hand mechanism, the two heads of kinesin made identical motions in successive steps, then kinesin would pirouette as it moved along a microtubule, making a 180° rotation for each 8-nm step (41). Such rotation is inconsistent both with multimotor motility (because torsional strain would accumulate) and the single-molecule data of Hua et al. (10). It is therefore likely that the heads make nonidentical motions and that kinesin moves by an asymmetric hand-over-hand mechanism, also called a waddle model (42). Such a mechanism is consistent with all of the existing experimental data, and, if the orientation of the cargo-binding domain is similar between successive steps, this model even accounts for the data of Hua et al. on which the inchworm model was based.

Rate Constants. The ADP-released-first mechanism with dead-end inhibition by ADP (schematized in Fig. 6) provided a good fit to the experiment data. The solid curves in Figs. 2, 4, and 5 correspond to the global fit of this model, and the fit values of the model parameters are collected in Table 3. These fit values, which are in agreement with the measured values shown in Table 1, were used to determine values or bounds for the individual rate constants and the dead-end inhibition constant (Table 4).

Table 3. Parameters of the ADP-released-first mechanism with dead-end inhibition by ADP.

Parameter	Value, mean ± SE
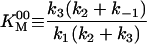	28.7 ± 0.8 μM
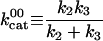	113.9 ± 0.8 s-1
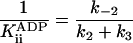	4.4 (±1.6) × 10-5 μM-1
k-3	0.6 ± 0.6 μM-1*
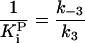	1.0 (±0.1) × 10-4 μM-1
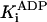	33.1 ± 1.6 μM*
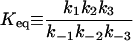	4.9 × 1011 μM†

The values and their uncertainties are obtained from global fits to the data.

^*k_-3 and 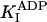were both determined by the competitive inhibition of ADP: .

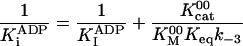^†From ref. 16.

Table 4. Rate constants for the ADP-released-first mechanism with dead-end inhibition by ADP.

ATP binding and hydrolysis, μM-1·s-1	Hydrolysis reversal and ATP unbinding, s-1	ADP release s-1	ADP rebinding, μM-1·s-1	Pi release, s-1	Pi rebinding, μM-1·s-1	Dead-end inhibition constant, μM
k1	k-1	k2	k-2	k3	k-3
4.0 ± 0.1	3.8 × 10-5 (≤7 × 10-4)*	116.3 ± 2.4	0.25 (≥0.02)†	5,600 (≥1,500)†	0.56 (≥0.1)†	33.1 ± 1.6

^*95% confidence upper bound.

^†95% confidence lower bound.

Our rate constants are consistent with almost all those published in the literature. First, the ADP dead-end inhibition constant 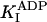= 33 μM is consistent with the dissociation constant for ADP unbinding from the nucleotide-free kinesin-microtubule complex measured by conventional fluorescence techniques [20 μM for recombinant human kinesin (24)] and by single-molecule assays [22 μM, recombinant Drosophila kinesin (12)]. Second, the second-order association rate for ATP binding of 4 μM^–1·s^–1 is consistent with that measured by using stopped-flow techniques [1–2 μM^–1·s^–1, human kinesin (24); 2.0 ± 0.8 μM^–1·s^–1, recombinant Drosophila kinesin (26)]. And third, the rate of ADP release of 116 s^–1 is consistent with stopped-flow measurements made in buffers with similar ionic strengths to those used in these experiments [100–110 s^–1, human kinesin (24), Neurospora kinesin (30)]. Note that other stopped-flow measurements gave faster ADP release rates [300 s^–1, Drosophila kinesin (26, 32)], perhaps because the attachment of the second head (and subsequent ADP release) is accelerated in the low-ionic-strength buffers used in those experiments.

Our analysis provides estimates of several additional rate constants. The unbinding of ATP is very slow, ≤7 × 10^–4 s^–1, and we interpret this as being due to the slow reversal of the hydrolysis step. Our value for the release of P_i and detachment of the rear head is high, >1,500 s^–1, but the ATP-induced detachment of myosin from actin is thought to occur at ≈5,000 s^–1 (43). The second-order rate constant for ADP rebinding of 0.25 μM^–1·s^–1 is a little smaller than that from other labs [e.g., 1.5 μM^–1·s^–1 (24)], but this could be due to their rate corresponding to ADP binding to the one-head-bound state, whereas ours is for ADP binding to the two-heads-bound state (Fig. 6). Importantly, our results support the conclusion that ADP release is rate limiting at low load and high ATP (44).

How the Rate Constants Lead to Precise Chemomechanical Coupling. At physiological ATP, ADP, and P_i concentrations (1, 0.01, and 1 mM respectively), the transitions between the various states (states 1, 2, and 3 in Fig. 6) will occur at the following rates (with units s^–1).

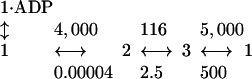[4]

The relative occupancies in the various states [Prob{2} to Prob{1} to Prob{1·ADP} to Prob{3}] are equal to 1 to 0.03 to 0.01 to (0.01–0.1) where we have given a range for the last ratio owing to the experimental uncertainty. Note that state 2 has the highest occupancy because the transition from state 2 to state 3 (attachment of the forward head and release of its ADP) is the rate-limiting step.

We now return to the question asked at the beginning of the Introduction: how does kinesin couple chemical changes to structural changes so that its motion is highly directed and processive? According to the ADP-released-first hand-over-hand model, the motor is highly directional because the hydrolysis cycle is essentially irreversible: the back transitions 2 → 1 and 3 → 2 are very rare. The motor is highly processive because the forward rates through the cycle are much faster than the rates of detachment. Detachment from the rigor state (state 1) is very slow [≈0.001 s^–1 (12)], a million times slower than k₁ (4,000 s^–1 at physiological [ATP]). Dissociation from state 3 is also very slow, because one of the heads is in the rigor state. The crucial step is the transition from state 2 to state 3: its rate of 116 s^–1 is only 100 times greater than the detachment from state 2 [≈1 s^–1 (12)]. For this reason, the ADP-first model predicts that there is only a small probability of both heads detaching during a cycle (≈1%), corresponding to a highly processive motor that takes on average ≈100 steps before dissociating. Thus the ADP-first model accounts for the precision of motility of kinesin under physiological nucleotide conditions. A limitation of this model is that it pertains only to situations where the mechanical load is low; whether the model can account for the precision of kinesin under high loads remains an open question.