A unified pharmacokinetic approach to individualized drug dosing

The ideal in drug therapy is to achieve the right dose, of the right drug, for the right time, in the right patient. Choice of drug dosage regimen in order to achieve optimal drug concentrations in an individual patient is based on the likely pharmacokinetics in that individual. In the case of loading doses it is the volume of distribution (V_d) that is the major determinant, while for maintenance dosing the most important determinant is clearance (CL). The half-life is important for choice of dose interval, time to steady-state and time for drug removal from the body. While the broad approach is well defined, adoption of the principles in clinical practice is far from universal. This is exacerbated by the fact that the details of how V_d and CL are affected by different covariates are often not well defined. A logical approach would assist clinical practice and help direct further research.

The initial doses chosen for an individual are based on an estimate of that individual's likely pharmacokinetic characteristics, usually by utilizing all known information about others in the population who resemble this individual. The population pharmacokinetic values are then adjusted for covariates such as age, weight, gender and any other characteristics that might make the individual different from the mean member of the population.

Underlying this process are simple equations for loading dose (LD), which is based on V_d, and maintenance dose-rate, which is based on CL for drugs with first order elimination. The aim of the LD is to achieve an initial target concentration (C_initial), whereas for the dose-rate it is to achieve a target steady state concentration (C_ss).

(1)

(2)

Both V_d and CL are usually estimated after intravenous administration. If calculated after oral administration then the oral availability needs to be considered. For simplicity in this paper we will ignore oral availability.

These equations can be adjusted to accommodate any factor known to explain some of the variance in V_d or CL. The main covariates of CL are shown in Table 1 and are similar for V_d. Some of these covariates may be interdependent and should not be accounted for twice. It would be useful if the effect of covariates could be incorporated into universal equations for dose-individualization.

Table 1.

Examples of covariates of clearance

Renal function

Hepatic metabolic function

Pharmacogenetics

Gender

Age

Weight

Pharmacokinetic drug interactions

As loading dose is often a single dose only, V_d matters less clinically than CL. The discussion is therefore focussed on CL and maintenance dosing.

Maintenance dose-rate adjustments for covariates of CL

The CL in a given individual (CL_Patient) is approximated by the population mean or median value (CL_Normal) and can be adjusted for covariates when known (see Table 1). Thus:

From the general equation for dose-rate (equation 2), the adjusted dose-rate for the patient to achieve the same C_ss as in the normal patient will be in proportion to the patient's decreased CL. i.e.

(3)

Variation in CL can be profound. For example, the CL of a drug that is entirely eliminated unchanged by the kidneys may vary from 100% in a patient with normal renal function to zero in a patient with absent renal function. Similarly, enzyme induction or gene multiplication can increase the CL of metabolized drugs many fold. It is therefore very important to be able to make dose adjustments based on an estimate of alterations in CL.

In this article, we propose a unified approach to maintenance dosing for adult patients. The approach separates out the two major mechanisms of drug elimination, renal and metabolic, and proposes how dose adjustments can be made for drugs eliminated by either or both mechanisms. For simplicity, it is assumed that the drug itself is the active component, but the principles apply equally to active metabolites.

Towards a universal equation for maintenance dose-rate adjustment

The approach to dose-rate adjustment is most clear for drugs with predominantly renal elimination (high fraction excreted renally unchanged, f_e).This has been summarized recently [1]. Dosing is adjusted for the renal fraction using an estimate of glomerular filtration rate (GFR), e.g. simplified Modification of Diet in Renal Disease equation [2], or a calculated creatinine clearance, e.g. using the Cockcroft & Gault formula [3]. The relative advantages and disadvantages of these methods have been well discussed in the literature.

By contrast with renal elimination, there is no clear index for dose-adjustment of metabolized drugs. This arises from the fact that there is no comparable index to GFR that reflects drug metabolic function. Further, the large number of covariates that alter metabolic function may need to be handled separately, e.g. progressive decline with age vs. quantal changes in relation to pharmacogenetics. A universal equation should be adaptable to handle the different scenarios.

The renal, metabolic and other components of drug elimination

The elimination of drugs is through renal (f_e), metabolic (f_m) and ‘other’ (f_other) mechanisms, as follows:

f_other includes elimination through spontaneous degradation, exhalation or via sweat, etc. For most drugs, this contribution is minor and can be ignored for the purposes of this article. Therefore, for most drugs:

(4)

It is easy to find information on f_e, but less easy to get information on f_m. However, f_m can be inferred from total elimination minus f_e:

It is useful to consider firstly the simple case of a drug with entirely renal elimination (i.e. f_e = 1). In this case, dose adjustment proceeds as follows:

which reduces to the following if f_e = 1:

(5)

The more general equation, for any f_e, and adding metabolic elimination (f_m) is conventionally calculated as follows:

Variation in f_m is often not considered when adjusting for renal function. We propose that it should be, to allow for any decrement in CL by metabolism. In its simplest form, for a drug eliminated entirely by metabolism (f_m = 1), the fractional adjustment can be considered analogous to the approach to drugs that are completely eliminated renally unchanged.

(6)

Many drugs are eliminated by both metabolism and renal elimination, and these can be handled by considering both components.

(7)

This can be considered a basic template for a universal equation for dosing adjustment. The following are some illustrative examples.

Drugs eliminated entirely by renal elimination (f_e = 1)

Atenolol has a f_e that approaches 1 and renal elimination that is entirely dependent upon the GFR. If GFR is calculated as being half normal, then by equation 5 the dose-rate would be reduced in proportion to the decrement in GFR i.e. half normal.

Renal CL of some drugs may also be altered by other processes such as active secretion such as by the organic acid or P-glycoprotein transporters, which may be subject to pharmacogenetic variation or drug interactions. In such cases the extent of these influences should be estimated and used in the dose adjustment.

Drugs eliminated entirely by metabolic elimination (f_m = 1)

For a drug that is completely metabolized, such as azathioprine, the dose is adjusted simply using equation 6. Azathioprine is a prodrug subject to metabolism to 6-thioguanines, which are the major active components. This involves an enzyme, thiopurine methyltransferase (TPMT), which is genetically determined. If the patient has normal genotype (wild type) for TPMT, and their liver function is normal, then normal doses apply. If the patient is homozygous for non-functional alleles, their CL is around one tenth of normal, and the dose-rate needs to be reduced to a one tenth using equation 6. i.e.

Therefore, if the normal dose is 100 mg day⁻¹, the adjusted dose should be 10 mg day⁻¹. With the available tablet form (50 mg, scored) it is not possible to do this simply, but could be approximated by 25 mg (by dividing the scored tablet) on alternate days.

Drugs with a mixture of renal and metabolic elimination

A drug such as ciprofloxacin, with a f_e of 0.5, and a f_m of 0.5 is handled by equation 7. The renal component (f_e) is adjusted by an estimate of the patient's GFR, while the metabolized component (f_m) is adjusted by an estimate of the altered metabolism (by whatever mechanism) in that patient. For example, if f_e is 0.5, f_m is 0.5 and the GFR is reduced by half but the metabolism is normal, the dose adjustment only needs to be made for the renal component, and in this case there would be an overall reduction of 25%. i.e. substituting in equation 7:

Again it may not be possible to achieve this exactly with the standard dosage forms, but a suitable dose regimen can be approximated.

A unifying equation for maintenance dose-rate adjustment based on readily available patient demographics

For drugs that are completely eliminated renally unchanged, estimates of GFR, such as the Cockcroft & Gault formula, include age and gender and often a size descriptor (e.g. weight) as covariates. For these drugs it is only necessary to use equation 5. The situation for metabolized drugs is less defined, but it is possible that age, weight and gender may be involved in like manner.

It is generally agreed that metabolic elimination is impaired in the elderly for high CL (flow dependent) drugs, and for low CL drugs with low protein binding [4]. However, there have been conflicting findings in relation to low CL drugs that are highly protein bound [5]. We believe that the conflicting findings are an artefact of assessment of total drug CL (CL_total), whereby decreased intrinsic CL, which would raise total concentrations, is offset by decreased protein binding, which would lower total concentrations, resulting perhaps in no net change. If unbound drug CL (CL_u) is measured, then a consistent decrease is observed for most drugs studied [5]. This allows the interesting prospect of a universal rule for metabolic drug CL in the elderly i.e. that there is an age-dependent decrease in metabolic CL for all drugs. Furthermore, the extent of the decrease in all three cases (high CL drugs, low CL drugs with low protein binding and low CL drugs with high protein binding) is remarkably similar, at around 30–50%, or an average of 40%, from age 40 to 80 years [5]. From this, and assuming a linear decline, a mean value of around 1% decline per year after the age of around 40 years can be used. An age correction factor to allow for this is thus hypothesized, for patients aged 40 years or over:

The age correction factor we propose, i.e. 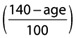, is based on our evaluation of the literature. This applies only to patients aged >40 years. If the patient is aged ≤40 years then the age correction factor can be replaced by 1. Others may disagree with the numbers involved, or may not accept our argument that all drug metabolism is affected by the same amount. The exact value, or method of calculating it, lends itself to further discussion and study. It is the principle of considering age as an important cause of possible variance that we are advocating.

If the logic of this background is accepted, and there is no additional reason for impaired metabolic function (e.g. hepatic failure) a simple index can be derived that allows appropriate dose-adjustment for metabolized drugs (f_m = 1) for any age above 40 years. This index (age is in years) can replace the right side of equation 6:

This means that, other things being equal, the average 80 year old should have a dose-rate around 60% of that in an average 20–40 year old who has normal metabolism for the particular drug. Obviously, this is an a priori dose-adjustment factor for a ‘mean’ member of the population, and it assumes a 1% decrement per year for every metabolic process. Clearly, there may be differences between different paths of metabolism, such as different cytochrome P450 enzymes (CYPs) or CYPs vs. glucuronidation. If the specific effect of age on CL related to a particular metabolic process is known for a particular drug, then the age correction factor can be adjusted appropriately, but the logic still applies. Any dose-adjustment should also take into account other covariates (as in any dose-adjustment situation) such as from Table 1.

For drugs that have both metabolic and renal elimination, the age correction factor can become an adjustment for the metabolized component in equation 7:

(8)

There may be other covariates that can be included within either bracket in equation 8. A useful covariate that could be added to the adjustment to the f_m is weight, which is already considered by some formulae for GFR such as that of Cockcroft & Gault.

Anderson & Holford [6] have shown that CL may be related to weight by a power function by the principle of allometric scaling i.e.

If W_Normal is considered to be 70 kg, then

Thus, the factor can be included in equation 8 above. Thus, equation 8 becomes:

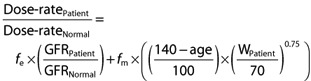(9)

For the renal component, GFR_Normal could be replaced by 100 if the Cockcroft & Gault formula was used to estimate GFR (units in ml min⁻¹).

In practice, most drugs are primarily cleared almost entirely by either renal (10% of drugs) or metabolic (70% of drugs) pathways [7], which allows simplification of equation 9 to the following pair of equations:

for renally cleared drugs and

for metabolically cleared drugs.

Examination of equation 9 yields some interesting findings that may direct further research. Firstly, the factors age and weight involved in the metabolic correction factor and the renal correction factor are similar. The renal correction factor, based on the GFR, also includes gender. The allometric scaling method of Anderson & Holford [6] assumes that the effects of gender are largely related to differences in weight and can be accommodated by a function based only on weight. It would be possible of course to have a separate weight descriptor for each gender. For example it has been argued that CL should relate best to lean body weight, as both are dependent on protein synthesis [8]. Since lean body weight as a fraction of total weight is lower in females, then there would be a separate adjustment factor for males and females if lean body weight was used. The metabolic adjustment factor in equation 9 does not include any biomarker for metabolic function. This is because there is no such predictive metabolic biomarker that is as useful as creatinine is as a renal biomarker. Serum albumin concentration is a potential candidate, based on the fact it may reflect liver enzyme synthetic activity. This could be the subject of more research.

The influences of other covariates on metabolism can be added to provide an increasingly complete picture of the patient's likely overall metabolic correction factor. Other factors noted above such as pharmacogenetics, drug interactions, and the effects of impaired hepatic function or other disease states could also be included. The extent of each effect will often be a best guess, where specific information is not available.

Equation 9 is contingent upon a number of assumptions. Oral availability has been assumed to be 100% for the sake of simplicity, but actual values and deviations from these could be accommodated using first principles. Renal clearance and metabolic clearance are assumed to be independent of each other, which may not always be so. The use of GFR to modify the f_e component assumes that the intact nephron theory holds true, such that other renal clearance pathways besides glomerular filtration, such as active transport, are reflected by the GFR. There are assumptions related to the f_m component of equation 9. The age correction factor assumes that the decline in metabolic clearance begins at 40 years, that the decrement is 1% per year and that there is no clear upper end of the age range. Allometric scaling according to weight makes the broad assumption that body size corresponds to body composition. Further, 70 kg is assumed to be the normal weight.

There are a number of practical limitations to the application of equation 9. The calculated adjusted doses may not be able to be accommodated precisely with available dose formulations and rounding may be necessary. Further, while we believe equation 9 is useful for most drug classes, we are unsure of its applicability to biological drugs such as antibodies.

Application of the above approach is likely to improve therapeutics. It is a starting point only, is pharmacokinetically based and is contingent upon various assumptions. Furthermore all other considerations for dose-individualization still apply, such as pharmacodynamic aspects. The approach also highlights areas of potential further research, in order to define the magnitude of likely alterations in CL related to all covariates.

Conclusion

A unified approach to individualizing drug dosing is proposed that allows maintenance dose-rate to be adjusted for altered drug metabolism and renal elimination. The general template for this is:

or:

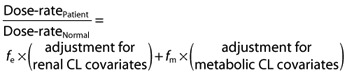The adjustment for renal CL covariates is usually a formula for estimation of GFR, such as the Cockcroft & Gault formula, which incorporates age, weight, gender and serum creatinine concentration. We propose a similar adjustment process for the metabolic CL covariates, utilizing age and weight. In the following formula, W is in kg and normal weight is assumed to be 70 kg. If the patient is aged ≤40 years, the age correction factor 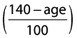can be replaced by 1.

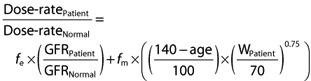In practice, since the majority of drugs can be considered to be eliminated either metabolically or by renal elimination, the dose adjustment for drugs eliminated primarily unchanged by the kidneys is:

and for drugs eliminated primarily by metabolism:

Competing Interests

There are no competing interests to declare.