Mechanism-based population pharmacokinetic modelling in diabetes: vildagliptin as a tight binding inhibitor and substrate of dipeptidyl peptidase IV

Abstract

AIMS

To assess the pharmacokinetics of vildagliptin at different doses and build a mechanism-based population model that simultaneously describes vildagliptin pharmacokinetics and its effects on DPP-4 activity based on underlying physiology and biology.

METHODS

Vildagliptin concentrations and DPP-4 activity vs. time from 13 type 2 diabetic patients after oral vildagliptin 10, 25 or 100 mg and placebo twice daily for 28 days were co-modelled. NONMEM VI and S-ADAPT were utilized for population modelling.

RESULTS

A target-mediated drug disposition (TMDD) model accounting for capacity-limited high affinity binding of vildagliptin to DPP-4 in plasma and tissues had good predictive performance. Modelling the full time course of the vildagliptin-DPP-4 interaction suggested parallel vildagliptin dissociation from DPP-4 by a slow first-order process and hydrolysis by DPP-4 to an inactive metabolite as a disposition mechanism. Due to limited amounts of DPP-4, vildagliptin concentrations increased slightly more than dose proportionally. This newly proposed model and the parameter estimates are supported by published in vitro studies. Mean parameter estimates (inter-individual coefficient of variation) were: non-saturable clearance 36 l h⁻¹ (25%), central volume of distribution 22 l (37%), half-life of dissociation from DPP-4 1.1 h (94%) and half-life of hydrolysis 6.3 h (81%).

CONCLUSIONS

Vildagliptin is both an inhibitor and substrate for DPP-4. By utilizing the TMDD approach, slow dissociation of vildagliptin from DPP-4 was found in patients and the half-life of hydrolysis by DPP-4 estimated. This model can be used to predict DPP-4 inhibition effects of other dosage regimens and be modified for other DPP-4 inhibitors to differentiate their properties.

WHAT IS ALREADY KNOWN ABOUT THIS SUBJECT

• Vildagliptin is a novel antidiabetic agent that acts by inhibiting dipeptidyl peptidase IV (DPP-4).

• DPP-4 inhibition results in higher active concentrations of incretin hormone, glucagon-like peptide 1 (GLP-1), leading to reduced glucose concentrations.

• Mechanism-based modelling of the pharmacokinetics (PK) of vildagliptin and its DPP-4 inhibition effects in type 2 diabetic patients has not been performed.

WHAT THIS STUDY ADDS

• Population pharmacokinetic modelling of the vildagliptin concentrations from three different doses indicated the presence of a small saturable elimination pathway for vildagliptin.

• Simultaneous population modelling of the pharmacokinetics and DPP-4 activity in patients with type 2 diabetes after treatment with vildagliptin revealed:

  1. Saturable binding of vildagliptin to DPP-4 in plasma and tissues and partial hydrolysis of vildagliptin by DPP-4.

  2. Vildagliptin is both an inhibitor and a substrate for DPP-4.

Introduction

Vildagliptin is a novel antidiabetic agent which belongs to the dipeptidyl peptidase IV (DPP-4) inhibitors and acts on the incretin system [1]. Glucagon-like peptide 1 (GLP-1) which is an incretin hormone is released from the L-cells in the gut wall after food ingestion. GLP-1 stimulates insulin secretion and inhibits glucagon secretion, but is eliminated rapidly by DPP-4 [2]. DPP-4 inhibition by vildagliptin therefore results in higher active GLP-1 concentrations and decreased glucose concentrations [3]. The pharmacokinetics (PK) of vildagliptin in diabetic patients and its effect on DPP-4 activity have not been modelled previously.

In a previous report, vildagliptin PK was assessed in diabetic patients using non-compartmental analysis (NCA) [4]. Standard NCA is an adequate method for preliminary exploration of the PK of a drug. However its value is limited in the potential presence of non-linear PK and if the relationship between drug concentrations and effects are studied based on the mechanism of action of the drug [5]. In contrast to compartmental modelling, the NCA cannot predict the DPP-4 activity vs. time profiles for other than the studied dosage regimens.

Mechanism-based compartmental modelling can explicitly account for the full time course of both drug concentrations and effects simultaneously for all doses and placebo (or baseline). In contrast to empirical models, mechanism-based models are more powerful at aiding understanding of the underlying kinetic mechanism and proposing likely mechanisms of action for a particular drug. They can be expanded to include additional physiological subsystems and support simulation of ‘what if’ scenarios. A mechanism-based model can be ultimately used in pharmacodynamic (PD) simulations to predict the probability of successful outcome of anti-diabetic treatment for different dosage regimens of a drug. In addition compartmental modelling by the full population approach utilizing state-of-the-art methodology, as reported here, takes into account between subject variability in both PK and drug effects.

The aims of our study were to assess the PK of vildagliptin at different dose levels by population PK modelling and to develop a mechanism-based population model that simultaneously describes the PK of vildagliptin and its effects on DPP-4 activity based on the underlying physiology and biology.

Methods

The study design and bioanalytical methods are briefly described below. A detailed report is provided in [4].

Study participants

The study included 13 patients with type 2 diabetes. The subjects had diabetes for at least 3 months prior to screening. A washout period from hypoglycaemic drugs for up to 4 weeks was required. All subjects had to undergo safety evaluations before, during and after the study. All adverse events were monitored and recorded and regular checks of blood and urine chemistry, vital signs and physical examination were conducted. All subjects gave their written informed consent. The study was approved by the local ethics committee and conducted in full compliance with the Declaration of Helsinki.

Study design and drug administration

A randomized, placebo-controlled, double-blind, four-way crossover study was conducted. The subjects received twice daily oral doses of 10, 25, and 100 mg vildagliptin (Galvus™) and placebo as tablets for 28 days. Patients were at the study site on day 1 and from the evening of day 26 to the morning of day 29 in each study period. During the confined periods the patients received a standard diet with identical meals for all four treatments. Breakfast and dinner were consumed at approximately 30 min after the doses. Subjects were requested to abstain from strenuous physical exercise and alcohol throughout the study and from xanthine-containing foods and beverages during the sampling periods.

Sampling schedule and bioanalysis

Blood samples for measurement of vildagliptin concentrations were obtained on day 28 of each period pre-dose and at 0.25, 0.5, 1, 1.5, 2, 3, 5, 8, 10, 11, 12, 16 and 24 h after the morning dose. Blood samples for determination of DPP-4 activity were collected prior to dosing and at 0.25, 0.75, 1, 2, 4, 5, 6, 7, 8, 10, 10.5, 11, 12, 14, 16 and 24 h after the morning dose. All samples were centrifuged and plasma was frozen at −70°C or lower until analysis.

Vildagliptin concentrations in plasma were determined by liquid chromatography-tandem mass spectrometry. The lower limit of quantification (LLQ) was 2 ng ml⁻¹, inter-day precision was 1.8−3.9% and accuracy was 99.1−104.5%. DPP-4 activity was measured by use of H-Gly-Pro-7-amino-4-methylcoumarin, which is cleaved by DPP-4 to yield the fluorescent product 7-amino-4-methylcoumarin. The LLQ for DPP-4 activity was 0.24 mU ml⁻¹ min⁻¹, inter-day precision was 3.6−7.9% and accuracy was 96.4−107.2%.

Data from absolute bioavailability study

In the process of PK model development, data from healthy volunteers after a single intravenous dose of 25 mg vildagliptin [6] were modelled simultaneously with the vildagliptin concentrations after oral administration from the type 2 diabetic patients. The intravenous data were included during model building to distinguish between elimination and absorption rate constants, and between distribution and absorption rate constants. The clearances and volumes were similar for models with and without the intravenous data. For the combined PK/PD model the bioavailability was fixed to the estimate from co-modelling intravenous and oral data. There was no indication for a change of bioavailability with dose and therefore bioavailability was assumed to be constant for the range of doses investigated.

Data analysis

The model for PK and DPP-4 activity was first developed utilizing the first order conditional estimation method (FOCE) with interaction in NONMEM VI version 1.1 [7]. For the combined PK/PD model including vildagliptin PK, DPP-4 activity, active GLP-1, glucose and insulin, S-ADAPT version 1.56 [8] was utilized due to the high level of complexity and long computation times. The PD part of the model, including active GLP-1, glucose and insulin, is described in the companion manuscript [9]. The parameter estimates and visual predictive checks of the PK and DPP-4 portions from simultaneous modelling of the full PK/PD model in S-ADAPT are shown in this report.

The PK and DPP-4 profiles from the three different dosing regimens and placebo from all patients were modelled simultaneously. Model discrimination was based on the following criteria: 1) visual inspection of the observed and predicted profiles, 2) visual comparison of the patterns of systematic and random residuals, 3) the objective function in NONMEM or S-ADAPT, 4) visual predictive checks and 5) precision of parameter estimates.

For the visual predictive checks, plasma concentration and DPP-4 activity time profiles were simulated for 5000 subjects in NONMEM or S-ADAPT for each competing model. From these data we calculated the median and the nonparametric 80% prediction interval (10% to 90% percentile) for the predicted vildagliptin concentrations and DPP-4 activity. These prediction interval lines were then overlaid on the observed data. If the model described the data adequately, then 10% of the observed data points should be below the 10^th percentile and 10% of the observed data points should be above the 90^th percentile over all time points. The median predicted concentrations and the 80% prediction interval were visually compared with the observed data. Competing models were examined to assess whether the median and the 80% prediction interval adequately mirrored the central tendency and the variability of the observed data.

Standard errors as a measure for precision of parameter estimates were obtained from the full PK/PD model by utilizing the type 1 bootstrap method as implemented in S-ADAPT [8]. By this method sets of patients are randomly selected from the dataset, and while refits of population parameters are not performed, the new population parameters and their variances are obtained from averaging the individual parameters and their intra-individual covariance matrices. The errors were obtained from 200 bootstrap runs. Performing a full bootstrap including refitting of population parameters was not feasible due to long run times of the full PK/PD model.

Structural models

One-, two- and three-compartment disposition models were tested for modelling the vildagliptin concentrations. The drug input was modelled as first order absorption with a lag time or an additional lag compartment for the absorption. The presence of target-mediated drug disposition (TMDD) was not suspected a priori for a small molecule drug such as vildagliptin. Therefore, initial attempts were made to explain nonlinearity in PK and explore potential reasons for the nonlinearity. Models with different bioavailabilities and absorption rate constants for the three different doses could not adequately describe the data. In addition models with three different volumes of distribution or three different clearances and models with linear, saturable and parallel linear and saturable elimination were tested.

For the effect of vildagliptin on DPP-4 activity, a simple I_max model and various models for TMDD [10, 11] were tested. The TMDD model had two disposition compartments for vildagliptin. Different structures of the TMDD model were tested: 1) binding of vildagliptin to DPP-4 only in the central compartment, 2) binding of vildagliptin in the central compartment to both DPP-4 in the central compartment and DPP-4 in the peripheral compartment and 3) binding of vildagliptin to DPP-4 in the central compartment and binding of vildagliptin to DPP-4 in the peripheral compartment. The structure of our final TMDD model is shown in Figure 1.

Figure 1.

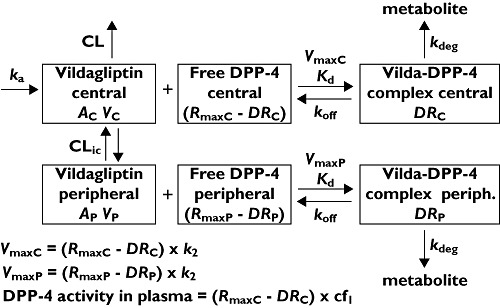
Model diagram. Symbols are defined in Table 1

Changes in amounts of vildagliptin in the gut compartment (A_G1, nmol) and initial conditions are:

where k_a1 is the first-order absorption rate constant (h⁻¹).

In order to describe a time lag in absorption, we included a second (sequential) absorption compartment (A_G2, nmol). This was numerically more stable than including a lag-time. The k_a1 was estimated as the sum of k_a2+dk_a with dk_a constrained to positive values to retain identifiability of the two absorption rate constants.

The amount of vildagliptin in the central (or plasma) compartment (A_C, nmol) is

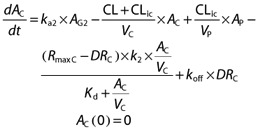where CL is the non-saturable linear clearance (l h^–1), CL_ic is the inter-compartmental clearance (l h^–1), V_C the central volume of distribution (l), V_P the volume of the peripheral (tissue) compartment (l), R_maxC the total amount of DPP-4 in V_C (nmol), DR_C the amount of vildagliptin – DPP-4 complex in V_C (nmol), k₂ the first order rate constant for conversion of the low affinity complex to the high affinity complex (h⁻¹), K_d the equilibrium dissociation constant (nmol l^–1), and k_off is the first order rate constant for dissociation of intact vildagliptin from DPP-4 (h⁻¹).

The equation for slow tight binding of vildagliptin was used to account for the fact that the rate constant for binding (k_on) changes with vildagliptin concentration. The k_on can be calculated as

The parameter k₂ is included in the model due to the slow tight binding of vildagliptin to DPP-4.

The maximum rate of binding of vildagliptin to DPP-4 in the central compartment (V_maxC, nmol h^–1) depends on the amount of free DPP-4 and can be calculated as

The amount of vildagliptin in the peripheral (or tissue) compartment (A_P, nmol) is

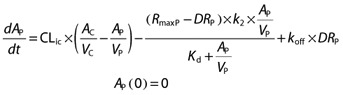where R_maxP is the total amount of DPP-4 in V_P (nmol), and DR_P the amount of vildagliptin – DPP-4 complex in V_P (nmol). The maximum rate of binding of vildagliptin to DPP-4 in the tissue compartment (V_maxP, nmol h^–1) can be calculated as

The amount of vildagliptin – DPP-4 complex in V_C (DR_C, nmol) is

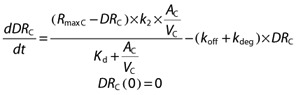where k_deg is the first order rate constant for hydrolysis of vildagliptin by DPP-4 (h⁻¹).

The amount of vildagliptin – DPP-4 complex in V_P (DR_P, nmol) is

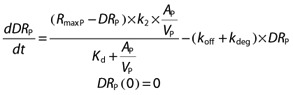The DPP-4 activity (mU ml^–1 min⁻¹) in the central (or plasma) compartment is calculated as

where cf₁ is the conversion factor between the free DPP-4 enzyme and DPP-4 activity. This output equation links the DPP-4 activity measured in plasma to the estimated time course of free DPP-4 in the central (plasma) compartment.

Between-subject variability model

The between-subject variability (BSV) was estimated for all parameters. A log-normal distribution was assumed for the PK parameters and a full variance-covariance matrix for the PK parameters was included in S-ADAPT. For convenient interpretation, the square root of the variance is reported for BSV, as this is an approximation to the apparent coefficient of variation of a normal distribution on log-scale. It was not feasible to include between-occasion variability (BOV) in the model due to high model complexity and long run times. The PK and PD (reported in the companion manuscript [9]) parts of the model were estimated simultaneously and including BOV would considerably increase the already long run times. In addition BOV should be used with caution in models including nonlinear PK, in order to prevent masking of potential systematic differences between the dose levels.

Residual error model

The residual unidentified variability was described by a combined additive and proportional error model for both vildagliptin concentrations and DPP-4 activity.

Results

Twelve subjects completed all four periods of the study and one patient only completed the 10 and 25 mg treatments. The average (range) weight was 91 (65–116) kg, height was 166 (148–183) cm and age was 53.5 (37–64) years. Six patients were male and seven were female.

The individual observed vildagliptin concentrations on day 28 of twice daily oral dosing are shown in Figure 2. For the 10 mg dose all concentrations at 10 h after each dose were below the limit of quantification (LOQ) of 2 ng ml⁻¹. For the 25 mg dose only part of the concentrations were below the LOQ. One subject had extremely high concentrations after the morning dose of 25 mg vildagliptin for unknown reasons and those results were included in the population analysis, although this resulted in an increased residual error for PK. Plotting the dose-normalized vildagliptin concentration−time profiles after all three doses for each individual subject revealed a faster decline with the two lower doses compared with the 100 mg dose (Figure 2D).

Figure 2.

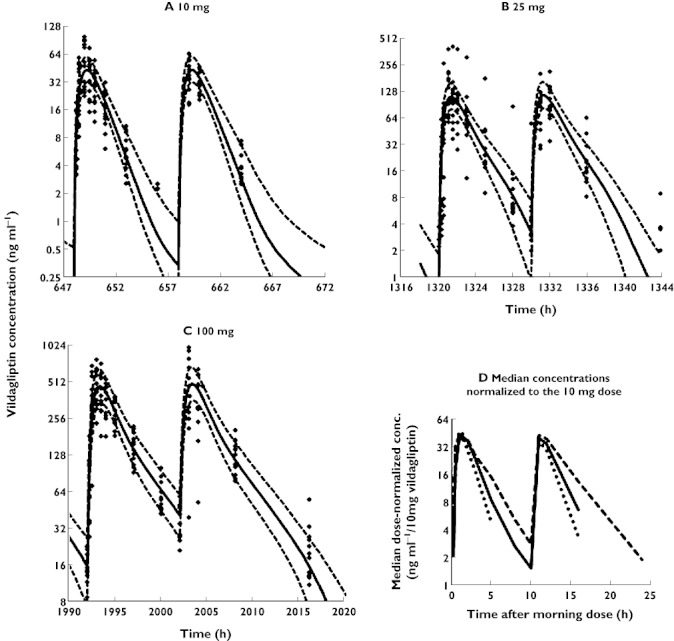
(A–C) Visual predictive checks for plasma concentrations of vildagliptin. The plots show the observed data (filled diamonds), the median predicted concentrations (solid line) and the 80% prediction interval (10–90% percentile, broken lines). In order to show all data from each dose level in the same plot it was assumed in the graphs that all virtual subjects received the doses in the same sequence. The doses on the observation days as shown in the figure were at 648 and 658 h for the 10 mg dose, 1320 and 1330 h for 25 mg and 1992 and 2002 h for 100 mg. The actual sequence of dosing in the randomized clinical trial for each individual patient was observed for all estimation model runs. (D) Median vildagliptin concentrations normalized to the 10 mg dose. Only four of 13 patients had a quantifiable concentration at 8 h after the 10 mg dose and only five of 13 patients had a quantifiable concentration at 24 h after the 25 mg dose. Those two time points were left out of the figure as otherwise the slopes of the curves would be biased. 10 mg (); 25 mg (); 100 mg ()

Observed DPP-4 activity after placebo and the three different vildagliptin doses is shown in Figure 3. For the placebo treatment the DPP-4 activity was relatively constant throughout the observation period, both overall and when considering the individual patients separately. For the population analysis three data points from three different patients during the placebo period were considered outliers and excluded from the analysis (DDP-4 activity 0.59, 1.4 and 5.3 mU ml⁻¹ min⁻¹) as no rational explanation was available for these low values.

Figure 3.

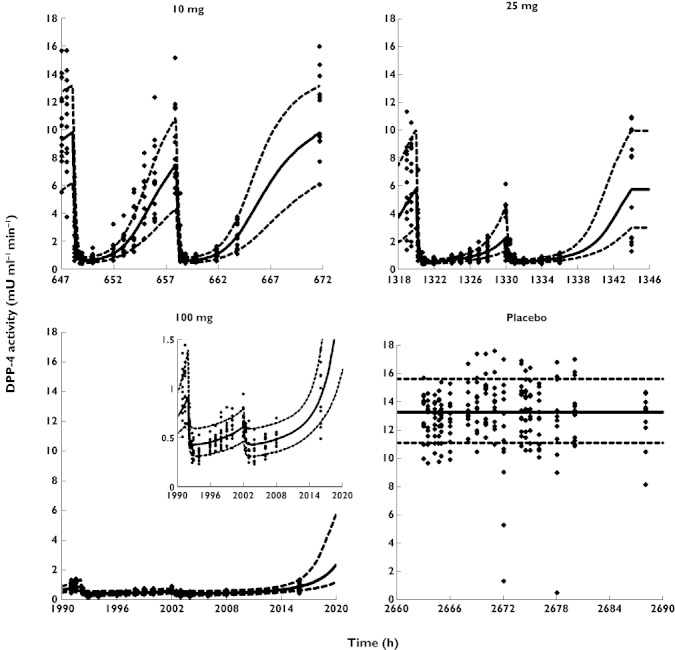
Visual predictive checks for DPP-4 activity. Symbols and x-axes are explained in Figure 2

After vildagliptin treatment the DPP-4 activity decreased with increasing vildagliptin concentrations and recovered when the vildagliptin concentrations were declining for all three doses. After the 100 mg vildagliptin dose the DPP-4 activity was inhibited almost completely over the entire 24 h observation period, which showed prolonged inhibition of DPP-4 by vildagliptin.

Non-compartmental analysis

The results from the NCA are reported by He et al. [4]. Average terminal half-life increased with dose from 1.32 h at the 10 mg dose to 2.43 h at the 100 mg dose, while clearance calculated from dose/AUC decreased from 84.0 l h⁻¹ at 10 mg to 53.5 l h⁻¹ at the 100 mg dose, indicating the presence of saturable elimination.

Compartmental modelling

The newly developed model which includes capacity-limited high-affinity binding of vildagliptin to DPP-4, parallel vildagliptin dissociation from DPP-4 by a slow first-order process and hydrolysis by DPP-4 to an inactive metabolite adequately describes the observed PK and DPP-4 activity. The visual predictive checks showed excellent predictive performance for both PK and DPP-4 activity for the three different doses and placebo (Figures 2 and 3).

The parameter estimates, their BSV and standard errors (SE) as a measure for precision are reported in Table 1. In the final model vildagliptin absorption could be described by dose-independent F and k_a parameters. A slight absorption delay was described by a lag time for absorption.

Table 1.

Population parameter estimates for vildagliptin pharmacokinetics

Parameter (units)	Definition	Estimate	BSV (%)	SE†(%)
CL (l h–1)	Non-saturable vildagliptin clearance	36.4	25	9
VC (l)	Volume of central compartment	22.2	37	11
VP (l)	Volume of tissue compartment	97.3	37	13
CLic (l h–1)	Intercompartmental clearance	40.1	34	11
ka1 (h−1)	Absorption rate constant	1.26	46	15
ka2 (h−1)	Absorption rate constant	1.05	14	4
F (%)	Bioavailability	77.2*	–	–
Kd (nmol l–1)	Equilibrium dissociation constant	71.9	54	16
k2 (h−1)	Rate constant for conversion of weak complex to high-affinity complex	23.4	70	22
koff (h−1)	Dissociation rate constant of intact vildagliptin from DPP-4	0.612	94	27
kdeg (h−1)	Rate constant for hydrolysis of vildagliptin by DPP-4	0.110	81	26
RmaxC (nmol)	DPP-4 in VC	5.0	12	4
RmaxP (µmol)	DPP-4 in VP	13.0	64	23
cf1 mU ml−1 min−1 nmol−1	Conversion factor between free DPP-4 enzyme and observed DPP-4 activity	2.80	17	5
CVVilda (%)	Proportional error for vildagliptin	48.7
SDVilda (ng ml–1)	Additive error for vildagliptin	0.99
CVDPP-4 (%)	Proportional error for DPP-4 activity	19.6
SDDPP-4 (mU ml–1 min−1)	Additive error for DPP-4 activity	0.061

^*Fixed to the estimate from the model including i.v. vildagliptin data.

^†Standard errors (SE) were obtained by bootstrap method 1 as implemented in S-ADAPT and are reported as coefficients of variation (%). Standard errors for BSV parameter estimates were between 25 and 57%.

The estimate for k_deg was 0.110 h⁻¹, which corresponds to a half-life for metabolism of vildagliptin by DPP-4 of 6.3 h. The estimate for k_off was about 5.6 times as high as k_deg, predicting that only a small part of the dose was metabolized by DPP-4 and the majority of the vildagliptin molecules dissociated unchanged from the vildagliptin-DPP-4 complex. Based on simulations, vildagliptin clearance was approximately 74 l h⁻¹ at an extremely low dose of 1 µg, suggesting that as vildagliptin concentrations approach zero the saturable clearance accounts for approximately half of total clearance. After a single dose of 100 mg, total clearance was 42.4 l h⁻¹ and the saturable clearance by DPP-4 accounted for approximately 14% of total. When concentrations approach infinity, total clearance approaches 36.4 l h⁻¹, the estimate for the non-saturable clearance.

The apparent amount of DPP-4 in the tissue compartment is estimated to be much higher (perhaps > 2000-fold) than in the central compartment, based on the population parameter estimates for R_maxC (5 nmol, BSV 12%, SE 4%) and R_maxP (13 µmol, BSV 64%, SE 23%). This suggests that the capacity of DPP-4 inhibition at the tissue level may be much higher than observed in plasma, and the tissue compartment is responsible for most of the non-linearity seen in vildagliptin PK. However the estimates for R_maxC and R_maxP as apparent amounts of available DPP-4 in the absence of vildagliptin should be interpreted carefully and might not represent the actual amounts of enzyme in plasma and tissue, as amounts of DPP-4 in plasma or tissue and DPP-4 activity in tissues were not available, and the factor cf₁ was estimated to relate measured DPP4 activity to R_maxP. In addition, estimates of R_max do not take into account, for example, spare receptors or effects of endogenous ligands [11]. Sensitivity analyses where R_maxC was fixed to several different higher values than the current estimate resulted in inadequate description of the observed DPP-4 activity profiles over time.

Signature profiles for vildagliptin and the vildagliptin-DPP-4 complex in the central and peripheral compartment based on model simulations are shown in Figure 4. Simulations suggest that the apparent amount of vildagliptin-DPP-4 complex is almost constant over the observation period in both compartments for the 100 mg dose and, therefore, DPP-4 activity is almost completely inhibited. Based on the simulations, DPP-4 enzyme in plasma is saturated at lower vildagliptin doses. However, the capacity of DPP-4 inhibition is larger in tissues due to the larger amount of enzyme available and therefore most of the non-linearity in PK is explained by DPP-4 inhibition in tissues in the model.

Figure 4.

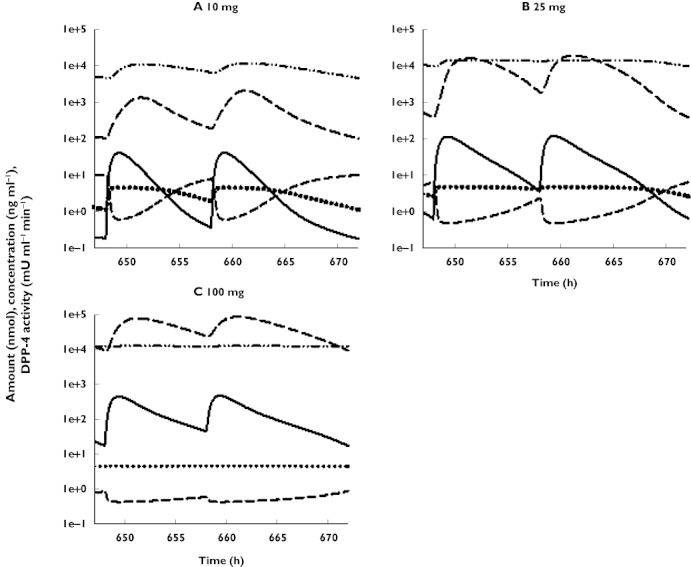
Simulations showing indicated model components vs. time for the three doses of vildagliptin. Vildagliptin central (ng ml⁻¹) (); DPP4 activity central (mU ml⁻¹min) (); Vildagliptin peripheral (nmol) (); Vilda-DPP4 complex central (nmol) (); Vilda-DPP4 complex peripheral (nmol) ()

Discussion

Overall diabetes has prevalence worldwide and approximately 50% of the population is likely to suffer from diabetes in 2050. Vildagliptin belongs to the DPP-4 inhibitors, one of the more recently introduced classes of antidiabetic agents. In this report the PK and effect on DPP-4 activity of vildagliptin is described and it is shown that insights into the mechanism of action of a drug in patients with type 2 diabetes can be gained by mechanism-based mathematical modelling. Population modelling of vildagliptin PK revealed slightly non-linear PK and co-modelling with data from the i.v. study suggested the existence of a deep peripheral compartment, such as may be observed due to binding in tissues. Vildagliptin, as a small molecule, was not expected a priori to exhibit TMDD, including metabolism by its own PD target. However, such a model could describe the data and results from a rat study which has meanwhile been published [12] confirmed DPP-4 as likely being responsible for part of vildagliptin elimination. In addition the slow tight binding found in in vitro studies could be confirmed also in humans and was necessary to be included into the model in order to describe the DPP-4 activity profiles. The current model allows quantification of the processes between vildagliptin and DPP-4.

Models for TMDD have been developed earlier [11] and were most frequently applied to large molecules such as interferons and monoclonal antibodies [13]. Such TMDD models describe the case that the PK of a drug is affected by binding of the drug to its target, with or without elimination of the drug through this process. Compared with those described earlier, our TMDD model for the current study required additional complexities: concentration dependent and slow tight binding of vildagliptin to DPP-4, and binding in tissues in addition to plasma.

A model with a simple k_on parameter for first order non-saturable binding, as generally utilized in TMDD models, did not result in adequate fittings of the DPP-activity vs. time profiles. Therefore, the concentration dependent, slow-tight added complexity was necessary for our model. The equations for binding of vildagliptin to DPP-4 were based on the Michaelis-Menten equation. Such an equation describes the situation that, upon binding of a substrate or inhibitor to the enzyme, first a low affinity complex is formed which is then converted to the final high affinity complex in a second step. As concluded from in vitro studies, vildagliptin is a slow-tight binding inhibitor with a two-step binding mode and saturable binding [14]. Preliminary modelling of the vildagliptin concentrations from the present study together with i.v. vildagliptin data indicated the presence of a deep third disposition compartment, which is in agreement with tight binding of vildagliptin to DPP-4 in tissues. The binding of DPP-728, a DPP-4 inhibitor with a similar molecular structure to vildagliptin, to DPP-4 in an in vitro study was fitted by the Michaelis-Menten equation [15]. Such slow and tight binding of vildagliptin to DPP-4, especially in tissues (simulations shown in Figure 4), as described by a Michaelis-Menten type process might reflect the sustained DPP-4 inhibition irrespective of the short half-life of 2 h in plasma.

Another complexity was to include the binding and metabolism of vildagliptin in both plasma and tissues. While the DPP-4 activity was measured only in plasma and it is not feasible to measure DPP-4 activity in tissues in a clinical trial, most DPP-4 actually resides in tissues [16]. In rats the measured DPP-4 activity per g of tissue was several thousand times higher than the activity per g of serum [16]. A model with binding of vildagliptin to and metabolism by DPP-4 only in plasma could not adequately describe the observed DPP-4 activity profiles. While the actual amount of DPP-4 in plasma was not known, the estimated apparent amount of DPP-4 in plasma available to metabolize vildagliptin was not large enough to account for the vildagliptin concentrations increasing slightly more than proportionally with dose. In addition, the total volume of distribution of vildagliptin at steady-state after i.v. administration to humans was 71 l [6], which indicates extensive tissue distribution and further supports the incorporation of the tissue vildagliptin DPP-4 interaction in the model. Overall, including the second part of the TMDD model which describes the interaction between vildagliptin and DPP-4 in tissue was necessary to describe adequately the nonlinearity of vildagliptin PK.

Mechanism-based population modelling of both vildagliptin concentrations and DPP-4 activity suggested that binding of vildagliptin to DPP-4 and partial metabolism by its pharmacodynamic target DPP-4, both in plasma and tissues, is responsible for the observed greater than proportional increase of vildagliptin concentrations with increasing dose. This proposed mechanism is supported by the findings of an in vitro microsomal and an in vivo metabolism study in DPP-4 deficient rats that received a large dose of 3 mg kg⁻¹ vildagliptin [12]. Those studies suggest that 20% of the cyano group hydrolysis is likely attributed to DPP-4 [12]. The cyano group hydrolysis forms the metabolite M20.7 and is the major elimination pathway of vildagliptin in rats and humans. It accounted for 56.5% of vildagliptin elimination in humans after a single dose of 100 mg [17]. In rats M20.7 represented 54% of the AUC in plasma [12]. Therefore DPP-4 may account for >10% of the elimination of vildagliptin at relatively high doses. This elimination process is likely to be saturable, as our model was able to explain adequately vildagliptin PK and DPP-4 activity after inclusion of capacity-limited elimination of vildagliptin by DPP-4 (as described by k_deg in the model diagram). Model predictions suggested a virtually constant amount of the drug-enzyme complex and therefore saturation of vildagliptin binding to and elimination by DPP-4 at the 100 mg dose. Simulations from our newly developed mechanism-based model suggest that around 14% of vildagliptin is metabolized by DPP-4 in humans after a single dose of 100 mg. This is consistent with the results observed in animals [12], as described above. Also the first order rate constant for dissociation of vildagliptin from DPP-4, k_off, which was estimated at 0.61 h⁻¹ (reflecting a dissociation half-life of 1.13 h) falls well within the range of 0.3 to 0.8 h⁻¹ which was reported from in vitro studies (investigator's brochure vildagliptin, 2006).

In order to compare our estimates with literature reports a value for k_on can be calculated as k₂/(K_d+C_vildagliptin). The binding coefficient k_on, calculated from parameter estimates, was 0.26 nm⁻¹× h⁻¹ at 5 ng ml⁻¹ vildagliptin, i.e. when the system was not saturated. Due to the saturable Michaelis-Menten type binding, the k_on changes with vildagliptin concentrations in relation to DPP-4 concentration, i.e. with the degree of saturation of DPP-4 by vildagliptin. From in vitro studies a k_on of 0.504 nm⁻¹× h⁻¹ was reported [14]. Because k_on changes with the degree of saturation, an inhibition coefficient K_i, which is also frequently calculated as k_off/k_on, changes in this case. At a vildagliptin concentration of 5 ng ml⁻¹, the K_i calculated from our estimates was 2.4 nm. An in vitro IC₅₀ of 2.7 nm in human plasma [18] was reported previously. The k₂ was 23.4 h⁻¹ as estimated from the current TMDD modelling based on clinical data from patients with type 2 diabetes, while 72 h⁻¹ was reported from in vitro studies [14]. Considering that our enzyme binding parameters were estimated based solely on clinical data in patients with type 2 diabetes without fixing parameters to the results from in vitro studies in the literature, the usefulness of the current TMDD model is shown and validated by the reasonably consistent estimates of binding kinetic parameters between the in vivo human data and the results from the in vitro studies. It is important to note that slightly inconsistent or different results exist among different in vitro studies, which might be due to the saturable binding of vildagliptin to DPP-4 and the fact that those in vitro studies were not all performed at the same concentrations of vildagliptin and DPP-4.

In addition to providing a mechanism-based description and explanation of the observed vildagliptin PK and DPP-4 activity, our model may be also used to predict the vildagliptin concentrations and DPP-4 activity profiles after administration of dosing regimens not studied in the present trial. While the specific model developed for vildagliptin most likely does not apply to the mechanism of action of other DPP-4 inhibitors such as sitagliptin or linagliptin, which are only DPP-4 inhibitors, the current modelling approach may be modified for the other DPP-4 inhibitors, and play a role in differentiating the different mechanisms of action of DPP-4 inhibitors. A TMDD model for linagliptin was recently published which was based on quasi-equilibrium conditions, assuming that the binding to DPP-4 was faster than all other processes [19]. Also a k_deg parameter or corresponding term was not necessary in that case as linagliptin is not a substrate of DPP-4, or in other words, metabolized by DPP-4.

There are several advantages in mechanism-based PK/PD models such as described here as they may be used to quantitate jointly all data, study the mechanisms of action, to differentiate the mechanisms of action of a variety of drug molecules by assessing the parameters estimated based on these models, to predict the effects of new dosage regimens and to optimize trial designs.

Our model adequately describes and predicts the drug concentrations and effects of the small molecule drug vildagliptin on DPP-4 activity. While results from previous studies indicated the presence of a slight non-linearity (over dose proportionality) in the vildagliptin PK studies, those studies were analyzed by NCA which generally does not provide much insight into the mechanism of action. Population PK modelling is the better method to explore and analyze the potential non-linearity in PK as shown by Jonsson et al. [20].

Different from sequential modelling, simultaneous modelling of PK and DPP-4 activity was important as the proposed mechanism includes both the effects of vildagliptin on DPP-4 activity and the effects of DPP-4 on the elimination of vildagliptin.

The mechanism-based population PK/DPP-4 analysis was conducted utilizing latest methodology including the Beal M3 method [21] to account for concentrations below the limit of quantification and the Monte Carlo parametric expectation maximization (MC-PEM) algorithm in parallelized S-ADAPT. The MC-PEM algorithm is an exact method to calculate the log-likelihood in contrast to the first order conditional estimation (FOCE) methods [22]. Application of the Beal M3 method in NONMEM VI requires the LAPLACIAN estimation method which decreases computation speed and can be unstable. Therefore it was not feasible to include the Beal M3 method in the NONMEM model. Utilizing parallelized S-ADAPT on a computer cluster including MC-PEM, a full variance-covariance matrix and the Beal M3 method allowed a >10-fold increase in computation speed compared with NONMEM VI FOCE. Therefore utilizing parallelized S-ADAPT with MC-PEM was found to be the preferable choice for the analysis described here, although most of the model development was performed in NONMEM VI FOCE.

In conclusion, population TMDD modelling of simultaneous PK and DPP-4 activity allowed adequate and unique description of the pharmacokinetics of vildagliptin and the kinetic binding and inhibition characteristics between vildagliptin and DPP-4. The current TMDD model could also be used to predict the pharmacokinetic profiles of vildagliptin and the time course of DPP-4 activity after treatment with a variety of dosing regimens of vildagliptin in patients with type 2 diabetes. The TMDD modelling indicated that vildagliptin is both a substrate and an inhibitor of DPP-4, which may be the unique feature of vildagliptin as a DPP-4 inhibitor.

Competing Interests

YLH is an employee of Novartis and holds Novartis stocks.