Division of labor among distinct subtypes of inhibitory neurons in a cortical microcircuit of working memory

Abstract

A conspicuous feature of cortical organization is the wide diversity of inhibitory interneurons; their differential computational functions remain unclear. Here we propose a local cortical circuit in which three major subtypes of interneurons play distinct roles. In a model designed for spatial working memory, stimulus tuning of persistent activity arises from the concerted action of widespread inhibition mediated by perisoma-targeting (parvalbumin-containing) interneurons and localized disinhibition of pyramidal cells via interneuron-targeting (calretinin-containing) interneurons. Moreover, resistance against distracting stimuli (a fundamental property of working memory) is dynamically controlled by dendrite-targeting (calbindin-containing) interneurons. The experimental observation of inverted tuning curves of monkey prefrontal neurons recorded during working memory supports a key model prediction. This work suggests a framework for understanding the division of labor and cooperation among different inhibitory cell types in a recurrent cortical circuit.

Synaptic inhibition is of paramount importance to cortical recurrent dynamics, sensory processing, and memory function. The complex inhibitory operation is likely to be accomplished by coordinated action of many subtypes of GABAergic (GABA, γ-aminobutyric acid) interneurons present in the cortex. Recent years have witnessed a dramatic accumulation of our knowledge about these inhibitory cells, their morphology, physiology, chemical markers, synaptic connections, short-term plasticity, and molecular characteristics (1–6). On the other hand, little is known about specific computations by the diverse interneuron subtypes in animal behavior.

To elucidate distinct operations performed by diverse interneurons, we have investigated a cortical microcircuit model that incorporates three interneuron subpopulations. Specifically, we report here a recurrent network model for working memory in the prefrontal cortex (PFC). PFC is a brain system critical to working memory, the ability to hold information actively in the mind for a short period of time (7, 8). Understanding the cellular and circuit mechanisms of stimulus-selective persistent activity associated with working memory is a subject of intense current experimental and computational research (9, 10). More generally, persistent activity is believed to be a hallmark of strong recurrency in a cortical microcircuit, therefore modeling a working memory circuit represents a testbed for our investigation of cortical organization and functions.

Methods

Model Architecture. The network model represents a local circuit of dorso-lateral prefrontal cortex in monkey. There are four cell populations: pyramidal (P) neurons and three subpopulations of inhibitory cells. Perisoma-targeting, dendrite-targeting, and interneuron-targeting interneurons are assumed to express parvalbumin (PV), calbindin (CB), and calretinin (CR) calcium-binding proteins, respectively (Fig. 1). P cells are four times more numerous than interneurons, and half of the interneurons are of the CR type in prefrontal cortex (11, 12). For the sake of computational efficiency, simulations reported here were done with N_P = 512, N_CR = 64, N_CB = 32, and N_PV = 32. Neurons are spatially distributed in a ring according to the preferred cues (0–360°). The strength of the recurrent connections between neurons in the network depends on the difference between their preferred cues. The conductance between neurons i and j is g_syn,ij = G_synW(θ_i – θ_j), where W(θ_i – θ_j) is the normalized connectivity profile. The W for excitatory projections (pyramid-to-interneurons and pyramid-to-pyramid) is chosen as W(θ_i – θ_j) = J^– + (J⁺ – J^–) exp (–(θ_i – θ_j)²/2σ²) (13). Our reference parameters are: 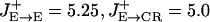, σ_E→E = 18°, σ_E→CR = 36° for the tuned projections. Excitatory projections to PV and CB are unstructured 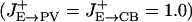, except for Fig. 3. Inhibitory projections are modeled as W(θ_i – θ_j) = A exp(–(θ_i – θ_j)²/(4π²σ²)), where A is a normalization constant. Inhibitory projections from CR and CB are narrow (σ_CB→P = σ_CR→CB = 9°), whereas projections from the PV neurons are unstructured. The recurrent excitatory N-methyl-d-aspartate (NMDA) synaptic conductances are (in mS/cm²): G_E→E = 1.63, G_E→PV = 1.09, G_E→CB = 1.12, G_E→CR = 0.94. GABAergic synaptic conductances are: G_PV→E = 0.93, G_PV→PV = 0.65, G_PV→CR = 0.98, G_CB→E = 0.75, and G_CR→CB = 2.81 (in mS/cm²).

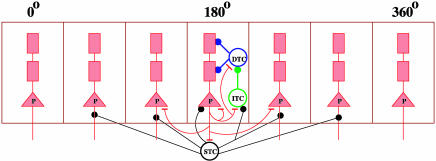
Fig. 1.

Schematic architecture of the biophysically based cortical network model. Pyramidal (P) neurons are arranged according to their preferred cues (0–360°). There are localized recurrent excitatory connections and broad inhibitory projections from perisoma-targeting (PV) fast-spiking neurons to P cells. Within a column, CB interneurons target the dendrites of P neurons, whereas CR interneurons preferentially project to CB cells. Excitation of a group of P cells locally recruits CR neurons, which sends enhanced inhibition to CB neurons, leading to dendritic disinhibition of the same P cells. STC, perisoma-targeting cell (PV); DTC, peridendrite-targeting cell (CB); ITC, interneuron-targeting cell (CR).

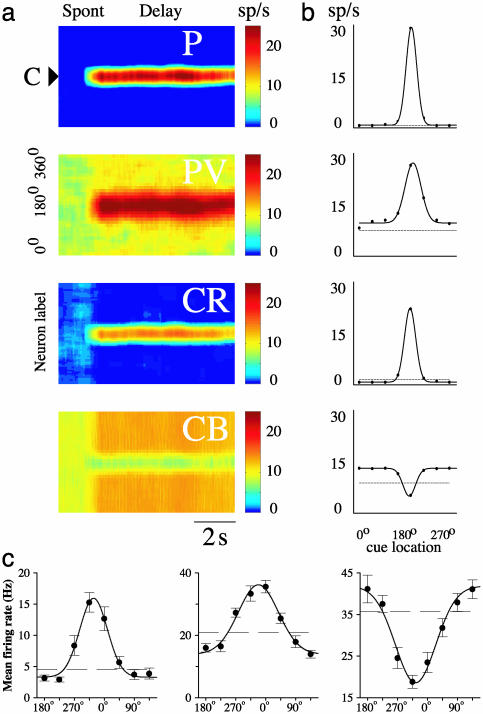
Fig. 3.

Comparison between the model and recorded PFC neuronal tuning curves. (a) Rastergrams for the P and the three (PV, CB, and CR) inhibitory neuron populations during the cue and delay periods. Instantaneous firing rates are color-coded. (b) Observed neuronal tuning curves (solid lines) during the delay period in the model simulations. Eight different cue positions are used. Dashed lines, spontaneous firing rate during the resting state. Parameter values that differ from the reference parameter set are 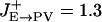, σ_E→PV = 162°, and 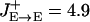. (c) Three kinds of recorded tuning curves in dorsolateral PFC during an oculomotor delayed response task, with the same conventions as in b. Solid line, the best Gaussian fit; dotted line, average firing rate during the last second of fixation. Note that the fast-spiking putative PV cell (Center) has a higher spontaneous firing rate and wider tuning than the regular-spiking putative P cell (Left), similar to what is found in the network simulations (b). An example of the inverted tuning curve is shown (Right). (Left and Center) Based on data from ref. 17.

All neurons receive unspecified external excitatory inputs mediated by α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA) receptors. This external input is modeled as Poisson spike trains to each neuron at a rate of ν_ext = 1,000 Hz per cell, where the synaptic conductances are: g_ext,E = 0.2, g_ext,PV = 0.04, g_ext,CB = 0.025, and g_ext,CR = 0.055.

Neuron Models. We used Hodgkin-Huxley-type conductance-based models for single pyramidal cells and interneurons, which were calibrated by in vitro physiological measurements. Pyramidal neurons have three compartments, representing a soma/initial axonal segment(s) and a proximal (d1) and a distal (d2) dendrite. The neuronal input–output relation and the shape of the somatic and dendritic action potential were tuned to cortical slice data. Several ion conductances that have been identified in prefrontal pyramidal neurons are included in the model [see Tegnér et al. (14) and Supporting Text, which is published as supporting information on the PNAS web site]. The somatic compartment contains spike-generating currents (I_Na and I_K), a high-threshold calcium current I_Ca, and a slow calcium-dependent cationic current I_Can. The proximal dendritic compartment has a persistent sodium current I_NaP and a slowly inactivating potassium current I_KS. The distal dendritic compartment has an I_Ca and a transient A type potassium current I_A. The somatic voltage V_s, proximal dendritic voltage V_d1, and distal dendritic voltage V_d2 obey the following membrane equations: C_mdV_s/dt = –I_Na – I_K – I_Ca – I_L – I_Can – gc₁ (V_s – V_d1)/p₁ – I_syn, C_mdV_d1/dt =–I_NaP – I_KS – I_L – gc₁(V_d1 – V_s)/p₂ – gc₂(V_d1 – V_d2)/p₂ – I_syn and C_mdV_d2/dt = –I_A – I_Ca – I_L – gc₂(V_d2 – V_d1)/(1 – p₁ – p₂) – I_syn.

Perisoma-targeting (PV) interneurons are modeled as C_mdV/dt = – I_Na – I_K – I_L – I_syn, hence they include only spike-generating sodium and potassium currents and show tonic fast-spiking behavior. Dendritic targeting CB interneurons are modeled as C_mdV/dt = – I_Na – I_K – I_h – I_Ca – I_KCa – I_L – I_syn. These cells show spike-frequency adaptation due to I_Ca and I_KCa as well as postinhibitory rebound due to the hyperpolarization-activated current I_h (3). CR interneurons follow C_mdV/dt = –I_Na – I_K – I_Ca – I_KCa – I_Ca,T – I_NaP – I_L – I_syn. They contain a low-threshold calcium current I_Ca,T, which can generate a transient burst response, adaptation currents I_Ca and I_KCa, and a persistent sodium current I_NaP. The interplay between these currents produces irregular firing patterns as observed experimentally (4).

A complete description of neuron models, with details of ion channel kinetics and conductance parameters, can be found in Supporting Text.

Synapses. Synaptic currents are modeled according to I_syn = g_syns(V – E_syn), where g_syn represents the maximal synaptic conductance, and the synaptic reversal potential E_syn (in mV) is 0 for excitation and –75 for inhibition. The gating variable s models the fraction of open synaptic ion channels and follows first-order kinetics for α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA) and (GABA) transmission; ds/dt = α_sF(V_pre)(1 – s) – s/τ_s; with α_s = 12 (1/ms). The synaptic channels decay as τ_s = 2 (ms) (AMPA) and τ_s = 10 (ms) (GABA). The normalized concentration of the postsynaptic transmitter–receptor complex, F(V_pre), is 1/(1 + exp(–(V_pre)/2)). The dynamics of the voltage-dependent N-methyl-d-aspartate channel is modeled by second-order kinetics as: dx/dt = α_xF(V_pre)(1 – x) – x/τ_x: ds/dt = α_sx(1 – s) – s/τ_s; α_x = 10, τ_x = 2 ms, α_s = 0.5, and τ_s = 100 ms. Due to the voltage-dependent magnesium block, an additional multiplicative factor is introduced in the current equation 1/(1+[Mg²⁺] exp(–0.062V)/3.57), [Mg²⁺] = 1.0 mM.

Simulation Protocol. The simulation protocol used here follows the experimental procedure of a delayed oculomotor response task (15). The details were described previously (13, 14, 16).

Numerical Integration. The model was programmed in C and was integrated by using a fourth-order Runge–Kutta algorithm.

Physiological Experiments. Neurons were recorded from two male rhesus monkeys Macaca mulatta during a delayed oculomotor response task. The behavioral paradigm and recording methods have been described in detail (17). Neurons were classified as fast- and regular-spiking, as reported previously, according to our narrow classification criterion (17). In the present study, we identified neurons with inverted tuning curves as those that exhibited firing rates significantly lower in the delay than the baseline fixation period (0.5 s before cue presentation) and spatial tuning evidenced by significantly different delay-period firing rates across the eight target locations (ANOVA test, P < 0.05).

Results

Our model (Fig. 1) is designed to describe a local prefrontal microcircuit, which is endowed with extensive horizontal connections between pyramidal neurons within layers 2 and 3 (9, 18, 19). In the model, P neurons are labeled according to their preferred stimulus cues: synaptic connection strength between P neurons decreases with the difference of their preferred cues. The model also includes three subpopulations of inhibitory cells: perisoma-, dendrite-, and interneuron-targeting interneurons. We assume they express, respectively, PV, CB, and CR calcium-binding proteins. The three interneuron classes contribute to recurrent synaptic inhibition in specific ways (Fig. 1). PV interneurons, presumably of the large basket-cell type, provide widespread perisomatic inhibition to P cells (20). By contrast, CB and CR interneurons have narrow dendritic and axonal arbors and subserve local inhibition. CB interneurons project onto the dendritic sites of P cells (2, 5), whereas CR interneurons target other interneurons, preferentially CB cells (21–24). When CR interneurons are activated by elevated activity of local P cells, they strongly inhibit neighboring CB cells, leading to a feedback disinhibition of the same P neurons.

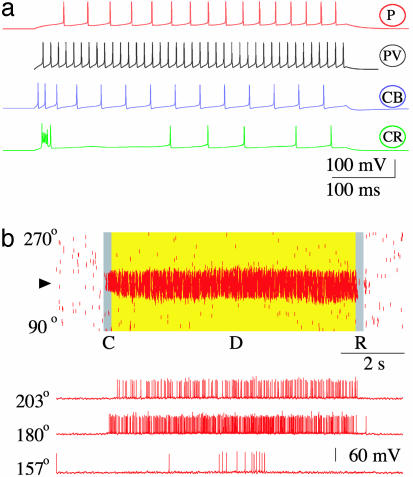
Spatially Tuned Persistent Activity. In our model, cells and diverse interneuron subtypes display distinct spike-firing patterns (Fig. 2a). PV cells are fast-spiking (25), CB cells show spike-frequency adaptation (26), and CR cells are characterized by irregular spiking patterns (4). Fig. 2b shows a network model simulation of the oculomotor delayed-response experiment (15). The network is initially in a resting state, with P neurons firing at a low rate (0.5–2 Hz) due to background inputs. A transient spatial cue triggers an increase of spike discharges in a subset of P cells (those for which the cue is the preferred stimulus): this activity persists after the stimulus offset due to excitatory reverberation in the recurrent network. The elevated firing (typically 30 Hz) remains spatially confined during the delay period. The visual cue is encoded and maintained in active memory by the peak location of the spatially tuned persistent activity pattern or bump attractor. At the end of the delay, a transient excitation terminates delay-period activity and switches the network back into the spontaneous-activity state. Therefore, our biophysically based model captures the main firing characteristics of PFC neurons described during a delayed oculomotor experiment.

Fig. 2.

Working memory behavior of the biophysically based network model. (a) Single-cell firing patterns: distinct response to an injected current pulse for each of the four neuron types, in agreement with physiological data. PV neurons are fast-spiking, CB interneurons show spike-frequency adaptation, and CR interneurons display irregular firing patterns. (b) Network simulation of the visuospatial working memory task. (Upper) Rastergram for the P cell population. A tick corresponds to an action potential from a P cell indexed by its preferred cue (0–360°) (along the y axis) at time (along the x axis). C, cue; D, delay period; R, response. A transient cue stimulus (0.5 μA/cm², 250 ms) induces a spatially localized persistent activity pattern during the delay period. At the end of the trial, the network is switched back to the resting state, and the memory is erased by a transient nonspecific current injection to neurons. (Lower) Sample voltage traces from three P neurons.

To gain insight into how a spatially tuned mnemonic firing pattern is generated, we examined the coordinated activity across the four types of neurons (P, PV, CR, CB) (Fig. 3a). During the resting state, all four neuronal populations exhibit untuned activity with low firing rates. A cue stimulus produces a localized increase of activity in a subset of P neurons, which in turn recruit CR neurons with similar preferred cues (Fig. 3a). Activation of CR neurons then increases inhibition transmitted to CB neurons likewise tuned to the similar preferred cues, thereby reducing CB inhibition on P cells during the delay period (Fig. 3a). On the other hand, on the flanks of the bump, the enhanced activity of PV interneurons suppresses CR cells, consequently CB neurons receive reduced inhibition from CR cells (possibly also increased excitation from P neurons), hence they fire at higher rates during the delay period (Fig. 3a). The end result is that CB interneurons send enhanced inhibition to those P cells that are selective to other stimuli. Lower delay activity of P cells after a nonpreferred cue, compared to spontaneous activity, is consistent with prefrontal recordings from behaving monkeys (15) and in line with our network model of working memory (9, 13, 14).

On another trial, a different stimulus triggers a bump attractor of the same shape but peaks at a new cue location. Using different stimuli across trials, a given model neuron would display stimulus-selective persistent activity, with a tuning curve that can be compared with the experimental data (Fig. 3b). In conformity with a previous model (13), fast-spiking PV cells typically show higher spontaneous firing rates during the resting state (dashed horizontal line, Fig. 3b) and broader tuning of delay-period activity (solid line, Fig. 3b) compared with P cells. Moreover, CB interneurons (Fig. 3b) have relatively high spontaneous activity and inverted tuning curve (defined by a lower firing rate during delay than spontaneous activity, for some cues).

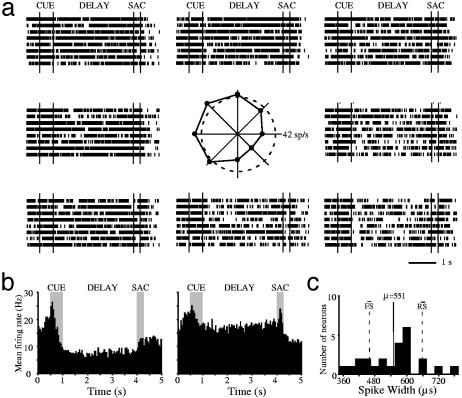
Inverted Tuning Curves. The model predicts inverted tuning curves as an indication of the proposed disinhibition mechanism for tuned persistent activity. Moreover, we expect only a small fraction of PFC neurons to exhibit inverted tuning curves, because the overall number of CB neurons is small in PFC (≈5%) (12). To test this prediction, we examined data from monkey PFC neurons recorded during an oculomotor delayed response task. In the previous work (17), putative regular-spiking P cells and fast-spiking inhibitory interneurons were differentiated according to the widths of their action potentials and firing rates. The tuning curve of delay-period activity is reproduced here for each of the two cell types (Fig. 3c Left and Center). Note that interneurons show higher spontaneous activity levels (horizontal line) and broader tuning curves, than P cells (Fig. 3c), in agreement with model predictions [(13), Fig. 3b]. Motivated by the present modeling results, we reanalyzed our database of 526 neurons that showed significant task-related activity. We found that 24 neurons (≈4.5%) displayed an inverted tuning curve of delay-period activity. An example is shown in Fig. 3c Right. As is evident in the rasters of the same neuron (Fig. 4a), delay-period activity is about the same as in (or slightly larger than) the spontaneous state for some stimuli and much lower for other stimuli. Fig. 4b shows the population poststimulus time histogram, averaging responses from all 24 neurons with inverted tuning. These neurons typically exhibit broad spatial tuning. The average baseline fixation firing rate of neurons with inverted tuning curves was 20.5 spikes per second. This is virtually identical to the baseline firing of fast-spiking (FS) neurons (19.9 spikes per second), as opposed to the firing rate of regular-spiking (RS) neurons (4.0 spikes per second). Interestingly, the spike widths of these cells fell between the distributions of the FS and RS neurons. The mean spike width of neurons with inverted tuning curves is 551 μs compared with the average FS (460) and RS (658) spike widths (Fig. 4c). This observation can be taken as evidence that they may be CB interneurons, because intracellular recording in vitro showed that, in rat frontal cortex, CB-containing interneurons have an average spike width at half-amplitude (≈1 msec) intermediate between those of fast-spiking interneurons (0.6 ms) and P cells (1.3 ms) (26). The existence of inverted tuning curves from putative CB cells in the prefrontal cortex of monkeys performing working memory tasks thus provides strong experimental support of a key prediction of our model and the model itself.

Fig. 4.

Inverted tuning of monkey prefrontal neurons recorded during spatial working memory. (a) An example of a neuron (same as in Fig. 3c) with inverted tuning during the delay period. Rasters represent responses for the eight cue locations, arranged to indicate the location of the corresponding cue. The polar plot in the center depicts the average delay period firing rate for each location; the dotted circle represents the average firing rate during the last second of fixation. (b) Population poststimulus time histogram, averaging responses from 24 of 526 (4.5%) neurons with inverted tuning curves. (Left) Responses for the location with the lowest (most-inhibited) delay period activity for each neuron. (Right) Responses for the location with the highest delay-period activity. (c) Spike-width distribution of neurons with inverted tuning curves during the delay period. The solid line represents the average spike width; dotted lines represent the average spike widths of the fast- and regular-spiking neuron distributions in our database.

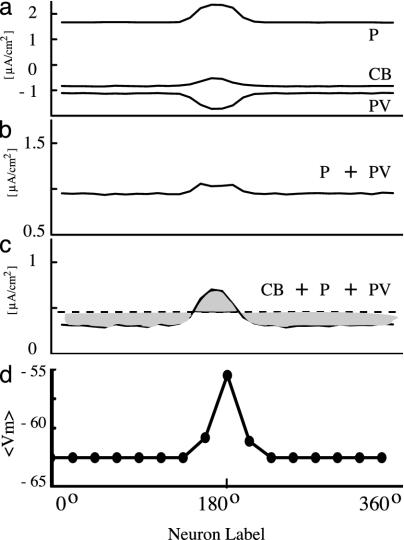
Mexican Hat. Is this disinhibition mechanism important for the generation of tuned persistent activity? We investigated this question by focusing on the Mexican-hat-type network connectivity (with local excitation and lateral inhibition) underlying the generation of spatially confined activity patterns (27). Specifically, we calculated the average synaptic currents from different cell types feeding into the P cell population (Fig. 5a). Recurrent collaterals between P cells produce a Gaussian profile of excitatory current (P, Fig. 5a), whereas CB neurons produce a spatial profile of inhibitory current with a minimum at the peak of the bump state (CB, Fig. 5a). Surprisingly, although the PV-to-P axonal projection is widespread, the resulting inhibitory postsynaptic current on the P cell population turns out to be narrowly tuned and maximal at the peak of the bump (PV, Fig. 5a). As a result, the sum of I_P and I_PV yields an almost flat spatial profile (Fig. 5b). However, when combined with I_CB (which shows a dip at the peak activity), the total recurrent synaptic input does show localized excitation and more widespread inhibition, like a Mexican hat (Fig. 5c). Therefore, dendritic disinhibition plays an important role in the generation of bump-activity patterns in our model.

Fig. 5.

Mexican-hat-type connectivity depends on dendritic disinhibition of P cells. (a) Average synaptic currents of different types to P neurons in a bell-shaped persistent activity pattern. Recurrent excitation from P cells is localized; recurrent inhibition from PV neurons is maximal, whereas inhibition from CB neurons shows a dip at the center of the bump. (b) Summation of synaptic currents from P and PV cells is almost flat. (c) When the synaptic contribution from CB neurons is also included, the total synaptic current shows a Mexican-hat-type shape, with local excitation and lateral inhibition. (d) The average membrane potential of a conductance-based P cell increases with its firing rate. Therefore, the driving force (V_P – E_inh) of the inhibitory synaptic current mediated by PV cells and the current itself (as shown in a) is about twice as large at the peak of the bump (where neurons fire at ≈30 Hz) than on the sides (where neurons are inactive).

The spatial tuning of the PV-to-P inhibition originates from the tuned driving force of the inhibitory postsynaptic currents (IPSC). Namely, if the PV-to-P IPSC is I_PV = g_PV(V_P – E_GABAA), then unstructured projection means that g_PV is the same for all P cells. However, the membrane potential V_P of a P cell increases with its firing rate (28). In the example of Fig. 5a, 〈V_P〉 = –56 mV at the peak of the bump, whereas 〈V_P〉 = –64 mV on the flanks (Fig. 5d). As a result, for a shunting inhibition, V_P – E_GABAA is about twice as large at the peak of the bump as on the flanks. Interestingly, this driving-force effect is not present in a network model of integrate- and-fire neurons (13). In that model, the average voltage actually decreases with increasing firing rate of a postsynaptic cell, due to the voltage reset after a spike, leading to minimum (rather than maximum) inhibition at the peak of the bump. Disinhibition, through the other (CB and CR) interneuron types, helps to produce stable bump states in a network model of Hodgkin–Huxley-type neurons.

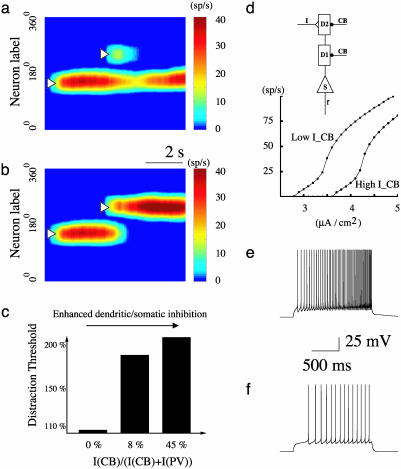
Dendritic Inhibition and Resistance Against Distractors. For a neural network to maintain memory storage, it should not be easily interrupted by behaviorally irrelevant stimuli (distractors). We examined the network's ability to filter out distractor stimuli, a characteristic of robust working memory in PFC (29). We analyzed how resistance against distractors depends on the relative inhibitory contributions from the CB and PV populations to P cells. A distractor stimulus was introduced during the delay period at a location different from the initial cue (13, 30). We fixed its location and determined the intensity threshold above which it is powerful enough to distract the network from the stored initial cue (Fig. 6 a and b). We found that dendritic inhibition mediated by CB cells is more efficient than perisomatic inhibition mediated by PV cells in filtering out distractor stimuli. For the simulations shown in Fig. 6, when dendritic inhibition is insignificant (as in the classical two-population model), a bump state can be activated but is not stable and shows systematic drifts over time (14). In this case, a distractor of a strength comparable to that of the initial cue is able to disrupt the working memory (Fig. 6c). Increasing the relative inhibition from the CB population increases dramatically the threshold above which a distractor can disrupt the memory of the initial cue, therefore the network's ability to filter out distractors is greatly enhanced (Fig. 6c).

Fig. 6.

Robustness against distracting stimuli is enhanced by an increased ratio of the dendritic/somatic inhibition. (a and b) Simulation protocol. A transient cue (0.8 μA/cm², 250 ms) elicits a spatially localized persistent activity pattern, which is resistant (a) to a weak distractor (1.125 μA/cm², 250 ms) but not (b) when the distractor (2.25 μA/cm²), is stronger than a distraction threshold. I_CB/(I_CB + I_PV) is 8%. (c) Increased resistance against distractors with a larger dendritic/somatic inhibition ratio (I_CB/(I_CB + I_PV)). (d) Input–output relation for an isolated P neuron, in response to current inputs to distal dendrite and in the presence of dendritic inhibition mediated by CB interneurons. The amount of inhibition from CB neurons was estimated from the network simulation, when the remembered stimulus is opposite from the preferred cue of the cell, either for the resting state (upper curve) (–0.529μA/cm² to both dendritic compartments, d1 and d2) or the delay period (lower curve) (–0.845 μA/cm²). Two examples with the same input current intensity but two different levels of dendritic inhibition are shown in e and f. The P cell's responsiveness is greatly reduced during the delay period because of enhanced dendritic inhibition, which provides a mechanism for filtering out distractor stimuli.

CB cells enhance resistance against distractors, because their inputs target the same dendritic sites as the external stimuli (such as a distractor) hence are well positioned to reduce the efficacy of external inputs. Furthermore, away from the bump's peak activity, CB interneurons show higher firing rates during the delay period than in the spontaneous state, therefore they provide stronger dendritic inhibition to those P cells not storing the initial cue. To quantitatively show this effect, we considered a single P cell whose preferred cue is opposite to the initial cue. As shown in Fig. 6 d–f, given the same external input, the cell's response is significantly reduced, with a higher level of dendritic inhibition (as in the delay period) compared to the case with a lower dendritic inhibition (in the resting state). Therefore, our results show that a working memory network endowed with synaptic inhibition is more robust against distractors when compared with a conventional two-population model.

Discussion

Widespread lateral inhibition is a general assumption in recurrent neural models with a Mexican-hat architecture (13, 16, 27, 31, 32). However, whether, in a cortical microcircuit, inhibition is broader than excitation is still a matter of debate (33). Moreover, here we showed that, even if axonal projection from interneurons is broad, the resulting distribution of inhibitory current in P cells can be narrowly tuned due to the driving force effect. Most previous models used the leaky integrate-and-fire neuron, for which this effect is absent. In a Hodgkin–Huxley model of spatial working memory, persistent activity generally shows systematic drifts in time, thus appears to be dynamically unstable (14). In a recent paper (34), bump attractors were reported in a two-population model of Hodgkin–Huxley-type neurons. However, in that study, the average membrane potential of a model neuron is basically independent of the firing rate, unlike real P cells (28). Further analysis will be worthwhile to clarify under what conditions, or whether, bump attractors can be generated with only one inhibitory population in a biologically realistic model. Regardless, we propose that, in addition to broad inhibition, local disinhibition contributes critically to the robust realization of Mexican-hat input distribution, thus stable spatially tuned persistent activity.

We emphasize that the three interneuron types in our model should be more appropriately interpreted according to their synaptic targets rather than calcium-binding protein expressions. For example, PV cells display a variety of axonal arbors, among which the large basket cells (20) are likely candidates for our widely projecting cells. Similarly, CB interneurons show a high degree of heterogeneity, but some of them (such as double-bouquet cells) are known to act locally and preferentially target dendritic spines and shafts of P cells (2, 5). Finally, although many CR interneurons do project to P cells (2), a subset of CR cells appear to avoid P cells (22), at least in the same cortical layer (23), and preferentially target CB interneurons (21). Electrophysiological evidence is presently lacking of the preferred innervations of CR interneurons onto GABAergic cells; progress in this direction would be most desirable.

Because Mexican-hat connectivity is an architecture widely used in recurrent cortical microcircuit models (13, 16, 27, 31, 32), our four-population model is of general relevance. At the same time, there could also be significant differences among cortical areas serving different functions. It would be interesting to compare quantitatively the distributions of interneuron subtypes in association vs. sensory cortices (21, 35–38). In particular, experiments are needed to test the hypothesis that our proposed disinhibition mechanism is especially prominent in those cortical regions capable of persistent activity.

According to the disinhibition mechanism, dendritic inhibition is reduced locally in activated P cells and increased in those P cells not engaged in encoding the shown stimulus. Our results suggest that, in a working memory network, this mechanism mediated by CB interneurons could serve to filter out distracting stimuli, thereby rendering memory storage robust. We showed that this mechanism is enhanced with a larger dendritic/somatic inhibition ratio (Fig. 6), which could be hard-wired or dynamically controlled by neuromodulation. Interestingly, recent work suggests that dopamine D1 receptor activation precisely increases the ratio of dendritic/somatic inhibition onto P cells in the prefrontal cortex (39). Dopamine was found to reduce the efficacy of inhibitory synapses onto the perisomatic domains of a P cell, mediated by fast-spiking interneurons, whereas it enhances inhibition at synapses from accommodating or low-threshold spiking interneurons that target the dendritic domains of a P cell (39). Our model predicts a specific function for such a dual dopamine action, namely it could boost the ability of a working memory network to filter out behaviorally irrelevant distracting stimuli. By the same token, the model also suggests one possible scenario for how impaired dopamine modulation of PFC could lead to working memory deficits and abnormal distractability in schizophrenia (8).