Control of calcium oscillations by membrane fluxes

Abstract

It is known that Ca²⁺ influx plays an important role in the modulation of inositol trisphosphate-generated Ca²⁺ oscillations, but controversy over the mechanisms underlying these effects exists. In addition, the effects of blocking membrane transport or reducing Ca²⁺ entry vary from one cell type to another; in some cell types oscillations persist in the absence of Ca²⁺ entry (although their frequency is affected), whereas in other cell types oscillations depend on Ca²⁺ entry. We present theoretical and experimental evidence that membrane transport can control oscillations by controlling the total amount of Ca²⁺ in the cell (the Ca²⁺ load). Our model predicts that the cell can be balanced at a point where small changes in the Ca²⁺ load can move the cell into or out of oscillatory regions, resulting in the appearance or disappearance of oscillations. Our theoretical predictions are verified by experimental results from HEK293 cells. We predict that the role of Ca²⁺ influx during an oscillation is to replenish the Ca²⁺ load of the cell. Despite this prediction, even during the peak of an oscillation the cell or the endoplasmic reticulum may not be measurably depleted of Ca²⁺.

In response to an increased concentration of inositol trisphosphate (IP₃), oscillations in the concentration of free intracellular calcium (Ca²⁺) occur in many cell types and are important for the control of many cellular functions (1–4). In nonexcitable cells, such as epithelial cells, these oscillations occur as the result of Ca²⁺ flux into and out of the endoplasmic reticulum (ER). However, although the oscillations result from the cycling of Ca²⁺ between the ER and the cytoplasm, the transport of Ca²⁺ across the cell membrane can have a dramatic effect on these oscillations.

Although Ca²⁺ influx is known to be important, disagreement exists, first, over the mechanisms by which Ca²⁺ influx is modulated during a Ca²⁺ oscillation, and, second, over the role played by Ca²⁺ influx. The capacitative entry hypothesis proposes that depletion of ER Ca²⁺ causes enhanced entry of Ca²⁺ across the plasma membrane (5–9). Often, although not necessarily, in this scenario, Ca²⁺ entry is necessary for the refilling of the ER, and thus oscillation frequency is controlled by the refilling time (10, 11). Although capacitative entry is certainly an important factor during the response to a maximal stimulus, other investigators have pointed to a lack of direct evidence that it plays an important role during smaller stimuli that generate oscillatory behavior (12). They maintain that Ca²⁺ influx, under these conditions, is controlled by a noncapacitative pathway involving arachidonic acid and that the purpose of the influx is to increase the likelihood that low levels of IP₃ will induce Ca²⁺ release from internal stores (13). This controversy is complicated by the fact that, in some cell types, Ca²⁺ oscillations persist in the absence of Ca²⁺ influx (14–16), whereas in other cell types, oscillations depend absolutely on influx (17, 18). Even in a single cell type, the effect of Ca²⁺ influx on agonist-induced oscillations varies according to the agonist (19), and the effect of removal of extracellular Ca²⁺ depends on when it is removed (17).

Using a combination of theoretical and experimental work, we attempt to resolve this controversy by studying how Ca²⁺ transport across the cell membrane can affect ER-based oscillations. We conclude that small changes in Ca²⁺ load can have a large impact on Ca²⁺ oscillations. By Ca²⁺ load we mean the total amount of Ca²⁺ in the cell, including the ER, the cytoplasm, and the Ca²⁺ buffers. (For the purposes of the model here, we neglect mitochondrial Ca²⁺, but its inclusion would have no qualitative effect on our results.) The amount of Ca²⁺ in the ER is directly related to the Ca²⁺ load, and thus our model predicts that Ca²⁺ oscillations will also be highly sensitive to ER Ca²⁺ concentration.

Our results are independent of the mechanism by which Ca²⁺ influx is controlled and thus cannot be used to distinguish between capacitative entry or noncapacitative, arachidonic acid-dependent entry, but they provide a way in which seemingly contradictory experimental results can be understood. In addition, they show that direct control of Ca²⁺ influx by the cytosolic or ER Ca²⁺ concentration is not necessary for Ca²⁺ influx to play a crucial role in the control of oscillations. Finally, our results do not depend on the precise details of the model, but they occur in at least four different models of Ca²⁺ oscillations.

The Model

Our model for Ca²⁺ oscillations is based on a dynamic model of the IP₃ receptor (IPR) (20) and assumes that oscillations in [IP₃] are not necessary for the generation of Ca²⁺ oscillations. A schematic diagram of the cell is given in Fig. 1. From there we see that the conservation equations for Ca²⁺ are

[1]

[2]

where c and c_e denote [Ca²⁺] in the cytoplasm and ER, respectively, γ is the cytoplasmic-to-ER volume ratio, and δ is a dimensionless parameter that controls the relative magnitudes of membrane and ER fluxes without changing the steady-state concentrations.

Fig. 1.

Schematic diagram of the model fluxes.

Calcium release through the IPR is described by the model of ref. 20, slightly modified for the context of a whole-cell model. Thus,

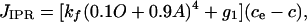[3]

where g₁ models a constant background leak from the ER at zero [IP₃]. O and A denote the probability the IPR is in the open and activated state, respectively, and are governed by differential equations with parameters determined by fitting to experimental data from the type II hepatocyte IPR (21).

Calcium pumping into the ER (J_serca) and extrusion across the plasma membrane (J_pm) are modeled by

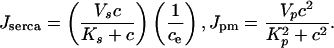[4]

These expressions are the ones used by ref. 22 and are discussed in detail there. Ca²⁺ entry is modeled as a linear, increasing function of [IP₃] (p), and thus

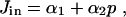[5]

where α₁ and α₂ are constants. This form for J_in is entirely arbitrary; we know that J_in must be an increasing function of p but do not know the exact relationship. Thus, we just choose the simplest possible form. Using a more complex function for J_in makes no qualitative difference to the model results.

Buffering is taken into account by assuming each flux to be an effective flux, scaled by the effects of fast linear buffers. Inclusion of slower nonlinear buffers will not alter the qualitative results of our analysis.

The parameter values are given in the legend to Fig. 2.

Fig. 2.

Blue lines are the bifurcation diagram of the closed-cell model with c_t as the bifurcation parameter. Parameter values of the IPR model are taken from ref. 20. Other parameter values (adapted from ref. 22) are γ = 5.4, k_f = 0.96 s^–1, g₁ = 0.002 s^–1, V_s = 120 μM²·s^–1, K_s = 0.18 μM, V_p = 28 μM·s^–1, K_p = 0.42 μM, α₁ = 0.03 μM·s^–1, and α₂ = 0.2 s^–1. The dotted red line is a solution of the open-cell model superimposed on the bifurcation diagram of the closed-cell model and calculated by using p = 10 and δ = 0.01. ss, steady states; max osc, maximum of the oscillation.

Analysis of the Model

Introduction of the new variable, c_t = c + (1/γ)c_e gives the system

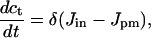[6]

[7]

The new variable c_t is the total number of moles of Ca²⁺ in the cell divided by the cytoplasmic volume. We shall call c_t the Ca²⁺ load of the cell. When δ is small, c_t can change only slowly, and in the limit, as δ → 0, the cell becomes closed, i.e., when δ = 0 no Ca²⁺ exchange occurs with the external medium.

We study the model by treating c_t as a bifurcation parameter and analyzing the model's behavior for a range of fixed values of c_t, a procedure that was used by refs. 23–25 (for a general introduction, see ref. 26) in a classic study of bursting oscillations, and by refs. 27 and 28 in the context of Ca²⁺ oscillations in neurosecretory cells. If c_t is constant, we replace c_e by γ(c_t – c) and consider just Eq. 1. We call this the closed-cell model. The bifurcation diagram is given in Fig. 2 (blue curve). Stable oscillations exist only for an intermediate range of values of c_t between the homoclinic (HC) and saddle node of periodics (SNP) bifurcations. In other words, when Ca²⁺ transport across the plasma membrane is blocked, oscillations can occur only if neither too much nor too little Ca²⁺ is inside the cell.

When c_t is allowed to vary, we obtain the open-cell model. A typical solution (drawn in the c, c_t phase plane and superimposed on the closed-cell bifurcation diagram) is sketched in Fig. 2 (red dotted curve). Suppose that, when p = 0 and δ = 0.01, c_t ≈ 12 at rest (see IPR_open.ode, which is published as supporting information on the PNAS web site). Raising p to 10 will cause immediate Ca²⁺ oscillations, with a gradually decreasing baseline as c_t decreases (Fig. 2, red dotted line). These oscillations are pseudosteady; the solution is trying to follow the oscillatory solutions of the closed-cell model, but cannot exactly, because δ is nonzero. Once c_t gets low enough, the oscillations change their character. During the interspike intervals, the solution approximately follows the lower stable steady state. (As δ → 0 the solution follows the lower stable steady state more closely. The agreement in Fig. 2 is not exact, but it is the general trend we are considering here.) Because the lower steady state is below the line where dc_t/dt = 0, c_t is increasing there. Once the solution reaches the limit point (the bend) it can no longer follow this branch, and “falls off,” moving toward the long period limit cycle close to the HC orbit. However, once on the other side of the dc_t/dt = 0 line, c_t starts to decrease, the solution returns to the lower stable steady state, and the cycle repeats.

Thus, in response to an increase in [IP₃], the model cell exhibits transient pseudosteady oscillations that tend to a stable steady-state limit cycle, in which the oscillation is a degenerate bursting oscillation having only a single peak during each bursting phase. This slow modulation of the oscillations is caused by a gradual decrease in c_t, and so the speed with which the model reaches the steady-state oscillation is governed by the value of δ, which controls the speed at which c_t reaches a steady-state limit cycle.

If an open cell exhibits Ca²⁺ oscillations, how will these oscillations be affected if membrane transport is stopped? This is most easily studied with the bifurcation diagram shown in Fig. 3. The loci of HC and SNP bifurcations as p and c_t vary in the closed-cell model are shown by the red curves. Thus, for each value of p, the closed-cell model will exhibit oscillations only when c_t lies between these two curves. Superimposed on this we plot bifurcation diagrams of the open-cell model (broken curves), plotting the maximum and minimum of c_t over an oscillation as a function of p. For each value of p where steady oscillations exist in the open-cell model, c_t moves between the appropriate broken curves. (For instance, when δ = 0.1, the broken curves are labeled max and min, and denote, respectively, the maximum and minimum values of c_t over an oscillation.) It follows that oscillations can occur in both the closed-cell and open-cell models only when the broken curves lie between the solid curves.

Fig. 3.

The broken lines are the maximum (max) and minimum (min) of oscillations in the open-cell model for different values of δ. The curves labeled HC and SNP are two-parameter continuations of the points labeled HC and SNP in Fig. 2. Thus, for each value of δ, oscillations exist in the closed-cell model only for values of c_t between the HC and SNP curves.

Consider the behavior at p = 1 and δ = 0.01. If the open-cell model is allowed to reach its steady-state oscillation, c_t will be moving between the blue short-dashed curves (over the point labeled A). If δ is now reduced to zero, i.e., membrane transport is shut off, c_t will now be held constant at point A and will not lie between the HC and SNP curves. Hence, the closed-cell model cannot oscillate and the oscillations stop. To restore the oscillations, c_t could be increased until it crosses the HC curve (point B). Alternatively, oscillations can be restored by increasing p (point C).

When p = 40 and δ = 0.01, we see that stable oscillations coexist in both the open-cell and closed-cell model, but for only a relatively small region (region D). If p and c_t are such that the cell sits in region D, blockage of membrane transport will not eliminate Ca²⁺ oscillations. When δ = 0.001, i.e., when membrane transport in the open-cell model is very slow, the open-cell bifurcation curves (the broken lines) begin to superimpose on the HC curve of the closed-cell model, thus showing how, in the limit as δ → 0, the open-cell oscillations get progressively restricted to planes of constant c_t. In addition, the p interval for which stable-steady oscillations coexist in the open-cell and the closed-cell models gets wider (region E).

From Fig. 2 we see that, immediately after an increase in [IP₃], the open-cell model exhibits oscillations with a gradually decreasing baseline and with a decreasing average c_t. This finding suggests that the effects of blocking membrane transport will depend on the timing of the block. If the block occurs soon after, or before, the increase in [IP₃], oscillations can continue because c_t has not yet fallen far enough to make oscillations impossible. However, if the block occurs later, after c_t has decreased past HC, then the block will be expected to eliminate oscillations.

Influx of Ca²⁺ from outside the cell is known to affect the frequency of Ca²⁺ oscillations and waves. We investigate this in the open-cell model by varying the background rate of Ca²⁺ influx, α₁. In Fig. 4 we plot lines in the α₁ – p plane that separate regions where Ca²⁺ oscillations occur from regions where they do not. For a fixed p, an increase in Ca²⁺ influx will lead to oscillations or to a decrease in the oscillation period. Similarly, for a fixed α₁, an increase in p will have the same effect. This occurs even when membrane transport is slow (δ = 0.001). Oscillations can be eliminated by a decrease in influx but can then be restored by increasing p.

Fig. 4.

Two-parameter bifurcation diagram of the open-cell model. The lines (for three different values of δ) divide the α₁ – p plane into regions for which oscillations do or do not exist.

Physiological Interpretation of the Analysis

A model cell can fire a Ca²⁺ spike only if its Ca²⁺ load (c_t) is above threshold. This is because enough cytosolic Ca²⁺ must be present to activate the IP₃ receptor, and enough ER Ca²⁺ must be available to provide sufficient driving force for efflux from the ER. Once c_t drops below threshold, these conditions are violated and the cell cannot fire a Ca²⁺ spike.

At rest, the model cell has a high resting Ca²⁺ load (c_t). On agonist stimulation, the rise in cytosolic Ca²⁺ causes a net loss of Ca²⁺ from the cell (as it is removed by the plasma membrane pumps), even though the influx of Ca²⁺ has been increased. Thus, c_t gradually declines, resulting in oscillations with a gradually decreasing baseline. If membrane transport is blocked during this phase of the response, c_t is still high enough to maintain oscillations, which would then occur purely by recycling Ca²⁺ to and from the ER.

Eventually, c_t declines to a new steady-state average level. Now, at the peak of each oscillation, the high cytosolic concentration causes a net loss of Ca²⁺ from the cell. The Ca²⁺ load thus drops below threshold, and the cell cannot fire another spike until this Ca²⁺ loss is restored by Ca²⁺ influx. Because each oscillation involves the loss and reuptake of Ca²⁺ from the cell (possibly only a small amount), these oscillations depend on Ca²⁺ influx and will be eliminated by blockage of membrane transport.

An increase in Ca²⁺ influx will increase oscillation frequency, as it increases the rate at which the Ca²⁺ lost during each spike is regained. In addition, an increase in Ca²⁺ influx will increase the average steady-state Ca²⁺ load, which will also increase oscillation frequency, even when the oscillations are not dependent on Ca²⁺ influx. A decrease in Ca²⁺ influx can eliminate oscillations, which can then be restored by an increase in [IP₃].

When membrane transport is slow enough, Ca²⁺ oscillations can persist in the absence of membrane transport, although their frequency is affected by Ca²⁺ influx.

A closed cell needs a higher Ca²⁺ load to support an oscillation than does an open cell. In the closed cell, because the Ca²⁺ load is constant, oscillations are possible only if the Ca²⁺ load is always over threshold. In the open cell this constraint is relaxed. For a large part of the oscillatory cycle, the Ca²⁺ load can be below threshold. It is only when Ca²⁺ influx from the outside drives the Ca²⁺ load over threshold that a spike occurs. Some of the Ca²⁺ released from the ER is then pumped out of the cell, the Ca²⁺ load drops below threshold, and the cycle repeats. Thus, when averaged over one cycle, the Ca²⁺ load is lower for the open cell than for the closed cell. For open-cell oscillations, Ca²⁺ influx serves to increase the Ca²⁺ load to a level where another oscillation can occur, and an increase in Ca²⁺ influx increases the oscillation frequency. However, although it is cell refilling that is governing the oscillation period, the amount of Ca²⁺ actually lost from the cell during each oscillation can be small and not easily detectable.

From our analysis we predict the following:

• Prediction 1. Blocking membrane transport can eliminate Ca²⁺ oscillations. An increase in the Ca²⁺ load of the cell will restore oscillations that have been eliminated by the block.

• Prediction 2. The effects of blocking membrane transport will depend on the timing of the block. If the block occurs soon after, or before, the increase of [IP₃], it will not eliminate oscillations, whereas if it occurs after the cell has reached a steady-state oscillation, it will eliminate the oscillations.

Experimental Verification

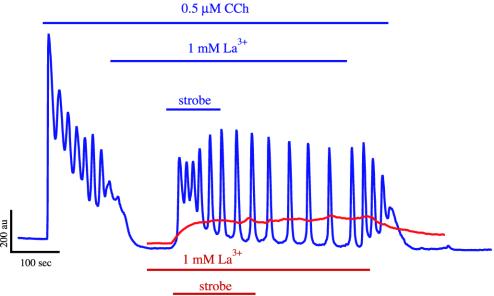
We tested our predictions experimentally in the following way. HEK293 cells were stably transfected with the m3 human muscarinic receptor and loaded with fluo-4. They were imaged on a TILL Photonics system with a monochromator (TILL Photonics, Planegg, Germany) and a progressive line-scan digital camera (Imago, Scientific Instruments, Madison, WI). The cells were stimulated with 0.5 μM carbamylcholine (CCh) to induce Ca²⁺ oscillations, then 1 mM La³⁺ was added to block both Ca²⁺ entry and the plasma membrane Ca²⁺ pump (29–33). Fig. 5 shows the effects of the addition of La³⁺ at two different times: after steady oscillations had appeared (Upper) and immediately before the addition of CCh (Lower). As predicted, oscillations were eliminated in the first case but not in the second (20 cells in four separate experiments). In the first case, the effect of La³⁺ was reversible. This result is similar to previous results showing that removal of extracellular Ca²⁺ before application of CCh to pancreatic acinar cells did not prevent oscillations, whereas removal of extracellular Ca²⁺ from a cell exhibiting Ca²⁺ oscillations terminated oscillations (17).

Fig. 5.

Addition of La³⁺ to HEK293 cells after addition of CCh eliminates oscillations (Upper), whereas addition of La³⁺ before CCh does not prevent oscillations (Lower).

In a second set of experiments, the cells were also loaded with caged Ca²⁺. Then, after the addition of La³⁺, intracellular Ca²⁺ was increased by uncaging the Ca²⁺ with the “strobe” mode on the TILL flash unit. This mode releases Ca²⁺ by brief low-energy flashes of UV light at 12 Hz. This strobing typically lasted for ≈1–1.5 min (Fig. 6). Then the La³⁺ was washed out, still in the presence of 0.5 μM CCh. A typical result (from seven cells in three separate experiments) is shown in Fig. 6. On addition of CCh, the cell exhibited Ca²⁺ oscillations, which terminated on blockage of membrane transport, even though the Ca²⁺ load of the cell remained unchanged by the addition of La³⁺. Thus, it is not the Ca²⁺ load alone that is controlling the oscillations, it is the combination of the Ca²⁺ load and the transport across the plasma membrane. An increase in c_t by the strobe then leads to the resumption of Ca²⁺ oscillations, which persist even when the strobe is turned off. Thus, once c_t is increased sufficiently, Ca²⁺ oscillations persist even in the absence of membrane transport, as predicted by the model. When membrane transport is restored by the removal of La³⁺, the oscillations continue.

Fig. 6.

Addition of CCh initiates oscillations that terminate on addition of La³⁺. Increasing c_t by strobed photorelease of cytosolic Ca²⁺ restores oscillations even during continued blockage of membrane transport (blue lines). This is equivalent to moving from point A to point B in Fig. 3. The red lines show the effect of the strobe in the presence of La³⁺ alone (done in a separate experiment, but plotted here on the same graph for ease of comparison). Note how, when the strobe is removed, [Ca²⁺] does not decline until the La³⁺ is removed.

Application of the strobe in the absence of CCh, but the presence of La³⁺, resulted in a small increase in resting [Ca²⁺] (Fig. 6, red line). On removal of the strobe, [Ca²⁺] remained unchanged, because the La³⁺ prevented it from leaving the cell; on removal of the La³⁺, [Ca²⁺] returned to baseline. Application of the strobe in the absence of caged Ca²⁺ has no effect on oscillations (34).

Discussion

Our results suggest that membrane transport of Ca²⁺ controls oscillations by controlling the Ca²⁺ load of the cell. It is already well known that Ca²⁺ influx affects oscillation frequency in many cell types (10, 13, 35–37). In Xenopus oocytes, which have a very small surface-to-volume ratio and thus a small δ, Ca²⁺ oscillations persist in the absence of external Ca²⁺, as found in the model. Nevertheless, an increase in Ca²⁺ influx increases oscillation frequency and wave speed (16, 35). In pancreatic acinar cells application of acetylcholine gives rise to Ca²⁺ oscillations, which disappear on reduction of external Ca²⁺. However, these oscillations reappear when the concentration of acetylcholine is increased (38), as expected from the results in Fig. 4. The effects of Ca²⁺ load on oscillations and waves have also been well characterized in cardiac cells (39–41).

Our model is also consistent with the results of ref. 42, which showed that blockage of Ca²⁺ influx during the interspike period eliminated further spikes, whereas, if the block occurred during a spike, the spike occurred as usual. According to our model, this is because only a small amount of Ca²⁺ influx during the interspike period is needed to push the Ca²⁺ load of the cell over threshold, whereas the majority of the Ca²⁺ in a spike is released from the ER.

We have shown that it is not the Ca²⁺ load per se that is the controlling factor, but it is rather the interplay between Ca²⁺ load and membrane transport. In HEK293 cells, addition of CCh stimulates Ca²⁺ oscillations with a gradually decreasing baseline (Fig. 6). If membrane transport is then blocked, the oscillations terminate, even though the cell's Ca²⁺ load remains unchanged. A subsequent increase in the Ca²⁺ load restores oscillations (Fig. 6), even though membrane transport of Ca²⁺ still does not occur. Furthermore, the effects of blocking membrane transport depend on the timing of the block. If the block occurs while the Ca²⁺ load is high, i.e., before application of agonist, an increase in [IP₃] will cause oscillations, whereas if the block occurs later, after the Ca²⁺ load has declined, agonist-induced oscillations will be eliminated (Fig. 5). Thus, our model can also explain previous puzzling results of ref. 17, which showed that removal of extracellular Ca²⁺ before the application of CCh did not eliminate oscillations, whereas, if Ca²⁺ oscillations had already developed, they were eliminated by the removal of extracellular Ca²⁺.

That small changes in Ca²⁺ load can have large effects on oscillations suggests a possible resolution of the controversy over the role of Ca²⁺ entry. Since experimental data have been unable to show conclusively that the ER is significantly depleted during an oscillation (43), it has been argued that ER depletion, and hence capacitative Ca²⁺ entry, does not play a significant role (12). In contrast, our model shows that cell depletion (i.e., a decrease in cytosolic and ER Ca²⁺) can play a crucial role, even when depletion is so small as to be unmeasurable. Our analysis also provides a consistent framework for understanding why removal of extracellular Ca²⁺ has such different effects, depending on the cell type, and it can explain why the timing of removal is so important (17, 42).

The same qualitative behavior occurs in at least three other models of Ca²⁺ oscillations: the Li–Rinzel model (44), and modified versions of the Atri model (45) and the LeBeau model (38) (computations not shown), all of which have different models for the IP₃ receptor and Ca²⁺ pumps. This finding suggests that our predictions do not depend on the precise model details, but they are instead a generic feature of models that have the structure shown in Fig. 1. We hypothesize that every model to follow this basic structure will exhibit the same behavior, no matter what the exact details are of the various pumps and release processes.