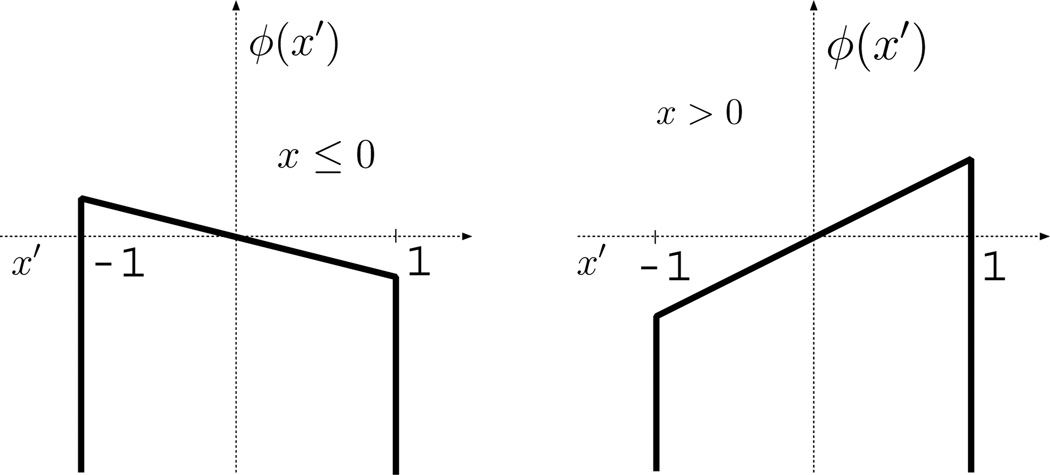Convex optimization problem prototyping for image reconstruction in computed tomography with the Chambolle-Pock algorithm

Abstract

The primal-dual optimization algorithm developed in Chambolle and Pock (CP), 2011 is applied to various convex optimization problems of interest in computed tomography (CT) image reconstruction. This algorithm allows for rapid prototyping of optimization problems for the purpose of designing iterative image reconstruction algorithms for CT. The primal-dual algorithm is briefly summarized in the article, and its potential for prototyping is demonstrated by explicitly deriving CP algorithm instances for many optimization problems relevant to CT. An example application modeling breast CT with low-intensity X-ray illumination is presented.

I. Introduction

Optimization-based image reconstruction algorithms for CT have been investigated heavily recently due to their potential to allow for reduced scanning effort while maintaining or improving image quality [1], [2]. Such methods have been considered for many years, but within the past five years computational barriers have been lowered enough such that iterative image reconstruction can be considered for practical application in CT [3]. The transition to practice has been taking place alongside further theoretical development particularly with algorithms based on the sparsity-motivated ℓ₁-norm [4], [5], [6], [7], [8], [9], [10], [11], [12]. Despite the recent interest in sparsity, optimization-based image reconstruction algorithm development continues to proceed along many fronts and there is as of yet no consensus on a particular optimization problem for the CT system. In fact, it is beginning to look like the optimization problem, upon which the iterative image reconstruction algorithms are based, will themselves be subject to design depending on the particular properties of each scanner type and imaging task.

Considering the possibility of tailoring optimization problems to a class of CT scanners, makes design of iterative image reconstruction algorithms a daunting task. Optimization formulations generally construct an objective function comprised of a data fidelity term and possible penalty terms discouraging unphysical behavior in the reconstructed image, and they possibly include hard constraints on the image. The image estimate is arrived at by extremizing the objective subject to any constraints placed on the estimate. The optimization problems for image reconstruction can take many forms depending on image representation, projection model, and objective and constraint design. On top of this, it is difficult to solve many of the optimization problems of interest. A change in optimization problem formulation can mean many weeks or months of algorithm development to account for the modification.

Due to this complexity, it would be quite desirable to have an algorithmic tool to facilitate design of optimization problems for CT image reconstruction. This tool would consist of a well-defined set of mechanical steps that generate a convergent algorithm from a specific optimization problem for CT image reconstruction. The goal of this tool would be to allow for rapid prototyping of various optimization formulations; one could design the optimization problem free of any restrictions imposed by a lack of an algorithm to solve it. The resulting algorithm might not be the most efficient solver for the particular optimization problem, but it would be guaranteed to give the answer.

In this article we consider convex optimization problems for CT image reconstruction, including non-smooth objectives, unconstrained and constrained formulations. One general algorithmic tool is to use steepest descent or projected steepest descent [13]. Such algorithms, however, do not address non-smooth objective functions and they have difficulty with constrained optimization, being applicable for only simple constraints such as non-negativity. Another general strategy involves some form of evolving quadratic approximation to the objective. The literature on this flavor of algorithm design is enormous, including non-linear conjugate gradient methods [13], parabolic surrogates [10], [14], and iteratively reweighted least-squares [15]. For the CT system these strategies often require quite a bit of know-how due to the very large scale and ill-posedness of the imaging model. Once the optimization formulation is established, however, these quadratic methods provide a good option to gain in efficiency.

One of the main barriers to prototyping alternative optimization problems for CT image reconstruction is the size of the imaging model; volumes can contain millions of voxels and the sinogram data can correspondingly consist of millions of X-ray transmission measurements. For large-scale systems there has been some resurgence of first-order methods [16], [17], [18], [19], [20], [21] and recently there has been applications of first-order methods specifically for optimization-based image reconstruction in CT [21], [22], [23]. These methods are interesting because they can be adapted to a wide range of optimization problems involving non-smooth functions such as those involving ℓ₁-based norms. In particular, the algorithm that we pursue further in this paper is a first-order primal-dual algorithm for convex problems by Chambolle and Pock [20]. This algorithm goes a long way toward the goal of optimization problem prototyping, because it covers a very general class of optimization problems that contain many optimization formulations of interest to the CT community.

For a selection of optimization problems of relevance to CT image reconstruction, we work through the details of setting up the Chambolle-Pock algorithm. We refer to these dedicated algorithms as algorithm instances. Our numerical results demonstrate that the algorithm instances achieve the solution of difficult convex optimization problems under challenging conditions in reasonable time and without parameter tuning. In Sec. II the CP methodology and algorithm is summarized; in Sec. III various optimization problems for CT image reconstruction are presented along with their corresponding CP algorithm instance; and Sec. IV shows a limited study on a breast CT simulation that demonstrates the application of the derived CP algorithm instances.

II. Summary of the generic Chambolle-Pock algorithm

The Chambolle-Pock (CP) algorithm [20] is primal-dual meaning that it solves an optimization problem simultaneously with its dual. On the face of it, it would seem to involve extra work by solving two problems instead of one, but the algorithm comes with convergence guarantees and solving both problems provides a robust, non-heuristic convergence check – the duality gap.

The CP algorithm applies to a general form of the primal minimization:

$$\underset{x}{\text{min}}\{F(\mathit{\text{Kx}})+G(x)\},$$ (1)

and a dual maximization:

$$\underset{y}{\text{max}}\{-F^{*}(y)-G^{*}(-K^{T}y)\},$$ (2)

where x and y are finite dimensional vectors in the spaces X and Y; respectively; K is a linear transform from X to Y; G and F are convex, possibly non-smooth, functions mapping the respective X and Y spaces to non-negative real numbers; and the superscript “*” in the dual maximization problem refers to convex conjugation, defined in Eqs. (3) and (4). We note that the matrix K need not be square; X and Y will in general have different dimension. Given a convex function H of a vector z ∈ Z, its conjugate can be computed by the Legendre transform [24], and the original function can be recovered by applying conjugation again:

$$H^{*}(z)=\underset{z\prime }{\text{max}}\{{\langle z,z\prime \rangle }_Z-H(z\prime )\},$$ (3)

$$H(z\prime )=\underset{z}{\text{max}}\{{\langle z\prime ,z\rangle }_Z-H^{*}(z)\}.$$ (4)

The notation 〈·, ·〉_Z refers to the inner product in the vector space Z.

Formally, the primal and dual problems are connected in a generic saddle point optimization problem:

$$\underset{x}{\text{min}}\underset{y}{\text{max}}\{{\langle Kx,y\rangle }_Y+G(x)-F^{*}(y)\}.$$ (5)

By performing the maximization over y in Eq. (5), using Eq. (4) with Kx associated with y′, the primal minimization Eq. (1) is derived. Similarly, performing the minimization over x in Eq. (5), using Eq. (3) and the identity 〈K x, y〉 = 〈x, K^T y〉, yields the dual maximization Eq. (2), where the T superscript denotes matrix transposition.

The minimization problem in Eq. (1), though compact, covers many minimization problems of interest to tomographic image reconstruction. Solving the dual problem, Eq. (2), simultaneously allows for assessment of algorithm convergence. For intermediate estimates x and y of the primal minimization and the dual maximization, respectively, the primal objective will be greater than or equal to the dual objective. The difference between these objectives is referred to as the duality gap, and convergence is achieved when this gap is zero. Plenty of examples of useful optimization problems for tomographic image reconstruction will be described in detail in Sec. III, but first we summarize Algorithm 1 from Ref. [20].

Algorithm 1.

Pseudocode for N-steps of the basic Chambolle-Pock algorithm. The constant L is the ℓ₂-norm of the matrix K; τ and σ are non-negative CP algorithm parameters, which are both set to 1/L in the present application; θ ∈ [0, 1] is another CP algorithm parameter, which is set to 1; and n is the iteration index. The proximal operators prox_σ and prox_τ are defined in Eq. (6).

1:	L ← ‖K‖2; τ ← 1/L; σ ← 1/L; θ ← 1; n ← 0
2:	initialize x0 and y0 to zero values
3:	x̄0 ← x0
4:	repeat
5:	yn+1 ← proxσ[F*](yn + σKx̄n)
6:	xn+1 ← proxτ [G](xn − τKT yn+1)
7:	x̄n+1 ← xn+1 + θ(xn+1 − xn)
8:	n ← n + 1
9:	untiln ≥ N

A. Chambolle-Pock: Algorithm 1

The CP algorithm simultaneously solves Eqs. (1) and (2). As presented in Ref. [20] the algorithm is simple, yet extremely effective. We repeat the steps here in Listing 1 for completeness, providing the parameters that we use for all results shown below. The parameter descriptions are provided in Ref. [20], but note that in our usage specified above there are no free parameters. This is an extremely important feature for our purpose of optimization prototyping. One caveat is that technically the proof of convergence for the CP algorithm assumes L²στ < 1, but in practice we have never encountered a case where the choice σ = τ = 1/L failed to tend to convergence. We stress that in Eq. (6) the matrix K^T needs to be the transpose of the matrix K; this point can sometimes be confusing because K for imaging applications is often intended to be an approximation to some continuous operator such as projection or differentiation and often K^T is taken to mean the approximation to the continuous operator’s adjoint, which may or may not be the matrix transpose of K. The constant L is the magnitude of the matrix K, its largest singular value. Appendix A gives the details on computing L via the power method. Key to deriving the particular algorithm instances are the proximal mappings prox_σ[F*] and prox_τ[G] (called resolvent operators in Ref. [20]).

The proximal mapping is used to generate a descent direction for the convex function H and it is obtained by the following minimization:

$${\mathit{\text{prox}}}_{\sigma }[H](z)=\underset{z\prime }{\text{arg min}}\{H(z\prime )+\frac{{\Vert z-z\prime \Vert }_2^2}{2\sigma }\}$$ (6)

This operation does admit non-smooth convex functions, but H does need to be simple enough that the above minimization can be solved in closed form. For CT applications the ability to handle non-smooth F and G allows the study of many optimization problems of recent interest, and the simplicity limitation is not that restrictive as will be seen.

B. The CP algorithm for prototyping of convex optimization problems

To prototype a particular convex optimization problem for CT image reconstruction with the CP algorithm, there are five basic steps:

1. Map the optimization problem to the generic minimization problem in Eq. (1).

2. Derive the dual maximization problem, Eq. (2), by computing the convex conjugates of F and G using the Legendre transform Eq. (3).

3. Derive the proximal mappings of F and G using Eq. (6).

4. Substitute the results of (3) into the generic CP algorithm in Listing 1 to obtain a CP algorithm instance.

5. Run the algorithm, monitoring the primal-dual gap for convergence.

As will be seen below, a great variety of constrained and unconstrained optimization problems can be written in the form of Eq. (1). Specifically, using the algebra of convex functions [24], that the sum of two convex functions is convex and that the composition of a convex function with a linear transform is a convex function, many interesting optimization formulations can be put in the form of Eq. (1). We will also make use of convex functions which are not smooth – notably ℓ₁ based norms and indicator functions δ_S(x):

$${\delta }_S(x)\equiv \{\begin{array}{cc}0\hfill & x\in S\hfill \\ \mathrm{\infty }\hfill & x\notin S\hfill \end{array},$$ (7)

where S is a convex set. The indicator function is particularly handy for imposing constraints. In computing the convex conjugate and proximal mapping of convex functions, we make much use of the standard calculus rule for extremization, ∇f = 0, but such computations are augmented also with geometric reasoning, which may be unfamiliar. Accordingly, we have included appendices to show some of these computation steps. With this quick introduction, we are now in a position to derive various algorithm instances for CT image reconstruction from different convex optimization problems.

III. Chambolle-Pock algorithm instances for CT

For this article, we only consider optimization problems involving the linear imaging model for X-ray projection, where the data are considered as line integrals over the object’s X-ray attenuation coefficient. Generically, maintaining consistent notation with Ref. [20], the discrete-to-discrete CT system model [25] can be written as:

$$\mathit{\text{Au}}=g,$$ (8)

where A is the projection matrix taking an object represented by expansion coefficients u and generating a set of line-integration values g. This model covers a multitude of expansion functions and CT configurations, including both 2D fan-beam and 3D cone-beam projection data models.

A few notes on notation are in order. In the following, we largely avoid indexing of the various vector spaces in order that the equations and pseudocode listings are brief and clear. Any of the standard algebraic operations between vectors is to be interpreted in a component-wise manner unless explicitly stated. Also, an algebraic operation between a scalar and a vector is to be distributed among all components of the vector; e.g., 1 + v adds one to all components of v. For the optimization problems below, we employ three vector spaces: I the space of discrete images in either 2 or 3 dimensions; D the space of the CT sinograms (or projection data); and V the space of spatial-vector-valued image arrays, V = I^d where d = 2 or 3 for 2D and 3D-space, respectively. For the CT system model Eq. (8), u ∈ I, and g ∈ D, but we note that the space D can also include sinograms which are not consistent with the linear system matrix A. The vector space V will be used below for forming the total variation (TV) semi-norm; an example of such a vector v ∈ V is the spatial-gradient of an image u. Although the pixel representation is used, much of the following can be applied to other image expansion functions. As we will be making much use of certain indicator functions, we define two important sets, Box(a) and Ball(a), through their indicator function:

$${\delta }_{\mathit{\text{Box}}(a)}(x)\equiv \{\begin{array}{cc}0\hfill & {\Vert x\Vert }_{\mathrm{\infty }}\le a\hfill \\ \mathrm{\infty }\hfill & {\Vert x\Vert }_{\mathrm{\infty }}>a\hfill \end{array},$$ (9)

and

$${\delta }_{\mathit{\text{Ball}}(a)}(x)\equiv \{\begin{array}{cc}0\hfill & {\Vert x\Vert }_2\le a\hfill \\ \mathrm{\infty }\hfill & {\Vert x\Vert }_2>a\hfill \end{array}.$$ (10)

Recall that the ‖ · ‖_∞ norm selects the largest component of the argument, thus Box(a) comprises vectors with no component larger than a (in 2D Box(a) is a square centered on the origin with width 2a). We also employ 0_X and 1_X to mean a vector from the space X with all components set to 0 and 1, respectively.

A. Image reconstruction by least-squares

Perhaps the simplest optimization method for performing image reconstruction is to minimize the the quadratic data error function. We present this familiar case in order to gain some experience with the mechanics of deriving CP algorithm instances, and because the quadratic data error term will play a role in other optimization problems below. The primal problem of interest is:

$$\underset{u}{\text{min}}\frac{1}{2}{\Vert \mathit{\text{Au}}-g\Vert }_2^2.$$ (11)

To derive the CP algorithm instance, we make the following mechanical associations with the primal problem Eq. (1):

$$F(y)=\frac{1}{2}{\Vert y-g\Vert }_2^2,$$ (12)

$$G(x)=0,$$ (13)

$$x=u,y=\mathit{\text{Au}}$$ (14)

$$K=A.$$ (15)

Applying Eq. 3, we obtain the convex conjugates of F and G:

$$F^{*}(p)=\frac{1}{2}{\Vert p\Vert }_2^2+{\langle p,g\rangle }_D,$$ (16)

$$G^{*}(q)={\delta }_{0_I}(q),$$ (17)

where p ∈ D and q ∈ I. While obtaining F* in this case involves elementary calculus for extremization of Eq. (3), finding G* needs some comment for those unfamiliar with convex analysis. Using the definition of the Legendre transform for G(x) = 0, we have:

$$G^{*}(q)=\underset{x}{\text{max}}{\langle q,x\rangle }_I.$$ (18)

There are two possibilities: (1) q = 0_I, in which case the maximum value of 〈q, x〉_I is 0, and (2) q ≠ 0_I, in which case this inner product can increase without bound, resulting in a maximum value of ∞. Putting these two cases together yields the indicator function in Eq. (16). With F, G, and their conjugates, the optimization problem dual to Eq. (11) can be written down from Eq. (2):

$$\underset{p}{\text{max}}\{-\frac{1}{2}{\Vert p\Vert }_2^2-{\langle p,g\rangle }_D-{\delta }_{0_I}(-A^{T}p)\}.$$ (19)

For deriving the CP algorithm instance, it is not strictly necessary to have this dual problem, but it is useful for evaluating convergence.

The CP algorithm solves Eqs. (11) and (19) simultaneously. In principle, the values of the primal and dual objective functions provide a test of convergence. During the iteration the objective of the primal problem will by greater than the objective of the dual problem, and when the solutions of the respective problems are reached, these objectives will be equal. Comparing the duality gap, i.e. the difference between the primal objective and the dual objective, with 0 thus provides a test of convergence. The presence of the indicator function in the dual problem, however, complicates this test. Due to the negative sign in front of the indicator, when the argument is not the zero vector, this term and therefore the whole dual objective is assigned to a value of −∞. The dual objective achieves a finite, testable value only when the indicator function attains the value of 0, when A^T p = 0_I. Effectively, the indicator function becomes a way to write down a constraint in the form of a convex function, in this case an equality constraint. The dual optimization problem can thus alternately be written as a conventional constrained maximization:

$$\underset{p}{\text{max}}\{-\frac{1}{2}{\Vert p\Vert }_2^2-{\langle p,g\rangle }_D\}\text{ such that }{A}^{T}p={\mathbf{0}}_I.$$ (20)

The convergence check is a bit problematic, because the equality constraint will not likely be strictly satisfied in numerical computation. Instead, we introduce a conditional primal-dual gap (the difference between the primal and dual objectives ignoring the indicator function) given the estimates u′ and p′:

$$\mathit{\text{cPD}}(u\prime ,p\prime )={\Vert \mathit{\text{Au}}\prime -g\Vert }_2^2+\frac{1}{2}{\Vert p\prime \Vert }_2^2+{\langle p\prime ,g\rangle }_D,$$ (21)

and separately monitor A^T p′ to see if it is tending to 0_I. Note that the conditional primal-dual gap need not be positive, but it should tend to zero.

To finally attain the CP algorithm instance for image reconstruction by least-squares, we derive lines 5 and 6 in Alg. 1. The proximal mapping prox_σ[F*](y), y ∈ D, for this problem results from a quadratic minimization:

$${\mathit{\text{prox}}}_{\sigma }[F^{*}](y)=\underset{y\prime }{\text{arg min}}\{\frac{1}{2}{\Vert y\prime \Vert }_2^2+{\langle y\prime ,g\rangle }_D+\frac{{\Vert y-y\prime \Vert }_2^2}{2\sigma }\}=\frac{y-\sigma g}{1+\sigma },$$ (22)

and as G(x) = 0, x ∈ I, the corresponding proximal mapping is

$${\mathit{\text{prox}}}_{\tau }[G](x)=x.$$ (23)

Substituting in the arguments from the generic algorithm, leads to the update steps in Listing 2. The constant L = ‖A‖₂ is the largest singular value of A (see Appendix A for details on the power method). Crucial to the implementation of the CP algorithm instance is that A^T be the exact transpose of A, which is a non-trivial matter for tomographic applications, because the projection matrix A is usually computed on-the-fly [26], [27], [28]. Convergence of the CP algorithm is only guaranteed when A^T is the exact transpose of A, although it may be possible to extend the CP algorithm to mismatched projector/back-projector pairs by employing the analysis in Ref. [29].

Algorithm 2.

Pseudocode for N-steps of the least-squares Chambolle-Pock algorithm instance.

1:	L ← ‖A‖2; τ ← 1/L; σ ← 1/L; θ ← 1; n ← 0
2:	initialize u0 and p0 to zero values
3:	ū0 ← u0
4:	repeat
5:	pn+1 ← (pn + σ(Aūn − g))/(1 + σ)
6:	un+1 ← un − τAT pn+1
7:	ūn+1 ← un+1 + θ(un+1 − un)
8:	n ← n + 1
9:	untiln ≥ N

This derivation of the CP least-squares algorithm instance illustrates the method on a familiar optimization problem, and it provides a point of comparison with standard algorithms; this quadratic minimization problem can be solved straight-forwardly with the basic, linear conjugate gradients (CG) algorithm. Another important point for this particular algorithm instance, where limited projection data can lead to an underdetermined system, is that the CP algorithm will yield a minimizer of the objective ${\Vert \mathit{\text{Au}}-g\Vert }_2^2$ which depends on the initial image u₀. In this case, it is recommended to take advantage of the prototyping capability of the CP framework to augment the optimization problem so that it selects a unique image independent of initialization. For example, one often seeks an image closest to either 0_I or a prior image, which can be formulated by adding a quadratic term ${\Vert u\Vert }_2^2$ or ${\Vert u-u_{\text{prior}}\Vert }_2^2$ with a small combination coefficient.

1) Adding in non-negativity constraints

One of the flexibilities of the CP method becomes apparent in adding bound constraints. While CG is also flexible tool for dealing with large and small quadratic optimization, modification to include constraints, such as non-negativity, considerably complicates the CG algorithm. For CP, adding in bound constraints is simply a matter of introducing the appropriate indicator function into the primal problem:

$$\underset{u}{\text{min}}\{\frac{1}{2}{\Vert \mathit{\text{Au}}-g\Vert }_2^2+{\delta }_P(u)\},$$ (24)

where the set P is all u with non-negative components. Again, we make the mechanical associations with the primal problem Eq. (1):

$$F(y)=\frac{1}{2}{\Vert y-g\Vert }_2^2,$$ (25)

$$G(x)={\delta }_P(x),$$ (26)

$$x=u,y=\mathit{\text{Kx}},$$ (27)

$$K=A.$$ (28)

The difference from the unconstrained problem is the function G(x). It turns out that the convex conjugate of δ_P (x) is:

$${\delta }_P^{*}(x)={\delta }_P(-x),$$ (29)

see Appendix B for insight on convex conjugate of indicator functions. Straight substitution of G* and F* into Eq. (2), yields the dual problem:

$$\underset{p}{\text{max}}\{-\frac{1}{2}{\Vert p\Vert }_2^2-{\langle p,g\rangle }_D-{\delta }_P(A^{T}p)\}.$$ (30)

As a result the conditional primal-dual gap is the same as before. The difference now is that the constraint checks are that A^T p and u should be non-negative.

To derive the algorithm instance, we need the proximal mapping prox_τ[G], which by definition is:

$${\mathit{\text{prox}}}_{\tau }[{\delta }_P](x)=\underset{x\prime }{\text{arg min}}\{{\delta }_P(x\prime )+\frac{{\Vert x-x\prime \Vert }_2^2}{2\tau }\}.$$ (31)

The indicator in the objective prevents consideration of negative components of x′. The ℓ₂ term can be regarded as a sum over the square difference between components of x and x′; thus the objective is separable and can be minimized by constructing x′ such that $x_i^{\prime }=x_i$ when x_i > 0 and $x_i^{\prime }=0$ when x_i ≤ 0. Thus this proximal mapping becomes a non-negativity thresholding on each component of x:

$${[{\mathit{\text{prox}}}_{\tau }[{\delta }_P](x)]}_i={[\mathit{\text{pos}}(x)]}_i\equiv \{\begin{array}{cc}{x}_i\hfill & x_i>0\hfill \\ 0\hfill & x_i\le 0\hfill \end{array}.$$ (32)

Substituting into the generic pseudocode yields Listing 3. Again, we have L = ‖A‖₂. The indicator function δ_P leads to the intuitive modification that non-negativity thresholding is introduced in line 6 of Listing 3. In this case the non-negativity constraint in u will be automatically satisfied by all iterates u_n. Upper bound constraints are equally simple to include.

Algorithm 3.

Pseudocode for N-steps of the least-squares with non-negativity constraint, CP algorithm instance.

1:	L ← ‖A‖2; τ ← 1/L; σ ← 1/L; θ ← 1; n ← 0
2:	initialize u0 and p0 to zero values
3:	ū0 ← u0
4:	repeat
5:	pn+1 ← (pn + σ(Aūn − g))/(1 + σ)
6:	un+1 ← pos(un − τAT pn+1)
7:	ūn+1 ← un+1 + θ(un+1 − un)
8:	n ← n + 1
9:	untiln ≥ N

B. Optimization problems based on the Total Variation (TV) semi-norm

Optimization problems with the TV semi-norm have received much attention for CT image reconstruction lately because of their potential to provide high quality images from sparse view sampling [8], [30], [22], [9], [31], [32], [33]. The TV semi-norm has been known to be useful for performing edge-preserving regularization, and recent developments in compressive sensing have sparked even greater interest in the use of this semi-norm. Algorithm-wise the TV semi-norm is difficult to handle. Although it is convex, it is not linear, quadratic or even everywhere-differentiable, and the lack of differentiability precludes the use of standard gradient-based optimization algorithms. In this sub-section we go through, in detail, the derivation of a CP algorithm instance for a TV-regularized least squares data error norm. We then consider the Kullback-Leibler (KL) data divergence, which is implicitly employed by many iterative algorithms based on maximum likelihood expectation maximization (MLEM). We also consider a data error norm based on ℓ₁ which can have some advantage in reducing the impact of image discretization error, which generally leads to a highly non-uniform error in the data domain. Finally, we derive a CP algorithm instance for constrained TV-minimization, which is mathematically equivalent to the least-squares-plus-TV problem [34], but whose data-error constraint parameter has more physical meaning than the parameter used in the corresponding unconstrained minimization. While the previous CP instances solve optimization problems, which can be solved efficiently by well-known algorithms, the following CP instances are new for the application of CT image reconstruction.

The optimization problem of interest is

$$\underset{u}{\text{min}}\{\frac{1}{2}{\Vert \mathit{\text{Au}}-g\Vert }_2^2+\lambda {\Vert (|{\nabla }_u|)\Vert }_1\},$$ (33)

where the last term, the ℓ₁-norm of the gradient-magnitude image, is the isotropic TV semi-norm. The spatial-vector image ∇u represents a discrete approximation to the image gradient which is in the vector space V, i.e., the space of spatial-vector-valued image arrays. The expression |∇u| is the gradient-magnitude image, an image array whose pixel values are the gradient magnitude at the pixel location. Thus, ∇u ∈ V and |∇u| ∈ I. Because ∇ is defined in terms of finite differencing, it is a linear transform from an image array to a vector-valued image array, the precise form of which is covered in Appendix D. This problem was not explicitly covered in Ref. [20], and we fill in the details here. For this case, matching the primal problem to Eq. (1) is not as obvious as the previous examples. We recognize in Eq. (33) that both terms involve a linear transform, thus the whole objective function can be written in the form F(Kx) with the following assignments:

$$F(y,z)=F_1(y)+F_2(z),F_1(y)=\frac{1}{2}{\Vert y-g\Vert }_2^2,F_2(z)=\lambda {\Vert (|z|)\Vert }_1,$$ (34)

$$G(x)=0,$$ (35)

$$x=u,y=\mathit{\text{Au}},z=\nabla u,$$ (36)

$$K=\left(\begin{array}{c}\hfill A\hfill \\ \hfill \nabla \hfill \end{array}\right),$$ (37)

where u ∈ I, y ∈ D, and z ∈ V. Note that F(y, z) is convex because it is the sum of two convex functions. Also the linear transform K takes an image vector x and gives a data vector y and an image gradient vector z. The transpose of K, K^T = (A^T, −div), will produce an image vector from a data vector y and an image gradient vector z:

$$x\leftarrow A^{T}y-\mathit{\text{div }}z,$$ (38)

where we use the same convention as in Ref. [20] that −div ≡ ∇^T, see Appendix D.

In order to get the convex conjugate of F we need $F_2^{*}$. For readers unfamiliar with the Legendre transform of indicator functions Appendix B illustrates the transform of some common cases. By definition,

$$F_2^{*}(q)=\underset{z}{\text{max}}\{{\langle q,z\rangle }_V-\lambda {\Vert (|z|)\Vert }_1\},$$ (39)

where q ∈ V, like z, is a vector-valued image array. There are two cases to consider: (1) the magnitude image |q| at all pixels is less than or equal to λ, i.e. |q| ∈ Box(λ) and (2) the magnitude image |q| has at least one pixel greater than λ, i.e. |q| ∉ Box(λ). It turns out that for the former case the maximization in Eq. (39) yields 0, while the latter cause yields ∞. Putting these two cases together, we have

$$F_2^{*}(q)={\delta }_{\mathit{\text{Box}}(\lambda )}(|q|).$$ (40)

The conjugates of F and G are:

$$F^{*}(p,q)=\frac{1}{2}{\Vert p\Vert }_2^2+{\langle p,g\rangle }_D+{\delta }_{\mathit{\text{Box}}(\lambda )}(|q|),$$ (41)

$$G^{*}(r)={\delta }_{{\mathbf{0}}_I}(r),$$ (42)

where p ∈ D, q ∈ V, and r ∈ I.

The problem dual to Eq. (33) becomes:

$$\underset{p,q}{\text{max}}\{-\frac{1}{2}{\Vert p\Vert }_2^2-{\langle p,g\rangle }_D-{\delta }_{\mathit{\text{Box}}(\lambda )}(|q|)-{\delta }_{{\mathbf{0}}_I}(\mathit{\text{div }}q-A^{T}p)\}.$$ (43)

The resulting conditional primal-dual gap is

$$\mathit{\text{cPD}}(u\prime ,p\prime ,q\prime )=\frac{1}{2}{\Vert \mathit{\text{Au}}\prime -g\Vert }_2^2+\lambda {\Vert (|\nabla u|)\Vert }_1+\frac{1}{2}{\Vert p\prime \Vert }_2^2+{\langle p\prime ,g\rangle }_P$$ (44)

with additional constraints |q′| ∈ Box(λ) and A^T p′ − div q′ = 0_I. The final piece needed for putting together the CP algorithm instance for Eq. (33) is the proximal mapping:

$${\mathit{\text{prox}}}_{\sigma }[F^{*}](y,z)=(\frac{y-\sigma g}{1+\sigma },\frac{\lambda z}{\text{max}(\lambda {\mathbf{1}}_I,|z|)}).$$ (45)

The proximal mapping of the data term was covered previously, and that of the TV term is explained in Appendix C. With the necessary pieces in place, the CP algorithm instance for the ${\ell }_2^2$-TV objective can be written down in Listing 4. Line 6, and the corresponding expression in Eq. (45), require some explanation, because the division operation is non-standard as the numerator is in V and the denominator is in I. The effect of this line is to threshold the magnitude of the spatial-vectors at each pixel in q_n + σ∇ū_n to the value λ: spatial-vectors larger than λ have their magnitude rescaled to λ. The resulting thresholded, spatial-vector image is then assigned to q_n+1. Recall that 1_I at line 6 is an image with all pixels set to 1. The operator |·| in this line converts a vector-valued image in V to a magnitude image in I, and the max(λ1_I, ·) operation thresholds the lower bound of the magnitude image to λ pixel-wise. Operationally, the division is performed by dividing the spatial-vector at each pixel of the numerator by the scalar in the corresponding pixel of the denominator. Another potential source of confusion is computing the magnitude ‖(A, ∇)‖₂. The power method for doing this is covered explicitly in Appendix A. If it is desired to enforce the positivity constraint, the indicator δ_P(u) can be added to the primal objective, and the effect of this is indicator is the same as for Listing 3; namely the right hand side of line 7 goes inside the pos(·) operator.

Algorithm 4.

Pseudocode for N-steps of the ${\ell }_2^2$-TV CP algorithm instance.

1:	L ← ‖(A, ∇)‖2; τ ← 1/L; σ ← 1/L; θ ← 1; n ← 0
2:	initialize u0, p0, and q0 to zero values
3:	ū0 ← u0
4:	repeat
5:	pn+1 ← (pn + σ(Aūn − g))/(1 + σ)
6:	qn+1 ← λ(qn + σ∇ūn)/max(λ1I, |qn + σ∇ūn|)
7:	un+1 ← un − τAT pn+1 + τdiv qn+1
8:	ūn+1 ← un+1 + θ(un+1 − un)
9:	n ← n + 1
10:	untiln ≥ N

1) Alternate data divergences

For a number of reasons motivated by the physical model of imaging systems, it may be of use to formulate optimization problems for CT image reconstruction with alternate data-error terms. A natural extension of the quadratic data divergence is to include a diagonal weighting matrix. The corresponding CP algorithm instance can be easily derived following the steps mentioned above. As pointed out above, the CP method is not limited to quadratic objective functions and other important convex functions can be used. We derive, here, three additional CP algorithm instances. For alternate data divergences we consider the oft-used KL divergence, and one not so commonly used, ℓ₁ data-error norm. For the following, we need only analyze the function F₁, as everything else remains the same as for the ${\ell }_2^2$-TV objective in Eq. (33).

TV plus KL data divergence

One data divergence of particular interest for tomographic image reconstruction is KL. Objectives based on KL are what is being optimized in the various forms of MLEM, and it is used often when data noise is a significant physical factor and the data are modeled as being drawn from a multivariate Poisson probability distribution [25]. For the situation where the view-sampling is also sparse, it might be of interest to combine a KL data error term with the TV semi-norm in the following primal optimization:

$$\underset{u}{\text{min}}\{{\displaystyle \sum _i}{[\mathit{\text{Au}}-g+g\text{ ln }g-g\text{ ln}(\mathit{\text{pos}}(\mathit{\text{Au}}))]}_i+{\delta }_P(\mathit{\text{Au}})+\lambda {\Vert (|\nabla u|)\Vert }_1\},$$ (46)

where ∑_i[·]_i performs summation over all components of the vector argument. This example proceeds as above except that the F₁ function is different:

$$F_1(y)={\displaystyle \sum _i}{[y-g+g\text{ ln }g-g\text{ ln}(\mathit{\text{pos}}(y))]}_i+{\delta }_P(y)$$ (47)

where y ∈ D, and the function ln operates on the components of its argument. Use of the KL data divergence makes sense only with positive linear systems A and non-negative pixel values u and data g. However, by defining the function over the whole space and using an indicator function to restrict the domain [24], a wide variety of optimization problems can be treated in a uniform manner. Accordingly, δ_P is introduced into the F₁ objective and the pos operator is used just so that this objective is defined in the real numbers. The derivation of $F_1^{*}$, though mechanical, is a little bit too long to be included here. We simply state the resulting conjugate function:

$$F_1^{*}(p)={\displaystyle \sum _i}{[-g\text{ ln}\mathit{\text{pos}}({\mathbf{1}}_D-p)]}_i+{\delta }_P({\mathbf{1}}_D-p).$$ (48)

The resulting dual problem to Eq. (46) is thus:

$$\underset{p,q}{\text{max}}\{{\displaystyle \sum _i}[g\text{ ln }{(\mathit{\text{pos}}({\mathbf{1}}_D-p)]}_i-{\delta }_P({\mathbf{1}}_D-p)-{\delta }_{\mathit{\text{Box}}(\lambda )}(|q|)-{\delta }_{{\mathbf{0}}_I}(\mathit{\text{div }}q-A^{T}p)\}.$$ (49)

To form the algorithm instance, we need the proximal mapping ${\mathit{\text{prox}}}_{\sigma }[F_1^{*}](y)$

$${\mathit{\text{prox}}}_{\sigma }[F_1^{*}](y)=\frac{1}{2}({\mathbf{1}}_D+y-\sqrt{{(y-{\mathbf{1}}_D)}^2+4\sigma g}).$$ (50)

An interesting point in the derivation, shown partially in Appendix C, of ${\mathit{\text{prox}}}_{\sigma }[F_1^{*}](y)$ is that the quadratic equation is needed, and the support function in $F_1^{*}(p)$ is used to select the correct (in this case negative) root of the discriminant in the quadratic formula. With the new function F₁, its conjugate, and the conjugate’s proximal mapping, we can write down the CP algorithm instance. Listing 5 gives the CP algorithm instance minimizing a KL plus TV semi-norm objective. The difference between this algorithm instance and the previous ${\ell }_2^2$-TV case comes only at the update at line 5. This algorithm instance has the interesting property that the intermediate image estimates u_n can have negative values even though the converged solution will be non-negative. If it is desirable to have the intermediate image estimates be non-negative, the non-negativity constraint can be easily introduced by adding the indicator δ_P (u) to the primal objective, resulting in the addition of the pos(·) operator at line 7 as was shown in Listing 3.

Algorithm 5.

Pseudocode for N-steps of the KL-TV CP algorithm instance.

1:	L ← ‖(A, ∇)‖2; τ ← 1/L; σ ← 1/L; θ ← 1; n ← 0
2:	initialize u0, p0, and q0 to zero values
3:	ū0 ← u0
4:	repeat
5:	$p_{n+1}\leftarrow \frac{1}{2}({\mathbf{1}}_D+p_n+\sigma A{ū}_n-\sqrt{{(p_n+\sigma A{ū}_n-{\mathbf{1}}_D)}^2+4\sigma g})$
6:	qn+1 ← λ(qn + σ∇ūn)/max(λ1I, |qn + σ∇ūn|)
7:	un+1 ← un − τAT pn+1 + τdiv qn+1
8:	ūn+1 ← un+1 + θ(un+1 − un)
9:	n ← n + 1
10:	untiln ≥ N

TV plus ℓ₁ data-error norm

The combination of TV semi-norm regularization and ℓ₁ data-error norm has been proposed for image denoising and it has some interesting properties for that purpose [35]. This objective is also presented in Ref. [20]. For tomography, this combination may be of interest because the ℓ₁ data-error term is an example of a robust fit to the data. The idea of robust approximation is to weakly penalize data that are outliers [36]. Fitting with the commonly used quadratic error function, clearly puts heavy weight on outlying measurements which in some situations can lead to streak artifacts in the images. In particular, for tomographic image reconstruction with a pixel basis, discretization error and metal objects can lead to highly non-uniform error in the data model. Use of the ℓ₁ data-error term may allow for large errors for measurements along the tangent rays to internal structures, where discretization can have a large effect. The ℓ₁ data-error term also puts greater emphasis on fitting the data that lie close to the model. The primal problem of interest is:

$$\underset{u}{\text{min}}\{{\Vert \mathit{\text{Au}}-g\Vert }_1+\lambda {\Vert (|\nabla u|)\Vert }_1\}.$$ (51)

For this objective, the function F₁ is:

$$F_1(y)={\Vert y-g\Vert }_1.$$ (52)

Computing the convex conjugate $F_1^{*}$ yields

$$F_1^{*}(p)={\delta }_{\mathit{\text{Box}}(1)}(p)+{\langle p,g\rangle }_D,$$ (53)

and the resulting dual problem is:

$$\underset{p,q}{\text{max}}\{-{\delta }_{\mathit{\text{Box}}(1)}(p)-{\langle p,g\rangle }_D-{\delta }_{\mathit{\text{Box}}(\lambda )}(|q|)-{\delta }_{{\mathbf{0}}_I}(\mathit{\text{div }}q-A^{T}p)\}.$$ (54)

The proximal mapping necessary for completing the algorithm instance is

$${\mathit{\text{prox}}}_{\sigma }[F_1^{*}](y)=\frac{y-g\sigma }{\text{max}({\mathbf{1}}_D,|y-g\sigma |)},$$ (55)

where 1_D is a data array with each component set to one and the max operation is performed component-wise. The corresponding pseudo-code for minimizing Eq. (51) is given in Listing 6, where the only difference between this code and the previous two occurs at line 5. The ability to deal with non-smooth objectives uncomplicates this particular problem substantially. If smoothness were required, there would have to be smoothing parameters on both the ℓ₁ and TV terms, adding two more parameters than necessary to a study of the image properties as a function of the optimization-problem parameters.

Algorithm 6.

Pseudocode for N-steps of the ℓ₁-TV CP algorithm instance.

1:	L ← ‖(A, ∇)‖2; τ ← 1/L; σ ← 1/L; θ ← 1; n ← 0
2:	initialize u0, p0, and q0 to zero values
3:	ū0 ← u0
4:	repeat
5:	pn+1 ← (pn + σ(Aūn − g))/max(1D, |pn + σ(Aūn − g)|)
6:	qn+1 ← λ(qn + σ∇ūn)/max(λ1I, |qn + σ∇ūn|)
7:	un+1 ← un − τAT pn+1 + τdiv qn+1
8:	ūn+1 ← un+1 + θ(un+1 − un)
9:	n ← n + 1
10:	untiln ≥ N

2) Constrained, TV-minimization

The previous three optimization problems combine a data fidelity term with a TV-penalty, and the balance of the two terms is controlled by the parameter λ. An inconvenience of such optimization problems is that it is difficult to physically interpret λ. Focusing on combining an ℓ₂ data-error norm with TV, reformulating Eq. (33) as a constrained, TV-minimization leads to the following primal problem:

$$\underset{u}{\text{min}}\{{\Vert (|\nabla u|)\Vert }_1+{\delta }_{\mathit{\text{Ball}}(\epsilon )}(\mathit{\text{Au}}-g)\},$$ (56)

where δ_Ball(ε)(Au − g) is zero for ‖Au − g‖₂ ≤ ε. When ε > 0, this problem is equivalent to the unconstrained optimization Eq. (33), see e.g. Ref. [34], in the sense that for each positive ε there is a corresponding λ yielding the same solution. For this constrained, TV-minimization, the function F₁ is

$$F_1(y)={\delta }_{\mathit{\text{Ball}}(\epsilon )}(y-g).$$ (57)

The corresponding conjugate is

$$F_1^{*}(p)=\epsilon {\Vert p\Vert }_2+{\langle p,g\rangle }_D,$$ (58)

leading to the dual problem:

$$\underset{p,q}{\text{max}}\{-\epsilon {\Vert p\Vert }_2-{\langle p,g\rangle }_D-{\delta }_{\mathit{\text{Box}}(1)}(q)-{\delta }_{{\mathbf{0}}_I}(\mathit{\text{div }}q-A^{T}p)\}.$$ (59)

Again, for the algorithm instance we need the proximal mapping ${\mathit{\text{prox}}}_{\sigma }[F_1^{*}]$:

$${\mathit{\text{prox}}}_{\sigma }[F_1^{*}](y)=\text{max}({\Vert y-\sigma g\Vert }_2-\sigma \epsilon ,0)(y-\sigma g).$$ (60)

The main points in deriving this proximal mapping are discussed in Appendix C, and it is an example where geometric/symmetry arguments play a large role. Listing 7 shows the algorithm instance solving Eq. (56), where once again only line 5 is modified. This algorithm instance essentially achieves the same goal as Listing 4, the only difference is that the parameter ε has an actual physical interpretation, being the data-error bound.

Algorithm 7.

Pseudocode for N-steps of the ℓ₂-constrained, TV-minimization CP algorithm instance.

1:	L ← ‖(A, ∇)‖2; τ ← 1/L; σ ← 1/L; θ ← 1; n ← 0
2:	initialize u0, p0, and q0 to zero values
3:	ū0 ← u0
4:	repeat
5:	pn+1 ← max(‖pn + σ(Aūn − g)‖2 − σε, 0) (pn + σ(Aūn − g))
6:	qn+1 ← (qn + σ∇ūn)/max(1I, |qn + σ∇ūn|)
7:	un+1 ← un − τAT pn+1 + τdiv qn+1
8:	ūn+1 ← un+1 + θ(un+1 − un)
9:	n ← n + 1
10:	untiln ≥ N

IV. Demonstration of CP algorithm instances for tomographic image reconstruction

In the previous section, we have derived CP algorithm instances covering many optimization problems of interest to CT image reconstruction. Not only are there the seven optimization problems, but within each case the system model/matrix A, the data g, and optimization problem parameters can vary. For each of these, practically infinite number of optimization problems, the corresponding CP algorithm instances are guaranteed to converge [20]. The purpose of this results section is not to advocate one optimization problem over another; rather to demonstrate the utility of the CP algorithm for optimization problem prototyping. For this purpose, we present example image reconstructions that could be performed in a study for investigating the impact of matching the data-divergence with data noise model for image reconstruction in breast CT.

A. Sparse-view experiments for image reconstruction from simulated CT data

We briefly describe the significance of the experiments, but we point out that the main goal here is to demonstrate the CP algorithm instances. Much of the recent interest in employing the TV semi-norm in optimization problems for CT image reconstruction has been generated by compressive sensing (CS). CS seeks to relate sampling conditions on a sensing device with sparsity in the object being scanned. So far, mathematical results have been limited to various types of random sampling [37]. System matrices such as those representing CT projection fall outside of the scope of mathematical results for CS [8]. As a result, the only current option for investigating CS in CT is through numerical experiments with computer phantoms.

A next logical step for bridging theoretical results for CS to actual application is to consider physical factors in the data model. One such factor is a noise model, which can be quite important for low-dose CT applications such as breast CT. While much work has been performed on iterative image reconstruction with various noise models under conditions of full sampling, little is known about the impact of noise on sparse-view image reconstruction. In the following limited study, we set up a breast CT simulation to investigate the impact of correct modeling of data noise with the purpose of demonstrating that the CP algorithm instances can be applied to the CT system.

B. Sparse-view reconstruction with a Poisson noise model

For the following study, we employ a digital 256 × 256 breast phantom, described in Ref. [23], [38], and used in our previous study on investigating sufficient sampling conditions for TV-based CT image reconstruction [12]. The phantom models for tissue types: the background fat tissue is a assigned a value of 1.0, the modeled fibro-glandular tissue takes a value of 1.1, the outer skin layer is set to 1.15, and the micro-calcifications are assigned values in the range [1.8,2.3].

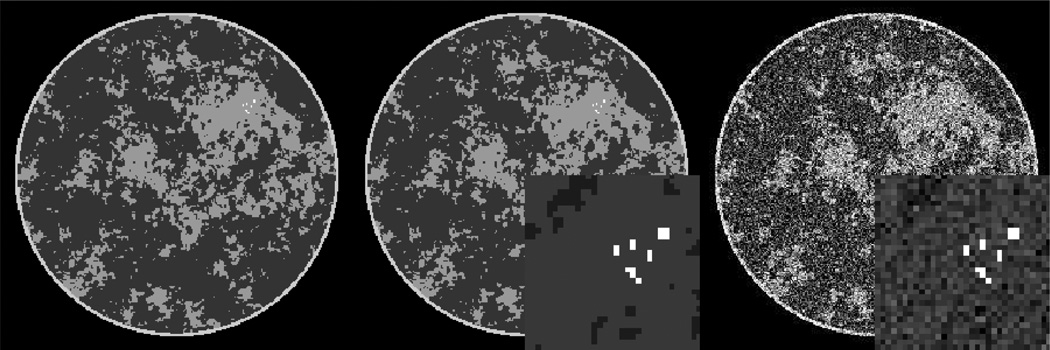
For the present case, we focus on circular, fan-beam scanning with 60 projections equally distributed over a full 360° angular range. The simulated radius of the X-ray source trajectory is 40cm with a source-detector distance of 80cm. The detector sampling consists of 512 bins of size 200 microns. The system matrix for the X-ray projection is computed by the line-intersection method where the matrix elements of A are determined by the length of traversal in each image pixel of each source/detector-bin ray. For this phantom under ideal conditions, we have found that accurate recovery is possible with constrained, TV-minimization with as few as 50 projections. In the present study, we add Poisson noise to the data model at a level consistent with what might be expect in a typical breast CT scan. The Poisson noise model is chosen in order to investigate the impact of matching the data-error term to the noise model. For reference, the phantom is shown in Fig. 1. To have a sense of the noise level, a standard fan-beam filtered back-projection reconstruction is shown alongside the phantom for simulated Poisson noise.

Fig. 1.

Breast phantom for CT and FBP reconstructed image for a 512-view data set with Poisson distributed noise. Left is the phantom in the gray scale window [0.95,1.15]; middle is the same phantom with a blow-up on the micro-calcification ROI displayed in the gray scale window [0.9,1.8]; and right is the FBP image reconstructed from the noisy data. The middle panel is the reference for all image reconstruction algorithm results. The FBP image is shown only to provide a sense of the noise level.

For this noise model, the maximum likelihood method prescribes minimizing the KL data divergence between the available and estimated data. To gauge the importance of selecting a maximum likelihood image, we compare the results from two optimization problems: a KL data divergence plus a TV-penalty, Eq. (46) above; and a least-squares data error norm plus a TV-penalty, Eq. (33) above. With the CP framework, these two optimization problems can be easily prototyped: the solutions to both problems can be obtained without worrying about smoothing the TV semi-norm, setting algorithm parameters, or proving convergence.

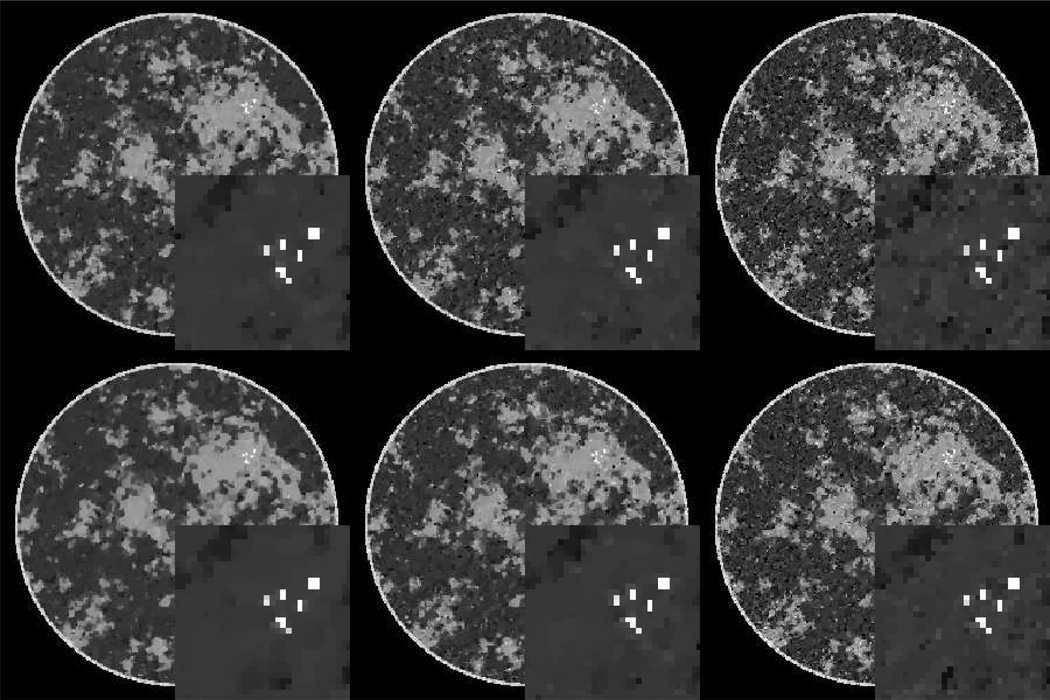
For the phantom and data conditions, described above, the images for different values of the TV-penalty parameter λ are shown in Fig. 2. An ROI of the micro-calcification cluster is also shown. The overall and ROI images give an impression of two different visual tasks important for breast imaging: discerning the fibro-glandular tissue morphology and detection/classification of micro-calcifications. The images show some difference between the two optimization problems; most notably there is a perceptible reduction in noise in the ROIs from the KL-TV images. A firm conclusion, however, awaits a more complete study with multiple noise realizations.

Fig. 2.

Images reconstructed from 60-view projection data with a Poisson distributed noise model. The top row of images result from minimizing the ${\ell }_2^2$-TV objective in Eq. (33) for λ = 1 × 10⁻⁴, 5 × 10⁻⁵, and 2 × 10⁻⁵, going from left to right. The bottom row of images result from minimizing the KL-TV objective in Eq. (46) for the same values of λ. Note that λ does not necessarily have the same impact on each of these optimization problems. Nevertheless, we see similar trends for the chosen values of λ.

The most critical feature of the CP algorithm that we wish to promote is the rapid prototyping of a convex optimization problem for CT image reconstruction. The above study is aimed at a combination of using a data divergence based on maximum likelihood estimation with a TV-penalty, which takes advantage of sparsity in the gradient magnitude of the underlying object. The CP framework facilitates the use of many other convex optimization problems, particularly those based on some form of sparsity, which often entail some form of the non-smooth ℓ₁-norm. For example, in Ref. [8] we have found it useful for sparse-view X-ray phase-contrast imaging to perform image reconstruction with a combination of a least-squares data fidelity term, an ℓ₁-penalty promoting object sparseness, and an image TV constraint to further reduce streak artifacts from angular under-sampling. Under the CP framework, prototyping various combinations of these terms as constrained or unconstrained optimization problems becomes possible and the corresponding derivation of CP algorithm instances follows from the steps described in Sec. II-B. Alternative, convex data fidelity terms and image constraints motivated by various physical models may also be prototyped.

As a practical matter, though, it is important to have some sense of the convergence of the CP algorithm instances. To this end, we take an in depth look at individual runs for the KL-TV algorithm instance for CT image reconstruction.

C. Iteration dependence of the CP algorithm

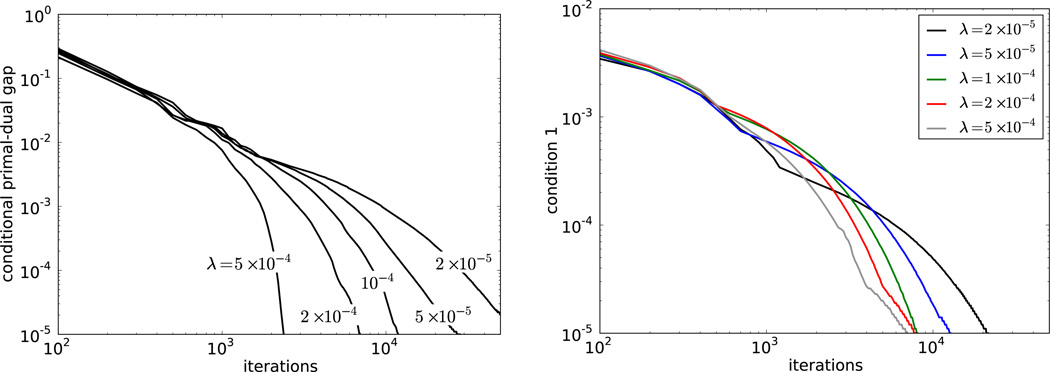
Through the methods described above, many useful algorithm instances can be derived for CT image reconstruction. It is obviously important that the resulting algorithm instance reaches the solution of the prescribed optimization problem. To illustrate the convergence of a resulting algorithm instance we focus on the TV-penalized KL data divergence, Eq. (46), and plot the conditional primal-dual gap for the different runs with varying λ in Fig. 3. Included in this figure is a plot indicating the convergence to agreement with the most challenging condition set by the indicator functions in Eq. (49). For the present results we terminated the iteration at a conditional primal-dual gap of 10⁻⁵, which appears to happen on the scale of thousands of iterations with smaller λ requiring more iterations. Interestingly, a simple pre-conditioned form of the CP algorithm was proposed in Ref. [39], which appears to perform efficiently for small λ. The pre-conditioned CP algorithm instance for this problem is reported in Appendix E.

Fig. 3.

(Left) Convergence of the partial primal-dual gap for the CP algorithm instance solving Eq. (46) for different values of λ. (Right) Plot indicating agreement with condition 1: ‖div q − A^T p‖_∞, the magnitude of the largest component of the argument of the last indicator function of Eq. (49). Collecting all the indicator functions of the primal, Eq. (46), and dual, Eq. (49), KL-TV optimization problems, we have four conditions to check in addition to the conditional primal-dual gap: (1) div q − A^T p = 0_I, (2) Au ≥ 0_D, (3) p ≤ 1_D, and (4) |q| < λ. The agreement with condition 1 is illustrated in the plot; agreement with condition 2 has a similar dependence; condition 3 is satisfied early on in the iteration; and condition 4 is automatically enforced by the CP algorithm instance for KL-TV. Because the curves are bunched together in the condition 1 plot, they are differentiated in color.

V. DISCUSSION

This article has presented the application of the Chambolle-Pock algorithm to prototyping of optimization problems for CT image reconstruction. The algorithm covers many optimization problems of interest allowing for non-smooth functions. It also comes with solid convergence criteria to check the image estimates.

The use of the CP algorithm we are promoting here is for prototyping; namely, when the image reconstruction algorithm development is at the early stage of determining important factors in formulating the optimization problem. As an example, we illustrated a scenario for sparse-view breast CT considering two different data-error terms. In this stage of development it is helpful to not have to bother with algorithm parameters, and questions of whether or not the algorithm will converge. After the final optimization problem is determined, then the focus shifts from prototyping to efficiency.

Optimization problem prototyping for CT image reconstruction does have its limitations. For example, in the breast CT simulation presented above, a more complete conclusion requires reconstruction from multiple realizations of the data under the Poisson noise model. Additional important dimensions of the study are generation of an ensemble of breast phantoms and considering alternate image representations/projector models. Considering the size of CT image reconstruction systems and huge parameter space of possible optimization problems, it is not yet realistic to completely characterize a particular CT system. But at least we are assured of solving isolated setups and it is conceivable to perform a study along one aspect of the system, i.e. consider multiple realizations of the random data model. Given the current state of affairs for optimization-based image reconstruction, it is crucial that simulations be as realistic as possible. There is great need for realistic phantoms, and data simulation software.

We point out that it is likely at least within the immediate future, that optimization-based image reconstruction will have to operate at severely truncated iteration numbers. Current clinical applications of iterative image reconstruction often operate in the range of one to ten iterations, which is likely far too few for claiming that the image estimate is an accurate solution to the designed optimization problem. But at least the ability to prototype an optimization problem can potentially simplify the design phase by separating optimization parameters from algorithm parameters.

APPENDIX A

Computing the norm of K

The matrix norm used for the parameter L in the CP algorithm instances is the largest singular value of K. This singular value can be obtained by the standard power method specified in Listing 8. When K represents the discrete X-ray transform, our experience has been that the power method converges to numerical precision in twenty iterations or less. In implementing the CP algorithm instance for TV-penalized minimization, the norm of the combined linear transform ‖(A, ∇)‖₂ is needed. For this case, the program is the same as Listing 8 where K^T Kx_n becomes A^T Ax_n − div∇x_n; recall that −div = ∇^T. Furthermore, to obtain s, the explicit computation is $s=\sqrt{{\Vert {\mathit{\text{Ax}}}_{n+1}\Vert }_2^2+{\Vert \nabla x_{n+1}\Vert }_2^2}$.

Algorithm 8.

Pseudocode for N-steps of the generic power method. The scalar s tends to ‖K‖₂ as N increases.

1:	initialize x0 ∈ I to a non-zero image
2:	n ← 0
3:	repeat
4:	xn+1 ← KTKxn
5:	xn+1 ← xn+1/‖xn+1‖2
6:	s ← ‖Kxn+1‖2
7:	n ← n + 1
8:	untiln ≥ N

APPENDIX B

The convex conjugate of certain indicator functions of interest illustrated in one-dimension

This appendix covers the convex conjugate of a couple of indicator functions in one dimension, serving to illustrate how geometry plays a role in the computation and to provide a mental picture on the conjugate of higher dimensional indicator functions.

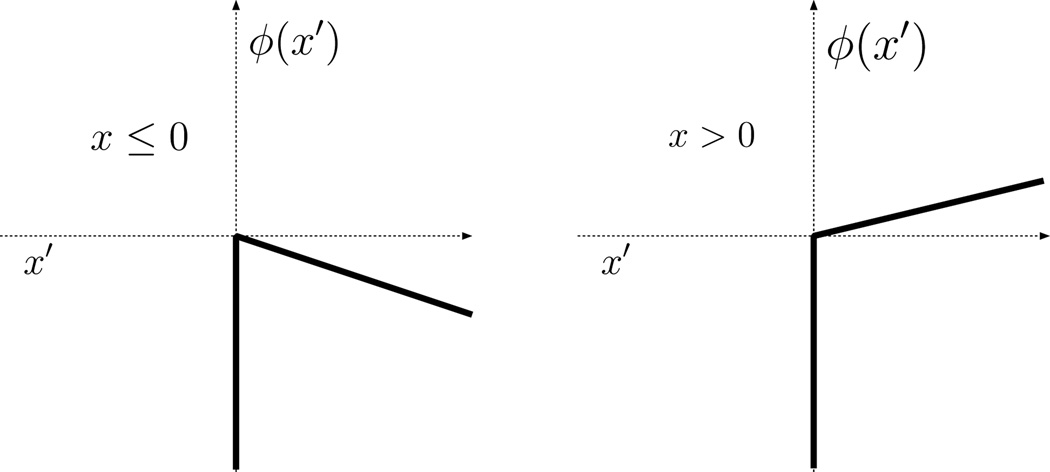
Consider first the indicator δ_P(x), which is zero for x ≥ 0. The conjugate of this indicator is computed from:

$${\delta }_P^{*}(x)=\underset{x\prime }{\text{max}}\varphi (x\prime )=\underset{x\prime }{\text{max}}\{x\prime x-\delta p(x\prime )\}.$$ (61)

To perform this maximization, we analyze the cases, x ≤ 0 and x > 0, separately. As a visual aid, we plot the objective for these two cases in Fig. 4. From this figure it is clear that when x ≤ 0, the objective’s maximum is attained at x′ = 0 and this maximum value is 0 (note that this is true even for x = 0). When x > 0, the objective can increase without bound as x′ tends to ∞, resulting in a maximum value of ∞. Putting these two cases together yields:

$${\delta }_P^{*}(x)={\delta }_P(-x).$$

Fig. 4.

Illustration of the objective function, labeled ϕ(x′), in the maximization described by Eq. (61). Shown are the two cases discussed in the text.

Generalizing this argument to multi-dimensional x, yields Eq. (29).

Next we consider δ_Box(1) (x), which in one dimension is the same as δ_Ball(1)(x). This functions is zero only for −1 ≤ x ≤ 1. Its conjugate is computed from:

$${\delta }_{\mathit{\text{Box}}(1)}^{*}(x)=\underset{x\prime }{\text{max}}\varphi (x\prime )=\underset{x\prime }{\text{max}}\{x\prime x-{\delta }_{\mathit{\text{Box}}(1)}(x\prime )\}.$$ (62)

Again, we have two cases, x ≤ 0 and x > 0, illustrated in Fig. 5. In the former case the maximum value of the objective is attained at x′ = −1, and this maximum value is −x. In the latter case the maximum value is x, and it is attained at x′ = 1. Hence, we have:

$${\delta }_{\mathit{\text{Box}}(1)}^{*}(x)=|x|.$$

Fig. 5.

Illustration of the objective function, labeled ϕ(x′), in the maximization described by Eq. (62). Shown are the two cases discussed in the text.

For multi-dimensional x, δ_Box(1)(x) ≠ δ_Ball(1)(x), and this is also reflected in the conjugates:

$$\begin{array}{c}{\delta }_{\mathit{\text{Box}}(1)}^{*}(x)={\Vert x\Vert }_1,\hfill \\ {\delta }_{\mathit{\text{Ball}}(1)}^{*}(x)={\Vert x\Vert }_2.\hfill \end{array}$$

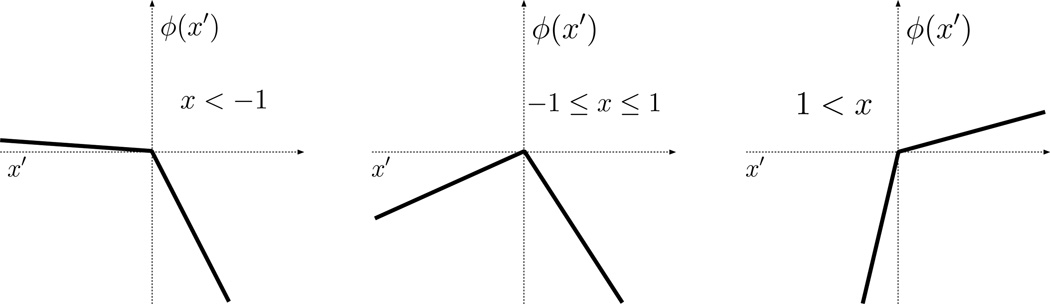
It is also interesting to verify that ${\delta }_{\mathit{\text{Box}}(1)}^{**}(x)$ is indeed δ_Box(1)(x) by showing, again in one dimension, that |x|* = δ_Box(1)(x). Illustrating this example helps in understanding the convex conjugate of multi-dimensional ℓ₁-based semi-norms. The relevant conjugate is computed from:

$${|x|}^{*}=\underset{x\prime }{\text{max}}\varphi (x\prime )=\underset{x\prime }{\text{max}}\{x\prime x-|x\prime |\}.$$ (63)

Here, we need to analyze three cases: x < −1, −1 ≤ x ≤ 1, and x > 1. The corresponding sketch is in Fig. 6. The −|x| term in the objective makes an upside-down wedge, and the x′x term serves to tip this wedge. In the second case, the wedge is tipped, but still opens up downward so that the objective is maximized at x′ = 0, attaining there the value of 0. In the first and third cases, the wedge is tipped so much that part of it points upward and the objective can increase without bound, attaining the value of ∞. Putting these cases together does indeed yield:

$${|x|}^{*}={\delta }_{\mathit{\text{Box}}(1)}(x).$$

Fig. 6.

Illustration of the objective function, labeled ϕ(x′), in the maximization described by Eq. (63). Shown are the three cases discussed in the text.

Similar reasoning is used to obtain Eq. (40) from Eq. (39).

APPENDIX C

Computation of important proximal mappings

This appendix fills in important steps in computing some of the proximal mappings in the text, where it is necessary to use geometrical reasoning in addition to setting the gradient of the objective to zero.

The conjugate of the TV semi-norm in Eq. (40) leads to the following proximal mapping computation:

$${\mathit{\text{prox}}}_{\sigma }[F^{*}](z)=\underset{z\prime }{\text{arg min }}\{{\delta }_{\mathit{\text{Box}}(\lambda )}(|z\prime |)+\frac{{\Vert z-z\prime \Vert }_2^2}{2\sigma }\},$$

where z, z′ ∈ V, and absolute value, |·|, of a spatial-vector image V yields an image, in I, of the spatial-vector-magnitude. The quadratic term is minimized when z = z′, but the indicator function excludes this minimizer when z ∉ Box(λ). To solve this problem, we write the quadratic as a sum over pixels:

$$\frac{{\Vert z-z\prime \Vert }_2^2}{2\sigma }=\frac{{\displaystyle {\sum }_i}{|z_i-z_i^{\prime }|}^2}{2\sigma },$$

where i indexes the image pixels and each z_i and $z_i^{\prime }$ is a spatial-vector. The indicator function places an upper bound on the magnitude of each spatial-vector $|z_i^{\prime }|\le \lambda$. The proximal mapping is built pixel-by-pixel considering two cases: if |z_i| ≤ λ, then prox_σ[F*](z)_i = z_i; if |z_i| > λ, then $z_i^{\prime }$ is chosen to be closest to z_i while respecting $|z_i^{\prime }|\le \lambda$ which leads to a scaling of the magnitude of z_i and prox_σ[F*](z)_i = λz_i/|z_i|. Note that the constant σ does not enter into this calculation. Putting the cases and components all together yields the second part of the proximal mapping in Eq. (45).

For the KL-TV problem the proximal mapping for the data term is computed from Eq. (48):

$${\mathit{\text{prox}}}_{\sigma }[F_1^{*}](p)=\underset{p\prime }{\text{arg min }}\{\frac{{\Vert p-p\prime \Vert }_2^2}{2\sigma }-{\displaystyle \sum _i}{[g\text{ ln}\mathit{\text{pos}}({\mathbf{1}}_D-p\prime )]}_i+{\delta }_P({\mathbf{1}}_D-p\prime )\}.$$

We note that the objective is a smooth function in the positive orthant of p′ ∈ D. Accordingly, we differentiate the objective with respect to p′ ignoring the pos(·) and indicator functions, keeping in mind that we have to check that the minimizer p′ is non-negative. Performing the differentiation and setting to zero yields the following quadratic equation:

$${p\prime }^2-({\mathbf{1}}_D+p)p\prime +p-\sigma g=0,$$

and substituting into the quadratic equation yields:

$$p\prime =\frac{1}{2}({\mathbf{1}}_D+p\pm \sqrt{{({\mathbf{1}}_D-p)}^2+4\sigma g)}.$$

We have two possible solutions, but it turns out that applying the restriction 1_D − p′ ≥ 0 selects the negative root. To see this, we evaluate 1_D − p′ at both roots:

$${\mathbf{1}}_D-p\prime =\frac{1}{2}({\mathbf{1}}_D-p\mp \sqrt{{({\mathbf{1}}_D-p)}^2+4\sigma g)}.$$

Using the fact that the data are non-negative, we have

$$\sqrt{{({\mathbf{1}}_D-p)}^2+4\sigma g}\ge |({\mathbf{1}}_D-p|;$$

the positive root clearly leads to possible negative values for 1_D −p′ while the negative root respects 1_D −p′ ≥ 0 and yields Eq. (50).

For the final computation of a proximal mapping, we take a look at the data term of the constrained, TV-minimization problem. From Eq. (58), the proximal mapping of interest is evaluated by:

$${\mathit{\text{prox}}}_{\sigma }[F_1^{*}](p)=\underset{p\prime }{\text{arg min }}\{\frac{{\Vert p-p\prime \Vert }_2^2}{2\sigma }+\epsilon {\Vert p\prime \Vert }_2+{\langle p\prime ,g\rangle }_D\}.$$

Note the first term in the objective is spherically symmetric about p and increasing with distance from p, and the second term is also spherically symmetric about 0_D and increasing with distance from 0_D. If just these two terms were present the minimum would lie on the line segment between 0_D and p. The third term, however, complicates the situation a little. We note that this term is linear in p′, and it can be combined with the first term by completing the square. Performing this manipulation and ignoring constant terms (independent of p′) yields:

$${\mathit{\text{prox}}}_{\sigma }[F_1^{*}](p)=\underset{p\prime }{\text{arg min }}\{\frac{{\Vert p-p\prime -\sigma g\Vert }_2^2}{2\sigma }+\epsilon {\Vert p\prime \Vert }_2\}.$$

By the geometric considerations discussed above, the minimizer lies on the line segment between 0_D and p − σg. Analyzing this one-dimensional minimization leads to Eq. (60).

APPENDIX D

The finite differencing form of the image gradient and divergence

In this appendix we write down the explicit forms of the finite differencing approximations of ∇ and −div in two dimensions used in this article. We use x ∈ I to represent an M × M image and x_i,j to refer to the (i, j)th pixel of x. To specify the linear transform ∇, we introduce the differencing images Δ_sx ∈ I and Δ_tx ∈ I:

$$\begin{array}{cc}{\mathrm{\Delta }}_s{x}_{i,j}=\hfill & \{\begin{array}{cc}{x}_{i+1,j}-x_{i,j}\hfill & i<M\hfill \\ -x_{i,j}\hfill & i=M\hfill \end{array},\hfill \\ {\mathrm{\Delta }}_t{x}_{i,j}=\hfill & \{\begin{array}{cc}{x}_{i,j+1}-x_{i,j}\hfill & j<M\hfill \\ -x_{i,j}\hfill & j=M\hfill \end{array}.\hfill \end{array}$$

Using these definitions, ∇ can be written as:

$$\nabla x=\left(\begin{array}{c}\hfill {\mathrm{\Delta }}_{s}x\hfill \\ \hfill {\mathrm{\Delta }}_{t}x\hfill \end{array}\right).$$

With this form of ∇, its transpose −div becomes:

$$-\mathit{\text{div }}\left(\begin{array}{c}\hfill {\mathrm{\Delta }}_{s}x\hfill \\ \hfill {\mathrm{\Delta }}_{t}x\hfill \end{array}\right)=\{-({\mathrm{\Delta }}_s{x}_{i,j}-{\mathrm{\Delta }}_s{x}_{i-1,j})-({\mathrm{\Delta }}_t{x}_{i,j}-{\mathrm{\Delta }}_t{x}_{i,j-1}),i\text{ and }j\in [1,M]\},$$

where the elements referred to outside the image border are set to zero: Δ_sx_0,j = Δ_sx_i,0 = Δ_tx_0,j = Δ_tx_i,0 = 0. What the particular form of ∇ is in its discrete form is not that important, but it is critical that the discrete forms of −div and ∇ are the transposes of each other.

APPENDIX E

Preconditioned chambolle-pock algorithm demonstrated on the kl-tv optimization problem

Chambolle and Pock followed their article, Ref. [20], with a pre-conditioned version of their algorithm that suits our purpose of optimization problem proto-typing while potentially improving algorithm efficiency substantially for the ${\ell }_2^2$-TV and KL-TV optimization problems with small λ. The new algorithm replaces the constants σ and τ with vector quantities that are computed directly from the system matrix K, which yields a vector in space Y from a vector in space X. One form of the suggested, diagonal pre-conditioners uses the following weights:

$$\mathrm{\Sigma }=\frac{{\mathbf{1}}_Y}{|K|{\mathbf{1}}_X},$$ (64)

$$\mathrm{T}=\frac{{\mathbf{1}}_X}{{|K|}^T{\mathbf{1}}_Y},$$ (65)

where Σ ∈ Y, T ∈ X, and |K| is the matrix formed by taking the absolute value of each element of K. In order to generate the CP algorithm instance incorporating pre-conditioning, the proximal mapping needs to be modified:

$${\mathit{\text{prox}}}_{\mathrm{\Sigma }}[F](y)=\underset{y\prime }{\text{arg min }}\{F(y\prime )+\frac{1}{2}{(y-y\prime )}^T(\frac{y-y\prime }{\mathrm{\Sigma }}\left)\right\}.$$ (66)

The second term in this minimization is still quadratic but no longer spherically symmetric. The difficulty in deriving the pre-conditioned CP algorithm instances is similar to that of the original algorithm. On the one hand there is no need for finding ‖K‖₂, but on the other hand deriving the proximal mapping may become more involved. For the ${\ell }_2^2$-TV and the KL-TV optimization problems, the proximal mapping is simple to derive and it turns out that the mappings can be arrived at by replacing σ by Σ and τ by T.

The gain in efficiency for small λ comes from being able to absorb this parameter into the TV term and allowing Σ to account for the mismatch between TV and data agreement terms. We modify the definitions of ∇ and −div matrices from Appendix D:

$${\nabla }_{\lambda }x=\left(\begin{array}{c}\hfill \lambda {\mathrm{\Delta }}_{s}x\hfill \\ \hfill \lambda {\mathrm{\Delta }}_{t}x\hfill \end{array}\right),$$

and

$$-{\mathit{\text{div}}}_{\lambda }\left(\begin{array}{c}\hfill {\mathrm{\Delta }}_{s}x\hfill \\ \hfill {\mathrm{\Delta }}_{t}x\hfill \end{array}\right)=\{-\lambda ({\mathrm{\Delta }}_s{x}_{i,j}-{\mathrm{\Delta }}_s{x}_{i-1,j})-\lambda ({\mathrm{\Delta }}_t{x}_{i,j}-{\mathrm{\Delta }}_t{x}_{i,j-1}),i\text{ and }j\in [1,M]\},$$

where again the elements referred to outside the image border are set to zero: Δ_sx_0,j = Δ_sx_i,0 = Δ_tx_0,j = Δ_tx_i,0 = 0.

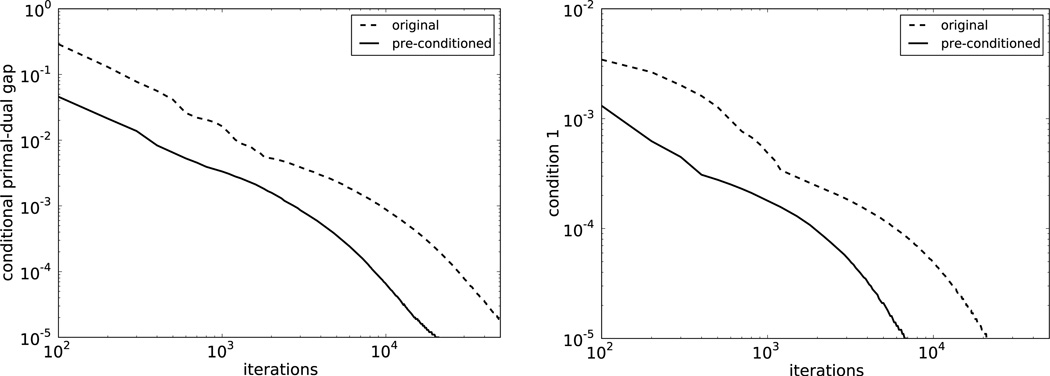
For a complete example, we write the pre-conditioned CP algorithm instance for KL-TV in Listing 9 To illustrate the potential gain in efficiency, we show the condition primal-dual gap as a function of iteration number for the KL-TV problem with λ = 2 × 10⁻⁵ in Fig. 7. While we have presented the pre-conditioned CP algorithm as a patch for the small λ case, it really provides an alternative prototyping algorithm and it can be used instead of the original CP algorithm.

Algorithm 9.

Pseudocode for N-steps of the KL-TV pre-conditioned CP algorithm instance.

1:	Σ1 ← 1D/(|A|1I); Σ2 ← 1V/(|∇λ|1I); T ← 1I/(|AT |1D + |divλ|1V)
2:	θ ← 1; n ← 0
3:	initialize u0, p0, and q0 to zero values
4:	ū0 ← u0
5:	repeat
6:	$p_{n+1}\leftarrow \frac{1}{2}({\mathbf{1}}_D+p_n+{\mathrm{\Sigma }}_{1}A{ū}_n-\sqrt{{(p_n+{\mathrm{\Sigma }}_{1}A{ū}_n-{\mathbf{1}}_D)}^2+4{\mathrm{\Sigma }}_{1}g})$
7:	qn+1 ← (qn + Σ2∇λūn)/max(1I, |qn + Σ2∇λūn|)
8:	un+1 ← un − TAT pn+1 + Tdivλqn+1
9:	ūn+1 ← un+1 + θ(un+1 − un)
10:	n ← n + 1
11:	untiln ≥ N

Fig. 7.

(Left) Convergence of the partial primal-dual gap for the CP algorithm instance solving Eq. (46) for λ = 2 × 10⁻⁵ for the original and pre-conditioned CP algorithm. (Right) Plot indicating agreement with condition 1 for the KL-TV optimization problem. See Fig. 3 for explanation.