Abstract
The ability to extract a pitch from complex harmonic sounds, such as human speech, animal vocalizations, and musical instruments, is a fundamental attribute of hearing. Some theories of pitch rely on the frequency-to-place mapping, or tonotopy, in the inner ear (cochlea), but most current models are based solely on the relative timing of spikes in the auditory nerve. So far, it has proved to be difficult to distinguish between these two possible representations, primarily because temporal and place information usually covary in the cochlea. In this study, “transposed stimuli” were used to dissociate temporal from place information. By presenting the temporal information of low-frequency sinusoids to locations in the cochlea tuned to high frequencies, we found that human subjects displayed poor pitch perception for single tones. More importantly, none of the subjects was able to extract the fundamental frequency from multiple low-frequency harmonics presented to high-frequency regions of the cochlea. The experiments demonstrate that tonotopic representation is crucial to complex pitch perception and provide a new tool in the search for the neural basis of pitch.
Pitch is one of the primary attributes of auditory sensation, playing a crucial role in music and speech perception, and in analyzing complex auditory scenes (1, 2). For most sounds, pitch is an emergent perceptual property, formed by the integration of many harmonically related components into a single pitch, usually corresponding to the sound's fundamental frequency (F0). The ability to extract the F0 from a complex tone, even in the absence of energy at the F0 itself, is shared by a wide variety of species (3, 4) and is present from an early developmental stage in humans (5).
The question of how pitch is encoded by the auditory system has a long and distinguished history, with lively debates on the subject going back to the time of Ohm (6) and Helmholtz (7). Although the debate has evolved considerably since its inception, one of the basic questions, whether timing (8, 9) or place information (10–12) (or both) from the cochlea is used to derive pitch, remains basically unanswered. In recent years, the weight of opinion and investigation has favored temporal codes (13–17). With few exceptions (18), recent models of pitch perception have been based solely on the timing information available in the interspike intervals represented in the simulated (17, 19–21) or actual (22, 23) auditory nerve. Such temporal models derive a pitch estimate by pooling timing information across auditory-nerve fibers without regard to the frequency-to-place mapping (tonotopic organization) of the peripheral auditory system.
Temporal models of pitch perception are attractive for at least two reasons. First, they provide a unified and parsimonious way of dealing with a diverse range of pitch phenomena (20). Second, the postulated neural mechanisms are essentially identical to those required of the binaural system when performing interaural timing comparisons for spatial localization; whereas temporal pitch theories postulate an autocorrelation function to extract underlying periodicities (9), binaural theories postulate a crosscorrelation function to determine interaural delays (24). Because both temporal pitch and binaural coding require neural temporal acuity on the order of microseconds, it is appealing to speculate that the same highly specialized brainstem structures [as found in the mammalian medial superior olivary complex (25) and the inferior colliculus (26) for binaural hearing] underlie both phenomena.
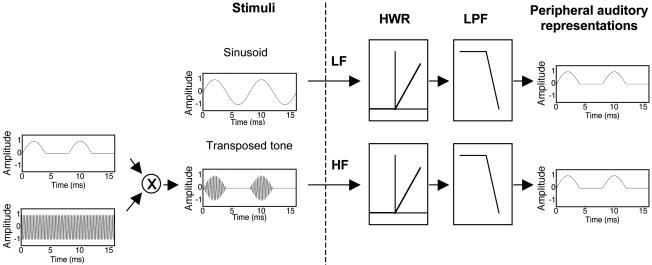
The goal of this study was to investigate whether pitch perception can be accounted for purely in terms of a temporal code (as assumed by most modern models) or whether the tonotopic representation of frequency is a necessary ingredient in the neural code for pitch. We approached the issue by using “transposed stimuli,” which have been used previously to investigate the relative sensitivity of the auditory system to low- and high-frequency binaural timing information (27–29). A transposed stimulus is designed to present low-frequency temporal fine-structure information to high-frequency regions of the cochlea. In this way, the place information is dissociated from the temporal information. When a low-frequency sinusoid is processed by the cochlea, the inner hair cells effectively half-wave rectify and low-pass filter the sinusoid (Fig. 1 Upper). To produce a comparable temporal pattern in inner hair cells tuned to high frequencies, a high-frequency carrier is modulated with a low-frequency, half-wave rectified sinusoid (Fig. 1 Lower). Thus, in this highly simplified scheme, the temporal pattern is determined by the low-frequency modulator, and the place of cochlear activity is determined by the high-frequency carrier. The temporal fine structure of the high-frequency carrier is not expected to be strongly represented because of the limits of synchronization in the auditory nerve (30). We tested the ability of human subjects to perceive pitch and make discrimination judgments for simple tones (single frequencies) and complex harmonic tones (multiple frequencies with a common F0), where the stimuli were either pure tones (sinusoids) or transposed tones. If pitch is based on a purely temporal code, performance with transposed tones should be similar to that found with sinusoids. If, on the other hand, place representation is important for pitch, then performance with transposed tones should be markedly poorer.
Fig. 1.
Schematic diagram of a pure tone (Upper) and a transposed tone (Lower). The transposed tone is generated by multiplying a high-frequency sinusoidal carrier with a half-wave rectified low-frequency sinusoidal modulator. As a first-order approximation, the peripheral auditory system acts as a half-wave rectifier (HWR) and low-pass filter (LPF), so that the temporal representations of both the low-frequency (LF) pure tone and the high-frequency (HF) transposed tone are similar.
Methods
Stimulus Generation and Presentation. The stimuli consisted of either pure tones or transposed tones. The transposed tones were generated by multiplying a half-wave rectified low-frequency sinusoid with a high-frequency sinusoidal carrier (Fig. 1 Lower). Before multiplication, the half-wave rectified sinusoid was low-pass filtered (Butterworth fourth order) at 0.2 fc (where fc is the carrier frequency) to limit its spectral spread of energy (28). The stimuli were generated digitally and presented with 24-bit resolution at a sampling rate of 32 kHz. After digital-to-analog conversion, the stimuli were passed through programmable attenuators and a headphone amplifier and presented with HD580 circumaural headphones (Sennheiser, Old Lyme, CT) in a double-walled sound-attenuating chamber.
Experiment 1. This experiment compared the abilities of human subjects to discriminate small frequency differences and interaural time differences (ITDs) in pure tones and in transposed tones. Four young (<30 years old) adult subjects with normal hearing participated. The two sets of conditions (frequency differences and ITDs) were run in counterbalanced order. Within each set, conditions were run in random order. Subjects received at least 1 h of training in each of the two tasks. The 500-ms stimuli (pure tones and transposed tones, generated as illustrated in Fig. 1) were gated with 100-ms raised-cosine onset and offset ramps and were presented binaurally over headphones at a loudness level of 70 phons (31). A low-pass filtered (600-Hz cutoff) Gaussian white noise was presented with the transposed stimuli at a spectrum level 27 dB below the overall sound pressure level of the tones to prevent the detection of low-frequency aural distortion products. Thresholds in both tasks were measured adaptively by using a 2-down 1-up tracking procedure (32) in a three-interval, three-alternative forced-choice task. In each three-interval trial, two intervals contained the reference stimulus, and the other interval (chosen at random) contained the test stimulus. For the frequency discrimination task, the test interval contained a stimulus with a higher (modulator) frequency than the reference stimulus. Pure-tone frequencies between 55 and 320 Hz in roughly one-third octave steps were tested. The transposed-tone carrier frequency of 4, 6.35, or 10.08 kHz was modulated with the same frequencies as were used for the pure tones. For the ITD task, all three intervals contained tones at the same frequency, but the reference intervals contained a stimulus with no ITD, whereas the test interval contained a stimulus with an ITD (right ear leading). The stimuli in both ears were always gated on and off synchronously, so that the ITD was only present in the ongoing portion of the stimulus, not in the onset or offset ramps. Again, pure-tone frequencies between 55 and 320 Hz were tested. However, as the ITD condition was essentially a replication of an earlier study (29) undertaken in the same subjects who completed the frequency-discrimination task, only one carrier frequency (4 kHz) was used for the transposed tones. Visual feedback was provided after each trial in all tasks. Individual threshold estimates were based on three repetitions of each condition.
Experiment 2. This experiment examined the ability of subjects to extract the F0 from three upper harmonics (harmonics 3–5) by requiring them to perform a two-interval F0 discrimination task, where one interval contained only the frequency component at F0 and the other interval contained only the three upper harmonics. Four different young (<30 years old) adult normal-hearing subjects participated in this experiment. In each two-interval trial, the subjects were instructed to select the interval with the higher F0. The stimuli were either pure tones or transposed tones. For the transposed stimuli in the three-tone case, harmonics 3, 4, and 5 were used to modulate carrier frequencies of 4, 6.35, and 10.08 kHz, respectively; in the transposed single-tone case, all three carrier frequencies were modulated with the same frequency (the F0). A two-track interleaved adaptive procedure was used to measure thresholds. In one track, the upper harmonics had a higher F0 than the frequency of the single tone; in the other track, the single tone had a higher frequency than the F0 of the upper harmonics. The lower and upper F0s were geometrically positioned around a nominal reference frequency of 100 Hz, which was roved by ±10% on each trial. Thresholds from the two tracks were combined to eliminate any potential bias (33). The 500-ms equal-amplitude tones were gated with 100-ms raised-cosine ramps and were presented at an overall sound pressure level of ≈65 dB. All stimuli were presented in a background of bandpass-filtered (31.25–1,000 Hz) pink noise at a sound pressure level of 57 dB per third-octave band to mask possible aural distortion products. Visual feedback was provided after each trial. Each reported threshold is the mean of six individual threshold estimates.
Experiment 3. The purpose of this experiment was to produce direct estimates of the perceived pitch produced by upper harmonics consisting of either pure tones or transposed tones. Pitch matches were measured for the same stimuli as in experiment 2 by using three of the four subjects from that experiment; the fourth subject was no longer available for testing. Sequential pairs of stimuli were presented, in which the first was fixed and the second could be adjusted in frequency (or F0) by the subject at will in large (4-semitone), medium (1-semitone), or small (¼-semitone) steps. Subjects were encouraged to bracket the point of subjective pitch equality before making a final decision on each run. No feedback was provided for this subjective task. Half the runs were done with the upper harmonics fixed, and half were done with the single tone fixed. The frequency (or F0) of the reference was 90, 100, or 110 Hz. Each condition was repeated six times. The six repetitions of three reference frequencies and two orders of presentation were pooled to provide a total of 36 pitch matches per subject for both the pure tones and the transposed tones.
Model Simulations. A recent temporal model of pitch processing (20) was implemented to verify that the transposed stimuli do indeed provide similar temporal information to that provided by low-frequency pure tones at the level of the auditory nerve. The simulations involve passing the stimulus through a bank of linear gammatone bandpass filters to simulate cochlear filtering. The output of each filter is passed through a model of inner hair cell transduction and auditory-nerve response (34), the output of which is a temporal representation of instantaneous auditory-nerve firing probability. The autocorrelation of this output is then calculated. To provide a summary of the temporal patterns in the individual channels, the autocorrelation functions from all frequency channels are summed to provide what has been termed a summary autocorrelation function (SACF). In our simulations, the complex-tone conditions used in experiment 3 were reproduced within the model, and the SACFs were examined. To avoid complications of simulating the response to stochastic stimuli, the pink background noise was omitted, and the levels of the tones were set to be ≈20 dB above the model's rate threshold, such that the model auditory nerve fibers were operating within their narrow dynamic range.
Results
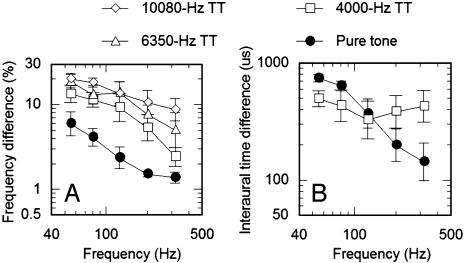
Experiment 1: Frequency and ITD Discrimination with Pure and Transposed Tones. Subjects performed more poorly with transposed tones than with pure tones in all of the conditions involving frequency discrimination (Fig. 2A). A within-subjects (repeated-measures) ANOVA with factors of presentation mode (four levels: pure tones and transposed tones with carrier frequencies of 4, 6.35, and 10.08 kHz) and frequency (55–318 Hz) found both main effects to be significant (P < 0.0001). Post hoc comparisons, using Fisher's least-significant difference test, confirmed that the results with pure tones were significantly different from those with transposed tones (P < 0.0001 in all cases). Furthermore, there was an increase in overall thresholds for transposed tones with increasing carrier frequency; thresholds with a 10.08-kHz carrier were significantly higher than thresholds with a 6.35-kHz carrier (P < 0.05), which in turn were significantly higher than thresholds with a 4-kHz carrier (P < 0.01). Subjecting the same data to an analysis of covariance confirmed the visible trend of a systematic decrease in thresholds with increasing frequency, from 55 to 318 Hz (P < 0.01). Within the analysis of covariance, the lack of an interaction (P > 0.1) between presentation mode and frequency suggests that the decrease in thresholds with increasing frequency is shared by both transposed and pure tones.
Fig. 2.
Mean performance in frequency discrimination (A) and interaural time discrimination (B) as a function of frequency. Open symbols represent performance with transposed tones (TT) on carrier frequencies ranging from 4,000 to 10,000 Hz. •, performance with pure tones.
In contrast to frequency discrimination, the ITD thresholds for transposed tones were equal to or lower than those for pure tones at frequencies ≤150 Hz (Fig. 2B) and higher at frequencies >150 Hz. The pattern of results in the ITD condition is in good agreement with previous studies (28, 29, †) and confirms that transposed stimuli are able to convey temporal information with microsecond accuracy to the binaural system. A within-subjects analysis of covariance revealed a significant effect of frequency (P < 0.05) and a significant interaction between frequency and presentation mode (P < 0.005) but no main effect of presentation mode (P > 0.1). This reflects the fact that thresholds in the pure-tone condition tend to decrease with increasing frequency, whereas thresholds in the transposed-tone condition do not.
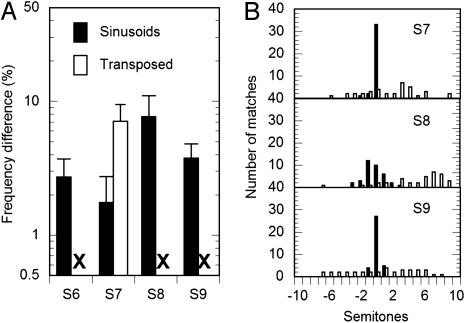
Experiment 2: F0 Discrimination with Pure and Transposed Tones. With pure tones, all four subjects were able to make meaningful comparisons of the pitch of a single tone and the composite pitch of the third through the fifth harmonics (Fig. 3A, filled bars). This is consistent with the well known finding that humans, along with many other species (3, 4, 35), are able to extract the F0 from a harmonic complex even if there is no spectral energy at the F0 itself.
Fig. 3.
Behavioral results using harmonic complex tones consisting of either pure tones (filled bars) or transposed tones (open bars). F0 difference limens (A) using transposed tones were not measurable for three of the four subjects. All three subjects tested on an F0 matching task (B) showed good performance for pure tones but no indication of complex pitch perception for the transposed tones.
The situation was very different for the transposed tones. For three of the four subjects, the threshold-tracking procedure exceeded the maximum allowable F0 difference of 32%, and no measurable threshold estimates could be made (Fig. 3A, X). For the remaining subject (S7; Fig. 3A, open bar), threshold estimates could be made but were significantly higher than that subject's threshold in the pure-tone condition (Student's t test, P < 0.001).
Experiment 3: Pitch Matching. Three of the four subjects took part in this experiment; the other subject (S6) was no longer available. The results are shown in Fig. 3B. A clear pitch sensation would be represented by a sharp peak in the matching histogram; a veridical pitch match (where the F0 of the upper harmonics is perceptually equated with the same frequency of the single tone) would be reflected by the peak occurring at a difference of 0 semitones. The results from all three subjects are very similar: the upper harmonics comprising pure tones elicited a pitch that was matched with reasonable accuracy to a single frequency corresponding to the F0 (Fig. 3B, filled bars), whereas the upper harmonics comprising transposed tones failed to elicit a reliable pitch (Fig. 3B, open bars).
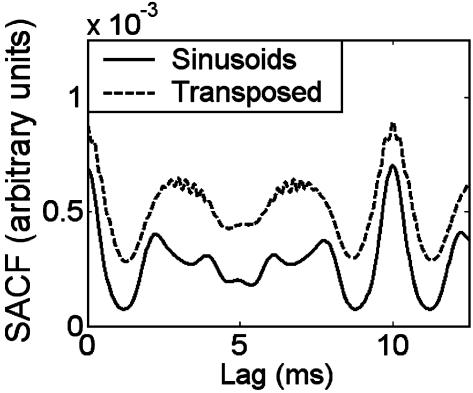
Model Simulations. By examining the output of a computational model of the auditory periphery (20), we verified that the temporal response to transposed tones in individual auditory nerve fibers was similar to the response produced by low-frequency pure tones at the sensation levels used in the experiment (data not shown). Similarly, the pure and transposed three-tone harmonic complexes used in experiments 2 and 3 produce very similar SACFs (Fig. 4). Both stimuli show a distinct peak at a time interval corresponding to the reciprocal of the F0. Thus, the model correctly predicts that the F0 will be perceived in the case of the pure tones, but it incorrectly predicts a similar pitch percept in the case of the transposed tones.
Fig. 4.
An SACF model (20) representation of harmonic complex tones consisting of either pure tones (solid curve) or transposed tones (dashed curve). Both representations in the model show a clear peak at a 10-ms lag, the inverse of the F0 of 100 Hz. In contrast, the F0 was perceived by human subjects only in the case of the pure tones.
Discussion
Simple (Single-Frequency) Pitch Perception. Frequency discrimination with transposed tones was markedly worse than for pure tones in all conditions tested (Fig. 2 A). This cannot be because of a failure of transposed stimuli to accurately convey temporal information to the auditory periphery; in line with previous studies, the same subjects were able to use the temporal cues in the transposed stimuli to make binaural judgments requiring temporal acuity on the order of microseconds (Fig. 2B). What then accounts for the failure of transposed stimuli to provide accurate pitch information?
A number of earlier studies have reported rather poor F0 discrimination when spectral cues are eliminated and perception is based only on the repetition rate in the envelope (36–38). It could be argued that these previous studies used envelopes that did not approximate the response produced by single low-frequency sinusoids and were therefore in some way nonoptimal for auditory processing. This was less likely to be the case here, where efforts were made to make the temporal response to the transposed stimuli in the peripheral auditory system resemble as closely as possible the response to low-frequency pure tones. It seems that the temporal information in the envelope is processed differently from that in the fine structure. Temporal envelope and fine structure are thought to play different roles in auditory perception (39), and so it is perhaps not surprising that they are processed differently. However, it is difficult to conceive of a processing scheme that could differentiate between temporal fine structure and envelope, based solely on the temporal pattern of neural activity in single auditory-nerve fibers. Coding schemes that could potentially differentiate between temporal envelope and fine structure with the addition of place information are discussed below.
Complex (Multifrequency) Pitch Perception. Most sounds in our environment, including speech, music, and animal vocalizations, derive their pitch from the first few low-numbered harmonics (40, 41). These are also the harmonics that tend to be resolved, or processed individually, in the peripheral auditory system (38, 42). Unlike high, unresolved harmonics, which interact in the auditory periphery to produce a complex waveform with a repetition rate corresponding to the reciprocal of the F0, the frequencies of the low harmonics must be estimated individually and combined within the auditory system to produce a pitch percept corresponding to the F0. Because this integration of information seems to be subject to higher level perceptual grouping constraints (43), it is likely that the integration occurs only at a cortical level. This conclusion is also consistent with a number of recent functional imaging studies in humans, suggesting a pitch-processing center in anterolateral Heschl's gyrus (14, 44, 45).
The present results suggest that this integration does not occur if the temporal information from the individual tones is presented to tonotopic locations that are inconsistent with the respective frequencies. In contrast to the results from single tones, where some, albeit impaired, pitch perception was possible (experiment 1), complex tones presented by means of independent transposed carriers produced no measurable pitch sensation at the F0 (experiments 2 and 3). This is in direct contradiction to all current temporal models of pitch perception, in which temporal interval information is pooled to provide an estimate of the underlying F0; such models will tend to predict equally good perception of the F0 for both pure tones and transposed tones, as illustrated for one such model (20) in Fig. 4.
Implications for Neural Coding. Our findings present an interesting dichotomy between pitch and spatial perception: transposed tones provide peripheral temporal information that is sufficiently accurate for binaural spatial processing but produce poor simple, and nonexistent complex, pitch perception. This insight should provide a valuable tool in the search for the neural code of pitch. In particular, any candidate neural code must demonstrate a tonotopic sensitivity, such that similar temporal patterns in the auditory nerve are transformed differently at higher stations in the auditory pathways, depending on the characteristic frequency of the neurons.
An early theory of pitch coding (46) suggested that periodicity tuning in neurons in the brainstem or higher may depend on the characteristic frequency of the neuron. In this way, the representation of periodicity at a given characteristic frequency would diminish with decreasing F0, thereby accounting for why low-order harmonics produce a stronger pitch percept than high-order harmonics. Although this arrangement could account for why simple pitch is poorer with transposed than with pure tones, it could not account for why no complex pitch percept was reported with the combinations of transposed tones that themselves produced simple pitches.
A class of theory based on place–time transformations is, in principle, consistent with the current data. In one formulation, the output of each cochlear filter is expressed as an interval histogram and is then passed through a temporal filter matched to the characteristic frequency of the cochlear filter, providing a spatial representation of a temporal code (47). A different approach uses the rapid change in group delay that occurs in the cochlea's traveling-wave response to tones around characteristic frequency as a mechanical delay line (48–50). Networks of coincidence cells tuned to slightly disparate spatial locations along the cochlear partition could thus be used to signal small changes in frequency. Such a model has been extended to account for complex pitch perception (51), and would (correctly) predict no complex pitch perception if the temporal information is presented to tonotopically incorrect locations in the cochlea. Note that these accounts require both accurate timing information and accurate place information. Our findings, which are broadly consistent with these place–time formulations, also provide stimuli that should assist in locating the putative neural mechanisms required for such coding schemes.
Implications for Implanted Auditory Prostheses. Cochlear implants are a form of auditory prostheses in which an array of electrodes is inserted into the cochlea in an attempt to electrically stimulate the auditory nerve. Most current systems concentrate on presenting only the temporal envelope of sounds to electrodes within the array. This approach is supported by findings showing that good speech perception in quiet can be achieved with only temporal envelope information in a limited number of spectral bands (52). However, temporal fine-structure information seems to be crucial for speech in more complex backgrounds (53) and for binaural and pitch perception (39). Given its apparent importance, much recent effort has gone into finding ways of representing temporal fine structure in cochlear implants (54, 55). The current results suggest that this effort may not be fruitful unless the information is mapped accurately to the correct place along the cochlea. Even then, it will be extremely challenging to recreate the complex pattern of activity produced within each cycle of the cochlear traveling wave, should the neural code be based on spatiotemporal excitation patterns.
Acknowledgments
We thank Ray Meddis for supplying the code for the pitch model and Christophe Micheyl for helpful comments on earlier drafts of this article. This work was supported by National Institutes of Health National Institute on Deafness and Other Communication Disorders Grants R01 DC 05216 and T32 DC 00038.
This paper was submitted directly (Track II) to the PNAS office.
Abbreviations: F0, fundamental frequency; ITD, interaural time difference; SACF, summary autocorrelation function.
See Commentary on page 1114.
Footnotes
Threshold values here are somewhat higher than in the most comparable earlier study (29). This may be because of the higher level of threshold sensitivity produced by a three-alternative, as opposed to a two-alternative, forced-choice procedure (d′ = 1.27, as opposed to d′ = 0.77) and to the fact that we introduced ITDs only to the ongoing (steady-state) portion of the stimulus and not to the onset and offset ramps.
References
- 1.Bregman, A. S. (1990) Auditory Scene Analysis: The Perceptual Organisation of Sound (MIT Press, Cambridge, MA).
- 2.Darwin, C. J. & Carlyon, R. P. (1995) in Handbook of Perception and Cognition, Volume 6: Hearing, ed. Moore, B. C. J. (Academic, San Diego).
- 3.Heffner, H. & Whitfield, I. C. (1976) J. Acoust. Soc. Am. 59, 915–919. [DOI] [PubMed] [Google Scholar]
- 4.Cynx, J. & Shapiro, M. (1986) J. Comp. Psychol. 100, 356–360. [PubMed] [Google Scholar]
- 5.Montgomery, C. R. & Clarkson, M. G. (1997) J. Acoust. Soc. Am. 102, 3665–3672. [DOI] [PubMed] [Google Scholar]
- 6.Ohm, G. S. (1843) Ann. Phys. Chem. 59, 513–565. [Google Scholar]
- 7.Helmholtz, H. L. F. (1885) On the Sensations of Tone (Dover, New York).
- 8.Schouten, J. F. (1940) Proc. Kon. Akad. Wetenschap. 43, 991–999. [Google Scholar]
- 9.Licklider, J. C. R. (1951) Experientia 7, 128–133. [DOI] [PubMed] [Google Scholar]
- 10.Goldstein, J. L. (1973) J. Acoust. Soc. Am. 54, 1496–1516. [DOI] [PubMed] [Google Scholar]
- 11.Terhardt, E. (1974) J. Acoust. Soc. Am. 55, 1061–1069. [DOI] [PubMed] [Google Scholar]
- 12.Wightman, F. L. (1973) J. Acoust. Soc. Am. 54, 407–416. [DOI] [PubMed] [Google Scholar]
- 13.Schulze, H. & Langner, G. (1997) J. Comp. Physiol. A 181, 651–663. [DOI] [PubMed] [Google Scholar]
- 14.Griffiths, T. D., Buchel, C., Frackowiak, R. S. & Patterson, R. D. (1998) Nat. Neurosci. 1, 422–427. [DOI] [PubMed] [Google Scholar]
- 15.Griffiths, T. D., Uppenkamp, S., Johnsrude, I., Josephs, O. & Patterson, R. D. (2001) Nat. Neurosci. 4, 633–637. [DOI] [PubMed] [Google Scholar]
- 16.Lu, T., Liang, L. & Wang, X. (2001) Nat. Neurosci. 4, 1131–1138. [DOI] [PubMed] [Google Scholar]
- 17.Krumbholz, K., Patterson, R. D., Nobbe, A. & Fastl, H. (2003) J. Acoust. Soc. Am. 113, 2790–2800. [DOI] [PubMed] [Google Scholar]
- 18.Cohen, M. A., Grossberg, S. & Wyse, L. L. (1995) J. Acoust. Soc. Am. 98, 862–879. [DOI] [PubMed] [Google Scholar]
- 19.Patterson, R. D., Allerhand, M. H. & Giguère, C. (1995) J. Acoust. Soc. Am. 98, 1890–1894. [DOI] [PubMed] [Google Scholar]
- 20.Meddis, R. & O'Mard, L. (1997) J. Acoust. Soc. Am. 102, 1811–1820. [DOI] [PubMed] [Google Scholar]
- 21.de Cheveigné, A. (1998) J. Acoust. Soc. Am. 103, 1261–1271. [DOI] [PubMed] [Google Scholar]
- 22.Cariani, P. A. & Delgutte, B. (1996) J. Neurophysiol. 76, 1698–1716. [DOI] [PubMed] [Google Scholar]
- 23.Cariani, P. A. & Delgutte, B. (1996) J. Neurophysiol. 76, 1717–1734. [DOI] [PubMed] [Google Scholar]
- 24.Jeffress, L. A. (1948) J. Comp. Physiol. Psychol. 41, 35–39. [DOI] [PubMed] [Google Scholar]
- 25.Brand, A., Behrend, O., Marquardt, T., McAlpine, D. & Grothe, B. (2002) Nature 417, 543–547. [DOI] [PubMed] [Google Scholar]
- 26.McAlpine, D., Jiang, D. & Palmer, A. R. (2001) Nat. Neurosci. 4, 396–401. [DOI] [PubMed] [Google Scholar]
- 27.van de Par, S. & Kohlrausch, A. (1997) J. Acoust. Soc. Am. 101, 1671–1680. [DOI] [PubMed] [Google Scholar]
- 28.Bernstein, L. R. (2001) J. Neurosci. Res. 66, 1035–1046. [DOI] [PubMed] [Google Scholar]
- 29.Bernstein, L. R. & Trahiotis, C. (2002) J. Acoust. Soc. Am. 112, 1026–1036. [DOI] [PubMed] [Google Scholar]
- 30.Rose, J. E., Brugge, J. F., Anderson, D. J. & Hind, J. E. (1967) J. Neurophysiol. 30, 769–793. [DOI] [PubMed] [Google Scholar]
- 31.ISO 226. (1987) Acoustics: Normal Equal-Loudness Contours (International Organization for Standardization, Geneva).
- 32.Levitt, H. (1971) J. Acoust. Soc. Am. 49, 467–477. [PubMed] [Google Scholar]
- 33.Oxenham, A. J. & Buus, S. (2000) J. Acoust. Soc. Am. 107, 1605–1614. [DOI] [PubMed] [Google Scholar]
- 34.Sumner, C. J., Lopez-Poveda, E. A., O'Mard, L. P. & Meddis, R. (2002) J. Acoust. Soc. Am. 111, 2178–2188. [DOI] [PubMed] [Google Scholar]
- 35.Tomlinson, R. W. W. & Schwartz, D. W. F. (1988) J. Acoust. Soc. Am. 84, 560–565. [DOI] [PubMed] [Google Scholar]
- 36.Burns, E. M. & Viemeister, N. F. (1981) J. Acoust. Soc. Am. 70, 1655–1660. [Google Scholar]
- 37.Houtsma, A. J. M. & Smurzynski, J. (1990) J. Acoust. Soc. Am. 87, 304–310. [Google Scholar]
- 38.Shackleton, T. M. & Carlyon, R. P. (1994) J. Acoust. Soc. Am. 95, 3529–3540. [DOI] [PubMed] [Google Scholar]
- 39.Smith, Z. M., Delgutte, B. & Oxenham, A. J. (2002) Nature 416, 87–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Moore, B. C. J., Glasberg, B. R. & Peters, R. W. (1985) J. Acoust. Soc. Am. 77, 1853–1860. [DOI] [PubMed] [Google Scholar]
- 41.Bird, J. & Darwin, C. J. (1998) in Psychophysical and Physiological Advances in Hearing, eds. Palmer, A. R., Rees, A., Summerfield, A. Q. & Meddis, R. (Whurr, London), pp. 263–269.
- 42.Bernstein, J. G. & Oxenham, A. J. (2003) J. Acoust. Soc. Am. 113, 3323–3334. [DOI] [PubMed] [Google Scholar]
- 43.Darwin, C. J., Hukin, R. W. & al-Khatib, B. Y. (1995) J. Acoust. Soc. Am. 98, 880–885. [DOI] [PubMed] [Google Scholar]
- 44.Patterson, R. D., Uppenkamp, S., Johnsrude, I. S. & Griffiths, T. D. (2002) Neuron 36, 767–776. [DOI] [PubMed] [Google Scholar]
- 45.Krumbholz, K., Patterson, R. D., Seither-Preisler, A., Lammertmann, C. & Lütkenhöner, B. (2003) Cereb. Cortex 13, 765–772. [DOI] [PubMed] [Google Scholar]
- 46.Moore, B. C. J. (1982) An Introduction to the Psychology of Hearing, 2nd Ed. (Academic, London).
- 47.Srulovicz, P. & Goldstein, J. L. (1983) J. Acoust. Soc. Am. 73, 1266–1276. [DOI] [PubMed] [Google Scholar]
- 48.Loeb, G. E., White, M. W. & Merzenich, M. M. (1983) Biol. Cybern. 47, 149–163. [DOI] [PubMed] [Google Scholar]
- 49.Shamma, S. A. (1985) J. Acoust. Soc. Am. 78, 1612–1621. [DOI] [PubMed] [Google Scholar]
- 50.Shamma, S. A. (1985) J. Acoust. Soc. Am. 78, 1622–1632. [DOI] [PubMed] [Google Scholar]
- 51.Shamma, S. & Klein, D. (2000) J. Acoust. Soc. Am. 107, 2631–2644. [DOI] [PubMed] [Google Scholar]
- 52.Shannon, R. V., Zeng, F. G., Kamath, V., Wygonski, J. & Ekelid, M. (1995) Science 270, 303–304. [DOI] [PubMed] [Google Scholar]
- 53.Qin, M. K. & Oxenham, A. J. (2003) J. Acoust. Soc. Am. 114, 446–454. [DOI] [PubMed] [Google Scholar]
- 54.Rubenstein, J. T., Wilson, B. S., Finley, C. C. & Abbas, P. J. (1999) Hear. Res. 127, 108–118. [DOI] [PubMed] [Google Scholar]
- 55.Litvak, L. M., Delgutte, B. & Eddington, D. K. (2003) J. Acoust. Soc. Am. 114, 2079–2098. [DOI] [PMC free article] [PubMed] [Google Scholar]