The Influence of Taxon Sampling and Tree Shape on Molecular Dating: An Empirical Example from Mammalian Mitochondrial Genomes

Abstract

Over the last decade, molecular dating methods have been among the most studied subjects in statistical phylogenetics. Although the evolutionary modelling of substitution rates and the handling of calibration information are the primary focus of species divergence time research, parameters that influence topological estimation, such as taxon sampling and tree shape, also have the potential to influence evolutionary age estimates. However, the impact of topological parameters on chronological estimates is rarely considered. In this study, we use mitochondrial genomes to evaluate the influence of tree shape and taxon sampling on the divergence times of selected nodes of the mammalian tree. Our results show that taxon sampling affects divergence time estimates; the credibility intervals for age estimates decrease as taxonomic sampling increases (i.e., estimates become more precise). The influence of taxonomic sampling was not observed on nodes that lay deep in the mammalian phylogeny, although the means of the posterior distributions tend to converge with increased taxon sampling, an effect that is independent of the location of the node. In the majority of cases, the effect of tree shape was negligible.

Introduction

After early debates on the relative contribution of increased taxon sampling to phylogenetic inference,^1–3 it is now generally accepted that the inclusion of new terminals has a positive impact on phylogenetic reconstruction by reducing the effect of long branch attraction and other topological anomalies.^4–6 Studies evaluating the influence of taxon sampling on phylogenies, however, have been generally focused on tree topology estimation alone.^7,8 An exception to this rule are works that investigate the robustness of parameter estimates for the diversification/extinction of lineages.⁹

The chronological scale is another feature inherent in phylogenies that has long been ignored by studies on the effects of taxonomic sampling. Divergence time inference has been a fundamental tool for elucidating evolutionary scenarios.¹⁰ Thus, it is a critical point to envisage how chronological parameters are influenced by the composition of the sequences used. The relevance of such an analysis is also magnified by implementations of the relaxed molecular clock, which emerged over the last decade. Recently, the performance of relaxed clock method have been investigated with respect to the modelling of evolutionary rates among branches,^11–13 the position of calibration nodes^14,15 as well as the probability distributions used to incorporate calibration information as priors.^16,17

Nevertheless, few studies have conducted a detailed evaluation of the impact of taxon sampling on divergence time inference, and the current picture is inconclusive. For example, Linder et al.¹⁸ found that varying taxonomic sampling impacts the African Restionaceae time scale, while Hug and Roger¹⁴ reported that the position of the calibration information along the phylogeny is much more significant than taxonomic sampling alone. In line with this finding, Xiang et al.¹⁹ concluded that a reduced data sample produced estimates that were congruent with the larger data sample, while calibration information played a major role in affecting the time scale.

One difficulty with these evaluations of the impact of taxon sampling on divergence time estimates is that they were not specifically designed to test this issue and thus are only marginal assessments. To overcome this issue, we have analysed how the number of sequences used during the construction of phylogenetic trees impacts divergence time estimates. To define the impact of varying taxonomic compositions on time-scale inferences, we employed a standard molecular marker, the mitochondrial genome, and several tree topologies to evaluate the influence of taxon sampling on the divergence times of selected placental mammals. We conclude that taxon sampling is an important parameter for estimating divergence times, as well as for inferring phylogenies. In general, increased taxonomic sampling reduced the variance of age estimates. This effect, however, was dependent on the position of the node relative to the calibration information.

Methods

Sequences and alignment

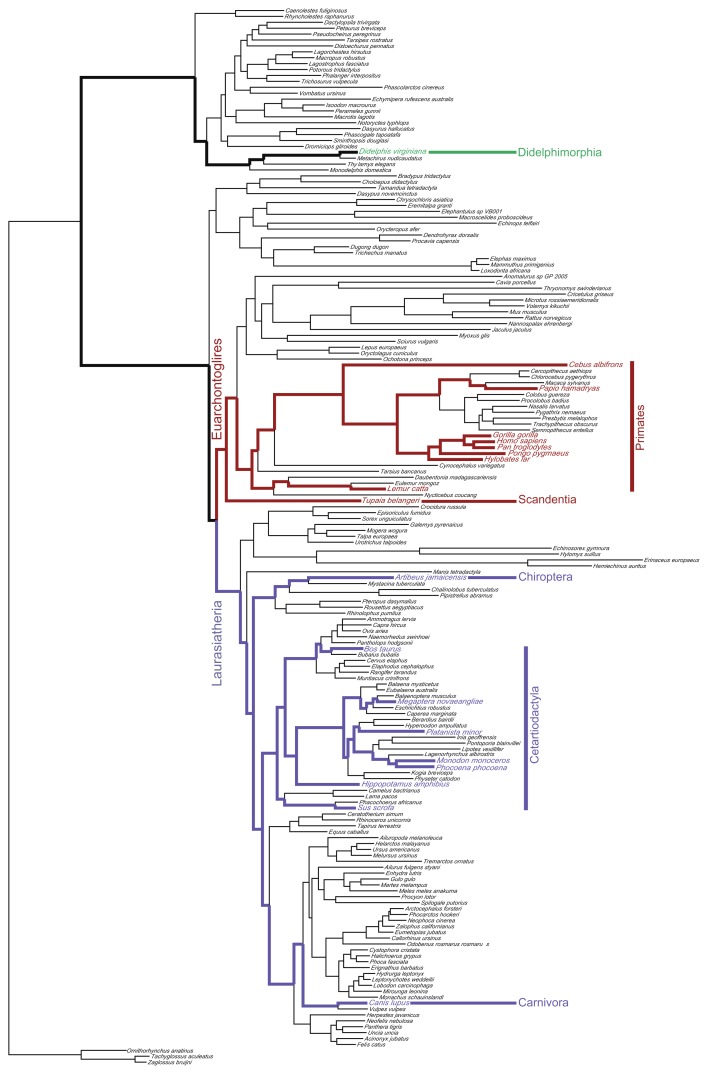
The complete mitochondrial genomes of 179 mammalian species (shown in Fig. 1) were retrieved from the NCBI database (http://www.ncbi.nlm.nih.gov/genomes/). Mammalian sequences were chosen because both the phylogeny of the lineage and its evolutionary time-scale are well studied. All 13 mitochondrial coding genes were used in the analysis. The translated amino acid sequences of these genes were aligned using the ClustalW algorithm²⁰ as implemented by MEGA 4.0.²¹ After manual inspection of the alignments, the data were separated into three partition sets that corresponded to the first, second and third positions of each codon. This approach maximises the heterogeneity of evolutionary rates in each partition because rate heterogeneity is greater among codon positions than among mitochondrial genes.²² Inspection of the evolutionary distances revealed that the third codon positions were saturated. Therefore, only the first and second codon positions were included in our analysis.

Figure 1.

The phylogeny of mammalian species inferred from 179 mitochondrial genomes.

Notes: The branches indicated in red and blue were sampled to compose the tree topology used in the study. The red branches are part of the Euarchontoglires clade, that includes, among others, the Primates and Scandentia (tree shrews) orders. The blue branches are part of the Laurasiatheria clade, including the Chiroptera (bats), Cetartiodactyla (cetaceans, ruminants and swines) and Carnivora (carnivores) orders. A member of the Didelphimorphia order (opossums) was used as outgroup.

Molecular dating

Divergence time estimation was conducted in BEAST 1.6.2 using the uncorrelated lognormal model of rate evolution described in Drummond et al.¹¹ under the GTR + G8 model of substitution. This prior distribution model does not assume the autocorrelation of evolutionary rates, and rate estimates are sampled independently from a lognormal prior distribution. Markov chains were submitted to a pre-burn-in period of 1,000,000 generations and sampled every 1,000 cycles over 30,000,000 generations. An additional 10% were discarded as part of the burn-in required to build the posterior distributions. All analyses were run with fixed topologies by removing operators that act on the treeModel (see BEAST program manual). We used the age of the root (Metatheria/Eutheria divergence) and the separation of Laurasiatheria and Euarchontoglires as calibration information in the analysis. According to Benton and Donoghue,¹⁰ the Metatheria/Eutheria divergence took place between 124.6 and 138.4 Ma and the Laurasiatheria and Euarchontoglires split occurred between 95.3 and 113 Ma. Thus, we have used normal distributions with average limiting values as the means. Standard deviations were determined based on the minimum and maximum bounds of the borders the 95% confidence interval. This approach yields the prior distributions N(131.5, 4) and N(104.2, 5) for the Metatheria/Eutheria and Euarchontoglires/Laurasiatheria splits, respectively.

Taxon sampling strategy

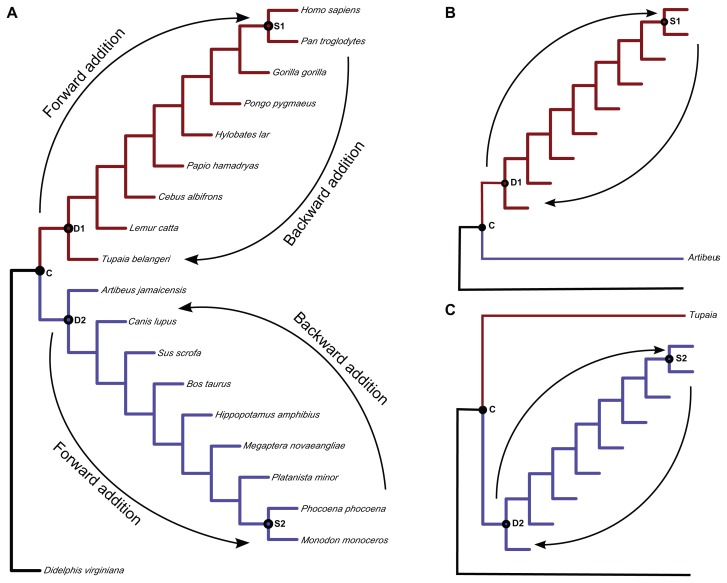
The influence of taxon sampling on divergence times was investigated using a reduced set of the full mammal tree shown in Figure 1. Samples that produced a balanced tree of placental lineages with well supported phylogenetic affinities were selected.²³ Specifically, we evaluated the inferred ages of two pairs of nodes that represent deep (D1 and D2) and shallow (S1 and S2) divergences (Fig. 2A). Divergence times at these nodes were estimated by successively increasing the number of terminal taxa according to two different schemes. The schemes were separated according to the number of terminals present in the left and right child subtrees that originated from the calibration node. In the first scheme (balanced), the number of terminals in each of the child subtrees was equal and the occurrence of the cladogenetic events was mirrored (Fig. 2A). These trees presented modified Fusco and Cronk’s I statistic = 0 at the calibration node,^24,25 indicating maximum balance (symmetric subtrees). In the second scheme, unbalanced, the tree has a pectinate shape, which means that one of the child subtrees originating from the calibration node contained only one terminal taxon (Fig. 1B and C). The I statistic measured at the calibration node ranged from 0.75 to 1.0, indicating that subtrees under this node were near maximum imbalance (1.0).

Figure 2.

The experimental design used to evaluate the impact of tree shape and taxon sampling on divergence time estimates. (A) Balanced topology. Arrows show the direction of the progressive forward and backward additions. (B) Unbalanced topology representing the Euarchontoglires lineages. Arrows show the direction of the progressive taxonomic addition. (C) Unbalanced topology of the Laurasiatheria lineages. Arrows show the direction of the progressive taxonomic addition.

The differential taxon sampling applied in the first scheme (balanced) was performed as follows. A balanced subtree under the calibration node was maintained through the successive addition of taxa from the shallowest to the deepest nodes in both groups (backward addition). Then taxa were added from the deepest (Tupaia/Lemur and Artibeus/Canis splits) to the shallowest nodes (forward addition) (Fig. 2A).

In the second scheme (unbalanced), unbalanced subtrees under the calibration node were created by eliminating either all laurasiatherians (Fig. 2B) or euarchontoglires (Fig. 2C), with the exception of one deep representative of each lineage (Tupaia or Artibeus) that was kept to validate the Laurasiatheria/Euarchontoglires calibration node. Then, for each composition of the tree, taxa were added from the shallowest to the deepest node (backward addition) and from the deepest to the shallowest node (forward addition) (Fig. 2B and C). It is important to note that a fundamental difference exists between the trees resulting from backward and forward additions of taxa. The backward addition of taxa increased the number of terminals between the calibration node and shallow (S1 and S2) nodes, while the forward addition of taxa resulted in the insertion of terminals after the deep nodes (D1 and D2). Thus, no new terminal taxon was added between the calibration node and D1 and D2 nodes. Details of all of the topological tree compositions evaluated in this study can be found in Figure 3 (Supplementary section). Topologies composed during the backward addition (balanced and unbalanced) are shown in Figure 3A and B. Topologies used during the forward addition (balanced and unbalanced) are shown in Figure 3C and D.

The sampling strategy implemented here allows for the investigation of node divergence times under increased taxonomic sampling (backward or forward additions) on two different topological shapes regarding the child subtrees of the calibration node (balanced and unbalanced). Our hypothesis is that if taxon sampling is not an issue in divergence time inference, then the estimated ages of both shallow (S1 and S2) and deep (D1 and D2) nodes should be the same for the backward and forward terminal additions. Likewise, if the tree shape does not affect divergence time inference, we expect that the balanced and unbalanced counterparts of each taxonomic composition will yield similar chronological estimates. For instance, if tree shape is not an issue in molecular dating, the estimated divergence time of node S1 should be equivalent in topologies S1-B-0 and S1-U-0 (Fig. 3). In both, there is no extra node on the path between the calibration and S1. However, in S1-B-0 tree, the (Homo/Pan) subtree is mirrored by the (Monodon/Phocoena) subtree, while in S1-U-0, the other child subtree contains only Artibeus.

Comparison of node estimates from the reduced data with the larger data set

Empirical studies seeking to verify the performance of statistical methods frequently lack the capabilities of simulation-based analysis, where the accuracy of parametric estimation can be measured. Thus, for the sake of comparison, node estimates were also obtained using the larger data set (hereafter referred to as the full data set) of 179 mammalian genomes. The chronological time-scale of the full data set was also inferred in BEAST using the evolutionary parameters and calibration information previously described. The tree topology analysed in BEAST was fixed using the tree inferred from the first and second codon positions in MrBayes 3²⁶ under the GTR + G8 model of sequence evolution. Markov chain Monte Carlo analysis sampled 80,000 trees from two independent runs of 5,000,000 generations with four chains each, which were visited every 100th cycle. Ten thousand trees were discarded as part of the burn-in in each run.

Results

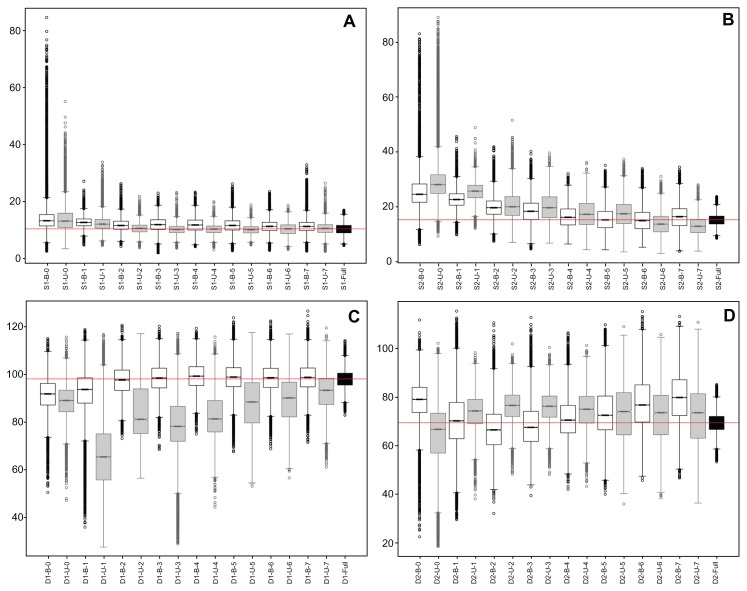
Significant variation was observed among divergence time estimates for different tree topologies. The timing of the Homo/Pan split, represented by the S1 node, was estimated to be between 10.1 ± 2.5 and 14.2 ± 5.5 Ma (Table 1). The number of nodes separating the calibration node and S1 nodes impacted the range of age estimates; the minimum estimate was obtained with 5 nodes present, while the maximum estimate was given in the absence of additional nodes (Fig. 4A). The topological composition that lacked nodes between the calibration and S1 nodes had the highest posterior distribution variance (5.5 Ma). A comparison of tree shapes revealed that trees (balanced and unbalanced) with 3 nodes between the calibration node and S1 nodes showed the greatest difference in posterior distribution means, 1.7 Ma (Fig. 4A, S1-B-3 × S1-U-3 boxplots). The minimum difference between balanced and unbalanced tree estimates was obtained under the topological composition that lacked nodes between the calibration node and S1 nodes (0.1 Ma) (Fig. 4A, S1-B-1 × S1-U-1 boxplots).

Table 1.

Divergence time estimates for the nodes under investigation.

	S1		S2		D1		D2
	Min.	Max.	Min.	Max.	Min.	Max.	Min.	Max.
Mean	10.1	14.2	13.1	29.3	67.3	99.3	63.7	79.8
SD	1.7	5.5	3.4	7.7	5.9	15.6	6.7	13.8
Difference*	0.1	1.7	0.7	3.8	2.8	25.1	0.6	14.5

Note:

^*Absolute difference between the balanced and unbalanced topology pairs.

Figure 4.

Boxplots of the posterior distributions of the evaluated taxonomic compositions. Labels represent the balanced (B) and unbalanced (U) topologies. In (A and B), the label numbers identify the number of new terminals between the calibration node and nodes S1 and S2. In (C and D), label numbers identify the number of new terminals inserted after nodes D1 and D2.

Estimates relating to the timing of the Monodon/Phocoena divergence, represented by the S2 node, followed a trend similar to the S1 node estimates. The minimum age of the split was inferred when 7 nodes separated the calibration node and S2 node (13.1 ± 3.4 Ma), while the absence of nodes between the calibration node and S2 node yielded the maximum estimate (29.3 ± 7.7 Ma). The maximum standard deviation of the posterior distribution was also obtained in the absence of nodes separating the calibration node and S2 node (7.7 Ma), whereas the minimum estimate was calculated for the topological composition with 7 nodes between the calibration node and the Monodon/Phocoena split (Table 1). When tree shape was evaluated, the difference in age between the balanced and unbalanced topologies ranged from 0.7 to 3.8 Ma. The minimum value was calculated when 3 nodes existed between the calibration node and S2 nodes (Fig. 4B, S2-B-1 × S2-U-1 boxplots), and the maximum value was estimated for the simplest topological composition, ie, no extra node (Fig. 4B, S2-B-1 × S2-U-1 boxplots).

Contrary to the shallow node estimates, estimates for the timing of the deep splits did not present decreasing variances while taxon sampling increased, and no obvious trend was detected. For instance, the Tupaia divergence time, represented by node D1, varied greatly. In this set of experiments, the minimum divergence estimate, 67.4 ± 15.6 Ma, was obtained for the composition with one extra node after the Tupaia divergence (Table 1). The maximum estimate, 99.3 ± 5.6 Ma, was obtained for the tree topology with 4 nodes after the split (Fig. 4C). The inverse scenario was depicted for standard deviation measurements; the estimate with the lowest mean had the highest associated standard deviation (67.4 ± 15.6 Ma), and that with the highest mean yielded the lowest (99.3 ± 5.6 Ma) (Table 1). The greatest difference between the balanced and unbalanced topologies was found for the tree configuration with one extra node after the Tupaia split (25.1 Ma). The minimum difference was obtained for the simplest topological composition (2.8 Ma). For the D1 node, it is clear that balanced trees resulted in posterior distributions with lower variance (Fig. 4C). This type of pattern was not observed for the shallow nodes.

The other deep divergence investigated in this study was the Artibeus split (node D2). Similar to the results for the D1 split, estimates of divergence for the D2 node did not display a predictable pattern under increased taxon sampling, although the estimates obtained from balanced and unbalanced topologies were more homogeneous than those of the D1 divergence (Fig. 4D). In the absence of nodes after the Artibeus split, divergence was dated at 63.7 ± 13.8 Ma, while the estimated timing shifted to 79.8 ± 9.7 Ma for the complete taxonomical composition (Table 1). Posterior distribution standard deviations varied less than those obtained for the D1 divergence—between 6.7 and 13.8 Ma for the topologies with 2 and no nodes after the Artibeus split, respectively. The differences between the balanced and unbalanced topologies were also more homogeneous than those calculated for the D1 split, varying from 0.6 (5 nodes) to 15.5 Ma (no nodes after the Artibeus split) (Fig. 4D).

In the full data set (Table 2), the width of the 95% highest probability density (HPD) intervals of the divergence time inferences were considerably smaller than those previously described (Fig. 4, Full boxplots). In the shallow data sets, as taxon sampling increased, estimates tended to approximate the value of the full data set. For instance, the smaller taxonomic tree compositions showed the greatest differences in divergence times between the trees that underwent progressive taxonomic addition and full tree inferences (3.8 Ma for S1 and 14.0 Ma for S2, Table 2). Similarly, the larger taxonomic tree compositions had the fewest differences with the full tree (0.1 Ma for S1 and S2, Table 2). Comparison with the full data set revealed that divergence times that were inferred from balanced tree topologies were significantly closer to those given by the full tree for node D1 (Fig. 4C). This trend was not observed for node D2, which presented large 95% HPD intervals throughout the progressive addition of taxa (Fig. 4D).

Table 2.

Divergence time estimates and 95% HPD intervals of the investigated shallow and deep nodes in the full data set with 179 mammalian mitochondrial genomes.

Node	Divergence time	Difference
		Max.	Min.
S1	10.4 (6.9–14.1)	3.8 (0-U)*	0.1 (7-B)
S2	15.3 (11.4–19.3)	14.0 (0-U)	0.1 (6-B)
D1	98.1 (90.9–105.3)	30.8 (1-U)	0.3 (3-B)
D2	69.5 (62.3–77.3)	10.3 (7-B)	0.9 (3-B)

Note:

^*Topology composition code is as detailed in Figure 3.

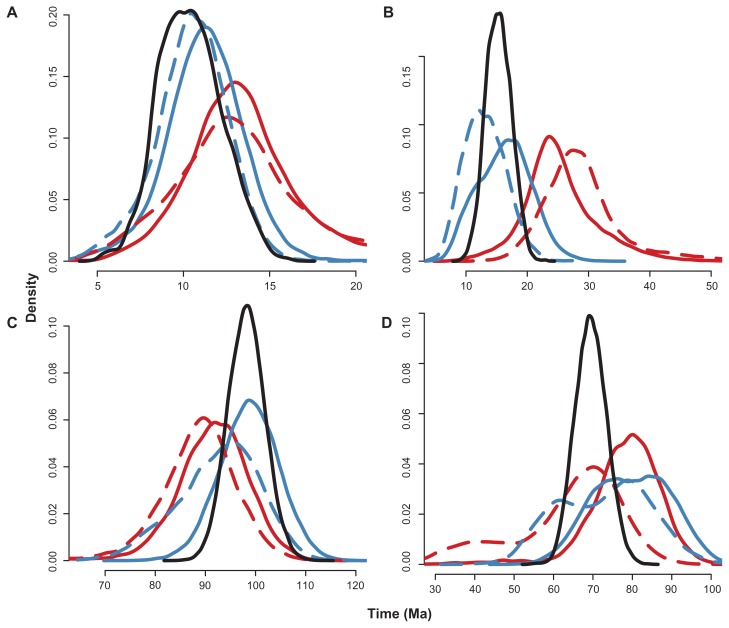
In general, when topologies with taxonomic compositions with 0 or 7 terminals were compared (Fig. 5), it was explicit that for the shallow nodes, the greatest difference from the full data set occurred between the 0-B/0-U and the 7-B/7-U data sets. Congruent posterior distributions were obtained for both the 0-B and 0-U and the 7-B and 7-U tree compositions (Fig. 5A and B). A similar result was obtained for the deep node D1 (Fig. 5C). The Artibeus divergence time (node D2) was the only parameter for which posterior distributions did not fit this pattern.

Figure 5.

Posterior distributions of divergence time estimates for the evaluated nodes: (A) S1, (B) S2, (C) D1 and (D) D2.

Notes: Black solid line: full tree; blue solid line: B-7 compositions; blue dashed line: U-7 compositions; red solid line: B-0 compositions; red dashed line: U-0 compositions.

Discussion

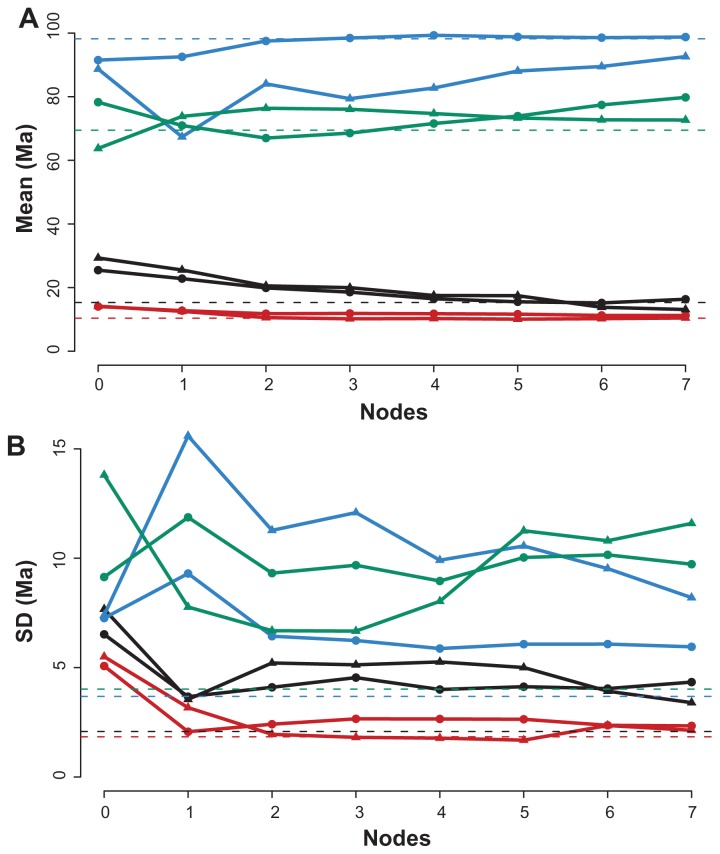
Our analyses show that the effect of taxon sampling on mammalian divergence time estimates depends on the number of terminals between the node of interest and the node that bears the calibration information. In general, as taxonomic sampling increased, the mean of the posterior distribution gradually approaches the value inferred from the full data set (Fig. 6A). Beyond their effects on the mean, differential taxonomic sampling schemes significantly affected the credibility intervals of the estimates. For both shallow nodes, representing the Homo/Pan and the Monodon/Phocoena splits, the variance of the estimates decreased when taxon sampling increased. Moreover, the width of the 95% HPD interval approached the value obtained for the full data set. The same effect was not observed for the estimates obtained from the deep nodes (D1 and D2), where the variance of posterior distributions varied greatly among taxonomic samplings (Fig. 6B). Therefore, while increasing the number of terminals between the calibration node and the shallow nodes improved the age estimates of S1 and S2, the addition of taxa after the deep nodes had no equivalent effect on the age estimates of D1 and D2.

Figure 6.

(A) Mean and (B) SD of the posterior distributions for the evaluated taxonomic compositions.

Notes: Numbers on the horizontal axis identify either the number of new taxon terminals between the calibration node and nodes S1 and S2 or the number of new taxon terminals after nodes D1 and D2. Red line with circles: node S1 for balanced trees; red line with triangles: node S1 for unbalanced trees; black line with circles: node S2 for balanced trees; black line with triangles: node S2 for unbalanced trees; blue line with circles: node D1 for balanced trees; blue line with triangles: node D1 for unbalanced trees; green line with circles: node D2 for balanced trees; green line with triangles: node D2 for unbalanced trees. Dashed lines indicate the mean and SD under the full data set.

We hypothesise that the behaviour of variances for the deep nodes are explained by the smaller effective sample sizes (ESS) obtained during the MCMC run. Although all ESS were greater than 400, the values were much smaller for deep nodes than for those inferred for the shallow nodes, which were frequently greater than 1,000. Indeed, the standard deviation of the estimates obtained for nodes D1 and D2 are negatively associated with their ESS (D1, Spearman ρ = −87.6, P-value < 0.001 and D2, ρ = −60.9, P-value < 0.01). The small ESS of deep nodes might reflect topological uncertainty because of insufficient phylogenetic signal resultant of the rapid inter-ordinal diversification of mammals.²⁷ Although tree topology was fixed, this issue could still influence the rate of acceptance of new divergence time values proposed during MCMC. One solution to this issue would be to reduce the 95% HPD interval by running the MCMC algorithm for more generations.

In this study, topological shape was not an issue for divergence time estimation. The differences between the balanced/unbalanced pair estimates were generally small. This means that for a given set of calibration information, simply augmenting the number of sequences would not be sufficient to improve divergence time estimates. The best strategy would be to insert nodes on the path between the calibration node and the node of interest. For instance, it is better to add two sequences (nodes) on the path between the calibration node and the node of interest than it is to add one on this path and the other on the sister group. Augmenting the number of sequences should generally have a positive effect on divergence time inference in cases where the number of nodes bearing calibration information increases and they are distributed evenly along the topology.

Our analyses are in agreement with Linder et al.¹⁸ showing that taxonomic sampling indeed impacts molecular dating. However, the authors of this study verified that the undersampling effect they detected was positively correlated with the distance from the calibration point; this correlation was not observed in our data. Under severe undersampling (the 0-B/0-U compositions), the posterior distribution means of divergence times for both deep and shallow nodes were equally distant from the full data set mean (Fig. 6A). In fact, the Homo/Pan split was the node that was least influenced by taxon sampling. On the other hand, we found that variance of the divergence time estimates were negatively correlated with the distance from the calibration node.

None of the aforementioned studies, however, have considered the influence of taxon sampling on the variance of the posterior distribution of divergence times, as measured here by the width of the 95% HPD interval. For instance, the inclusion of an extra node on the path between the calibration node and nodes S1 or S2 drastically reduced the standard deviation of the posterior distribution for shallow nodes (Fig. 4B). One possibility is that the inclusion of nodes between the calibration node and the shallow nodes augmented the inheritance of the chronological information present on the calibration prior. For instance, Lapage et al.¹² has shown that correlated models of sequence evolution perform better than independent-rate models because the correlation between branches enhances the possibility that the information will be carried from ancestral to descendent branches.

The model of evolutionary rate evolution used in this work, however, does not assume correlation along the branches of the phylogeny.¹¹ Nevertheless, it is possible that, even under an uncorrelated lognormal model, additional taxa could reduce the overall variance of the mean evolutionary rate among branches and consequently decrease the variance of individual time estimates. The problem with this hypothesis is that it would not explain why the variance of the posterior distribution of the ages of deep nodes was unresponsive to increased taxonomic sampling (Fig. 6B). As previously noted, reduced ESS is one possible explanation.

Of relevance to the influence of taxon sampling on divergence time estimates is whether the time scales obtained under different sampling would lead to significantly distinct historical scenarios of lineage evolution. Our results have demonstrated that this possibility cannot be ruled out. For instance, under the composition S2-U-0, the Monodon/Phocoena split was dated at approximately 29 Ma, while under the S2-U-7 composition, the value fell to 13 Ma. If only the mean of the posterior distribution was considered, the divergence would shift from the Early Oligocene to the Middle Miocene. When the 95% HPD intervals are compared, the difference is still drastic (from 17 to 45 Ma in S2-U-0 and from 7 to 19 Ma in S2-U-7). Previous studies estimating the age of the Monodon/Phocoena divergence also recovered dates as different as 10.5 Ma²⁸ and 21.0 Ma.²⁹ Curiously, the work with the oldest estimate was also the one with fewer taxonomic samplings,²⁹ supporting the results found here. Therefore, it is possible that many of the discrepancies found among molecular dating studies are caused by differential taxon sampling.

In conclusion, mammalian divergence time estimates were influenced by taxonomic sampling. This influence was more associated with the number of nodes between the calibration node and the node of interest than it was with the distance between nodes. Furthermore, the width of the credibility interval of the posterior distribution was affected to a greater extend by taxonomic sampling than the mean. Tree shape was a minor issue for Bayesian divergence time inference using mammal mitogenomes.

Supplementary Figure

Figure 3

Tree topologies used for divergence time inference. Tree names are coded so as to represent the balanced (B) and unbalanced (U) topologies. The calibration node is identified by the green circle. Red circles identify nodes S1 and D1, while purple circles identify nodes S2 and D2. (A) Node S1, applying the backward addition of taxa. Numbers in tree names identify the number of new terminals between the calibration node and node S1. (B) Node S2, applying the backward addition of taxa. Numbers in tree names identify the number of new terminals between the calibration node and node S2. (C) Node D1, applying the forward addition of taxa. Numbers in tree names identify the number of new terminals inserted after node D1. (D) Node D2, applying the forward addition of taxa. Numbers in tree names identify the number of new terminals inserted after node D2.

Abbreviation

Ma

mega annum.