Abstract
For centuries, it has been known that humans can rapidly and accurately enumerate small sets of items, a process referred to as subitizing. However, there is still active debate regarding the mechanisms that mediate this ability. For example, some have argued that subitizing reflects the operation of a fixed-capacity individuation mechanism that enables concurrent access to a small number of items. However, others have argued that subitizing reflects the operation of a continuous numerical estimation mechanism whose precision varies with numerosity in a manner consistent with Weber's law. Critically, quantitative models based on either of these predictions can provide a reasonable description of subitizing performance, making it difficult to discriminate between these alternatives solely on the basis of subjects' behavioral performance. Here, we attempted to discriminate between fixed-capacity and continuous estimation models of subitizing using neural measures. In two experiments, we recorded EEGs while subjects performed a demanding subitizing task and examined set-size-dependent changes in a neurophysiological marker of visual selection (the N2pc event-related potential component) evoked by an array of to-be-enumerated items. In both experiments, N2pc amplitudes increased monotonically within the subitizing range before reaching an asymptotic limit at approximately three items. Moreover, inter-participant differences in the location of this asymptote were strongly predictive of behavioral estimates of subitizing span derived from a fixed-capacity model. Thus, neural activity linked with subitizing ability shows evidence of an early and discrete limit in the number of items that can be concurrently apprehended, supporting a fixed-capacity model of this process.
Introduction
Humans are able to rapidly and accurately enumerate small sets of objects (Jevons, 1871), a process referred to as “subitizing” (Kaufman et al., 1949). In a typical enumeration task, subjects are asked to rapidly and accurately count the number of stimuli present in a visual display. When subjects' response latencies (or error rates) are plotted as a function of set size, a typical pattern emerges: the slope of this function is shallow for displays that contain fewer than three to four objects but increases drastically for larger displays. This discontinuity has led many to propose that subitizing is governed by a fixed-capacity individuation mechanism that enables concurrent access to a small number of items (Mandler and Shebo, 1982; Trick and Pylyshyn, 1994; Revkin et al., 2008; Piazza et al., 2011), whereas the enumeration of larger sets is governed by a separate numerical process. However, other studies have demonstrated that this profile is also well approximated by quantitative models assuming a single continuous numerical estimation mechanism whose precision varies with numerosity according to Weber's law (Balakrishnan and Ashby, 1991, 1992; Gallistel and Gelman, 1992; Dehaene and Changeux, 1993). Thus, the mechanisms that enable subitizing remain a matter of substantial debate.
Here, we present neural evidence supporting a fixed-capacity model of subitizing. In two experiments, subjects were asked to report the number of targets present in brief visual displays. In both experiments, subjects' behavioral performance on was equally well described by quantitative functions derived from fixed-capacity and continuous estimation models of subitizing. However, concurrent electrophysiological [electroencephalogram (EEG)] recordings allowed us to distinguish between these models. Specifically, we examined set-size-dependent changes in a neurophysiological marker of visual selection evoked by the target array: the N2pc event-related potential (ERP) component. The N2pc is a transient contralateral negative-going wave appearing over posterior electrodes ∼200 ms after the onset of an attended stimulus (Luck and Hillyard, 1994; Eimer, 1996; Woodman and Luck, 1999), and its amplitude scales with the number of stimuli that must be selected or remembered before reaching an asymptotic limit with behavioral estimates of multiple-object tracking (Drew and Vogel, 2008) and working memory capacity (Anderson et al., 2011). Here, we reasoned that if subitizing reflects the operation of a fixed-capacity individuation mechanism, then N2pc amplitudes evoked by a subitizing array should reach an asymptotic limit at or near behavioral estimates of subitizing span. Alternately, if subitizing reflects the operation of a continuous numerical estimation mechanism, then N2pc amplitudes should increase monotonically with target numerosity across a much larger range of set sizes. In both experiments, we found that N2pc amplitudes increased monotonically with set size before reaching an asymptotic limit at approximately three items. Moreover, individual differences in the location of this asymptote were strongly correlated with behavioral estimates of subitizing span derived from a fixed-capacity model of this process. These findings suggest that subitizing reflects the operation of a fixed-capacity individuation mechanism that enables concurrent access to a small number of items.
Materials and Methods
Subjects.
Eighteen and 24 students (10 and 14 males, respectively) from the University of Oregon participated in experiments 1 and 2, respectively. All subjects were tested in a single 2 h session in exchange for monetary compensation. All subjects reported normal or corrected-to-normal visual acuity and color vision, and all gave both written and oral informed consent. Data from one subject in experiment 1 and two subjects in experiment 2 were discarded as a result of an excessive number of eye movements or blinks (which contaminated concurrent electrophysiological recordings); the data reported here reflect the remaining 17 and 22 participants, respectively.
Stimuli and apparatus.
Stimuli were generated in MATLAB (MathWorks) and rendered on an 18-inch CRT monitor cycling at 60 Hz via Psychophysics Toolbox software (Brainard, 1997; Pelli, 1997). Subjects were seated ∼80 cm from the display (head position was unconstrained) and instructed to maintain fixation on a small dot (subtending 0.2°) for the duration of each trial. Stimuli (subtending 1.1°) were rendered on the vertices of invisible 12 × 12 grids centered within each hemifield of the display.
Experiment 1.
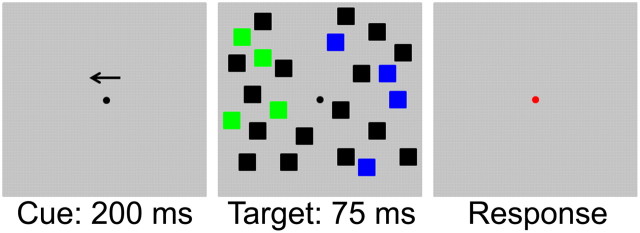
A representative trial from experiment 1 is shown in Figure 1. Before beginning the experiment, participants were instructed to enumerate blue or green squares (counterbalanced across subjects; no differences were observed as a function of target color in either experiment reported here, and this factor was excluded from all analyses). Each trial began with a fixation display for 300–500 ms (the exact duration was randomly chosen on each trial). A small arrow cue was then rendered immediately above the fixation point for 200 ms; this indicated the visual hemifield where targets would subsequently appear. After a 200 ms post-cue interval, the target display was presented for 75 ms. On each trial, 12 or 14 squares were rendered in each hemifield (total numerosity was varied in this manner to prevent subjects from enumerating non-target items and then subtracting this value from the total number of items in the display to infer the number of targets present). In the cued hemifield, 1–6, 8, or 10 of these squares were rendered in the target color (e.g., green), and the remainder were black (distractors). An equivalent number of non-targets (e.g., blue) and distractors were rendered in the opposite hemifield; this was done to eliminate sensory confounds that could account for set-size-dependent changes in the N2pc, a lateralized ERP component. The target display was followed by a 300 ms blank interval and response probe. Subjects were instructed to report the number of target items present in this display using the number pad of a standard American keyboard to enter their response (the “0” key was used to denote 10 items). Trials were separated by a 300–500 ms interval (randomly chosen on each trial independently of the random fixation interval that began each trial; thus the interstimulus interval separating the subject's response from the appearance of the arrow cue on the subsequent trial ranged from 600 to 1000 ms). Participants were instructed to prioritize accuracy, and no response deadline was imposed. Subjects completed a total of 200 trials (100 per visual hemifield) in each set size condition (1600 trials total).
Figure 1.
The behavioral task used in experiment 1. Subjects were required to enumerate the number of blue or green squares (target color was counterbalanced across observers) appearing in one hemifield of a visual display. Before the onset of the target display, subjects were shown a spatial cue that indicated the hemifield where targets would subsequently appear with 100% validity. The target display was followed by a 300 ms blank interval and a response cue.
Experiment 2.
The design of experiment 2 was similar to that of experiment 1, with the following exceptions. First, distractors (Fig. 1, black squares) were removed from both hemifields of the target array. This allowed us to examine whether the findings of experiment 1 would generalize to a more “traditional” subitizing task that omits distractors. Second, because the target arrays used in experiment 1 contained an equal number of target and non-target items in the relevant and irrelevant visual hemifields, we considered the possibility that subjects ignored the initial hemifield cue and simply counted the number of squares presented on a randomly chosen side of the screen. The results of experiment 1 (see Fig. 3) suggest that this is unlikely. Specifically, if subjects simply oriented to a randomly chosen hemifield on each trial, it would obscure set-size-dependent changes in N2pc amplitudes contralateral to the cued hemifield, as well as any correlations between N2pc slopes and behavioral performance. However, robust N2pc set size effects were observed, and set-size-dependent changes in N2pc amplitudes were strongly correlated with subjects' performance. Nevertheless, we modified the design of experiment 2 in an effort to further discourage subjects from ignoring the hemifield cue. Specifically, on 50% of trials, an equivalent number of non-target items were presented in the non-cued hemifield (as in experiment 1). On the remaining 50% of trials, the non-cued hemifield contained both non-target and white squares (“catch” trials). The number of non-target and white squares was randomly chosen for each trial, with the constraints that at least one item of each color was presented, and the total number of squares was equal to the number of targets present in the cued hemifield so that physical stimulation was balanced across contralateral and ipsilateral visual fields. During set size 1 trials, the non-cued hemifield always contained a non-target colored square. Assuming that subjects can only enumerate a single “set” of items (defined here by color) at one time, then the inclusion of catch trials precludes a strategy of simply enumerating the items present in a randomly chosen hemifield. Although a recent study by Halberda et al. (2006) suggests that human observers can enumerate at least two sets of items in a short period, we note that this study used relatively dense stimulus arrays (e.g., 20–30 items) designed to engage an “approximate number system” that operates independently of subitizing mechanisms (Dehaene et al., 1998). Indeed, subjects' estimates of numerosity for these displays were highly variable (average coefficient of variance = 0.21). Moreover, the stimulus displays used in this study were presented for 500 ms (more than five times the duration of the target arrays used here), which could allow for the serial enumeration of multiple sets. Finally, subjects were tested on a wider range of set sizes (1–6, 8, 10, and 12) relative to experiment 1. Responses were made using the number pad on a standard keyboard; the “0” and “.” keys were used to denote 10 and 12 items, respectively.
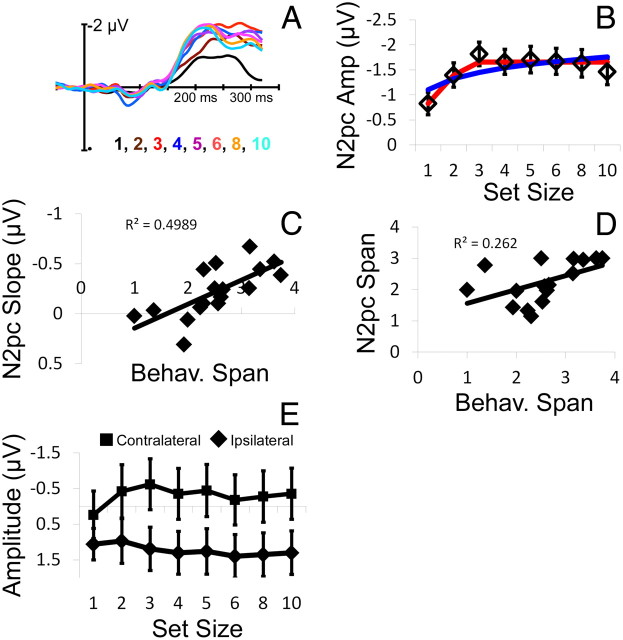
Figure 3.
Electrophysiological responses observed in experiment 1. A, Grand-averaged ERP difference waves (defined as the difference in amplitude between contralateral and ipsilateral electrode sites O1/2, OL/R, and PO3/4) time locked to the onset of the target array are plotted as a function of set size (colors). By convention, negative is plotted upward. We defined the N2pc as the mean amplitude observed during a period 200–300 ms after the onset of the target array. B, Mean N2pc amplitudes (diamond symbols, error bars are ±1 SEM) are plotted as a function of set size. Note that N2pc amplitudes increase monotonically with set size from set sizes 1–3 before reaching a stable asymptote at set sizes 4–10. The best-fitting fixed-capacity (red line) and continuous estimation (blue line) models are overlaid. C, Individual differences in subitizing span (defined via the inflection point of a bilinear function fit to each subject's error rate by set size function) were strongly correlated with N2pc slopes (defined as the difference in mean amplitude between set sizes 2 and 5). D, Individual differences in subitizing span derived from subjects' behavioral performance (abscissa) were strongly correlated with estimates of subitizing span derived by fitting each subject's N2pc by set size profile with a bilinear function (ordinate). E, Mean electrophysiological responses observed during a period from 200–300 ms after the onset of the target array are plotted as a function of set size (abscissa) and electrode site (contralateral vs ipsilateral to the cued hemifield; square and diamond symbols, respectively). Set-size-dependent changes in electrophysiological responses were observed over contralateral, but not ipsilateral, electrode sites (see Results). Error bars are ±1 SEM.
Analysis of behavioral data.
To compare fixed-capacity and continuous estimation models of subitizing, we fit each subject's error rate (i.e., 1 minus percentage correct) by set size profile with quantitative functions that encapsulate key predictions of these models. For example, according to the continuous estimation model of subitizing, the enumeration of small and large sets is mediated by a single numerical estimation mechanism whose precision varies with set size according to Weber's law. Thus, the enumeration of small sets should be highly accurate (i.e., error rates should be low) but should become less precise (i.e., error rates should increase) as set size increases. Following other studies (Balakrishnan and Ashby, 1991, 1992), we expressed these predictions using an exponential function of the following form:
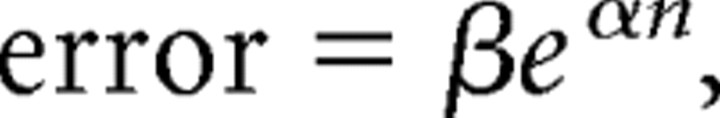 |
where n refers to set size, and e is the base of the natural logarithm. β and α are free parameters. In contrast, the fixed-capacity model of subitizing assumes that separate numerical mechanisms enable the enumeration of small and large sets. Specifically, the enumeration of small sets is thought to be mediated by a fixed-capacity individuation mechanism that enables concurrent access to a small number of items, whereas the enumeration of larger sets is thought to be mediated by a second numerical process (perhaps similar to the estimation procedure posited by the continuous estimation model; we take an agnostic view on this issue). Thus, the enumeration of sets within the subitizing range (e.g., one to four items) should be virtually perfect (i.e., error rates should be near 0), but performance should decrease monotonically with increases in set size once this limit is exceeded. Following earlier studies (Balakrishnan and Ashby, 1991, 1992; Trick and Pylyshyn, 1994), we expressed these predictions using a bilinear function with three parameters: the height of a flat line (whose slope was fixed at 0) used to account for performance in subitizing range, and the slope and intercept of a positively increasing line used to account for performance outside of subitizing range. Finally, we computed the adjusted r2 statistic for both models on a subject-by-subject basis to quantify their explanatory power. The adjusted r2 statistic expresses the proportion of variance explained by a model weighted by its number of free parameters; models with a greater number of free parameters are penalized relative to those with fewer free parameters. Thus, this statistic ensures a fair comparison between the two-parameter continuous estimation model and the three-parameter fixed-capacity model.
Electrophysiological recording and analysis.
ERPs were recorded and analyzed using standard procedures that have been described in detail previously (McCollough et al., 2007). Briefly, we recorded from 22 electrodes spanning the scalp, including International 10/20 Standard sites F3, F4, C3, C4, P3, P4, O1, O2, PO3, PO4, T5, and T6, as well as non-standard sites OL and OR (midway between O1/2 and T5/6). The horizontal electrooculogram (EOG) was recorded from electrodes placed 1 cm to the left and right of the external canthai, and the vertical EOG was recorded from an electrode beneath the right eye. All electrodes were referenced to an electrode placed on the right mastoid. Trials contaminated by blinks or large (>1°) eye movements were excluded from all analyses. EEG and EOG were amplified by an SA Instrumentation amplifier with a bandpass of 0.01–80 Hz (half-power cutoff, Butterworth filters) and digitized at 250 Hz by a personal-computer-compatible microcomputer. Contralateral waveforms were computed by averaging the activity recorded over right hemisphere electrodes when observers attended the left visual field and vice versa when observers attended the right visual field. This was done separately for each set size. In both experiments, the N2pc was defined as the difference in mean amplitude between contralateral and ipsilateral waveforms measured at standard electrode sites O1/2, OL/OR, and PO3/4 during a period 200–300 ms after the onset of the target display.
Results
Experiment 1
Mean response error across participants is plotted as a function of set size in Figure 2A, and response errors from a representative participant are shown in Figure 2B. To characterize performance, we fit each subject's response error by set size function with the continuous estimation and fixed-capacity models described in Materials and Methods (see Modeling behavioral performance) using a nonlinear maximum likelihood estimation routine (the Nedler–Mead simplex method as implemented in MATLAB). For many analyses, modeling was performed using data from set sizes 1–5. This was done for two reasons. First, the primary goal of this experiment was to discriminate between fixed-capacity and continuous estimation models of subitizing. Critically, both models predict substantial changes in error rates with large arrays, either because items could not be individuated (fixed-capacity model) or because of greater variability representations of large relative to small numbers (continuous estimation model). However, the models predict very different response profiles at lower set sizes. For example, if subitizing is mediated by a fixed-capacity mechanism that enables concurrent access to a limited number of items, then the enumeration of subcapacity arrays should be virtually perfect. However, error rates should climb dramatically once putative capacity limits are exceeded (i.e., there should be a sharp discontinuity in error rates and/or N2pc by set size functions). In contrast, if subitizing is mediated by a continuous numerical mechanism whose precision is inversely related to set size, then one would expect to observe gradual changes in error rates (or N2pc amplitudes) with increases in set size. With respect to discriminating between these models, the most informative data points lie around putative capacity limits in subitizing, typically estimated at approximately three to four items (Pylyshyn and Storm, 1993, 1994).
Figure 2.
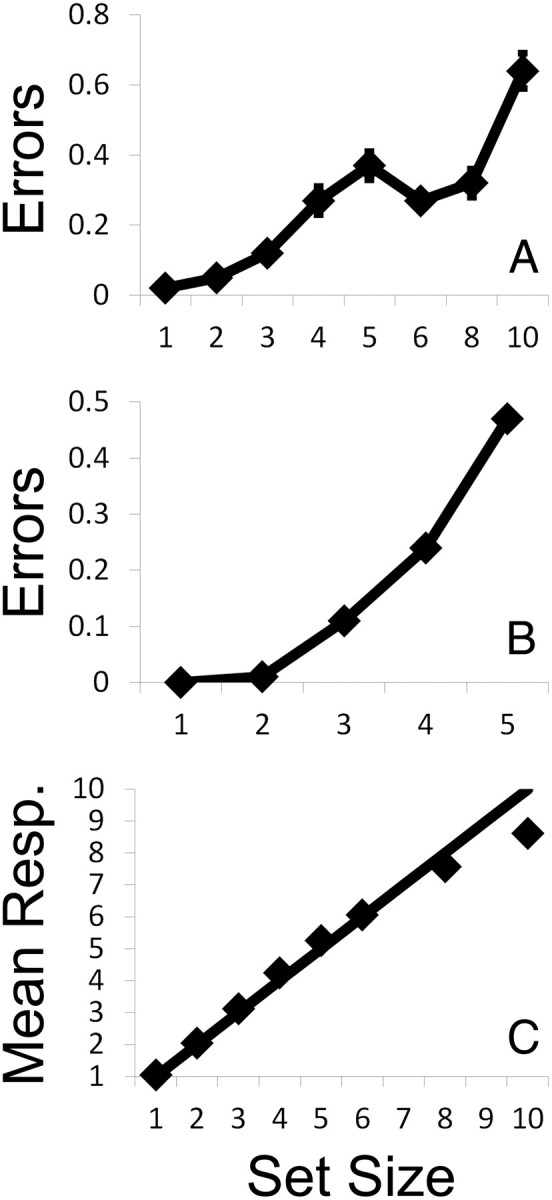
Behavioral performance in experiment 1. A, Mean response error (±1 SEM) across subjects is plotted as a function of set size. B, Data from a representative participant. To distinguish between fixed-capacity and continuous estimation models of subitizing, each subject's error rate by set size function was fit with exponential and bilinear functions (see Materials and Methods). C, Subjects' mean responses (ordinate) are plotted as a function of set size (abscissa). Error bars (±1 SEM) are subsumed by the data symbols at all set sizes. Values above the unity line reflect a proclivity to overestimate the number of targets present, whereas values below it reflect a proclivity to underestimate the number of targets present. Because subjects tended to systematically underestimate the number of targets present in large arrays (e.g., set sizes 8 and 10), most modeling was performed using data from set sizes 1–5.
A second reason why we restricted our analysis to set sizes 1–5 was because our data revealed a bias in which subjects tended to systematically underreport the number of targets present at higher set sizes (a similar bias has been reported in many other studies of subitizing; Mandler and Shebo, 1982). To illustrate this, Figure 2C plots subjects' mean responses as a function of set size. Note that mean responses are well below the unity line for set sizes 8 and 10, suggesting that subjects frequently underestimated the number of targets present during these trials. It is likely that this bias also influenced subjects' performance at set size 6. For example, given that subjects were hesitant to report large values, they may have simply been more likely to report that six items were present when they were unsure of the exact target numerosity. This would explain why error rates at set size 6 are somewhat lower than error rates at either set sizes 5 or 8 (Fig. 2A; a similar bias was also observed in experiment 2; see Fig. 5B). To ensure that modeling solutions were not unduly influenced by this bias, we focused on data from set sizes 1–5 (although qualitatively similar findings emerged when all set sizes were included, as described below).
Figure 5.
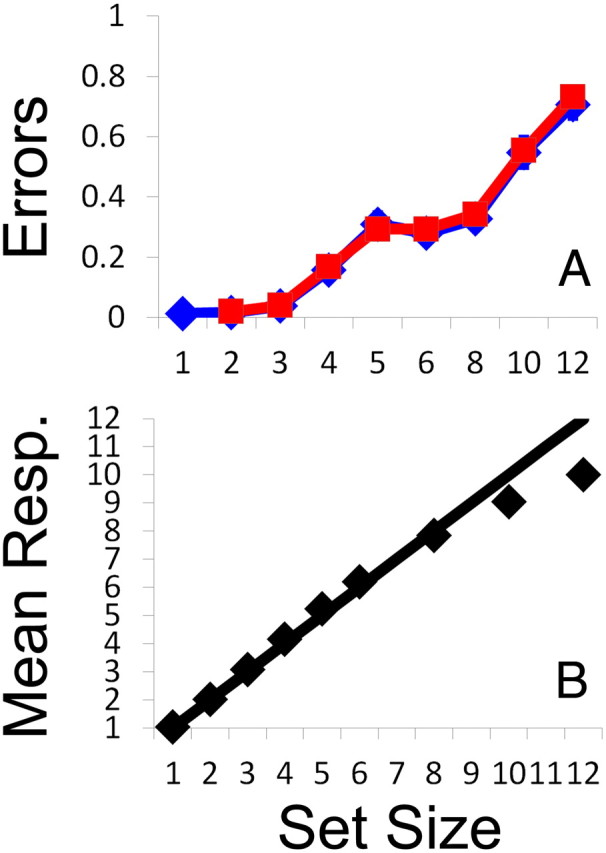
Behavioral performance in experiment 2. A, Mean response errors across subjects are plotted as a function of set size and trial type (i.e., non-catch vs catch trials; blue and red lines, respectively). Error bars are ±1 SEM. B, As in experiment 1, subjects typically underestimated the number of targets present in large arrays. Thus, we modeled each subject's error rate by set size function using data from set sizes 1–5.
As shown in Table 1, both the fixed-capacity and continuous estimation models provided a good description of subjects' performance, accounting for >90% of the variance in behavioral responses. Direct statistical comparisons revealed a small advantage in adjusted r2 values for the fixed-capacity relative to the continuous estimation model (t(16) = 2.30, p = 0.03). Qualitatively similar findings were also observed when we fit each subject's error rate-by-set size profile using data from set sizes 1–10 (although adjusted r2 values were much lower, presumably because of greater response variability at higher set sizes; Fig. 2A,C, Table 1). In fact, the continuous estimation model actually bested the fixed-capacity model under these conditions (t(16) = 3.12, p < 0.01). These results are unsurprising insofar as many studies have shown that subitizing performance can be reasonably well approximated by either or both models. However, one can also attempt to distinguish between these models by examining electrophysiological responses evoked by the presentation of a to-be-enumerated array. Thus, we examined set-size-dependent changes in N2pc amplitudes evoked by the presentation of the target array. As discussed in Introduction, the N2pc is a transient contralateral negative-going wave appearing over posterior electrodes ∼200 ms after the onset of an attended stimulus, and its amplitude scales with the number of stimuli that must be selected or remembered before reaching an asymptotic limit with behavioral estimates of multiple-object tracking (Drew and Vogel, 2008) and working memory capacity (Anderson et al., 2011). Moreover, a recent study by Mazza and Caramazza (2011) suggests that the N2pc amplitudes scale with the number of to-be-enumerated targets in a display. These authors recorded EEGs while subjects performed an enumeration task that required them to rapidly and accurately indicate whether one, two, or three targets were present in a lateralized display (as in the current study, targets were embedded among distractors) and observed monotonic increases in N2pc amplitudes with increases in target numerosity. Critically, these results were contingent on the subjects' intent to enumerate the target items—in a second experiment, subjects were shown displays identical to those described above and asked to indicate whether any targets were present (regardless of their numerosity). Under these conditions, N2pc set size effects were eliminated. These results demonstrate that the N2pc can be taken as a measure of the number of to-be-enumerated items present in a visual display. Here, we exploited these findings to compare fixed-capacity and continuous estimation models of subitizing. Specifically, we reasoned that if subitizing reflects the operation of a fixed-capacity individuation mechanism, then N2pc amplitudes should saturate or asymptote once putative capacity limits are exceeded. Alternately, if the enumeration of small and large sets is mediated by a single continuous numerical estimation procedure, then one would expect N2pc amplitudes to increase monotonically across a much larger range of set sizes.
Table 1.
Model fitting summary for experiment 1
| Mean adjusted r2 | Minimum adjusted r2 | Maximum adjusted r2 | |
|---|---|---|---|
| Fixed-capacity set sizes 1–5 | 0.94 | 0.72 | 0.99 |
| Continuous estimation set sizes 1–5 | 0.87 | 0.58 | 0.99 |
| Fixed-capacity set sizes 1–10 | 0.56 | 0.13 | 0.99 |
| Continuous estimation set sizes 1–10 | 0.62 | 0.14 | 0.98 |
ERP difference waves time locked to the onset of the target display are shown as a function of set size in Figure 3A, and mean N2pc amplitudes during a period 200–300 ms after the onset of the target display are depicted in Figure 3B. As shown in Figure 3B, N2pc amplitudes increased from set sizes 1–3 before reaching a clear asymptote at larger set sizes. At the group level, this profile was well approximated by a bilinear function derived from a fixed-capacity model of subitizing (adjusted r2 = 0.83; Fig. 3B, red line) and poorly described by a logarithmic function (i.e., the inverse of the exponential function used to model subjects' behavioral performance; this function was chosen because, in contrast to subjects' behavioral performance, N2pc amplitudes increased from set sizes 1–3 before leveling off) of the following form:
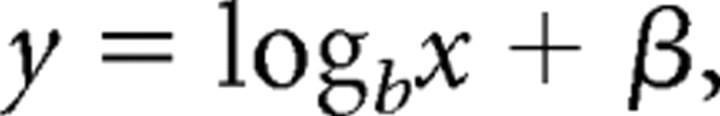 |
where b is the base of the logarithm and β is a scalar (both were allowed to vary; adjusted r2 = 0.44; Fig. 3B, blue line). Similar findings were also observed at the level of individual subjects: N2pc response profiles were well approximated by a bilinear function (mean adjusted r2 across participants = 0.46; set sizes 1–10) and poorly approximated by a logarithmic function. In the latter case, 11 of 17 subjects had negative adjusted r2 values, indicating that the error variance associated with their model fits were larger than what would be expected given a model in which the mean of the sample (in this case, the mean N2pc amplitude across set sizes) is the sole parameter (this fact precluded direct statistical comparisons between the single-subject fits for the fixed-capacity and continuous estimation models). Thus, set-size-dependent changes in N2pc responses evoked by the target array were well characterized by a bilinear function derived from a fixed-capacity model of subitizing and poorly characterized by a logarithmic function derived from a continuous estimation model of this process.
Next, we asked whether N2pc response profiles were related to subjects' subitizing performance. To do so, we first computed the inflection point (i.e., the intersection of the flat and linear components) of the bilinear function derived from the fixed-capacity model of subitizing that was fit to each subject's behavioral data (using data from set sizes 1–5 so as to avoid contamination from response biases at higher set sizes; see above); the location of this inflection point was taken as a behavioral estimate of subitizing span. Next, we computed the slope of each subject's N2pc by set size function by subtracting the mean amplitude observed at set size 2 from the mean amplitude at set size 5 (following an approach described by Vogel and Machizawa, 2004). Our reasoning was that, if N2pc amplitudes reach a stable asymptote with putative capacity limits in subitizing (as predicted by a fixed-capacity model of subitizing), then N2pc amplitudes should saturate at lower set sizes for subjects with low subitizing spans. Consequently, the slopes of these subjects' N2pc by set size functions should be smaller than those observed for high-span subjects. As shown in Figure 3C, inter-subject differences in behavioral estimates of subitizing span were indeed positively correlated with N2pc slopes (r = 0.70, p = 0.001). A similar trend was also observed when subitizing span was estimated by fitting each subject's error rate by set size function using data from set sizes 1–8 (r = 0.51, p = 0.05; stable inflection points could not be estimated for two subjects in this case; this correlation reflects the remaining 15 subjects), as well as when N2pc slope was defined as the difference between the mean amplitude observed at set sizes 2 and 3 (r = 0.59, p < 0.05). Moreover, mean N2pc amplitudes observed at larger set sizes (e.g., set sizes 4–6) were not predicted by individual differences in subitizing span (all p values > 0.30), suggesting that correlations between estimates of subitizing span and N2pc slope cannot be explained by overall differences in mean N2pc amplitudes across high- and low-span subjects.
Given that the N2pc by set size function depicted in Figure 3B is well approximated by a bilinear function, one can also ask whether individual differences in the inflection point of this function predict estimates of subitizing span. To examine this possibility, we fit each participant's N2pc amplitude by set size profile with a bilinear function similar to that used to characterize subjects' behavioral performance (using data from set sizes 1–5 so as to match the model applied to subjects' behavioral data; see above). The inflection point of this function was then taken as an electrophysiological estimate of subitizing span. Data from one subject could not be modeled (i.e., there was no evidence for a bilinear or any other orderly profile across set sizes); the data reported here reflect the remaining 16 subjects. Critically, as shown in Figure 3D, inter-participant differences in the inflection point of this function were strongly correlated with behavioral estimates of subitizing span (r = 0.52, p < 0.05). A similar relationship was also observed when both behavioral and N2pc inflection points were estimated using data from set sizes 1–6 (r = 0.54, p < 0.05), suggesting that the relationship between behavioral and electrophysiological measures of subitizing span was not attributable to arbitrary choices regarding which set sizes to model. These findings provide additional evidence that subitizing reflects the operation of a fixed-capacity individuation mechanism that enables concurrent access to a fixed number of items.
Critically, the N2pc is defined as the difference in amplitudes measured at contralateral and ipsilateral electrode sites. Based on the extant literature, we have assumed that set-size-dependent changes in the N2pc reflect the selection and/or individuation of items in the cued hemifield and that this process manifests as a greater negativity over electrode sites contralateral to this hemifield. However, a second possibility is that these set-size-dependent changes reflect a suppression of information in the irrelevant visual hemifield, perhaps manifesting as a greater positivity over electrode sites ipsilateral to the cued hemifield. Alternately, set-size-dependent changes in N2pc amplitudes might reflect a greater negativity over contralateral electrodes coupled with a greater positivity over ipsilateral electrodes. To discriminate between these alternatives, we examined set-size-dependent changes in activity measured at contralateral and ipsilateral electrodes separately. Mean response amplitudes observed in contralateral (squares) and ipsilateral (diamonds) electrodes during a period 200–300 ms after the onset of the target array are depicted as a function of set size in Figure 3E. To characterize set-size-dependent changes in response amplitudes, data were subjected to a 2 (electrode site; contralateral vs ipsilateral) × 8 (set size; 1–6, 8, or 10 targets) ANOVA. This analysis revealed a significant main effect of electrode site (F(1,16) = 37.02, p < 0.001) and a significant interaction between electrode site and set size (F(7,112) = 19.42, p < 0.001). The main effect of set size was not significant (F(7,112) = 1.51, p = 0.17). Visual inspection of Figure 3E suggests that response amplitudes over contralateral electrodes became progressively more negative from set sizes 1–3, whereas amplitudes observed over ipsilateral electrodes remained relatively constant across this range. To formally examine this possibility, electrode responses for set sizes 1–3 were subjected to a 2 (electrode site) × 3 (set size; 1, 2, or 3 targets) ANOVA. This analysis revealed a significant main effect of electrode site (F(1,16) = 42.62, p < 0.001), a marginally significant effect of set size (F(2,32) = 2.76, p = 0.08), and a significant interaction between these factors (F(2,32) = 52.32, p < 0.001). Thus, separate one-way ANOVAs were performed on contralateral and ipsilateral responses. This analysis revealed a significant main effect of set size for contralateral, but not ipsilateral, electrodes (F(1,26) = 8.66, p < 0.005 and F(1,26) = 0.611, p = 0.55, respectively). These findings demonstrate that set-size-dependent changes in N2pc amplitudes were primarily driven by greater negative responses over electrode sites contralateral to the cued hemifield and support our assumption that the N2pc reflects the selection and individuation of items from this hemifield rather than the processing or suppression of information in the irrelevant hemifield.
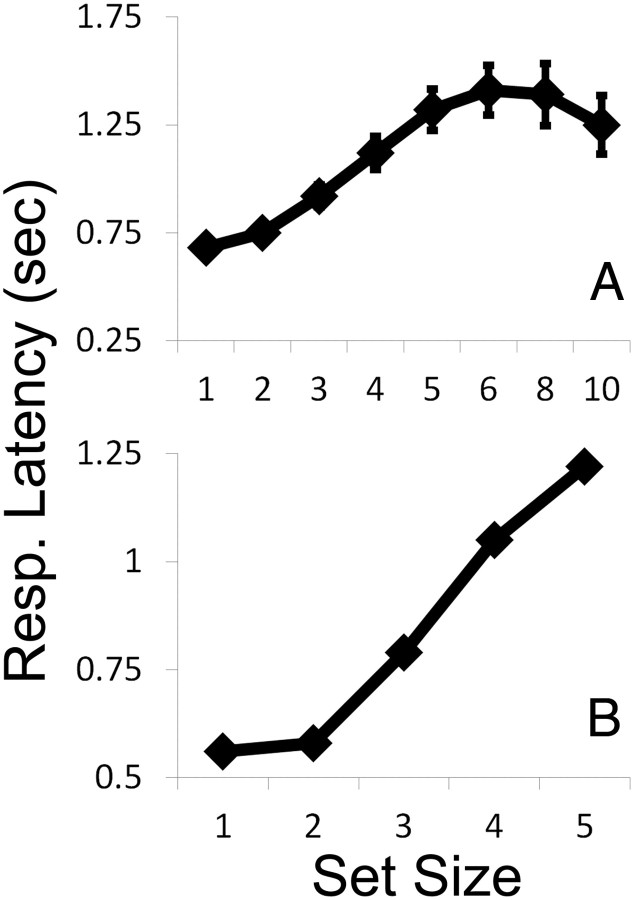
Finally, many (in fact, most) previous studies of subitizing report response times (RT) as the primary dependent measure and error rates as a secondary measure (for examples of subitizing studies that have relied on accuracy as the primary dependent measure, see Green and Bavelier, 2006; Palomares and Egeth, 2010; Palomares et al., 2011). Although one could conceivably argue that the results observed in the current study are idiosyncratic to situations in which subjects are instructed to prioritize accuracy, we believe that this is unlikely. In many studies of subitizing, the profile observed when mean RTs and error rates are plotted as a function of set size are nearly identical. Although subjects in the current study were instructed to prioritize accuracy over speed, we also collected RT data. Mean RTs across subjects in experiment 1 are plotted as a function of set size in Figure 4A, and data from a representative subject are plotted in Figure 4B. Note that these functions bear a strong resemblance to the error rate data depicted in Figure 2, A and B. Individual subjects' mean RT by set size functions were well approximated by a bilinear function identical to that used to model error rate data. However, individual differences in the inflection point of this function did not predict estimates of subitizing span derived by modeling each subject's error rate by set size function (r = 0.14, p > 0.05), presumably because subjects were instructed to prioritize response accuracy over speed. Nevertheless, the response latency data depicted in Figure 4 suggest that our task engages the same core subitizing mechanism that has been described in numerous other studies.
Figure 4.
RT data from experiment 1. A, Mean RTs across subjects are plotted as a function of set size. Error bars are ±1 SEM. B, Data from a representative participant. Note that the profiles depicted in both panels are similar to the group- and single-subject error rates depicted in Figure 2, A and B.
Experiment 2
In experiment 1, we included distractors (black squares) in our subitizing arrays because a substantial body of evidence suggests that the N2pc is much larger and more robust when subjects are required to select targets from among distractors (Luck and Hillyard, 1994). Indeed, recent evidence suggests that the N2pc indexes the selection and/or individuation of targets as well as the suppression of distractors (Hickey et al., 2009; Carlisle and Woodman, 2011; Sawaki and Luck, 2011). However, few studies of subitizing have used distractors. Thus, a primary goal of experiment 2 was to determine whether our basic findings would generalize to a subitizing task that omitted distractors in the target hemifield. Moreover, in experiment 1, an equivalent number of targets and non-targets were presented in opposite hemifields. Thus, we considered the possibility that subjects ignored instructions (e.g., “count blue squares”) and simply enumerated the items in a randomly chosen hemifield. The robust correlations between subjects' behavioral performance and N2pc slopes observed in experiment 1 cast doubt on this hypothesis, but it cannot be summarily excluded based on the extant data. Thus, a secondary goal of experiment 2 was to examine this possibility. Subjects were once again instructed to count blue or green squares and cued to one hemifield before the onset of the target array. Distractors (black squares) were omitted from both hemifields of the target array. On 50% of trials, an equal number of targets (e.g., blue) and non-targets (e.g., green) appeared in the cued and uncued hemifields, respectively (as in experiment 1). On the remaining 50% of trials, the uncued hemifield contained a heterogeneous array of non-targets (catch trials; e.g., green and white squares). We reasoned that, if subjects simply chose to enumerate the items in a randomly chosen hemifield on each trial, then their performance on catch trials should be substantially worse than their performance on non-catch trials.
Subjects' mean response errors are plotted as a function of set size and trial type (catch vs non-catch) in Figure 5A. To examine differences in performance across trial types, these data were submitted to a 2 (trial type) × 8 (set size; only set sizes 2–6, 8, 10, and 12 were included in this analysis because set size 1 trials required homogeneous non-target arrays) ANOVA. This analysis revealed main effects of trial type and set size (F(1,21) = 4.96, p = 0.037 and F(7,147) = 91.69, p < 0.001, respectively) but no interaction between these factors (F(7,147) = 1.47, p = 0.18). Post hoc comparisons revealed that the main effect of trial type was driven exclusively by set size 12 trials (mean error = 0.73 vs 0.70 for catch vs no-catch trials; two-tailed paired-samples t test, p < 0.05); no differences between trial types were observed at any other set size (all p values > 0.12). Thus, in general, subjects' performance was equivalent during catch and no-catch trials, casting additional doubt on the hypothesis that subjects ignored instructions and simply chose to enumerate the items present in a randomly chosen hemifield. Thus, data were subsequently pooled across catch and non-catch trials and fit with the continuous estimation and fixed-capacity models described above. As in experiment 1, both models provided a good description of the observed data (Table 2), and we observed no differences in the amount of variance explained by these models regardless of what set sizes we chose to model (t(21) = 1.55, p = 0.14 and t(21) = 0.53, p = 0.60 for set sizes 1–5 and 1–12, respectively).
Table 2.
Model fitting summary for experiment 2
| Mean adjusted r2 | Minimum adjusted r2 | Maximum adjusted r2 | |
|---|---|---|---|
| Fixed-capacity set sizes 1–5 | 0.89 | 0.32 | 0.99 |
| Continuous estimation set sizes 1–5 | 0.87 | 0.43 | 0.99 |
| Fixed-capacity set sizes 1–12 | 0.81 | 0.17 | 0.96 |
| Continuous estimation set sizes 1–12 | 0.82 | 0.15 | 0.97 |
Grand-averaged ERP difference waves time locked to the onset of the target array are plotted in Figure 6A, and mean N2pc amplitudes during a period 200–300 ms after the onset of the target array are depicted in Figure 6B. As in experiment 1, N2pc amplitudes increased monotonically from set sizes 1–3 before reaching a stable asymptote at larger set sizes. In general, N2pc responses in this experiment were lower in amplitude and more variable than those observed in experiment 1 (compare Figs. 3A, 6A), presumably because distractors were no longer present in the target array. Nevertheless, subjects' N2pc by set size functions were once again better described by a bilinear than a logarithmic function (set sizes 1–12; adjusted r2 values = 0.93 and 0.69, respectively). Moreover, as shown in Figure 6C, estimates of subitizing span (defined as the inflection point of the bilinear function fit to each subject's behavioral data) were strongly predictive of individual differences in N2pc slope, defined here as the difference in mean amplitude between set sizes 1 and 3 (r = 0.67, p < 0.001), 1 and 4 (r = 0.54, p < 0.01), or 1 and 5 (r = 0.53, p = 0.01). Next, we examined whether these set-size-dependent changes in N2pc amplitude were attributable to increases in negative-going potentials over electrode sites contralateral to the cued hemifield, increases in positive-going potentials over ipsilateral electrode sites, or both. Mean response amplitudes observed in contralateral (squares) and ipsilateral (diamonds) electrodes during a period 200–300 ms after the onset of the target array are depicted as a function of set size in Figure 6E. Electrode responses for set sizes 1–3 were first subjected to a separate 2 (electrode site) × 3 (set size; 1, 2, or 3 targets) ANOVA. This analysis revealed main effects of electrode site and set size (F(1,21) = 13.39, p < 0.001 and F(2,42) = 4.28, p < 0.05, respectively), as well as a significant interaction between these factors (F(2,42) = 10.24, p < 0.001). Thus, separate one-way ANOVAs were performed on contralateral and ipsilateral responses. These analyses revealed a significant main effect of set size for contralateral, but not ipsilateral, electrodes (F(1,21) = 9.48, p < 0.001 and F(1,21) = 0.728, p = 0.49, respectively). Thus, set-size-dependent changes in N2pc amplitudes were driven primarily by greater negative responses over electrode sites contralateral to the cued hemifield.
Figure 6.
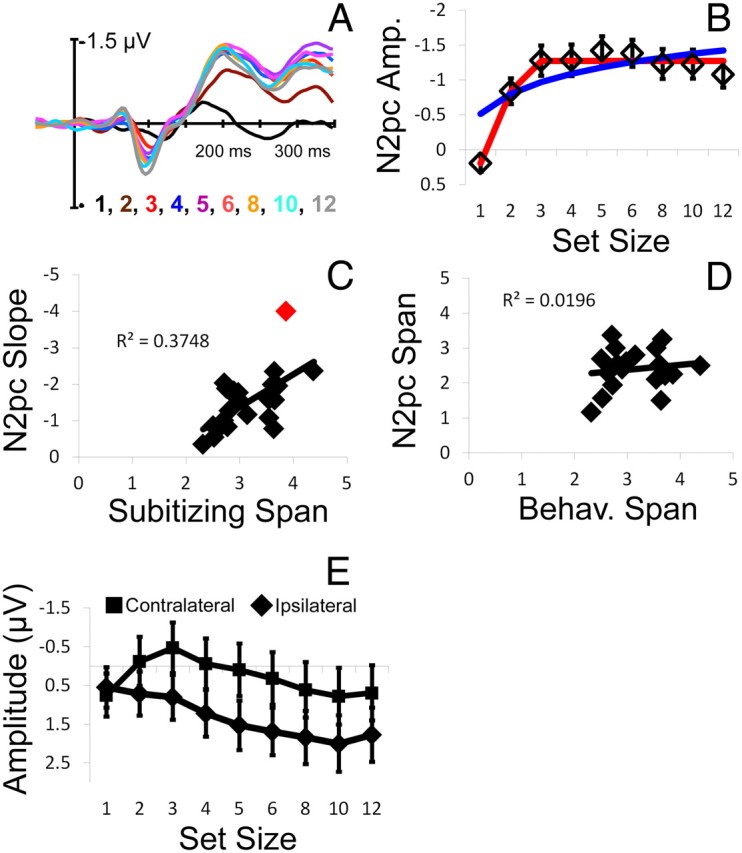
Electrophysiological responses observed in experiment 2. A, Grand-averaged ERP difference waves time locked to the onset of the target array are plotted as a function of set size. B, Mean N2pc amplitudes (diamond symbols; units are microvolts; error bars are ±1 SEM) are plotted as a function of set size. As in experiment 1, N2pc amplitudes increased monotonically across set sizes 1–3. C, Like experiment 1, individual differences in subitizing span were strongly correlated with N2pc slopes (defined here as the mean difference in amplitude between set sizes 1 and 3, 1 and 4, and 1 and 5; this correlation was significant when each of these set size pairs were considered independently; see Results). The relationship between subitizing span and N2pc slopes remained significant when the obvious outlier (red diamond) was removed (r = 0.59, p < 0.01). D, In contrast to the results of experiment 1, individual differences in estimates of subitizing span derived from subjects' behavioral performance did not predict span estimates obtained by modeling each subject's N2pc by set size response profile. E, Mean electrophysiological responses observed during a period from 200–300 ms after the onset of the target array are plotted as a function of set size (abscissa) and electrode site (contralateral vs ipsilateral to the cued hemifield; squares and diamonds, respectively). As in experiment 1, set-size-dependent changes in electrophysiological responses were observed over contralateral, but not ipsilateral, electrode sites (see Results). Error bars are ±1 SEM.
In contrast to the results of experiment 1, electrophysiological estimates of subitizing span obtained by fitting each subject's N2pc by set size profile with a bilinear function did not predict behavioral estimates of subitizing span (r = 0.13, p = 0.56; Fig. 6D). We suspect that this lack of generality reflects noise or instability introduced into the N2pc response by the removal of distractors from the target array. Nevertheless, the observed N2pc by set size profiles were bilinear in shape (Fig. 6B), and N2pc slopes were predictive of individual differences in subitizing span (Fig. 6C). Thus, these findings demonstrate that the core aspects of the empirical pattern found for experiment 1 were not contingent on the intermixing of targets and distractors. Moreover, we also observed a bilinear N2pc response profile in a variant of experiment 2 (n = 16; data not shown) that omitted catch trials, and individual differences in the slope of this response profile were robustly correlated with behavioral estimates of subitizing span (r = 0.54, p < 0.05). Together, our results strongly suggest that subitizing reflects the operation of a fixed-capacity individuation mechanism that enables concurrent access to a small number of items.
Discussion
Here, we attempted to distinguish between fixed-capacity and continuous estimation models of subitizing by examining set-size-dependent changes in the N2pc, an ERP component sensitive to the number of targets present in an array of to-be-enumerated items (Mazza and Caramazza, 2011). In the fixed-capacity model, the enumeration of small sets (e.g., fewer than three to four items) is mediated by a limited-capacity individuation mechanism, whereas the enumeration of larger sets requires a more sluggish (and perhaps serial) mechanism. In the continuous estimation model, a single mechanism is invoked to enumerate small and large sets. However, the precision of this mechanism is inversely related to numerosity (per Weber's law); thus, the enumeration of small sets should be fast and accurate, whereas the enumeration of larger sets should be relatively slow and error prone. Our findings strongly support a fixed-capacity model of subitizing. In two experiments, subjects were asked to report the number of targets present in a brief visual display as accurately as possible. In both cases, subjects' behavioral performance was equally well described by quantitative functions derived from fixed-capacity and continuous estimation models of subitizing. However, N2pc amplitudes evoked by the presentation of a target array scaled monotonically with the number of targets present before reaching an asymptotic limit at approximately three items, consistent with the operation of a fixed-capacity mechanism. Critically, individual differences in the location of this asymptotic limit were strongly predictive of behavioral estimates of subitizing span derived from a fixed-capacity model. Thus, our data strongly support the view that subitizing reflects the operation of a fixed-capacity individuation mechanism.
Multiple sources of evidence suggest that the N2pc can be used to measure the number of items an individual can subitize. First, Mazza and Caramazza (2011) have recently reported that N2pc amplitudes scale with the number of to-be-enumerated items in a display. Critically, this pattern depends on subjects' intent to enumerate these items: when subjects were shown identical stimulus displays and simply asked to report whether any targets were present, set-size-dependent changes in N2pc amplitudes were eliminated. Second, the current experiment demonstrates that individual differences in N2pc slopes (experiments 1 and 2) and individual differences in the inflection point of subjects' N2pc by set size functions (experiment 1) are strongly correlated with behavioral measures of subitizing span. Although correlations alone cannot establish a causal relationship between N2pc amplitudes and subitizing ability, the current findings complement previous reports linking these factors (Mazza and Caramazza, 2011) and demonstrate that asymptotic limits in N2pc amplitudes are positively correlated with individual differences in subitizing span. A fixed-capacity model of subitizing provides a straightforward explanation for this result: once span is exceeded, a slower, perhaps serial counting mechanism must be invoked to enumerate the remaining items in a display. In contrast, it is unclear how a continuous estimation model might account for our findings, because these models predict that a capacity-unlimited numerical mechanism has access to information about each to-be-enumerated item in a display, although the precision of this information dwindles as numerosity increases.
The findings depicted in Figures 3B and 6B suggest that, although the N2pc is a sensitive measure of individual differences in subitizing span, it is insensitive to the slower (and perhaps serial) counting mechanism that must be deployed once span is exceeded (e.g., N2pc amplitudes saturated once putative capacity limits in subitizing were reached, but subjects' error rates and response latencies continued to increase well beyond this range). This result is somewhat surprising insofar as previous work (Woodman and Luck, 1999, 2003) has demonstrated that the N2pc can be used to index serial mechanisms under some circumstances. For example, Woodman and Luck (1999, 2003) observed rapid changes in the sign of the N2pc (i.e., positive vs negative going relative to a given visual hemifield) in a visual search task that required subjects to switch attention between visual hemifields. However, one salient difference between the present study and previous work is that, in the latter, subjects were required to report the presence or absence of a single target whose location was unknown. In contrast, the present study required subjects to count the number of targets present in a prespecified visual hemifield. Moreover, target displays in the current study were presented very briefly (75 ms), which presumably precluded serial shifts of attention to different items (or groups of items) in the relevant hemifield. Thus, the current work cannot exclude the possibility that the N2pc can also be used to measure the deployment of a serial counting mechanism invoked once capacity limits in subitizing are exceeded. Nevertheless, the bilinear N2pc profiles depicted in Figures 3B and 6B, coupled with strong correlations between N2pc slopes and behavioral estimates of subitizing span, strongly support a two-component model of enumeration.
It is well known that N2pc amplitudes are influenced by the presence of distractors (Luck and Hillyard, 1994; Hickey et al., 2009). Thus, one possibility is that set-size-dependent changes in N2pc amplitude reflect the suppression of irrelevant information (distractors or non-targets) rather than the enumeration of targets. Indeed, overall N2pc amplitudes observed in experiment 2 (in which distractors were removed from the target array) were substantially lower than those observed in experiment 1 (compare Figs. 3B, 6B). However, this modulation was akin to a simple main effect: clear bilinear N2pc response profiles were observed in the presence and absence of distractors, and strong correlations between individual differences in behavioral estimates of subitizing span and N2pc slopes were observed in both cases. Thus, although it is clear that distractors can have substantial effects on N2pc amplitudes, these effects appear to be orthogonal to those related to the subitizing process scrutinized here.
In a typical enumeration study, subjects are told to prioritize both speed and accuracy, and the array of to-be-enumerated information remains present until a response is made (for exceptions, see Green and Bavelier, 2006; Palomares and Egeth, 2010; Palomares et al., 2011). Here, subjects were shown the target array for 75 ms (followed by a 300 ms blank interval and response cue). Thus, one could argue that the fixed-capacity limits observed in our study reflect the encoding or storage of information in working memory rather than a limit in the number of items a subject can concurrently access or enumerate. This possibility is rendered even more plausible in light of recent evidence suggesting that the short-term storage of visual information (e.g., in working memory) is subject to a capacity limit of approximately three to four discrete units (Awh et al., 2007; Zhang and Luck, 2008; Fukuda et al., 2010; Anderson et al., 2011). However, we suspect that similar memory limits could also be invoked to explain performance in a response-limited subitizing tasks that afford subjects unlimited viewing time. Broadly speaking, simply leaving a display on the screen until the subject responds does necessarily eliminate contributions from memory processes to performance. With respect to subitizing and enumeration, the subject must encode and create an internal representation of the stimulus display regardless of whether it is presented for a brief or lengthy interval. Moreover, even if the data-limited displays used in the present study rely on working memory processes to a greater extent than traditional response-limited subitizing tasks, we note that subjects' performance nevertheless exhibits many of the stereotypical patterns (e.g., an “elbow-like” function in error rates and response latencies) observed in traditional enumeration tasks. This suggests that the primary limiting factor that determined subjects' performance in our task was their ability to access, individuate, and enumerate information rather than their ability to encode and store this information in working memory.
More generally, the current findings suggest that there may be a fixed upper limit in the number of items that humans can concurrently access. This point is not without controversy. For example, numerous studies have demonstrated that participants can rapidly identify a salient target embedded amid hundreds of distractors (Triesman and Gelade, 1980), implying parallel access to a very large number of stimuli. However, this finding can be explained by assuming that observers perceive the large number of (typically uniform) distractors as a texture (attributable to Gestalt cues, top-down grouping strategies, or both), enabling rapid and efficient access to the pop-out target. In contrast, the subitizing task used in this study requires observers to select individuated representations of target stimuli to arrive at a precise numerosity judgment. Thus, we suggest that the capacity limits observed in this study reflect a fixed limit in the number of individuated object representations observers could select simultaneously (Mitchell and Cusack, 2008; Xu and Chun, 2009; Cusack et al., 2010; Piazza et al., 2011).
In summary, our findings provide strong evidence that subitizing reflects a fixed limit in the number of items that can be selected. The existence of such a limit is inconsistent with models that assume a single continuous estimation process and instead suggests that subitizing reflects the operation of a fixed-capacity individuation mechanism.
Footnotes
This work was supported by National Institutes of Health Grant R01-MH087214 (E.A. and E.K.V.).
The authors declare no competing financial interests.
References
- Anderson DE, Vogel EK, Awh E. Precision in visual working memory reaches a stable plateau when individual item limits are exceeded. J Neurosci. 2011;31:1128–1138. doi: 10.1523/JNEUROSCI.4125-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- Awh E, Barton B, Vogel EK. Visual working memory represents a fixed number of items regardless of complexity. Psychol Sci. 2007;18:622–628. doi: 10.1111/j.1467-9280.2007.01949.x. [DOI] [PubMed] [Google Scholar]
- Balakrishnan JD, Ashby FG. Is subitizing a unique numerical ability? Percept Psychophys. 1991;50:555–564. doi: 10.3758/bf03207540. [DOI] [PubMed] [Google Scholar]
- Balakrishnan JD, Ashby FG. Subitizing: magical numbers or mere superstition? Psychol Res. 1992;54:80–90. doi: 10.1007/BF00937136. [DOI] [PubMed] [Google Scholar]
- Brainard DH. The psychophysics toolbox. Spat Vis. 1997;10:433–436. [PubMed] [Google Scholar]
- Carlisle NB, Woodman GF. When memory is not enough: electrophysiological evidence for goal-dependent use of working memory representations in guiding visual attention. J Cogn Neurosci. 2011;23:2650–2664. doi: 10.1162/jocn.2011.21602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cusack R, Mitchell DJ, Duncan J. Discrete object representation, attention switching, and task difficulty in the parietal lobe. J Cogn Neurosci. 2010;22:32–47. doi: 10.1162/jocn.2009.21194. [DOI] [PubMed] [Google Scholar]
- Dehaene S, Changeux JP. Development of elementary numerical abilities: a neuronal model. J Cogn Neurosci. 1993;5:390–407. doi: 10.1162/jocn.1993.5.4.390. [DOI] [PubMed] [Google Scholar]
- Dehaene S, Dehaene-Lambertz G, Cohen L. Abstract representations of numbers in the animal and human brain. Trends Neurosci. 1998;21:355–361. doi: 10.1016/s0166-2236(98)01263-6. [DOI] [PubMed] [Google Scholar]
- Drew T, Vogel EK. Neural measures of individual differences in selecting and tracking multiple moving objects. J Neurosci. 2008;28:4183–4191. doi: 10.1523/JNEUROSCI.0556-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eimer M. The N2pc component as an indicator of attentional selectivity. Electroencephalogr Clin Neurophysiol. 1996;99:225–234. doi: 10.1016/0013-4694(96)95711-9. [DOI] [PubMed] [Google Scholar]
- Fukuda K, Awh E, Vogel EK. Discrete capacity limits in visual working memory. Curr Opin Neurobiol. 2010;20:177–182. doi: 10.1016/j.conb.2010.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallistel CR, Gelman R. Preverbal and verbal counting and computation. Cognition. 1992;44:43–74. doi: 10.1016/0010-0277(92)90050-r. [DOI] [PubMed] [Google Scholar]
- Green CS, Bavelier D. Enumeration versus multiple-object tracking: the case of action video game players. Cognition. 2006;101:217–245. doi: 10.1016/j.cognition.2005.10.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halberda J, Sires SF, Feigenson L. Multiple spatially overlapping sets can be enumerated in parallel. Psychol Sci. 2006;17:572–576. doi: 10.1111/j.1467-9280.2006.01746.x. [DOI] [PubMed] [Google Scholar]
- Hickey C, Di Lollo V, McDonald JJ. Electrophysiological indices of target and distractor processing in visual search. J Cogn Neurosci. 2009;21:760–775. doi: 10.1162/jocn.2009.21039. [DOI] [PubMed] [Google Scholar]
- Jevons WS. The power of numerical discrimination. Nature. 1871;3:281–282. [Google Scholar]
- Kaufman EL, Lord MW. The discrimination of visual number. Am J Psychol. 1949;62:498–525. [PubMed] [Google Scholar]
- Luck SJ, Hillyard SA. Spatial filtering during visual search: evidence from human electrophysiology. J Exp Psychol Hum Percept Perform. 1994;20:1000–1014. doi: 10.1037//0096-1523.20.5.1000. [DOI] [PubMed] [Google Scholar]
- Mandler G, Shebo BJ. Subitizing: an analysis of its component processes. J Exp Psychol Gen. 1982;111:1–22. doi: 10.1037//0096-3445.111.1.1. [DOI] [PubMed] [Google Scholar]
- Mazza V, Caramazza A. Temporal brain dynamics of multiple object processing: the flexibility of individuation. PLoS One. 2011;6:e17453. doi: 10.1371/journal.pone.0017453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCollough AW, Machizawa MG, Vogel EK. Electrophysiological measures of maintaining representations in visual working memory. Cortex. 2007;43:77–94. doi: 10.1016/s0010-9452(08)70447-7. [DOI] [PubMed] [Google Scholar]
- Mitchell DJ, Cusack R. Flexible, capacity-limited activity of posterior parietal cortex in perceptual as well as visual short-term memory tasks. Cereb Cortex. 2008;18:1788–1798. doi: 10.1093/cercor/bhm205. [DOI] [PubMed] [Google Scholar]
- Palomares M, Egeth H. How element visibility affects visual enumeration. Vis Res. 2010;50:2000–2007. doi: 10.1016/j.visres.2010.07.011. [DOI] [PubMed] [Google Scholar]
- Palomares M, Smith PR, Pitts CH, Carter BM. The effect of viewing eccentricity on enumeration. PLoS One. 2011;6:e20779. doi: 10.1371/journal.pone.0020779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pelli DG. The VideoToolbox software for visual psychophysics: transforming numbers into movies. Spat Vis. 1997;10:437–442. [PubMed] [Google Scholar]
- Piazza M, Fumarola A, Chinello A, Melcher D. Subitizing reflects visuo-spatial object individuation capacity. Cognition. 2011;121:147–153. doi: 10.1016/j.cognition.2011.05.007. [DOI] [PubMed] [Google Scholar]
- Revkin SK, Piazza M, Izard V, Cohen L, Dehaene S. Does subitizing reflect numerical estimation? Psychol Sci. 2008;19:607–614. doi: 10.1111/j.1467-9280.2008.02130.x. [DOI] [PubMed] [Google Scholar]
- Sawaki R, Luck SJ. Active suppression of distractors that match the contents of visual working memory. Vis Cogn. 2011;19:956–972. doi: 10.1080/13506285.2011.603709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sperling G. The information available in brief visual presentations. Psychol Monogr. 1960;74:1–29. [Google Scholar]
- Treisman AM, Gelade G. A feature-integration theory of attention. Cogn Psychol. 1980;12:97–136. doi: 10.1016/0010-0285(80)90005-5. [DOI] [PubMed] [Google Scholar]
- Trick LM. More than superstition: differential effects of featural heterogeneity and change on subitizing and counting. Percept Psychophys. 2008;70:743–760. doi: 10.3758/pp.70.5.743. [DOI] [PubMed] [Google Scholar]
- Trick LM, Pylyshyn ZW. What enumeration studies can show us about spatial attention: evidence for limited capacity preattentive processing. J Exp Psychol Hum Percept Perform. 1993;19:331–351. doi: 10.1037//0096-1523.19.2.331. [DOI] [PubMed] [Google Scholar]
- Trick LM, Pylyshyn ZW. Why are small and large numbers enumerated differently? A limited-capacity preattentive stage in vision. Psychol Rev. 1994;101:80–102. doi: 10.1037/0033-295x.101.1.80. [DOI] [PubMed] [Google Scholar]
- Vogel EK, Machizawa MG. Neural activity predicts individual differences in visual working memory capacity. Nature. 2004;428:748–751. doi: 10.1038/nature02447. [DOI] [PubMed] [Google Scholar]
- Woodman GF, Luck SJ. Electrophysiological measurement of rapid shifts of attention during visual search. Nature. 1999;400:867–869. doi: 10.1038/23698. [DOI] [PubMed] [Google Scholar]
- Woodman GF, Luck SJ. Serial deployment of attention during visual search. J Exp Psychol Hum Percept Perform. 2003;29:121–138. doi: 10.1037//0096-1523.29.1.121. [DOI] [PubMed] [Google Scholar]
- Xu Y, Chun MM. Selecting and perceiving multiple visual objects. Trends Cogn Sci. 2009;13:167–174. doi: 10.1016/j.tics.2009.01.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang W, Luck SJ. Discrete fixed-resolution representations in visual working memory. Nature. 2008;453:233–235. doi: 10.1038/nature06860. [DOI] [PMC free article] [PubMed] [Google Scholar]