Review of tissue simulating phantoms with controllable optical, mechanical and structural properties for use in optical coherence tomography

Abstract

We review the development of phantoms for optical coherence tomography (OCT) designed to replicate the optical, mechanical and structural properties of a range of tissues. Such phantoms are a key requirement for the continued development of OCT techniques and applications. We focus on phantoms based on silicone, fibrin and poly(vinyl alcohol) cryogels (PVA-C), as we believe these materials hold the most promise for durable and accurate replication of tissue properties.

1. Introduction

In optical coherence tomography (OCT), it is vitally important to develop tissue-simulating phantoms for the validation of new methods, technologies and applications [1,2]. To date, the main focus has been on developing phantoms with optical properties in the range of those of tissues [3], but other important properties include durability, mechanical behavior and three-dimensional structure. The continued advancement of OCT methods, such as optical coherence elastography (OCE) [4] and magneto-motive OCT [5], technologies, such as needle OCT [6], and applications, such as intravascular OCT [7], will depend upon the availability of phantoms simulating the optical and mechanical properties and the three-dimensional structure of tissues. Such phantoms are needed to form the basis for durable, transferable standard imaging targets.

In this paper, we review progress on the development of phantoms that simulate the optical and mechanical properties as well as the complex structures found in tissue, whilst concentrating on materials that provide durability of at least one month.

Many early OCT phantoms were based on hydrogels, two of the most common of which are agar [8] and gelatin [9]. These semisolid matrices allow for the inclusion of both organic and non-organic additives as optical scatterers. The tissue-like mechanical properties of these hydrogels have also been utilized in early OCE experiments [4]. However, there are several major issues with hydrogel phantoms. They have a short durability on the order of a week and are not rigid at room temperature [1], which makes forming them into complex shapes impractical. Resin phantoms, by contrast, are very durable; they can be used for years whilst maintaining their optical properties [10,11] and have the potential to be fabricated into complex shapes. However, resin phantoms are much stiffer than soft tissue, which limits their utility in intravascular OCT [7] and elastography [4,12].

In this paper, we focus on phantoms based on three materials: silicone [13]; fibrin [14]; and poly(vinyl alcohol) cryogels (PVA-C) [15], which we believe to be the best candidates for the development of versatile tissue-simulating phantoms.

Silicone is a convenient base material for flexible and straightforward fabrication of phantoms. It provides ready compatibility with a wide range of suitable scatterers for adjustment of the optical properties. The mechanical properties can be adjusted over a wide range by controlling the amount of cross-linking within the silicone formulation. Silicone is also well suited for fabrication of phantoms with complex structures due to its low viscosity prior to curing and high toughness, i.e., resistance to fracture.

A disadvantage is that silicone is not compatible with organic materials, such as tissue constituents. In simulating the optical properties of tissue, a convenient option is to employ material systems to which tissue constituents may be readily added [1]. Fibrin phantoms [14] meet this need, providing a transparent organic matrix to which both organic and inorganic scatterers and absorbers may be added. Fibrin is a naturally occurring protein in humans that provides structural support for blood clots [16]. Fibrin is readily synthesised and has a shelf life of up to one month.

Poly(vinyl alcohol) cryogels (PVA-C), the other class of phantom materials we consider, have been used extensively to fabricate phantoms for other medical imaging modalities, particularly ultrasound and magnetic resonance imaging [15]. PVA-C is especially attractive for its mechanical properties, which are readily controllable over the range found in tissue. In biomedical optics, PVA-C phantoms have been used for photoacoustic imaging [17], diffuse optical imaging [18] and optical elastography [19]. However, their use in OCT has been less extensive [20–22].

In the following, we review in detail the development of phantoms based on the three candidate material systems. The structure of the remainder of the paper is as follows: in Section 2, we review the optical properties of OCT phantoms, with particular emphasis on backscatter amplitude and attenuation; in Section 3, the mechanical properties of phantoms are discussed and reviewed in the context of both elasticity and viscoelasticity; in Section 4, the development of phantoms with complex shapes is reviewed; and in Section 5, we summarize and draw some conclusions.

2. Optical properties

2.1. Details of optical properties

2.1.1. Description of optical properties

The most important optical properties of tissue for OCT imaging are backscattering and attenuation. Light propagating in tissue is scattered by constituents such as cells, organelles and fibers and absorbed by pigments such as hemoglobin and melanin, and by water [3]. In OCT, light from the source is attenuated (scattered and absorbed) on the incident path, backscattered, and attenuated again on the return path. The detected OCT signal is that component of backscattered light coupled into the collection optics. The strength of backscattering is influenced by the attenuation coefficient and its anisotropy, and provides the contrast mechanism to differentiate tissue structures. Contrast in OCT imaging can be augmented by measurement of the attenuation coefficient, which has been demonstrated as a means for identifying lesions in cancer imaging [23–26] and plaque components in atherosclerotic arteries [27,28].

2.1.2. Measuring optical properties

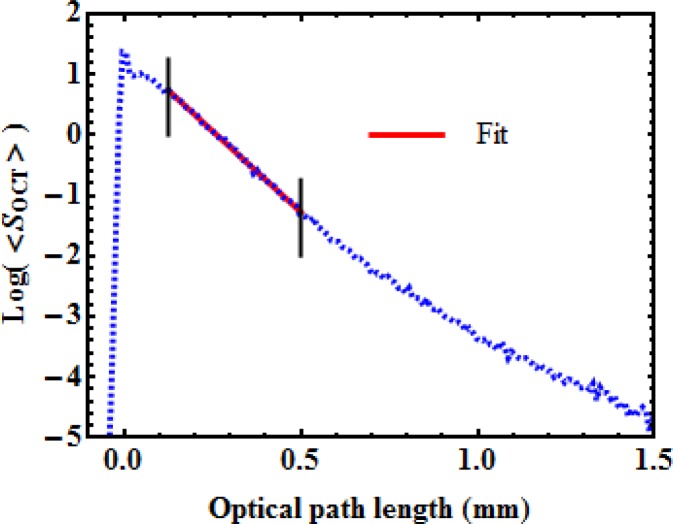
Figure 1 presents a typical OCT average depth scan (A-scan) of a homogeneous sample for which the optical properties are to be extracted. Averaging is important as it allows for the reduction of the high spatial frequency fluctuations caused by speckle. Accounting for the focusing effect of the optics used for illumination and detection is also important, and has been performed in the data presented in Fig. 1 [29,30]. In this figure, the surface of the sample is located at 0 mm optical path length, corresponding to a sharp increase in the OCT signal strength.

Fig. 1.

Typical average OCT signal, on a logarithmic scale, as a function of depth. The straight line illustrates a fit performed between the two vertical lines to extract the parameters A and μ_t.

We extract two parameters from the OCT measurement: the backscattering amplitude, A, (reflectance) and the total attenuation coefficient, μ_t. To develop a phantom simulating a certain tissue, the values of A and μ_t must be measured and the phantom fabricated to match them. Use of a reference measurement ensures that the optical characterization is independent of variations in system response, either inter-system or intra-system, accounting, for example, for polarization effects or variations in the optical source power. The backscattering amplitude measurement can be calibrated against a known value from a low-scattering dilute microsphere solution [27].

An alternative solution which does not require prior knowledge of the backscattering amplitude normalizes the average OCT amplitude by dividing it by a reference value [31]. Fitting the variation of the normalized averaged OCT amplitude <S_OCT > as a function of optical path length, z, with an exponential decay from the sample surface, located at z₀, provides

$$\text{log}(<S_{OCT}>)=\log (A)-{\mu }_t\frac{(z-z_0)}{n},$$ (1)

where n is the group refractive index of the sample.

In Fig. 1, deviations from the expected single exponential dependence are observed near the surface and deep within the sample, which is common when performing such measurements. The collected OCT signal is composed of ballistic and quasi-ballistic photons, i.e., photons that have undergone a number of shallow forward-scattering events before being backscattered [32]. A possible explanation for this behavior close to the surface is an increased contribution of quasi-ballistic photons, but a more complete model including the anisotropy is necessary to fully explain this effect. It is common practice to neglect this region and begin the fitting procedure at some distance from the surface, e.g., to the right of the first black vertical line in Fig. 1.

For larger depths, the increase in the OCT signal is a clear signature of multiple scattering [33]. In this region, the OCT signal is not solely due to ballistic and quasi-ballistic photons, but also to multiply scattered photons. Departure from a single exponential decay may be due to other factors, such as heterogeneities in the sample. When using a linear fit to extract the attenuation coefficient, this region is avoided such that the fit does not extend beyond the second black vertical line in Fig. 1. In [26], an automated method to select the greatest depth boundary is proposed; it is based on a threshold value for the integrated logarithmic backscattered intensity.

2.1.3. Comments on optical properties and phantom fabrication

When fabricating an OCT phantom, one usually introduces scatterers and absorbers into a matrix. The main contribution to the backscattering is expected from the scatterers but there are often contributions from both the matrix and the absorbers, which are used to increase the attenuation if necessary.

In this review, we have not considered the scattering anisotropy, which determines the angular distribution over which light is scattered. Ignoring the anisotropy in phantom design may result in phantoms that exhibit an OCT response that depends on numerical aperture. The development of OCT phantoms with controlled anisotropy represents an important topic for future research.

An important consideration for OCT imaging is speckle. Speckle is not an optical property of the tissue, but the result of imaging the tissue with a coherent technique. The collected backscattered light is the summation of the light waves returning from multiple scatterers contained within the probed volume (resolution volume), which is determined by the coherence length of the source and the illumination spot size at that depth. The coherent interference of these backscattered components, plus any multiply scattered components, gives rise to the grainy structure observed in OCT images [34]. The inverse problem of reconstructing the sub-resolution scatterer distribution that produces a speckle pattern is grossly ill-conditioned. Hence, only the statistics of speckle patterns are relevant when designing tissue-simulating phantoms. Nonetheless, speckle patterns of fully developed speckle, i.e., with no spatial or temporal averaging present, have first- and second-order statistics that are independent of scatterer distribution, other than in cases where the effective number of scatterers in the resolution volume is very small [35] or where multiple scattering is present [36]. The first-order statistics of speckle in OCT depart from a Rayleigh distribution only if the number of scatterers in a resolution volume is less than around 5 [35]. This should be taken into consideration when determining the concentration of scatterers during phantom fabrication. Speckle contrast ratio serves as a useful parameter for speckle characterization. Speckle contrast ratio is defined as the standard deviation of the OCT amplitude divided by the average amplitude in an image. Assuming a Rayleigh distribution, the speckle contrast ratio corresponding to fully developed speckle in homogenous tissue is 0.52. This also implies that the scatterers have dimensions much smaller than the volume probed by the OCT system. All the phantoms discussed in this review are based on a matrix containing discrete scatterers and will, thus, provide fully developed Rayleigh-distributed speckle patterns.

2.2. Silicone phantoms

Silicone phantoms, previously reviewed in the context of biomedical optics by Pogue and Patterson [1], were first introduced in the context of OCT by Oldenburg et al. [5], who made use of their mechanical properties to demonstrate magnetomotive contrast in OCT.

Commercial silicone kits, that include compound and catalyst, can be purchased from numerous manufacturers. When mixed, the two components cure at room temperature. Curing can also be accelerated by heating. As discussed in Section 3.2, adding polydimethylsiloxane (PDMS) oil softens the silicone, but these formulations require weeks to cure if not heated, due to the reduction in cross-linking brought about by the PDMS oil. Silicone provides a soft matrix to which one can integrate a variety of inorganic scatterers and absorbers. These additives are introduced prior to adding the catalyst. For OCT phantoms, the following scatterers have been reported: titanium dioxide [5,12,37–40], silica microspheres [30], alumina [31], and, more recently, gold nanoshells [41]. The following absorbing agents have been reported: carbon black [31] and dye [39]. Graphite and dry ink have also been used as absorbers in [42], but without success as this resulted in an inhomogeneous solution.

The largest challenge in fabricating a silicone phantom is obtaining a homogeneous distribution of scatterers and absorbers without aggregates, sedimentation or air bubbles. Different techniques can be used separately or in combination to ensure a homogeneous distribution of scatterers and absorbers in the silicone matrix: e.g., sonication [5,12,30,31,38–40], thinning of silicone before curing with hexane followed by evaporation [30,40], and degassing under vacuum [39].

The silicone matrix has a very uniform group refractive index that is close to that of tissues and contributes very little to the scattering. For example, Sylgard 184 (Dow Corning) has a group refractive index of about 1.4 [42] at a wavelength of 1.3 μm and an attenuation coefficient of less than 0.5 mm⁻¹. A shortcoming of silicone phantoms is that the most often used inorganic scatterers have refractive indices that are much larger than biological structures. For example, alumina has a refractive index of 1.76 and titanium dioxide has a refractive index of 2.3. Silica microspheres have more relevant refractive index values but have been less often used to fabricate OCT phantoms.

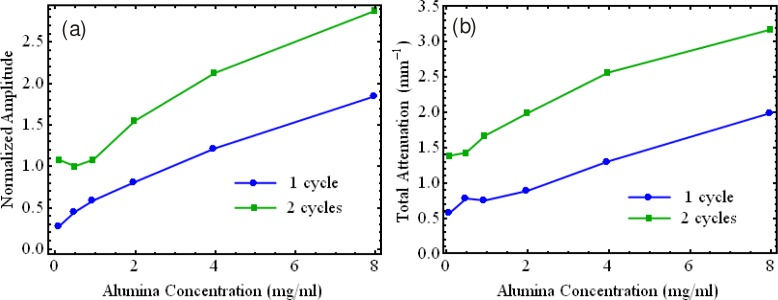
Figure 2 shows a typical calibration curve for a silicone matrix containing alumina. It demonstrates that a wide range of attenuation coefficients similar to those of tissue can be obtained. This figure also exhibits an important feature: the backscattered amplitude increases as the square root of the concentration. This is related to the fact that OCT is a coherent detection technique and that the OCT signal is generated by a large number of scatterers in the probed volume [30,31]. The optical properties of silicone phantoms with inorganic scatterers and absorbers have been shown to remain stable for at least one year after fabrication [31,43].

Fig. 2.

(a) Backscattered amplitude and (b) total attenuation coefficient of silicone phantoms with different concentrations of alumina. Red line in (a) illustrates a fitted square-law dependency of the backscattered amplitude upon the concentration of alumina.

2.3. Fibrin phantoms

Silicone offers many key advantages as a synthetic phantom material. However, a limitation of silicone is its incompatibility with biological tissue constituents. Fibrin phantoms overcome this limitation. A fibrin matrix improves upon key attributes associated with commonly used biologically compatible materials, such as agar and gelatin, including time-efficient fabrication, long lifetime, rigidity at room temperature, and low scattering [14]. Fibrin is a naturally occurring protein in humans that provides structural support for blood clots [16] and is formed from the protein fibrinogen by proteolysis induced by the enzyme thrombin. It is employed as an adhesive in surgical procedures and wound closures [44].

Its fabrication involves fibrinogen and thrombin powder dissolved separately in saline and then mixed forming a gel. The gel formation (clotting) time can be reduced by adding calcium chloride (CaCl₂), which increases the gel’s elasticity [44]. A scanning electron microscope image of a fibrin phantom is shown in Fig. 3(a) . During the clotting process, the fibrin fibers aggregate and branch to form a 3-D matrix seen in Fig. 3(a). The nano-scale of the structure results in a sufficiently low optical scattering cross-section for the phantom to be optically transparent at wavelengths used for OCT.

Fig. 3.

(a) SEM image of fibrin gel, and; (b) Attenuation coefficient, μ_t, measured for phantoms with different % w/v concentrations of Intralipid.

To introduce scattering to fibrin phantoms, a range of materials can be used, from tissue constituents, such as blood and lipids (fat), to inorganic powders, such as titanium dioxide and alumina. To demonstrate fibrin’s potential, phantoms have initially been demonstrated using Intralipid as a scatterer [14]. The measured values of μ_t using OCT for phantoms with varying concentrations of Intralipid are presented in Fig. 3(b). For each concentration, measurements were recorded at intervals, in the x-direction, of 600 μm and averaged. The error bars represent one standard deviation, calculated from five lateral positions. A monotonic increase in scattering was measured for increasing Intralipid concentration. The curve deviates from the expected logarithmic increase [45], possibly due to leaching of intralipid and scattering from the fibrin matrix. The values of μ_t presented in Fig. 3(b) are within the range of previously measured values for both tissue [3] and Intralipid [45].

2.4. PVA-C phantoms

Poly(vinyl alcohol) cryogel (PVA-C) is formulated using solutions of varying concentrations of poly(vinyl alcohol), a solid polymer, most commonly dissolved in water or dimethyl sulfoxide (DMSO) to form a thick, liquid hydrogel. These solutions cross-link to become a solid gel when they are successively submitted to freezing and thawing, hence the term “cryogel.” The sequence in which the temperature is decreased below freezing point and then thawed, preferably at controlled rates, is called a freeze/thaw cycle (FTC). PVA-C phantoms need to be stored in water or wet in sealed containers. Mano et al. [46] reported that the relaxation properties for MRI were stable over a 6-month period.

In optical coherence tomography, PVA-C phantoms have been used mainly for their mechanical properties: to develop OCT-based elastography [20–22] and to provide more realistic mechanical behavior of artery phantoms [47,48].

The optical properties of PVA-C phantoms are affected by the solvent (water, dimethyl sulfoxide), FTCs (number, rate of thawing) and additives. PVA combined with water produces a translucent material becoming increasingly opaque with increased PVA concentration. The use of a water/DMSO mixture as a solvent can result in a nearly clear material; a 95% visible-light transmittance has been reported for a 0.6 mm thick sample with 30/70 water/DMSO weight ratio [49].

The optical properties of PVA-C may be adjusted by introducing scatterers and absorbers into the matrix. This was achieved in [47] and [48], using alumina and block-printing ink. The PVA used had a molecular weight between 146,000 and 180,000 g/mol (Aldrich Chemicals). A 10% w/w PVA/water solution was prepared by heating and mixing in a standard reflux column/flask combination. The FTCs employed freezing and thawing temperature extremes of −20°C and +20°C cycled at 0.1°C/min in an environmental chamber with a one hour hold at −20°C. A uniform mixture of alumina in the cryogel was obtained by dispersing the particles in the solution using an ultrasonic bath maintained at 60°C for 5 hours, which decreases the viscosity of the PVA solution. To increase the total attenuation in PVA cryogels, both carbon black and India ink were used, but could not be mixed uniformly in the PVA solutions. A good uniformity was obtained by mixing block printing ink (brand “Speedball”) manually in the PVA solution at 60°C. Figure 4 presents the variation in backscattered amplitude and total attenuation with the concentration of alumina for a PVA-C phantom resulting from one and two FTCs.

Fig. 4.

(a) Backscattered amplitude and (b) total attenuation coefficient for PVA-C with one and two FTCs for various concentrations of alumina.

3. Mechanical properties

Although contrast in OCT is determined by optical properties, a number of OCT’s derivative techniques are also influenced by mechanical properties. For example, optical coherence elastography (OCE) provides images based on mechanical contrast [4]; magnetomotive OCT (MM-OCT) [5] and photothermal OCT [50] measure tissue deformation induced using nanoparticles to enhance image contrast; and intravascular OCT [7] can image the inside of vessels which deform in response to intra-arterial pressure or percutaneous interventions such as angioplasty [51,52]. In addition, needle [6] and hand-held [53] probes, developed to broaden the clinical applications of OCT, come into direct contact with soft tissue during image acquisition, such that the mechanical properties significantly influence image quality. To optimize these techniques and technologies, it is critical to develop phantoms that accurately simulate tissue mechanical properties. In this section, we review the development of phantoms with controllable mechanical properties simulating those of tissue.

3.1. Definition of Mechanical properties

Mechanical properties characterize a material’s response to an applied load and the two most important such properties are elasticity and viscoelasticity.

3.1.1. Elasticity

The elasticity of a material is often characterized using the elastic modulus, defined as the ratio of stress, the force per unit area, to strain, the fractional change in length of a sample:

$$E=\frac{\sigma }{{\epsilon }_0}=\frac{\raisebox{1ex}{$F$}\!\left/ \!\raisebox{-1ex}{$A$}\right.}{\raisebox{1ex}{$\Delta l$}\!\left/ \!\raisebox{-1ex}{$l_0$}\right.},$$ (2)

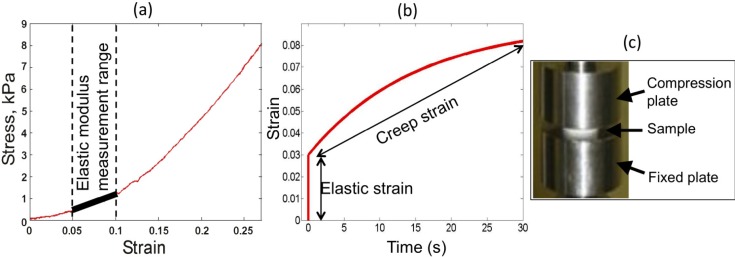
where E is the elastic modulus, σ is the stress, ε₀ is the strain, F is the applied force, A is the area, Δl is the change in length, and l₀ is the original length of the sample. For a linearly elastic material, the elastic modulus is defined as the slope of the stress-strain curve. However, most biological tissues exhibit nonlinear elastic behavior at strains higher than ~0.1 [54]. Therefore, a representative elastic modulus for these materials is usually calculated in the regime of low strain, as illustrated in Fig. 5(a) . Although the mechanical behavior of biological tissues can be highly nonlinear, the elastic modulus provides a convenient measure for comparison of tissue types, as well as a means to distinguish between pathological and benign tissue [54]. The elastic modulus of soft, healthy tissues, such as adipose, muscle, and liver ranges from 1 to 34 kPa [55,56], whereas, the elastic modulus of some common types of cancerous tumors has been measured between 112 kPa [54] and 638 kPa [56].

Fig. 5.

Measurements of elasticity and viscoelasticity of materials and apparatus. (a) Stress-strain curve, highlighting the region of linear elasticity from which elastic modulus is calculated. (b) Creep curve for characterization of viscoelastic materials. (c) Photograph of Instron compression tester.

3.1.2. Viscoelasticicty

Soft biological tissues are typically viscoelastic, i.e., they exhibit both elastic, or time-independent, and viscous, or time-dependent, components in their mechanical behavior. The viscous component inherently causes a time-dependent strain in response to a constant stress. This phenomenon is known as creep. The strain of a viscoelastic material is described by [57]

_{$\epsilon (t)={\epsilon }_0+{\epsilon }_1\left(1-\exp \left(\frac{-t}{T_1}\right)\right),$} (3)

where ε₀ is the elastic strain, ε₁ is the viscoelastic strain, and T₁ is the retardation time constant, defined as the time at which the strain has risen to within 1/e of its final value [57]. The strain induced in a viscoelastic material is illustrated in Fig. 5(b), where both the elastic strain, the instantaneous material response to an applied load, and viscoelastic strain, the time-dependent response to a constant load, are observed. Viscoelasticity is known to vary significantly between different tissues types [58] and, in ultrasound, has been proposed as a contrast mechanism to distinguish between diseased and healthy tissue [59]. Analysis of tissue mechanical properties in OCT has focused predominantly on elastic properties; however, in order to accurately characterize mechanical behavior, the viscoelastic properties should also be taken into account. The viscoelastic properties of tissue have been exploited in OCT for gaining additional contrast [60] and reducing speckle noise [37].

3.2. Measuring mechanical properties

The elasticity of materials can be measured by performing a standard uniaxial load test using a materials testing machine. These devices apply either a tensile or compressive load to a sample positioned between two rigid plates. In the tensile case, a sample is clamped between two fixtures, and one fixture is moved away from the other at a constant rate (strain rate), stretching the sample. In the compressive case, a moving plate compresses the sample against an underlying stationary plate, as shown in Fig. 5(c). In both tensile and compressive cases, during loading, a sensor measures the overall force applied to the sample, while a separate sensor measures the displacement introduced to the sample. The stress-strain curve may then be generated from the recorded force and displacement data using Eq. (2), as shown in Fig. 5(a) for the compressive case. When the strain rate is changed (increased) the stress-strain curve of a viscoelastic material will also change. For tissues this curve is non-linear. Therefore the elastic modulus will be different for different parts of the curve, referred to as “strain hardening”. If the force is held constant, a creep curve such as that in Fig. 5(b) may also be generated using these devices. Other methods for testing the viscoelastic response of materials include a stress relaxation test (measuring time-dependent stress for a constant strain), or dynamic mechanical analysis that uses opposite rotation of two plates contacting the specimen (measuring the time lag of the material response to a periodic load).

3.2. Controlling the mechanical properties of OCT phantoms

3.2.1. Silicone

The mechanical properties of silicone phantoms are controlled by varying the cross-link density; i.e., by varying the ratio of catalyst to cross-linker. This was explored by Jiang et al. [61] and later implemented in phantoms for magnetomotive OCT [5] and OCE [12]. Importantly for OCT techniques, the optical and mechanical properties of silicone phantoms can be controlled independently [61]. Table 1 illustrates the effect of varying the ratio of cross-linker to catalyst for a particular commercially available silicone, Wacker Elastosil 601, used previously for phantoms in OCE [12]. This material has similar mechanical properties to other silicones that have been used for fabrication of OCT phantoms [5,31]. Using this silicone, an elastic modulus range of ~100 kPa to ~5 MPa is achievable [12], which covers a wide range of tissue elasticities. However, unlike tissues, these silicone phantoms have very low viscoelasticity. This is readily observed in the creep curve in Fig. 6(a) for Elastosil 601 in a 1:5 cross-linker:catalyst ratio, where the strain remains unchanging over time for a constant load.

Table 1. Elastic modulus of various mixing ratios (Cross-linker: Catalyst) for Wacker Elastosil 601 silicone phantoms.

Mixing ratio	Elastic modulus (kPa)
1:5	4910
1:15	3060
1:20	1483
1:30	1008
1:40	286
1:50	127

Fig. 6.

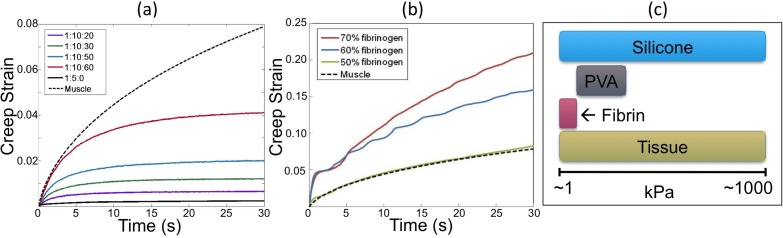
Creep strain curves for: (a) silicone fluid phantoms; and (b) fibrin phantoms. (c) Comparison of range of elastic moduli of phantom materials and soft tissue

Very soft tissues such as adipose, brain and liver, have elastic moduli below 10 kPa [55]. To optimize the OCT techniques described at the start of this section, OCT phantoms should be able to simulate these soft tissues. To further reduce the elastic modulus of silicone phantoms to be in the range of very soft tissues, silicone fluid such as PDMS oil may be added prior to curing [5,38]. Silicone fluid does not participate in the curing process, but remains as a fluid within the cross-linked polymer network of the cured silicone, resulting in a softer material [62]. Table 2 lists the measured elastic modulus of Wacker Elastosil 601 silicone with varying concentrations of silicone fluid. Note that by adding PDMS oil, an elastic modulus as low as 10 kPa was achieved. The PDMS oil also alters the viscoelastic properties of silicone phantoms [62] making the system more or less viscous depending on the viscosity of the silicone fluid added. This is illustrated in the creep curves for silicone with various ratios of PDMS oil (50 cSt viscosity) in Fig. 6(a). For all samples, a 1.1 N load was applied and held constant. The samples become more viscoelastic, i.e., have a higher creep time constant, with increasing proportions of silicone fluid. In Fig. 6(a), the result obtained from a representative tissue sample (chicken muscle) is also included for comparison. This demonstrates the ability to fabricate silicone phantoms with viscoelasticity in the range of tissue using this technique.

Table 2. Elastic Modulus of various mixing ratios (Cross-linker: Catalyst: PDMS oil) for Wacker Elastosil 601 silicone and Wacker AK50 PDMS oil phantoms.

Mixing ratio	Elastic modulus (kPa)
1:10:10	316
1:10:20	122
1:10:30	81
1:10:40	38
1:10:50	23
1:10:60	10

While addition of silicone fluid provides a convenient solution for adjusting the mechanical properties of phantoms, the polymer network for any given silicone elastomer can hold only a limited percentage weight of silicone fluid before reaching saturation. Manufacturers of silicones have suggested that exceeding this limit can result in a gradual exudation of the oil [62], leading to large variations of the phantom’s mechanical properties over time. This is a major limitation of this phantom fabrication technique.

Silicone with very low hardness, such as silicone gels, liquid silicone rubbers and some elastomers provide a more durable and reliable alternative to the silicone fluid phantoms for simulating very soft tissues.

Such silicones have not previously been implemented in OCT phantoms, but are commonly used in biomechanics studies of deformation of very soft tissues [63,64]. Table 3 presents results obtained for the elasticity of some soft silicones. The elastic modulus of these materials is certainly in the range of very soft tissues such as adipose, and much lower than the silicone materials presented in Table 1. The mechanical properties of these silicones could also be finely adjusted by adding small quantities of silicone fluid, if needed, without the concern of exudation of the fluid. Characterization of the viscoelastic properties of these materials is still needed to assess how closely they simulate the full range of tissue mechanical behavior.

Table 3. Elastic modulus of soft silicone phantoms.

Product	Mixing ratio	Elastic modulus (kPa)
Wacker LR3003/03	1:1	18.1
Wacker P7676	1:1	6.4
Wacker SilGel 612	1:1	1.6
Nusil LS3441	1:1	1.3

By choosing the appropriate silicone and fabrication process, it is possible to obtain phantoms that mimic the mechanical properties of tissue over a wide range, as illustrated by the graph in Fig. 6(c).

3.2.2. Fibrin

The mechanical properties of fibrin phantoms can be controlled by changing the ratio of fibrinogen to thrombin, which has been demonstrated in application of fibrin to surgical sealants [16]. Fibrin can be used to achieve very low elastic modulus (<5 kPa) [14], but fabrication of phantoms stiffer than 10 kPa is challenging, limiting the range of tissues it can simulate. A comparison of the elasticity achievable with fibrin phantoms in comparison to soft tissue, silicone phantoms and PVA phantoms is presented in Fig. 6(c). Varying the concentration of fibrinogen also changes the viscoelastic properties of fibrin phantoms, as illustrated in the creep data in Fig. 6(b). As may be expected from a phantom with biological constituents, fibrin phantoms can exhibit viscoelastic behavior very similar to that of real tissue. This is evident in the creep curve for 50% fibrinogen, which closely matches the creep curve for muscle.

3.2.3. PVA-C

The mechanical properties of PVA-C phantoms are influenced by several parameters: PVA grade (molecular weight, degree of saponification), the polymer concentration in the initial solution, the presence of additives and conditions of cryogenic treatment: temperature and rate of thawing and number of cycles [15,19,65,66]. The sensitivity to variations in processing parameters has some advantages when using the gel to create test specimens as a substitute for biological soft tissues, where sample-to-sample variations and changes in the elastic properties, within a certain range, could be desired. However, this sensitivity is a drawback when reproducibility is required (calibration phantoms, for example).

Crystal nuclei are generated by freezing, and on thawing these sites grow into crystals that act as cross-linking sites for the polymer. Subsequent freeze-thaw cycles produce larger and/or more numerous cross-linking sites until a rubber-like gel is produced. The length of time frozen does not have a large influence on the mechanical properties [67].

The capability of adjusting mechanical properties of PVA-C phantoms in OCT has mainly been used to perform OCE [20–22]. In these studies, both mechanical and optical properties were obtained by adjusting the number of FTCs. For example, in [20,21], a biliayer phantom with a 1.5:1 ratio in dynamic stiffness was obtained with 7 and 5 FTCs, respectively, for a 20% PVA-C.

Studies [65,66,68] have shown that PVA-C exhibits non-linear elastic behavior [69]. In [47] and [48], the aim was to develop artery phantoms that provided not only relevant optical properties, but also tissue-simulating non-linear elasticity and viscoelasticity. The optical properties were controlled by the number of FTCs as well as additives, whilst the mechanical properties were controlled by the number of FTCs only. Figure 7 presents results of a tensile elasticity test, i.e., a stress-stretch curve, for a multilayer PVA-C phantom and a multilayer silicone phantom. The PVA-C phantom exhibits non-linear elasticity and viscoelasticity, in the form of hysteresis, whereas, the silicone phantom does not. Figure 7 also shows stress-stretch curves for the intima and the media layers of arteries stretched in the circumferential direction. They show that even if some strain hardening is obtained with the PVA-C phantom, it is insufficient to accurately simulate the behavior of the artery layers [48].

Fig. 7.

Tensile test results for a PVA-C artery phantom, a silicone artery phantom and human media and intima. Reproduced from [48] with permission.

A significant challenge in fabricating OCT phantoms with PVA-C is that the freeze-thaw cycles adjust both the optical and mechanical properties simultaneously. The experimental results in [47] suggest that the addition of scatterers and absorbers does not affect the mechanical properties. Also DMSO can be used to reduce the scattering induced by the FTCs [49]. These two features provide the potential for independent control of the optical and mechanical properties

4. Complex structures

Organs to be imaged by OCT are usually composed of tissues assembled in complex structures. Such structures include layers of different cell types, cavities and vessels containing fluid and blood, and diseased tissue manifesting as altered morphology. It is important to simulate such structures using phantoms. Additionally, incorporation of 2D and 3D structures with known geometry allows such phantoms to be used to validate and verify system performance and techniques. For example, such phantoms could enable the resolution and sensitivity of the OCT system to be determined and the ability to perform diagnosis through segmentation of structures or attenuation measurements. As the development and application of OCT continues to advance, the need for phantoms with complex shapes is growing for both inter-laboratory and inter-system comparison.

In other imaging modalities such as ultrasound, 2D and 3D structured phantoms have received much attention [70,71] and, indeed, are now available commercially [72]. In comparison, the OCT community is in the relatively early stages of developing phantoms with complex shapes. Simple bi-layer (slab) phantoms representing morphological change in 1D have been proposed with different materials, including agar, gelatin, PVA, fibrin and silicone [8,12,14,20,33]. An early example of a phantom containing 2D structure was presented in 1997, and was used to study the effect of multiple scattering in OCT [73]. Phantoms containing randomly dispersed inclusions, used to validate various speckle-reduction techniques, have also been proposed [74].

4.1. Silicone phantoms

Silicone lends itself well to the fabrication of phantoms with complex shapes, due to its low viscosity prior to curing and high toughness. Phantoms have been developed for point-spread function measurements at controlled positions, using femtosecond laser subsurface micro-inscription [75]. Structures can easily be formed in silicone phantoms through sequential molding, i.e., by curing each desired feature sequentially. For a layered phantom, this involves stacking layers by adding and curing one layer at a time [5,12]. Strong inherent adhesion between layers ensures fabrication of a solid block bearing the desired features. Recently, an even simpler fabrication technique was proposed which involves stacking pre-molded and cured layers [39]. This technique has been used to simulate complex 2D wave-like structures and narrow linear channels, which are shown in Fig. 8 . Another recent work has demonstrated a novel skin-simulating phantom. This phantom consists of a positive replica of human skin; fabricated using a negative imprint of skin obtained by impressing wax on the skin surface [76]. This phantom represents an important advance in that a real biological structure (the skin’s surface relief) is used in the fabrication of the phantom.

Fig. 8.

OCT imaging of 2D-structured silicone phantoms: (a) Skin simulating phantom; (b) Its 3-D reconstruction; (c) 200-μm channel filled with 20% Intralipid; and (d) its 3-D reconstruction. Reproduced from [39] with permission.

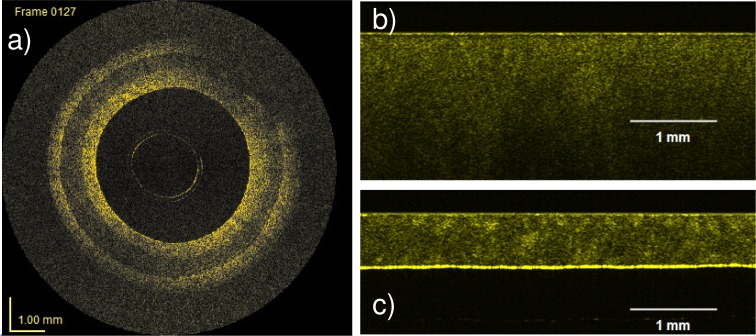
A further advance has been the fabrication of 3D-structured silicone phantoms using a more advanced and highly flexible soft-lithographic molding technique known as replica molding [77]. This technique is based on a master produced by UV photolithography, which is used in a two-step casting procedure. An example of a 3D-structured phantom fabricated with this technique is presented in Fig. 9 . The 3D features, the letters “O B E L”, protrude from the first (feature) casting and are encased on both sides by the second (embedding) casting. The letter dimensions ranged from 250 μm in height to between 180 μm and 220 μm in width. The smallest features were 45 μm wide and the spacing between the letters was 50 μm. The smallest feature size is set by the optical lithography system resolution (2 μm) and the largest feature size can exceed 1 mm. Optical profiling suggested that the sharpness of the optical features was very high, the deviation from the normal to the protrusion casting background being less than 1°. The authors demonstrated its use in assessing feature contrast enhancement and the associated effects on image resolution. This method provides for well-defined, reproducible and independently controllable structures with a wide range of structures possible, but it requires access to complex and costly soft lithography apparatus.

Fig. 9.

Cross-sectional OCT images of a 3D-structured phantom: (a) B-scan view (x-z plane); (b) y-z plane view; (c) en face view (x-y plane); (Scale bars: 100 μm) and (d) Orientation of planes with respect to the features. Solid renderings of: (e) Phantom with no scatterers in surrounding layer; and (f) Phantom with scatterers in surrounding layer. Reproduced from [77] with permission.

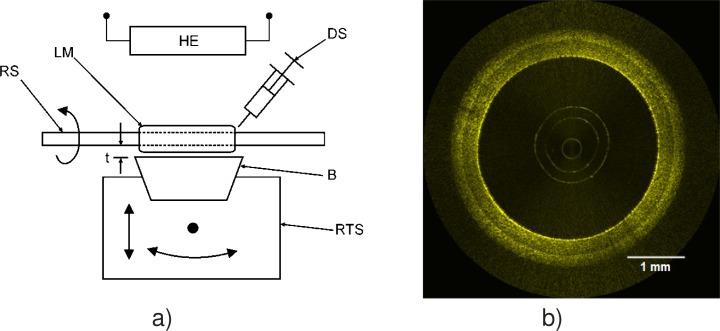
Yet another approach to silicone molding is to allow the silicone to cure as it is deposited. This allows complex structures to be fabricated in a much simpler and more precise manner than sequential molding. This technique has been used to fabricate artery phantoms with controlled optical and mechanical properties for each layer [31]. The experimental setup is depicted in Fig. 10(a) . The silicone mixture is deposited with a syringe over a rotating shaft. The material is wiped by a blade mounted on a precision translation stage. The blade distance from the rotating shaft determines the layer thickness. Curing is accelerated by the presence of a heating element. Once a layer is cured, the blade is retracted to the desired thickness for the next layer and a different mixture is applied. The process is repeated until the required number of layers is obtained. Figure 10(b) presents an OCT image of an artery phantom with three layers simulating the intima, the media, and the adventitia. By slightly modifying the fabrication process, more complex structures simulating diseased artery phantoms can be fabricated [78]. The technique can be used to fabricate phantoms for any tubular multilayered organ.

Fig. 10.

(a) Experimental setup to fabricate multilayer tubular silicone phantoms and (b) OCT image of an artery phantom. (RS rotating shaft, LM layer mixture, DS deposition syringe, B blade, RTS rotation and translation stage, HE heating element, t thickness). Reproduced from [31] with permission.

4.2. Fibrin phantoms

Complex shapes can also be included in fibrin phantoms [14]. Layered phantoms have been fabricated by pouring fibrin into the base of a mold in two steps. By controlling the volume of solution added to the mold, a thin layer with 1% w/v Intralipid was fabricated, followed by a thicker layer with 13% w/v Intralipid added 10 min later. An OCT B-scan of a bilayer fibrin phantom is presented in Fig. 11 . Higher scattering in the thicker layer is visible. The values of μ_t measured in the thin and thick layers were 1.7 and 3.3 mm⁻¹, respectively. μ_t in the thin layer is higher than expected, while μ_t in the thick layer is lower than expected. It has been suggested that these differences are due to leaching of Intralipid from the thick layer to the thin layer during fabrication. Fabricating the phantoms at lower temperature could potentially reduce this leaching; nonetheless, it represents a significant disadvantage. Furthermore, it may be difficult to fabricate fibrin phantoms with 2D and 3D-structure due to their high viscosity and low toughness.

Fig. 11.

Bilayer fibrin phantom, with different Intralipid concentration in both layers.

4.3. PVA phantoms

PVA-C phantoms with complex structures can be obtained using successive molding. Bilayer PVA-C phantoms were fabricated to study OCT elastography [20–22]. Single-layer cylindrical PVA-C phantoms were reported in [22]. Multilayered tubular phantoms to mimic arteries were reported in [47] and [48]. A PVA-C multilayered tubular artery phantom obtained by an over-molding process is depicted in Fig. 12(a) . The multilayers employed 4 FTCs for the first layer (intima), 2 FTCs for the second layer (media), and 1 FTC for the outer layer (adventitia). Alumina was used for the outer layer only with a concentration of 20 mg/ml.

Fig. 12.

OCT images of: (a) a multilayer PVA-C artery phantom; (b) a 4 mm-thick PVA-C sample with 2 FTCs; and (c) a 0.380 mm-thick PVA-C sample with 2FTCs. Reproduced from [48] with permission.

There are two main challenges when fabricating a complex structure in PVA-C. The first arises because the number of FTCs affects both the mechanical and optical properties. Compounded by the fact that each phantom component is not submitted to the same number of FTCs, it is challenging to correctly set these properties for each component. Using additives to separately control scattering and absorption helps to overcome this issue. The second challenge is the difficulty of molding PVA-C phantoms. As can be seen in Fig. 12(a), the multilayer artery phantom is not perfectly homogeneous. This was investigated in [48], where it was observed that thin layers molded with PVA appear less optically homogeneous than thick layers, even in absence of additional scatterers and absorbers. This is shown in Figs. 12(b) and 12(c), which present OCT images of two PVA-C samples. Both were made of 10% PVA-H without additives, and both were subjected to 2 FTCs. The phantoms were fabricated in flat stainless steel molds. The first was fabricated with 4 mm spacing between plates, and the second with 0.380 mm spacing. The OCT image of the 4 mm sample is more homogeneous than that of the 0.380 mm sample, where several clusters of high signal can be observed. Methods of fabricating PVA-C phantoms with complex structures and good optical homogeneity within each structure require further refinement.

5. Conclusion

In conclusion, we have reviewed the development of OCT phantoms capable of simulating the optical, mechanical and structural properties of tissue. We focused on three materials: silicone, fibrin and PVA-C, each providing the prospect of durable and reproducible phantoms with complementary properties. We discussed the advantages and disadvantages of each material, supported by results obtained both in our laboratories and by others. These results demonstrate that no one phantom can provide the flexibility necessary to simulate all properties of tissue: each material system has its respective strengths and weaknesses. For example, silicone is preferable to fibrin if a phantom is required with 3D structure, but fibrin is preferable to silicone if a phantom is required to incorporate tissue constituents for optical scattering. PVA-C phantoms can provide controlled complex mechanical properties, although obtaining good control over optical properties still represents a challenge. We believe fabricating OCT phantoms using one of the selected materials will allow researchers to obtain the required tissue properties for the majority of OCT experiments.

The continued advancement of OCT methods, technologies and applications depends upon the development of reproducible and reliable phantoms. We trust this paper will assist in efforts to design such phantoms, which could then form the basis for durable, transferable standard imaging targets for OCT.