Abstract
Purpose: Accurately segmenting breast tumors in ultrasound (US) images is a difficult problem due to their specular nature and appearance of sonographic tumors. The current paper presents a variant of the normalized cut (NCut) algorithm based on homogeneous patches (HP-NCut) for the segmentation of ultrasonic breast tumors.
Methods: A novel boundary-detection function is defined by combining texture and intensity information to find the fuzzy boundaries in US images. Subsequently, based on the precalculated boundary map, an adaptive neighborhood according to image location referred to as a homogeneous patch (HP) is proposed. HPs are guaranteed to spread within the same tissue region; thus, the statistics of primary features within the HPs is more reliable in distinguishing the different tissues and benefits subsequent segmentation. Finally, the fuzzy distribution of textons within HPs is used as final image features, and the segmentation is obtained using the NCut framework.
Results: The HP-NCut algorithm was evaluated on a large dataset of 100 breast US images (50 benign and 50 malignant). The mean Hausdorff distance measure, the mean minimum Euclidean distance measure and similarity measure achieved 7.1 pixels, 1.58 pixels, and 86.67%, respectively, for benign tumors while those achieved 10.57 pixels, 1.98 pixels, and 84.41%, respectively, for malignant tumors.
Conclusions: The HP-NCut algorithm provided the improvement in accuracy and robustness compared with state-of-the-art methods. A conclusion that the HP-NCut algorithm is suitable for ultrasonic tumor segmentation problems can be drawn.
Keywords: breast tumor, image segmentation, homogeneous patch, normalized cut, ultrasound
INTRODUCTION
Breast cancer is one of the most common malignancies in women. Its incidence and mortality are on the top of the list in female diseases.1 Early diagnosis and treatment are crucial to improve the survival rate. X-ray mammography and ultrasonic examination have been widely used for early diagnosis and treatment. Compared with mammography, ultrasonic examination has unique advantages in breast cancer detection and classification because of its low cost and minimal ionizing radiation. However, due to its low-image resolution and signal-to-noise ratio (SNR), the interpretation of ultrasound (US) images is more difficult and highly dependent on expert clinical experience. This setback entails the development of computer-aided diagnosis (CAD) systems that can help experts recognize abnormal regions in US images. As an important component of the CAD system,2 US image segmentation has been the focus of extensive research recently.3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23 An intensive review was conducted by Ref. 2.
Manual segmentation is time consuming and varies from case to case, so automatic or semiautomatic segmentation of ultrasonic images is clinically desired. In the segmentation of ultrasonic breast tumors, there are two types of difficulties that should be considered:2, 3, 4, 24, 25 (1) The existence of inherent artifacts, such as attenuation, shadows, speckle, and so on, makes the tumor region less distinguishable in the image. For instance, posterior acoustic shadowing usually presents a black region below the tumor and tends to merge with the tumor region. The intensity inhomogeneity caused by attenuation leads to blurry boundaries, and speckle noise seriously decreases the SNR of the image. All these findings make the segmentation of lesions more difficult.3, 4, 5, 24 (2) Handling tumor-like structures in images is difficult, e.g., glandular tissue, Cooper’s ligaments, and subcutaneous fat,3, 25 which always present similar appearances to tumors and are hard to differentiate from true lesions by traditional image features.
In this section, we will review the state-of-the-art algorithms of US image segmentation and present motivations for developing a novel algorithm to overcome current limitations.
Related work
Several approaches have been reported in the literature for US image segmentation. These approaches can be roughly categorized into three groups, namely, random field-based methods, active contour-based methods, and normalized cut (NCut) based methods.
Markov random field (MRF) based methods are used to segment US images due to their capability of coping with noise in images.5, 6, 7 For instance, Cheng et al.7 introduced a MRF-Gibbs random field-based framework to segment breast tumors in US images. To suppress noise, a four-neighbor system with a newly defined local energy was adopted to capture the pixel correlations. Furthermore, the expectation– maximization (EM) method was utilized to obtain optimal parameters of the model. Unfortunately, the attenuation field was not considered in this model. Xiao et al.5 presented a combined maximum a posteriori (MAP) and a MRF model to eliminate the effect of attenuation artifact. The attenuation field and labels of image regions can be estimated simultaneously under this framework. However, the proposed model seemed invalid in the case of severe artifacts, and the authors pointed out that an accurate segmentation of the object of interest cannot be guaranteed for some cases. The main limitation of random field-based approaches is the difficulty of integrating high-dimension image features aside from pixel intensity into their segmentation framework, whereas intensity feature is not sufficiently descriptive to distinguish the lesion from the background due to the high amounts of artifacts in US images.
Active contour supplies another popular framework for US image segmentation. According to the type of adopted image features, the active contour models can be divided into region-driven models8, 9, 13 and edge-driven models.10, 11, 12, 13, 14, 15 For region-driven models, energy function is constructed using the region-based image features, i.e., some kinds of statistics of the primary image features in a region. Liu et al.9 formulated an energy function based on probability density functions of intensities in lesions and background regions. The authors suggested that a good segmentation could be obtained even if the apparent edge between the target and background is missed. Obviously, the larger region leads to more reliable statistics; thus, it is more robust to the noise. However, the localization capability of region-based features decreases along the enlarged region and the accuracy of segmentation would be affected. Alternatively, edge-driven models depend on edge-based image features, i.e., local intensity gradients, outputs of edge indicator, and so on. Traditional edge extraction methods are commonly sensitive to noise, so appropriate denoising and edge detection methods are usually necessary for edge-driven models. For example, anisotropic filters for speckle noise reduction and phase-based edge indicator functions were used in Refs. 10, 12 and Refs. 14, 15, respectively. Chang et al.10 took an anisotropic filter, a stick operation and an automatic threshold method as the preprocessing steps. Subsequently, they applied active contour method to extract contours of a breast tumor from US images and finally extended their work to three dimensional case. Alternatively, Chang et al.11 used stick operation followed by morphologic process as preprocessing steps before applying active contour. In addition to noise, the intensity inhomogeneity caused by the attenuation artifacts often occurs in US images. To overcome this problem, Belaid et al.14 presented a phase-based level set (PBLS) method to segment the left ventricle from US images. In their approach, phase-based image features that are intensity invariant were adopted. The results showed that PBLS is robust to attenuation artifact and speckle noise and captures the missing boundaries well. Gao et al.15 extended this work to the segmentation of breast US images, by extracting phase-based edge feature and then using it to calculate the generalized gradient vector flow. Their method achieved good tumor segmentations but was tested on a limited dataset. In summary, region-based features and edge-based features have their own advantages and disadvantages. A new feature-extraction scheme that can combine region and edge information together should supply more descriptive clues and would benefit the segmentation of US images. Moreover, the intensity-invariant nature of image features is an important factor that should be taken into account emphatically. Liu et al.13 presented a combined region and edge-based active contour method where global information was extracted from the original image for modeling tissues and edge information was extracted from a denoised and edge-enhanced image for capturing boundaries of breast tumors. This work can segment breast tumors efficiently and automatically, however, did not explicitly account for intensity-invariant nature.
The location and shape information of tumors are usually introduced into the segmentation framework as priors to prevent tumor-like structures from being erroneously merged with the tumor region. For instance, Horsch et al.16, 17 proposed a breast lesion-segmentation method that can exclude the subcutaneous fat from the lesion region by manually defining the lesion center and subsequently cropping the top part of the image. Madabhushi and Metaxas3 integrated empirical domain knowledge, including shape, intensity, texture, and so on, into a deformable model to eliminate the effects of gland tissue, subcutaneous fat, and shadowing on the segmentation. In the previous works,3, 16, 17 the authors showed that their methods can segment cysts, benign masses, and malignant masses from US images.
Notably, as graph-based method, NCut,26, 27 extensively used for nature image segmentation,28, 29 has been applied in US image segmentation.18, 19, 20 NCut-based approaches mainly include two steps. First, a weighted graph is constructed, where nodes of the graph correspond to image pixels, and the weight of the edge reflects the similarity between two joined nodes. A graph can be represented by a weight matrix. Second, the image segmentation is performed by solving the eigenvectors and eigenvalues of the weight matrix. This step follows a partitioning criterion that maximizes the total similarity within groups and minimizes the total similarity between different groups. Using NCut-based approaches, an image is usually segmented into several distinct regions rather than the target and the background, and the pixels have high similarity within each region. A priori knowledge is usually introduced into the segmentation process through manual interactions to obtain the complete target.29 As a semiautomatic segmentation method, it has received significant attention.20, 30, 31 Another way to separate the target from the background is to combine multiple segmentation methods. For example, Huang et al.21 used the graph-based method as the initial contour estimation for active contour to find breast tumor boundaries in US images. The biggest innovation of NCut is that the similarity and the spatial relationship of pixels are taken into account simultaneously during the segmentation. Through NCut, an optimal solution can be calculated elaborately by solving the eigenvectors and eigenvalues of the weight matrix. NCut is a very flexible segmentation framework where appropriate image feature-extraction methods and similarity metrics can be selected according to the specific segmentation task. At the same time, it is convenient to integrate priors into the framework by simple manual interactions. These advantages motivate us to develop a NCut-based method to segment tumors from breast US images.
Our contributions
In the current paper, we present a novel semiautomatic NCut-based method (referred to as HP-NCut) to segment tumors from breast US images. Our methodology is novel in the following ways:
-
(1)
In Refs. 26, 27, 28, 32, 19, 20, a fixed window is used to extract local region-based image features. Traditional fixed window-based feature extraction suffers from the fact that the narrow window bears poor statistical information and the wide window yields poor boundary localization. Our goal is to overcome the current tradeoff and propose a novel feature-extraction scheme. To this end, we constructed a kind of adaptive neighborhood, i.e., homogeneous patch (HP). The boundary information is used to determine the shape and size of HP, which guarantees that HP cannot spread across the strong edges and is limited within the same tissue region. Thus, the statistics of primary features within the HP is more reliable in distinguishing different tissues, and this helps to avoid including tumor-like structures as part of the tumor region. Obviously, HP plays an important role in improving the accuracy and robustness in tumor segmentation.
-
(2)
A new boundary-detection function is proposed to create the boundary map for HP construction. Unlike traditional edge detector methods, such as Sobel and Canny detectors33, 34 where the intensity gradient information is mainly used for edge extraction, we incorporate the texture and intensity information into the detector function, and the experiment shows that proposed boundary-detection approach can find the fuzzy boundaries of the target object in US images.
-
(3)
In view of the importance of intensity-invariant features for US image segmentation as described in Sec. 1A, the outputs of intensity invariant-oriented filters bank are adopted as primary features in the currently proposed method. Based on these primary features, a texton-like scheme is explored to describe the texture information. Furthermore, each HP is considered as a fuzzy set, and the fuzzy distribution of textons within the HP is used as image feature for the segmentation. The proposed feature-extraction scheme ensures the intensity-invariant nature of the final-used features and has the capability of coping with the inhomogeneity problems caused by attenuation artifact in US images. Meanwhile, the denoising property of the oriented filters is helpful to suppress the speckle noise.
The presented method was evaluated on a database of 100 breast US images (50 benign and 50 malignant). The results are promising and show that the current approach can segment breast tumors from US images accurately and efficiently compared with other semiautomatic segmentation methods, i.e., the well-studied interactive NCut tool of Yu and Shi29 and the recently published PBLS method of Belaid et al.14
The remainder of the current paper is organized as follows: Sec. 2 briefly describes the background of NCut and introduces the HP-NCut algorithm. Experimental results are presented and discussed in Sec. 3. Finally, conclusions are given in Sec. 4.
METHODS
Background of normalized cut
The HP-NCut algorithm is based on NCut. In this section, we briefly describe the principle of NCut. NCut is an unsupervised segmentation method proposed by Shi and Malik26, 27 that casts image segmentation as a graph-partitioning problem. In the NCut framework, a given image is represented as a weighted undirected graph G = (V,E,W), where V is the set of nodes and E is the set of edges connecting the nodes. W = {w(p, q)} is a weight matrix, and one of its elements, w(p, q), is a function of the similarity between the nodes p and q, and usually defined as
| (1) |
where F(p) is the image features of the node p and X(p) is the spatial location of that node. σI and σX are two positive scaling factors that determine the similarity in the feature and spatial domains, respectively. Meanwhile, ‖·‖2 represents the Euclidean metric and r is a threshold. When the spatial distance between nodes p and q is larger than r, w(p,q) is set as zero.
In the graph theory, a graph can be partitioned into disjoint sets A and B, satisfying A ∪ B = V, A ∩ B = Φ. The degree of similarity between these two sets is commonly called cut26, 27
| (2) |
The above graph partitioning can be achieved by minimizing the cut function. To find a balanced partition, the disassociation measure was defined as26, 27
| (3) |
where A represents the set of all pixel nodes, asso(A, V) and asso(B, V) are defined similarly as the total connection from nodes in A to all nodes in the graph.
To maximize the total dissimilarity and total similarity between and within sets A and B, Eq. 3 can be transformed into the following generalized eigensystem:
| (4) |
where D denotes a diagonal matrix with diagonal elements and λ and x are the eigenvalue and the eigenvector, respectively.
As mentioned in Sec. 1, NCut supplies a flexible segmentation framework where the appropriate image feature-extraction method can be selected according to the specific segmentation task. The current study mainly focuses on a novel HP-based feature extraction, which is very different from the fixed window-based feature extraction usually adopted by traditional NCut-based methods.
Overview of the proposed HP-NCut algorithm
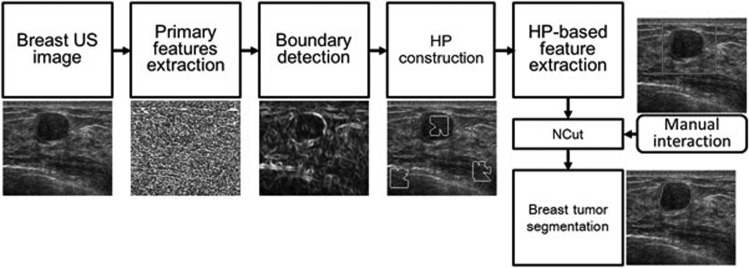
The HP-NCut algorithm consists of five components, namely, primary feature extraction, boundary detection, HP construction, HP-based feature extraction, and manual interaction. The flowchart of the method is illustrated in Fig. 1, and the corresponding implementations are briefly described in the succeeding paragraphs.
Figure 1.
Flowchart of the HP-NCut algorithm.
First, by fully considering the necessity of the intensity-invariant nature of the features for US image segmentation, the oriented filter is adopted for the primary feature extraction. The outputs of the oriented filter bank are used to capture the intensity variation at local points, and then, the texture information is represented using a texton-like scheme. These two types of features are all intensity invariant and treated as primary features for the following boundary detection and segmentation. Second, a boundary-detection method is proposed to find the potential boundaries of the target objects. Here, the intensity and texture features are combined by introducing a novel boundary-detection function. Third, based on the precalculated boundary map in the previous step, a search algorithm is proposed for the HP construction. In this step, the adaptive neighbor of each pixel, which is spatial homogeneous, is determined. Fourth, the histograms of the textons within the HPs are calculated as final image features for the segmentation. Last, a rectangle region of interest (ROI), which includes the tumor region in the image, is integrated into the algorithm by manual interaction. Final segmentation is obtained using the NCut framework. The details of each component are described in the rest of this section.
Primary feature extraction
For breast US images, texture information is associated with internal echo pattern and can provide important clues for distinguishing different tissues. Accordingly, the texture features are used in the proposed methods as primary features for boundary detection and segmentation.
To describe the local texture information, a variable of filter banks, such as Gabor filter bank23 and oriented filter bank,28, 35 are available. In the current research, the outputs of the oriented filter bank are used for its simplicity and effectiveness. The used filter bank is the same as the paper.28, 35 This filter bank contains a set of even-symmetric and odd-symmetric filters at six orientations, coupled with a center-surround filter. The even-symmetric filter is a second derivative of a two-dimensional Gaussian function, and the odd-symmetric one is its Hilbert transform. The center-surround filter is a difference of Gaussians (DoG). Mathematically, three types of filters can be formulated as follows:
| (5) |
where , , θt = nπ/N, n = 0, 1, …, N − l, and N is the total number of orientations. In the current paper, we use the same parameter settings as Ref. 35, where σx:σy = 3:1, C = 2, N = 6, and σx = 0.7% of the image diagonal. We have tested other parameters and found that the current setting yields the best results. The filters defined by Eq. 5 are plotted in Fig. 2a.
Figure 2.
The illustration of filter bank and texton map (a) first to sixth rows: even and odd filter bank consisting of one scale and six orientations; seventh row: center-surround filter fDoG. (b) The original image. (c) The texton map derived from a universal dictionary. (d) The texton map created using the proposed approach. (e) Zoom-in view of the region inside the white square outlined in (d). The ground truth tumor boundary indicated in dark color (green in online version), is overlaid to all texton maps.
By convolving a breast US image I with the above filter bank, for one pixel located at (x,y), we can get a feature vector Ffilter(x,y), as follows:
| (6) |
where
and
where , , and represent the outputs at location (x,y) by convolving the image with the filters , , and fDoG, respectively. Notably, in the current implementation, six orientations are considered; thus, and are vectors containing six elements, respectively. Accordingly, Ffilter(x,y) is a vector that lies in a 13D feature space.
Building the statistics of features directly in a high-dimension feature space is difficult. On the other hand, texture usually has spatially repeated properties, so it is possible to represent the texture feature vectors approximately using some conspicuous prototype vectors.28 In the proposed method, we introduce a texton-like scheme to obtain a concise representation of the texture feature. First, the feature vectors are clustered into a small set of groups using K-means algorithm. Each group center is called a texton, and all textons compose a dictionary. Then, each feature vector is mapped to the nearest texton and assigned a label according to the precalculated dictionary, i.e., K group centers. Thus, a high-dimension feature vector can be represented just by a label, which is convenient in the local distribution estimations of textons. The difference between the currently proposed scheme and the traditional texton scheme28 is that we use only the feature vectors extracted from the image under segmentation rather than an image dataset for training to create the dictionary. This setup makes the created dictionary more image-specific, namely, with the same dictionary size, an image-specific dictionary makes a better representation of the feature vectors of the image under segmentation than a universal dictionary.
The proposed feature-extraction scheme offers several advantages. First, the responses of the oriented filter band reflect intensity variation along a specific direction, thus, it is intensity invariant. This attribute is very important in US image segmentation. Furthermore, the multiorientation representation of the filter bank is capable of edge orientation detection and benefits the subsequent boundary detection. Second, the filtering operation can suppress the effect of noise in images. With the Gaussian factor in the filter bank, the noise in US images, such as speckle, can be smoothed or removed.22
An experiment was performed to test and compare the texton maps derived from image-specific dictionary and universal dictionary. Figure 2b illustrates a breast US image of a malignant tumor that has heterogeneous internal echo. The texton maps created using universal dictionary and image-specific dictionary are shown in Figs. 2c, 2d, respectively. In Figs. 2c, 2d, 2e, different gray colors are assigned to textons for better display, and a zoom-in view of the region inside the square in Fig. 2d is shown in Fig. 2d. In this example, the number of texton channel, K = 20 is used. Our training dataset contained 20 breast US images to construct a universal dictionary. From Figs. 2d, 2e, we can see that the texton map derived from image-specific dictionary can accurately capture the internal echo pattern of the tumor. In fact, for most breast US images, our experiments in Sec. 4 show that the extracted texton feature is sufficient in characterizing image textures. In addition, from Figs. 2c, 2d, we can see that two texton maps derived from image-specific dictionary and universal dictionary, respectively, present the visually similar appearances, which indicates that the image-specific dictionary is compared powerful to universal one for capturing the texture information of images at least. Furthermore, the root mean square errors (RMSEs) between the original feature vectors and their corresponding words in the dictionaries of 20 images are calculated to quantify the accuracy of the two dictionaries for representation of the original feature vectors. The results show that, compared to universal dictionary, the image-specific dictionary improves the RMSE from 0.0503 to 0.0488 with 2.83% gains. These results reveal that using the proposed approach leads to the improved feature-extraction behavior.
Boundary detection
An appropriate boundary map that can accurately capture the boundary of the target object is necessary for the construction of the HP. The boundaries of tumors in US images are usually fuzzy, so intensity gradient-based edge detectors, such as the Sobel detector, become invalid [Fig. 4a]. Previous reports19, 22, 23, 36 indicate that the abrupt changes of texture and intensity play critical roles for US image edge detection. Thus, in the proposed method, the texture features described in Sec. 3A and the oriented energy (OE) capturing local intensity variation28, 35 are integrated into a novel boundary-detection function and used to find the boundaries of the tumors in US images.
Figure 4.
Boundary map comparison of different methods. (a) Original image. (b) Boundary map obtained by Sobel operator. (c) Boundary map obtained using the texton histograms. (d) Boundary map obtained by the proposed approach. The ground truth tumor boundary indicated in light color (green in online version), is overlaid to all boundary maps. Three dark color (red in online version) rectangles are drawn to indicate the differences among the detected boundary maps.
Detection function
Suppose there exists a boundary at a point, and its neighborhoods are divided into two subregions along the boundary, the image information (intensity and texture) should have big differences between these two subregions. These differences can indicate the strength of the boundary. In the proposed method, a detection function is introduced to measure these differences.
At a pixel point p in an image, its circular neighborhood NP with radius r1 is selected and divided along the direction θt. The left and right half-disc neighborhoods are denoted as Lp and Rp, respectively (Fig. 3).
Figure 3.
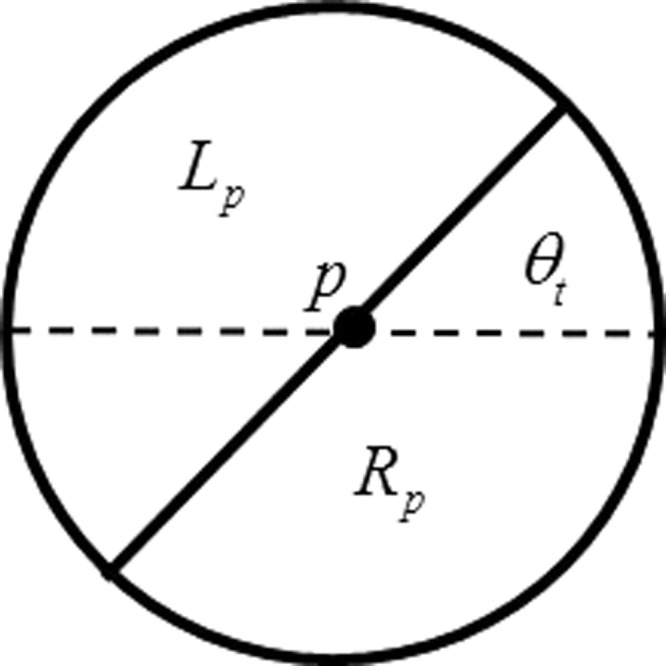
An illustration of partitioning neighborhood.
Naturally, the boundary-detection function is designed by comparing the energies associated with the image information of two half-disc neighborhoods. Accordingly, the boundary-detection function is defined as
| (7) |
where E(p,θt) is the boundary energy at p with the direction θt. The larger value of E(p,θt) indicates the stronger boundary in the direction θt. Two elements, and , represent the image energies of Lp and Rp at the kth texton channel, respectively. Texton channels refer to the collection of discrete pixel point sets with the same texton labels. Part I of Eq. 7 is the Manhattan distance, whereas part II is the χ2 distance for measuring the difference between the energies of Lp and Rp. The combination of these two types of distance metrics is expected to improve the robustness of the proposed function.
In Refs. 28, 35, the distributions of textons, i.e., the texton histograms within Lp and Rp, are used as energies directly. Accordingly, and are formulated as
| (8) |
and
| (9) |
where T(p′) refers to the texton label of a pixel point p′. Count (LP) and count (RP) are the numbers of pixel points in LP and RP, respectively. δ(·) is the Kronecker’s delta function given by
| (10) |
In the proposed method, besides the above-mentioned texture information, abrupt intensity changes are considered as well. Thus, the new energies are defined as
| (11) |
and
| (12) |
The new terms dk(p, θt) are designed to integrate the effects of intensity changes into the energies. The definition of dk(p, θt) is mainly based on the following assumption: For a certain direction, once the abrupt intensity change occurs only at a candidate point but seldom appears in its neighborhood, there exists a boundary with high probability. In other words, the discontinuity of can provide useful clues for boundary detection. Based on this idea, dk(p, θt) are defined in following way.
First, OE is introduced to capture intensity changes in the images. Given an image I, OE can be expressed as
| (13) |
where the filters and are defined in Eq. 5. Intensity edges in direction θt can be captured by , with being strongly positive.28, 35
Second, for a point p, the average of its neighborhood Np with respect to the kth texton channel is defined as
| (14) |
where δ(T(p′), k) is defined in Eq. 10.
Finally, dk(p, θt) is formulated as
| (15) |
Actually, in Eq. 15, dk(p, θt) is designed to measure discontinuity of by comparing current point p and its neighborhood. Larger dk implies stronger boundary, accordingly, it is reasonable to assume that the texton channels associated with higher dk should be emphasized by adjusting their corresponding weights according to Eqs. 11, 12.
Finally, to extract the final result, oriented nonmaximal suppression can be used.28 Mathematically, the final boundary map can be given as
| (16) |
E* is normalized to 0–1.
The Sobel operator and texton histogram-based approaches28, 35 and the proposed approach were tested on a US image with malignant tumor [Fig. 4a]. The results are shown in Fig. 4. As can be seen, the Sobel operator using the default parameter setting performed poorly. A large number of tumor boundaries were missed and there were spurious edges inside the tumor region. The texton histogram-based approach yielded better result, but failed in some regions, for example, the region outlined by a red rectangle in the images. In addition, spurious edges inside the tumor region still remained. The proposed method performed best among these three methods in that it correctly extracted tumor boundary while eliminating spurious detection in the tumor region.
HP construction
As described in Sec. 1, for the traditional region-based image feature-extraction schemes,26, 27, 28, 29, 32 fixed neighborhood windows with the same size and shape are usually used to gather statistical information around the candidate points. The drawback of fixed window-based feature extraction is that the narrow window bears poor statistical information, whereas the wide window yields poor boundary localization. The larger window corresponds to the stronger ability to hold reliable information. Conversely, the smaller window leads to the stronger ability to localize boundary. Obviously, fixed window-based feature-extraction scheme is not an appropriate way to handle this trade-off problem. In this section, we propose the concept of HP, i.e., a novel type of adaptive neighborhood consisting of similar neighboring pixels. The boundary map described in Sec. 3B is used to construct the HPs, which guarantees that a HP cannot spread across the strong boundaries and is limited within the same tissue region. Thus, the statistics of primary features within the HPs is more reliable in distinguishing different tissues and benefits the subsequent segmentation. The details of HP construction are discussed in the rest of this section.
The basic idea of the construction of HPs is to look for the homogeneous pixels in terms of a boundary map in a large search window centered on the current pixels. At the same time, the system demands these pixels compose a connective region that includes the current pixels. The construction of HP includes three stages, namely, search window determination, energy reassignment, and HP determination.
Search window determination
The square windows are used to search for the homogeneous pixels in the proposed method. For a pixel point p at location (x, y), the search window is defined as
| (17) |
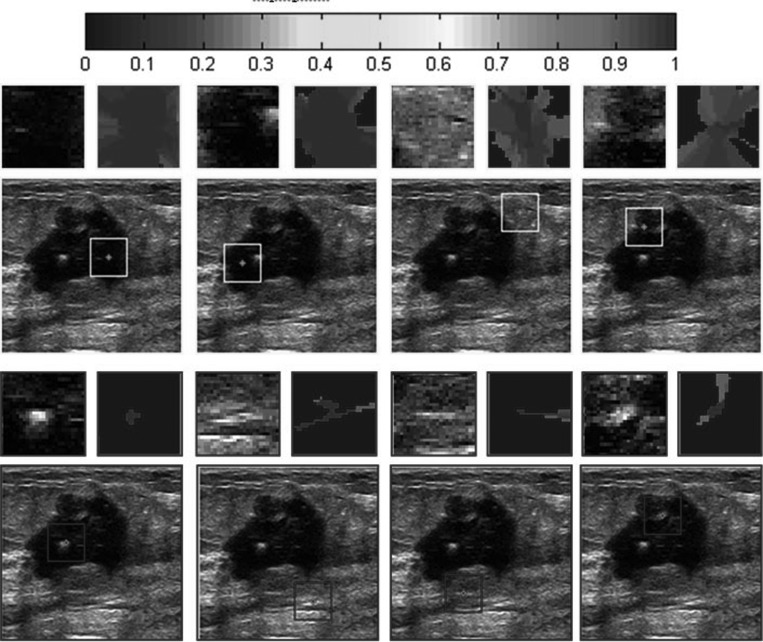
where R is the size of window. Figure 5 gives some demonstrations of the search windows, where the yellow and blue squares represent the search windows for some pixels.
Figure 5.
Examples of HPs on a breast US image. Eight search windows located in smooth region (outlined with light color (yellow in online version) squares) or nonsmooth region (outlined with dark color (blue in online version) squares) are listed in a test image. The specified area inside each search window is zoomed and displayed above the images. The corresponding HPs are displayed on the right and shown in color-coding. Along with the increase of the membership, the color varies from blue to darker red as shown by the color bar displayed at the top of the figure (available in online version).
Energy reassignment
The boundary energy calculated according to Eq. 17 needs to be reassigned for every point in the search window to guarantee that a HP cannot spread across the boundaries. Given a point p′ within wp, i.e., p′ ∈ wp, its maximal boundary energy with respect to point p, noted as is calculated and assigned to point p′. The definition of is similar to that in Ref. 28 and formulated as
| (18) |
where L(p,p′) represents the set of points lying on the line pp′ between the pixel points p and p′, and E* is the boundary energy defined in Eq. 16. represents the maximal boundary energy that needs to be conquered when the HP spreads from points p to p′. Accordingly, a point with a higher Emax should have lower potential to be incorporated into the HP.
HP determination
HP is considered a fuzzy set, where each point in the search window belongs to a HP according to a fuzzy membership. The membership reflects the probability of being integrated into the HP for a point, and is defined as follows:
| (19) |
Reasonably, a point p′ with higher mp(p′) which associates with a lower has a higher potential to belong to the HP of point p, and vice versa. Furthermore, to reduce the computation cost for the following feature extraction, a threshold method is introduced to remove the points that have low memberships from the HP. Given a threshold τ, the points with memberships lower than τ are removed from the HP directly. Mathematically, HP denoted as Ωp is defined below.
Definition I (HP):
Given a point, its HP Ωp is
| (20) |
HPs have something similar to the superpixels37, 38, 39 in that they are both representative forms of homogeneous and spatially coherent regions. However, the main differences between the superpixels and HPs include the following aspects. First, HP is an adaptive neighborhood system according to image location for the image feature extraction, and HPs of adjacent pixels usually have the overlap. Otherwise, a superpixel is a collection of the adjacent pixels that have the similar intensity, and superpixels have no overlap with each other. Second, HP imposes the soft homogeneity constraint during its construction, which is fundamentally different from the superpixel. Namely, a HP is defined as a fuzzy set of pixels rather than the traditional set as the superpixel.
Some examples of HPs are shown in Fig. 5. The previously constructed HPs are adaptive to different regions with varying sizes and shapes. In the smooth regions, the sizes of the HPs are relatively large because there are more homogeneous points in the search windows. In the nonsmooth regions, the sizes of the HPs are relatively small as there are more boundary points in the search windows. In addition, the homogeneities in the large regions are maintained. At the same time, the small-scale details are preserved.
HP-Based feature extraction
A novel feature-extraction scheme is proposed in this section. In the proposed methods, the distributions of textons within HPs are used as the final features for the segmentation. To obtain the features at one point, only the textons located in its HP rather than the fixed windows of the traditional scheme are accumulated to build the texton histogram. In addition, the fuzzy memberships of points are used to adjust the importance of textons for the histogram calculation. The points with higher membership in HP play a more important role for histogram calculation. Accordingly, a HP-based texton histogram can be defined as
| (21) |
where hp(k) is the kth bin of the histogram and δ(T(p′),k) is defined in Eq. 10. This histogram which describes the fuzzy distributions of the textons within a HP is called fuzzy histogram in current paper.
χ2 distance is introduced to measure the differences between the features. The difference between image features extracted from points p and q can be defined as
| (22) |
Finally, the weight function of NCut described in Sec. 2 can be rewritten as
| (23) |
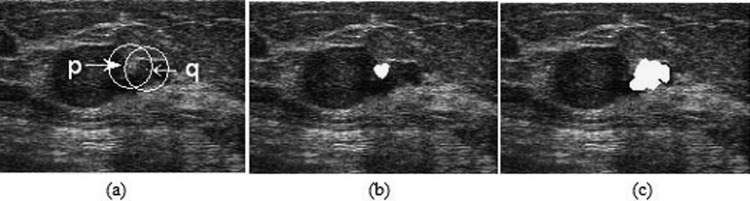
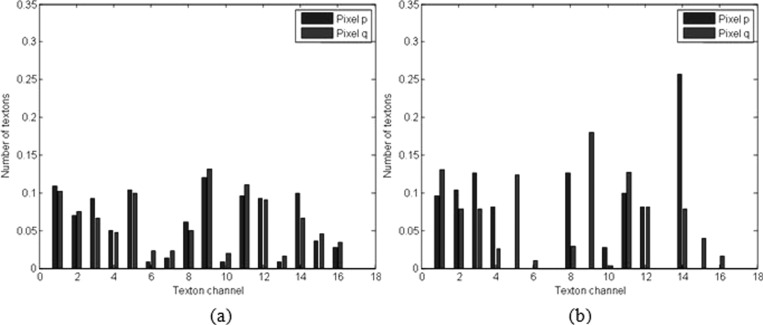
As described above, an attractive aspect of the HPs is that image features extracted from them are more discriminative in distinguishing different tissues in US images. We give an example to illustrate this point. A test was performed in a breast US image with a malignant tumor, as shown in Fig. 6a. Point p in the normal tissue region and point q in the tumor region were selected for comparison. The texton histograms of the fixed round neighborhoods (outlined in Fig. 6a with white circles) and HPs [as shown in Figs. 6b, 6c with yellow color] of these two points are calculated and displayed in Fig. 7. As can be seen, the large overlap of these two round neighborhoods makes their texton histograms very similar, as illustrated in Fig. 7a. This finding implies that by relying on such texton histograms, points p and q would have been mistakenly assigned to the same object, i.e., either tumor or normal tissues. Conversely, two HPs of p and q overlap less. Accordingly, the texton histograms computed based on the HPs [Fig. 7b], show a significant difference, and therefore, can help to separate p and q effectively.
Figure 6.
An illustration of the major challenge of using textures for successful segmentation of tumor from breast US images. (a) The two white arrows indicate two points located in the tumor and normal tissue regions, respectively. The white circles represent their round neighborhoods. (b) The HP of point p. (c) The HP of point q.
Figure 7.
For the points p and q in Fig. 6, two texton histograms were computed over: (a) the fixed round neighborhoods and (b) the HPs.
Manual interaction
As described in Sec. 1, prior knowledge is very helpful in US image segmentation. The location and shape information of the tumor are usually integrated into the segmentation framework to prevent tumor-like structures from being erroneously merged with the tumor region. In the proposed method, the location of the tumor is introduced into the NCut by manual interaction. Manual determination of the ROI is required using a rectangle in the image. The ROI as spatial information is a region that contains the breast tumor, as shown in Fig. 8a. Automatic segmentation only functions in the ROI. By setting the number of categories as 2, the proposed NCut-based algorithm can give the final segmentation directly.
Figure 8.
The segmentation of a breast US image with irregular shape and posterior acoustic shadowing. (a) The original image with a rectangular ROI placed by user. (b) Manual segmentation. The segmentation results using (c) HP-NCut, (d) Interactive-NCut, and (e) PBLS after 380 iterations. (f) The edge detection result of PBLS (the intensity value ranges from 0 to 1, with the values close to one indicating an edge pixel and the values close to zero indicating a background pixel).
RESULTS AND DISCUSSIONS
Data acquisition
The clinical study was carried out at the Shanghai Sixth People’s Hospital in China. Patients who received biopsy or surgery were recruited in the study. Informed consent to the protocol was obtained from all patients. Patient information about age, menopausal status, number of pregnancies or year of first full-term pregnancy, and personal and family history of breast cancer were acquired from a self-reporting patient history datasheet. A radiologist determined whether the breast mass is benign or malignant according to surgery and pathological examinations or biopsy.
In the present paper, a set of breast US images of Chinese women was built. The dataset contained 100 tumors, including 50 benign and 50 malignant tumors. Histologically, most of the benign tumors were fibroadenomas (FA) and most malignant tumors were invasive ductal carcinomas (IDCs). Table TABLE I. presents the pathological type of each tumor. The average tumor size was 31.6 mm (median size, 30 mm; size range, 10–70 mm) for benign tumors and 37.8 mm (median size, 40 mm; size range, 15–70 mm) for malignant tumors. The patient ages ranged from 18 to 75 yr. The breast US images were collected using three kinds of machines, i.e., ESAOTEDU8 (Esaote Medical Systems, Genoa, Italy), SEQUOIA 512 (Siemens, Mountain View, CA), or ESAOTEMYLAB90 (Esaote Medical Systems, Genoa, Italy) with 5.5–12.5 MHz, 8–14 MHz, and 5.5–12.5 MHz linear transducers and freeze-frame capabilities during the period 2003–2009. We only selected images which did not contain overlaid cursors and in which pathology was clearly available. For the images with heavy posterior acoustic shadowing, the expert radiologist was unable to distinguish the tumor region visually; thus, these images were excluded. The images in the current study were captured at the largest diameters of the masses.
TABLE I.
The pathological type of breast tumors.
| Lesion nature | Pathological type | Number of cases |
|---|---|---|
| Benign | Fibroadenoma | 30 |
| Breast disease | 12 | |
| Intraductal papilloma | 3 | |
| Inflammatory | 3 | |
| Normal breast tissue | 1 | |
| Cyst | 1 | |
| Subtotal | 50 | |
| Malignant | Invasive ductal carcinoma | 37 |
| Medullary carcinoma | 3 | |
| Invasive lobular carcinoma | 2 | |
| Ductal carcinoma in situ | 4 | |
| Intraductal papillary carcinoma | 3 | |
| Neuroendocrine carcinoma | 1 | |
| Subtotal | 50 | |
| Total | 100 |
Manual segmentation results outlined by a trained radiologist with more than 20 yr of clinical experience were considered the golden standard. They were performed using specially designed software and saved for validating the performance of the proposed method. The trained radiologist ensured that the segmented images covered the entire tumor.
The images in our dataset included glandular tissue, subcutaneous fat, and varying degrees of shadowing. In most of the images, blurred boundaries existed between different regions because of speckle noise. The complexity of breast US images renders the correct tumor segmentation very difficult.
Validation methods
In the current experiments, HP-NCut was compared with two other well-studied approaches to validate its performance, which were the PBLS method proposed by Belaid et al.14 and a close related interactive NCut approach presented by Yu and Shi.29 (Noted as Interactive-NCut in the rest of current paper for simplicity).
We carefully considered the initialization and parameter setting of PBLS and Interactive-NCut during our experiments so that fair comparisons can be made. For PBLS, the initial contours were placed manually according to the author’s suggestion. They were placed close to the tumor boundary. In addition, the critical parameters μ, λ, and v of PBLS were well-tuned to obtain the best segmentation for all images. For Interactive-NCut, we used the code downloaded from the website given in Ref. 40 for performance testing. The same spatial prior (ROI) was introduced into HP-NCut and Interactive-NCut. The parameter r defined in Eq. 24 was set to 8 for these two methods. The parameter σ defined in Eq. 23 was set empirically, with the range from 0.1 to 0.15 for Interactive-NCut and the range from 0.03 to 0.1 for HP-NCut, to yield optimal segmentation results. A summary of the parameter setting of HP-NCut is listed in Table TABLE II..
TABLE II.
The summary of parameter setting of HP-NCut.
| Parameter | Description | Setting |
|---|---|---|
| R | Defined in Eq. 17 | 12 |
| r | Defined in Eq. 23 | 8 |
| σ | Defined in Eq. 23 | range from 0.03 to 0.1 |
| K | Number of the texton channels | 16 |
| r1 | Radius of window used in boundary-detection function | 2% of the image diagonal |
| τ | Defined in Eq. 20 | About one minus mean boundary energies over the image domain. Described in Sec. IV.E |
Qualitative results
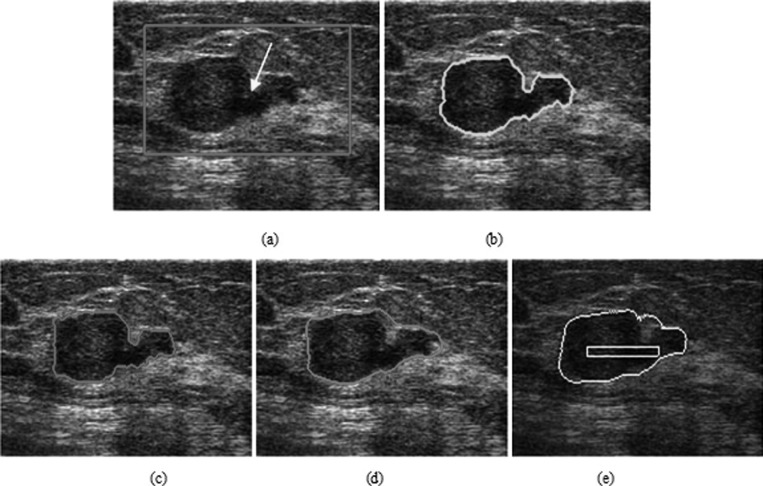
The advantage of the proposed HP-NCut algorithm is most significant when handling highly corrupted images with local intensity variations. Experiment 1 applied these three methods to a breast US image that contains a malignant (IDC) tumor with gradually changing intensity and irregular shape, as show in Fig. 8a. In particular, posterior acoustic shadowing was observed, corresponding to the dark area in the bottom section of the tumor. When initialized as a yellow rectangle in Fig. 8e, PBLS converged after 380 iterations (with parameters μ = 1, λ = 0.6, and v = −0.3). The result is illustrated in Fig. 8e. Although PBLS showed a certain ability to cope with intensity inhomogeneity, it indicated an inaccurate location of the part of tumor boundary. This result can be partly understood by the essence of the PBLS model, which is only dependent on the edge map. Figure 8f shows the corresponding edge map where a large part of the tumor boundary is missing in the region indicated by the yellow arrows. Therefore, the PBLS model went beyond a large gap and incorrectly converged to the nontumor boundary. Using the same ROI shown as a red rectangle in Fig. 8a, the segmentation results of the Interactive-NCut (with parameters σ = 0.15) and HP-NCut (with parameters σ = 0.07 and τ = 0.36) are shown in Figs. 8c, 8d, respectively. Although both Interactive-NCut and the proposed method are variants of the NCut, the image features used are very different. Specifically, Interactive-NCut relies only on edge information. That is, if a boundary consists of strong edges, using this method can accurately extract the object boundary. By contrast, HP-NCut integrates boundary information and texture information due to the use of HPs. The difference between the tumor and the surrounding normal tissue is sufficiently large, so the strong tumor boundary at the top can be found by Interactive-NCut. However, this method failed to detect the weak tumor boundary on the bottom due to the slight difference between the tumor region and the shadowing region. The HPs constructed in the proposed method enabled the accurate extraction of the entire tumor boundaries at the top and bottom, which proved very useful in handling intensity inhomogeneity. In addition, the segmentation result using HP-NCut was in agreement with the manual segmentation [Fig. 8b].
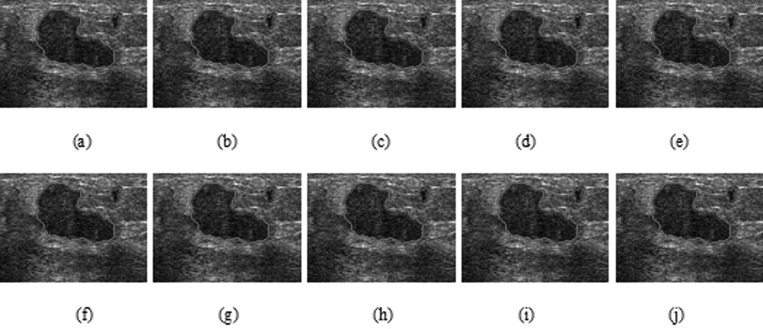
Experiment 2 applied these methods to a breast US image, as shown in Fig. 9. This image contained a malignant tumor (papillary carcinoma) connected to the normal tissues with similar texture distribution. In this experiment, we used the following settings: μ = 1, λ = 1.5, and v = −1 for PBLS; σ = 0.15 for Interactive-NCut; and σ = 0.07 and τ = 0.4 for HP-NCut. In Fig. 9e, the yellow rectangle represents the initial contour of PBLS. When initialized close to the tumor boundary, however, PBLS failed to find the boundary concavities indicated by a yellow arrow after 240 iterations. This behavior also occurs in the other types of level set models dependent on edge information or image gradient. The reason is that these models could not converge into the top of the U-shaped object, even when given good initialization. Given an ROI indicated by red rectangle [Fig. 9a], the segmentation results using HP-NCut and Interactive-NCut are illustrated in Figs. 9c, 9d. We can see that Interactive-NCut failed to detect the true tumor boundary at the top. This result can be partly explained by the essence of Interactive-NCut, which relies on image edge information alone. Therefore, when there are strong edges outside the tumor, the Interactive-NCut incorrectly interprets them; thus, an incorrect segmentation was achieved. In this situation, integrating boundary and texture information are crucial in improving the segmentation performance due to their complementary effects. For HP-NCut, the edge information was first used to define the HP centered at each pixel. Very often, the sizes of HPs are relatively large in smooth regions and relatively small near boundaries [Figs. 6b, 6c]. Accordingly, the interior texture statistics of the HPs are adaptively changed according to pixel location [Fig. 7b] and the weight matrix construction is consequently influenced by these changing region information. Eventually, the HP-NCut algorithm prevents the inclusion of the surrounding normal tissues and successfully extracts the tumor boundary, as shown in Fig. 9c.
Figure 9.
The segmentation of a breast tumor with similarity to the surrounding normal tissue. (a) The original image with a rectangular ROI placed by user. (b) Manual segmentation. The segmentation results using (c) HP-NCut, (d) Interactive-NCut, and (e) PBLS after 240 iterations.
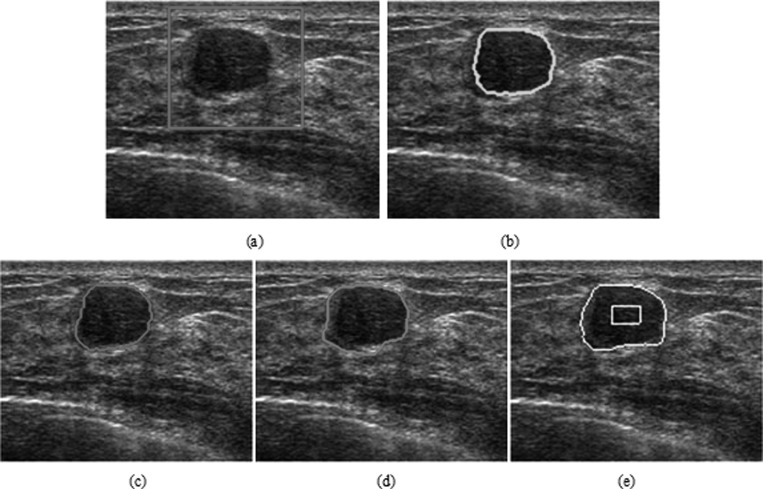
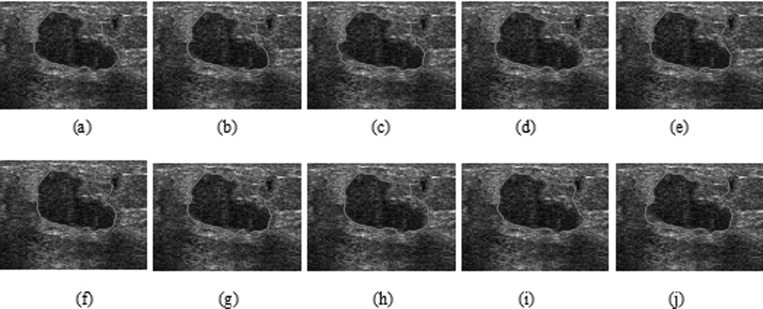
Experiment 3 applied these three methods to a relatively smooth benign tumor (FA), as illustrated in Fig. 10a. This FA is encapsulated and has distinct boundaries, where the transition of intensity from the inside of the tumor to the outside of the tumor is sharp but is associated with lateral acoustic shadowing. The echo pattern is homogeneous inside the FA. In this experiment, we used parameters μ = 1, λ = 1.5, and v = −1 for PBLS; σ = 0.1 for Interactive-NCut; and σ = 0.1 and τ = 0.45 for HP-NCut. Using the manually placed initial contour shown as a yellow rectangle, PBLS converged after 300 iterations and the result is illustrated in Fig. 10e. The segmentation results for HP-NCut and Interactive-NCut are illustrated in Figs. 10c, 10d, respectively, using the manually chosen ROI on the original image [Fig. 10a]. In this case, the texture and intensity of the tumor differed from the surrounding gland breast tissue region. Therefore, the edge between them is strong, except for a small part of the weak edge on the left side of the image. Therefore, Interactive-NCut and PBLS extracted a large part of the tumor boundary but failed with the boundary on the left. Interestingly, using the HPs, HP-NCut produced a correct segmentation, including the strong and weak edges. The result is much closer to the manual segmentation [Fig. 10e].
Figure 10.
The segmentation of a breast tumor with regular shape. (a) The original image with a rectangular ROI placed by user. (b) The manual segmentation. The segmentation results using (c) HP-NCut, (d) Interactive-NCut, and (e) PBLS after 300 iterations.
Based on Figs. 8910, the segmentation results obtained by the proposed algorithm are visually superior to those of the other two methods. The proposed HP-NCut method produces contours that are very close to the manual segmentation results. More experimental results of the proposed system support the same claims.
Quantitative results
We numerically evaluated our algorithm on a database of 100 breast sonograms to evaluate the effectiveness of the proposed algorithm. Two boundary-based error metrics and three overlapping area error metrics were used to evaluate the accuracy of HP-NCut.
Boundary-based error metrics
Hausdorff distance (HD)41 and average minimum Euclidean (AMED)42 were selected as boundary-based error metrics in the current experiments.
If A is a contour which has m points noted as {a1, …, am}, and another contour B is defined the same way, HD (A, B) and AMED (A, B) are, respectively, defined as
| (24) |
| (25) |
where MED (a, B) is the minimum Euclidean distance between point a and contour B
| (26) |
AMED measures the average distance between two contours, whereas HD measures the maximum distance between two contours.
Overlapping area error metrics
We also used three overlapping area error metrics,43 the true positive ratio (TP), the false positive ratio (FP), and the similarity (SI), to measure the similarity between semiautomatic segmentation results and the golden standard. Defining S as the set of points in the segmented region, G as the set of points in the golden standard, and Area(G) as the area of G, the three error metrics are
| (27) |
| (28) |
and
| (29) |
The higher the TP ratio, the more the true tumor regions are covered by the segmented tumor regions. On the other hand, the lower the FP ratio, the fewer the normal tissue regions are covered by the segmented tumor regions. SI is a very intuitive metric that ranges from 0 to 1. The higher the value of SI, the better the overall performance of the segmentation will be. SI equal to 1 suggests a good match between manual and semiautomatic segmentation.
Experiment results
The experiments results of 100 breast US images are listed in Tables 3, TABLE IV..
TABLE III.
Distance error metrics of three different image segmentation methods.
| Average HD (pixels) | Average AD (pixels) | |
|---|---|---|
| Benign | ||
| Interactive-NCut | Mean = 15.86 | Mean = 4.55 |
| Std = 8.57 | Std = 3.47 | |
| PBLS | Mean = 8.27 | Mean = 2.21 |
| Std = 3.26 | Std = 1.23 | |
| HP-NCut | Mean = 7.10 | Mean = 1.58 |
| Std = 3.20 | Std = 0.72 | |
| Malignant | ||
| Interactive-NCut | Mean = 22.34 | Mean = 7.03 |
| Std = 11.08 | Std = 4.64 | |
| PBLS | Mean = 12.81 | Mean = 3.16 |
| Std = 4.75 | Std = 1.81 | |
| HP-NCut | Mean = 10.57 | Mean = 1.98 |
| Std = 3.96 | Std = 0.59 | |
TABLE IV.
Overlapping area error metric of three different image segmentation methods.
| TP ratio (%) | FP ratio (%) | SI (%) | |
|---|---|---|---|
| Benign | |||
| Interactive-Ncut | Mean = 96.98 | Mean = 40.95 | Mean = 72.81 |
| Std = 4.14 | Std = 41.29 | Std = 14.56 | |
| PBLS | Mean = 92.61 | Mean = 11.74 | Mean = 83.48 |
| Std = 5.62 | Std = 12.05 | Std = 7.41 | |
| HP-NCut | Mean = 92.90 | Mean = 7.32 | Mean = 86.67 |
| Std = 3.92 | Std = 4.17 | Std = 4.73 | |
| Malignant | |||
| Interactive-Ncut | Mean = 97.07 | Mean = 65.01 | Mean = 64.81 |
| Std = 6.37 | Std = 62.36 | Std = 17.74 | |
| PBLS | Mean = 91.35 | Mean = 18.00 | Mean = 78.73 |
| Std = 7.22 | Std = 20.21 | Std = 9.90 | |
| HP-NCut | Mean = 90.91 | Mean = 7.99 | Mean = 84.41 |
| Std = 4.45 | Std = 5.73 | Std = 5.91 | |
For both benign tumors and malignant tumors, HP-NCut gives the best accuracy among the three methods tested (Table TABLE III.). HP-NCut has the smallest average mean error and the smallest average stand deviation in terms of HD and AD. Concretely, compared with Interactive-NCut and PBLS, for benign tumors, HP-NCut improved average HD from 15.86 and 8.27 to 7.10, respectively. In addition, the average AD is improved from 4.55 (Interactive-NCut) and 2.21 (PBLS) to 1.58. For malignant tumors, the average HD is improved from 22.34 (Interactive-NCut) and 12.81 (PBLS) to 10.57, and average AD from 7.03 (Interactive-NCut) and 3.16 (PBLS) to 1.98. Evidently, the tabulated results reveal better correlation between the results of the HP-NCut algorithm and manual segmentations.
For both benign tumors and malignant tumors, the TP ratios of the above methods are higher than 90% (Table TABLE IV.), which means that most of the tumor regions can be segmented by the above methods. The TP ratio of HP-NCut (92.90% for benign cases and 90.91% for malignant cases) is less than that of Interactive-NCut (96.98% for benign cases and 97.07% for malignant cases) because there are many blurry regions near the boundaries in most cases. Finding the true boundaries in these blurry regions is very difficult, so the manual segmentation results include some blurry regions. However, with the HP, the HP-NCut algorithm can deal with blurry regions well and locate true boundaries accurately. Hence, some regions generated by the manual segmentation are not in the tumor regions segmented by the HP-NCut algorithm, leading to slightly lower TP ratios. Using Interactive-NCut, many normal issues are misclassified as the tumors, including some blurry regions. The TP ratios are higher, as well. However, its segmentation results remain undesirable, as illustrated by the higher FP ratios.
Using Interactive-NCut, the FP ratio is very high (40.95% for benign cases and 65.01% for malignant cases), as shown in Figs. 8910. Despite the fact that this method nearly covers the whole tumor region, it simultaneously contains many nontumor regions, which has an adverse effect on the feature-extraction process for the CAD system. PBLS does not deal with all the blurry boundaries and some normal regions are included, so a relatively lower FP ratio (11.74% for benign cases and 18.00% for malignant cases) is obtained. Using HP-NCut, the lowest FP ratio (7.32% for benign cases and 7.99% for malignant cases) is achieved. In other words, few normal tissue regions are covered by the segmented tumor regions, and more accurate segmentation results are achieved.
HP-NCut achieves the highest similarity (86.67% for benign cases and 84.41% for malignant cases). It is higher than Interactive-NCut (72.81% for benign cases and 64.81% for malignant cases) and PBLS (83.48% for benign cases and 78.73% for malignant cases), which supports the effectiveness of HP. Remarkably, HP-NCut obtains the best performance among the three methods.
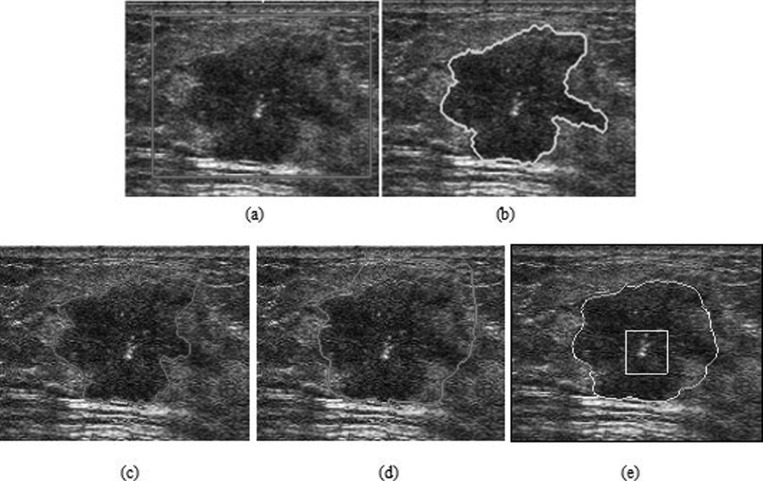
Tables 3, TABLE IV. reveal that the segmentation results of HP-NCut are satisfactory. However, there are still some cases that cannot be dealt with well by HP-NCut. Figure 11 shows the worst segmentation result of the proposed method. In Fig. 11a, a malignant (IDC) tumor is depicted with a highly irregular shape, spiculation, ill-defined margins, microclacification, and heterogeneous internal echo pattern. This IDC is associated with posterior enhancement. The manual segmentation includes the overall tumor region. Part of the manual segmentation image covers blurry regions between the tumor and normal tissue region, as shown in Fig. 11b. HP-NCut cannot get the whole tumor region, as shown in Fig. 11c. However, the other two methods did not yield good segmentation results. Although the segmentations of Interactive-NCut and PBLS included more tumor regions, the compensation for them is a significant increase in the false positives, as illustrated in Figs. 11d, 11e. In this extreme case, the performance of HP-NCut (SI = 86.51%) is higher than that of Interactive-NCut (SI = 66.64%) and the PBLS method (SI = 80.10%). On the other hand, this example indicates that further research is required to improve the proposed HP-NCut algorithm.
Figure 11.
The worst segmentation result. (a) The original image with a rectangular ROI placed by the user. (b) Manual segmentation. The segmentation results using (c) HP-NCut, (d) Interactive-NCut, and (e) PBLS.
Influence of parameter choices
The radius r1 of the circular neighborhood described in Sec. 3B is a minor parameter for boundary detection. We performed an experiment to show the effect of parameter r1 on a breast US image [Fig. 2a]. Figure 12 shows the boundary maps using three different radius values r1 = {1%, 2%, 3%} of the image diagonal. The smallest radius size resulted in spurious edges, but preserved continuity of boundaries. The largest radius size lost the continuity of boundaries, but suppressed spurious edges. The intermediate radius size gave a good detection result. In all the experiments, we fixed r1 at 2% of the image diagonal.
Figure 12.
Examples of the boundary-detection function using three different radius values. From left to right r1 = {1%, 2%, 3%} of the image diagonal.
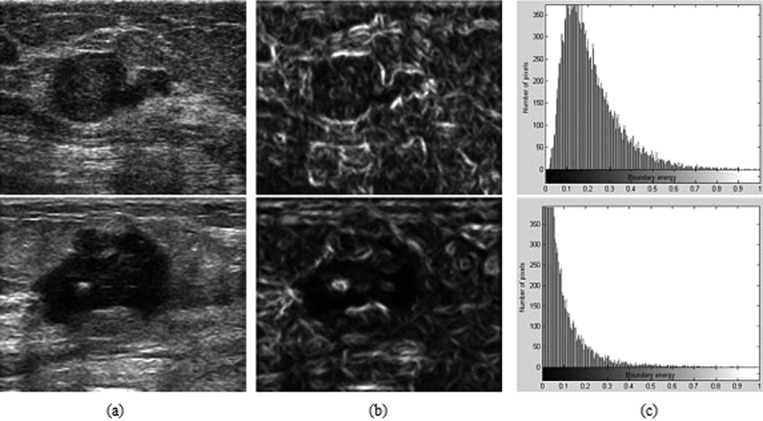
The fuzzy membership threshold τ (described in Sec. 3C) is a major parameter for constructing HPs. For most of the breast US images in the current dataset, the energy threshold was usually determined as about one minus the mean boundary energy over the entire image domain. For example, given two breast US images with malignant tumors [Fig. 13a], we first extracted the boundary maps using Eq. 7, as shown in Fig. 13b. Then, the corresponding histograms of the boundary maps were constructed, where horizontal axes gave boundary energies and vertical axes gave the number of pixels at boundary energy level [Fig. 13c]. The mean boundary energy was 0.24 in the first histogram, whereas the mean boundary energy was 0.1 in the second histogram. Thus, we set the energy thresholds as τ = 1 − 0.24 = 0.76 and τ = 1 − 0.1 = 0.9.
Figure 13.
(a) Original images. (b) The boundary maps. (c) The histograms of the boundary energies over the entire image domain.
Furthermore, we tested the effect of threshold τ for HP construction. We took the two images in Figs. 9a, 2a as examples. Figure 14 shows the results using three different values, i.e., τ = {0.86, 0.76, 0.66} for row 1 and τ = {0.95, 0.9, 0.8} for row 2. The areas enclosed by yellow contours represent HPs in the smooth regions, whereas those enclosed by blue contours are HPs in the nonsmooth regions. Red dots are the central pixels. We observed that the smaller the threshold, the larger the sizes of the HPs. Second, when the largest or the smallest threshold was adopted, the shapes of the HPs themselves did not adopt the local image contents and the homogeneities of the HPs were violated. When the intermediate threshold was adopted, the shape of the HPs changed in response to the geometry of the structure. Third, the largest threshold resulted in incorrect HP representations, which were too local for the task at hand. The smallest threshold resulted in incorrect representations, which were too global. This experiment demonstrated that the thresholds that were too large or too small might lead to incorrect results. In the present study, the thresholds that were set to one minus the mean boundary energy [e.g., τ = 0.76 for Fig. 9a and τ = 0.9 for Fig. 2a] were good candidates for HP determination.
Figure 14.
Influence of the energy threshold τ for HP construction. The areas enclosed by light color (yellow in online version) contours represent HPs in the smooth regions, whereas those enclosed by dark color (blue in online version) contours are HPs in the nonsmooth regions. Gray (red in online version) dots are the central pixels. From left to right threshold τ = {0.86, 0.76, 0.66} for row 1 and τ = {0.95, 0.9, 0.8} for row 2. The original images can be seen in Fig. 9a in row 1 and Fig. 2a in row 2.
Robustness analysis
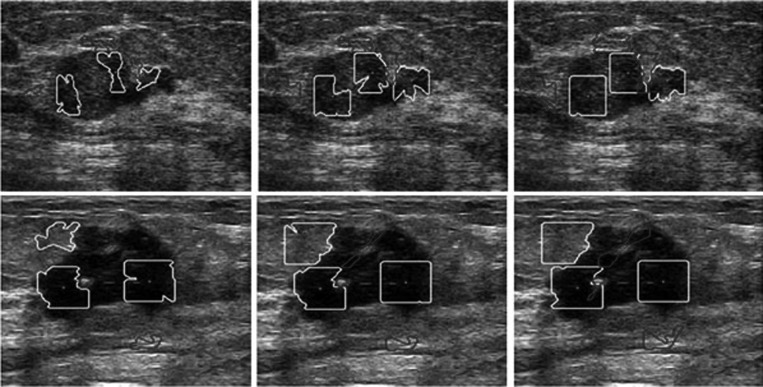
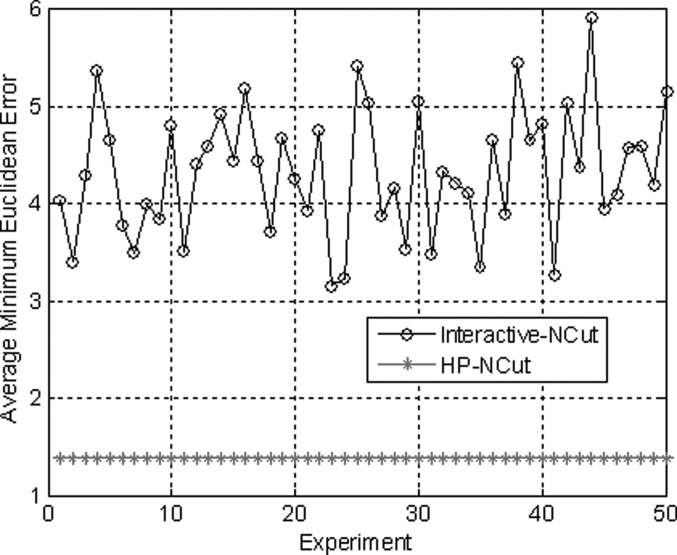
HP-NCut and Interactive-NCut used the same sampling strategy to speed up the segmentation process. An important factor in the two methods that may affect the segmentation results was the sampling points. We fixed all the parameters including the sample size to examine the robustness of the two methods with respect to random samples. The sampling rate can be very low (e.g., 1% of all pixels in an image or even less).44 We obtained the sample size by setting the number of samples to 1.5% of the number of image pixels. Then, we repeatedly conducted 50 random experiments on the same image. By varying the random samples and comparing the results with manual segmentation, we can get the AMEDs for the two methods (Fig. 15). Out of 50 experiments visually inspected, only ten segmentation results from both Interactive-NCut and the proposed HP-NCut algorithm are displayed in Figs. 1617, respectively. Interactive-NCut was observed to be sensitive to the random samples, whereas the proposed algorithm is not. This finding could be explained as follows. First, although the sampling strategy applied to our algorithm was the same as that applied to Interactive-NCut, they have quite different constructions in weight matrix. The construction of the weight matrix in Interactive-NCut is dependent on the image pixels. A pixel contains limited image information and suffers from poor quality of the breast US image, and the sampled image pixels could barely reflect the original image well. However, instead of using image pixels, the construction of the weight matrix in the proposed algorithm depended on the HPs. Local pattern was introduced into the HPs before sampling. Each HP was constructed by the pixels with similar properties inside a large neighborhood, thus including more reliable image information than a single pixel and can effectively reflect breast US image. Second, by binning the neighboring pixels within the HP to the textons, the problem arising from small speckle noise and intensity inhomogeneity was avoided. Even if some pixels are mapped to the wrong textons, it does not greatly influence the texton histograms. Hence, feature difference between HPs is larger and more robust than between the pixels after the sampling process. These overcome the problem on sensitivity. In addition, identical segmentation results were produced every time. The proposed HP-NCut algorithm guarantees good stability and reproducibility with respect to the random samples. From these results, the proposed algorithm is deemed suitable for ultrasonic tumor segmentation problems.
Figure 15.
The average minimum Euclidean error in the two methods after repeating 50 experiments with different sampling points selected randomly.
Figure 16.
Ten segmentation results (a)–(j) on a breast US image using Interactive-NCut with different sampling points selected randomly.
Figure 17.
Ten segmentation results (a)–(j) on a breast US image using HP-NCut with different sampling points selected randomly.
Runtimes
The run-times of the three methods, i.e., Interactive-NCut, PBLS and the proposed HP-NCut, are listed in Table TABLE V.. All the methods were performed on a computer with the following configuration: Intel Core 2 CPU 7200 at 2 GHz, 0.99 GB of RAM.
TABLE V.
Average run-time of three different image segmentation methods.
| Interactive-NCut (s) | PBLS (s) | HP-NCut (s) |
|---|---|---|
| 57.35 | 77.34 | 191.75 |
Comparing to Interactive-NCut and PBLS, the proposed HP-NCut algorithm required more time consuming due to the HPs computation and texture extraction. However, our HP-NCut algorithm can achieve tumor segmentation more accurately and efficiently. Moreover, the HP-NCut algorithm is more robust than the Interactive-NCut.
CONCLUSIONS
We have developed a novel algorithm for segmenting breast tumors in US images. Many of these tumors have textures and/or intensities similar to the surrounding structures in the ultrasonic images, such as glandular tissue, subcutaneous fat, and so on. In the boundary-detection phase, a boundary-detection function is designed by combining texture information and intensity information. By describing the similar relationships between neighboring pixels in a local neighborhood, the HP-NCut algorithm defines a HP for each pixel using the boundary map from the boundary-detection function. Based on the HPs, a novel feature-extraction scheme is proposed. Using the HPs is equivalent to using both the edge information and region statistical information. The proposed HP-NCut algorithm yields better results in cases where shadowing artifacts are encountered.
The proposed algorithm has been evaluated using a large number of breast US images. The results show that the proposed method achieves more accurate segmentation results compared with Interactive-NCut and PBLS. Nevertheless, the proposed HP-NCut algorithm cannot deal well with the cases where the tumors have highly irregular contours (e.g., deep lobulation or spiculation) or very blurry boundaries. Thus, further study on the proposed algorithm is recommended. Moreover, future work will consider optimizing our codes to speed up the algorithm. As some parts of our algorithm, e.g., the HPs computation, can be decomposed into a parallel framework and achieved by using GPU, we hope the parallel processing technique will render our algorithm more appropriate for real-time application.
ACKNOWLEDGMENTS
This research was supported by the grants from the National Basic Research Program of China (973 Program) (Grant No. 2010CB732501) and National Natural Science Funds of China (Grant Nos. 30900380, 30730036, and 60873102). The authors would like to thank the anonymous reviewers for their valuable comments.
References
- Zheng Y., Greenleaf J. F., and Gisvold J. J., “Reduction of breast biopsies with a modified self-organizing map,” IEEE Trans. Neural Netw. 8, 1386–1396 (1997). 10.1109/72.641462 [DOI] [PubMed] [Google Scholar]
- Noble J. A. and Boukerroui D., “Ultrasound image segmentation: A survey,” IEEE Trans. Med. Imaging 25, 987–1010 (2006). 10.1109/TMI.2006.877092 [DOI] [PubMed] [Google Scholar]
- Madabhushi A. and Metaxas D. N., “Combining low-, high-level and empirical domain knowledge for automated segmentation of ultrasonic breast lesions,” IEEE Trans. Med. Imaging 22, 155–169 (2003). 10.1109/TMI.2002.808364 [DOI] [PubMed] [Google Scholar]
- Liu B., Cheng H. D., Huang J. H., Tian J. W., Tang X. L, and Liu J. F., “Fully automatic and segmentation-robust classification of breast tumors based on local texture analysis of ultrasound images,” Pattern Recogn. 43, 280–298 (2010). 10.1016/j.patcog.2009.06.002 [DOI] [Google Scholar]
- Xiao G. F., Brady M., Noble J. A., and Zhang Y. Y., “Segmentation of ultrasound B-mode images with intensity inhomogeneity correction,” IEEE Trans. Med. Imaging 21, 48–57 (2002). 10.1109/42.981233 [DOI] [PubMed] [Google Scholar]
- Boukerroui D., Baskurt A., Noble J. A., and Basset O., “Segmentation of ultrasound images-multiresolution 2D and 3D algorithm based on global and local statistics,” Pattern Recogn. Lett. 24, 779–790 (2003). 10.1016/S0167-8655(02)00181-2 [DOI] [Google Scholar]
- Cheng H. D., Hu L., Tian J., and Sun L., “A novel Markov random field segmentation algorithm and its application to breast ultrasound image analysis,” in Proceedings of International conference on Computer Vision, Pattern Recognition and Image Processing (Salt Lake City, 2005).
- Sarti A., Corsi C., Mazzini E., and Lamberti C., “Maximum likelihood segmentation of ultrasound images with Rayleigh distribution,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 52, 947–960 (2005). 10.1109/TUFFC.2005.1504017 [DOI] [PubMed] [Google Scholar]
- Liu B., Cheng H. D., Huang J. H., Tian J. W., Tang X. L, and Liu J. F., “Probability density difference-based active contour for ultrasound image segmentation,” Pattern Recogn. 43, 2028–2042 (2010). 10.1016/j.patcog.2010.01.002 [DOI] [Google Scholar]
- Chang R. F., Wu W. J., Tseng C. C., Chen D. R., and Moon W. K., “3-D snake for US in margin evaluation for malignant breast tumor excision using mammotome,” IEEE Trans. Inf. Tech. Biomed. 7, 197–201 (2003). 10.1109/TITB.2003.816560 [DOI] [PubMed] [Google Scholar]
- Chang R. F., Wu W. J., Moon W. K., Chen W. M., Lee W., and Chen D. R., “Segmentation of breast tumor in three-dimensional ultrasound images using three-dimensional discrete active contour model,” Ultrasound Med. Biol. 29, 1571–1581 (2003). 10.1016/S0301-5629(03)00992-X [DOI] [PubMed] [Google Scholar]
- Alemán-Flores M., Álvarez L., and Caselles V., “Texture-oriented anisotropic filtering and geodesic active contours in breast tumor ultrasound segmentation,” J. Math. Imaging Vision 28, 81–97 (2007). 10.1007/s10851-007-0015-8 [DOI] [Google Scholar]
- Liu B., Cheng H. D., Huang J. H., Tian J. W., Liu J. F., and Tang X. L., “Automated segmentation of ultrasonic breast lesions using statistical texture classification and active contour based on probability distance,” Ultrasound Med. Biol. 35, 1309–1324 (2009). 10.1016/j.ultrasmedbio.2008.12.007 [DOI] [PubMed] [Google Scholar]
- Belaid A., Boukerroui D., Maingourd Y., and Lerallut J. F., “Phase-based level set Segmentation of Ultrasound Images,” IEEE Trans. Inf. Technol. Biomed. 15, 138–147 (2011). 10.1109/TITB.2010.2090889 [DOI] [PubMed] [Google Scholar]
- Gao L., Liu X. Y., and Chen W. F, “Phase- and GVF-based level set segmentation of ultrasonic breast tumors,” J. Appl. Math. 2012, 22 p. (2012). 10.1155/2012/810805 [DOI] [Google Scholar]
- Horsch K., Giger M. L., Venta L. A., and Vyborny C. J., “Automatic segmentation of breast lesions on ultrasound,” Med. Phys. 28, 1652–1659 (2001). 10.1118/1.1386426 [DOI] [PubMed] [Google Scholar]
- Horsch K., Giger M. L., Venta L. A., and Vyborny C. J., “Computerized diagnosis of breast lesions on ultrasound,” Med. Phys. 29, 157–164 (2002). 10.1118/1.1429239 [DOI] [PubMed] [Google Scholar]
- Liu X., Huo Z. M., and Zhang J. W., “Automated segmentation of breast lesions in ultrasound images,” in Proceedings of IEEE Annual International Conference on Engineering in Medical Biology (IEEE Comput. Soc., Shanghai, China, 2005), pp. 7433–7435. [DOI] [PubMed]
- Zhu C. M., Gu G. C., Liu H. B., Shen J., and Yu H. L., “Segmentation of ultrasound image based on texture feature and graph cut,” in Proceedings of International Conference on Computer Science Software Engineering (IEEE Comput. Soc., Hubei, China, 2008), pp. 795–798.
- Chen S. Y., Chang H. H., Hung S. H., and Chu W. C., “Breast tumor identification in ultrasound images using the normalized cuts with partial grouping constraints,” in Proceedings of IEEE International Conference on Biomedical Engineering and Informatics (IEEE Comput. Soc., Sanya, China, 2008), pp. 28–32.
- Huang Q. H., Lee S. Y., Liu L. Z., Lu M. H., Jin L. W., and Li A. H., “A robust graph-based segmentation method for breast tumors in ultrasound images,” Ultrasonics 52, 266–275 (2012). 10.1016/j.ultras.2011.08.011 [DOI] [PubMed] [Google Scholar]
- Shen D. G., Zhan Y. Q., and Davatzikos C., “Segmentation of prostate boundaries from ultrasound images using statistical shape model,” IEEE Trans. Med. Imaging 22, 539–551 (2003). 10.1109/TMI.2003.809057 [DOI] [PubMed] [Google Scholar]
- Zhan Y. Q. and Shen D. G., “Deformable segmentation of 3-D ultrasound prostate images using statistical texture matching method,” IEEE Trans. Med. Imaging 25, 256–272 (2006). 10.1109/TMI.2005.862744 [DOI] [PubMed] [Google Scholar]
- Burckhardt C. B., “Speckle in ultrasound B-mode scans,” IEEE Trans. Sonics Ultrason. 25, 1–6 (1978). 10.1109/T-SU.1978.30978 [DOI] [Google Scholar]
- Leucht W. and Leucht D., Teaching Atlas of Breast Ultrasound, 2nd ed. (Thieme Medical, Inc., New York, 2000). [Google Scholar]
- Shi J. B. and Malik J., “Normalized cuts and image segmentation,” in Proceedings of IEEE Conference on Computer Vision Pattern Recognition (IEEE Comput. Soc., San Juan, Puerto Rico, 1997), pp. 731–737.
- Shi J. B. and Malik J., “Normalized cuts and image segmentation,” IEEE Trans. Pattern Anal. Mach. Intell. 22, 888–905 (2000). 10.1109/34.868688 [DOI] [Google Scholar]
- Malik J., Belongie S., Leung T., and Shi J., “Contour and texture analysis for image segmentation,” Int. J. Comput. Vis. 43, 7–27 (2001). 10.1023/A:1011174803800 [DOI] [Google Scholar]
- Yu X. and Shi J. B., “Segmentation given partial grouping constraints,” IEEE Trans. Pattern Anal. Mach. Intell. 26, 173–183 (2004). 10.1109/TPAMI.2004.1262179 [DOI] [PubMed] [Google Scholar]
- Wu X., Ngo C. W., and Hauptmann A. G., “Multimodal news story clustering with pairwise visual near-duplicate constraint,” IEEE Trans. Multimedia 10, 188–199 (2008). 10.1109/TMM.2007.911778 [DOI] [Google Scholar]
- Bria K., Sugato B., Inderjit D., and Raymond M., “Semi-supervised graph clustering: A kernel approach,” Mach. Learn. 74, 1–22 (2009). 10.1007/s10994-008-5084-4 [DOI] [Google Scholar]
- Carballido-Gamio J., Belongie S. J., and Majumdar S., “Normalized cuts in 3-D for spinal MRI segmentation,” IEEE Trans. Med. Imaging 23, 36–44 (2004). 10.1109/TMI.2003.819929 [DOI] [PubMed] [Google Scholar]
- Pratt W. K., Digital Image Processing, 3rd ed. (John Wiley & Sons, Inc., New York, 1978). [Google Scholar]
- Canny J., “A computational approach to edge detection,” IEEE Trans. Pattern Anal. Mach. Intell. 8, 679–698 (1986). 10.1109/TPAMI.1986.4767851 [DOI] [PubMed] [Google Scholar]
- Martin D. R., Fowlkes C. C., and Malik J., “Learning to detect natural image boundaries using local brightness, color and texture cues,” IEEE Trans. Pattern Anal. Mach. Intell. 26, 530–549 (2004). 10.1109/TPAMI.2004.1273918 [DOI] [PubMed] [Google Scholar]
- Somkantha K., Theera-Umpon N., and Auephanwiriyakul S., “Boundary detection in medical images using edge following algorithm based on intensity gradient and texture gradient features,” IEEE Trans. Inf. Technol. Biomed. 58, 567–573 (2011). [DOI] [PubMed] [Google Scholar]
- Ren X. and Malik J., “Learning a classification model for segmentation,” in Proceedings of IEEE International Conference on Computer Vision (IEEE Comput. Soc., Nice, France, 2003), pp. 10–17.
- Levinshtein A., Stere A., Kutulakos K. N., Fleet D. J., Dickinson S. J., and Siddiqi K., “Turbopixels: Fast superpixels using geometric flows,” IEEE Trans. Pattern Anal. Mach. Intell. 31, 2290–2297 (2009). 10.1109/TPAMI.2009.96 [DOI] [PubMed] [Google Scholar]
- Xiang S. M., Pan C. H., Nie F. P., and Zhang C. S., “Turbopixel segmentation using eigen-images,” IEEE Trans. Image Process. 19, 3024–3034 (2010). 10.1109/TIP.2010.2052268 [DOI] [PubMed] [Google Scholar]
- http://www.eecs.berkeley.edu/Research/Projects/CS/vision/stellayu/code.html
- Huttenlocher D. P., Klanderman G. A., and Rucklidge W. J., “Comparing images using the Hausdorff distance,” IEEE Trans. Pattern Anal. Mach. Intell. 15, 850–863 (1993). 10.1109/34.232073 [DOI] [Google Scholar]
- Sahiner B., Petrick N., Chan H.-P., Hadjiiski L. M., Paramagul C., Helvie M. A., and Gurcan M. N., “Computer-aided characterization of mammographic masses: Accuracy of mass segmentation and its effects on characterization,” IEEE Trans. Med. Imaging 20, 1275–1284 (2001). 10.1109/42.974922 [DOI] [PubMed] [Google Scholar]
- Udupa J. K., LaBlanc V. R., Schmidt H., Imielinska C., Saha P. K., Grevera G. J., Zhuge Y., Molholt P., Jin Y. P., and Currie L. M., “A methodology for evaluating image segmentation algorithms,” Proc. SPIE 2, 266–277 (2002). 10.1117/12.467166 [DOI] [Google Scholar]
- Wang Q., Wu G. R., Yap P.-T., and Shen D. G., “Attribute vector guided groupwise registration,” Neuroimage 50, 1485–1496 (2010). 10.1016/j.neuroimage.2010.01.040 [DOI] [PMC free article] [PubMed] [Google Scholar]