Real-Time Brain Oscillation Detection and Phase-Locked Stimulation Using Autoregressive Spectral Estimation and Time-Series Forward Prediction

Abstract

Neural oscillations are important features in a working central nervous system, facilitating efficient communication across large networks of neurons. They are implicated in a diverse range of processes such as synchronization and synaptic plasticity, and can be seen in a variety of cognitive processes. For example, hippocampal theta oscillations are thought to be a crucial component of memory encoding and retrieval. To better study the role of these oscillations in various cognitive processes, and to be able to build clinical applications around them, accurate and precise estimations of the instantaneous frequency and phase are required. Here, we present methodology based on autoregressive modeling to accomplish this in real time. This allows the targeting of stimulation to a specific phase of a detected oscillation. We first assess performance of the algorithm on two signals where the exact phase and frequency are known. Then, using intracranial EEG recorded from two patients performing a Sternberg memory task, we characterize our algorithm’s phase-locking performance on physiologic theta oscillations: optimizing algorithm parameters on the first patient using a genetic algorithm, we carried out cross-validation procedures on subsequent trials and electrodes within the same patient, as well as on data recorded from the second patient.

I. INTRODUCTION

Neural oscillations are fundamental to the normal functioning of a working central nervous system. They can be observed in single neurons as rhythmic changes of either the subthreshold membrane potential or in cellular spiking behavior. Large populations of such neurons can give rise to synchronous activity, which may correspond to rhythmic oscillations in the local field potential (LFP). These oscillations can in turn modulate the excitability of other individual neurons. Therefore, a key function of these oscillations is to facilitate efficient communication across large neuronal networks, as the synchronous excitation of groups of neurons allow them to form functional networks [1]. Additionally, network oscillations bias input selection, temporally link neurons into assemblies, and facilitate synaptic plasticity, mechanisms that all support the long-term consolidation of information [2].

There are distinct oscillators in various brain regions that are governed by different physiological mechanisms. We are only beginning to uncover the various roles these oscillators play in different aspects of cognition. Numerous EEG, MEG, ECoG, and single unit recording studies have shown that oscillations at certain frequencies can be elicited or modulated by specific task demands, and that their amplitude or power have correlations to the outcome of those tasks [3], [4]. For example, prominent oscillations in the theta frequency range can be detected in the hippocampus and entorhinal cortex of rats during locomotion, orienting, conditioning, or while they are performing learning or memory tasks [5], as well as in humans performing various memory and spatial navigation tasks [6], [7], [8], [9], [10], [11], [12], [13], [14]. Because of the role of hippocampal theta oscillations in modulating long-term potentiation (LTP), they are thought to be an important component of memory encoding [15], [16], [17], [18], [19], [20]. Synchronization and coherence of theta oscillations between the hippocampus and other brain regions such as the prefrontal cortex have also been shown to be an important factor in successful learning and memory [21], [22], [23], [24].

The phase of these neural oscillations can possibly be used to store and carry information [25], [2], as well as to modulate physiological activity such as LTP. For example, stimulation applied to the perforant pathway at the peak of hippocampal theta rhythms induced LTP while stimulation applied at the trough induced long-term depression [17]. Theta also serves to temporally organize the firing activity of single neurons involved in memory encoding [26], [27], such that the degree to which single spikes are phase-locked to the theta-frequency field oscillations is predictive of how well the corresponding memory item is transferred to long-term memory [14]. Such temporal patterns of neural activity are potentially important considerations in the design of future neural interface systems.

Phase relationships are typically characterized through post hoc analysis in most studies, as accurate measures of frequency and phase and their complex relationships with other phenomena require analysis in the time-frequency domain. Real-time systems that could potentially utilize oscillation phase information, for example brain-computer interfaces [28], or responsive closed-loop stimulator devices that combine neural ensemble decoding with simultaneous electrical stimulation feedback [29], [30], [31], would require precise and accurate measurements of the instantaneous phase. Phase-specific stimulation could also aid in experimental research on the temporal patterns of neural ensemble activity and their correlations with cognitive processes and behavior. A few studies have performed such phase-specific electrical stimulation on animals. Pavlides et al. [15] and Hölscher et al. [16] built analog circuits that triggered stimulation pulses at the peak, zero-crossing, and troughs of the hippocampal LFP signal. This approach assumes a sufficiently narrow bandwidth such that the peak, zero-crossing, and troughs of the input signal approximates these values of the actual underlying oscillation. Hyman et al. used a dual-window discrimination method for peak detection, whereby two windows of variable-time widths and heights were manually created to fit each individual animals typical theta frequency and amplitude, and the stimulator set to be delay-triggered if the input waveform successfully passed through both windows [17]. Because this approach requires manual calibration to a specific setting, real-time operation in the face of dynamic amplitude or frequency changes would not be possible. These systems would not be sufficient for neural interfaces operating in real time or experiments requiring higher-resolution phase detection. As such, an alternative approach is needed.

Here, we present methods to accurately estimate the instantaneous frequency and phase of an intracranial EEG oscillation signal in real time. At the core of our methodology is an autoregressive model of the EEG signal, which we use to both optimize the bandwidth of the narrow-band signal using estimations of the power spectral density, as well as to perform time-series forward-predictions. These two steps in conjunction allows us to make precise and accurate estimates of the instantaneous frequency and phase of an oscillation, which we then use to target output stimulation pulses to a specific phase of the oscillation.

II. METHODS

A. Algorithm Overview

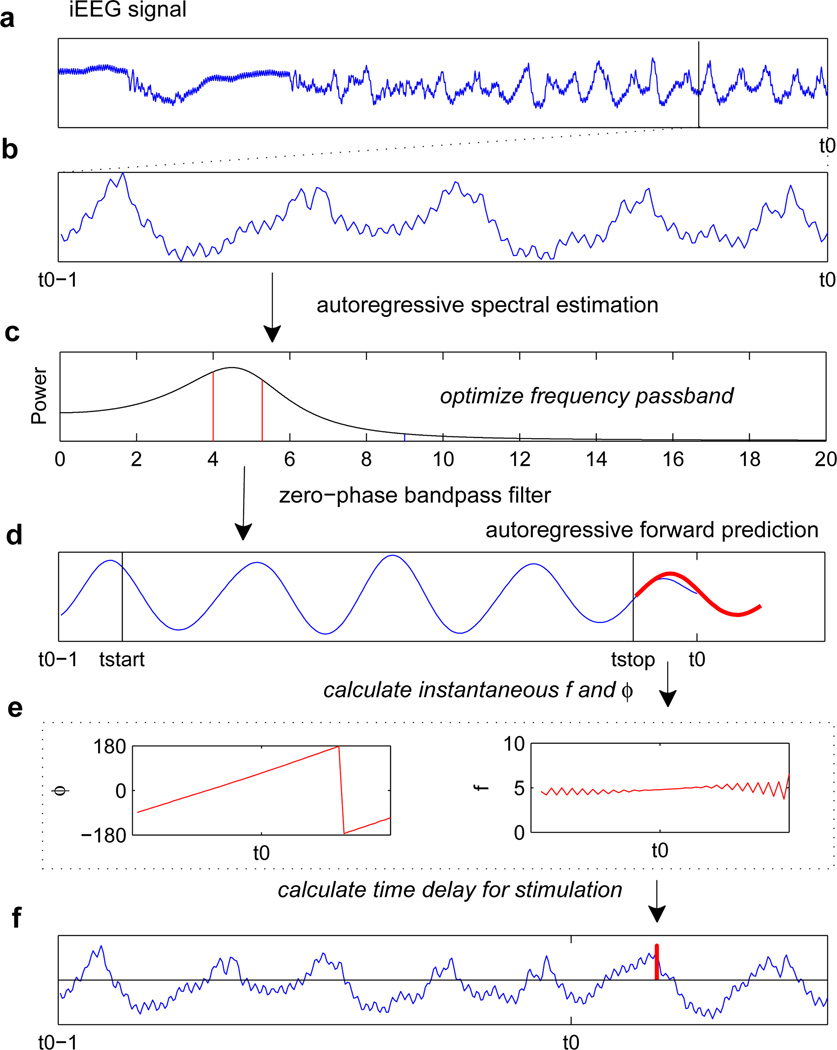
The ultimate goal of our algorithm is to be able to calculate the instantaneous frequency and phase of a neurophysiological signal at a specific point in time with the necessary accuracy and precision to be able to deliver phase-locked stimulation pulses in real time. The algorithm is comprised of several sequential steps: 1. Frequency band optimization within a predefined frequency band (for theta, we use 4–9 Hz), utilizing autoregressive spectral estimation, 2. Zero-phase bandpass filtering, based on the results of the frequency band optimization procedure, 3. Estimating the future signal by autoregressive time-series prediction, 4. Calculating the instantaneous frequency and phase via the Hilbert-transform analytic signal, and 5. Calculating the time lag until the desired phase for the output stimulation pulse. A graphical representation of these steps is depicted in Fig. 1. It must be noted, however, that there are several parameters used by the algorithm that are optimized offline prior to its online operation. The procedure for the offline optimization of these parameters using a genetic algorithm is discussed in section 2I.

Fig. 1.

Overview of algorithm. (a) Raw iEEG signal, where t₀ represents the current time in a real-time acquisition process. (b) Analyze the last 1-second segment of iEEG signal. (c) Use autoregressive spectral estimation to calculate the power spectral density in the 1-second segment. The frequency band optimization procedure is carried out. (d) The 1-second segment is bandpass filtered in both the forward and backward directions, based on the optimized passband. (e) Using the bandpass-filtered signal from t_start to t_stop, time-series forward predictions (shown in red) are made using the autoregressive model. (f) The instantaneous phase and frequency of this forward-predicted segment are calculated. (g) Using the instantaneous phase and frequency of the forward-predicted segment at t₀, a time delay from t₀ is calculated. Output stimulation is triggered after this time delay (shown in red). Overlaid is the raw iEEG signal from (b) plus some additional time.

B. Autoregressive Model

Autoregressive (AR) modeling has been successfully applied to EEG signal analysis for diverse applications such as data compression, segmentation, classification, sharp transient detection, and rejection or canceling of artifacts [32], [33]. Although the processes underlying EEG signals may be nonlinear, traditional linear AR modeling has been shown to be as good as, or even slightly better than, non-linear models in at least one study [34], in terms of the correlation coefficient between forecasted and real time series. It was found that processes with spectra limited to certain frequencies plus white noise can be well described by an AR model, while processes with power spectra characterized by multiple very narrow peaks are described poorly by an AR model. Therefore, for brain oscillation detection, AR modeling is a natural choice. Furthermore, parameters can be updated in an adaptive manner using the Kalman filtering algorithm or chosen to give the best fit to a segment of data samples, using either the Levinson-Durbin algorithm or the Burg algorithm [33]. Particularly with strong, coherent oscillations, small segments of the EEG are presumed to be locally-stationary, and thus a non-adaptive model is suitable. Autoregressive modeling provides a robust method of estimating the power spectrum for short (1–2 s) EEG segments, and is less susceptible to spurious results [33].

An autoregressive model AR(p) of order p is a random process defined as:

$$X_t=c+{\displaystyle \sum _{k=1}^p}{\alpha }_k{X}_{t-k}+{\epsilon }_t,$$ (1)

where α₁, …, α_p are the parameters of the model, c is a constant, and ε_t is white noise. If a is the vector of model parameters, for a given time-series sequence x(t) and model output x̂(t, a), the forward prediction error is given by:

$$e(t,\mathbf{a})=x(t)-\mathrm{x̂}(t,\mathbf{a}),$$ (2)

where a is found by minimizing the mean squared error

$$E(\mathbf{a})=\frac{1}{N}{\displaystyle \sum _{t=1}^N}{e}^2(t,\mathbf{a}),$$ (3)

where N is the segment length of x(t). The autoregressive model can be constructed using one of several algorithms to calculate model coefficients. They include the least-squares approach, which minimizes the prediction error in the least squares sense (either forward prediction error or both forward and backward prediction errors), the Burg lattice method, which solves the lattice filter equations using the mean (either harmonic or geometric) of forward and backward squared prediction errors, and the Yule-Walker method, which solves the Yule-Walker equations formed from sample covariances, minimizing the forward prediction error. The Burg and Yule-Walker methods always produce stable models, but because we are only interested in forward prediction, we use the Yule-Walker method here.

One issue that is of critical importance in the successful application of AR modeling is the selection of the model order [33], [32], [35], [36], [37], [38]. There have been many criteria formulated over the years for determining the optimal model order. The most well-known of these is Akaike’s Information Criterion (AIC) [39]. Other criteria that have been developed, such as the Bayesian Information Criterion, Final Prediction Error, Minimal Description Length differ essentially in the degree of the penalty applied to higher orders [40]. These are useful guides that can serve as useful starting points, but because estimated optimal order varies by the criterion, the sampling rate, and the characteristics of the input data, order selection ultimately depends upon the resulting performance of the system [36], [37]. Thus, it is empirically determined.

C. Frequency Band Optimization

An AR model can also be formulated in the frequency domain as a spectral matching problem. For EEG applications, AR spectral estimation has been demonstrated to be superior to traditional nonparametric methods such as the periodogram–due to the clear, higher-resolution spectra that it generates [41], [33]. The estimated AR spectrum of a data sequence is a continuous function of frequency and can be evaluated at any given frequency. This is why AR spectral estimation is much more powerful in discriminating narrow-band peaks, such as those produced by brain oscillations. Here, the AR model order becomes important in that a low model order will give an overly smoothed spectrum while an overly high order will result in spurious peaks. Two poles are needed to resolve each sinusoidal peak, and thus 2 is the minimum model order required [33]. Depending on the spectral band of interest, much higher orders may be necessary, as greater power is concentrated in the lower frequencies. The power spectrum is estimated by the following equation [42]:

$$S_{\text{AR}}(f)=\frac{{\sigma }^2}{{\left|1+{\displaystyle {\sum }_{k=1}^p}{\alpha }_k{e}^{-j^{2\pi \mathit{\text{fk}}}}\right|}^2},$$ (4)

where σ² is the noise variance and α_k are AR the model coefficients. The coefficients α_k are the same as the time-domain parameters in Equation 1.

To isolate a particular brain oscillation and accurately determine its instantaneous phase, we must perform bandpass filtering around its central frequency. Instantaneous phase only becomes accurate and meaningful if the filter bandwidth is sufficiently narrow [43]. Using predetermined cutoff frequencies may lead to either an insufficiently narrow band, where noise and extraneous signals will interfere with the brain oscillation signal, or an overly narrow band, in which frequency components of the brain oscillation are lost due to crossing over the range of the passband. Therefore, we developed an adaptive method that optimizes the cutoff frequencies using the AR power spectrum estimate, where the power contained in the optimized band does not fall below a specified threshold level. First, for the raw EEG signal, we calculate the total power contained in a particular frequency band of interest:

$$P(f_L,f_H)={\displaystyle {\int }_{f_L}^{f_H}}{S}_{\text{AR}}(f)\mathit{\text{ df}}.$$ (5)

We then iteratively increase f_L or decrease f_H by a specified step-size δ_f until

$$P({\mathrm{f̂}}_L,{\mathrm{f̂}}_H)\le \lambda P(f_L,f_H),$$ (6)

where f̂_L and f̂_H are the optimized passband cutoff frequencies, and λ is a fractional multiplier. For every iteration:

$$({\mathrm{f̂}}_L,{\mathrm{f̂}}_H)=\{\begin{array}{cc}\hfill (f_L+{\delta }_f,f_H)\hfill & \hfill \text{ if }{S}_{\text{AR}}(f_L)<S_{\text{AR}}(f_H)\hfill \\ (f_L,f_H-{\delta }_f)\hfill & \text{ if }{S}_{\text{AR}}(f_L)\ge S_{\text{AR}}(f_H)\hfill \end{array}.$$ (7)

The selection of a value for λ defines the tradeoff between an insufficiently narrow band (λ close to 1) and an overly narrow band (λ close to 0). Here, we set λ to be greater than 0.5, with the justification that we are ensuring the majority of the power contained within the frequency band of interest is contained within the bounds of f̂_L and f̂_H. It is important to note that the optimal value of λ may be context-dependent. We are using the assumption that for a particular brain oscillation, there is a certain characteristic frequency, and some amount of variance about that central frequency, rather than the assumption that the oscillation is comprised of many component frequencies. Using this relative measure λ, we are able to ensure that the filter passband is locally optimized within each time segment. A bandpass filter with cutoff bands f̂_L and f̂_H is then applied to the original EEG segment. To prevent phase distortion, we use a zero-phase digital filter that processes input signals in both the forward and reverse directions.

D. Time-Series Forward Prediction

Once we have filtered a signal through the optimized bandpass filter, we can calculate the instantaneous frequency and phase. However, when operating in real time, the relevant f(t) and ϕ(t) are its values at the current time, which we will define as t₀. Using a zero-phase filter, distortions will occur near t₀ as only the signal in the reverse direction is available. To make more accurate estimates of f(t₀) and ϕ(t₀), we make use of an autoregressive model. The autoregressive model as formulated in equation 1 provides a basis for linear forward prediction. For a given EEG segment, we use the bandpass filtered signal from X_tstart to X_tstop to predict a signal of length 2(t₀−t_stop) from t_stop (see Fig. 1). Therefore, the midpoint of this predicted signal corresponds to t₀. We predict a signal of length 2(t₀ − t_stop) to ensure a smooth and continuous instantaneous phase function at t₀, so that the calculation of the instantaneous frequency and phase at t₀ will not be affected by the edge effects of the Hilbert transform. The Hilbert transform will be used to calculate the instantaneous phase and frequency (see section 2E). An example of its edge effect can be seen in the ripples in Fig. 1e.

Because filter distortions occur at both ends of the signal segment, we set the length from t_start to t_stop symmetric about the signal segment midpoint, such that t_start = (t₀−T)+(t₀−t_stop), where T is the length of the original signal segment (here, T is 1 second). If the length between t_start and t_stop is set too small, then the amount of data used as the basis for the AR model will be insufficient, whereas if t_stop is set too close to t₀, then too much distortion will remain present in the predicted signal. In our genetic algorithm for optimizing the algorithm parameters offline (see section 2I), we have set the bounds of t₀ − t_stop to be between 0.05 and 0.45 seconds. In other words, the fraction of the signal segment used as input to the autoregressive model can range from the middle 0.1 to 0.9 seconds. An additional point of consideration is that both the filter type and filter order will influence the amount of distortion in the filtered signal, and thus it will be necessary to optimize the filter in relation to both t₀−t_stop and the input data.

E. Instantaneous Phase and Frequency

The instantaneous phase is calculated by first constructing the analytic signal, a combination of the original data and its Hilbert transform [44]. For the real signal x(_t), the complex analytic signal z_x(t) can be formulated as:

$$z_x(t)=x(t)+\mathit{\text{jH}}\{x(t)\},$$ (8)

where H{x(t)} is the Hilbert transform of x(t), and is defined as:

$$H\{x(t)\}=\frac{1}{\pi }\mathrm{p}.\mathrm{v}.{\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}}\frac{x(\tau )}{t-\tau }d\tau ,$$ (9)

where p.v. denotes Cauchy’s principal value.

The instantaneous phase of x(t) can be calculated from the complex analytic signal z_x(t) as:

$${\varphi }_x(t)=\text{arg }{z}_x(t)=\{\begin{array}{cc}\text{arctan}\frac{H\{x(t)\}}{x(t)}\hfill & x(t)\ge 0\hfill \\ \text{arctan}\frac{H\{x(t)\}}{x(t)}+\pi \hfill & x(t)<0,H\{x(t)\}\ge 0.\hfill \\ \text{arctan}\frac{H\{x(t)\}}{x(t)}-\pi \hfill & x(t)<0,H\{x(t)\}<0\hfill \end{array}$$

The instantaneous frequency f_x(t) can then be calculated in terms of the instantaneous phase:

$$f_x(t)=\frac{1}{2\pi }\frac{d}{\mathit{\text{dt}}}{\varphi }_x^{\mathrm{\text{uw}}}(t),$$ (10)

where ${\varphi }_x^{\text{uw}}(t)$ is the unwrapped instantaneous phase. Because the domain of ϕ_x(t) is (−π, π], discontinuities are present in the form of 2πn jumps, where n is an integer. The unwrapping procedure chooses the appropriate n at each discontinuity such that ϕ_x(t) becomes continuous.

In our algorithm, the two steps that are based on autoregressive modeling, frequency band optimization and time-series forward prediction, are strategies to attempt to maximize the accuracy of instantaneous phase and frequency estimations.

F. Implementation

Our algorithm was implemented in the LabView 9.0 environment (National Instruments, Austin, TX) as well as in MATLAB 7.11 (MathWorks, Natick, MA). The LabView implementation is used for real-time operation and the MATLAB implementation is used for offline analysis. The analyses carried out in this paper were performed in MATLAB with simulated input data.

The maximum signal segment analysis rate (which translates to the maximum stimulation rate) for the determination of stimulation timing should be greater than the frequency of the oscillation of interest. However, if this frequency is set too high, then spurious outputs will be generated. For theta oscillations, we have set this frequency to be 10 Hz, corresponding to a time window shift every 100 ms. For every period of this analysis cycle, f(t₀) and ϕ(t₀) are calculated, and the time delay until the output stimulation is delivered is calculated by the following formula:

$$t_{\text{delay}}=\frac{1}{f(t_0)}\frac{(\phi -\varphi (t_0)+2\pi )\text{ mod }2\pi }{2\pi },$$ (11)

where φ is the desired phase of the output stimulation (φ = 0 corresponds to the waveform peak, while φ = π corresponds to the trough). Note that 2π is added as the output of ϕ lies in the interval (−π, π].

G. Patients and Data

For the first part of our performance studies, we used signals where the exact phase and frequency are known–first, a simple 6 Hz cosine waveform and second, a 10-second intracranial EEG signal recorded from a single subdural contact electrode over the parahippocampal gyrus of a patient with temporal lobe epilepsy exhibiting epileptiform theta discharges.

For the second part of our performance studies, we assessed phase-locking accuracy on physiologic theta oscillations from two epilepsy patients performing a memory task, who had been surgically implanted with subdural electrodes. The clinical team determined the placement of these electrodes to best localize epileptogenic regions. All subjects had normal-range intelligence and were able to perform the task within normal limits. Our research protocol was approved by the institutional review board at the Brigham and Women’s Hospital. Informed consent was obtained from the subjects prior to the surgical implantation. Subject 1 had electrodes covering the frontal, parietal and subtemporal areas (73 channels). Subject 2 had electrodes covering the middle, inferior and subtemporal regions (38 channels). The experimental protocol was a version of the Sternberg task adapted from [10]. Four list items (consonant letters) were presented sequentially on the computer screen. Each item was presented for 1.2–2 seconds, with 0.2–1 second intervals between items. The termination of the last item in the list was followed by a 2–4 second delay and the presentation of a probe, a single consonant that may or may not have been in the list. The subject was instructed to press the ’y’ key on the keyboard if the probe item was in the list and ’n’ key if the item was not. After each response, the subject was given feedback on accuracy, and another trial could be initiated by key press. After this key press, a subsequent trial began in 1–2 seconds. TTL pulses marked the presentation of the four items and the probe item in the iEEG recordings. We obtained 40 trials from subject 1 and 11 trials from subject 2. Both the correct and incorrect trials were pooled for this analysis. Intracranial (iEEG) signals were recorded from grids and strips electrode arrays containing multiple platinum electrodes (3 mm diameter), with an inter-electrode spacing of 1 cm. The locations of the electrodes were determined by post-operative co-registered computed tomography (CT) scans. The signal was amplified, sampled at 500 Hz, and bandpass filtered between 0.1 and 70 Hz.

For the cosine waveform and the epileptiform theta discharges waveform, we optimized the algorithm parameters on the data and ran simulations with these parameters on the same data. For the Sternberg task patient datasets, we optimized the algorithm parameters on the first trial for subject 1 with the single electrode with the largest average theta power. We then used these parameters to perform simulation runs on all electrode channels in subject 1 for all subsequent trials (trials 2–40). Phase-locking performance was assessed at each electrode channel (1–73) collectively over trials 2– 40. These same parameters were then tested on subject 2 at each electrode channel (1–38) and assessed collectively over all trials (1–11).

H. Assessment of Phase-Locking Performance

We are interested in two measures of phase-locking accuracy. The first is the difference between the mean stimulation phase ϕ̄ and the desired phase φ. The second is the variance of stimulation phases. Perfect accuracy would be a value of 0 for both measures. We calculated the spread of ϕ several ways, including the circular variance:

$${\sigma }_{\text{circ}}^2=1-\Vert \frac{1}{N}{\displaystyle \sum _{i=1}^N}\left(\begin{array}{c}\text{cos }{\varphi }_i\hfill \\ \hfill \text{sin }{\varphi }_i\hfill \end{array}\right)\Vert ,$$ (12)

which ranges from 0 to 1 [45]. We also calculated the 95% confidence interval of the mean phase ϕ̄ and applied Rayleigh’s test for circular non-uniformity.

Not every channel may provide a suitable input signal, perhaps due to the properties of the underlying physiological processes. Therefore, we looked at phase-locking performance in the context of the electrode channel’s theta power level and theta temporal coherence. The temporal coherence τ_c is calculated by determining the length of time it takes for the amplitude of the autocorrelation function of the theta-bandpassed signal to decrease to half the maximal value at t = 0. As an example, for a 1-second truncated sine wave segment, τ_c = 0.5 seconds. We placed electrode channels into four bins: high theta power/high theta coherence, high theta power/low theta coherence, low theta power/high theta coherence, and low theta power/low theta coherence. Electrode channels that did not produce stimulation output were discarded. High theta power was defined as being greater than the median theta power across all remaining electrodes, whereas high theta coherence was defined as being greater than the midpoint of the range of τ_c values. The theta power for each electrode was averaged over trials 2–40 for subject 1 and trials 1–11 for subject 2.

I. Optimizing Parameters Using a Genetic Algorithm

There are multiple parameters in our algorithm that require selection and optimization. Because these variables interact in non-obvious ways, depending on, most of all, the characteristics of the input data, we sought to optimize these parameters simultaneously through a multi-dimensional search. However, the search space is extremely large and complex. An exhaustive search is a practical impossibility. Therefore, we used a genetic algorithm to arrive at an optimal parameter combination for a particular input signal. A genetic algorithm is a stochastic global search and optimization method that mimics biological evolution through its natural selection of a population of potential solutions according to some measure of fitness. The population undergoes selection, crossover, and mutation to simultaneously generate diversity while converging towards an optimal solution. Though it is possible that the solution arrived at is only a local optimum for any given run, we are constrained by computational resources and time.

The five parameters to be optimized include the AR order p, λ for frequency band optimization, the bandpass filter order and type, and the length t₀ − t_stop for time-series forward prediction. The ranges of acceptable values for these parameters are listed in Table II. Phase-locking performance is characterized by both accuracy (stimulation phases should be close to the target phase) and precision (stimulation phases should be within a narrow range). In addition, similar to the basis for Akaike’s Information Criterion and similar order estimation methods, we want to find the minimum AR order that yields good performance. The fitness function we use is a sum of terms reflecting these three objectives:

$$y=\frac{\left|\phi -\mathrm{\varphi ̄}\right|}{\pi }+\frac{\left|{\mathrm{\varphi ̄}}_{\text{upper }95\%}-{\mathrm{\varphi ̄}}_{\text{lower }95\%}\right|}{\pi }+\frac{p}{100}.$$ (13)

TABLE II.

Optimal Parameters Found By Genetic Algorithm

Dataset	AR Order	λ	Filter Order	Filter Type	t0 − tstop
Cosine	6	0.89	2	Elliptic	0.14
Seizure	13	0.50	1	Butterworth	0.10
Subject 1	22	0.79	2	Chebyshev	0.05

For each case, the number of trials performed was 5, the desired phase of the stimulation output was set to the input waveform peak, or 0°, and the AR model order p was set to 9. The unit of ϕ is degrees.

The first term captures the difference between the mean stimulation phase and the target phase. The second term captures the spread of the stimulation phases. One could also use the circular variance for this term, but unlike the confidence interval, the circular variance does not take into account the number of stimulation pulses. The third and last term is the AR model order. The weighting of these terms is to ensure that each term has a range of 0 to 1 so that each term has roughly an equal contribution to the overall fitness.

We implemented the genetic algorithm in MATLAB 7.11 with the Global Optimization Toolbox 3.1 (Mathworks, Natick, MA). We used a population size of 200, an elite count of 20, crossover fraction of 0.7, the heuristic crossover function, the roulette selection function, and the adaptive feasible mutation function. The initial population was generated randomly within the bounds listed in Table I. We set the stopping criterion to be a cumulative change in fitness of less than 0.0001 between generations.

TABLE I.

Genetic Algorithm Search Space

Parameter	Values
AR order (p)	2–100
λ	0.5–1
Filter order	1–5
Filter type	1–5
t0 − tstop	0.05–0.45

The filter type corresponds to: 1=Butterworth, 2=Chebyshev (0.1 dB of peak-to-peak ripple in the passband), 3=Inverse Chebyshev (stopband attenuation of 60 dB), 4=Elliptic (1 dB of ripple in the passband, and a stopband 60 dB down from the peak value in the passband), 5=Bessel.

III. Results

A. Cosine Waveform

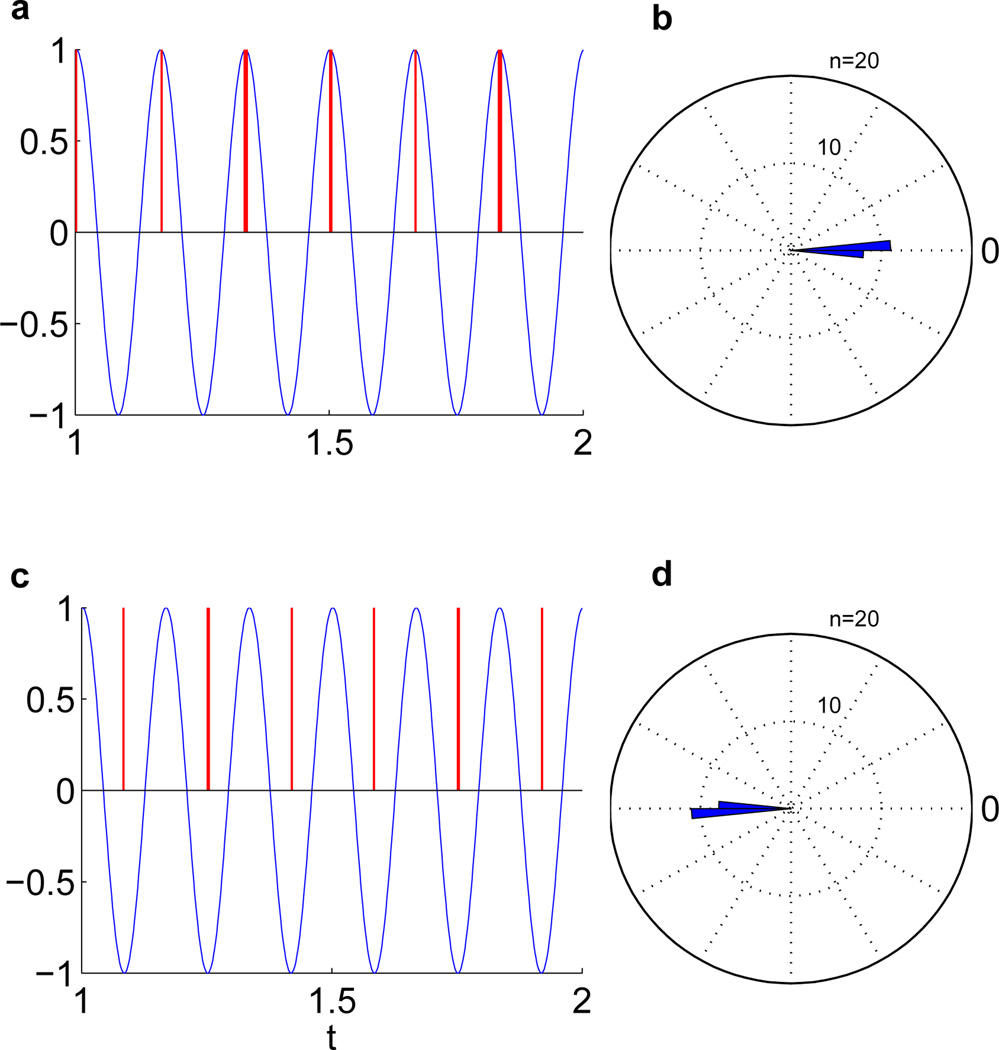
For the simple cosine function, it is reassuring that the phase-locking performance is excellent, as shown in Fig. 2. The parameters used are listed in Table II. While these parameters were optimized using the genetic algorithm, in reality many more parameter combinations yield similarly excellent results. The same parameters were also used to target stimulation at the trough of the waveform. The measures of phase-locking accuracy are also listed in Table III.

Fig. 2.

Results for 6 Hz cosine function. (a) Stimulation at the peak. (b) Rose plot of phases at which stimulation occurred, targeting the peak. (c) Stimulation at the trough. (d) Rose plot of phases at which stimulation occurred, targeting the trough.

TABLE III.

Performance for Each Dataset

Dataset	ϕ̄	ϕ̄lower 95%	ϕ̄upper 95%	Circular Variance	Rayleigh p-value
Cosine	−0.53	−2.06	0.99	0.0016	9.65 × 10−14
Seizure	−2.49	−17.64	12.65	0.2651	2.00 × 10−11
Sub. 1 (45)	−0.91	−7.60	5.77	0.5611	2.27 × 10−59
Sub. 1 (57)	1.60	−2.59	5.79	0.4490	2.02 × 10−145
Sub. 1 (68)	−0.56	−3.49	2.37	0.4848	9.19 × 10−299
Sub. 2 (6)	−11.36	−17.59	−5.14	0.6449	1.81 × 10−69
Sub. 2 (18)	−61.45	−89.21	−33.70	0.7404	1.60 × 10−4
Sub. 2 (20)	−0.19	−8.10	7.72	0.5894	5.79 × 10−43

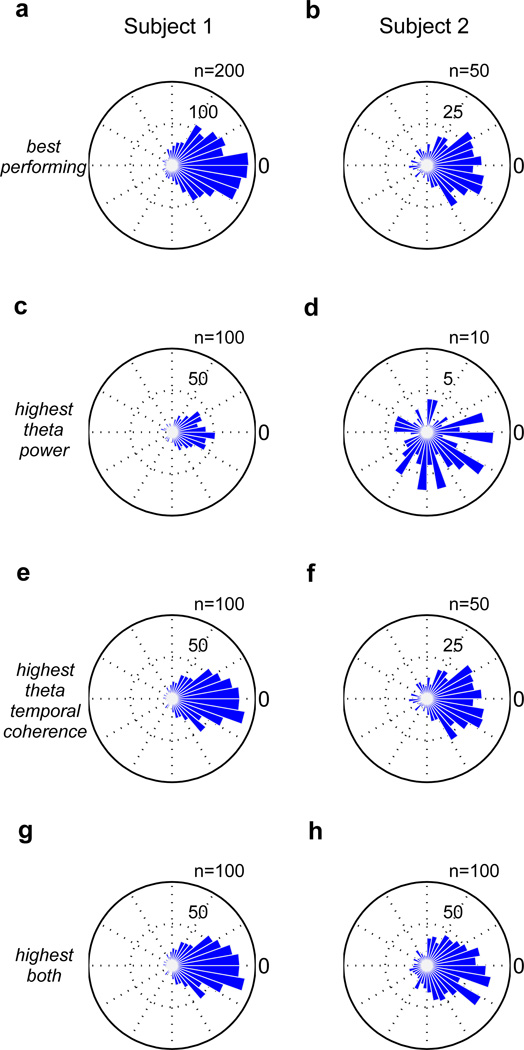
In each case, the target phase of stimulation was the peak of the input waveform, or 0°. The unit of ϕ here is in degrees. For subject 1, channel 68 was the best-performing, channel 45 had the highest theta power, and channel 57 had both the highest theta temporal coherence and highest combined metric (theta power and theta temporal coherence). For subject 2, channel 20 was the best-performing, channel 18 had the highest theta power, channel 20 had the highest theta temporal coherence, and channel 6 had the highest combined metric (theta power and theta temporal coherence).

B. Epileptiform Theta Discharges

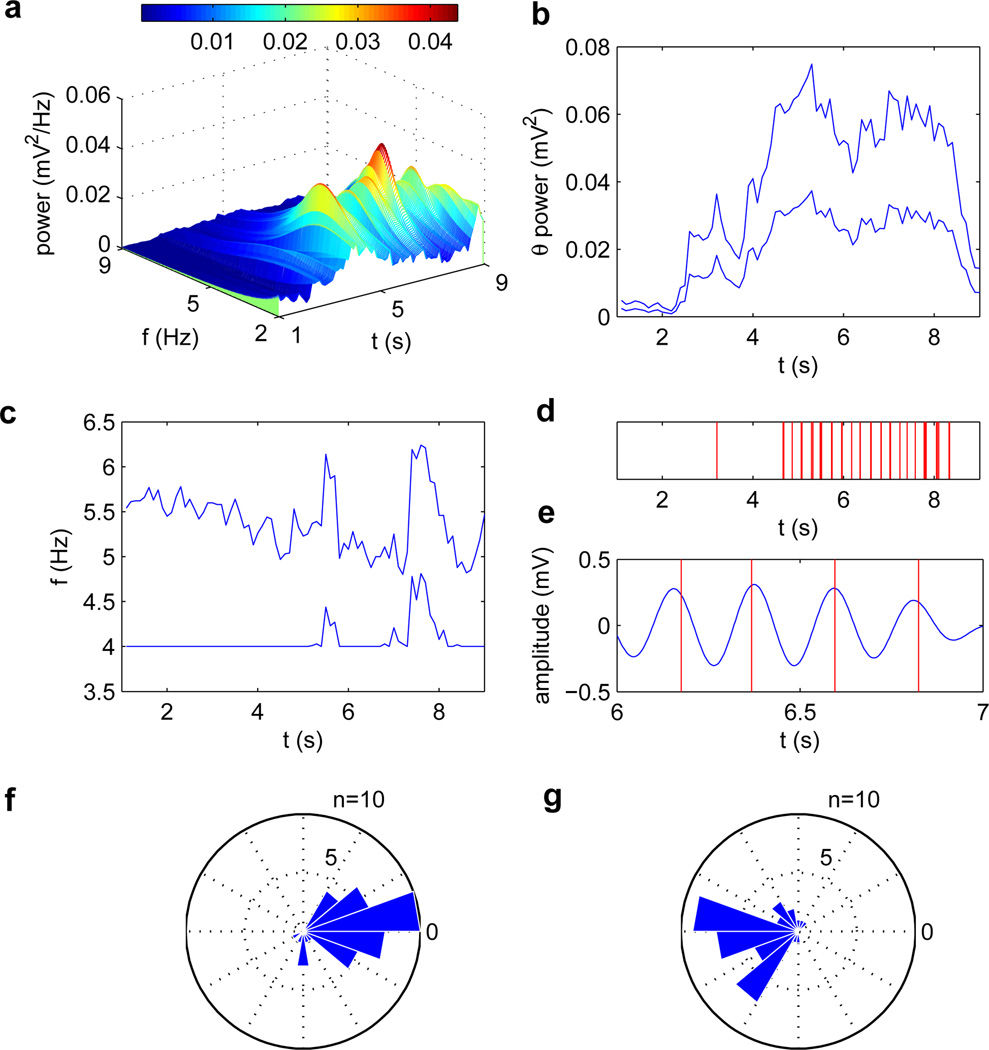
As illustrated in Fig. 3a, the advantage of using an AR model comes from its ability to accurately discern single peaks. Fig. 3 shows the results for the epileptiform theta discharges data. The parameters used–optimized based on targeting the peak–are listed in Table II. The same parameters were then used to test the algorithm for stimulation targeting the trough. For stimulation targeting the peak, the mean resulting phase ϕ̄ was −2.49° degrees (95% confidence interval: −17.64°–12.65°, circular variance: 0.2651). For stimulation targeting the trough, the mean resulting phase ϕ̄ was −178.42° (95% confidence interval: −162.64°–165.79°, circular variance: 0.2867).

Fig. 3.

Results for epileptiform theta discharges data (data is 10-second iEEG signal recorded from a single subdural contact electrode over the parahippocampal gyrus of a patient with temporal lobe epilepsy exhibiting epileptiform theta discharges). (a) Power spectral density over time, using autoregressive estimation. The model order here is 13. (b) Total power in the theta (4–9 Hz) frequency band over time (top curve), and power within the optimized frequency band (bottom curve). (c) The optimized frequency band limits f̂_L (bottom curve) and f̂_H (top curve) over time. Note that as the theta power increases due to the appearance of a theta oscillation, the optimized frequency band becomes narrower. (d) Times at which stimulation output were generated, over the entire 10-second segment. (e) Signal during 6–7 seconds, bandpass filtered between 4 and 5 Hz using a first-order Butterworth filter. Overlaid are times at which stimulation output were generated from 6–7 seconds. (f) Rose plot of stimulation phases, where target phase was 0 degrees, or at the peak. (g) Rose plot of stimulation phases, where target phase was 180 degrees, or at the trough.

C. Sternberg Task

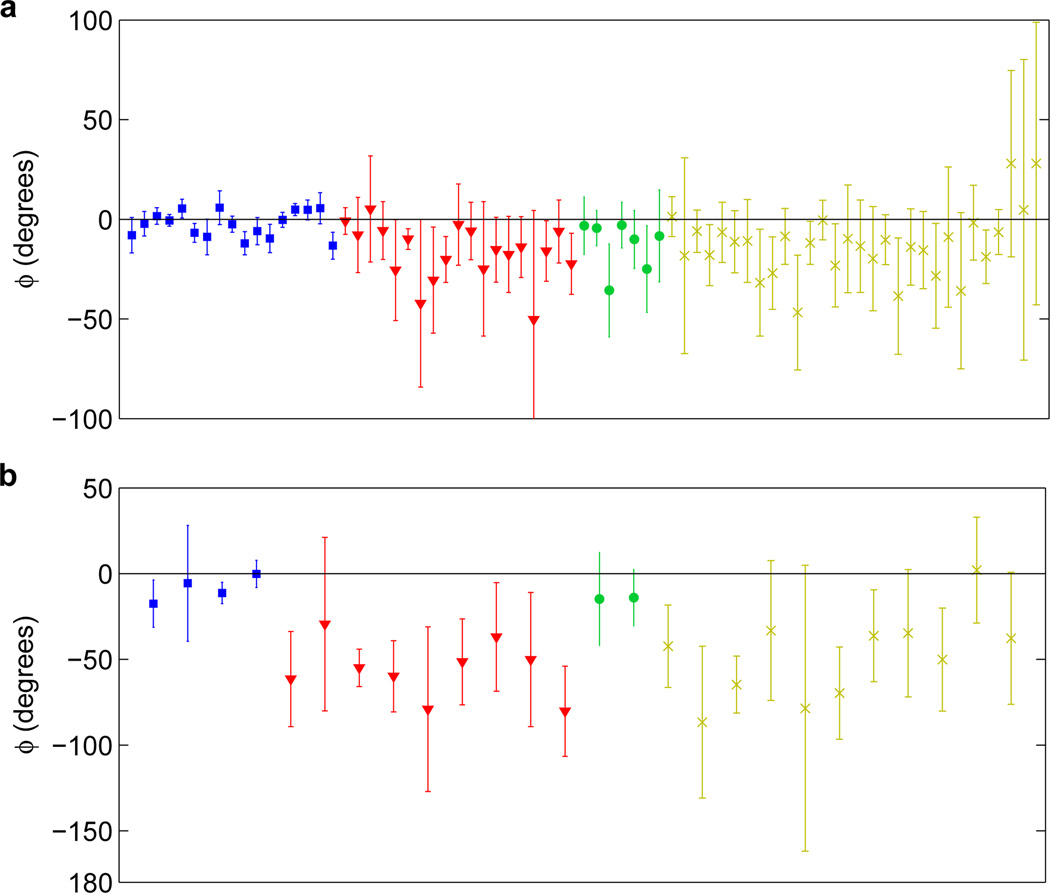
For subject 1, in the first trial, electrode 45 had the largest average theta power (2300 µV²), and thus the algorithm parameters were optimized on this data. The resulting optimized parameters are listed in Table II. Results of simulation runs on trials 2–40 are shown in Fig. 4a. Not all electrode channels had equal phase-locking performance. Channels with both high theta power and high theta temporal coherence resulted in the best performance. The median theta power averaged across trials 2–40 was 570 µV², and the theta temporal coherence τ_c averaged across trials 2–40 ranged from 0.0812 to 0.1308 seconds. A rose plot of stimulation phases for the electrode with the overall best performance is shown in Fig. 5a, and the performance measures are listed in Table III. For this channel (68), the theta power averaged across the trials was 1576 µV² and the theta coherence averaged across the trials, τ̄_c, was 0.1205 seconds. Results for the channel with the highest theta power, channel 45, are shown in Fig. 5c. The average theta power was 2533 µV² and the average theta temporal coherence τ_c for this channel was 0.0907 seconds. Results for the channel with the highest theta temporal coherence as well as the highest combined metric (both high theta power and theta temporal coherence), channel 57, are shown in Fig. 5e and Fig. 5g. The average theta power was 1610 µV² and the average theta temporal coherence τ̄_c for this channel was 0.1308 seconds.

Fig. 4.

Phase-locking performance on signals recorded during the Sternberg task (ϕ̄, error bars represent the 95% confidence interval for ϕ̄). Electrodes are sorted by high theta power/high theta coherence (blue squares), high theta power/low theta coherence (red triangles), low theta power/high theta coherence (green circles), and low theta power/low theta coherence (yellow crosses). (a) For subject 1, signals from 73 out of 73 electrodes generated output stimulation cumulatively over 39 trials (2–40). (b) For subject 2, signals from 26 out of 38 electrodes generated output stimulation cumulatively over 11 trials (1–11).

Fig. 5.

Rose plots for (a) the best performing electrode channel in subject 1 (68), (b) the best performing electrode channel in subject 2 (20), (c) the channel with the highest theta power in subject 1 (45), (d) the channel with the highest theta power in subject 2 (18), (e) the channel with the highest theta temporal coherence in subject 1 (57), (f) the channel with the highest theta temporal coherence in subject 2 (20), (g) the channel with the highest combined metric (both theta power and theta temporal coherence) in subject 1 (57), and (h) the channel with the highest combined metric (both theta power and theta temporal coherence) in subject 2 (6).

The same parameters from subject 1 were tested on subject 2. Out of 38 electrodes, 26 generated output stimulation, and for these electrodes, the median theta power averaged across trials 1–11 was 1500 µV² and the theta coherence averaged across trials 1–11 ranged from 0.0690 to 0.1087 seconds. Results are shown in Fig. 4b. Here, electrode channels with both high theta power and high theta temporal coherence resulted in the best performance. Furthermore, it appears that high theta temporal coherence is more important than high theta power. A rose plot of stimulation phases for the electrode with the overall best performance in subject 2 is shown in Fig. 5b, and the performance measures are listed in Table III. For this channel (20), the theta power averaged across the trials was 1508 µV² and the theta coherence averaged across the trials, τ̄_c, was 0.1087 seconds. Results for the channel with the highest theta power, channel 18, are shown in Fig. 5d. The average theta power was 5740 µV² and the average theta temporal coherence τ̄_c for this channel was 0.0806 seconds. Channel 20, the best-performing channel, happened to also have the highest theta temporal coherence (Fig. 5f). Channel 6 had the highest combined metric (both high theta power and theta temporal coherence), and results for this channel are shown in Fig. 5h. The average theta power for this channel was 2117 µV² and the average theta temporal coherence τ̄_c was 0.0959 seconds.

These results show that while both high theta power and high theta temporal coherence are important in determining performance, high theta temporal coherence is the more important factor. For example, while channel 18 in subject 2 exhibited very large theta power (5740 µV²), it exhibited relatively low theta temporal coherence (0.0806 seconds), and thus performed very poorly (Fig. 5d). On the other hand, channel 20 exhibited lower theta power (1508 µV²), but had higher theta temporal coherence (0.1087 seconds), which explains its better performance (Fig. 5f)

IV. Discussion

We have presented here a system for brain oscillation detection and phase-locked stimulation. Though we have tested our system only on theta oscillations, this system can conceivably be used to also study oscillations in other frequency bands. Autoregressive modeling provides an excellent method to estimate the instantaneous frequency and phase, from which we can accurately deliver phase-locked stimulation in real time.

Optimal selection of the AR model order and other algorithm parameters are important considerations. Because these parameters interact with each other and the input data, we used a genetic algorithm method to optimize these parameters simultaneously. This optimization procedure requires intensive computational resources, and thus cannot be done in real time. It must be manually performed on a separate experimental trial (or set of trials) before the algorithm can be deployed. Here, in subject 1 performing the Sternberg task, we performed this optimization on the first trial and used the parameters derived from this optimization on subsequent trials. In subject 2, we used the parameters that were optimized on subject 1. In reality, it may be more appropriate to optimize the parameters on a patient-by-patient basis, as there will be subtle differences in the physiology between patients, such as in the dominant theta frequencies, timing, and spatial characteristics. For example, hippocampi will differ between patients, especially in the presence of underlying pathology such as mesial temporal sclerosis. In addition, our system may further be improved upon in the future by adopting an online adaptive strategy in selecting algorithm parameters, rather than performing an offline optimization procedure prior to online operation.

Our approach for accurately estimating instantaneous phase and frequency relies on optimizing the narrow passband. Alternate methods have been proposed for estimating the instantaneous phase, such as using wavelet ridge extraction [46]. One advantage of this method is that it is robust even when multiple oscillatory regimes are simultaneously present and are highly variable in time. However, such a time-frequency based method may be too computationally intensive to implement in real time. Another method that has been proposed for oscillation detection is to use an adaptive filter that dynamically tracks the central frequency of the oscillation by adjusting its transfer function coefficients [47]. While this method allows for accurate frequency tracking, the bandwidth of the adaptive filter must still be set manually, and thus remains susceptible to suboptimal bandwidth selection. In these methods, real-time operation would also be limited by edge effects, as only data in the reverse direction is available.

How accurate and precise in phase-locking to an oscillation does one have to be for neurostimulation applications such as memory augmentation? While our method performs relatively well, it remains to be seen if meaningful clinical effects can be elicited by the phase-locking performance demonstrated here. An important consideration is that while we demonstrated our algorithm on subdural electrodes located over widely-distributed spatial areas, in reality our algorithm would be applied to depth electrodes targeting deep mesial temporal lobe structures. Continuous theta oscillations have been recorded from within the hippocampus in humans performing a memory task [14], exhibiting what appears to be a high degree of theta temporal coherence. Because our results show that the performance of our algorithm is correlated with the temporal coherence of detected oscillations, it is reasonable to assume that our algorithm will result in even better performance on depth electrodes targeting the hippocampus directly.

In our implementation of the system, stimulation can be triggered to occur within specified time intervals, for example in synchrony with novel external stimuli or memory task items, or it can be triggered to occur when oscillations above a certain power threshold are detected. The former setup may be useful for experimental paradigms, and the latter setup may be useful in a therapeutic setting. For potential clinical applications, it may be worthwhile to consider further extensions to multi-electrode arrays. This may simply be a matter of setting up multiple parallel channels of analysis and output stimulation delivery, or it could be more sophisticated and use a distributed approach. Because the phase of an underlying brain oscillation may vary across time and anatomical space, more advanced algorithms may be needed to phase-lock to a specific traveling oscillation [48], or a superposition of oscillations from multiple sources. Even with a single channel, the system described here will provide a useful tool for studying the properties of brain oscillation and their interactions with cognitive processes, as well as allow the development of future therapeutic devices that utilize phase-specific information. However, as demonstrated here, the relative success of phase-locked stimulation is a function of both the power and the coherence of the underlying oscillation. Oscillations generated by neural ensembles may be inherently transient in nature [49], and thus future improvements would need to take this into account.

Biographies

L. Leon Chen received the Bachelor of Science (B.S.) degree in electrical engineering from the University of Washington in 2005. He is currently pursuing the M.D. degree at Harvard Medical School, with academic interests in computational neuroscience, neuroengineering, and neurosurgery.

Radhika Madhavan received the B.S. degree in electrical engineering and the M.S. degree in biomedical engineering from the Indian Institute of Technology, Bombay, India in 2001, and the Ph.D. degree in bioengineering from the Georgia Institute of Technology, Atlanta, GA in 2007. She is currently a postdoctoral researcher at the Brigham and Women’s Hospital and Children’s Hospital Boston. Her research interests include understanding the network correlates of learning and memory, using electrophysiology and optical methods.

Benjamin I. Rapoport (S’07) received the A.B. degree in physics and mathematics and the A.M. degree in physics from Harvard University in 2003; the M.Sc. degree in mathematics from Oxford University in 2004; and the S.M. degree in physics from the Massachusetts Institute of Technology (MIT) in 2007. He is presently a student in the M.D.-Ph.D. program at Harvard Medical School and is jointly pursuing his M.D. at Harvard Medical School and his Ph.D. in electrical engineering at MIT. His research and professional interests include bioimplantable electronic interfaces with the brain and nervous system, biological and computational neuroscience, and clinical neurosurgery.

William S. Anderson received the B.S. degree in physics from Texas A&M University, the M.A. and Ph.D. degrees in physics from Princeton University, and the M.D. degree from the Johns Hopkins University School of Medicine. He is currently an Instructor in Surgery at Harvard Medical School, and Associate Neurosurgeon at the Brigham and Women’s Hospital, Boston. His research interests include computational modeling of epileptiform neural networks, cortical and subcortical recording techniques, and closed-loop therapeutic neurostimulation systems.