An event-based approach for comparing the performance of methods for prospective medical product monitoring

Abstract

Prospective medical product monitoring is intended to alert stakeholders about whether and when safety problems are identifiable in a continuous stream of longitudinal electronic healthcare data. In comparing the performance of methods to generate these alerts, three factors must be considered: (1) accuracy in alerting; (2) timeliness of alerting; and (3) the trade-offs between the costs of false negative and false positive alerting. Using illustrative examples, we show that traditional scenario-based measures of accuracy, such as sensitivity and specificity, which classify only at the end of monitoring, fail to appreciate timeliness of alerting. We propose an event-based approach that classifies exposed outcomes according to whether or not a prior alert was generated. We provide event-based extensions to existing metrics and discuss why these metrics are limited in this setting because of inherent tradeoffs that they impose between the relative consequences of false positives versus false negatives. We provide an expression that summarizes event-based sensitivity (the proportion of exposed events that occur after alerting among all exposed events in scenarios with true safety issues) and event-based specificity (the proportion of exposed events that occur in the absence of alerting among all exposed events in scenarios with no true safety issues) by taking an average weighted by the relative costs of false positive and false negative alerting. This approach explicitly accounts for accuracy in alerting, timeliness in alerting, and the trade-offs between the costs of false negative and false positive alerting. Subsequent work will involve applying the metric to simulated data.

INTRODUCTION

With the initial development of FDA’s Sentinel System, and with similar initiatives around the world, regulators and other stakeholders may soon use longitudinal electronic healthcare data to actively and prospectively monitor the safety of medical products.^1-3 As data flow through prospective medical product safety monitoring systems, stakeholders will need to decide whether and when safety information rises to the level of a safety alert.⁴

Many investigators are developing, testing, and implementing methods for prospective monitoring,^5-8 which will generate alerts directing stakeholders to associations that require closer scrutiny and, possibly, subsequent action.⁹ Optimal methods would minimize false positive alert generation (i.e. have high specificity), identify all safety issues of interest (i.e. have high sensitivity), and generate true positives alerts as early as possible to facilitate timely follow-up. False positives can have serious adverse clinical and public health consequences when a medical safe product is unjustly withdrawn or when patients stop using an efficacious product.⁴ Further, regulatory resources may be wasted in pursuit of false positive associations and manufacturers may incur untoward consequences. False negative and delayed true positive alerts can also associated with serious consequences as patients may be inadvertently exposed to harmful products.

In order to select and implement optimal methods for prospective monitoring, stakeholders must first decide how to compare candidate methods. Traditional operating characteristics, such as sensitivity and specificity, do not capture the importance of time-to-alerting and existing indices that summarize performance impose fixed tradeoffs among various operating characteristics that may not reflect reasonable tradeoffs for active monitoring. In this paper, we explore the aspects of prospective medical product safety monitoring that should be considered when comparing method performance, we review existing metrics with respect to these characteristics, and we propose an approach that incorporates events as a measure of time. We use the term ‘method’ generically to refer to any approach to prospective monitoring that can be used to generate alerts, from specific procedures (e.g. sequential probability ratio tests or group sequential monitoring methods), to monitoring designs (e.g. cohort vs. self-controlled designs), to entire monitoring systems that comprise different constellations of design and analytic processes.

PERFORMANCE CHARACTERISTICS

As in other contexts, the performance characteristics of methods for prospective medical product safety monitoring can only be compared in the presence of a gold standard, or a reasonable reference standard with an assumed ground truth. For example, the sensitivity of different screening tests can be compared only if it is known which members of the screening population actually have the condition of interest. Similarly, if a particular method for prospective medical product monitoring generates an alert for a particular product-outcome pair, determining whether the alert is a true positive or false positive requires knowledge of the underlying true association between the product and outcome. An alert is the output of a monitoring method (whether a true positive or a false positive) that prompts further attention from stakeholders regarding a possible safety issue. Further attention may entail some form of verification (e.g. data quality checks, sensitivity analyses, consulting experts or external data sources) and response, including no action. In general, alerting does not influence scenarios. A scenario in prospective monitoring is a single product-outcome pair, for which certain characteristics are known (such as those defined by the investigator in statistical simulations) or assumed from contextual knowledge in empirical settings. These parameters include outcome risk (or rate) in the unexposed or referent group, exposure prevalence, the relative or absolute increase (or decrease) in outcome risk (or rate) conferred by the monitoring product, and the duration of monitoring, which could be defined in several ways, such as the number of monitoring periods, a fixed number of events, or a set number of “looks” at the accumulated data. The underlying truth (or gold standard) in a scenario is a reflection of the causal relation between the monitoring product and the outcome of interest and whether the magnitude of this relation is alert-worthy. Importantly, a single scenario can contribute only to sensitivity or specificity, but not to both. That is, in a scenario in which a true safety issue exists, an alert would be a true positive and an absence of an alert would be a false negative; thus, in either case the scenario contributes information only to sensitivity, but not to specificity. Therefore, to compare methods, a simulation study might include 100,000 scenarios (i.e. product-outcome pairs) across which the underlying rate differences vary to include both scenarios with and without true safety issues. Alternatively, one may be interested in comparing methods in real-world data among a set of scenarios for which the truth is assumed. For example, scenarios with true underlying safety issues might include cerivastatin-induced rhabdomyolysis¹⁰ and angioedema related to angiotensin-converting enzyme inhibitors.¹¹

Accuracy (i.e. whether) and timeliness (i.e. when)

By cross-classifying the results of prospective monitoring methods according to the known or assumed truth in each scenario (i.e. the gold or reference standard), usual performance characteristics, such as sensitivity, specificity, positive predictive value, and negative predictive value, can be easily computed to compare the extent to which methods correctly classify the scenarios. However, when comparing methods for prospective monitoring among an accumulating number of subjects, interpreting measures of accuracy is less straightforward than in static settings.

If hypothetical monitoring methods A and B each identify 1 out of every 2 true medical product safety issues, but A identifies them, on average, more quickly than B, then we prefer A over B (assuming equal specificity) even though they have the same value for overall sensitivity (i.e. 0.5). Delayed alerting and action on true safety issues can have adverse public health consequences.⁴

Event-based operating characteristics

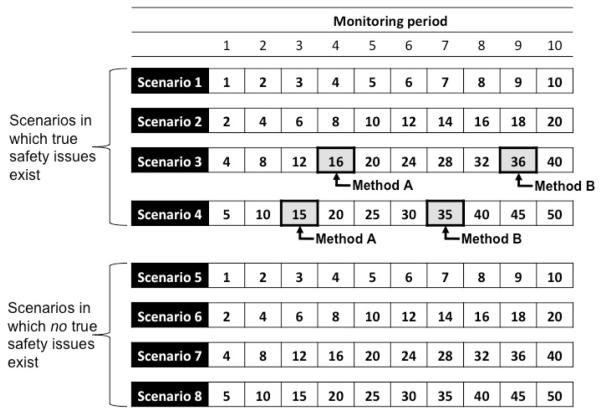
To incorporate time into performance measurement, we propose the use of event-based, rather than scenario-based, classification. Whereas scenario-based classification looks only to the classification of products at the end of monitoring, event-based operating characteristics classify each outcome that occurs following exposure to a medical product according to whether or not an alert has been generated at the time of its occurrence. Figure 1 depicts a matrix of cumulative exposed events that occur at each of 10 monitoring periods (horizontal axis) across eight monitoring scenarios (i.e. product-outcome pairs; vertical axis). If hypothetical Method A generates an alert in the fourth period of Scenario 3 and in the third period in Scenario 4, hypothetical Method B generates an alert in the ninth period of Scenario 3 and the seventh period of scenario 4, and neither method generates alerts in Scenarios 1 and 2, then both methods have conventional scenario-based sensitivities of 0.50 (i.e. 2/4). However, Method A is preferred because it identified alerts in Scenarios 3 and 4 earlier than did Method B. If this were an actual application of a monitoring system, then the 40 exposed events that accumulated between alerting by Method A and Method B in Scenarios 3 and 4 combined could, in theory, have been modified, illustrating that, from a public health perspective, Method A is better than Method B in this set of scenarios. It should be noted that the quantity of 40 events represents the maximum counterfactual advantage of A over B since instantaneous decision-making and action is unlikely in practice.

Figure 1.

Cumulative numbers of exposed events and alerting indications for two hypothetical monitoring methods across eight hypothetical monitoring scenarios (i.e. medical product-outcome pairs)

Each cell indicates the number of cumulative hypothetical exposed events observed at each of ten monitoring periods across eight hypothetical scenarios (i.e. product-outcome pairs). Scenarios 1-4 are ones in which true safety issues exist such that alerts are true positives. Scenarios 5-8 are ones in which no true safety issues exist such that alerts would be false positives. The arrows indicate when each of two hypothetical monitoring methods generated alerts in each scenario. Neither method generated an alert in scenarios 1, 2, 5, 6, 7, and 8. Both methods generated alerts in Scenarios 3 and 4, but at different times.

Now, let us assume that the exposed events in the scenarios 1 through 4 in Figure 1 are exchangeable; that is, the opportunity to modify each event is equally important regardless of both the scenario in which it occurs and the time at which it occurs. If, instead of computing scenario-based sensitivity, we computed sensitivity based on event classification, Method A would have an event-based sensitivity of 0.49 and Method B would have an event-based sensitivity of 0.16. That is, among all exposed events that occur in the four scenarios in which a true safety issue existed, 49% would have occurred after alerting by Method A as compared to only 16% that would have occurred after alerting by Method B. Thus, we define the event-based sensitivity of a method, across a given set of scenarios, as the proportion of exposed events that occur after alerting by the method in scenarios in which true safety issues of interest exist. Based on the 2×2 table in Table 1, event-based sensitivity equals a/(a+c), where a is the number of exposed events that occur after alerting in scenarios in which true safety issues exist and c is the number of exposed events that occur prior to (as in Scenarios 3 and 4 in Figure 1) or in the absence of (as in Scenarios 1 and 2 in Figure 2) alerting in scenarios in which true safety issues exist.

Table 1. Cross–classification of exposed events according to true safety status and alerting status of a particular method.

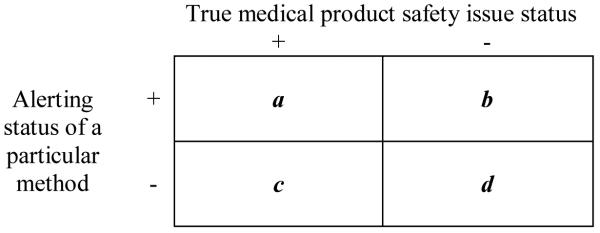a corresponds to exposed events that occur after alerting in scenarios (i.e. product-outcome pairs) in which a true safety issue exists

b corresponds to exposed events that occur after alerting in scenarios in which no true safety issue exists

c corresponds to exposed events that occur prior to or in the absence of alerting in scenarios in which a true safety issue exists

d corresponds to exposed events that occur prior to or in the absence of alerting in scenarios in which no true safety issue exists

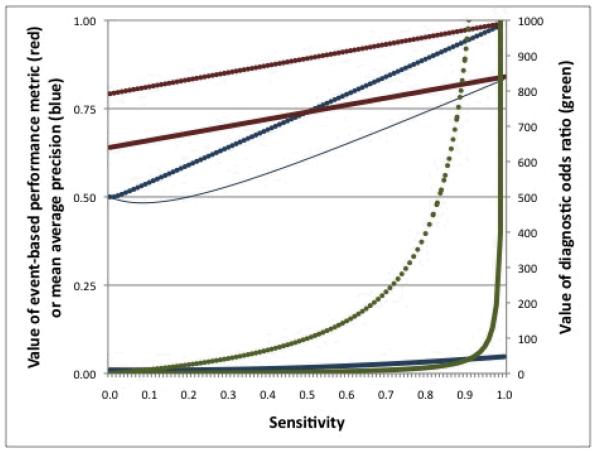
Figure 2.

Behaviors of three metrics at varying parameter values

Plotted is the event-based performance (EBP) metric with w = 0.20 (red; left vertical axis), the diagnostic odds ratio (DOR; green; right vertical axis), and mean average precision (blue; left vertical axis) across values of sensitivity (horizontal axis) when prevalence (i.e. proportion of all scenarios that contain true safety issues) = 0.50 and specificity = 0.80 (thin solid lines), prevalence = 0.50 and specificity = 0.99 (dotted lines), and prevalence = 0.01 and specificity = 0.80 (think solid lines). The thin solid and thick solid lines are superimposed for EBP and for DOR.

Similarly, we define event-based specificity of a method, across a given set of scenarios, as the proportion of exposed events that occur before or in the absence of alerting by the method in scenarios in which no true safety issues exist. Based on Table 1, event-based specificity equals d/(b+d), where d is the count of exposed events that occur prior to or in the absence of alerting in scenarios in which no true safety issues exists and b is the count of exposed events that occur after alerting in scenarios in which no true safety issues exist.

In addition to being modifiable, exposed events are the main driver of whether and when methods generate alerts in prospective monitoring and therefore are a natural unit of measurement for comparing method performance. Focusing only on exposed events, rather than on both exposed and unexposed or on excess events, permits greater flexibility in measurement since not all methods rely directly on observed unexposed event counts. For example, some methods, such as the maximized sequential probability ratio test for Poisson data,¹⁶ may use expected event rates, which could be determined from historical data or estimates from the literature. Moreover, in situations in which no safety issues exist, excess events are, by definition, non-existent, and therefore of no use for determining measures of specificity or other characteristics that rely on the b and d cells.

Summarizing event-based performance

Event-based operating characteristics, such as event-based sensitivity and event-based specificity, offer a simple way to incorporate time into performance evaluation. However, when comparing methods, a single numeric index that summarizes the relevant characteristics is often desired. Several different metrics that are used to evaluate binary classifiers in other fields such as information retrieval, machine learning, bioinformatics, and diagnostic screening, provide single scores to reflect various configurations of operating characteristics (Table 2). While all of these metrics have hitherto focused on scenario-rather than event-based classification, and have not been adapted to settings in which time is an important dimension, they all exploit the contents of 2×2 classification tables and, as such, can be based on event-classification. However, the configuration of each metric implicitly weighs the tradeoffs between false positive and false negative costs in a fixed way that may not be relevant to prospective medical product safety monitoring in general or to any specific monitoring scenario. In a given scenario the relative consequences of false positive alert generation may vastly outweigh the consequences of false negative alert generation, and vice versa, depending on the severity of the outcome, the availability of treatment alternatives, and the relative benefit of the particular medical product as compared to alternatives.

Table 2. Event-based extensions of existing metrics to compare binary classifiers that could be considered to evaluate the performance of methods in prospective medical product safety monitoring.

Metric	Brief description	Extension to event-based classification
Accuracy (A)	Accuracy is the proportion of all exposed events that are correctly classified. Range: (0,1).	$\frac{a+d}{a+b+c+d}$
Diagnostic odds ratio (DOR)11	The DOR is the ratio of odds of positivity in scenarios in which true safety issues exist to odds of positivity in scenarios in which no safety issue exists. Range: (0,∞). DOR approaches ∞ as either EB-sensitivity or EB- specificity approach 1. A method that cannot discriminate between scenarios with a true safety issue and those without would have DOR = 1. DOR is undefined when either EB-sensitivity = 1, or EB-specificity =1, or both	$\frac{ad}{bc}$
F1 score13	The F1 score is the harmonic mean (HM) of EB-sensitivity and EB-positive predictive value. HM is related to the arithmetic mean (AM) and the geometric mean (GM) by HM = GM2/AM. Range: (0,1).	$\frac{2a}{2a+b+c}$
Mean Average precision (MAP)8	MAP is most often used in non-binary settings when algorithms return ranked values, but can be adapted to binary classifiers. Range: (0,1). When EBspecificity is low, MAP can paradoxically increase as EB-sensitivity decreases.	$\frac{\frac{a^2}{a+b}+\frac{ac+c^2}{a+b+c+d}}{a+c}$
Matthews correlation coefficient (MCC)14	The MCC is the Pearson correlation coefficient for two binary variables. Range: (−1,1). MCC = 0 indicates random alert generation.	$\frac{ad-bc}{\sqrt{(a+b)\cdot (c+d)\cdot (a+c)\cdot (b+d)}}$
Youden’s J statistic15	Youden’s J is algebraically equal to the risk difference from a 2×2 table. Range: (−1, 1). J represents the net amount by which sensitivity and specificity differ from 0.5.	$\frac{a}{a+c}-\frac{b}{b+d}$

EB, event-based

a is the number of exposed events that occur after alerting in scenarios in which a true safety issue exists

b is the number of exposed events that occur after alerting in scenarios in which no true safety issue exists

c is the number of exposed events that occur prior to or in the absence of alerting in scenarios in which a true safety issue exists

d is the number of exposed events that occur prior to or in the absence of alerting in scenarios in which no true safety issue exists

A new metric

Ideally, a metric to compare methods for prospective safety monitoring would allow for the incorporation of different relative costs of false positives and false negatives in different scenarios. Thus, we propose a simple weighted average of event-based sensitivity and event-based specificity, which we call event-based performance (EBP):

$$EBP=w\left(\frac{a}{a+c}\right)+(1-w)\left(\frac{d}{b+d}\right)$$

where a/(a+c) is event-based sensitivity, d/(b+d) is event-based specificity, and w is a decisionmaker-defined weight reflecting the tradeoff between the costs of false positives and the costs of false negatives. Small values of w give preference to specificity implying relatively high false positive costs whereas larger weights reflect higher false negative costs. The selected weight for a given scenario will depend on the nature of the medical product under consideration (e.g. a life-saving drug with no reasonable alternative versus a marginally effective drug with many alternatives) and the characteristics of the monitored outcome (e.g. life threatening versus mild passing symptoms). Plausible values of w range from 0 to 1. Choosing a weight is analogous to specifying a tradeoff between α- (i.e. the probability of rejecting a true null hypothesis in statistical hypothesis testing) and β-risk (i.e. probability of failing to reject a false null hypothesis) for a given scenario. Conventionally, decision makers accept a β of 0.20 to identify a specified effect at an α-level of 0.05; thus, accepting a 4:1 β:α tradeoff, or a w of 0.20. Smaller weights would reflect a decision maker’s preference for methods that further limit the numbers of false positives, which is particularly important in the prospective monitoring setting that inherently involves multiple testing.

Above we assumed that events that occur in a set of scenarios are exchangeable, even if they occur in different scenarios. However, medical product monitoring systems will simultaneously consider many different exposures and health outcomes for which the relative false positive and false negative costs will vary. EBP can accommodate comparisons across scenarios with varying relative false positive and false negative costs by allowing for the application of different weights (w) in different scenarios that may have different outcomes or that may differ in other important ways that affect the tradeoff between sensitivity and specificity. For example, larger values of w might be applied to hepatotoxicity outcomes as compared to values that might be applied to outcomes for which the relative costs of false negatives are lower, such as for non-fatal gastrointestinal bleeding. Other considerations might include the implications of false positive alert generation on subsequent medical product utilization and its resultant public health consequences, the tradeoffs between the monitoring outcomes and the benefits of the monitoring product, and the availability of safe and effective alternatives. Ideally, w would be selected on the basis of a formal decision analytic model. It is important to note that, prior to weighting, scenarios with more exposed events contribute more information to EBP. Therefore, w might also consider the relative contribution of each scenario according to the number of events it contains.

It follows from above that, across a set of scenarios, the performance of methods can be ranked differently depending on the values of w chosen. If small w values are used in all scenarios, methods that generate few false positives will achieve relatively higher values of EBP, whereas if large values of w are used in all scenarios then methods with higher sensitivity will be ranked higher. Therefore, the choice of w for a given safety monitoring scenario will have important implications for selecting the most appropriate monitoring method. In the Appendix we provide an evaluation of EBP using hypothetical data.

In order to fully compare the relative performance of methods, they must be evaluated across sets of scenarios that contain both true safety issues (i.e. gold or reference standard is positive) and no true safety issues (i.e. gold or reference standard is negative), as single scenarios contribute either to event-based sensitivity or event-based specificity, but not both, just as a single scenario contributes only to conventional sensitivity or specificity. For example, an investigator may establish a specific type of scenario as defined by baseline outcome frequency among the unexposed and a fixed number of monitoring periods, and may simulate data with varying, but known, underlying relations between a medical product and the outcome. Different methods can then be applied to the simulated data and EBP can be calculated across the simulated scenarios to determine which methods achieve the highest EBP at given values of w. Alternatively, different scenarios could be created with varying parameter constellations and EBP could be used to compare methods across the range of scenarios while accommodating different w values. We provide the following expression to calculate EBP across multiple scenarios:

$$EBP=\frac{\sum _{j=1}^k{a}_j\cdot w_j}{\sum _{j=1}^k{a}_j+c_j}+\frac{\sum _{j=1}^k{d}_j\cdot (1-w_j)}{\sum _{j=1}^k{d}_j+b_j}$$

where j is an individual scenario and k is the total number of scenarios across which methods are compared. The remaining components are as described above, but are scenario specific.

Comparing EBP to other metrics

While the use of event-rather than scenario-classification is not specific to our proposed metric, EBP offers some particular advantages over existing metrics. For example, the diagnostic odds ratio (DOR) assigns very high values when either sensitivity or specificity (or both) is high as compared to when both are moderately high (Figure 2; green lines). A method with a sensitivity of 0.99 and a specificity of 0.70 achieves a DOR value of 231, whereas a method with a sensitivity of 0.90 and a specificity of 0.80 achieves a DOR of only 36. Moreover, because the numerator of the DOR is the product of true positives and true negatives and the denominator is the product of false positives and false negatives, applying a weight reflecting a preference for sensitivity or specificity is not straightforward. For example, applying a weight to the DOR numerator increases the value of correct classification as compared to incorrect classification but applies the increased value equally to true positives and true negatives. As a result, the DOR implicitly values sensitivity and specificity equally.

Other measures, such as the MCC, also cannot easily accommodate user-specified weights for false positive and false negative tradeoffs and others, such as the F₁ score, impose fixed tradeoffs that may not be meaningful for prospective medical product safety monitoring. Moreover, when used to compare binary classifiers, at some values of specificity the MAP can paradoxically increase with decreasing sensitivity, even though higher MAP values are considered better. For example, assuming a setting in which half of monitoring scenarios are situations in which a true safety issue exists (i.e. a “prevalence” of 0.50), a method with a specificity of 0.80 and a sensitivity of 0.01 has a MAP value of 0.50 whereas a method with a specificity of 0.80 and a sensitivity of 0.10 has a MAP value of 0.45 (Figure 2; blue lines).

DISCUSSION

The many methods that may be used to generate alerts in prospective medical product safety monitoring will differ in their ability to identify true safety issues in a timely fashion while minimizing false positivity, and this performance will vary from scenario-to-scenario depending on characteristics of the medical product and outcome of interest. In comparing the methods’ performance across a given set of scenarios, stakeholders must consider accuracy in alerting, timeliness of alerting, and the trade-offs between the costs of false negative and false positive alerting. Because hitherto conventional scenario-based measures of accuracy, such as sensitivity and specificity, look only to the classification of products at the end of monitoring, they do not account for differences in timeliness among methods. As an alternative, we propose the use of event-based operating characteristics, which classify outcomes that occur following exposure to a medical product according to whether or not a signal has been raised and offer a simple way of incorporating time into measures of accuracy.

We reviewed many metrics that combine operating characteristics into a single numeric index. Although these metrics have not relied on event-based classification in the past, they all exploit the contents of a 2×2 table and therefore can use scenario- or event classification. However, these metrics impose fixed trade-offs among the operating characteristics that they consider and these fixed arrangements may not reflect the relative costs of false positive and false negative alerting in any given medical product monitoring scenario.

We propose an event-based performance metric that uses event-based classification to integrate time into measures of accuracy and it allows users to explicitly incorporate tradeoffs between costs of false positives and false negatives, and allows the trade-off to vary in each monitoring scenario.. We plan to use this metric for comparing the performance of alerting methods for prospective safety monitoring in simulated data to inform selection of methods for applied monitoring. Unlike existing metrics, EBP allows users to specify a weight (w) to reflect their preference for sensitivity versus specificity for each scenario. Plausible values of w range from 0 to 1 with a weight of 0.5 reflecting no preference for sensitivity or specificity; a situation that is very much unlike general epidemiologic practice in which investigators typically focus on minimizing Type 1 error (i.e. minimizing the number of false positives) at the expense of Type 2 error (i.e. allowing some true safety issues to go undetected). As a rule-of-thumb, we recommend w values of less than 0.20, which is consistent with the conventional willingness to accept a 4:1 tradeoff between β- and α-risk, and appreciates the inherent multiplicity in sequential monitoring. However, selection of an appropriate w value for a given scenario will depend on many scenario-specific factors and would ideally be chosen on the basis of a comprehensive decision analytic model that considers all costs of false positive and false negative alerting. Choosing an appropriate weight for a given scenario is akin to determining a cut point on a receiver operating characteristic curve.

EBP may be a useful approach for comparing methods for prospective medical product safety monitoring within a defined set of scenarios for which the truth is known or can reasonably be assumed in each individual scenario. It is important to note that values of EBP are context-specific. For example, if the duration of monitoring were 15 periods in Figure 1, then the values of event-based sensitivity for Methods A and B would be different from those based on 10 periods. As such, EBP provides an approach to rank methods within defined sets of scenarios, but EBP values from one setting are not transportable to other settings.

Comparing methods for signal detection in spontaneous adverse event reporting data shares many similarities to the comparison of methods in active medical product monitoring. However, studies that have compared methods for signal detection have generally relied on scenario-based measures of sensitivity, specificity, and the false discovery rate. Our proposed metric can be readily applied to this setting as a way to incorporate time-to-signaling.

In conclusion, our proposed metric overcomes several limitations of existing metrics when applied to active medical product safety monitoring. The metric readily accommodates weights to reflect trade-offs between the costs of false positives and false negatives, and, most importantly, uses events, rather than scenarios, to incorporate time-to-alerting.

Key points.

• -Many stakeholder are currently developing and testing methods for medical product safety monitoring systems, but little attention has been paid to how methods should be evaluated
• -In comparing the performance of such methods, three factors must be considered: (1) accuracy in alerting; (2) timeliness of alerting; and (3) the trade-offs between the costs of false negative and false positive alerting
• -Traditional scenario-based measures of accuracy, such as sensitivity and specificity, fail to appreciate timeliness of alerting and other metrics impose arbitrary tradeoffs between false negatives and false positives
• -The authors propose an event-based classification approach that explicitly accounts for accuracy in alerting, timeliness in alerting, and the trade-offs between the costs of false negative and false positive alerting

APPENDIX

In this section, we use hypothetical data to evaluate EBP. Imagine a set of eight monitoring scenarios among which we wish to compare the performance of four different monitoring methods. Half of the scenarios (i.e. scenarios 1-4) are ones in which a true safety issue exists and half (i.e. scenarios 5-8) are scenarios in which no true safety issue exists. In Appendix Table 1 we show the hypothetical numbers of exposed events in each of the eight scenarios and the numbers of exposed events observed prior to signaling by each of the four methods.

Method 1 always generates an alert after 35 exposed events in a given scenario, regardless of whether the scenario is one in which a true safety issue exists. Thus, it generates alerts in scenarios 3, 4, 7, and 8, corresponding to an overall sensitivity of 0.500 and an overall specificity of 0.500 (Appendix Table 2). As an improvement, Method 2 also generates alerts after 35 exposed events in scenarios in which safety issues exist, but performs better in scenarios in which no safety issues exist by generating alerts after 40 events in such cases; yet these methods have identical overall performance characteristics. This improved performance of Method 2 over Method 1 is, however, reflected in the EBP metric, which results in a value of 0.700 for Method 1 and 0.767 for Method 2, based on a weight of 0.20 across all eight scenarios.

Method 3 generates alerts more quickly than Method 2, by signaling after 15 exposed events in scenarios in which a safety issue exists and after 35 events in scenarios in which no safety issue exists. This results in a substantially higher event-based sensitivity as compared to Method 2 (0.542 vs. 0.167) and a slightly lower event-based specificity (0.833 vs. 0.917) and a resulting higher EBP value for Method 3 versus Method 2 when using a weight of 0.20. Method 4 dominates the other methods by generating alerts after only 15 exposed events in true safety scenarios and after 45 events in scenarios in which no true safety issues exist, resulting in an EBP value of 0.875.

If we used a weight of 0.10 reflecting an even greater preference for specificity, Method 1 would still have the lowest EBP value and Method 4 the highest, but we would now prefer Method 2 to Method 3, because of the higher event-based specificity of Method 2. We could also have applied different weights to each of the eight scenarios.

Appendix Table 1. Summary of monitoring data from four hypothetical methods applied to eight hypothetical scenarios (i.e. medical product-outcome pairs).

Scenario no.	True safety issue?	Total no. exposed events	No. exposed events observed prior to alerting*
			Method 1	Method 2	Method 3	Method 4
1	□	10
2	□	20			15	15
3	□	40	35	35	15	15
4	□	50	35	35	15	15
5		10
6		20
7		40	35	40	35
8		50	35	40	35	45

^*Gray cells indicate that the method did not generate an alert

Appendix Table 2. Performance characteristics of 4 hypothetical methods across 10 hypothetical examples^*.

Hypothetical methods	Scenario-based approach						Event-based approach
	TP	FP	FN	TN	Overall sensitivity	Overall specificity	a	b	c	d	Event- based sensitivity	Event- based specificity	EBP*	EBP**
1	2	2	2	2	0.500	0.500	20	20	100	100	0.167	0.833	0.700	0.767
2	2	2	2	2	0.500	0.500	20	10	100	110	0.167	0.917	0.767	0.842
3	3	2	1	2	0.750	0.500	65	20	55	100	0.542	0.833	0.775	0.804
4	3	1	1	3	0.750	0.750	65	5	55	115	0.542	0.958	0.875	0.917

FN, false negatives; FP, false positives; TN, false negatives; TP, true positives

^*With w_i = 0.20

^**With w_i = 0.10