Improved Prediction of Disturbed Flow via Hemodynamically-Inspired Geometric Variables

Abstract

Arterial geometry has long been considered a pragmatic alternative for inferring arterial flow disturbances and their impact on the natural history and treatment of vascular diseases. Traditionally, definition of geometric variables is based on convenient shape descriptors, with only superficial consideration of their influence on flow and wall shear stress patterns. In the present study we demonstrate that a more studied consideration of the actual (c.f., nominal) local hemodynamics can lead to substantial improvements in the prediction of disturbed flow by geometry. Starting from a well-characterized computational fluid dynamics (CFD) dataset of 50 normal carotid bifurcations, we observed that disturbed flow tended to be confined proximal to the flow divider, whereas geometric variables previously shown to be significant predictors of disturbed flow included features distal to the flow divider in their definitions. Flaring of the bifurcation leading to flow separation was redefined as the maximum relative expansion of the common carotid artery (CCA), proximal to the flow divider. The beneficial effect of primary curvature on flow inertia, via suppression of flow separation, was characterized by the in-plane tortuosity of CCA as it enters the flare region. Multiple linear regressions of these redefined geometric variables against various metrics of disturbed flow revealed R² values approaching 0.6, better than the roughly 0.3 achieved using the conventional shape-based variables, while maintaining their demonstrated real-world reproducibility. Such a hemodynamically-inspired approach to the definition of geometric variables may reap benefits for other applications where geometry is used as a surrogate marker of local hemodynamics.

1. INTRODUCTION

Atherosclerosis develops primarily at bends and major branches of the arterial network, such as the carotid bifurcation (DeBakey et al., 1985). Numerous in vivo and in vitro experiments have proved that these regions experience “disturbed” flow patterns, characterized by low and oscillatory wall shear stress, which can lead to endothelial cell dysfunction (Slager et al., 2005). The CARDIA study has also recently shown that traditional systemic cardiovascular risk factors have weaker associations with intima-media thickening (IMT) when based on IMT at the carotid bulb vs. the common carotid artery (CCA), attributed to “bifurcation geometry and differences in hemodynamics” (Polak et al., 2010). While such indirect evidence suggests that hemodynamic forces could augment widely accepted systemic factors for atherosclerosis risk assessment, utility of such “local” risk factors remains unclear owing to challenges of quantifying hemodynamics using in vivo imaging methods or computational fluid dynamic (CFD) models (Taylor and Steinman, 2010).

Geometric features of an artery are key factors determining the hemodynamics (Friedman et al., 1983), and thus may be more practical surrogate markers for large-scale retrospective and prospective imaging studies, or indeed routine clinical use. Conventionally, geometric variables are defined to characterize the shape of an artery, whereas the link to the hemodynamics they are intending to predict is usually only presumed or nominal. As a result, such shape-based variables may be suboptimal predictors of disturbed flow. An explicit link between geometry and hemodynamics was recently demonstrated by Lee et al. (2008), who showed, for the normal carotid bifurcation at least, that area ratio and tortuosity, but not branch angle or planarity, significantly predict disturbed flow. The present study aims to close this conceptual loop by demonstrating, for the first time, how insights from the underlying hemodynamics can be effectively fed back to substantially improve the performance of its geometric predictors.

2. METHODS

The objects of this study were 50 carotid bifurcations, digitally reconstructed from high-resolution black blood MRI of 25 young adults, as described by Thomas et al. (2005). Starting from the 3D surface triangulation of each carotid bifurcation, geometric variables were automatically extracted using the open-source Vascular Modeling Toolkit (VMTK; www.vmtk.org). The centerline of each model was generated automatically along the CCA-ICA and CCA-ECA tracts using VMTK’s Voronoi-diagram-based algorithm (Antiga et al., 2008), which also provides the maximally inscribed sphere radius (MISR) at each point along the centerline. The centerline was decomposed into CCA, ICA and ECA branches (Antiga and Steinman, 2004), each parameterized using an objective distance metric based on the local MISR, as introduced byThomas et al. (2005); e.g., CCA3 identifies a location 3 CCA radii proximal to the bifurcation origin. Cross-sectional areas were calculated automatically via intersection of a plane normal to the centerline at the desired location.

2.1. Redefining Area Ratio

The expansion, or flare, of a bifurcation is traditionally characterized by the cross-sectional areas of the two daughter branches divided by that of parent artery (e.g., Fisher and Fieman, 1990; Schulz and Rothwell, 2001; Smedby, 1996). As shown in Figure 1A, this informed the definition of area ratio (AR1) used by Lee et al. On the other hand, by looking at the actual flow patterns, we observed that flow separation leading to low and oscillating shear tended to be confined proximal to the branching, as is evident from their Figure 3 and consistent with observations from colour Doppler ultrasound (Steinke et al., 1990). Since flow separation is precipitated by local expansion of the lumen, a new flare variable (FlareA) was defined as the ratio of the maximum CCA cross-sectional area proximal to the bifurcation flow divider (CCAmax), divided by the CCA3 area (Figure 1B). To identify CCAmax, a new centerline was computed, as the average of the CCA-ICA and CCA-ECA centerlines up to the flow divider, and sections were generated automatically and searched for the largest section area.

Figure 1.

Elements in the definition of geometric variables, as described in the Methods. In panels A and B, planes normal to the centerlines are used to define the original area ratio (AR1) and redefined flare (FlareA) variables. In panel B, the thin solid line is the average of the (dotted) ICA and ECA centerlines; the thicker (red) dashed lines identify the major axes used to compute FlareM, and the distance between planes for compute FlareR. In panel C, the thick (red) solid line identifies the centerline segment used to compute the original Tortuosity. In panel D, the pivot is identified as the point of maximum rate of change of the Frenet normals (vector direction), or equivalently the maximum torsion (vector colour). The thick (red) line identifies the centerline segment used as the basis for the redefined tortuosity, Tort3D. The projection of this centerline onto the best-fit plane is used to determine Tort2D or Curv2D.

Figure 3.

Distribution of disturbed flow for a representative case. Yellow highlights regions exposed to low WSS or high OSI beyond the respective the 80^th percentile value; red narrows this area to the 90^th percentile value. Dark grey identifies the surface area used to normalize the SA exposed to disturbed flow. Panel C isolates the disturbed flow and normalizing surface area to the outer wall of the CCA-ICA tract, as described in the Discussion.

Recognizing that the maximum flare tends to occur in the plane of the bifurcation, a second flare variable (FlareM) was defined the ratio of the major axes at CCAmax and CCA3, i.e., D_max/D_CCA3 as shown in Figure 1B. Finally, since the rate of flaring from locations CCA3 to CCAmax might be a factor in promoting flow separation, we defined a third flare variable (FlareR) as half the difference between the two major axes divided by the distance between the two planes, i.e., ½(D_max-D_CCA3)/L, approximating the mean slope of the flare.

2.2. Redefining Tortuosity

A convenient definition of vascular tortuosity is L/D-1, where L is the path length of the vessel between two end points, and D is its straight-line distance (e.g., Brinkman et al., 1994; Smedby and Bergstrand, 1996; Wood et al., 2006). As shown in Figure 1C, Lee et al. defined their Tortuosity in this way, using the 3D centerline from the proximal CCA to the distal ICA. They conclusively demonstrated that higher tortuosity tends to counteract the effect of area ratio on promoting disturbed flow, later explained by the stabilizing effect of curvature-induced secondary flow (Zhang et al., 2010). In this context, however, the influence of the distal ICA portion should be negligible, and possibly confounding if included in the tortuosity calculation. To isolate the influence of the proximal CCA on flow separation, we noted that the CCA-ICA tract typically possesses a sigmoidal shape, with an inflection point proximal to the flow divider, i.e., in the region where flow separation typically occurs. We therefore defined a new tortuosity variable, Tort3D, using the 3D centerline from CCA3 to this inflection point (Figure 1D), which was identified automatically as the location of the maximum centerline torsion (Piccinelli et al., 2009).

Since secondary flows are driven primarily by planar rather than out-of-plane curvature, we defined a second tortuosity variable (Tort2D) in which L and D were based on a projection of the 3D centerline onto a best fit plane between CCA3 and the inflection point. Finally, since curvature itself, rather than tortuosity, is more directly linked to the production of secondary flow, a third variable (Curv2D) was defined as the curvature of a circle fitted, via least squares, to the projected centerline segment between CCA3 and the inflection point.

2.3. Hemodynamic Characterization

CFD simulations were previously carried out on each of the 50 carotid bifurcation geometries using a well-validated in-house finite-element-based CFD solver. Fully developed (Womersley) velocity boundary conditions were imposed at the CCA inlet and ECA outlet, based on characteristic flow waveform shapes and allometric scaling of mean flow rates to the respective inlet and outlet areas. Rigid walls and constant blood viscosity of 0.035 cm²/s were assumed. Details of the meshing and boundary conditions are provided byLee et al. (2008).

From the resulting time-varying, 3D velocity fields, surface distributions of the following indicators of disturbed flow were calculated: cycle-averaged magnitude of the wall shear stress (WSS), oscillatory shear index (OSI); and relative residence time (RRT) (Himburg et al., 2004), each normalized to their nominal value at the CCA3 section. Following Lee et al. (2008), two threshold values were defined for each indicator, corresponding to the 80^th and 90^th percentiles of their cumulative distributions pooled across all 50 models. For an individual model, disturbed flow was quantified as the surface area (SA) exposed beyond these percentile values. Following Lee et al., each SA was normalized by the total surface area of the respective model clipped at planes CCA3, ICA5 and ECA2. These relative surface areas exposure to disturbed flow (SA_rel) are hereafter referred to as WSS80, WSS90, OSI80, OSI90, RRT80, and RRT90.

Since the redefined geometric variables focus on the flare region, and bifurcations with large flare by definition have larger total SA, normalization by total SA potentially biases the burden of disturbed flow. By way of introducing a less biased accounting for vessel size, we also investigated the effect of normalizing the SA of disturbed flow by the CCA3 cross-sectional area.

2.4. Data analysis

Multiple linear regressions were used to quantify the predictive ability of the different combinations of the flare and tortuosity variables as independent predictors, with each of the SA_rel variables (i.e., WSS80, etc.) in turn as dependent variables. The strength of each regression was reported as its coefficient of determination adjusted for the number of independent predictors, R² _adj.

Previously, Bijari et al. (2011) demonstrated excellent reproducibility of the original geometric variables, based on 3D-contrast-enhanced magnetic resonance angiography (CEMRA) of participants scanned twice as the part of the Atherosclerosis Risk in Communities (ARIC) Carotid MRI study (Wasserman et al., 2010). The intra-class correlation coefficient (ICC), also called the coefficient of reliability, was found to be on the order of 0.9. To determine whether the redefinitions of the geometric variables might degrade their reproducibility, we computed their ICC values starting from the same segmented 3D surfaces previously used by Bijari et al. (2011).

3. RESULTS

As summarized in Table 1, R² _adj values from the multiple regressions reveal that substitution of either the original AR1 or Tortuosity by the respective redefined variables, alone or together, improves the prediction of disturbed flow irrespective of the disturbed flow metric. For a given flare variable (i.e., looking down each column of Table 1), Tort3D offers a consistent improvement in R² _adj, which is further enhanced by its planar variant, Tort2D, but not Curv2D.

Table 1.

Coefficients of determination (R²_adj) for multiple regressions of SA_rel, determined by different hemodynamic parameters, as predicted by various permutations of original and redefined flare and tortuosity variables.

Tortuosity Variables	Flare Variables
	AR1	FlareA	FlareM	FlareR	AR1	FlareA	FlareM	FlareR	AR1	FlareA	FlareM	FlareR
	WSS80				OSI80				RRT80
Tortuosity	0.314	0.385	0.354	0.325	0.311	0.244	0.315	0.265	0.358	0.383	0.397	0.354
Tort3D	0.391	0.438	0.429	0.406	0.326	0.233	0.336	0.289	0.421	0.417	0.462	0.425
Tort2D	0.444	0.542	0.434	0.417	0.435	0.388	0.386	0.349	0.501	0.549	0.485	0.457
Curv2D	0.441	0.462	0.429	0.399	0.345	0.269	0.322	0.225	0.452	0.401	0.446	0.417
	WSS90				OSI90				RRT90
Tortuosity	0.375	0.421	0.326	0.421	0.321	0.245	0.377	0.313	0.389	0.372	0.413	0.365
Tort3D	0.410	0.422	0.365	0.353	0.336	0.235	0.401	0.340	0.437	0.388	0.465	0.423
Tort2D	0.460	0.523	0.373	0.364	0.422	0.355	0.433	0.381	0.495	0.490	0.470	0.436
Curv2D	0.416	0.312	0.322	0.394	0.314	0.287	0.356	0.183	0.402	0.348	0.400	0.314

All correlations significant to p<0.001. Values in bold identify the best flare-tortuosity pairing(s) for each 4×4 table.

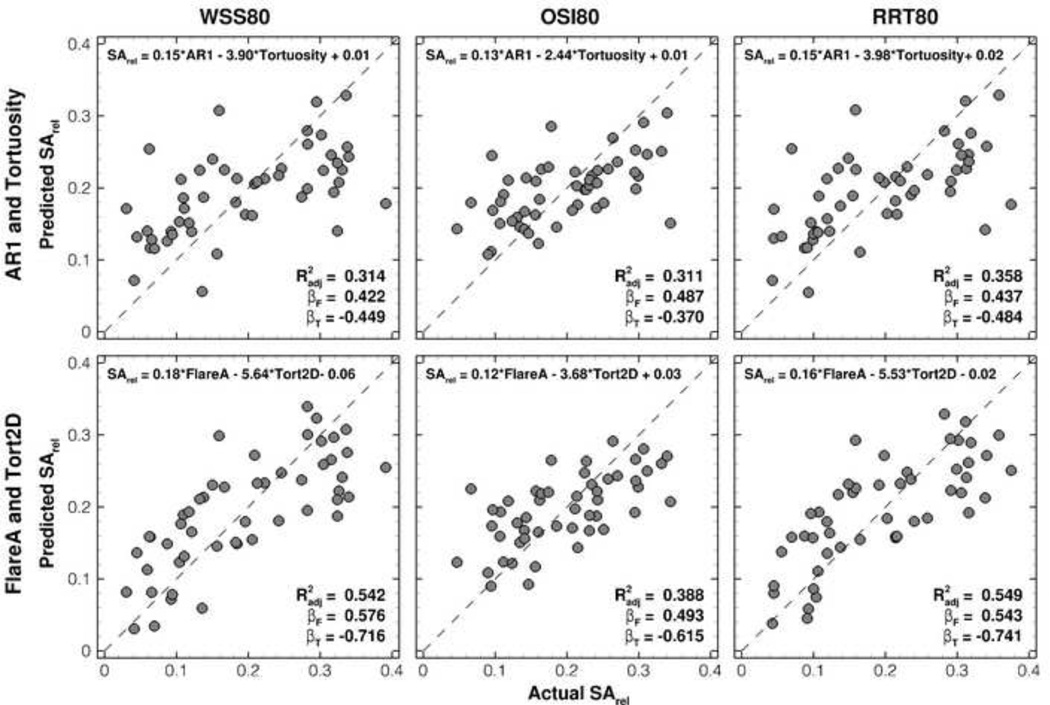
The trend is less clear for the redefined flare variables (i.e., looking across each column of Table 1). For WSS, the Tort2D-FlareA pairing provides the consistently strongest improvement in R² _adj compared to the original two variables (0.542 vs. 0.314 for WSS80; 0.523 vs. 0.375 for WSS90). Figure 2 shows that these improvements can be attributed largely to several cases that are poorly predicted by the original geometric variables. On the other hand, for OSI80 the best correlations are found using AR1 vs. FlareM for OSI90, but inferior to those using WSS80 and WSS90. Regressions for RRT are comparable to those for WSS, although again the trends across the flare variables are less clear.

Figure 2.

Scatter plots illustrating the improved prediction of SA_rel using the original (AR1 and Tortuosity) vs. redefined (FlareA and Tort2D) geometric variables. The upper left of each plot shows the regression equation used to generate the predictions; the lower right shows the coefficient of determination (R² _adj) and standardized regression coefficients for the respective flare and tortuosity variables (β_F and β_T).

As shown in Table 2, the improved prediction of SA_rel by the redefined vs. original variables was consistent irrespective of the SA normalization; however, normalizing by the CCA3 area had a net beneficial effect on all correlations. The excellent reproducibility previously demonstrated byBijari et al. (2011) for the original AR1 and Tortuosity were also found to be unchanged for the respective redefined variables, FlareA (ICC = 0.90) and Tort2D (ICC = 0.93).

Table 2.

Effect of surface area normalization on multiple regressions (R²_adj) of original vs. redefined variable pairings.

	AR1 and Tortuosity			FlareA and Tort2D
SA normalized to:	WSS80	OSI80	RRT80	WSS80	OSI80	RRT80
Bifurcation surface area	0.314	0.311	0.358	0.542	0.388	0.549
CCA3 section area	0.369	0.433	0.420	0.596	0.492	0.607

All correlations significant to p<0.001. Similar trends were seen for WSS90, OSI90 and RRT90, see Supplementary Table 5.

4. DISCUSSION

The present study clearly demonstrates that modest redefinitions of geometric variables, when informed by a studied consideration of the actual hemodynamics they are intending to predict, can lead to marked improvement in those predictions without a loss of reproducibility. In fact, the combination of just two such hemodynamically-inspired variable, Tort2D and FlareA, was comparable or superior to regressions based on the combination of 14 shape-based variables, as derived byZhang et al. (2010) using principal components analysis. Those authors reported R² _adj of 0.439 and 0.520 for WSS80 and WSS90, compared to our 0.542 and 0.523, respectively. Similar comparisons were found for OSI and RRT metrics. Of course PCA could be used to further improve the prediction of disturbed flow by combining shape-based and/or hemodynamically-inspired variables, but at the loss of conceptual simplicity and perhaps consequently, clinical acceptance (Lieber et al., 2005).

4.1. Choice of Optimal Redefined Variables

Our study has clearly shown that the conventional definition of outflow, just distal to the bifurcation, is not the primary determinant of flow expansion in this area. Rather, the maximum area proximal to the bifurcation is a better predictor of flare-induced disturbed flow. Generally speaking, the relative area expansion (FlareA) outperformed its planar variants, FlareM and FlareR. The latter two were chosen to highlight dominant flaring in the bifurcation plane, but overlook the out-of-plane flaring that clearly contributes to flow separation and disturbance. We expected that flare rate (FlareR) would be a better predictor of disturbed flow, at least compared to FlareM, by virtue of accounting for the suddenness of the flaring; however, this was not the case. A possible explanation is that CCA3, while a convenient reference point for the nominal CCA3 diameter, does not necessarily reflect the start of the flare. Attempts to account for this, by automatically searching for the start of the flare along the averaged CCA centerline did not markedly improve R² _adj.

We expected that curvature of the ICA distal to the flow divider would have a confounding effect on the prediction of flow stabilization, and this was demonstrated by the superior correlations obtained using the redefined tortuosity variables. Moreover, inspection of the underlying flow patterns at the bifurcation suggested that stronger secondary flow toward the outer walls of the proximal ICA is induced by the in-plane curvature of the S-shape of the proximal CCA-ICA tract (Morbiducci et al., 2010). Per Table 1, tortuosity derived from the centerline projected onto its best-fit plane was indeed a stronger predictor of disturbed flow compared to 3D tortuosity. On the other hand, it was not entirely clear why Curv2D was a relatively poor predictor of disturbed flow. Initially, we assumed this was because it is a dimensional quantity, but even after normalizing to the inverse of the CCA3 radius the correlations did not improve. A possible reason is that the projected centerline segment is not strictly a circular arc, or at least local variations in curvature have a non-negligible effect on the production of secondary flows.

In the end we have shown that exposure of an individual carotid bifurcation to disturbed flow can be predicted by a relatively simple relationship: SA_rel ∝ FlareA – C×Tort2D, where C is a positive constant falling between 30 and 38, depending on the choice of disturbed flow metric. This is different from the 19–27 range for C reported by Lee et al., which can be explained by the fact that FlareA and Tort2D have values (2.18±0.34 and 0.023±0.013, respectively) different from those of their original counterparts (1.82±0.28 and 0.025±0.012, respectively).

4.2. Impact of Disturbed Flow Indicator

A striking finding was that correlations for the OSI metrics were weaker and less consistent than those for WSS and RRT metrics. By way of explanation, we note that extreme values of OSI can be found at the outer wall of the ECA, whereas this region is typically spared extremes of WSS (e.g., Figure 3, or Figure 3 ofLee et al. (2008)). We speculated that this difference in typical spatial distribution is behind the discrepancy in effectiveness of the redefined geometric variables. To demonstrate this, we recomputed the regressions based on disturbed flow along the outer wall of the CCA-ICA tract (Figure 3C). As summarized by Table 3, this served to align the prediction of OSI metrics with those of WSS and RRT. This is notable, since our ultimate goal is to incorporate these geometric variables into the wider ARIC Carotid MRI study of risk factors for early atherosclerosis, for which wall thickness was measured at the CCA and ICA only (Wasserman et al., 2010).

Table 3.

Effect of the choice of disturbed flow region on multiple regressions (R²_adj) for various pairings of original and redefined variables.

		Whole Surface			CCA-ICA Outer Wall
Geometric Variables		WSS80	OSI80	RRT80	WSS80	OSI80	RRT80
Tortuosity	AR1	0.314	0.311	0.358	0.338	0.365	0.366
Tortuosity	FlareA	0.385	0.244	0.383	0.417	0.342	0.426
Tort2D	AR1	0.444	0.435	0.501	0.453	0.573	0.524
Tort2D	FlareA	0.542	0.388	0.549	0.553	0.580	0.611

All correlations significant to p<0.001. Similar trends were seen for WSS90, OSI90 and RRT90, see Supplementary Table 6.

The choice of CCA3 location as the basis for redefined (and indeed original) geometric variables was somewhat arbitrary, being originally based on the fact that all 50 cases extended to CCA3, whereas only 39 of the cases extended as far as CCA4. As summarized by Table 4, we observed that extending the centerline to CCA4 had a consistently beneficial effect on regressions using Tort2D. Conversely, there was a consistently detrimental effect of truncating the centerline to CCA2. This is likely because the CCA is continuing to curve even down to CCA4, and because the overall increase in the lengths of L and D may afford more dynamic range and higher sensitivity for this geometric variable. On the other hand, there was no consistent effect of CCA location on FlareA, as might be expected since CCA area does not change appreciably between CCA2 and CCA4. Thus, we may anticipate a beneficial, albeit probably modest, effect of considering a more objective definition of the proximal location, particularly as longer CCA segments are available from larger field-of-view acquisitions (e.g., Hoi et al., 2010b).

Table 4.

Effect of proximal CCA location on multiple regressions (R²_adj) using redefined flare and tortuosity pairings, with one of the variable fixed.

	Effect on Tort2D			Effect on FlareA
CCA Location	WSS80	OSI80	RRT80	WSS80	OSI80	RRT80
CCA2	0.447	0.354	0.461	0.498	0.367	0.566
CCA3	0.542	0.388	0.549	0.542	0.387	0.603
CCA4	0.591	0.424	0.603	0.561	0.341	0.577

All correlations significant to p<0.001. Similar trends were seen for WSS90, OSI90 and RRT90, see Supplementary Table 7.

4.3. Potential Limitations

A potential limitation of our study, and indeed that of Lee et al.’s, is that CFD models were truncated near CCA3, whereas our group has recently demonstrated that at least three CCA diameters (i.e., CCA7) may be required to reliably characterize the extent and distribution of disturbed flow (Hoi et al., 2010b)). Including more of the CCA may allow consideration of bulk flow metrics such as helicity, induced by CCA entrance geometry and shown to be closely linked to shear stress and mass transport mechanisms underlying atherosclerosis (Morbiducci et al., 2007). This may provide further clues about how the 3D characteristics of the centerline may be exploited to better predict how disturbed flow is suppressed or amplified by vessel curvature and tortuosity. Having said this, it is worth noting that Lee et al.’s original findings, based on same truncated models considered here, are broadly consistent with in vivo measurements by Markl et al. (2010), which implicitly included the full length of CCA.

Subject-specific flow rates were not available for these cases, and so we employed scaled boundary conditions proposed by Lee et al. (2008). Those authors demonstrated insensitivity of their regressions to the choice of flow boundary conditions, and Hoi et al. (2010a) later showed that use of subject-specific vs. assumed flow rates has only a modest impact on the exposure to disturbed flow. Our study also made the usual assumptions of Newtonian rheology and rigid walls, both demonstrated to have a negligible effect on flow patterns at the carotid bifurcation (Lee and Steinman, 2007; Younis et al., 2004).

In summary, the results of the present study are conclusive that combining only two individual geometric variables, inspired by the influence of flare and tortuosity on hemodynamics at the human carotid bifurcation, can strongly predict the burden of disturbed flow. This reinforces the possibility of using lumen geometry to tease out the influence of local hemodynamic forces vs. systemic risk factors in the development of atherosclerosis. More broadly, the novel approach taken here may reap benefits for other applications where geometry is used as a clinically expedient surrogate marker of disturbed flow, such as for cerebral aneurysm rupture risk assessment (e.g., Xiang et al., 2011).