Abstract
Purpose
To develop a post-processing method to correct saturation of arterial input function (AIF) in T1-weighted DCE-MRI for quantification of hepatic perfusion.
Materials and Methods
The saturated AIF is corrected by parameterizing the first pass of the AIF as a smooth function with a single peak and minimizing a least squares error in fitting the liver DCE-MRI data to a dual-input single-compartment model. Sensitivities of the method to the degree of saturation in the AIF first-pass peak and the image contrast-to-noise ratio were assessed. The method was also evaluated by correlating portal venous perfusion with an independent overall liver function measurement.
Results
The proposed method corrects the distorted AIF with a saturation ratio up to 0.45. The corrected AIF improves hepatic arterial perfusion by −23.4% and portal venous perfusion by 26.9% in a study of 12 patients with liver cancers. The correlation between the mean voxelwise portal venous perfusion and overall liver function measurement was improved by using the corrected AIFs (R2=0.67) compared with the saturated AIFs (R2=0.39).
Conclusion
The method is robust for correcting AIF distortion, and has the potential to improve quantification of hepatic perfusion for assessment of liver tissue response to treatment in patients with hepatic cancers.
Keywords: DCE MRI, AIF saturation, correction, liver, dual-input single compartment model
INTRODUCTION
Dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) in the liver has shown its clinical value for detection of hepatic cancers, diagnosis of cirrhosis and its severity, assessment of therapy effectiveness of liver cancers, and prediction of normal tissue treatment toxicity (1,2). Although semi-quantitative indices of contrast uptake have been used previously (3), compartment kinetic models of DCE MRI have become increasingly important for quantitative analysis of hepatic perfusion. Hepatic perfusion comprises two phases, the arterial and portal venous phases of perfusion. The phases of hepatic perfusion are generally estimated using a dual-input single-compartment model (1), in which the liver is considered to be a single compartment and receives two blood inflows from the hepatic artery and portal vein. Therefore, fitting DCE images to this liver perfusion model requires two input functions, artery and portal vein. An error in either input function can result in a miscalculation of both arterial and portal venous perfusion.
MRI signal intensities are altered by the paramagnetic contrast agent (CA) during a bolus injection of contrast via a change in the longitudinal relaxation rate (R1) of water. A linear relationship between the CA concentration and the change in R1 has been used explicitly or implicitly in DCE MRI quantification. Careful investigations by gel and water phantom studies at different field strengths indicate a departure from this linear relationship, particularly at high CA concentrations and high field strengths (4-9). The factors that affect the linear relationship are multiple and complex, and still a subject of study. In tissue, an effect of magnetic spin water exchange among the major compartments – intravascular, extravascular extracellular, and extravascular intracellular spaces – have been investigated and appear to be one of the factors that complicate the linear relationship between the CA concentration and the change in R1 (5,6,10,11). Furthermore, a finite TE, even 1 or 2 seconds long, used in T1-weighted gradient-echo DCE-MRI acquisition at a high magnetic field can cause a reduction in contrast-enhanced signal intensities due to the susceptibility effect (9,12). This effect is pronounced at high paramagnetic contrast agent concentrations, as during the first pass of the bolus in arterial blood. MRI acquisition parameters, e.g., temporal sampling rate and slice orientation, can also affect quality of the AIF (13). An improper treatment of these effects on the AIF in a rapid contrast uptake experiment and at a high magnetic field can lead to miscalculation of perfusion parameters (9,14).
In this study, we propose a method to correct the distorted AIF delineated from an aorta in T1-weighted DCE-MRI for hepatic perfusion quantification. Considering the complexity of modeling the dual-input single-compartment kinetics in the liver, we used a different approach to parameterize the AIF, and designed a cost function in order to decrease the number of unknown parameters and increase robustness of the solution. This method was evaluated by simulated data and experimental MRI data from 12 patients for accuracy and stability of hepatic perfusion parameters estimated using the dual-input single-compartment model and the AIF corrected by our method. Sensitivities of the method to the degree of saturation in the first-pass peak of the AIF and the contrast-to-noise ratio were also assessed. The physiological evaluation of the method was done by correlating portal venous perfusion with an independent overall liver function measurement.
MATERIALS AND METHODS
Liver Perfusion Model
Using the dual-input single-compartment kinetic model (Figure 1), a change in the CA concentration of the liver is given by the following differential equation:
| [1] |
where Ca, Cp, Cl are CA concentrations in the respective artery, portal vein and liver tissue; ta and tp are time delays of CA bolus arrival from the respective artery and portal vein to a liver voxel of interest; ka and kp are transfer constants of the CA from the respective arterial and portal venous plasma to liver tissue, and k2 is a transfer constant of the CA from liver tissue to the central vein.
Figure 1.
Dual-input single-compartment kinetic model of hepatic perfusion. Ca(t), Cp(t) and Cl(t) represent concentrations of the contrast agent at time t in hepatic artery, portal vein, and liver tissue, respectively. kp, ka and k2 are transfer constants of the contrast agent from hepatic artery to the liver, from portal vein to the liver, and from the liver to central vein, respectively.
To estimate ka, kp and k2 in the kinetic model, concentration-time curves of Ca(t) and Cp(t) are usually determined from volumes of interest (VOIs) drawn on the aorta and portal vein of the T1-weighted MRI, respectively. The relative large sizes of the blood vessels alleviate the partial volume effect on the input functions, and also improve the signal-to-noise ratio (SNR) of the input functions. However, as discussed in the Introduction, the first pass of the AIF, during which the CA concentration is high, has been noticed to present distortion. Figure 2 shows an example of a distorted AIF obtained from an aorta during liver DCE acquisition on a 3T magnet with an intravenous injection of one standard dose of Gd-DTPA at a rate of 2 cc/s. The distorted AIF can lead to a miscalculation of ka and kp. Therefore, we developed a robust method to correct this distortion based on a liver kinetic model.
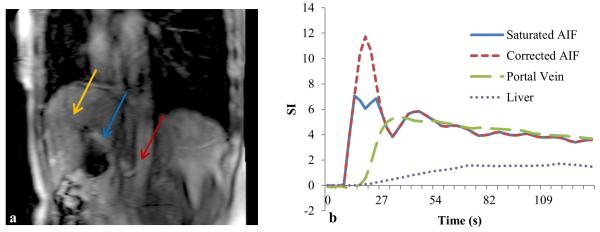
Figure 2.
A slice of DCE-MRI of a patient (Figure a) and the contrast concentration-time curves of the original and corrected AIFs, the portal venous input and the liver parenchyma (Figure b). The first pass of the original AIF shows 42% saturation compared with the corrected one. Arrows in left panel mark locations of aorta, portal vein and liver voxels where the contrast concentration-time curves are obtained.
Formulation of Corrected AIF
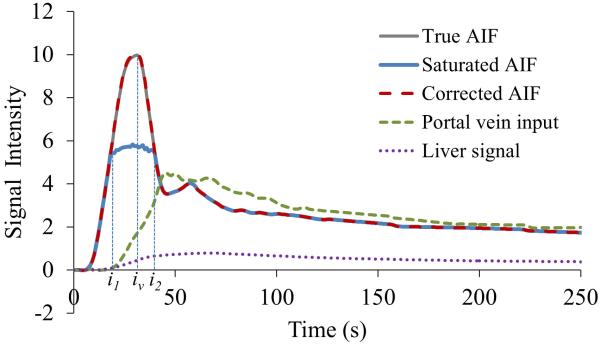
An error in the first pass of the AIF, particularly the peak amplitude, has been shown to significantly affect the fitted kinetic parameters (9,15). Therefore, we propose a method to correct the amplitude of the first pass of the AIF. We assume that the corrected AIF is a smooth function with a single peak at iv between time indices of i1 and i2, and the corrected portion of the AIF is smoothly connected to the measured portions of the curve (at the low CA concentrations) at i1 and i2, as illustrated in Figure 3. The corrected AIF is determined by the best fit of Eq. [1].
Figure 3.
Contrast concentration-time curves of simulated Cl(t), simulated saturated AIF, corrected AIF, true AIF and Cp(t). The simulated AIF is saturated between i1 and i2 with a saturation ratio of 0.45. The corrected AIF by the proposed method is coincident with the true one.
Instead of directly pursuing , we estimate a smooth function f(i) that is defined between i1 − 1 ≤ i ≤ i2 + 1 as follows. For i1 ≤ i ≤ iv where is assumed to monotonically increase until reaching a peak at iv, f(i) is defined as a backward difference of between consecutive points, ; while for iv + 1 ≤ i ≤ i2 where is assumed to monotonically decrease from the peak, f(i) is the forward difference between consecutive points, . Therefore, is computed as:
| [2] |
where Ca(i) is the acquired AIF, and f(i) is constrained to be greater than zero to ensure that has a single peak at iv. To maintain continuity of the curve at the boundary points of i1 and i2 where the corrected portion connects to the measured portions, f(i) at both end points is computed as f (i1 − 1) = Ca(i1 − 1) − Ca (i1 − 2) and f(i2 + 1) = Ca (i2) − Ca(i2 + 1).
The number of unknown parameters (or degree of freedom) in the f(i) estimation is i2 - i1 +1, which is affected by the temporal sampling interval (Δt) of dynamic image acquisition. In order to decrease the degree of freedom in the estimation, f(i) is estimated on only a small number of selected knot points between i2 and i1 . Then, values of f(i) on the other time points are approximated by cubic spline interpolation of the values of knot points. To define the knot points, first the peak point iv and the two end points of (i1-1) and (i2+1) are selected. For the remaining knot points, one knot point is chosen for every D original sampling point. D reduces the number of points in the f(i) estimation and can be adjusted according to the temporal sampling rate. Also, selecting D ≥ 2 ensures a smoother function of f(i) by interpolation between the knot points. In our application, D is chosen to be two. We denote f(i) at the knot points as fknot(p), where p = i1 − 1, i1 − 1 + D, …, iv, iv + D, …, i2 + 1, an index of the knot points in the time course. Therefore, correction of AIF includes (a) estimation of fknot(p) at the knot points, (b) cubic spline approximation of f(i) at all the sampling points from fknot(p), and (c) computation of from f(i) using Eq. [2].
Cost Function for Correction of AIF
The corrected AIF of and the kinetic parameters are assumed to satisfy the dual-input single-compartment model of Eq. [1] by minimizing the least squares error of E as:
| [3] |
where the time derivative , which is computed by the central difference of Cl(i), and is a function of fknot(p), as described previously. To improve SNR in the estimation of Eq. [3], the concentration-time curve Cl(i) is measured from a VOI of uniform normal liver tissue. As discussed above, the constraint of fknot(p)> 0 ensures a single peak in the corrected AIF. The unknown variables in Eq. [3] include the three perfusion parameters (kp, ka, k2), the two time delays (ia, ip) and the values of fknot(p) at the knot points.
Using a matrix format, the least squares function E in Eq. [3] can be rewritten as E = ||∇tCl − S × K||2, where is an N × 3 matrix, and K = (kp, ka, k2)T is a column vector (T is the matrix transpose operator). The linear least squares solution K of E is given by K = (ST S)−1 ST∇tCl. Then, the matrix S can be decomposed to a product of an orthogonal matrix Q and an upper triangular matrix R as S=QR (so QTQ=I), which is implemented by the Gram-Schmidt Orthogonalization (16). Substituting the K into E, the cost function in Eq. [3] becomes E = ||∇tCl − S(STS)−1 ST ∇tCl||2 = (∇tCl)T ∇tCl − (∇tCl)T QTQ∇tCl. Ignoring the constant term, the cost function becomes:
| [4] |
Note that the three kinetic parameters (kp, ka, k2) are removed in Eq [4], and only the time delays and the values of fknot(p) at the knot points remain to be determined.
Minimization of the Cost Function
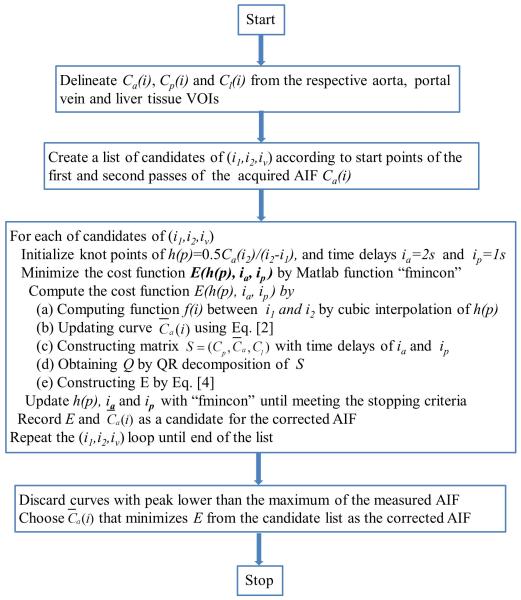
To determine the corrected AIF, Matlab function “fmincon” with the algorithm of “interior-point” is used to find a minimum of the nonlinear multivariable function of Eq. [4] with the constraint of fknot(p) > 0. The iterative minimization terminates when the relative tolerance of the unknowns reaches 10−6, or the number of iterations reaches 800. As discussed previously, the proposed method seeks to correct the values of the AIF between i1 and i2. The start and end points of the distortion can vary markedly across imaging sessions and/or subjects. Note that the time course of the first pass is very dynamic and usually lasts less than 20 sec for an intraveneous injection of a single dose of Gd-DTPA at a rate of 2 cc/s or faster (Figure 2). According to our observation on patient data and the reports of other groups (15), i1 is approximately 4 s after the beginning of the first pass and i2 before the beginning of the second pass. Therefore, candidates of (i1, i2) are limited in the first pass of the AIF. We exhaustively examine each possible pair of (i1, i2) in the first pass, and each possible iv between i1 and i2. After minimizing E with all possible choices of i1, i2, and iv, we first discard the curves with peak concentration lower than the maximum of the measured AIF, and then select the corrected AIF as the one that minimizes the least squares cost function E. Note that this procedure is only done once per imaging session and per patient. A flowchart of the proposed method for AIF correction is given in Figure 4.
Figure 4.
Flow chart of the proposed method for AIF correction
Simulation Study
Simulated data with the true AIF and known perfusion parameters are used to evaluate the influence of AIF distortion on quantification of hepatic perfusion and to assess the performance of the corrected AIF on the estimated perfusion parameters. We first obtained an undistorted AIF and a portal venous input Cp(t) from our previous IRB-approved DCE-CT study (17,18), in which the DCE-CT was sampled at a temporal resolution of 1 s and scanned for 2 min. The liver CA concentration-time curve Cl(t) was then simulated by the solution of the differential Eq. [1] as:
| [5] |
where ka, kp and k2 were 20, 100 and 400 ml/100g/min, respectively, and ta and tp were 1 and 2 s, respectively. These parameters are typical for normal hepatic perfusion (17).
The first pass of the AIF measured from DCE-MRI can be distorted to various degrees. In order to quantify the degree of distortion, we defined a saturation ratio as . We then simulated the distorted AIFs with saturation ratios varying from 0.05 to 0.45 and incremented with a step size of 0.05. For a given saturation ratio r, the intensities of Ca(i1-1) and Ca(i2+1) as well as the indices of i1 and i2 can be determined. The distorted AIF was then obtained by replacing between i1 and i2 by a smooth curve that is spline interpolated from the values of at the point i1 and i2.
Gaussian-distributed random noise was added to Cp(i) and the simulated Ca(i) and Cl(i) to evaluate the effect of noise on the proposed method for AIF correction. The contrast-to-noise ratio (CNR), defined as the ratio of the maximal CA concentration of the dynamic curve to the standard deviation of intensities at the baseline prior to CA administration, was used to describe the level of noise added onto the dynamic data. Ca(i) and Cp(i) were set to have the typical CNRs of 100 and 50, respectively. The CNRs of Cl(i) were 100, 50, 35, 25, 20 and 15. For each combination of CNRs and saturation ratios, the data were simulated 250 times. For each of the simulated data sets, the proposed method was performed to correct the distorted AIF. Then, the perfusion parameters were estimated by nonlinear least squares fitting of simulated DCE data to Eq. [5] using the distorted and corrected AIFs (17). The relative mean and standard deviation (STD) of each perfusion parameter over 250 simulations for each combination of CNRs and saturation rates were computed with respect to the true parameter value. In addition, the simulated data were down-sampled from a temporal resolution of 1 s to 2s or 3s to evaluate the effect of the temporal resolution on the AIF correction. Again, noise was added into Ca(i), Cp(i) and Cl(i) to yield CNRs of 100, 50 and 50, respectively. Similar statistical analyses were performed.
Patient Liver Perfusion Study
DCE-MRI data of 12 patients with intra-hepatic cancers were acquired before radiation therapy in a prospective IRB-approved protocol. The DCE MRI data were acquired during a bolus injection of 15mL Gd-DTPA at a rate of 2 mL/sec on a clinical 3T MR scanner (Philips Achieva 3.0T; Philips Heathcare, Netherlands). 3D volumetric MRI of the whole liver was obtained every 2 seconds for a total of 2 minutes with a gradient echo pulse sequence (TR/TE/FA: 4.48/2.15/20°; Matrix: 320×320×66; FOV: 33×33×19.8 cm; SENSE factor: 2 in 2 different directions). The 3D DCE MRI was acquired in sagittal/coronal orientation to avoid the inflow effect. In order to reduce breathing-related motion artifacts in the DCE images, patients were coached to hold their breath as long as possible at the beginning of image acquisition, followed by repeated cycles of rapid inhale for 2-3s and short breath-holding for 10-12s until the completion of acquisition.
An arterial input function (Ca(t)) and a portal vein input function (Cp(t)) were obtained from VOIs of aorta and portal vein delineated, respectively, on MR images. Another VOI in normal liver tissue was delineated to obtain the CA concentration-time course of Cl(t). Care was taken to choose the liver tissue VOI that had uniform CA concentration-time curves across voxels. The numbers of voxels in these VOIs were approximately 800, 400, and 350 for Ca(t), Cp(t) and Cl(t), respectively. The MR intensity-time curves from these VOIs were related to the CA concentration-time curves by using the linear relationship between the CA concentration and the R1 enhancement after CA administration, while ignoring the effect of T2* on the data. The AIFs obtained from the DCE MRI data of these patients show substantial distortion on the first pass. We applied the proposed method to correct the measured AIFs from the MRI data of each patient.
To examine the effect of the AIF correction on perfusion measurements in normal tissue of the liver, the perfusion parameters in the liver VOIs were estimated by the conventional least squares fitting method using the original and corrected AIFs (17). In addition, perfusion of the whole liver was quantified voxel-by-voxel using the original and corrected AIFs. The goodness-of-fit of voxel-by-voxel perfusion computations using the corrected AIFs was compared with using the original AIFs. Furthermore, we performed physiological evaluations of the proposed method. The liver is considered as a parallel organ, the overall function of which is a sum of the function of sub-units (19-22). We measured overall liver function of the patients within 1-2 days of MRI scans by an established method -- Indocyanine green (ICG) clearance. A previous DCE-CT study has shown a strong correlation between the mean of portal venous perfusion in the whole liver and ICG clearance (18). Here, we tested the correlation between the mean of voxel-by-voxel portal venous perfusion over the whole non-tumor liver, derived from DCE MRI using the corrected or original AIF, with the ICG clearance rate (1/T1/2).
RESULTS
Simulation study
We evaluated the effect of the saturation ratio on the perfusion parameters. The saturated AIF caused overestimation in ka, underestimation in kp, and little change in k2 compared to the true values (Figure 5). As the saturation ratio in the distorted AIF increased from 0.20 to 0.45, overestimation in ka increased from 18% to 92%, and underestimation in kp changed from 3% to 17%, where CNRs for Cp(t), Ca(t) and Cl(t) were 50, 100 and 50, respectively (Figure 5). After correcting the distorted AIF by the proposed method, errors in the estimated perfusion parameters were less than 5% for ka and 3% for kp compared with the true values (Figure 5). The relative STDs of the estimated perfusion parameters over 250 simulations, an indicator of stability of the method, showed a less than 5% difference between using the corrected and saturated AIFs (Figure 5). Note that additional free parameters were introduced in the optimization for correcting the AIF, which could affect stability of each of the individual perfusion parameters. Figure 3 shows an example in which the proposed method restores the first pass curve of the AIF from the simulated distorted AIF that has a saturation ratio of 0.45.
Figure 5.
Relative mean values (left column) and relative standard deviations (right column) of estimated kp, ka, k2 to the true values using the saturated AIF and corrected AIF vs saturation ratios. The CNRs of the concentration-time signals of Ca(t), Cp(t) and Cl(t) are of 100, 50 and 50, respectively. Descriptive statistics were obtained from 250 simulations.
Sensitivity of the estimated perfusion parameters using the distorted and corrected AIFs to CNR and saturation ratio are given in Figure 5. Overall, the estimated perfusion parameters are less sensitive to CNR than level of saturation independent of using corrected or saturated AIFs (Figure 6). Using the corrected AIF, the estimated parameters of kp, ka and k2 differed from the true values by less than 5% when the CNR of Cl was equal to or greater than 20, demonstrating the robustness of the proposed method. The effects of temporal resolution of DCE-MRI on the AIF correction and subsequent perfusion-parameter estimation are shown in Figure 7. For the sampling intervals of 1s, 2s and 3s, estimated values of kp and k2, using the corrected AIF deviated from the true values less than 3% and 2%, respectively, regardless of the saturation ratios. The errors in the ka estimation were less than 3% and 10% for 2s and 3s of temporal resolution, respectively.
Figure 6.
Relative mean values of kp, ka, k2 estimated from the saturated (left) and corrected AIFs (right) vs CNRs and saturation ratios. Each of relative means was obtained from 250 simulations.
Figure 7.
Relative mean values of kp, ka, k2 estimated using the corrected AIF vs saturation ratio. The dynamic contrast-activity time curves have sampling time intervals of 1s, 2s and 3s
Human study
The proposed method has been applied to correct the AIFs in a DCE-MRI study of 12 patients with intrahepatic cancers. A slice of the DCE-MRI of a patient in Figure 2a illustrates locations of the aorta, portal vein and liver voxels, where the AIF, portal vein input and liver dynamic curve were delineated. Figure 2b shows there is severe saturation, approximately 0.4 in the saturation ratio, in the first pass of the acquired AIF, which can substantially overestimate ka and underestimate kp.
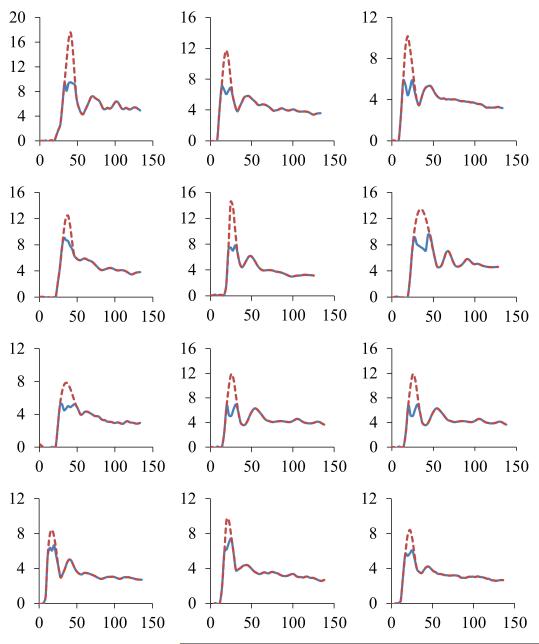
The original and corrected AIFs of the 12 patients are plotted in Figure 8. The original AIFs in all patients show marked saturation during the first pass, in contrast to the corrected AIFs. Compared with the corrected AIFs, the original AIFs of the 12 patients had a mean saturation ratio of 0.36 ± 0.12. Figure 8 also shows considerable variations in the AIFs, including the amplitude, width, and shape across the patients, which suggests it is necessary to determine the AIF individually in a DCE study.
Figure 8.
The original AIFs (solid curve) and the corrected AIFs (dash line) obtained from DCE-MRI of 12 patients with intraphepatic cancers. Each plot is for one of the patients.
Perfusion parameters were estimated using the original and corrected AIFs in the VOIs of normal liver tissue in the 12 patients (Table I). The corrected AIFs resulted in an average increase in estimated kp by 26.9% and an average decrease in ka by 23.4%, consistent with the findings in the simulated data. Note that there was only a 2.7% change in estimated k2 using the corrected AIFs compared to the original ones. The pair-t test indicated significant alterations in estimated ka and kp values using the corrected AIFs, compared with using the measured ones (p < 0.05). Applying the corrected AIF to DCE MRI for volumetric perfusion quantification, the estimates of time delay ta and tp showed substantial changes throughout the liver, in which ta varied from 1 s to 10 s and tp ranged from 0 s to 8 s.
Table 1.
Hepatic perfusion parameters estimated by the original and corrected AIF in normal liver tissue of 12 patients. The change in percentage is the difference between the parameters estimated using the corrected and original AIFs as a fraction of the estimates with the corrected AIF
| Original AIF (ml/100g/min) |
Corrected AIF (ml/100g/min) |
Change (%) | P-Value | |
|---|---|---|---|---|
| kp | 94.9 ± 24.3 | 120.5 ± 30.0 | 19.4 | 0.004 |
| ka | 29.3 ± 9.3 | 22.4 ± 8.0 | −30.5 | 0.002 |
| k2 | 378.0 ± 82.2 | 388.0 ± 71.5 | 2.6 | 0.595 |
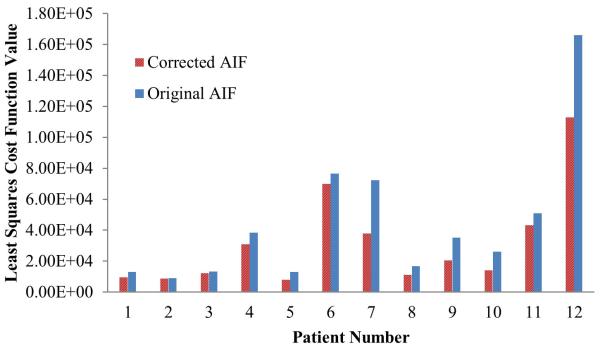
When evaluating goodness-of-fit of the voxel-by-voxel estimation of the hepatic perfusion parameters by minimizing the least-squares cost function in fitting DCE MRI to Eq [5], averages of residual cost function values over all voxels were smaller using the corrected AIFs than using the original AIFs in all patients (Figure 9). Finally, when evaluating MRI-derived portal venous perfusion with an independent liver function measurement, the correlation between the mean of voxel-by-voxel portal venous perfusion in the whole non-tumor liver volume and the ICG clearance rate was stronger using the corrected AIF than using the measured AIF (R2=0.67 vs R2=0.39, Figure 10).
Figure 9.
The least squares cost function values of the perfusion quantification using the original and corrected AIF for the 12 patients. The value of a patient is the mean cost of the voxel-by voxel perfusion estimations in the liver.
Figure 10.
Means of portal venous perfusions (kp) in the non-tumor liver volumes vs ICG clearance rates (1/T1/2) in the 12 patients. A better correlation was achieved by using the corrected AIFs (diamonds) than using the saturated ones (squares).
DISCUSSION
In this study, we proposed a post-processing method to correct the distorted AIF for quantification of hepatic perfusion parameters from DCE MRI. This method is based upon minimization of a cost function of the dual-input single-compartment kinetic model in a VOI of liver tissue. We evaluated the method by using simulated data generated from liver DCE-CT data that had the known AIF and perfusion parameter values, DCE-MRI data from the 12 patients with intrahepatice cancer, and independent physiological data of overall liver function. Also, we assessed the sensitivity and stability of the method to CNR in the image data and the degree of distortion in the AIF. The results show that our method is very robust to noise in DCE images and can correct an AIF with a saturation ratio up to 0.45. The DCE-MRI-derived AIF without correction underestimated hepatic arterial perfusion by 23.4% and overestimated portal venous perfusion by 26.9%, resulting in a poor correlation with the overall liver function measure. Our method is a robust and practical approach to dealing with measurement errors in the AIF, regardless of causes and mechanisms.
As discussed in the Introduction, the causes of measurement errors in the AIF from DCE MRI are multiple and complex. Many of these causes become pronounced at a high CA concentration in the tissue, e.g., the T2* effect, and the departure of the linear relationship between the R1 change and the CA concentration. An intuitive way to alleviate some of the effects on the AIF is to lower the CA concentration by administrating a low dose of the contrast agent, or by slowing the injection rate. However, a low CA concentration administrated in the blood decreases the contrast-to-noise ratio in DCE MRI by a square root, which can result in an increase in the error and variation in perfusion quantification and thus is not desirable (17). A population-average AIF has been suggested to avoid difficulty in measurement of individual AIFs (23), but neglecting intra- and inter-subject physiological variations in the distribution and elimination of CA in the blood causes errors in the perfusion parameters greater than using individual AIFs (24,25). The reference tissue method shows its value as an alternative modeling approach by avoiding large errors in the measured AIFs for cerebral perfusion quantification (26,27), but relies on either literature perfusion values of the reference tissue (27) or published empirical models of the AIF in the reference tissue (28,29). For a longitudinal study, it is challenging to choose reference tissues in a liver undergoing anti-cancer chemo and radiation therapy. Another approach to the problem is to address one fundamental effect at a time, e.g., the T2* effect, by using a double gradient echo pulse sequence (12,30,31), but neglecting others. The prolonged acquisition time and repetition time in the double-echo approach also have negative effects on quality of the AIF and DCE MRI data. Another approach is to delineate the AIF from the phase change in the DCE MRI signals (32-34), instead of from the amplitude change. Knutsson et al (35) propose to generate an AIF by amplifying the concentration curve from a smaller vein, which needs carefully match the curve from the vein with the concentration curve of the superior sagittal sinus. Recently, the methods that model the whole AIF curve as a parameterized function for cerebral DCE MRI have shown promise (36,37). However, the modeling often becomes to a large nonlinear minimization problem. In another study of DSC-MRI cerebral perfusion, only the saturated portion of the AIF is reconstructed as two third-order polynomial functions based upon the transport-diffusion theory (15). In this study, we adopt the similar strategy to correct the distorted AIF for quantification of hepatic perfusion from liver DCE MRI. Given the complexity in modeling the AIF using the dual-input single-compartment liver model, we carefully parameterize the AIF, design a robust cost function in which the number of free parameters are reduced to a minimum (by removing three hepatic perfusion parameters and limiting the number of fitting points in the AIF), and choose an effective optimization method.
The most substantial distortion in the AIF is observed in the first pass by the presence of a high CA concentration (Figures 3 and 8). At a low CA concentration and slow contrast uptake, the effects of T2*, water exchange of spins between tissue compartments, and sampling rate on the AIF diminish. Although errors could present in the second pass and steady state phase of the AIF, particularly in the case of excessive contrast administration, previous studies have indicated that the first pass of the AIF is the most crucial for perfusion quantification (38). Meanwhile, fitting the whole AIF curve increases the number of free parameters dramatically, which often results in individual perfusion parameters that are less robust and unstable under influence of noise even though the overall goodness-of-fit can be improved. In addition, fitting the whole AIF curve requires determining an overall scaling factor, which is not trivial for each of the individual patients (36). Considering all these issues, we propose a robust method to correct the intensity errors in the first pass of the AIF.
The first pass of the contrast bolus in the aorta presents as a rapid increase followed by a sharp decrease. In order to fit a function to follow this rapid temporal curve change in the first pass of the AIF and avoid jitter in the fitted curve due to noise, we use intensity differences between consecutive points to parameterize the first pass of the AIF, and constrain the intensity differences before and after the peak to be greater than zero. In our implementation, we avoid the use of a presumed mathematic function or a combination of multiple functions to mimic the shape of the AIF, which often encounters a challenge due to inter-subject variation in the shape of the AIF. To decrease the number of free parameters in the optimization, we fit the intensity differences at the limited knot points rather than all sampling points of the first pass of the AIF, and then interpolate the fitting results onto all sampling points by a cubic spline. We find that using 3-4 knot points in the first pass, which is equivalent to one knot point for every two sampling points in our case, is sufficient. The results from our simulated data show that our strategy for selection of knot points produces very accurate restoration of the true AIF. In addition, performance of our method has the advantage of removing the three perfusion parameters from the cost function (Eq. [4]), which further decreases the degree of freedom in the optimization. Due to these designs and implementations, the proposed method successfully corrects the first pass distortion of the AIF with respect to a large range of saturation ratios and is robust to noise, as demonstrated in the simulation study.
The simulation study assumes the liver DCE signal follows the dual-input single compartmental model. This assumption limits the interpretation of the simulation results. However, the simulation and patient studies show the proposed method is adequate for MRI experiments like ours, in which we use one standard dose of Gd-DTPA with a modest injection rate of 2 cc/s. Using the corrected AIF, arterial and portal venous perfusion estimated in the normal liver VOIs of the patients from the DCE MRI is consistent with the findings in the DCE-CT studies (17,18). Most importantly, the correlation between the mean of voxel-by-voxel portal venous perfusion over the whole non-tumor liver and the overall liver function is improved using the corrected AIF instead of the original AIF.
In conclusion, we developed a method to correct the distortion in the first pass of arterial input function measured in the aorta for quantification of hepatic perfusion from T1-weighted DCE MRI using a dual-input single-compartment model. The design and implementation of our method show advantages in dealing with the complexity in the parameterization of the AIF and optimization of the compartment model. The evaluation of our method using simulated data, DCE MRI data from the patients, and physiological data demonstrates the stability and accuracy of estimated hepatic perfusion parameters with respect to the degree of distortion in the AIF and noise in the images. The proposed method may improve quantification of hepatic perfusion from DCE-MRI.
Acknowledgments
Grant Support: NIH P01 CA59827, RO1 CA132834
REFERENCES
- 1.Thng CH, Koh TS, Collins DJ, Koh DM. Perfusion magnetic resonance imaging of the liver. World J Gastroenterol. 2010;16:1598–1609. doi: 10.3748/wjg.v16.i13.1598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Van Beers BE, Leconte I, Materne R, Smith AM, Jamart J, Horsmans Y. Hepatic perfusion parameters in chronic liver disease: dynamic CT measurements correlated with disease severity. AJR Am J Roentgenol. 2001;176:667–673. doi: 10.2214/ajr.176.3.1760667. [DOI] [PubMed] [Google Scholar]
- 3.Miyazaki S, Murase K, Yoshikawa T, Morimoto S, Ohno Y, Sugimura K. A quantitative method for estimating hepatic blood flow using a dual-input single-compartment model. Br J Radiol. 2008;81:790–800. doi: 10.1259/bjr/52166324. [DOI] [PubMed] [Google Scholar]
- 4.Donahue KM, Burstein D, Manning WJ, Gray ML. Studies of Gd-DTPA relaxivity and proton exchange rates in tissue. Magn Reson Med. 1994;32:66–76. doi: 10.1002/mrm.1910320110. [DOI] [PubMed] [Google Scholar]
- 5.Landis CS, Li X, Telang FW, et al. Determination of the MRI contrast agent concentration time course in vivo following bolus injection: effect of equilibrium transcytolemmal water exchange. Magn Reson Med. 2000;44:563–574. doi: 10.1002/1522-2594(200010)44:4<563::aid-mrm10>3.0.co;2-#. [DOI] [PubMed] [Google Scholar]
- 6.Landis CS, Li X, Telang FW, et al. Equilibrium transcytolemmal water-exchange kinetics in skeletal muscle in vivo. Magn Reson Med. 1999;42:467–478. doi: 10.1002/(sici)1522-2594(199909)42:3<467::aid-mrm9>3.0.co;2-0. [DOI] [PubMed] [Google Scholar]
- 7.Stanisz GJ, Henkelman RM. Gd-DTPA relaxivity depends on macromolecular content. Magn Reson Med. 2000;44:665–667. doi: 10.1002/1522-2594(200011)44:5<665::aid-mrm1>3.0.co;2-m. [DOI] [PubMed] [Google Scholar]
- 8.Weinmann HJ, Brasch RC, Press WR, Wesbey GE. Characteristics of gadolinium-DTPA complex: a potential NMR contrast agent. AJR Am J Roentgenol. 1984;142:619–624. doi: 10.2214/ajr.142.3.619. [DOI] [PubMed] [Google Scholar]
- 9.de Bazelaire C, Rofsky NM, Duhamel G, et al. Combined T2* and T1 measurements for improved perfusion and permeability studies in high field using dynamic contrast enhancement. Eur Radiol. 2006;16:2083–2091. doi: 10.1007/s00330-006-0198-1. [DOI] [PubMed] [Google Scholar]
- 10.Cao Y, Brown SL, Knight RA, Fenstermacher JD, Ewing JR. Effect of intravascular-to extravascular water exchange on the determination of blood-to-tissue transfer constant by magnetic resonance imaging. Magn Reson Med. 2005;53:282–293. doi: 10.1002/mrm.20340. [DOI] [PubMed] [Google Scholar]
- 11.Ewing JR, Knight RA, Nagaraja TN, et al. Patlak plots of Gd-DTPA MRI data yield blood-brain transfer constants concordant with those of 14C-sucrose in areas of blood-brain opening. Magn Reson Med. 2003;50:283–292. doi: 10.1002/mrm.10524. [DOI] [PubMed] [Google Scholar]
- 12.Kuperman VY, Alley MT. Differentiation between the effects of T1 and T2* shortening in contrast-enhanced MRI of the breast. J Magn Reson Imaging. 1999;9:172–176. doi: 10.1002/(sici)1522-2586(199902)9:2<172::aid-jmri4>3.0.co;2-g. [DOI] [PubMed] [Google Scholar]
- 13.Cheng HL. Investigation and optimization of parameter accuracy in dynamic contrast-enhanced MRI. J Magn Reson Imaging. 2008;28:736–743. doi: 10.1002/jmri.21489. [DOI] [PubMed] [Google Scholar]
- 14.Ellinger R, Kremser C, Schocke MF, et al. The impact of peak saturation of the arterial input function on quantitative evaluation of dynamic susceptibility contrast-enhanced MR studies. J Comput Assist Tomogr. 2000;24:942–948. doi: 10.1097/00004728-200011000-00022. [DOI] [PubMed] [Google Scholar]
- 15.Brunecker P, Villringer A, Schultze J, et al. Correcting saturation effects of the arterial input function in dynamic susceptibility contrast-enhanced MRI: a Monte Carlo simulation. Magn Reson Imaging. 2007;25:1300–1311. doi: 10.1016/j.mri.2007.03.011. [DOI] [PubMed] [Google Scholar]
- 16.Arfken G. Gram-Schmidt Orthogonalization. Academic Press; Orlando,FL: 1985. [Google Scholar]
- 17.Cao Y, Alspaugh J, Shen Z, Balter JM, Lawrence TS, Ten Haken RK. A practical approach for quantitative estimates of voxel-by-voxel liver perfusion using DCE imaging and a compartmental model. Med Phys. 2006;33:3057–3062. doi: 10.1118/1.2219773. [DOI] [PubMed] [Google Scholar]
- 18.Cao Y, Platt JF, Francis IR, et al. The prediction of radiation-induced liver dysfunction using a local dose and regional venous perfusion model. Med Phys. 2007;34:604–612. doi: 10.1118/1.2431081. [DOI] [PubMed] [Google Scholar]
- 19.Yorke ED, Kutcher GJ, Jackson A, Ling CC. Probability of radiation-induced complications in normal tissues with parallel architecture under conditions of uniform whole or partial organ irradiation. Radiother Oncol. 1993;26:226–237. doi: 10.1016/0167-8140(93)90264-9. [DOI] [PubMed] [Google Scholar]
- 20.Withers HR, Taylor JM, Maciejewski B. Treatment volume and tissue tolerance. Int J Radiat Oncol Biol Phys. 1988;14:751–759. doi: 10.1016/0360-3016(88)90098-3. [DOI] [PubMed] [Google Scholar]
- 21.Jackson A, Ten Haken RK, Robertson JM, Kessler ML, Kutcher GJ, Lawrence TS. Analysis of clinical complication data for radiation hepatitis using a parallel architecture model. Int J Radiat Oncol Biol Phys. 1995;31:883–891. doi: 10.1016/0360-3016(94)00471-4. [DOI] [PubMed] [Google Scholar]
- 22.Jackson A, Kutcher GJ, Yorke ED. Probability of radiation-induced complications for normal tissues with parallel architecture subject to non-uniform irradiation. Med Phys. 1993;20:613–625. doi: 10.1118/1.597056. [DOI] [PubMed] [Google Scholar]
- 23.Shukla-Dave A, Lee N, Stambuk H, et al. Average arterial input function for quantitative dynamic contrast enhanced magnetic resonance imaging of neck nodal metastases. BMC Med Phys. 2009;9:4. doi: 10.1186/1756-6649-9-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ahearn TS, Staff RT, Redpath TW, Semple SI. The effects of renal variation upon measurements of perfusion and leakage volume in breast tumours. Phys Med Biol. 2004;49:2041–2051. doi: 10.1088/0031-9155/49/10/014. [DOI] [PubMed] [Google Scholar]
- 25.Meng R, Chang SD, Jones EC, Goldenberg SL, Kozlowski P. Comparison between population average and experimentally measured arterial input function in predicting biopsy results in prostate cancer. Acad Radiol. 2010;17:520–525. doi: 10.1016/j.acra.2009.11.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kovar Da Fau - Lewis M, Lewis M Fau - Karczmar GS, Karczmar GS. A new method for imaging perfusion and contrast extraction fraction: input functions derived from reference tissues. J Magn Reson Imaging. 1998;8:1126–1134. doi: 10.1002/jmri.1880080519. [DOI] [PubMed] [Google Scholar]
- 27.Yang C, Karczmar GS, Medved M, Stadler WM. Multiple reference tissue method for contrast agent arterial input function estimation. Magn Reson Med. 2007;58:1266–1275. doi: 10.1002/mrm.21311. [DOI] [PubMed] [Google Scholar]
- 28.Fan X, Haney CR, Mustafi D, et al. Use of a reference tissue and blood vessel to measure the arterial input function in DCEMRI. Magn Reson Med. 2010;64:1821–1826. doi: 10.1002/mrm.22551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Heisen M, Fan X, Buurman J, van Riel NA, Karczmar GS, ter Haar Romeny BM. The use of a reference tissue arterial input function with low-temporal-resolution DCE-MRI data. Phys Med Biol. 2010;55:4871–4883. doi: 10.1088/0031-9155/55/16/016. [DOI] [PubMed] [Google Scholar]
- 30.Kuperman VY, Karczmar GS, Blomley MJ, Lewis MZ, Lubich LM, Lipton MJ. Differentiating between T1 and T2* changes caused by gadopentetate dimeglumine in the kidney by using a double-echo dynamic MR imaging sequence. J Magn Reson Imaging. 1996;6:764–768. doi: 10.1002/jmri.1880060509. [DOI] [PubMed] [Google Scholar]
- 31.Uematsu H, Maeda M. Double-echo perfusion-weighted MR imaging: basic concepts and application in brain tumors for the assessment of tumor blood volume and vascular permeability. Eur Radiol. 2006;16:180–186. doi: 10.1007/s00330-005-2807-9. [DOI] [PubMed] [Google Scholar]
- 32.Bleeker EJ, van Buchem MA, Webb AG, van Osch MJ. Phase-based arterial input function measurements for dynamic susceptibility contrast MRI. Magn Reson Med. 2010;64:358–368. doi: 10.1002/mrm.22420. [DOI] [PubMed] [Google Scholar]
- 33.Cron GO, Foottit C, Yankeelov TE, Avruch LI, Schweitzer ME, Cameron I. Arterial input functions determined from MR signal magnitude and phase for quantitative dynamic contrast-enhanced MRI in the human pelvis. Magn Reson Med. 2011;66:498–504. doi: 10.1002/mrm.22856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Korporaal JG, van den Berg CA, van Osch MJ, Groenendaal G, van Vulpen M, van der Heide UA. Phase-based arterial input function measurements in the femoral arteries for quantification of dynamic contrast-enhanced (DCE) MRI and comparison with DCE-CT. Magn Reson Med. 2011;66:1267–1274. doi: 10.1002/mrm.22905. [DOI] [PubMed] [Google Scholar]
- 35.Knutsson L, Börjesson S, Larsson EM, Risberg J, Gustafson L, Passant U, Ståhlberg F, Wirestam R. Absolute quantification of cerebral blood flow in normal volunteers: correlation between Xe-133 SPECT and dynamic susceptibility contrast MRI. J Magn Reson Imaging. 2007;26:913–920. doi: 10.1002/jmri.21093. [DOI] [PubMed] [Google Scholar]
- 36.Schabel MC, DiBella EV, Jensen RL, Salzman KL. A model-constrained Monte Carlo method for blind arterial input function estimation in dynamic contrast-enhanced MRI: II. In vivo results. Phys Med Biol. 2010;55:4807–4823. doi: 10.1088/0031-9155/55/16/012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Schabel MC, Fluckiger JU, DiBella EV. A model-constrained Monte Carlo method for blind arterial input function estimation in dynamic contrast-enhanced MRI: I. Simulations. Phys Med Biol. 2010;55:4783–4806. doi: 10.1088/0031-9155/55/16/011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Murase K, Shinohara M, Yamazaki Y. Accuracy of deconvolution analysis based on singular value decomposition for quantification of cerebral blood flow using dynamic susceptibility contrast-enhanced magnetic resonance imaging. Phys Med Biol. 2001;46:3147–3159. doi: 10.1088/0031-9155/46/12/306. [DOI] [PubMed] [Google Scholar]