Recently, the funnel shape energy landscape theory has been successfully utilized to describe the folding (1–4) and binding (5) behavior in proteins. While in general the free energy landscape is depicted by a funnel-like shape, the details of the landscape surface of a folding funnel will be affected by changes in the surrounding environment. On the basis of Freire’s work in this issue of the Proceedings (6), we describe a shift in the energy landscape of a folding funnel, caused by a binding event. Shifts in energy landscapes portray shifts in the populations of the substates.
The exciting paper by Freire (6) presents a structure-based statistical thermodynamic approach to predict the stabilization effects observed following the binding of a ligand to a receptor. Interestingly, the structure-based thermodynamic analysis indicates that the stabilization effect is not distributed uniformly throughout the enzyme. Instead, upon the binding of the inhibitor, the stability constants of individual residues exhibit changes in their magnitudes. Of particular interest is the finding made by Freire and his colleagues that upon binding, large changes are observed in residues which are far away from the binding sites. These results are consistent with experiments (7) showing changes in amide hydrogen exchange rates in lysozyme, when complexed with three different antibodies. Regardless of the sites at which the (D44.1, D1.3, and HyHEL-5) antibodies bound, the remote residues were found to be protected by the binding events. Additional, consistent evidence comes from crystal structures of mutants of HIV-1 protease, which show that changes far away from the active site affect the conformation at this region (8).
Furthermore, a major finding of Freire is the dual character of active sites. Freire has applied the algorithm to a number of proteins, showing that binding sites characteristically have regions of high and low structural stability, with a significant fraction of their residues being flexible. While the less stable (more flexible) region allows “opening” of the active site, to allow the ligand to enter, the stable region contributes to the specificity and affinity of the binding. This dual character implies that there are minor changes between the bound and unbound conformations at the active site. Hence, the algorithm developed by Freire (6) addresses cases that do not illustrate large scale motions, typically included in Koshland’s classical induced fit model (9). The availability of a predictive scheme, which can predict changes in stability of residues that are distant from the binding sites, and its application to studies of the effects of binding on remote regions are important contributions to our understanding of protein folding and binding.
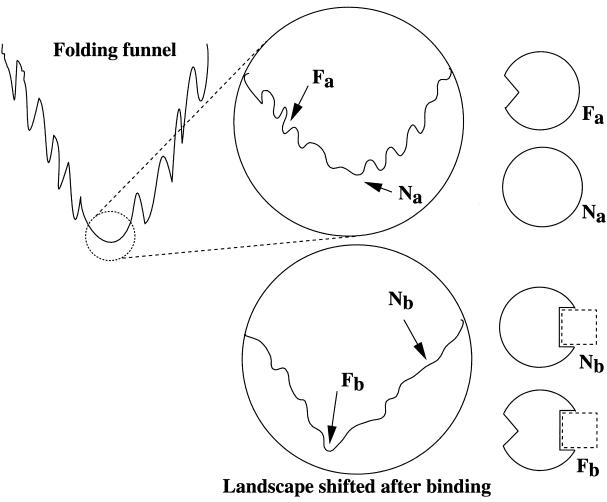
The implications of the paper by Freire are far reaching. They are in agreement with current notions on protein folding (10–13) and binding (14–16). Protein folding is now viewed as multiple conformations racing down the funnel slopes in multiple paths, with some more heavily traveled than others. In protein folding, energy landscapes have been depicted in terms of hills, corresponding to high energy conformations and valleys, having more favorable conformations than those in their energy-landscape vicinity. Around the bottom of the valleys there are populations of conformations. If the landscape is smooth, the native protein may be expected to have small fluctuations, with only small changes in its conformation. However, if the energy landscape is rugged, the ensemble of structures would include conformations that may be quite different, depending on the extent of the ruggedness. The conformer with the highest population time under certain conditions is not necessarily the one that binds to the ligand. Hence, while inspection of the crystal structures of the bound as compared with the free, unbound molecules may reveal differences in the conformations, these differences are not the outcome of conformational changes that are induced by the ligands (5, 14, 15). These changes simply illustrate that the conformation which is most favorable for crystallization when unbound to the ligand is not the one which is most favorable in the bound state. Because there is a range of conformations, the conformer that is most favorable for binding, even if its population in solution is lower than other, alternate conformations, is the one that will bind. The equilibrium will then shift in favor of this conformation. Fig. 1 depicts a folding funnel, with a rugged bottom, corresponding to a population of conformational isomers.
Figure 1.
At the bottom of a folding funnel (shown enclosed by a small circle, which is projected and magnified in the larger circle), there are many distinctive, accessible conformations around the most populated native structure. For clarity, only the native structure and the functional conformation are highlighted in the figure. They are indicated by the schematic drawings as Na and Fa, respectively. The conformational change responsible for the cascade reaction in binding is drawn opposite to the binding site to reflect that it is remote from the binding site. On binding (indicated by a dashed rectangle), the environment changes. The change in the environment has the effect of making the folding energy surface shift, to favor the functional conformation (Fb) instead of the native structure (Nb). Hence, in terms of the free energy landscape theory, the functional switch-on mechanism is not by induced and propagated conformational change of the protein molecule through binding; rather, it is a shift of the population toward the functional conformer.
The energy landscape model applies consistently to a range of short and long polypeptide chains and for intra- and intermolecular associations, that is, for folding and for binding (5). Binding and folding are similar processes (5, 16). Folding is a hierarchical process (5, 16–18), involving a combinatorial assembly of a set of conformationally fluctuating building blocks (5, 16). A building block is a fragment of the protein, with a transient, highly populated conformation. The conformation of the building block that we observe in the native structure is not necessarily the most highly populated conformation in the initial stages of the folding, or of the isolated fragment. Building blocks associate into hydrophobic folding units (19), which further associate to form domains, and subsequently, entire proteins (16). The hydrophobic collapse of the building blocks may be fast. However, the critical consideration is the barrier heights: If climbing out of the local minima takes time, trapped intermediates would be observed. If, however, the conformation of the mutually stabilizing, interacting building blocks in the collapsed state is similar to the one in the native state, with only minor alterations, the barriers are low, and a fast two-state-like folding is observed. Starting from the entire structure, it is progressively cut into smaller units, culminating in a set of building blocks. The initial formation of “microdomains” in protein folding in the collision–diffusion model (20) is also characterized by features similar to the formation of building blocks. The “foldon” approach (21), where a protein is built from an assembly of foldons, also corresponds nicely to the building blocks concept. With the exception of two differences, a building block in protein folding corresponds to a folded monomer in protein binding. The first important difference is the population time. The population time of the transient building block is likely to be significantly shorter than that of the monomer. The second difference is that the building blocks are covalently connected by the polypeptide backbone, whereas in binding there is no such connectivity. While bearing these differences in mind, it is not surprising that folding funnels resemble binding funnels, apart from the increasing complexity of the binding funnels. Hence, inspection of the ruggedness around of the bottom of the binding funnels would reveal the ensembles of conformers of the bound conformers. Just like the situation that is observed around the bottom of the folding funnel, the population times of conformers around the bottom of the binding funnel vary. Conformers with low conformation times in the folding funnels may show high conformation times in the binding funnels. This principle can be observed if we compare the schematic drawings of the bottoms of the funnels in Fig. 1.
From what we know today, with the exception of binding of inhibitors, it appears that in biological systems, none of the protein molecules functions through a single binding event. This means that such binding events cascade down through a series of binding events. For each such event, the population around the bottom of the corresponding (folding or binding) funnel serves as the repertoire of potentially available molecules for the following binding event in the chain. As in the case of the conformers present around the bottom of the folding funnel, here, too, it is not the conformer with the highest population times that will bind in the following step. Rather, it is the conformer whose structure in the current bound stage is most favorable for the next binding event. This is a general phenomenon that holds uniformly (5, 14) whether in allostery (15), molecular communication, or signal transduction. Conformers whose population times might have been very low in the folding funnels might be considerably enriched as they go down consecutive funnels. This principle is illustrated as we progress through the funnels schematically depicted in Fig. 1.
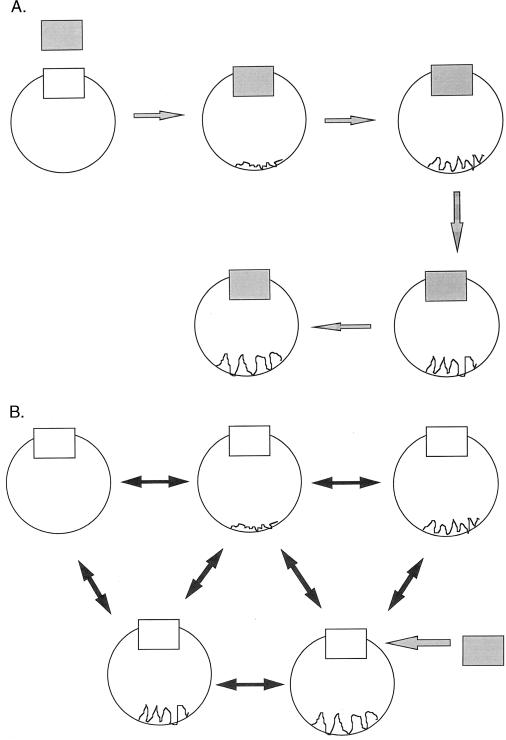
At each step, a potentially low-population time conformer that binds and gets depleted from the solution will shift the equilibrium in its favor. Thus, it is not a conformational change of a given molecule that is induced, i.e., brought about through the act of binding; Rather, it is a change induced by the shifting of the equilibrium (Fig. 2).
Figure 2.
(A). The traditional view of induced fit and allostery where binding in one site (shaded) causes changes at a remote site (rugged). (B) The concept of conformational substates described here, where preexisting conformations are in equilibrium. The equilibrium shifts to one of conformations that fits incoming ligand.
Hence, this is the reason why the implications of the paper by Freire in this issue of the Proceedings (6) are so important. We see how binding at one location of the molecule affects, through a redistribution of the probabilities of the conformations, the conformation at a site that is far away. While here only a limited series of a cascading chain of conformational redistributions has been presented, nevertheless, if we sequentially repeat each binding stage, such enrichment in the likelihood of a given conformer would be observed. Furthermore, Freire has equipped us with a tool for predicting local flexible regions, if the molecular structures are available.
Acknowledgments
We thank Drs. Jacob V. Maizel, S. Kumar, and N. Sinha for many helpful discussions. The research of R.N. in Israel has been supported in part by Grant 95–00208 from the Binational Science Foundation (Israel), by a grant from the Israel Science Foundation administered by the Israel Academy of Sciences, by a Magnet grant, by a Ministry of Science grant, and by grants from the Tel Aviv University Basic Research and Adams Brain Center. This project has been funded in whole or in part with Federal funds from the National Cancer Institute, National Institutes of Health, under contract number NO1-CO-56000.
Footnotes
The companion to this Commentary begins on page 10118.
References
- 1.Bryngelson J D, Wolynes P G. J Phys Chem. 1989;93:6902–6915. [Google Scholar]
- 2.Frauenfelder H, Sligar S G, Wolynes P G. Science. 1991;254:1598–1603. doi: 10.1126/science.1749933. [DOI] [PubMed] [Google Scholar]
- 3.Karplus M. Folding Design. 1997;2:S69–S75. doi: 10.1016/s1359-0278(97)00067-9. [DOI] [PubMed] [Google Scholar]
- 4.Dill K A, Chan H S. Nat Struct Biol. 1997;4:10–19. doi: 10.1038/nsb0197-10. [DOI] [PubMed] [Google Scholar]
- 5.Tsai C J, Kumar S, Ma B, Nussinov R. Protein Sci. 1999;8:1181–1190. doi: 10.1110/ps.8.6.1181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Freire E. Proc Natl Acad Sci USA. 1999;96:10118–10122. doi: 10.1073/pnas.96.18.10118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Williams D C, Benjamin D C, Poljak R J, Rule G S. J Mol Biol. 1996;257:866–876. doi: 10.1006/jmbi.1996.0207. [DOI] [PubMed] [Google Scholar]
- 8.Rose R B, Craik C S, Stroud R M. Biochemistry. 1998;37:2607–2621. doi: 10.1021/bi9716074. [DOI] [PubMed] [Google Scholar]
- 9.Koshland D E., Jr Proc Natl Acad Sci USA. 1958;44:98–123. doi: 10.1073/pnas.44.2.98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Baldwin R L. Nature (London) 1994;369:183–184. doi: 10.1038/369183a0. [DOI] [PubMed] [Google Scholar]
- 11.Bozko E M, Brooks C L., III Science. 1995;269:393–396. doi: 10.1126/science.7618103. [DOI] [PubMed] [Google Scholar]
- 12.Lazaridis T, Karplus M. Science. 1997;278:1928–1931. doi: 10.1126/science.278.5345.1928. [DOI] [PubMed] [Google Scholar]
- 13.Onuchic J N, Socci N D, Luthey-Schulten Z, Wolynes P G. Folding Design. 1996;1:441–450. doi: 10.1016/S1359-0278(96)00060-0. [DOI] [PubMed] [Google Scholar]
- 14.Ma, B., Kumar, S., Tsai, C. J. & Nussinov, R. (1999) Protein Eng., in press. [DOI] [PubMed]
- 15.Kumar, S., Ma, B., Tsai, C. J., Wolfson, H. & Nussinov, R. (1999) Cell Biochem. Biophys., in press. [DOI] [PubMed]
- 16.Tsai C-J, Xu D, Nussinov R. Folding Design. 1998;3:R71–R80. doi: 10.1016/S1359-0278(98)00032-7. [DOI] [PubMed] [Google Scholar]
- 17.Baldwin R L, Rose G D. Trends Biochem Sci. 1999;24:26–33. doi: 10.1016/s0968-0004(98)01346-2. [DOI] [PubMed] [Google Scholar]
- 18.Sinclair J F, Shortle D. Protein Sci. 1999;8:991–1000. doi: 10.1110/ps.8.5.991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tsai C-J, Nussinov R. Protein Sci. 1997;6:24–42. doi: 10.1002/pro.5560060104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Karplus M, Weaver D L. Protein Sci. 1994;3:650–668. doi: 10.1002/pro.5560030413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Panchenko A R, Luthey-Schulten Z, Wolynes P G. Proc Natl Acad Sci USA. 1996;93:2008–2013. doi: 10.1073/pnas.93.5.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]