A Multi-Scale Approach to Airway Hyperresponsiveness: From Molecule to Organ

Abstract

Airway hyperresponsiveness (AHR), a characteristic of asthma that involves an excessive reduction in airway caliber, is a complex mechanism reflecting multiple processes that manifest over a large range of length and time scales. At one extreme, molecular interactions determine the force generated by airway smooth muscle (ASM). At the other, the spatially distributed constriction of the branching airways leads to breathing difficulties. Similarly, asthma therapies act at the molecular scale while clinical outcomes are determined by lung function. These extremes are linked by events operating over intermediate scales of length and time. Thus, AHR is an emergent phenomenon that limits our understanding of asthma and confounds the interpretation of studies that address physiological mechanisms over a limited range of scales. A solution is a modular computational model that integrates experimental and mathematical data from multiple scales. This includes, at the molecular scale, kinetics, and force production of actin-myosin contractile proteins during cross-bridge and latch-state cycling; at the cellular scale, Ca²⁺ signaling mechanisms that regulate ASM force production; at the tissue scale, forces acting between contracting ASM and opposing viscoelastic tissue that determine airway narrowing; at the organ scale, the topographic distribution of ASM contraction dynamics that determine mechanical impedance of the lung. At each scale, models are constructed with iterations between theory and experimentation to identify the parameters that link adjacent scales. This modular model establishes algorithms for modeling over a wide range of scales and provides a framework for the inclusion of other responses such as inflammation or therapeutic regimes. The goal is to develop this lung model so that it can make predictions about bronchoconstriction and identify the pathophysiologic mechanisms having the greatest impact on AHR and its therapy.

Introduction

Airway hyperresponsiveness (AHR) is defined as an excessive and inappropriate narrowing of the airways in response to bronchoconstrictive challenge. While AHR and inflammation are hallmarks of asthma and are primarily responsible for patient dyspnea, we still have an incomplete understanding of how airway smooth muscle (ASM) activation leads to airway narrowing and why asthma exacerbates this response.

Nevertheless, it is clear that AHR involves a dynamic balance between the active forces generated by ASM and the opposing passive forces exerted by the airway and surrounding parenchymal tissues. Importantly, these forces manifest at many length and time scales; from molecular interactions within cells to changes in airway morphology at the level of the whole lung. Furthermore, these forces are dynamic and, in particular, are rhythmically modulated by the act of breathing. For practical reasons, traditional experimental approaches tend to focus on specific levels of time and length scale and this has resulted in the accumulation of numerous disparate facts about many of the individual mechanisms pertaining to AHR. However, a clear view of how these mechanisms interact to mediate AHR has remained elusive because of the difficulty of integrating the many different time and length scales involved.

It is our view that computational modeling provides a way forward, therefore our primary goal is to construct a multi-level computational model of the lung that embodies the key mechanisms impinging on the phenomenon of airway responsiveness. Such a model will not only contribute to a more complete understanding of the pathogenesis of AHR, but it will also provide a virtual laboratory for in silico investigation of potential new therapies for obstructive lung diseases and their modes of delivery. This is particularly important in the current era of evidence-based medicine in which advances in medical practice are driven by the outcomes of clinical trials. The expense and effort involved in such trials are considerable and only a very limited number of questions can be addressed. It is therefore crucial that these questions be selected on the basis of their having the greatest likelihood of yielding useful results. This can be greatly facilitated if the questions are first vetted on the basis of predictions made by a computational model of the lung that integrates experimental data relevant to AHR from all relevant length and time scales.

So far, our modeling and experimental studies have focused on the basic mechanisms of ASM contraction in the healthy state. The initial aim was to develop the basic model framework onto which pathological conditions could be imposed. The obvious next step will be to include, in the case of asthma, the complex process of inflammation. Unfortunately, at the current time, we have inadequate information or models reflecting the action of inflammation on ASM. Therefore, we have not attempted to extensively address this complex aspect of asthma in this review. However, experimental work is proposed to examine ASM responses from asthmatic tissues.

Multi-Scale Computational Modeling

An interest in creating multi-scale models of biological systems has developed rapidly in recent years along with the availability of the required computing power. However, models of biological systems should always be motivated by the need to address biological questions rather than a demonstration that a model can be created. Furthermore, the purpose of a multi-scale model must be more than just a representation of the biological system at different scales of length or time. Ideally, the model must provide scientific insight, particularly in terms of how changes in behavior at one level of scale influence behavior at other scales within the system.

Biological systems are hierarchical; organs are composed of tissues, tissues of cells, cells of organelles, and organelles of macromolecules, with each step exhibiting qualitatively different behaviors. Importantly, interactions between these scales often lead to emergent phenomena that cannot be envisaged when considering only a single scale. Thus, a key goal of multi-scale modeling is to understand how integration of system components at one level of scale produces emergent behavior at higher levels of scale. The model should also provide the reverse function to elucidate how high scale behavior can influence lower scale activity. Multi-scale modeling requires the distillation of these scale-dependent behavioral characteristics into their essential elements for inclusion into the model rather than the inclusion of every detailed interaction. This approach is more efficient from a computational viewpoint and facilitates the likelihood of gaining insight and understanding.

Principal length and time scales involved in AHR

Because ASM is the source of contractile force in the airway, AHR is a manifestation of its activity. This activity has consequences at four major scales: that of the molecular, the cell, the tissue, and the organ scale.

At the molecular scale

Airway smooth muscle cell (ASMC) contraction is produced by the cyclic cross-bridge formation between myosin and actin that generates force and movement; the kinetics of these cross-bridge interactions primarily determines force-velocity output. However, these cross-bridges can take a unique form called latch-bridges that maintain the ASMC at a shortened length to exert prolonged contraction. For the model, characterization, and understanding of these two cross-bridge mechanisms are required in order to predict their force output and how molecular alterations of actin-myosin interactions may be useful for the relaxation of ASMCs.

At the cellular scale

The contractile activity of the actin-myosin filaments is enzymatically regulated by the antagonistic activities of myosin light chain (MLC) kinase (MLCK) and MLC phosphatase (MLCP). The activity of MLCK is in turn regulated by complex spatiotemporal patterns of Ca²⁺ changes within the ASMC, while MLCP is regulated by a phosphorylation signaling cascade primarily involving Rho Kinase. Of equal importance are the signaling pathways that lead to ASMC relaxation; while this can simply involve the cessation of Ca²⁺ signals, the activation of relaxing signals mediated via protein kinase A (PKA; via β₂-adrenergic agonists) or protein kinase G (PKG; via NO production) is frequently involved. The contractile activity of the ASMC thus reflects a balance between opposing signaling cascades. Consequently, characterization of these regulatory mechanisms of ASMCs is required to make the model responsive to external contractile stimuli.

At the tissue scale

Airway constriction is a dynamic event reflecting the opposing influences of the active forces generated by ASMCs, which act to narrow the airway, and the passive mechanical forces of the airway wall and the surrounding parenchyma, which resist airway narrowing. The passive forces are due to numerous structures in and around the airways including the alveolar walls that tether the airway from the outside, the compressive stiffness of airway wall components such as the epithelium and basement membrane, and the intrinsic stiffness of the ASMC itself. All of these factors, including the force-generating capacity of the ASMC, have the potential to become markedly altered in diseases that involve significant degrees of airway remodeling, such as asthma. A particular challenge in modeling AHR at this level of scale is thus to identify those mechanisms that have the most influence on airway narrowing.

At the organ scale

The lung has a complex anatomy comprising of asymmetrically branching airway and vascular trees embedded in viscoelastic parenchymal tissue. In health, this structure brings air and blood in close juxtaposition over the enormous surface area that is required for adequate diffusive fluxes of oxygen and carbon dioxide, with regional variability in ventilation-perfusion matching having a small influence on total lung gas exchange. In a lung suffering from AHR, however, substantial heterogeneities of regional mechanical function may arise that severely alter the ventilation-perfusion ratios, compromising gas exchange. A computational model that is able to recapitulate this type of behavior, therefore, must incorporate accurate anatomical geometry together with local mechanical properties of both airway and tissue. The respiratory tract is in constant motion as a result of breathing. Consequently, the spatial distribution of local changes in airway constriction will determine the overall airway impedance, which in turn will influence the distribution and ease of ventilation. To understand this complex behavior, it is necessary to model breathing dynamics in addition to the branching geometry, material properties, and interdependence (through parenchymal tethering) of the airways and parenchyma in which they are embedded. This model incorporates the foregoing scales and thereby provides the ability to observe how emergent properties alter ventilation.

Approaches to modeling

Predictive modeling

It is common for models to be purely constructive, i.e., constructed in great detail and validated by comparison to existing experimental data. Because these models essentially provide a quantitative explanation for what was already known, they are constrained in their usefulness. By contrast, a model based on physiological principles that can predict novel outcomes that are not intuitively obvious, but which can be experimentally tested, is extremely valuable for advancing an understanding of a system. This modeling approach is successful because it inspires further investigation and thereby provides additional evidence with which to evaluate the predictions. This property of predictive models is the key reason for constructing a multi-scale model of the airway, because it is only with such a model that the complicated behavior of AHR can be evaluated. While experimental investigations are forced to accept limitations, predictive modeling is less constrained.

Functional modeling

A major caveat of building a multi-scale model is that, at least in the initial stages, it is undesirable to include all known complexities. From a practical viewpoint, an all-inclusive model is not feasible because such a model would require excessive computing. Importantly, the model should be constructed on fundamental principles of operation. Most researchers agree with this premise, but can quickly lose confidence in a model if specific details central to their work are not included. However, it is common that the significance of such details to the overall system is rarely known and therefore must be initially omitted. With a basic working model, additional complexity can be added, if validated by iterative testing between model and experiment.

Our approach to building an airway lung model initially follows the fundamental concept of force generation by myosin and actin that is primarily controlled by cellular Ca²⁺ and converted into airway narrowing by the mechanical properties of the lung as outlined across the four major scales. The auxiliary control processes and tissue characteristics can then be applied to this framework. In this review the important details of the physiological process will be initially addressed, for each of the four major scales, followed by the relevant modeling approaches to build the sub-models of each scale. It must be emphasized that this is an on-going endeavor and that the parameters currently included in the model only reflect current progress. The ultimate aim for the model is for it to become a predictive tool that can be used for clinical evaluation and insight. This will require substantially more complexity, but the first step is the construction of a robust foundation and a flexible open-source framework for future development.

Our approach to multi-scale modeling

To construct a multi-scale model there are two major problems that must be solved. Firstly, models for each level need to be constructed, validated against existing data, and improved iteratively with additional experimental data. In general, this first step uses traditional modeling methods and is largely based on existing approaches. Secondly, methods must be devised for coupling these scales together into a single unified model. At this stage, new mathematical methods may need to be developed. There are no standard procedures for the construction of such multi-scale models; every multi-scale model, particularly one that spans such a wide range of spatial scales as ours, will likely depend on the invention of new methods. In addition, the entire multi-scale model must be modular in order to avoid the rebuilding of the entire model with each new iteration or error correction at each scale.

Linking the various spatial scales requires connecting partial and ordinary differential equations, together with judicious use of linearization and interpolation methods. Our approach has been to retain, as far as possible, the richness of our cellular and sub-cellular models (an alternative would have been to parameterize a lumped-parameter model to represent their essential behaviors). This means that we can explore the sensitivity of the large-scale model behavior to perturbations at the smallest scales; for example, in our multi-scale model it is possible to predict how changes at the level of myosin and actin kinetics will affect ventilation or heterogeneity at the level of the entire lung. Without a multi-scale model, such predictions are simply not possible. One drawback is that computations for a whole lung are demanding. We minimize this problem by use of interpolation methods in the coupling of the spatial scales, but each full model simulation may still take many days of computer time.

The Molecular Scale

Contractile mechanisms and proteins

The contraction of ASM cells appears to be mediated by a two-step process; the first or precursor step is proposed to be a dynamic assembly of actin filaments into a cortical cytoskeleton that couples the cell membrane with more central and stable actin filaments to enable effective force transmission. This is followed by the traditional or familiar role of force generation by cyclic myosin interactions with the pre-formed or stable actin filaments.

The formation of the cortical cytoskeleton is reviewed by Gunst and Zhang (2008) and is only briefly summarized here. A key observation is that agonist-induced tension development is largely inhibited, in a manner independent of MLC phosphorylation, by preventing actin polymerization (Adler et al., 1983; Mauss et al., 1989; An et al., 2002; Shaw et al., 2003). This cytoskeletal assembly involves an increase of ∼20% F-actin (and decrease of ∼30% G-actin), occurs quickly (within ∼60 s) and involves the translocation and interaction of numerous actin-binding proteins and nucleation factors to the adhesion junctions that link the cytoskeleton to the extracellular matrix (Gunst and Zhang, 2008; Huang et al., 2010; Zhang et al., 2010b). Gunst and Zhang (2008) propose that this dynamically polymerizing actin is required to transmit and potentially amplify the forces generated by the more central actomyosin interactions to the cell-surface. However, it is unclear if this cytoskeletal formation is immediately reversed when the ASM relaxes (e.g., upon agonist removal) or if an extended relaxed state is required. At the current time, our modeling approach assumes a fixed anchorage of the actin-myosin filaments but the inclusion of a cortical cytoskeletal sub-model would be a desirable future direction.

The contractile or “functional” sarcomere

Airway smooth muscle cells generate force by the hydrolysis of MgATP (magnesium ion-adenosine trisphosphate) which provides the energy to power a sliding filament mechanism mediated by cyclic interactions between myosin filament heads and actin filament binding sites (Adelstein and Sellers, 1996). The actin filaments are approximately orientated along the length of the ASMCs (Stephens and Kroeger, 1980). Traditionally, it was believed that actin filaments were embedded in dense bodies that served as anchor points at the cell membrane or within the cell (Bond and Somlyo, 1982; Fay et al., 1983). However, more recent studies have observed that dense bodies are actually tubular structures that run parallel to the contractile filaments (Zhang et al., 2010a). Nevertheless, it is likely that actin filaments are anchored in some sort of alpha-actinin based structure, similar to the z-lines of skeletal muscle, so that contraction at the molecular level can be transmitted to the cellular scale (Gunst and Tang, 2000; Gunst and Zhang, 2008).

The myosin filaments are interspersed between the actin filaments and typically appear thicker being composed of multiple myosin dimers with the myosin heads projecting outward toward the actin filaments (Trybus, 1996). Whereas the myosin heads have a bi-polar orientation in striated muscles, in smooth muscle most of the myosin filaments have a side-polar orientation (Xu et al., 1996). The exact nature of the myosin filaments also varies with the contractile state (Ip et al., 2007). From electron microscopy observations, the thickest and longest myosin filaments appear to occur in relaxed ASMCs whereas myosin filaments appear to redistribute and are difficult to observe in contracted ASMCs (Chin and Seow, personal communication). A possible explanation for this is that unconnected myosin dimers may be able to mediate filament sliding.

Regulation of myosin cross-bridge activity

The ability of myosin to perform force-generating cross-bridge cycling is regulated by Ca²⁺/calmodulin-MLCK dependent phosphorylation of the regulatory MLCs (rMLC). Once phosphorylated, myosin can hydrolyze MgATP into MgADP and Pi and associate with actin filaments to generate force. It is believed that the faster kinetics of rapidly contracting phasic smooth muscle (e.g., in intestines), as compared to slower contracting tonic smooth muscle (e.g., in blood vessels), is caused by a faster regulatory and contractile system (Horiuti et al., 1989). However, it is unclear whether ASMC exhibits a tonic (Horiuti et al., 1989) or phasic (Malmqvist and Arner, 1991) phenotype. Furthermore, ASM may potentially change its behavior in disease (Souhrada and Dickey, 1976; Davis et al., 1982).

Several accessory proteins, including tropomyosin, caldesmon, calponin, and transgelin are all structurally associated with the actin filaments (Morgan and Gangopadhyay, 2001) and are proposed to play a role in contraction regulation. Tropomyosin appears to have similar properties as in skeletal muscle and facilitates cooperativity between cross-bridges (Morgan and Gangopadhyay, 2001) as well as the action of caldesmon (Shirinsky et al., 1992). Caldesmon inhibits actomyosin ATPase activity (Nagai et al., 1989) and decreases the actin sliding velocity (ν_max) in in vitro motility assays (Shirinsky et al., 1992; Horiuchi and Chacko, 1995). The inhibitory action of caldesmon is reversed by its phosphorylation that can be achieved by several agents including Ca²⁺-calmodulin, Cam Kinase II (Ngai and Walsh, 1984; Shirinsky et al., 1992).

Similarly, calponin inhibits actomyosin ATPase activity (Winder et al., 1998) and decreases ν_max in in vitro motility assays (Shirinsky et al., 1992). Contrary to the effect of calponin, this decrease in ν_max is more of an “all or none” mechanism. That is, some of the filaments are completely stopped rather than displaying a simple decrease in ν_max (Shirinsky et al., 1992). This inhibitory action of calponin is reversed by its phosphorylation by PKC or Cam Kinase II, etc. (Winder and Walsh, 1990; Winder et al., 1998).

Taken together, the above data suggest that activation (by phosphorylation) of actin regulatory proteins may be necessary for cross-bridge cycling and contraction (Winder et al., 1993; Gerthoffer et al., 1996; Pohl et al., 1997). However other studies reported the absence of phosphorylation in vivo (Gimona et al., 1992; Adam et al., 1995).

Transgelin (SM22α), a ubiquitous protein found in smooth muscle cells (Solway et al., 1995; Fu et al., 2000), is thought to interact with, or bind to, actin (Gimona and Mital, 1998; Fu et al., 2000) and potentially modulate actin cytoskeleton organization by increasing F-actin bundling to enhance contractility (Han et al., 2009). Studies on smooth muscle from SM22α knockout mice have demonstrated that SM22α is necessary for Ca²⁺ independent contraction but not for Ca²⁺ dependent force generation (Je and Sohn, 2007). Interestingly, SM22α appears to be significantly increased in asthmatic ASMCs, at least at the mRNA level (Leguillette et al., 2009).

Enhanced contraction rates in AHR

There are two isoforms of smooth muscle myosin heavy chain (SMMHC) that are generated by alternative mRNA splicing at the amino-terminus (Eddinger and Murphy, 1988; Nagai et al., 1989). These isoforms differ by the absence [(−)insert] or presence [(+)insert] of a seven amino acid sequence near the ATPase site (Kelley et al., 1993; White et al., 1993). The importance of this insert is that it doubles the actin-activated ATPase activity and actin filament movement in in vitro motility assays (ν_max; Kelley et al., 1993; Rovner et al., 1997; Lauzon et al., 1998). Myosin purified from multiple rat tissues shows a rank correlation between the (+)insert protein expression and ν_max (Leguillette et al., 2005).

Airway smooth muscle cells from asthmatics and animal models of asthma exhibit increased rates and extents of shortening (Jiang et al., 1992; Bramley et al., 1994; Mitchell et al., 1994; Fan et al., 1997; Wang et al., 1997). This increased shortening rate correlates with the over-expression of the fast SMMHC mRNA in asthmatic human ASMCs (Leguillette et al., 2009). Increased rates of ASM shortening have also been correlated with increased levels of MLCK (Jiang et al., 1992, 1995; Ma et al., 2002), but a direct link between rMLC phosphorylation and shortening velocity remains controversial (Gerthoffer, 1987; Merkel et al., 1990; Mitchell et al., 2001). Thus, the importance of increased activation or altered expression of contractile proteins in AHR is unknown.

The latch-state

The latch-bridge, or latch-state, is a unique form of the myosin cross-bridge and was originally defined as a state of force maintenance that occurs when rMLC is deactivated by dephosphorylation while the myosin head is still attached to actin (Dillon et al., 1981). Despite the wide acceptance of this hypothesis, a verification of the occurrence of latch-bridges at the molecular level is lacking in both animal and human tissues. This latch-bridge hypothesis also assumes that myosin must be initially phosphorylated in order to attach to actin (Hai and Murphy, 1988). However, tonic force can develop with little or no rMLC phosphorylation suggesting that latch-bridges can be formed by dephosphorylated or unphosphorylated myosin (Sato et al., 1992). Indeed, evidence is accumulating to suggest that unphosphorylated myosin can attach to actin (Leguillette et al., 2008) and our preliminary data also indicate that it can occur in the presence of actin regulatory proteins. Furthermore, the (−)insert SMMHC is preferentially expressed in tonic smooth muscle, where the latch-state is prevalent. This suggests that the unphosphorylated isoform might play a role in force maintenance (Leguillette et al., 2008).

In an alternative hypothesis for latch-bridge formation, the rMLC remains phosphorylated but force regulation is modulated by caldesmon and calponin (Hai and Kim, 2005). Because, in asthma, there is a possibility that contractile protein expression and function are altered by airway inflammation, latch-bridge formation may contribute to the force maintenance observed in AHR.

Dynamic relaxation of ASMCs

A striking feature of AHR in asthmatic subjects is an apparent failure of the ASMCs to relax in response to deep inspiration. The putative mechanisms for this clinically important effect (An et al., 2007) include an alteration of the molecular mechanisms of ASMC force production. Force generation in ASMCs normally results from rapidly cycling cross-bridges but may also result from slowly cycling latch-bridges. These latch-bridges have the potential for force maintenance and thereby prevent relaxation of asthmatic airways (Fredberg et al., 1997). Alternatively, sustained contraction may result from a reduced rate of myosin dephosphorylation; a condition consistent with increased Ca²⁺-sensitivity mediated by Rho activated Rho kinase (ROK; Somlyo and Somlyo, 2003).

Experimental approaches

Multiple studies have addressed and compared the mechanical properties of normal or asthmatic ASMCs, but none of these studies have performed a multi-level investigation of the component proteins in a single animal species. Our approach is to characterize how the basic properties of ASMC proteins (from mice, rats, and humans) influence actin-myosin interactions in terms of sliding velocity and force production. These studies will provide the parameters necessary to build our model of the normal and hyper-responsive lung.

Purification of ASMC proteins

The functional analysis of individual myosin molecules from animal models has only recently been made possible by our development of techniques to purify it from small tissue samples (Sobieszek, 1994; Leguillette et al., 2005). The main challenge in smooth muscle myosin purification is to detach it from actin. This is achieved by extracting myosin in folding conditions, decreasing its access to actin (Sobieszek, 1994) followed by myosin filament formation. Precipitation of myosin is then performed by ammonium sulfate fractionation. Myosin fractions are then dissolved and dialyzed against low-salt buffer to purify the myosin filaments from tropomyosin. The purified myosin is then thiophosphorylated, a stable form of phosphorylation that allows mechanics studies without the confounding effect of dephosphorylation. This purification procedure has made possible, for the first time, the study of ASM myosin from rat models of asthma (Leguillette et al., 2005).

In vitro motility assays

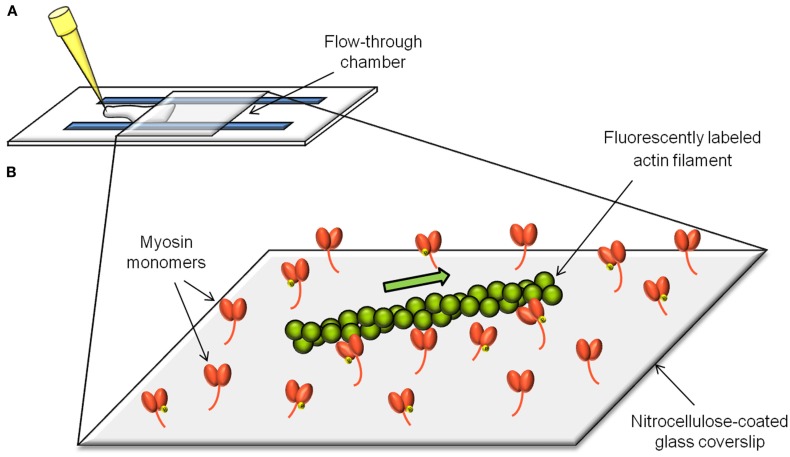
The in vitro motility assay (Figure 1) consists of observing the sliding velocity of fluorescently labeled actin filaments as they are propelled by myosin molecules randomly adhered to a nitrocellulose-coated coverslip (Warshaw et al., 1990; Leguillette et al., 2008). The role of the actin regulatory proteins can be addressed by adding them individually or in combination to the assay. The sliding velocity (ν_max) of single actin filaments is determined in presence of MgATP and is calculated by dividing the path length traveled by the elapsed time.

Figure 1.

The in vitro motility assay. The in vitro motility assay consists of measuring the velocity (ν_max) of actin filaments as they get propelled by myosin molecules randomly adhered to a microscope coverslip (B). The flow-through chamber to setup and perform the assay is constructed from a nitrocellulose-coated coverslip and a microscope slide separated by plastic shims (A).

Force measurements with optical tweezers

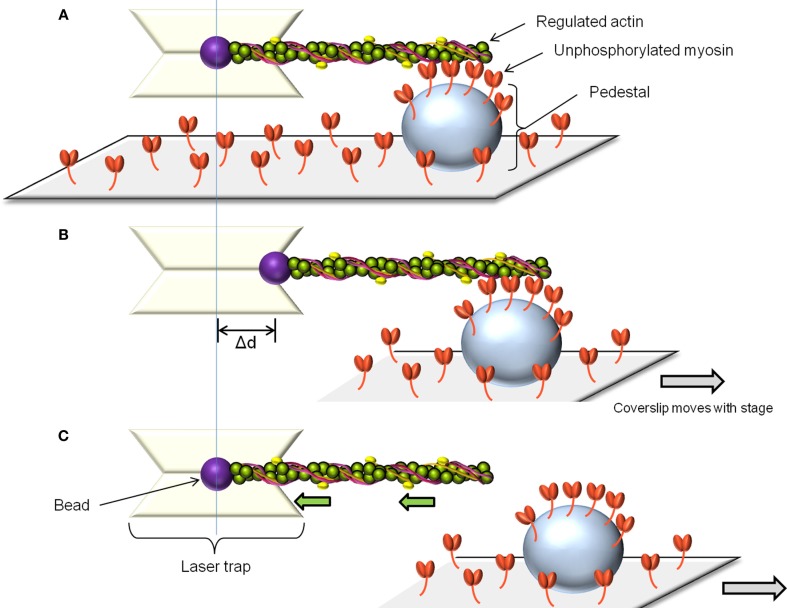
The laser trap assay is used to measure unitary displacement and force generated by myosin molecules. The assay uses laser light to create potential energy wells which are capable of capturing and manipulating beads in solution (Dupuis et al., 1997). By attaching actin filaments to two such beads, a single fluorescently labeled actin filament can be brought into contact with myosin molecules adhered to a pedestal on a coverslip. The displacement distance and attachment time of a single myosin molecule can be estimated by measuring the movement of one of the beads while myosin undergoes its power-stroke. Alternatively, the force generated by a single myosin molecule can be estimated by using a feedback system to prevent bead movement by generating an equal and opposite force. The laser trap can also be used to measure the behavior of several myosin molecules at a time (Leguillette et al., 2008; Figure 2A). In this case, only one bead is required to bring an actin filament in contact with multiple myosin molecules. Displacement and force will again be estimated from the displacement of the bead and normalized by the actin filament length or the estimated number of myosin molecules interacting with the filament. To estimate the force of binding of non-phosphorylated myosin to actin (myosin molecules that do not generate movement) the actin-attached bead is moved away from the pedestal at constant velocity (Figure 2B). When the pulling force exerted by the laser trap exceeds the binding force of the non-phosphorylated myosin molecules to actin, the trapped bead snaps back to its unloaded position (Figure 2C). The product of the laser trap stiffness (Dupuis et al., 1997) and the maximum distance between the bead and the trap center (Figure 2B) gives the binding force of the unphosphorylated myosin to actin. This force is then normalized as above.

Figure 2.

The laser trap assay. To measure the force of binding to actin of unphosphorylated myosin, a single beam laser trap assay is used as follows: The laser trap is used to capture a polystyrene bead coated with N-ethylmaleimide modified myosin. Such myosin can attach to actin but does not cycle, so it is used to glue the fluorescently labeled actin filament. The actin is then brought in contact with the randomly adhered unphosphorylated myosin on a pedestal on the coverslip (A). After allowing time for binding, the pedestal is moved away from the laser trap at constant speed (B). Initially, the bead remains offset from the trap center. When the pulling force exerted by the trap exceeds the binding force of the unphosphorylated myosin molecules, the bead springs back into the trap center, its unloaded position. (C) The unbinding force is the product of the maximal distance between the bead and the trap center (Δd) by the trap stiffness. This force can be normalized by the number of myosin molecules estimated to interact with the actin filament.

Modeling approaches at the molecular scale

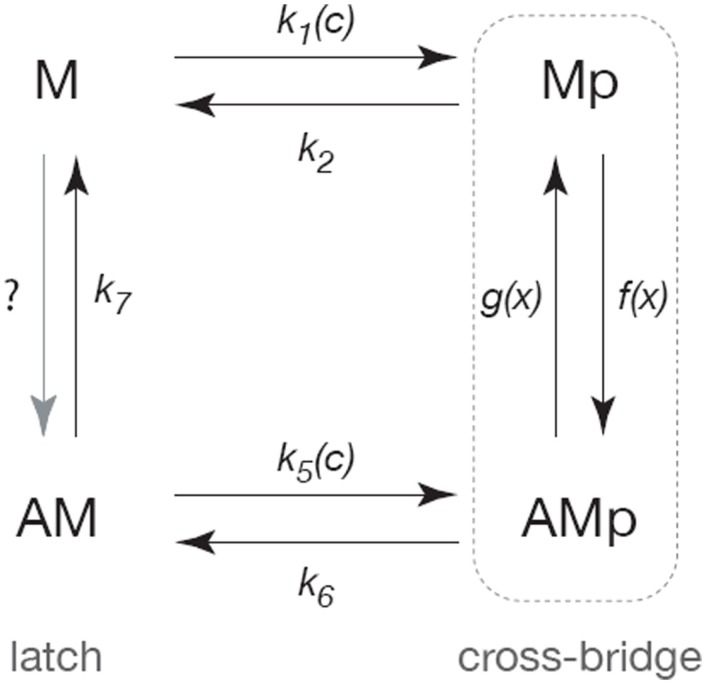
Our initial model of the smooth muscle cross-bridge cycle (Wang et al., 2008) is based on a modified version of the Hai–Murphy model (Hai and Murphy, 1988; Mijailovich et al., 2000; Hai and Kim, 2005; Figure 3). Myosin is assumed to exist in one of four states: the base state of myosin (M) that is neither phosphorylated nor attached to actin; a phosphorylated myosin that is not attached to actin (Mp); a phosphorylated myosin that is attached to actin (AMp); and a myosin that is attached to actin but not phosphorylated (AM).

Figure 3.

Schematic diagram of the cross-bridge model. Following Hai and Murphy (1988) the myosin is assumed to exist in four forms; unphosphorylated and unattached (M), phosphorylated and unattached (Mp), phosphorylated and attached (AMp), attached and unphosphorylated (AM). Cycling between the Mp and AMp states generates active force, while the AM state can maintain tension but cannot generate force (and is thus called the latch-state). Rates of phosphorylation are assumed to be sigmoidal functions of Ca²⁺ concentration (c). The rates of attachment and detachment are functions of the distance (x) to the actin-binding site, and thus the model is a system of partial differential equations of conservation type.

Myosin can only exert a force when it is attached to actin. The transition from Mp to AMp, i.e., the attachment of phosphorylated myosin to actin, is believed to occur upon hydrolysis of ATP. During the cross-bridge cycle, myosin cycles between the Mp and AMp states, continually binding to and unbinding from actin, and hence consuming ATP to generate force. By controlling the rate of myosin phosphorylation, the ASMC can presumably control the velocity of shortening and the amount of force generated. The Ca²⁺-dependent mechanisms by which myosin phosphorylation is regulated are discussed in Section “The Cellular Scale.”

In smooth muscle, myosin is believed to remain attached to actin after dephosphorylation (Dillon et al., 1981). As mentioned above, this state (AM) is called the latch-state. Because the rate of transition from AM to M is typically slow, this allows the smooth muscle to remain in a state where it can no longer relax or contract quickly, but requires less ATP to maintain contraction. The kinetics of the latch-state, as well as that of the cross-bridge cycle are vital for understanding ASMC contraction and relaxation.

This model plays two major roles. Firstly, it is the force-generating mechanism that, ultimately, results in airway narrowing in the full multi-scale model. To accomplish this, the model parameters are determined by comparison with data taken from molecular scale experiments, as well as data collected from muscle strips. Thus, we aim to ensure the model generates physiological levels of force when incorporated into the multi-scale model. Secondly, the model can be used as a predictive tool to understand the consequences of the possible binding of unphosphorylated myosin.

In addition to modeling the cross-bridges with a version of the Hai–Murphy model, our molecular scale model also includes a hypothetical type of binding protein, which we call a cross-linker (Donovan et al., 2010). Cross-linkers are included to give a biophysical basis for the plastic-like properties of unactivated smooth muscle, such as fluidization upon stretching. They are modeled similarly to cross-bridges, except that the attachment functions are symmetrical with respect to the distance variable. A cross-bridge generates active force as a result of the attachment function being asymmetrical, thus biasing the cross-bridge to bind in a position that exerts active force. An identical binding mechanism, but one with a symmetrical binding function, does not generate active force, but exhibits similar dynamic behavior upon stretching. Since the cross-linker model is validated mostly by comparison to data collected at the tissue scale, and has no known specific associated proteins, it is discussed further in Section “The Tissue Scale.”

The Cellular Scale

Physiological signaling mechanisms

Ca²⁺ oscillations and waves

A fundamental stimulus for ASMC contraction is an increase in [Ca²⁺]_i. This commonly occurs in ASMCs in response to agonist activation of G-protein coupled receptors (GPCRs; Sanderson et al., 2008; Figure 4). We have found that Ca²⁺ oscillations are induced in mouse, rat, and human ASMCs by methacholine, 5HT, histamine, NO, endothelin, and LTD₄ (Perez and Sanderson, 2005; Perez-Zoghbi and Sanderson, 2007, 2010; Bai et al., 2009; Ressmeyer et al., 2010). However, changes in membrane potential (e.g., induced with external KCl) can also lead to Ca²⁺ changes (Perez-Zoghbi et al., 2009; Figure 4). The key function of the increased [Ca²⁺]_i is the activation, via calmodulin, of MLCK to phosphorylate rMLC to initiate cross-bridge formation (Figure 3) Consequently, the form and magnitude of the Ca²⁺ signals influence the extent of force generation.

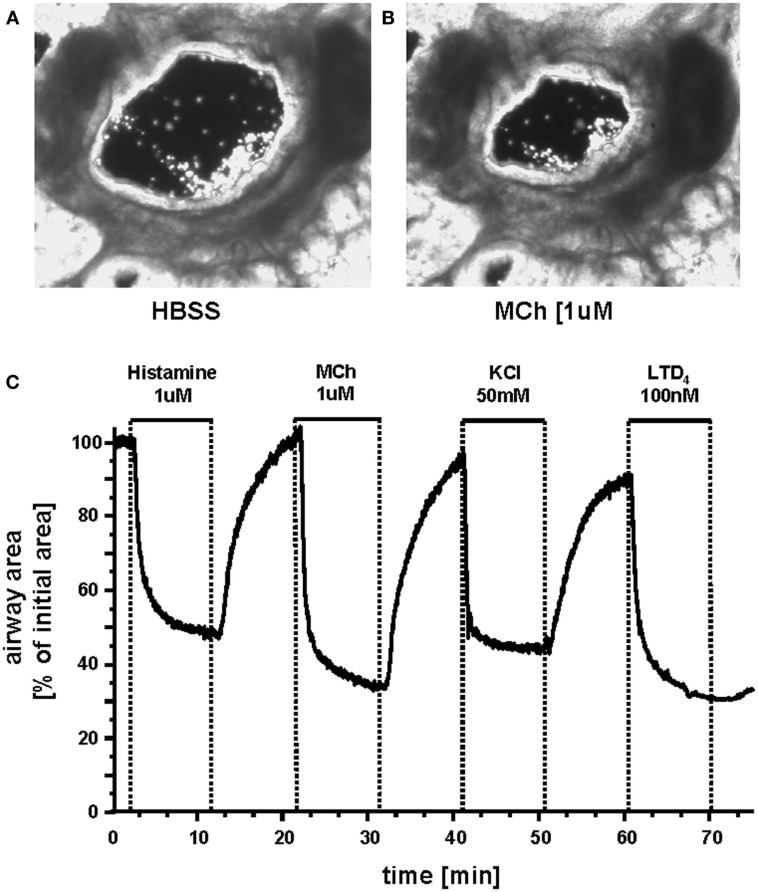
Figure 4.

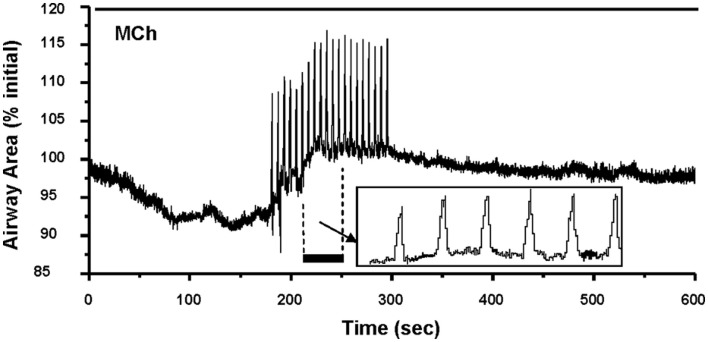
Airways in human lung slices. (A) A human small airway in Hanks’ balanced salt solution (HBSS). (B) In response to 1 μM MCH, the airway has contracted. (C) The change in airway cross section area (as a % of the initial area) in response to a variety of contractile stimuli. Agonists Histamine, Methacholine and leukotriene D4 and membrane depolarization with KCl induce airway contraction.

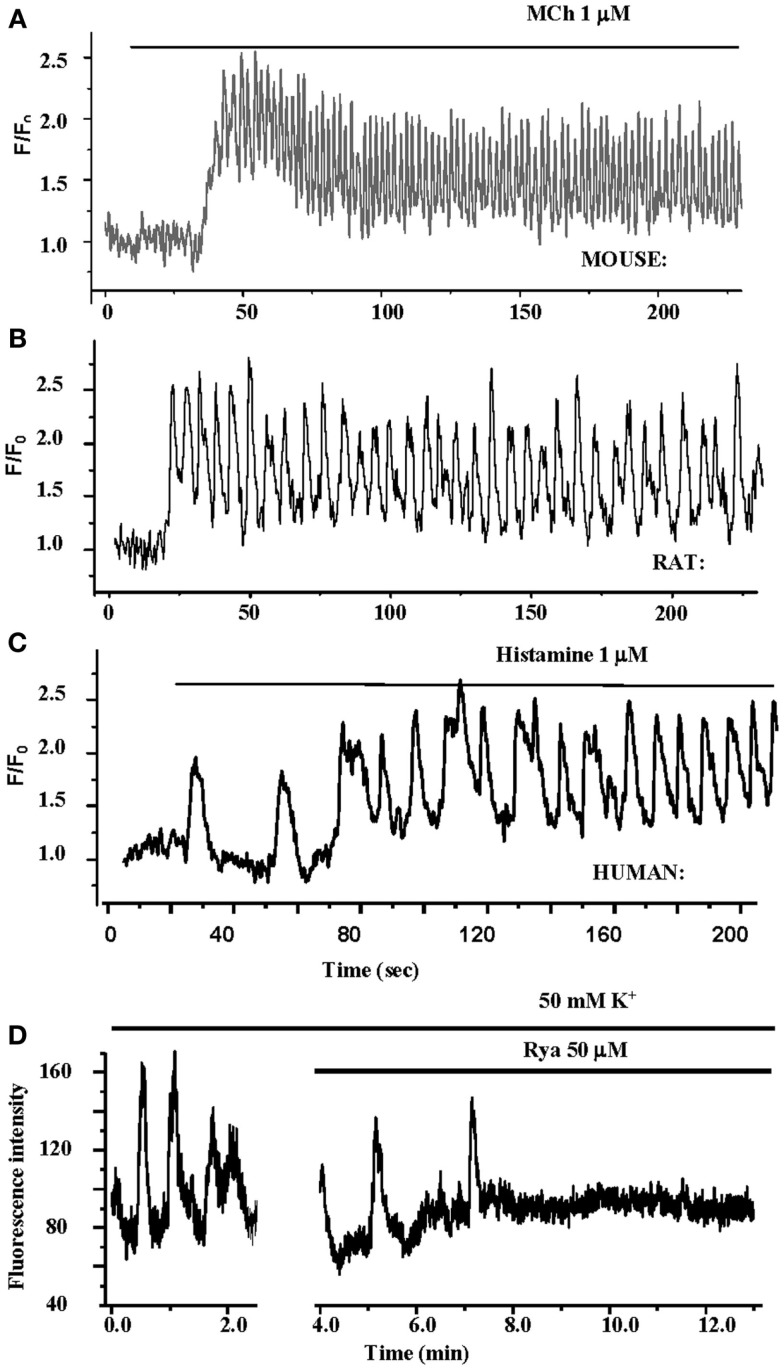
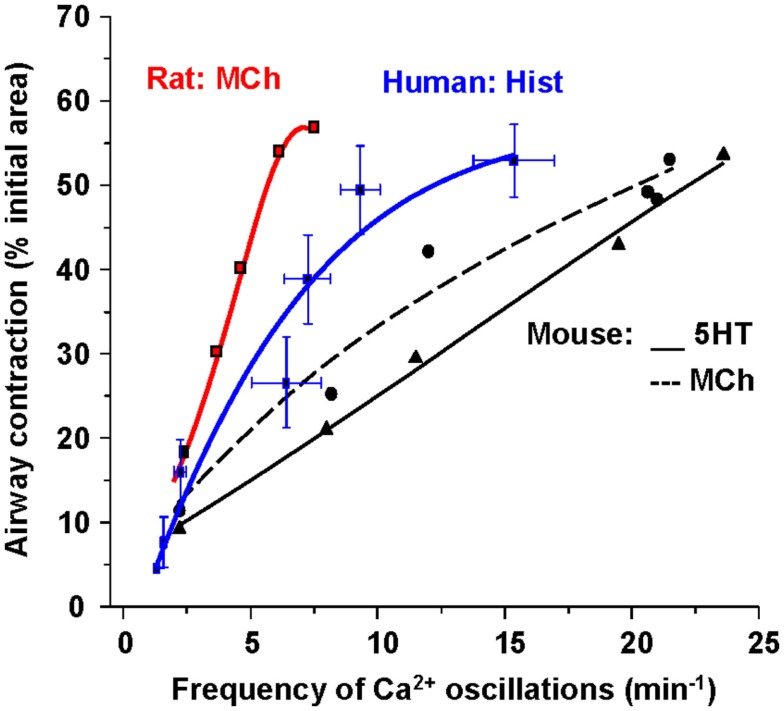
Importantly, these changes in [Ca²⁺]_i in ASMC from the small airways of a variety of species in near in situ conditions occur as sustained Ca²⁺ oscillations rather than static elevations of [Ca²⁺]_i while the agonist remains present (Figure 5; Sanderson et al., 2008; Bai et al., 2009; Delmotte and Sanderson, 2010; Perez-Zoghbi and Sanderson, 2010; Ressmeyer et al., 2010). Each Ca²⁺ oscillation is often initiated at one end of the cell and propagates along the cell as a Ca²⁺ wave. By correlating airway responses with the occurrence of agonist-induced Ca²⁺ oscillations, it has become clear that increased airway contraction correlates with an increased Ca²⁺ oscillation frequency (Figure 6; Sanderson et al., 2008; Delmotte et al., 2010; Ressmeyer et al., 2010). Because it appears that the frequency of the Ca²⁺ oscillations is important in force regulation, this relationship is termed frequency-modulated (FM) regulation (Berridge, 1997). However, the outcome of our modeling indicates that this form of control involves more than just the frequency aspect of the Ca²⁺ oscillation and probably relates to frequency-dependent changes in the form of the Ca²⁺ oscillations (Wang et al., 2010). A second interesting finding is that the relationship between contraction and the frequency of the Ca²⁺ oscillations differs between species (Figure 6; Bai and Sanderson, 2009). In mouse, Ca²⁺ oscillations of about 20–30 min⁻¹ induced a similar extent of airway contraction as 8–10 Ca²⁺ oscillations per minute in human airways (Ressmeyer et al., 2010). While some of this difference may be attributable to the form of the Ca²⁺ oscillation at different rates, it is likely that a second mechanism termed “Ca²⁺ sensitivity” is responsible (see later; Bai and Sanderson, 2009).

Figure 5.

Ca²⁺ oscillations in ASMCs in lung slices. (A–C) The contractile agonists methacholine and histamine induce Ca²⁺ Oscillations in mouse, rat, and human ASMCs in lung slices. The frequency of the Ca²⁺ oscillations varies between species. (D) KCl also induces Ca²⁺ oscillations in human ASMCs in lung slices. Theses Ca²⁺ oscillations are slow and are inhibited by RyR.

Figure 6.

The relationship between Ca²⁺ oscillation frequency of ASMCs and the extent of airway contraction. The gradient of the relationship is different for each species.

Mechanisms of agonist-induced Ca²⁺ signaling

Agonist-induced Ca²⁺ oscillations in ASMCs primarily rely on Ca²⁺ release from the sarcoplasmic/endoplasmic reticulum (S/ER). In general, agonist stimulation of GPCRs results in the production of inositol trisphosphate (IP₃). This, in turn, binds to and releases Ca²⁺ from the S/ER via IP₃ receptors (IP₃Rs). The sensitization of all the IP₃Rs of an ASMC with IP₃ primes the ASMC to display Ca²⁺ oscillations and waves. A Ca²⁺ transient occurring at one group or cluster of IP₃Rs leads to, by the diffusion of Ca²⁺ through the cytosol, the stimulation of other nearby IP₃Rs to release Ca²⁺, a process called Ca²⁺-induced Ca²⁺ release (CICR; Berridge et al., 2003; Berridge, 2009). The sequential repeat of this activity propagates a Ca²⁺ wave. Therefore, it appears that Ca²⁺ wave properties are a consequence of Ca²⁺ diffusion rates and IP₃R distribution and sensitivity. The S/ER Ca²⁺ ATPase (SERCA) pumps sequester much of the cytosolic Ca²⁺ back into the S/ER to allow the process to recycle. Although a direct role for Ca²⁺ influx is not required for Ca²⁺ oscillations, the long-term maintenance of Ca²⁺ oscillations does rely on the Ca²⁺ content of the SR (Perez and Sanderson, 2005). Most likely, Ca²⁺ enters the cell via a store-operated channel (SOC) influx mediated by membrane channels, Orai1, activated by STIM1, a Ca²⁺ sensor within the S/ER (Parekh and Putney, 2005; Putney and Bird, 2008). However, when the S/ER Ca²⁺ content is low, Ca²⁺ may also enter via receptor-operated channels, TRP channels, or the reversal of the Na⁺-Ca²⁺ exchanger (Rahman et al., 2012).

Ca²⁺ oscillations have also been proposed to be mediated by CICR via the ryanodine receptor (RyR) of the S/ER (Dai et al., 2007). These may result by a direct influx action of Ca²⁺ or following sensitization of the RyR by cADP-ribose (cADPR; Prakash et al., 1998; Jude et al., 2008). However, in all our experiments with normal lung slices, on-going Ca²⁺ oscillations or waves are not inhibited in anyway by ryanodine (Bai et al., 2009), an antagonist of the RyR or antagonists of cADP-ribose. While other RyR antagonists such as tetracaine do inhibit Ca²⁺ oscillations (Dai et al., 2007), these appear to result from their non-specific anesthetic effects that decrease IP₃ production or Ca²⁺ sensitivity (Bai et al., 2009).

Ca²⁺ signaling associated changes in membrane potential

Membrane depolarization has commonly been associated with smooth muscle contraction; and is believed to be mediated by the opening of voltage-dependent Ca²⁺ channels and the influx of Ca²⁺ perhaps followed by CICR via the RyR (Janssen, 2002). However, ASMCs in lung slices do not appear to follow this scheme. In response to membrane depolarization, induced by external KCl, ASMCs display Ca²⁺ oscillations with a very slow rate (1–2 min⁻¹) as compared to agonist-induced Ca²⁺ oscillations (Figure 5; Perez and Sanderson, 2005; Bai et al., 2009; Ressmeyer et al., 2010). Importantly, these Ca²⁺ oscillations have a significantly different appearance and occur as large prolonged increases in [Ca²⁺]_i that are preceded by numerous elemental Ca²⁺ responses. In contrast to agonist-induced oscillations, KCl-induced oscillations are inhibited by ryanodine (Figure 5) and the removal of extracellular Ca²⁺ (Perez and Sanderson, 2005; Bai et al., 2009). The implication is that KCl-induced oscillations are mediated by a slow Ca²⁺ influx that overfills the S/ER to sensitize the RyR to CICR.

It seems clear from these studies that both IP₃Rs and RyR are present in ASMCs, but they appear to function independently of each other during normal Ca²⁺ signaling. However, since both receptors rely on the same Ca²⁺ resource, they are unavoidably linked by the Ca²⁺content of the S/ER. Indeed, slow Ca²⁺ oscillations mediated by the RyR can be replaced by fast Ca²⁺ oscillations via the IP₃R. An explanation for this conversion is that the partial emptying of the S/ER Ca²⁺ inactivates the RyR (Wang et al., 2010) and this also explains why the RyR does participate in CICR Ca²⁺ signaling during IP₃-dependent Ca²⁺ oscillations.

Ca²⁺ sensitivity

A complementary mechanism enhancing ASMC that works in parallel to the activation of MLCK by Ca²⁺ is the inactivation of the antagonistic enzyme, MLCP that dephosphorylates rMLC to mediate ASMC relaxation (Schaafsma et al., 2008; Chiba et al., 2010; Mbikou et al., 2011). The inhibition of MLCP is commonly achieved by an increased activity of Rho kinase (ROK; by Rho A) in response to the same agonist stimulation that induced increases in Ca²⁺. Similar changes can be induced by PKC in response to activation by diacylglycerol. Phosphorylation of the regulatory or accessory proteins of MLCP by ROK or PKC prevent its association with rMLC; decreased MLCP activity allows the phosphorylation state of rMLC to persist (Somlyo and Somlyo, 2003; Sanderson et al., 2008).

ASMC relaxation by β₂-adrenergic receptor agonists

A major objective of therapies for AHR is the relaxation of contracted ASMCs and the prominent pharmaceuticals in this strategy are β₂-adrenergic receptor agonists. Although widely used, the mechanism of action of these compounds is not fully understood at the cellular level; a common belief is that increases in cAMP lead to Ca²⁺ decreases and thereby relaxation.

Because it will be important to include β₂-adrenergic receptor signaling in our lung model, we have initially explored this signaling pathway with lung slices (see below). An important finding was that both short-acting (albuterol) and long-acting (formoterol) β₂-adrenergic receptor agonists slowed the Ca²⁺ oscillations induced by methacholine or histamine in mouse or human airways (Delmotte et al., 2010). This appeared to be achieved by a reduced activation-sensitivity to IP₃ and increased inhibition-sensitivity to Ca²⁺ of the IP₃R (Bai and Sanderson, 2006a). The production of IP₃ may have also been reduced in the case of high formoterol concentrations (Delmotte and Sanderson, 2010). These conclusions appear to differ from earlier studies that proposed that increased cAMP reduced internal Ca²⁺ by activating Ca²⁺-dependent K⁺ channels that mediate membrane hyperpolarization to reduce Ca²⁺ influx (Kume et al., 1994). Although the earlier studies implied that this was a direct mechanism to reduce [Ca²⁺]_i, it is not totally incompatible with decreased Ca²⁺ oscillation frequency if the Ca²⁺ influx is directed to refilling the supportive Ca²⁺ store. This hypothesis has similar implications for the idea that spontaneous Ca²⁺ sparks, (mediated by RyRs) that also activate Ca²⁺-dependent K⁺ channels and observed in isolated ASMCs (Zhuge et al., 2010), serve as a relaxation mechanism.

In addition to Ca²⁺ reduction, β₂-adrenergic receptor agonists also reduce the Ca²⁺ sensitivity of ASMCs. Importantly, this effect is very potent with formoterol (Delmotte and Sanderson, 2010; Delmotte et al., 2010). At a low concentration (5 nM) that is insufficient to alter the Ca²⁺ oscillation frequency, formoterol induces a substantial relaxation of the ASM. A change in ASMC Ca²⁺ sensitivity may also explain some of the effects of membrane hyperpolarization; with the Ca²⁺ clamped in a lung slice, we have found that KCl (depolarization) also increased contraction. KCl can activate Rho kinase (Janssen et al., 2004) and this suggests that hyperpolarization will decrease Ca²⁺ sensitivity to help relax ASMCs. These mechanisms emphasize that Ca²⁺ sensitivity is an equally relevant signaling mechanism that must be considered when addressing the cause and relief of AHR (Chiba et al., 2010).

Experimental approaches

A major advance that has facilitated our investigation of the cellular regulation of airway contraction is our ability to examine changes in ASMC physiology while simultaneously measuring airway contraction. These correlations are made possible by a unique lung slice preparation that has been used with mouse, rat, guinea pig, horse, monkey (Sanderson, 2011), and most importantly, human airways (Ressmeyer et al., 2010; Figure 4).

Briefly, isolated lungs are re-inflated via the trachea to a normal size with a solution of warm agarose (∼2%). After cooling and gelling of the agarose, the lungs are sufficiently stiff to be cut into serial slices, ∼200 μm thick (Perez and Sanderson, 2005). Only lung slices containing airway cross sections that lack agarose within the lumen and have an intact epithelium and ciliary activity are selected for study. Lung slices are robust, being viable for 3 days and highly compatible with experimental imaging. By loading the cells of the lung slice with Ca²⁺ reporter dyes, changes in [Ca²⁺]_i in ASMCs can be observed with scanning laser microscopy during contraction.

The lung slices can also be used to investigate the mechanism of “Ca²⁺ sensitivity.” This requires that the [Ca²⁺]_i of the ASMCs is “clamped” to a constant level. This is achieved by irreversibly emptying the S/ER of Ca²⁺ by treatment with caffeine and ryanodine to invoke continuous Ca²⁺ influx via SOCs (Bai and Sanderson, 2006b; Cahalan, 2009). Increased force production under these conditions implies that an alternative method besides Ca²⁺ is acting.

Modeling approaches

Ca²⁺ oscillations

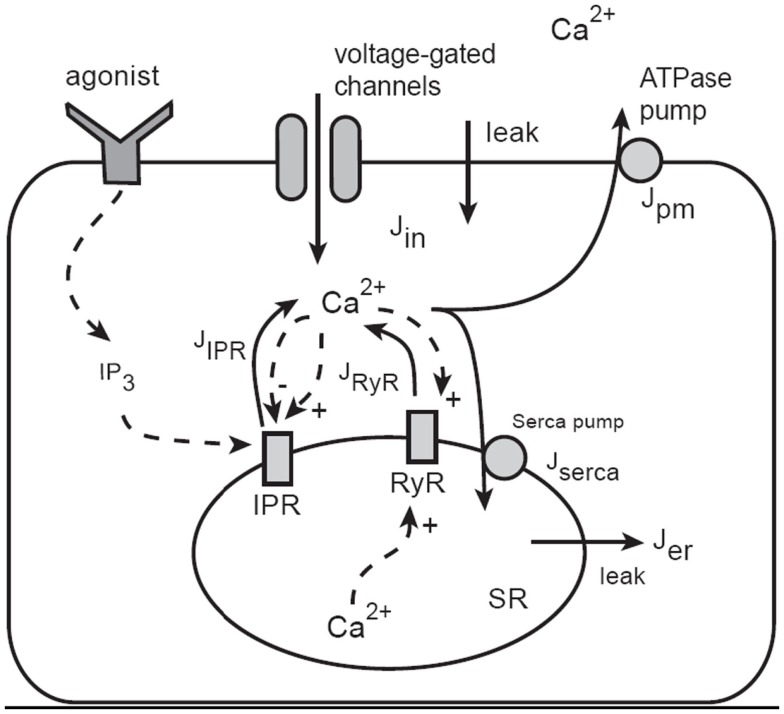
The model of Ca²⁺ oscillations is based on the dynamics of Ca²⁺ leaving or entering the cytosol (Figure 7). Ca²⁺ can enter the cytosol from outside the cell (J_in) or from the S/ER (J_SR). Conversely, Ca²⁺ can be removed from the cytoplasm by Ca²⁺ATPase pumps in the SR (J_serca) and the plasma membrane (J_pm). This model construction is well developed (Falcke, 2004) and has been used extensively to further develop our model and test predictions (Sneyd et al., 2004, 2006).

Figure 7.

Schematic diagram of the Ca²⁺ model. Calcium can enter the cytosol through IP₃ receptors (IPR), ryanodine receptors (RyR), or generic voltage-gated channels and leaks. Ca²⁺ is removed from the cytoplasm by ATPase pumps on the membrane of the SR and on the plasma cell membrane. IPR are activated by IP₃, which is produced as an end-product of agonist stimulation of cell-surface receptors. Calcium in the cytosol can diffuse, and is heavily buffered. The buffers are not shown explicitly as they are incorporated via an effective diffusion coefficient and effective reaction rates.

Although the overall structure is simple, each of the individual fluxes can be modeled in a complex way; J_SR includes Ca²⁺ flux through IP₃ receptors (J_IPR) as well as ryanodine receptors (J_RyR). The J_IPR flux also requires that we incorporate sensitivity to IP₃ binding and Ca²⁺ feedback. In the initial version of the model, this was achieved by using a model of the IP₃R developed by De Young and Keizer (1992), although more recent work uses more modern IP₃R models (Gin et al., 2009a,b,c; Siekmann et al., 2011). The RyR is modeled using the model of Keizer and Levine (1996).

J_in incorporates Ca²⁺ fluxes through voltage-gated Ca²⁺ channels and this is regulated by the membrane potential. Ca²⁺ influx via a capacitative Ca²⁺ entry mechanism or arachidonic-acid-regulated channels is incorporated in the current model of mouse ASMCs, but only in a simplistic way. More detailed models of Ca²⁺ influx in human ASMCs are being developed by an associated group (Croisier and Brook, unpublished).

Ca²⁺ buffering is modeled by incorporating a fast buffering approximation. Nuclear and mitochondrial Ca²⁺ fluxes, although present, have a secondary effect and are modeled as immobile buffers. The modulation of IP₃ production and degradation is not an important part of the mechanism underlying Ca²⁺ oscillations in ASMC (Sneyd et al., 2006) so these pathways are not included.

Our current model of Ca²⁺ dynamics does not attempt to include a wide variety of membrane ion channels that have been found in ASM, primarily because there are few data directly linking the activity of such channels to agonist-induced Ca²⁺ changes in ASM in situ. Although a correlation of ASM contraction and channel activity has been often observed, this is inadequate for Ca²⁺ modeling since the underlying Ca²⁺ changes cannot be assumed. The induction of slow Ca²⁺ oscillations by KCl is a good example of an unexpected form of Ca²⁺ signaling in response to a stimulus that is commonly expected to induce a sustained Ca²⁺ elevation in response to the opening of voltage-dependent Ca²⁺ channels. Ion channel activity may also affect Ca²⁺ sensitivity. From our experience, we emphasize that it is essential to collect information on contraction, Ca²⁺ changes and Ca²⁺ sensitivity, before mechanisms and conclusions can be made with models.

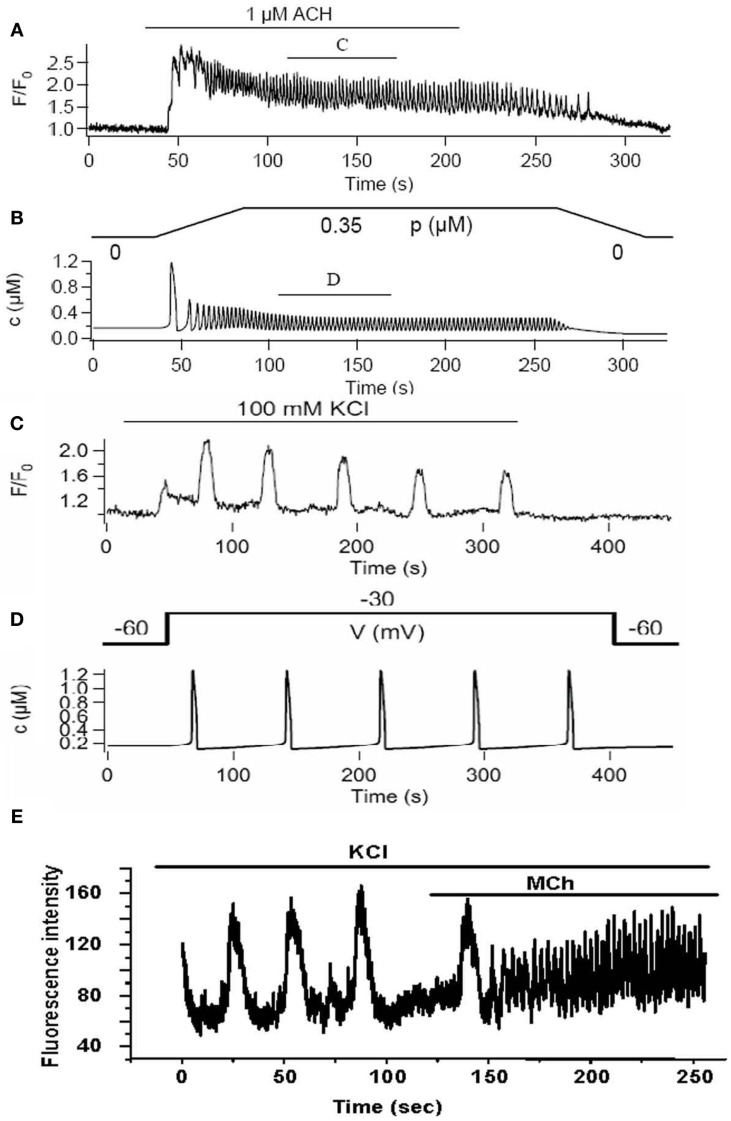
The full model provides a good fit to Ca²⁺ oscillations induced by stimulation with MCh (Figures 8A,B) and importantly has made some interesting predictions (Wang et al., 2010). Although experiments and model indicate that the RyR is not a key feature of on-going Ca²⁺ oscillations, the model surprisingly predicts that the first Ca²⁺ transient is dominated by RyR activity (Figure 8). This possibility was not original envisaged and resulted in experimental design that only added ryanodine to on-going Ca²⁺ oscillations. However, an initial role for RyR can be experimentally tested by having ryanodine present before the stimulation of Ca²⁺ oscillations with agonist. A second model prediction is that the S/ER Ca²⁺ content rapidly falls with each Ca²⁺ oscillation to reach a new but lower equilibrium. This lower S/ER Ca²⁺concentration predicts that the RyR will be insensitive to CICR and explains why the RyR cannot contribute to on-going Ca²⁺ oscillations. Importantly, the model also reproduces the experimental response of slow Ca²⁺ oscillations upon depolarization with KCl (Figures 8B,C). The prediction of this aspect of the model is that the SR becomes over-filled with Ca²⁺ to sensitize the RyR to CICR. The model further predicts that agonist-induced oscillations would empty the SR so that the KCl-induced Ca²⁺ oscillations operating through the RyR would become inoperative as a result of reduced SR Ca²⁺. This prediction was upheld in the experimental examination of cytosolic Ca²⁺ oscillations; measurement of SR Ca²⁺ is still required (Figure 8E).

Figure 8.

A comparison of experimental and model Ca²⁺ oscillations induced by agonist (A,B) and KCl (C,D). Agonist-induced Ca²⁺ oscillations are fast compared to KCl-induced Ca²⁺ oscillations. (E) Experimentally, we observe that slow Ca²⁺ oscillations induced by KCl are converted into fast Ca²⁺ oscillations by the addition of agonist in the presence of KCl.

Ca²⁺ waves

An important aspect of the Ca²⁺ signaling occurring within the ASMCs is their spatial organization; each Ca²⁺ oscillation propagates as a Ca²⁺ wave. This serves to distribute the stimulus equally across the cell but it also determines the duration of the signal at points within the cell. To model this spatial behavior, it is necessary to incorporate a spatial distribution for the release channels and to model the diffusion of Ca²⁺. The Ca²⁺ oscillations can then be visualized as propagating waves (for both agonist and KCl stimulation) that reflect the experimental data (Wang et al., 2010). However, the model predicts that both the IP₃Rs and RyRs need to be asymmetrically distributed; there appears to be a requirement for receptor density to be greater toward one end of the cell in order to reproduce the propensity for Ca²⁺ waves to initiate at one end of the cell, as well as show intermittent wave failure followed by a reversal of the wave propagation direction. It is not clear why this organization is required, or if it occurs biologically, but we intend to test this prediction by examining receptor distribution.

Coupling Ca²⁺ signal to force production

To incorporate the cellular signaling into the larger lung model, it is necessary to couple our Ca²⁺ dynamics model to our model for force generation. We discussed the cross-bridge model in Section “The Molecular Scale.” The coupling of Ca²⁺ to force generation requires the activation of MLCK by Ca²⁺/calmodulin and we use a Hill function to mimic cooperative binding of four Ca²⁺ ions to calmodulin.

Force generation also requires the consideration of myosin dephosphorylation by MLCP. This is influenced by both agonist and KCl. An additional complication is that in mouse but not human ASMCs, MLCP appears to be activated (on a slower time base relative to MLCK) by Ca²⁺ (Bai and Sanderson, 2006b, 2009; Ressmeyer et al., 2010). To model fast Ca²⁺ activation of MLCK followed by slower Ca²⁺ activation of MLCP, we introduced an additional differential equation for Q, the fraction of activated MLCP (Wang et al., 2008). The rate constants were determined by fitting to the airway response to a step increase in Ca²⁺ (Figure 3).

With this mouse model, that translates Ca²⁺ oscillations into force production, we were able to explore the hypothesis of FM regulation to identify the key features of the Ca²⁺ oscillations that are the most significant in force generation. Interestingly, whole-cell Ca²⁺ oscillations (a simultaneous uniform increase in Ca²⁺ throughout the whole-cell) induced greater force than propagating Ca²⁺ oscillations (i.e., Ca²⁺ waves), even through the frequency and mean Ca²⁺ concentration of the two processes were similar (Wang et al., 2010). It is important to point out that in this mouse model, a constant increase in [Ca²⁺]_i induced less force than either type of Ca²⁺ oscillation. This is believed to result, in part, from the slow activation of MLCP that can decrease force. Therefore, what appears to be important for force production is the shape or duration of the Ca²⁺ oscillation. If the Ca²⁺ oscillation becomes more like that of a constant increase in [Ca²⁺]_i, (i.e., it broadens) by becoming lower in magnitude but longer in duration in the case of a whole-cell Ca²⁺ oscillation or spatially broader in the case of the Ca²⁺ wave, it will induce less force even though the mean Ca²⁺ remains little changed. This relationship between oscillatory Ca²⁺ changes and force may be different in human ASM cells, in view of the fact that Ca²⁺ has less effect on Ca²⁺ sensitivity of human ASM cells.

By examining the proportion of cross-bridges in the latch-state, the model is used to determine the importance of the latch-state in controlling the speed of relaxation. Initial results from the model indicate that the gradual movement of cross-bridges into the latch-state causes a gradual decline in the speed of contraction, with a power-law decay profile (see The Tissue Scale). These model results agree qualitatively with experimental data. However, understanding of the relationship between the latch-state, muscle stiffness, and the speed of contraction remains incomplete.

Stochastic modeling of Ca²⁺ oscillations and waves

The current Ca²⁺ signaling models are deterministic. However, the behavior of channels such as the IP₃R, are for the most part, essentially stochastic. Stochastic behavior is observable in long-duration recordings of low frequency Ca²⁺ oscillations, which have an increased variance in the inter-spike interval. Even at higher IP₃ concentrations, i.e., at higher oscillation frequencies, there is clear stochastic variation in the oscillation period. Consequently, a major goal will be to convert our models to include stochastic behavior, in order to see how important stochastic effects are in force generation.

Our initial stochastic models have incorporated the most recent data on the dynamical behavior of IP₃R, collected from single channels in the nuclear membrane (Betzenhauser et al., 2008). By fitting new Markov models to these single channel data, the next generation of IP₃R models has more accurately determined the time scales of Ca²⁺ and IP₃ control of IP₃R open probability (Gin et al., 2009a,b; Siekmann et al., 2011). Initial simulations using a more accurate IP₃R model suggest that a stochastic IP₃R-based model is unable to generate long-period oscillations. How such long-period oscillations occur remains an open question.

Once stochastic effects are incorporated in the model, and their effects on force generation determined, the challenge will be to develop formulations of the stochastic model that allow for coupling to the next higher spatial scale. There is no standard methodology for such coupling, and new methods will have to be developed.

The Tissue Scale

The aim of the tissue scale model is to reproduce the active and passive mechanical properties of ASMCs and the viscoelastic properties of the surrounding tissue against which the ASMC shortens. However, ASMCs are complicated by the fact that their mechanical properties are malleable depending on the physiological circumstances.

ASMC and tissue mechanical properties

Inherent ASMC properties

Airway smooth muscle cells exhibit a hyperbolic force-velocity relationship (Hanks and Stephens, 1981) and a characteristic tension transient in response to step length changes (Fredberg et al., 1997; Bates et al., 2009). However, this force-length relationship is not fixed; when stimulated repeatedly, at a given length, ASMCs adapt in order to maintain their current length at the peak of the force-length relationship (Bullimore et al., 2011). This provides the ASMCs with the ability to generate maximal force even after shortening; a response that, if unregulated, would enhance AHR. In addition, and as mentioned earlier, ASMCs are able to form latch-bridges. Such latch-bridges maintain force for long periods with low energy consumption and a decreased ASMC shortening velocity (Dillon et al., 1981; Fredberg et al., 1997). Thus, by entering the latch-state the mechanical properties of ASMCs markedly change to a stiffened state. ASMCs also exhibit force adaptation; total force gradually increases when ASM is stimulated repeatedly in the presence of baseline tone (Gunst and Wu, 2001; Gunst et al., 2003).

Parenchyma tissue properties

The dynamic environment of the in vivo airway is determined to a substantial extent by the forces imparted by parenchymal tethering. Parenchymal attachments to the outside of the airway wall are responsible for conveying transpulmonary pressure from the pleural surface to the airway wall, and thus impart an outwardly directed force that opposes airway narrowing. Consequently, when the airways are challenged with a smooth muscle agonist, their contractile response is exquisitely sensitive to transpulmonary pressure.

The mechanical properties of the parenchyma can be described to a first approximation in terms of a linear single-valued stress-strain function such that transpulmonary pressure depends linearly on lung volume. This description accounts for the majority of the mechanical behavior that influences airways responsiveness over the range of volumes encountered during normal breathing. However, the stress-strain behavior of lung tissue exhibits significant strain stiffening beyond this volume range due to a variety of mechanisms; a key mechanism being the progressive recruitment of collagen fibers that become straight and bear the load as volume increases (Maksym and Bates, 1997; Maksym et al., 1998). Lung tissue is also highly viscoelastic (Bates et al., 1994), so the outward force it exerts on a tethered airway depends on volume history in addition to the current volume itself.

Experimental methods

ASM strips

We have made substantial progress toward understanding the mechanical behavior of activated and non-activated ASM by characterizing the dynamic force-length behavior of strips of rat trachealis muscle (Bates et al., 2009; Bullimore et al., 2011). We measured the slowing of contraction velocity during activation (a characteristic of the latch-state) and examined if the isotonic releases influence the degree of velocity slowing. This was done by comparing shortening velocity after 15 min of isometric activation with the shortening velocity of the same ASM strip when velocity was measured once per min for 15 min. Velocity at 15 min was very similar under the two conditions. We also studied velocity slowing over time in ASM from rat and sheep trachea and found that the time course of velocity slowing was similar in both preparations and could be described by a power-law.

Stretching lung slices

To explore if airway stretching associated with breathing relaxes airway ASM, lung slices can be stretched and changes in airway size recorded. To ensure tethering is active, the lung slice periphery must be stabilized and this can be achieved by attaching the lung slice edge to a silicon sheet with glue. By applying oscillating stretches to the preparation the airway appears to simulate the cyclic expansion during breathing. Preliminary data indicate that human airways contracted with MCh respond to rhythmic stretch by relaxing (Figure 9). When stretching ceased, the airway re-contracted. These results are consistent with the idea that stretching is a protective mechanism against agonist-induced contraction, which was inspired by studies in isolated strips of ASM (Fredberg et al., 1997; Wang et al., 2000) leading to the hypothesis that fluidization of the ASM causes its contractile state to be determined dynamically (Krishnan et al., 2008). On the other hand, evidence of this effect in vivo is scant, being limited to volume changes that are very large (Bates et al., 2007). Recent studies of the contractile response of isolated airways subjected to transmural pressure changes have also failed to show that pressure oscillations reduce airway contractility (LaPrad et al., 2010; Noble et al., 2011). Our working hypothesis is that the protective mechanism we observe in our explant preparation derives from the dynamic properties of the ASM cross-linkers and cross-bridges, which exhibit fluidization when stretched. Nevertheless, it will be interesting to see whether these effects manifest in a measurable way at the level of the whole organ when incorporated into a global model of lung responsiveness.

Figure 9.

Effect of stretch on airway contraction. A human airway contracted with MCh and exposed to sequential uni-axial stretching to mimic breathing (details of the effect of each stretch is shown in the insert box) responded with an increase in the baseline of airway size (relaxed). When stretching was terminated, the airway began to slowly re-contract in response to the continual presence of MCH.

Modeling approaches

Empirical models of ASM contraction dynamics

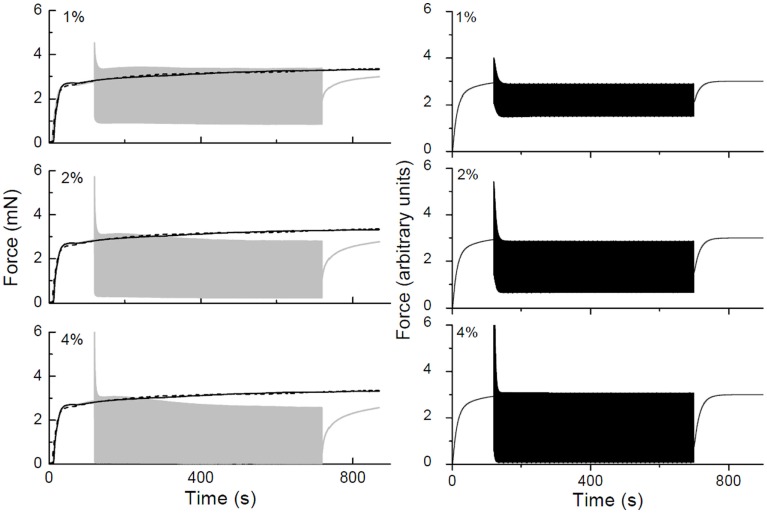
To model the dynamic force-length behavior of an ASM strip, we have used two complementary approaches. One uses traditional viscoelastic theory (Bates et al., 2009) based on spring-and-dashpot models and has the advantage that it is based on ordinary differential equations and is therefore relatively straightforward to simulate. Here, we assume that the contractile machinery in the ASMC is presented as a force generator that acts in concert with non-linear passive elements representing the connective tissues that are mechanically arranged both in series and parallel with the force generator. This model mimics the key features of the oscillatory force-length behavior of ASM strips both when they are passive and when the ASMCs are activated by an applied stimulus (Figure 10). Of particular note, in order to reproduce the rapid transient decrease in peak oscillatory force observed upon the initiation of activation (Figure 10), it is necessary to have the force-generating capacity of the ASMCs be reduced in proportion to the rate of change of ASM strip length. This mechanism is still empirical, but is motivated by the notion that cross-bridge attachment is impaired by relative movement of actin and myosin filaments (Fredberg et al., 1999).

Figure 10.

Force-time traces obtained in a strip of rat trachealis muscle. The gray curves show data obtained with 2 Hz length oscillations having amplitudes of ±1, ±2, and ±4% baseline length as indicated. Isometric force-time curves are shown in black (solid lines obtained prior to collecting oscillation data, dashed lines obtained afterward). The black curves in the right-hand panels show corresponding force-time plots simulated by a lumped-parameter model of the ASM strip that includes an empirical mechanism accounting for cross-bridge attachment and detachment kinetics.

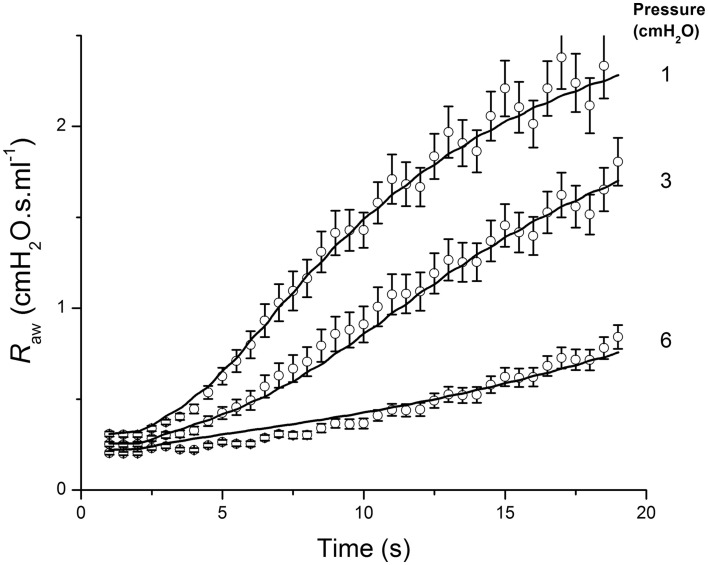
We have incorporated a simplified version of the above model into a model of the contraction of ASM around an airway embedded in the lung parenchyma in order to mimic the marked dependence of airway responsiveness on transpulmonary pressure. Here, it is necessary to take into account not only transpulmonary pressure itself, but also the increased translumenal pressure across the airway wall that arises from local distortion of the parenchyma caused by airway narrowing. The latter can be usefully approximated by a relationship derived by Lai-Fook (1979). Using this relationship, together with the classic hyperbolic description of the force-velocity relationship for ASM, the dynamic response of the airways to intravenous methacholine over a range of inflation pressures can be accurately reproduced by a model consisting of a single airway embedded within linearly elastic parenchyma (Bates and Lauzon, 2007; Cojocaru et al., 2008). Importantly, the adequacy of the model fit (Figure 11) relies on the inclusion of a finite stiffness to the airway wall, which provides a significant load opposing smooth muscle shortening in addition to that of the parenchyma itself. This approach to balancing the force of smooth muscle contraction against the opposing mechanical loads can be taken with respect to the individual airways in a model of the lung that includes the branching structure of the airway tree, thereby allowing regional differences in responsiveness to be taken into account (Politi et al., 2010).

Figure 11.

Airway resistance measured in mice (open circles: mean ± SEM) following an intravenous injection of methacholine at time 0, when the lung inflation pressure was set to the three different values indicated at the right of the figure. The solid line shows the fit provided by a computational model of an elastic airway embedded in parenchyma that contracts according to a hyperbolic force-velocity relationship. Adapted from Cojocaru et al. (2008).

Mechanistic models of ASM force-length dynamics

The second approach we have used to model the dynamic force-length behavior of the ASM strip takes the underlying cross-bridge mechanism specifically into account (Wang et al., 2008; Donovan et al., 2010). This approach has the advantage of a specific biophysical basis, but it is based on partial differential equations and is therefore more difficult to implement than the spring-and-dashpot model described above. Again, the dynamic mechanical properties of ASM are obtained experimentally from its transient force-length behavior during cyclic stretching, with peak force and stiffness being initially high but rapidly falling to become at or below isometric values. While some of this behavior can be predicted using an adaptation of Huxley’s cross-bridge model of skeletal muscle (Mijailovich et al., 2000) we have found that the non-linear viscoelastic properties of ASM tissue must also be taken into account (Bates and Lauzon, 2005). However, this still does not account for all the dynamic force-length behavior of ASM. In particular, when activated ASM is stretched to mimic deep inhalation, there is a protracted decrease in its subsequent ability to generate force that is not predicted by models based solely on cross-bridges. We have proposed that this loss of ASM force generation results from the disruption of the contractile apparatus (Bates et al., 2009), the actin cytoskeleton, or other proteins comprising ASM and its connections to the airway.

Models of passive parenchymal tissue

The modeling of soft tissue mechanics using empirical constructs such as assemblies of springs and dashpots is well-established (Fung, 1981). Such models do not, however, embody any particular underlying biophysical mechanisms for complex tissue rheology; indeed, this remains an active research field that has much attention from both biological and physical scientists (Suki and Bates, 2011). Recently, we have proposed a novel mechanism for the genesis of the rheological behavior that has been observed in lung tissue (Bates et al., 1994). This mechanism is based around the notion that stress is released within stressed tissue through a sequence of micro yield events that occur throughout the tissue (Bates, 2007), as opposed to the smooth relative sliding of multiple components as is implied by spring-and-dashpot models. The appeal of this model is that, although still empirical in terms of specific mechanisms, it exhibits quasi-linear viscoelastic behavior in which the static non-linear stress-strain behavior of the tissue is separable from the dynamic non-linear behavior. Furthermore, the latter is predicted to manifest as a power-law decay of stress with time following a step increase in strain, as is observed experimentally (Bates et al., 1994).

We have recently proposed a specific mechanism for the micro yield events described above that derives from the Huxley-type cross-bridge models of active ASM that are now well-established (Mijailovich et al., 2000). Specifically, we have proposed that the passive stress in ASM tissue is mediated by cross-linking proteins that temporarily bind protein fibers together within the tissue via thermodynamically driven interactions (Donovan et al., 2010). The cross-linkers extend from one filament and bind to attachment sites on an adjacent filament, and can account for many of the passive mechanical behaviors observed in ASMC such as the responses to cyclic stretching and deep inspirations and fluidization upon stretching. The cross-linker model also suggests a compelling unification between the mechanical mechanisms of passive and active tissue; both involve cross-bridges, the only difference being that the binding probabilities in passive tissue are symmetric functions of distance and are driven thermodynamically while the binding probabilities in active tissue are asymmetric and require the energy supplied by ATP (Donovan et al., 2010).

The Organ Scale

To this point we have described the balance of forces for a single airway. However, the mechanical properties of the lung vary significantly along the airway tree. For example, the amounts of collagen and ASM in the airway wall progressively decrease toward the periphery. In lung disease, it is also common that the properties of the airway wall and the parenchyma are altered, (e.g., airway remodeling associated with AHR). These regional passive (mechanical and structural) and active (force-generating) heterogeneities have a major influence on the overall mechanical behavior of the lungs. For example, when regions of the lung that are connected in parallel become mechanically disparate (so-called “parallel heterogeneities”), the apparent overall resistance of the lung, which normally has an inverse dependence on the frequency of oscillatory flow, decreases with frequency even more precipitously. Conversely, for mechanically disparate regions of the lung that are connected in series, some of the oscillatory flow can be shunted into the proximal elastic compartment (e.g., the central airways) which causes overall lung elastance to increase dramatically with frequency. Thus, the crucial question is: how does the function of the whole organ arise from the distributed nature of structure and function at the level of the individual airways?

Experimental methods

The state-of-the-art method to assess the overall mechanical properties of the lung is based on the measurement of input impedance. A broad-band flow perturbation is applied at the trachea while pressure is measured at the same site. This is achieved with a forced flow oscillation technique. In mice, a computer-controlled mechanical ventilator (Flexivent) can be used to apply and measure a controlled mechanical perturbation to the lungs at frequencies of up to 20 Hz or more (Schuessler and Bates, 1995). Although technically less challenging due to the larger lung volume, the approach is essentially the same for human subjects (Bates et al., 2011). However, flow perturbations in human subjects have to be applied via the mouth rather than the trachea so some shunting of flow into cheeks and pharynx can influence the results related to the lung.

The pressure [P(t)] and flow signals [V′(t)] are related in the frequency domain by the relationship P(f) = Z(f)V′(f), where frequency (f) indicates the Fourier transform of the corresponding function of time (t). The complex function Z(f) is the input impedance and is a model independent function that encapsulates the mechanical properties of the lung. The physiological information inferred from measurements of Z(f) depends on the frequency range of the flow oscillations applied to the lungs (Bates, 2009; Bates et al., 2011). By fitting physiologically motivated mathematical models to Z(f), the model parameters can be determined as measures of the physiological quantities they represent (Bates, 2009).

Increased lung impedance associated with AHR

Using these approaches, Hantos et al. (1992) proposed a model known as the constant-phase model. In this model, a uniformly ventilated lung is accessed by single airway that has a Newtonian resistance (R_n). This airway is coupled to a distal alveolar unit composed of viscoelastic tissue that has mechanical impedance with real and imaginary parts that have a constant ratio to each other with frequency (i.e., “constant-phase”). The dissipative component, G, of this tissue impedance reflects the resistive properties of the tissue, while the conservative component, H, is a measure of tissue stiffness.

We have used the constant-phase model in studies of AHR in mice to help identify the underlying mechanisms that are responsible for exaggerated responses to methacholine. For example, in BALB/c mice that were allergically sensitized to challenge with ovalbumin, we found that AHR to a methacholine aerosol resulted from a thickened epithelium and increased airway secretions, but not from increased shortening of ASM (Wagers et al., 2004). By contrast, when mice were treated with intra-tracheal cationic protein, which has the effect of damaging the epithelium, mice exhibited AHR characterized by increased ASM shortening (Bates et al., 2006). When both mechanisms were present simultaneously, mice were extremely hyperresponsive, arguably recapitulating the essential features of a severe asthma attack (Bates et al., 2008). However, when methacholine is administered via the peripheral circulation rather than as an aerosol, the ASM exhibits increased shortening relative to the control. We hypothesize that this exaggerated response to injection reflects an increased leakiness of an inflamed pulmonary endothelium, allowing a greater dose of methacholine to reach the ASM (Cojocaru et al., 2008). These results highlight the important role that inflammation plays in AHR. This role is well known in allergic asthma, which has been shown to lead to alterations in the excitation-contraction coupling behavior of ASM (Bjorck et al., 1992; Mitchell et al., 1994), in addition to the biophysical roles alluded to above.

The Multi-Scale Model of the Lung

Integrating across the scales to achieve a full lung model

To scale up to the level of the lung from a model of a single airway, we embed the conducting airway tree within a parenchymal tissue continuum (Figure 12 – organ scale). The airway tree geometry is generated using an asymmetrically branching, 3-D tree-generating algorithm that aims to be morphometrically accurate (Tawhai et al., 2004). There are several important reasons for scaling to a full lung topology instead of only studying the behavior of a limited number of airways. First, we can impose physiological boundary conditions that are consistent with the environment and function of the lung. Second, we can exploit medical lung imaging to create subject-specific models in order to test the sensitivity of regional bronchoconstriction to airway geometry. And third, it is only by correctly accounting for the spatial distribution of the airway tree within the lung parenchyma that the appropriate contribution of regional differences in tissue expansion (due to gravity and normal variability in material properties) can be assigned to the balance of forces on the airway wall during its constriction.

Figure 12.

The four spatial scales and their interactions in the multi-scale lung and airway model. The four scales of organ, tissue, cell, and molecule interact as follows: (A) anisotropic strain from the parenchymal continuum model (organ scale), linearized to an expression for parenchymal tethering, (B) Shortening velocity that is limited by the balance of active and passive forces, (C) Coupling of calcium to force generation via activation of MLCK, (D) Active and passive force generation from cross-bridges and cross-linkers, (E) Airway constriction and redistribution of ventilation.

To achieve computational feasibility when scaling the model to represent an entire human lung (that contains about 60,000 bronchial airways), we assume each airway is radially symmetric and that changes in airway mechanics during breathing are determined only by changes in radius and not length. At the tissue level, each airway is comprised of an airway wall and a surrounding ASM layer that interacts mechanically with the parenchyma (Figure 12 – tissue scale). In this way, we calculate the active contractive force generated by the ASM and the opposing passive mechanical forces provided by airway wall stiffness and outward parenchymal tethering. From the resulting balance of all these forces, we can determine the airway radius; this calculation is repeated for each airway with respect to time.

For computational simplification, we initially considered an arbitrary 3-D unit of lung tissue that is representative of the whole lung and its airways (this includes a range of airway sizes). The location of the unit is relatively unimportant for establishing an initial understanding of the system behavior, but it can be scaled to the whole lung and fitted to the anatomically based geometry of the full conducting airway tree – this is a question of computational rather than conceptual complexity. The tissue unit contains all the key elements of the airways embedded in a parenchymal continuum. The alveoli are not represented discretely, but are assumed to operate as a smooth, homogeneous material (as part of the organ scale parenchymal continuum) regardless of the airway size or order. The airways included in the unit have eight orders of branching (generated by a space-filling branching algorithm; Tawhai et al., 2004). Again, for simplification and scaling feasibility, each airway segment is assumed to be radially symmetric and longitudinally stiff. Length changes are assumed independent of radial changes.

We use a continuum approach to embed the airway tree within “lung tissue” that is a compressible, hyper-elastic material in 3-D (Tawhai et al., 2006, 2009). This “tissue” is essentially a homogenization of the elastic properties of the parenchyma, air, airways, and blood vessels. We assume material compressibility because the tissue contains air that is free to move into or out of the lung. Stress and strain are related by a strain energy density function, and the response parameters of the tissue are selected such that normal lung inflation pressures give rise to expected expansion volumes for the tissue (Tawhai et al., 2009). By solving the governing equations of finite elasticity (large deformation) mechanics using a finite element method, our model is capable of simulating tissue deformation due to both gravity and the expansion and recoil associated with cyclic changes in pressure on the model surface due to breathing. Figure 12 (organ level) illustrates a distribution of recoil pressures on a finite element model of the right lung in the upright position under gravitational load. Due to the inaccessibility of the lung tissue to direct measurement and limitation of high resolution imaging of supine or prone postures, data for the validation of the tissue mechanics model are limited (discussed later). However, we have validated the prediction of the distribution of tissue density due to the model’s deformation under gravity in the supine posture by comparing this against imaging data of subjects in the same posture (Tawhai et al., 2009). This model provides the boundary pressures and local elastic properties of the parenchyma that are required for interaction with the tissue level model. The airway lumen radii computed at the tissue level depend on their coupling with the organ level model, the non-linear properties of the airway wall, and ASM force generation.

Each airway segment is classified according to its Horsfield order and has three layers with properties that depend on the order: an inner wall layer that contributes passive stiffness, an active ASM layer that generates force, and an outer parenchymal layer, which serves as an interface with the parenchymal continuum that surrounds the lung segment, and mediates tethering (Figure 12 – tissue scale). Airway diameter is a function of transmural pressure generated by stress within the ASM layer, external forces acting via the parenchyma, and luminal air pressure (Lambert et al., 1982). To enable coupling across the tissue-organ scales, the model uses two representations of the parenchyma: a local layer and the conditions of the parenchymal continuum at the location of the airway. These layers are connected with the material properties of the local layer determined from a linearization of the anisotropic continuum at the location of the airway (Figure 12). That is, the lung tissue will have undergone local volumetric changes that depend on its location in the lung; tissue in the gravitationally dependent regions will generally be under less tension than tissue in the non-dependent regions, and the irregular curvilinear shape of the lung introduces variability in the distribution of strain. Note that this variability occurs independently of any assumptions of heterogeneity in the intrinsic tissue properties.

Airway smooth muscle stress is generated by a cross-bridge model of sliding filaments within the ASMCs (Figure 12 – molecule scale) under the regulation of Ca²⁺ signaling (Figure 12 – cell scale). The models defining these processes were addressed in detail earlier and are include in the whole lung model. Thus, overall airway diameter is regulated by ASMC contraction acting against parenchymal tethering which varies with gravity and breathing. We consider breathing that is driven by changes in force or displacement at the (pleural) surface of the model, as opposed to positive pressure ventilation that is driven by increasing the pressure at the mouth. We have therefore assumed that the air pressure remains small relative to the parenchymal and ASMC forces, and so does not make a significant contribution to the transmural pressure. This is in contrast to positive pressure models with fixed tidal volume in which the air pressure can make a significant contribution (Venegas et al., 2005).

Coupling of all of these models and solving simultaneously for each airway with respect to time is a significant computational problem. Not only must all models be solved simultaneously for force balance, but a numerical continuation is also required (Allgower and Georg, 2003) because of the bistability inherent in the Lambert model of the pressure-radius relationship for the small airways (Affonce and Lutchen, 2006). It is this computational complexity (i.e., modulating transitions between the two stable states for each airway) which most limits the computational scope. However, the process is inherently parallel and potentially amenable to parallel computing approaches.

Model outcomes

It should be initially emphasized that the major outcome of this multi-scale modeling is the first working, biologically based in silico lung and the proof-of concept of the feasibility of this approach (Politi et al., 2010). Although many aspects of lung physiology are not yet included in the current model, their incorporation is now more a function of time and experimentation rather than a major modeling concept.

Reduced airway contraction due to breathing

Our simulations of breathing with contractile agonist exposure demonstrated that, as expected, the extent of airway contraction was a function of pressure changes induced by breathing imposed on pressure changes induced by ASMC stress. Importantly, the organ model also revealed the emergent behavior of increased airway diameter associated with breathing as compared to static conditions. Sensitivity analysis suggested this response was (again, as expected from experimental work) a function of the ASMC cross-bridge kinetics determined by the attachment and detachment rates. However, the model also suggested that the maximal isometric force and the rMLC dephosphorylation rate were also important (Politi et al., 2010).

Although airway radius was increased by breathing, this increase was smaller than that proposed from experimental studies (Politi et al., 2010). This raises interesting questions about the significance of the effect and the conditions under which it is observed. Our model simulates tidal breathing rather than experimental deep inspiration which appears to have a large relaxation effect on ASMCs. More importantly, experimental approaches often examine isolated ASM strips which alter or abolish the organization constraints of the airway and remove the multi-scale interactions. Thus, a small change in airway diameter may be a more realistic response. On the other hand, passive ASMC properties, which exhibit fluidization responses, are not yet included in the multi-scale model and these are expected to enhance the magnitude of airway relaxation.

The importance of spatial heterogeneity at the cellular scale

Simulations at the scale of the individual ASMCs have shown that the amount of force generated by the ASMCs is especially sensitive to the spatial distributions of the Ca²⁺ responses (i.e., the shape of the Ca²⁺ waves; Wang et al., 2008, 2010). Thus, unexpectedly, overall airway contraction can be modified and controlled by relatively minor and subtle changes in Ca²⁺ signaling at the cellular scale.

The interplay between passive and active elements at the molecular scale

At the molecular scale, passive elements such as cross-linkers generate complex dynamic behavior, including fluidization, adaptation, and velocity-dependent force generation (Donovan et al., 2010). Hence, many of the mechanical properties of ASMCs are the emergent result of these molecular scale interactions, and are thus a blend of both active and passive processes. Tissue scale mechanical behavior cannot be understood by considering cross-bridges alone.

Slow transitions between open and closed airway states

A result which has emerged only from the coupling of multiple scales in the model is a slow and steady transition between an open and closed airway state, with the transition being modulated by cross-bridge dynamics (Politi et al., 2010). It s well known that bistability between open and closed states is an inherent characteristic of the Lambert airway wall model (Lambert et al., 1982; Affonce and Lutchen, 2006) but this static model allows for instantaneous transitions between the open and closed state. Only by coupling the tissue scale with the dynamics of the cross-bridge model of ASMCs are these airway transitions modulated into the slow and steady behavior seen experimentally (Latourelle et al., 2002; Oliver et al., 2007). This result cannot be obtained by considering either scale in isolation.

Heterogeneity and gravitational gradients

Heterogeneity in airway constriction is an important aspect in the manifestation of AHR and changes in ventilation and has been explained by changes in dynamic factors as opposed to structural factors. Some studies suggest the constriction pattern can be altered by deep inspiration while other studies suggest that clustered ventilation occurs preferentially in gravitationally dependent tissue (Venegas et al., 2005; Tgavalekos et al., 2007). The coupling of non-linear sub-scale models in the multi-scale model allows us to consider the degree of heterogeneity attributable to structural factors. A significant gravitational gradient is developed, and airways located in dependent tissue are exposed to parenchymal conditions which differ significantly (Politi et al., 2010). This suggests that some heterogeneity, particularly that found in dependent tissue, may be explained by structural phenomena; however, “resetting” of the constriction pattern still requires a dynamic explanation.

Passive tissue fluidization

One result which has the potential to significantly impact the dynamic equilibration of in vivo airways is strain-induced fluidization of passive ASM. When exposed to oscillatory strain, the force exerted by stretched, passive ASM is reduced. This reduction in force is proportional to the strain oscillation amplitude, and persists beyond a 30-s timescale; this occurs in both the experimental and modeling results (Donovan et al., 2010). This has the potential to reduced airway constriction due to tidal breathing and/or deep inspirations (Ijpma and Lauzon, 2012).

Future Directions

We emphasize here that the multi-scale model is a work-in-progress. Although there are a huge number of possible additions to the model, we propose a series of questions and modifications we consider to be most important to our current sub-scale models.

At the molecular scale

How important is the latch-state in the long-term modulation of force generation?

Can passive elements such as cross-linkers, independent of cross-bridges, reproduce any of the behaviors traditionally thought to be caused by the latch-state? This is question is closely related to the question of how the active and passive elements interact to control force generation in a single ASMC; the latch-state, being in a half-way state between active and passive, will play a central role in these investigations.

What happens if unphosphorylated myosin can bind to actin?

How will this influence AMSC stiffness as a function of time after stimulation or stretching? How should this best be modeled?

Should an ASMC be modeled using a Huxley-style formation for the cross-bridges and cross-linkers, or is a more continuous (a more complicated) approach necessary?

Data indicate that breakage of cross-linkers and cross-bridges after a large stretch plays an important role in decreasing the active force, but such breakage has not yet been included in our models.

At the cellular scale

How important are stochastic properties of Ca²⁺ release?

We have to develop a stochastic model of Ca²⁺ oscillations and waves and determine whether the measured single channel properties of the IP₃R are sufficient to generate the observed behavior.

How do the patterns of Ca²⁺ waves and oscillations modulate force generation?

Although we know that the shape of the Ca²⁺ oscillation plays a role in modulating force generation, and thus there is a measurable difference between the force generated by Ca²⁺ oscillations and the force generated by Ca²⁺ waves, we need to develop mathematical methods that can take these differences into account without greatly increasing the required computer time for simulations.

How will a human ASMC model differ from a mouse model?

As yet, we have only developed a mouse model. We need to develop a detailed model of Ca²⁺ signaling in human ASMC. This will require additional data from human tissues.

What are the effects of inflammation on force generation?

Inflammatory aspects of the Ca²⁺ signaling pathways and their connection (for example) to Ca²⁺ influx, need to be included in the model so that we can study the effects of inflammation on force generation.

What is the role of mechanotransduction in Ca²⁺ signaling in ASMCs?

Are stretch-activated or compression-activated calcium channels present? If so, how important are they? Can we use a model to predict how important such channels would be expected to be?

At the tissue scale

How important are the interactions between active and passive elements in force generation?

The passive adaptation of stress in lung tissue will change the stress acting on actively cycling cross-bridges and thereby affect their actin-binding probabilities. Conversely, active force generation within the ASM tissue will affect the stress bearing role of the passive connective tissue via the cross-linker mechanism.

How important are regional tissue heterogeneities in airway-parenchymal tethering?

So far, we have modeled the parenchyma as a homogeneous isotropic material, but this is far from reality, particularly in asthma that involves regional tissue remodeling. We have begun to simulate the parenchyma as heterogeneous networks of springs, some of which may be stiffened to represent fibrotic remodeling, in order to determine how parenchymal tethering modulates airway responsiveness.

How important is the complex rheology of lung tissue in determining AHR?

We have also modeled airway-parenchymal interactions under the assumption that the tissue is purely elastic, but we know it is markedly viscoelastic. We would therefore expect that the inflation history of the lung to also affect the extent to which the parenchyma is able to resist ASM contraction.

At the organ scale

Major assumptions and/or limitations in the model at the organ level are our definition of the material law, neglecting the potential influence of air pressure, weak coupling between the tissue and organ level mechanical models, and limitations on data against which we can validate the model function.

How important is surfactant dynamics to the regional tissue elasticity?

Our continuum model combines the contributions of tissue elasticity and surface forces into a single description of the elastic behavior of the lung parenchyma, parameterized to the expected pressure-volume relationship for an intact lung at only two volumes (functional residual capacity and total lung capacity). This approach has been shown to be satisfactory for simulating static lung deformations in the supine posture in two human subjects, however this single material law parameterization is likely to be inadequate for representing the mechanics of individual subjects, particularly those with chronic lung disease. We have treated the lung tissue mechanics as a sequence of static deformations, but in the dynamic lung the contribution of surfactant dynamics and how this changes with stretch (Majumdar et al., 2011) may be important in the force balances that influence emergent behavior.

Does airway pressure make a significant contribution to the balance of pressures in a breathing lung?

Our initial model has neglected the contribution of air pressure to the balance of forces on the airway. However, other breathing lung models driven by positive pressure inflation with fixed tidal volume have shown that the contribution of the air pressure can be significant (Venegas et al., 2005). We have recently developed a model that couples the tissue deformation model to pressure development and flow distribution in the full airway tree (Swan et al., 2012). This ventilation model is not yet a component of the multi-scale model, however we can control the degree and location of static bronchoconstriction in the model and evaluate the redistribution of alveolar and luminal pressures, which the model predicts are relatively modest. Figure 12 (organ scale) illustrates a “patchy” flow distribution in this model that results from the interaction of increased airway resistance (Figure 12E) and distributed tissue compliance.

How do we introduce bi-directionality in tissue and airway mechanics?

In our multi-scale model, the airways and parenchyma are not tightly coupled. That is, while the balance of forces acting on each airway includes input from the parenchymal mechanics, the deformation of the airway, or its closure does not act in the opposite direction to contribute to the balance of forces in the continuum model. Over long times scales this could exhibit as changes in the surface forces, as we have already described. This limitation in existing models means that we do not yet understand the dependence between local airway constriction and the cyclic pressures of breathing that are transmitted throughout the lung tissue: it is not clear whether airway-parenchymal interdependence will act to further impede flow or to maintain flow to constricted regions.

Can we define a new protocol for validating multi-scale models?

For single scale models that have been designed to test a hypothesis, the model is considered validated (at least to some degree) if it qualitatively and quantitatively predicts an independent set of experimental data. While the components of these large-scale physiome-type models are data driven, every component is not amenable to independent validation against experiment. This is partly due to limitations on the data that can be acquired for validation, and partly because the intrinsic structural and functional connections across the scales can render meaningless a “validation” that is performed at a single scale or under non-physiological conditions. It is important to emphasize that we have developed the multi-scale model to have a strong biophysical basis: it is grounded in physical conservation laws, and is constrained by physiological and biological parameters. The model’s foundation in physical laws means that we only rarely have to revisit our description of the fundamental behavior of its components; rather, our modeling iterations are usually a matter of revisiting the model’s parameterization, or our computational methods that allow us to couple different scales. And operating within physiological constraints considerably – and conveniently – reduces the range of parameters that can be chosen for the model. These two considerations provide some assurance that the model does not violate either physical laws or physiological behaviors; this is necessary to demonstrate, but it is not a sufficient “validation.” At the level of the integrated model we can say with confidence that the model is predictive of several emergent behaviors that are consistent with pulmonary physiology and asthmatic pathophysiology. This is one important and necessary validation, but it does not guarantee that each model scale is realistic. Understanding uncertainties at each scale in the model is therefore imperative to providing confidence in its integrated predictions.

There are uncertainties in the model parameterization, as well as natural variability in material properties and anatomical geometry in the population. Rather than implementing the multi-scale model in numerous subjects and/or computing a stochastic variant of the model, a more systematic approach can be taken to address uncertainty and to provide confidence in the model predictions. That is, the nature of the model enables us to discover which structural or functional aspects of the integrated system are most critical in the development of bronchoconstriction. Conversely – and just as important – we can identify which model components our predictions are not sensitive to. The most straightforward approach is to perform a sensitivity analysis: simulating whole model bronchoconstriction during systematic variation in the model parameters. This is a standard approach to address uncertainty in model parameterization, but we are not aware of it being used to address the contribution of airway topology to lung function. In terms of addressing population variability, this systematic approach is more useful than repeated analysis of multiple subjects because we can control the nature and extent of the anatomical variation and provide comment on how this contributes to local force balance. For example, a subject-specific definition of the distribution of airway wall thickness and stiffness, and distribution of ASM cell type would be desirable for a truly subject-specific prediction of bronchoconstriction. New insight into how, e.g., localized wall thickening impacts on regional ASM force development could be gained through pooling simulation data from (many) subject-specific modeling studies, but this introduces similar uncertainty to an experimental study. In contrast, a systematic sensitivity analysis can distinguish between the contribution of airway wall thickening and stiffening (which would not be separable experimentally in the subject-specific analysis), the thresholds at which they become significant, and whether their regional distribution is of importance in the development of localized ventilation defects. Because our model is amenable to implementation in a test unit or in the whole lung, we can test its emergent behavior at the whole organ level against clinical data. Lutchen et al. (Tgavalekos et al., 2003, 2005) have demonstrated the potential of this approach by validating complex global-level model behavior against multiple physiological measurements through their “image-function modeling” approach. In their studies they chose to constrict airways within imaged regions of ventilation defect, and – through trial and error – fit a constriction distribution throughout the conducting airway tree that gave realistic prediction of airway impedance. We now have the opportunity to extend this approach, by predicting the spatial distribution of airway closure, and validating the integrative behavior of the model against measurements of inert gas washout, oscillation mechanics, and gas exchange.

Conclusion

We focus here on developing a whole lung model to address the phenomenon of AHR, a cardinal feature of asthma. This is a challenging task in its entity because the lung is a complex organ within which qualitatively different behaviors manifest over an enormous range of length and time scales. So far, our approach has been to select what we consider to be the most important levels of scale involved in the genesis of AHR, and to model these phenomena at each level of scale separately before combining the resulting sub-models into a global model that links behaviors between scales. We have made considerable progress by establishing the fundamental framework for an in silico lung model that based on key experimental observations made at the levels of the molecule, the cell, the tissue, and the whole organ. Furthermore, at each level of scale these representations are, for the most, based on biophysical mechanisms operative at lower levels of scale, allowing us to trace the global response of the lung, following challenge with ASM agonist, to processes operative all the way down to the molecules involved in ASM force generation. In the future, we anticipate that many other aspects of lung physiology will be included and that the model will be developed to the stage where it can be used to gain further insight into the understanding of AHR and potential therapies.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.