A genome-wide analysis of common fragile sites: What features determine chromosomal instability in the human genome?

Abstract

Chromosomal common fragile sites (CFSs) are unstable genomic regions that break under replication stress and are involved in structural variation. They frequently are sites of chromosomal rearrangements in cancer and of viral integration. However, CFSs are undercharacterized at the molecular level and thus difficult to predict computationally. Newly available genome-wide profiling studies provide us with an unprecedented opportunity to associate CFSs with features of their local genomic contexts. Here, we contrasted the genomic landscape of cytogenetically defined aphidicolin-induced CFSs (aCFSs) to that of nonfragile sites, using multiple logistic regression. We also analyzed aCFS breakage frequencies as a function of their genomic landscape, using standard multiple regression. We show that local genomic features are effective predictors both of regions harboring aCFSs (explaining ∼77% of the deviance in logistic regression models) and of aCFS breakage frequencies (explaining ∼45% of the variance in standard regression models). In our optimal models (having highest explanatory power), aCFSs are predominantly located in G-negative chromosomal bands and away from centromeres, are enriched in Alu repeats, and have high DNA flexibility. In alternative models, CpG island density, transcription start site density, H3K4me1 coverage, and mononucleotide microsatellite coverage are significant predictors. Also, aCFSs have high fragility when colocated with evolutionarily conserved chromosomal breakpoints. Our models are predictive of the fragility of aCFSs mapped at a higher resolution. Importantly, the genomic features we identified here as significant predictors of fragility allow us to draw valuable inferences on the molecular mechanisms underlying aCFSs.

Chromosomal fragile sites are loci that are prone to gaps or breaks within metaphase chromosomes. Common fragile sites (CFSs) are observed in all humans and constitute a component of normal chromosome structure (Durkin and Glover 2007; Freudenreich 2007). Such regions have been documented in many other mammalian species, including chimpanzee, gorilla, orangutan (Smeets and van de Klundert 1990), baboon (Soulie and De Grouchy 1981), cat (Stone et al. 1993), dog (Stone et al. 1991a,b), mouse (Elder and Robinson 1989), and rat (Robinson and Elder 1987). CFSs have an important role in chromosome instability; they are associated with sister chromatid exchange hotspots (Glover and Stein 1987), viral integration sites (Bester et al. 2006; Dall et al. 2008), and sites of deletion, amplification, and translocation in various cancers (Arlt et al. 2006; Durkin et al. 2008; Burrow et al. 2011). Recently, CFSs have been shown to be preferred sites of structural variation in stem cells (Hussein et al. 2011). Clearly, CFSs play an important role in genome dynamics and are medically relevant.

A subset of CFSs can be specifically induced by cellular treatment with aphidicolin (APH), a DNA polymerase inhibitor. Several models have been proposed to explain the underlying mechanisms responsible for preferential DNA strand breakage at APH-induced CFSs (hereafter called aCFSs) (Durkin and Glover 2007). Replication delay or inherent DNA replication difficulties are believed to underlie the initiation of aCFS expression (Arlt et al. 2006). Some aCFS regions undergo delayed or prolonged DNA elongation in S phase, and cells can enter G2 phase with only 50% of some aCFS loci completely replicated (Palakodeti et al. 2004; Pelliccia et al. 2008). DNA breakage within aCFSs is thought to be a consequence of failing to complete replication and/or resolving the arrested forks prior to the end of telophase and chromosome segregation (Chan et al. 2009). Specific DNA sequences, such as [A/T]_n and [AT/TA]_n repeats, and/or the formation of non-B DNA secondary structures within aCFSs can inhibit replicative DNA polymerases (Shah et al. 2010) and replication fork progression (Zhang and Freudenreich 2007). AT-rich high DNA flexibility regions have been described within some aCFSs, and may affect replication by acting as sinks for the superhelical density generated ahead of the replication fork, hindering efficient topoisomerase activity (Zlotorynski et al. 2003). More recently, a paucity of replication origins, inefficient origin firing, and failure to activate latent origins have all been suggested to play a role in delayed replication at specific aCFSs (Palakodeti et al. 2010; Letessier et al. 2011; Ozeri-Galai et al. 2011).

Intrinsic DNA sequence features alone are sufficient to induce site-specific chromosomal breakage of aCFSs found at ectopic locations (Ragland et al. 2008). Unlike rare fragile sites that are associated with a single DNA element, many sequence motifs spread throughout the aCFS region may contribute to fragility (Ried et al. 2000; Durkin and Glover 2007; Ragland et al. 2008), making the characterization of aCFSs a computational challenge. Nevertheless, previous analyses of individual aCFS loci demonstrated that these regions may be enriched in several genomic features, such as Alu repeats (Tsantoulis et al. 2008), gene-containing regions (Helmrich et al. 2006), histone hypoacetylation (Jiang et al. 2009), highly AT-rich sequences, and high DNA flexibility sequences (Mishmar et al. 1998). Unfortunately, such studies have been mostly inconclusive at the genome-wide level. For example, a large fraction of the fragile site FRA3B is enriched in LINE1 elements, but these sequences are poorly represented in FRA16D; conversely, Alu repeats dominate FRA16D (Ried et al. 2000). Similarly, highly AT-rich sequence content was shown to be irrelevant (Helmrich et al. 2006) or even to have the opposite correlation (Tsantoulis et al. 2008) with fragility. The inconsistent results reported previously are best ascribed to two major factors. First, most studies considered only a few aCFSs, so the observed enrichment might not have reflected the global trend of genomic contexts surrounding such sites. Second, the studies analyzed the enrichment of single (and not multiple) genomic features at aCFSs, and compared these with control regions that differed from study to study (Mishmar et al. 1998; Helmrich et al. 2006; Ruiz-Herrera et al. 2006; Tsantoulis et al. 2008). Some of these studies previously used control regions that exhibited low-frequency breakage or were characterized as aCFSs in subsequent studies (Mrasek et al. 2010).

Traditionally, the organization of the human genome was interrogated using a variety of chromosomal banding techniques (Comings 1978). Differential banding patterns reflect variations in chromatin structure and base composition among chromosomal regions and have been correlated with various aspects of genome function (Craig and Bickmore 1993). For example, R bands have a higher gene and CpG island density than G bands, display higher levels of histone acetylation, and are enriched for SINE elements. S phase DNA replication is distinctly bimodal, and R bands correspond to early replicating regions, whereas G bands correspond to late replicating regions of the genome (Holmquist et al. 1982). Several types of fragile sites have been observed to lie more frequently in R bands or near the border of R and G bands (Yunis and Soreng 1984). It has also been suggested that aCFSs are located in G-band-like regions of R bands (Mishmar et al. 1999). T bands, a specific subset of R bands, have been shown to be sites of increased chromosomal rearrangement, both in cancer cells and during chromosomal evolution (Holmquist 1992). Interestingly, aCFSs may be depleted in evolutionarily homologous syntenic regions conserved between mammals and chicken (Ruiz-Herrera et al. 2006).

Current evidence suggests that aCFSs are caused by multiple interplaying genomic factors (Dillon et al. 2010). Fragility may result from several genomic properties characterizing a locus, instead of a single motif or genomic feature (Durkin and Glover 2007). The wealth of genome-wide profiling studies that are now available provides us with an unprecedented opportunity to investigate the underlying causes of chromosomal fragility. A model that considers multiple factors simultaneously is expected to be more biologically realistic and could illuminate how different genomic features interact to contribute to fragility. In addition, aCFSs vary in their breakage frequency, but previous studies have not incorporated this quantitation into their statistical models.

To advance our understanding of the relationship between aCFSs and genomic contexts, we built statistical models to explain the fragility of well-characterized autosomal aCFSs by considering their genomic landscape and contrasting them with nonfragile regions (NFRs) obtained from a genome-wide screening. We focused on CFSs induced by aphidicolin because they have been characterized genome-wide (Mrasek et al. 2010), are the most numerous CFSs, and CFSs induced by other agents might have different breakage mechanisms and characteristics. We used multiple logistic regression to predict the probability of a given region to be either an aCFS or an NFR and multiple linear regression to predict expected breakage frequency. Finally, to evaluate performance, we validated our models using mouse fragile sites.

Results

Defining aCFSs vs. NFRs

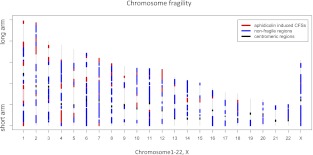
The cytogenetic locations of APH-induced CFSs from the genome-wide screening (Mrasek et al. 2010) were converted to genomic coordinates using the UCSC Genome Browser (Rhead et al. 2009). Among the known APH-induced CFSs, we focused on 76 well-characterized sites (Lukusa and Fryns 2008). These 76 aCFSs, which vary in size from 0.7 to 24.8 Mb, were originally defined by cytogenetic analyses (Lukusa and Fryns 2008; Mrasek et al. 2010). Notably, while some of the aCFS size variation may reflect actual biological differences, some might also be explained (especially in the upper size ranges) by the limited resolution of cytogenetic methods used to define the aCFSs (Durkin and Glover 2007). We did not use all 233 breakage regions identified by Mrasek and colleagues (2010) because their set included low-breakage-frequency sites (possibly representing experimental background) and rare fragile sites known to originate by a different molecular mechanism (Durkin and Glover 2007; Lukusa and Fryns 2008). From the 76 well-characterized aCFSs, initially we excluded sites located on sex chromosomes, because sex chromosomes possess very few aCFSs (three on chromosome X and none on chromosome Y) (Fig. 1) and are enriched in repetitive elements (Skaletsky et al. 2003; Ross et al. 2005), potentially biasing our analysis. A subsequent analysis including aCFSs on chromosome X led to similar results (see below). Our final data set, thus, consisted of 73 aCFSs that were distributed quite broadly across human autosomes (but none were located on chromosomes 19 and 21) and covered 462 Mb (or 14.90%) of the autosomal genome (Fig. 1; Supplemental Table S1). Visual inspection of their genome-wide distribution suggests that most autosomal aCFSs are located away from centromeres (Fig. 1).

Figure 1.

Locations of 76 APH-induced common fragile sites (aCFSs) and 131 nonfragile control regions (NFRs) used in this study. (Red) aCFSs (pink is used to differentiate among three fragile sites on chromosome 1). (Blue) NFRs. Gray regions were excluded from the analysis because they are either rare fragile sites or background breakage regions. (Black regions) Centromeres.

To define NFRs against which to contrast aCFSs, the set of 233 known fragile regions identified in a genome-wide screen (Mrasek et al. 2010), fragile regions from other studies (Kuwano et al. 1988; Borgaonkar 1994), heterochromatin, and centromeric regions were removed from the human autosomal genome (see Methods for details). After such removal, we defined the leftover 124 fragments as NFRs, ranging in size from 1.4 to 32.9 Mb and covering 1084 Mb (or 34.96%) of the autosomal genome (Supplemental Table S2).

Genomic features

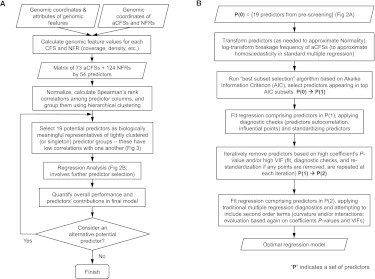
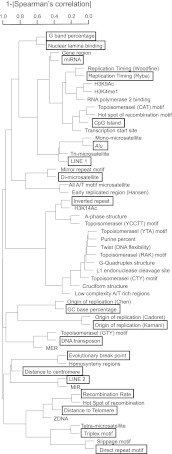
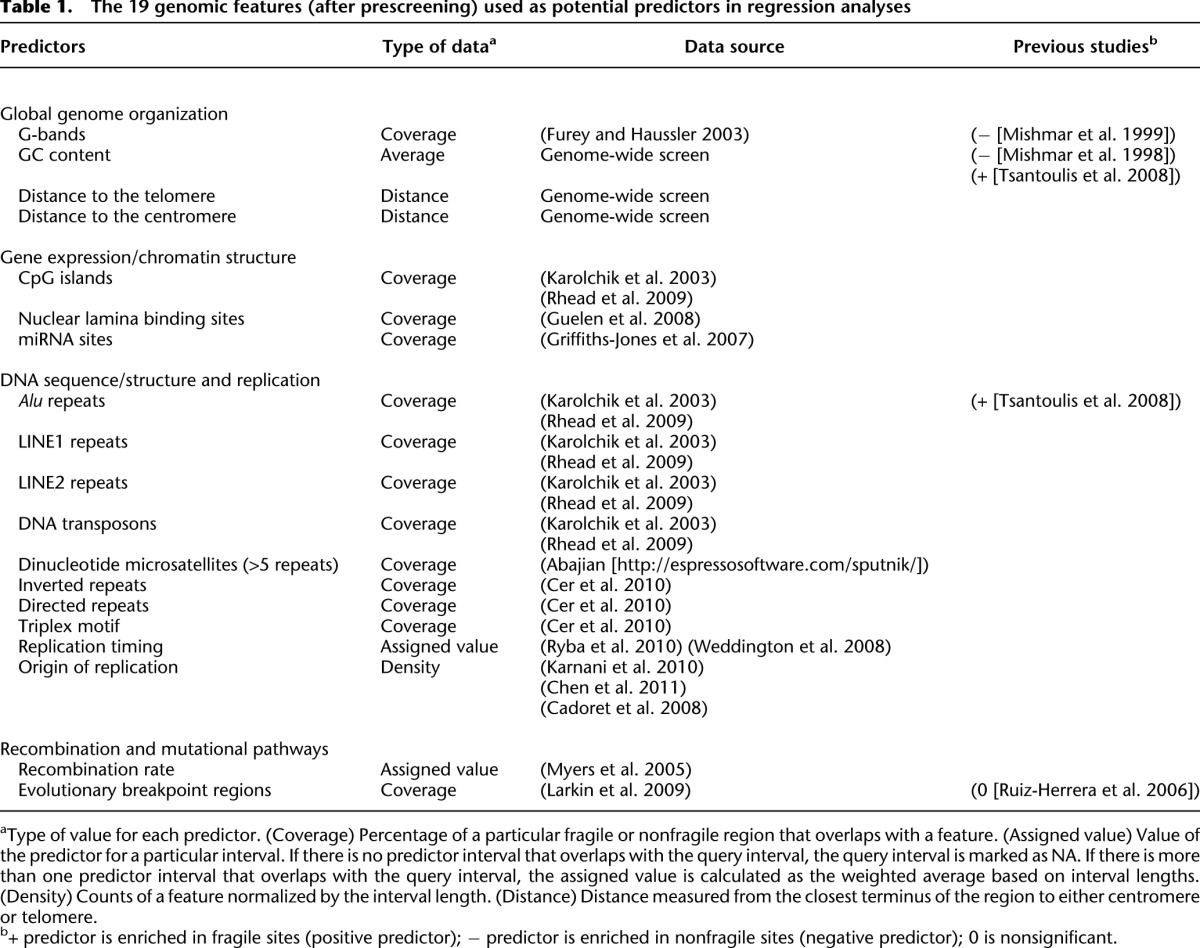
To assess the location of aCFSs relative to the global organization of the genome, we initially used G banding, GC content, distance to the centromere, and distance to the telomere as potential predictors of fragility. The advent of whole-genome sequencing and other genome-profiling techniques has overlaid this global organization with more specific landscape features. Therefore, we considered a larger set of 54 genomic features, including those for which an association with aCFSs has been suggested in previous studies (Supplemental Table S3). This set included the above features associated with global genome organization, as well as with gene expression and chromatin organization (CpG islands, transcription start sites, H3K4me1 histone modification sites, nuclear lamina binding sites, and microRNA occurrence), DNA replication (replication timing and replication origin density), recombination and mutation (recombination rates and evolutionarily breakpoint regions), and DNA sequence/structure (direct and inverted repeats, triplex motifs, microsatellites, low complexity A/T rich regions, non-B DNA structures, DNA flexibility, and transposable elements). The DNA flexibility parameter (Twist) measures potential local variations in the DNA structure, expressed as fluctuations in the twist angle of two adjacent base pairs (Sarai et al. 1989; Mishmar et al. 1998; Travers 2004). All these predictors were measured in each aCFS and NFR and prescreened based on their pairwise associations with other predictors (a flowchart with our predictor screening pipeline is depicted in Fig. 2A). More specifically, we clustered predictors using their Spearman's rank correlation coefficients (Fox 2002) and selected one “representative” predictor from each tight cluster to ensure that pairwise correlations between any selected predictors did not exceed 0.7 (Fig. 3). In subsequent regression fits, this avoided strong multicollinearities, keeping variance inflation factors (VIFs), which measure linear association among the predictors in a regression, below five (Fox 2002). “Representative” features from each tight cluster were selected based on prior evidence of association with CFSs (from the literature; see Introduction). This prescreening produced a set of 19 predictors (Table 1; Fig. 3) that were used for subsequent model selection in our regressions (Fig. 2B). Genome-wide computational modeling is limited by the resolution/accuracy of the genome annotations that are available for the predictors. Some of this annotation, in turn, is limited by the experimental approaches used to derive the data (e.g., many “genome-wide” sequencing studies exclude repetitive sequences). Because all approaches have inherent error, we considered other genomic features (from Supplemental Table S3) as alternatives at various stages of our analyses, with the logic that true molecular predictors of aCFSs will likely overlap with several genomic features.

Figure 2.

Statistical workflow. (A) Potential predictor selection (prescreening). (B) Regression analysis (box “Regression Analysis” in A).

Figure 3.

Hierarchical clustering of predictors using their Spearman correlation coefficients computed across all 73 aCFSs + 124 NFRs. (Y-axis) 1−|correlation coefficient|. The lower predictors merge in the dendrogram, the higher their correlation. Predictors in black boxes were selected as potential predictors to run our regression analysis (which includes further predictor selection steps).

Table 1.

The 19 genomic features (after prescreening) used as potential predictors in regression analyses

Contrasting genomic features between aCFSs and NFRs

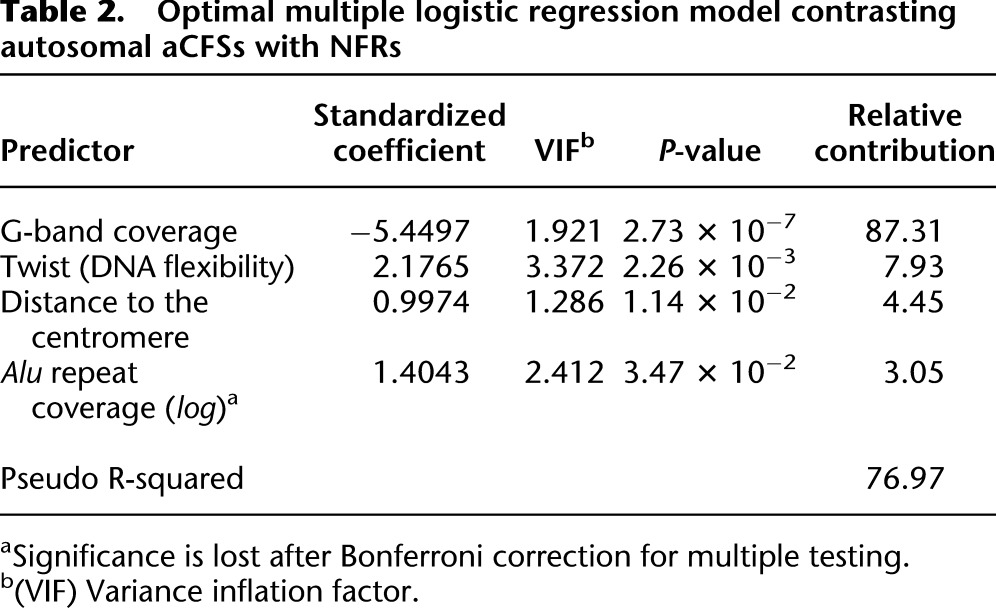
In this analysis, we used logistic regression to contrast genomic features between aCFSs and NFRs. Well-established techniques for model selection applied to the 19 prescreened predictors (Table 1) led to a model with the highest predictive power—later called the optimal logistic model (importantly, some of the 19 prescreened predictors were subsequently replaced with alternative choices, i.e., predictors highly correlated with them, to produce alternative models— see below). The optimal logistic model captures 76.97% of the null deviance and comprises four highly significant genomic features (Table 2; P-values are given in the table). The strongest feature discriminating between aCFSs and NFRs was G band coverage (individual contribution ∼87%). This was a negative predictor, indicating that aCFSs are positioned largely outside of G bands (e.g., in G-negative bands). Average twist value, distance to the centromere, and Alu repeat coverage were all significant positive predictors (individual contributions ∼8%, ∼4%, and ∼3%, respectively). Alu repeat coverage lost its significance after Bonferroni correction for multiple testing. Thus, known aCFSs appear to be located distant from the centromere and preferably in a genomic landscape depleted in G bands, yet characterized by high DNA flexibility and enrichment in Alu repeats. Note that the existence of correlations among predictors (despite low VIFs) implies that the sum of the relative contributions of individual predictors does not necessarily add to 100% (the total deviance explained by the model).

Table 2.

Optimal multiple logistic regression model contrasting autosomal aCFSs with NFRs

We attempted to further investigate the genomic features associated with aCFSs by replacing predictors in the optimal model (Table 2) with predictors that were excluded during prescreening (see above; Fig. 3) but can provide alternative interpretations (Table 3; Supplemental Table S4). For instance, we replaced average Twist value with the coverage of low-complexity A/T-rich regions that have been suggested to associate with aCFS breakage (Dillon et al. 2010). Coverage of low complexity A/T-rich regions was a significant positive predictor (P = 0.00031) (model 1 in Table 3), and the resulting model had a higher pseudo R-squared as compared with the optimal model (80.32% vs. 76.97%). However, low complexity A/T-rich regions had high VIFs (>5), reflecting multicollinearity (Supplemental Table S4), and therefore, we consider this model to be suboptimal. We also replaced Twist with negatively correlated predictors such as H3K4me1 site coverage (enriched in promoter regions) (Heintzman et al. 2009), CpG island coverage, or transcription start site density (models 2, 3, and 4 in Table 3, respectively). All of these predictors were significant (P = 0.047, P = 0.006, and P = 0.034, respectively; for H3K4me1 site coverage and transcription start site density, the significance was lost after Bonferroni correction for multiple testing). The resulting models had lower pseudo R-squared (72.69%, 76.27%, and 72.60%, respectively) as compared to that for the optimal model (76.97%).

Table 3.

Alternative multiple logistic regression models contrasting autosomal aCFSs with NFRs

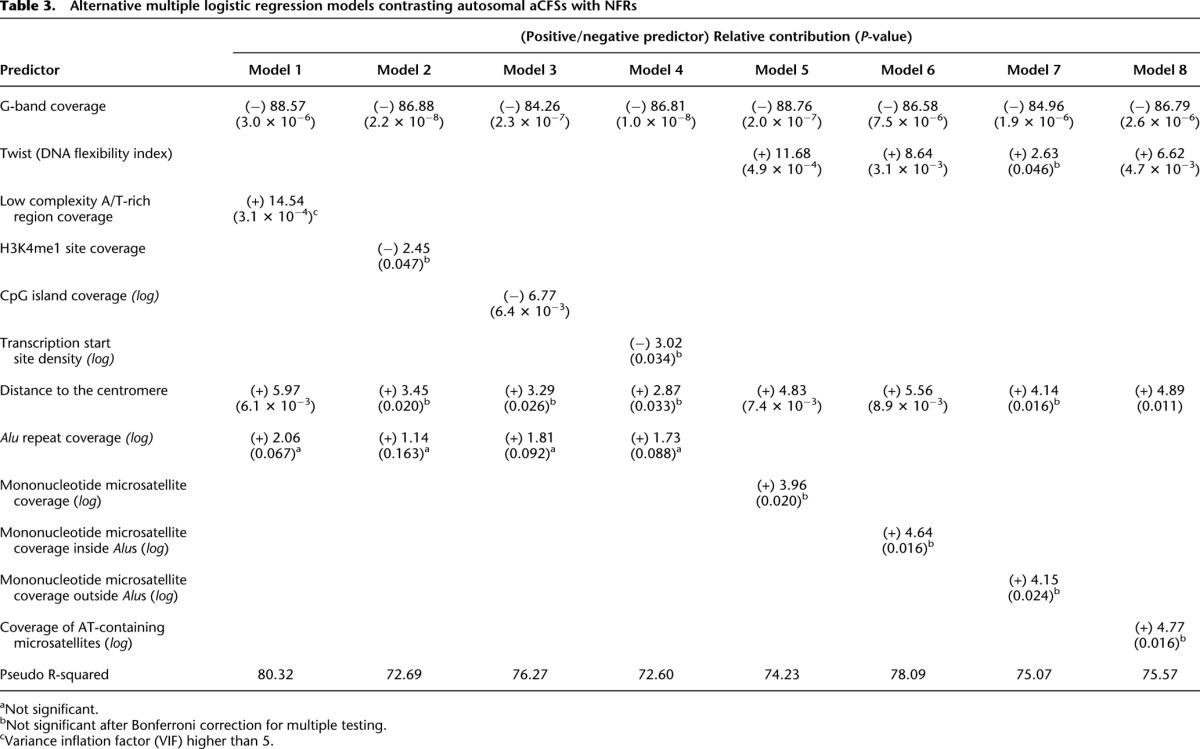
Alu sequences are composed of two long A-rich stretches frequently containing mononucleotide microsatellites (Arcot et al. 1995; Kelkar et al. 2011). Mononucleotide A/T repeats cause pausing of replicative DNA polymerases in vitro (Shah et al. 2010) and, thus, may contribute to replication difficulties within aCFSs. Thus, we replaced Alu repeat coverage with mononucleotide microsatellite coverage in our modeling (model 5 in Table 3). Mononucleotide microsatellite coverage was a significant positive predictor (only) prior to Bonferroni correction (P = 0.020), resulting in a model with a lower fit than the optimal model (74.23% vs. 76.97%). We also replaced Alu coverage with either the coverage of mononucleotide microsatellites within or outside of Alus (models 6 and 7 in Table 3). Interestingly, the model using mononucleotide microsatellites within Alu sequences had a better fit than the model utilizing mononucleotides outside of Alu sequences (78.09% vs. 75.07%) and the optimal model (78.09% vs. 76.97%). Replacing Alu coverage with A/T-containing microsatellite coverage (i.e., genome-wide microsatellites with repeats consisting of exclusively A and/or T bases) did not yield a more predictive model (75.57% for model 8 in Table 3). However, note that, in all these models, Alu coverage and other predictors used to replace it were significant only prior to Bonferroni correction for multiple testing and were, in fact, the predictors with the lowest explanatory power (among other predictors). Nevertheless, this analysis suggests that mononucleotide A/T-rich microsatellites, particularly when located within Alus, may substantially contribute to fragility.

Despite evidence that some aCFSs replicate late during the cell cycle (Le Beau et al. 1998; Hellman et al. 2000; Durkin and Glover 2007), replication timing was not a significant predictor of fragility in any of our models. Three independent replication timing data sets were tested (Woodfine et al. 2004; Hansen et al. 2009; Ryba et al. 2010). These data sets were found to be highly correlated (all pairwise Pearson correlation coefficients were above 0.7, data not shown) and therefore appear to be robust. The utilization of replication origins has been recently hypothesized to be altered in aCFSs (Palakodeti et al. 2010; Letessier et al. 2011). However, origin density was not significant in our models, independent of the three replication origin data sets used in our analyses (Cadoret et al. 2008; Karnani et al. 2010; Chen et al. 2011).

Finally, we repeated our analysis including X chromosomes (here, all 76 aCFSs and 131 NFRs were used; chromosome Y was excluded as female cells were analyzed by Mrasek and colleagues [Mrasek et al. 2010]). The results (pseudo R-squared of 77.16%) (Supplemental Table S5) were similar to those obtained for autosomes only (Table 2).

Effect of genomic features on the frequency of aCFS breakage

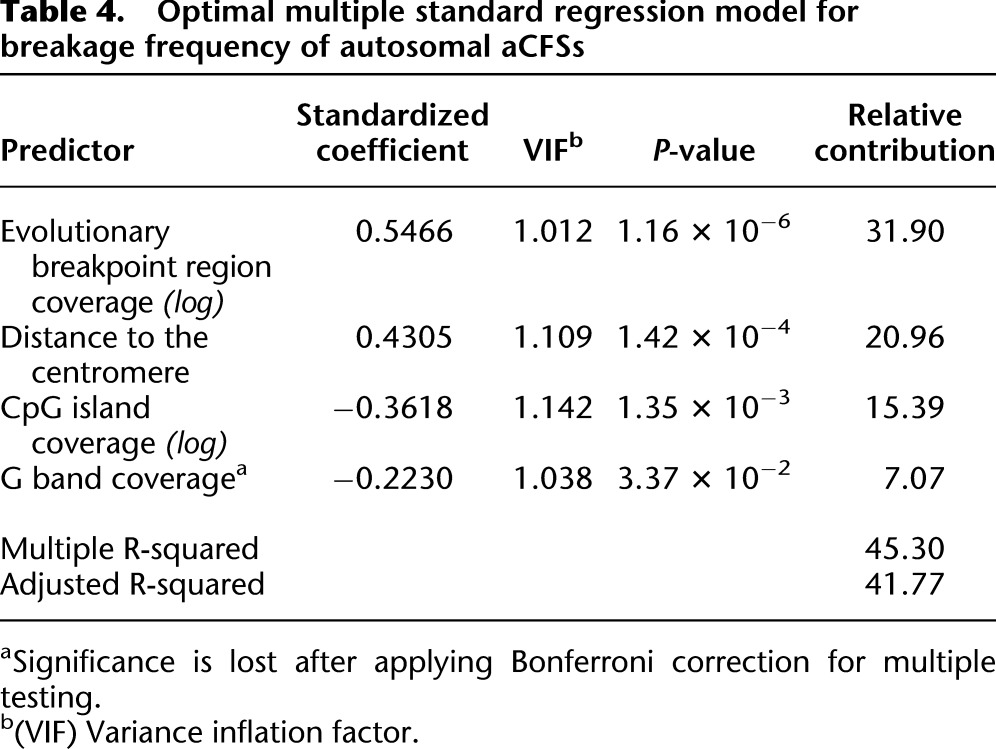
Across the genome, various aCFSs do not break with the same probability. Mrasek and colleagues (2010) evaluated breakage frequency of aCFSs within 25,000 peripheral blood lymphocyte-derived metaphase spreads and observed that only ∼10% of aCFSs detected were fragile at a frequency >1%. We used these data to examine genomic features potentially affecting aCFS breakage frequency, focusing on the 73 APH-induced autosomal aCFSs, and performing a standard multiple regression analysis. Different variable selection approaches starting from the 19 prescreened predictors (Table 1) all led to a model (later called the optimal standard model) accounting for ∼45% of variation in aCFS breakage frequency and containing four significant predictors (Table 4): distance to the centromere (P = 0.00014), G-band coverage (P = 0.0337; loses significance after Bonferroni correction for multiple testing), CpG island coverage (P = 0.00135), and evolutionary breakpoint region coverage (P = 0.00000116). Two of these features (distance to the centromere and G-band coverage) were also identified as discriminators (with the same sign) between aCFSs and NFRs in the optimal logistic regression model above (Table 2), and CpG island coverage was a significant predictor in an alternative logistic model (model 3 in Table 3). Most importantly, evolutionary breakpoint region coverage (individual contribution ∼31.9%) emerged as a new positive predictor highly relevant to aCFS breakage frequency. Our optimal standard model suggests that the frequency of breakage of aCFSs appears to increase in a genomic landscape rich in evolutionary breakpoints, distant from the centromere, located in G-negative bands, and depleted in CpG islands.

Table 4.

Optimal multiple standard regression model for breakage frequency of autosomal aCFSs

We next added to or replaced the four significant predictors identified above (Table 4) with predictors excluded during prescreening (Supplemental Table S6). Transcription start site density was found to be a significant (P = 0.0023) negative predictor, and the model including it (model 1 in Supplemental Table S6) had explanatory power only slightly lower than that for the optimal model (43.37% vs. 45.30%). Coverage of H3K4me1 histone modification sites, Twist, and coverage of low complexity A/T-rich regions (models 2, 3, and 4, respectively, in Supplemental Table S6) were not significant. All these alternative standard regression models had predictors with low VIFs (Supplemental Table S7).

The explanatory power (percentage of variance or deviance explained) for the breakage frequency model (45.30%) was lower than that obtained for the aCFS vs. NFR model (76.97%). There are two possible explanations. First, the breakage frequency data that we used came from one study (Mrasek et al. 2010). Therefore, some portion of the observed variation in breakage frequency across aCFSs may have actually been due to the stochastic nature of fragility in the APH-induced experimental assay. Second, even though the overall correlation in breakage frequency among individuals was high, some fragile sites exhibited a high degree of variability in breakage frequency between individuals (Supplemental Fig. S1).

Validation in cloned aCFSs

Because our models were derived and estimated using aCFSs initially defined by low-resolution cytogenetic methods, it was important to assess their predictive behavior for aCFSs mapped at higher resolution, i.e., with fluorescence probes around the breakage area (Ruiz-Herrera et al. 2006). We were able to find high-resolution genomic coordinates of 18 autosomal cloned aCFS either using BAC accession numbers (Ciullo et al. 2002; Fechter et al. 2007; Reshmi et al. 2007; Bosco et al. 2010; Pelliccia et al. 2010; Blumrich et al. 2011) or data collected by Ruiz-Herrera and colleagues (Ruiz-Herrera et al. 2006). Among these, 14 (FRA2C, FRA2G, FRA2H, FRA3B, FRA4F, FRA6E, FRA6F, FRA7B, FRA7G, FRA7H, FRA9E, FRA11F, FRA11G, and FRA13A) overlapped with aCFSs cytogenetically defined by Mrasek and colleagues (Mrasek et al. 2010), while high-resolution coordinates for the remaining four (FRA1E, FRA7E, FRA7I, and FRA16D) did not overlap with their cytogenetic coordinates (Supplemental Table S8). This was not completely unexpected, as both cytogenetic banding and fluorescent mapping methods have inherent technical limitations that contribute to variation among coordinates. Because of this uncertainty, these four aCFSs were excluded from further analysis.

We investigated genomic regions of the 14 cloned aCFSs defined by the intersection of their cytogenetically and clonally defined coordinates. Using the models described above (Tables 2, 4), we recalculated values for the significant predictors of the smaller genomic segments delineated by the intersection coordinates. Interestingly, in the logistic regression model, using genomic features defined at a higher resolution led to higher or equal expected probabilities of being fragile sites (as compared to using cytogenetic coordinates) for 10 of the 14 aCFSs tested (FRA2G, FRA2H, FRA3B, FRA4F, FRA6E, FRA7B, FRA7H, FRA9E, FRA11F, and FRA13A). The remaining four aCFSs (FRA2C, FRA6F, FRA7G, and FRA11G) had slightly lower probabilities (Supplemental Table S9). Similarly, using the high-resolution genomic features, our standard regression model predicted an equal or higher than expected breakage frequency (as compared with using cytogenetic coordinates) for 11 out of 14 aCFSs (Supplemental Fig. S2). This analysis illustrates that our models capture important aspects of the molecular biology underlying aCFSs and are not a by-product of the lack of resolution of current genome-wide aCFS data.

Validation in mouse fragile sites

For additional validation, we tested the ability of our models derived from human data to predict 24 known APH-induced mouse fragile sites (Elder and Robinson 1989; Helmrich et al. 2006). The use of the optimal (Table 2) and alternative (Table 3) logistic regression models resulted in 79% and 71%–79% correct predictions, respectively (Supplemental Table S10). Unfortunately, we cannot derive a false positive rate, as the lack of a genome-wide screen for mouse aCFSs precludes defining mouse NFRs. See Supplemental Note for details of the mouse fragile sites analyses.

Discussion

In this study, we posed the following questions. First, which genomic features are enriched or depleted in APH-induced CFSs, and how much does each feature contribute to fragility? Second, what are the genomic features that aggravate fragility of aCFSs? Third, are models built based on the analysis of cytogenetically mapped aCFSs also relevant for predicting the available finely mapped aCFSs? We showed that our models predict aCFSs with high accuracy, explain a large portion of the observed variation in breakage frequency, and validate finely mapped aCFSs.

In the genome-wide aCFS vs. NFR logistic regression model (Table 2), G-band coverage is the dominant predictor, while average Twist value, distance to the centromere, and Alu repeat coverage have important but smaller roles. The same observations emerge when validating aCFSs mapped at a higher resolution, suggesting the robustness of our conclusions. Moreover, the model has a high success rate for predicting aCFSs in the mouse genome, despite the limited number of identified mouse fragile sites and unavailability of a negative control for mouse. That G banding is the strongest predictor may be due, in part, to the scale at which aCFS fragility information is available to us. G-banding and aCFSs (Mrasek et al. 2010) were both identified at the cytogenetic level, while most of the other genomic features we examined were identified at the primary sequence level. Our study, thus, depends on the accuracy with which the cytogenetic G-banding map was annotated onto the genome sequence (Furey and Haussler 2003). Nevertheless, the preferential location of aCFSs in G-negative bands has been described previously (Yunis and Soreng 1984; Hecht 1988).

Two predictors of genome-wide aCFS breakage frequency (Table 4) coincide with features identified in the aCFS vs. NFR comparison, namely distance to the centromere and G-band coverage. CpG island coverage is a significant predictor in the optimal standard regression model (Table 4) and in one of the alternative logistic regression models (model 3 in Table 3). However, evolutionary breakpoint region coverage is a significant predictor only in the breakage frequency model (Table 4), while Alu repeat coverage is significant (prior to Bonferroni correction for multiple testing) only in the logistic model (Table 2). Therefore, our results suggest that genomic features differentiating between aCFSs and NFRs and genomic features that affect fragility level of aCFSs are not necessarily the same.

Our genome-wide model demonstrates that G-banding is negatively correlated with aCFSs; in other words, most aCFSs are located within G-negative (R) bands, which are also the functional regions of the genome (Mishmar et al. 1999). The additional predictors identified in our study provide further insight into the chromosomal organization surrounding aCFSs and the mechanisms underlying aCFS expression, as discussed below.

Alu repeat coverage

Alu repeats have been documented previously to be enriched in aCFSs (Tsantoulis et al. 2008), and our optimal logistic model including Alu repeats has high predictive value (Table 2). Mechanistically, Alu repeats have been studied extensively for their effect on nonhomologous recombination, which might impact chromosome stability (Cordaux and Batzer 2009; Konkel and Batzer 2010). Most Alu repeats contain mononucleotide microsatellites (Arcot et al. 1995; Kelkar et al. 2011) which are involved in replication slippage, unequal crossing over, secondary structure formation, and DNA polymerase inhibition (Bhargava and Fuentes 2009; Shah et al. 2010). Therefore, a role for mononucleotide microsatellites in genomic instability is well supported. We found mononucleotide microsatellite coverage to be a significant (prior to Bonferroni correction for multiple testing) positive predictor, although the model including it in place of Alu coverage had lower explanatory power (Table 3). Notably, the logistic regression model with mononucleotide microsatellites located within Alus had a slightly higher overall fit than the model including Alu coverage. Thus, it is possible that mononucleotide microsatellites may be the factor that actually contributes to aCFS fragility, due to a high correlation in occurrence of Alu repeats and mononucleotide microsatellites.

AT sequence content and DNA flexibility

Experimental studies have shown that long AT/TA palindromes and AT-rich sequences are associated with replication stalling and aCFS breakage (Dillon et al. 2010). G-negative bands are heterogeneous with regard to base composition and may contain AT-rich isochores (Costantini et al. 2006). We found Twist percentage (Sarai et al. 1989) to be a significant, positive predictor in the optimal logistic model contrasting aCFSs with NFRs (Table 2), which concurs with a previous study (Mishmar et al. 1998). Our results suggest that aCFSs tend to be located in G-negative banding regions that have AT-rich isochores with a high density of AT-rich repeats or a high A/T-base pair content (Mishmar et al. 1998, 1999). Therefore, our results agree with the notion that aCFSs might be located in G-band-like regions of R bands (Mishmar et al. 1999).

CpG island coverage

We found that CpG island coverage is negatively associated with both breakage frequency and the probability of being an aCFS (Table 4 and model 3 in Table 3, respectively). Also, in some alternative logistic regression models, transcription start site coverage and H3K4me were also significant negative predictors (H3K4me1 loses its significance after Bonferroni correction for multiple testing) (models 4 and 2 in Table 3, respectively). This finding is counterintuitive, given the dogma that G-negative bands display a higher density of genes, CpG islands, and histone acetylation, relative to G-positive bands (Craig and Bickmore 1993). One interpretation of our results is that aCFSs reside within G-negative chromosomal isochores that adopt a less open chromatin structure, relative to NFRs. Because DNA repair mechanisms are known to be more efficient in open chromatin and active gene regions (Mellon et al. 1986), NFRs may be able to repair DNA more efficiently than aCFS regions.

Replication timing

Delayed replication has been considered to be a key molecular feature associated with aCFS expression (Arlt et al. 2006; Palumbo et al. 2010). However, we found G-negative banding to be the dominant predictor of fragility in our aCFS vs. NFR model, and initial studies examining G vs. R banding patterns and S-phase replication timing showed that G-negative bands are replicated early in S phase (Holmquist et al. 1982). Thus, despite the observation that some aCFSs remain incompletely replicated at the end of S phase (Palakodeti et al. 2004; Pelliccia et al. 2008), late replication of G bands per se is not a genome-wide predictor of fragility (see below). Instead, our modeling suggests that aCFSs may be sequences that experience replication delays but that lie within otherwise early replicating regions of the genome.

Late-replicating regions of the genome are known to harbor heterochromatin and centromeres, both highly repetitive sequences (Holmquist et al. 1982). Recently, genome-wide studies of replication timing have been performed, primarily examining replication dynamics within unique and low-complexity sequences of the genome. In these studies, repetitive DNA sequences are excluded from the sequencing analyses (Hansen et al. 2009), or arrays are used that are underrepresented for heterochromatic regions of the genome and do not contain centromeric DNA (Woodfine et al. 2004). These methodological limitations notwithstanding, we used the replication timing data from three studies (Woodfine et al. 2004; Hansen et al. 2009; Ryba et al. 2010) to determine whether it is a predictor of chromosomal fragility. However, we found neither replication timing nor content of early replicated regions to be a significant predictor in any of our models. Possibly, some aCFSs have average replication timing under normal physiological conditions but exhibit delayed or late replication under APH-induced stress. Replication timing can change with developmental stage and cell type (Hansen et al. 2009; Pope et al. 2010).

Density of replication origins

Recent studies of FRA3B suggest that differential utilization of replication origins contributes to fragility of aCFSs (Palakodeti et al. 2010; Letessier et al. 2011). However, we did not find the density of replication origins to be a significant genome-wide predictor in our models. We utilized origin-mapping data derived both computationally and experimentally (Cadoret et al. 2008; Karnani et al. 2010; Chen et al. 2011). Notably, the densities of computationally predicted vs. experimentally mapped replication origins were not highly correlated (Fig. 3), suggesting limitations in one or both of these approaches. The computational prediction of replication origins uses abrupt base skew changes to partially differentiate leading versus lagging DNA strand switches (Chen et al. 2011). However, a similar signal can be generated from a transcription start site. Experimental mapping of replication origins exhibits substantial variation among platforms utilized in the same laboratory (Karnani et al. 2010), and the set of origins identified by several platforms has a high false negative rate (low sensitivity). While aCFSs and NFRs appear to have a similar density of replication origins, they might differ in replication origin efficiency (Palakodeti et al. 2010; Letessier et al. 2011) or utilization (Gilbert 2010). In fact, a recent analysis suggested that the failure to activate origins in response to replication stress and fork stalling was involved in FRA16C instability (Ozeri-Galai et al. 2011).

Distance from the centromere

We observed a positive association between the presence of aCFSs and distance from the centromere, suggesting that chromosomal regions located farther away from the centromere have a higher probability of being aCFSs. Moreover, the farther away from the centromere, the higher is the breakage frequency of aCFSs. Several genomic contexts/features are known to vary along the length of a chromosome, creating a change in genomic landscape that affects the rates of various mutational events (Hardison et al. 2003; Kvikstad et al. 2007; Ananda et al. 2011). The best subset selection procedure we applied to select the optimal set of predictors in our regressions favors models with a small number of predictors. Therefore, in reality, distance from the centromere might be selected as an effective proxy capturing the effects on fragility of multiple genomic features as they vary along the length of the chromosome.

Enrichment of evolutionary breakpoint regions

Evolutionary breakpoint regions are genomic sites of intra- and inter-chromosomal breakages that were found to be frequently reused among ten amniote genomes analyzed (Larkin et al. 2009). From our study, this predictor is significant only in the breakage frequency model, where it is, in fact, the dominant predictor. Since the aCFS vs. NFR model includes a larger data set (73 aCFSs + 124 NFRs) than the breakage frequency model (73 aCFSs), the lack of predictive power of evolutionary breakpoints in the former model cannot be explained by sample size limitations. Our results suggest that evolutionary breakpoint regions are enriched specifically in highly fragile aCFSs.

Statistically, we cannot establish a causality direction, i.e., whether (1) evolutionary breakpoint regions make existing aCFSs more fragile, or (2) aCFSs are, indeed, hotspots of evolutionary breakpoints. Some human aCFSs were found to have orthologous aCFSs in other mammals, e.g., other primates (Smeets and van de Klundert 1990; Ruiz-Herrera et al. 2004), carnivores (Stone et al. 1991a,b, 1993), and mouse (Glover et al. 1998; Shiraishi et al. 2001; Krummel et al. 2002; Matsuyama et al. 2003; Rozier et al. 2004; Helmrich et al. 2006, 2007). Analysis of such loci is expected to shed light on the causative agents of fragility (CFSs vs. evolutionary breakpoints). A locus-specific analysis indicated that, for instance, both human and mouse orthologous CFSs are enriched in AT-repeats (Shiraishi et al. 2001). In addition, recent evidence suggests that evolutionary breakpoint regions are enriched for repeats that might alter chromatin conformation or recruit transposable elements and trigger genome instability (Farré et al. 2011). For a definite answer to this puzzling question, a genome-wide analysis of sequence features still conserved for such orthologous aCFSs is required. Nevertheless, our modeling suggests that some features of chromosomal regions that are conserved in their evolutionary fragility across species separated by hundreds of million of years (Larkin et al. 2009) are also associated with fragility of these regions in the human genome under conditions of replication stress. This implies similarity in the mechanisms of chromosomal fragility at micro- and macroevolutionary levels. Larkin and colleagues (2009) discovered that evolutionary breakpoint regions are enriched in structural variants, SNPs, genes, and pseudogenes, and depleted in recombination hotspots and most conserved elements. The significance of evolutionary breakpoint regions in our modeling might capture a combination of some of these factors.

Summary

The ultimate goal of our computational analysis is to develop accurate and reliable models that can aid in the prediction of locations and fragility levels of aCFSs within individual human genomes. Using the models we describe here, we can currently predict the probability that a given chromosomal region is an aCFS and its corresponding breakage frequency, based on genomic context. We demonstrate that our models remain valid when we apply them to a handful of aCFSs that have been mapped using fine-scale fluorescence probe labeling. Our models did not identify several “expected” genomic features as being significant predictors of genome-wide chromosomal fragility. This does not eliminate these characteristics, which include replication timing and replication origin density, from the list of potential contributors to aCFS instability. Rather, our findings support the idea that, although aCFSs share characteristics that predict fragility globally (such as those found in our optimal models), other genome features might be contributors to only a unique subset of aCFSs. A full understanding of the mechanisms of aCFS instability will require further computational and experimental analyses. With advances in genome-wide sequencing technologies, we will soon be in a position to identify locations of chromosome breakage at the base pair level, allowing a more detailed analysis of aCFSs in individual genomes.

Methods

Mapping genomic locations of aCFSs and NFRs

The cytogenetically determined locations of all 73 autosomal aCFSs, as determined previously (Lukusa and Fryns 2008; Mrasek et al. 2010), were converted to human genomic coordinates (hg18) using the UCSC Genome Browser (Rhead et al. 2009). Breakage frequencies were obtained for three distinct individuals but presented high inter-individual concordance (correlations around 0.96–0.99); we, therefore, used the average breakage frequency across the three individuals for each aCFS.

The NFR set was constructed from regions that did not exhibit breakage after induction by aphidicolin in the genome-wide screen by Mrasek and colleagues (Mrasek et al. 2010) and were not indicated as fragile sites in other studies (Kuwano et al. 1988; Borgaonkar 1994). From these, we further excluded centromeric regions because they are enriched in minisatellites (Vergnaud and Denoeud 2000) and heterochromatin regions that do not have DNA sequence available. Sex chromosomes were also excluded from our initial analyses because of their high repetitive element content (Skaletsky et al. 2003; Ross et al. 2005). In all, we utilized 124 autosomal NFRs.

Calculating and prescreening predictors

Genomic features (Supplemental Table S3), as assigned to each aCFS and NFR, were downloaded from the UCSC Genome Browser (Rhead et al. 2009) or from the literature (see Supplemental Table S3 for references). The hg18 human genome annotations were used for most features, and those available only for other human genome assemblies were mapped to hg18 with the lift-over tool in Galaxy (Blankenberg et al. 2011). Most features were available in the corresponding data sets as genomic intervals and were intersected with aCFS or NFR cytogenetic coordinates to calculate coverage (percentage of overlap) for large-scale genomic features or density for small motifs. For replication timing, we used a weighted average value when several data intervals overlapped with an aCFS or an NFR. Features were measured as coverage (percentage), motif density, or average value across an interval, depending on their type (Table 1; Supplemental Table S3), and each was transformed to approximate a Gaussian distribution. The gaps in assembly were subtracted from each aCFS and NFR prior to calculating coverage, density, or assigned value.

In order to limit the number of, and correlations among, features used as potential predictors for our regression models, we performed a prescreening (Fig. 2A). We used hierarchical clustering based on pairwise Spearman's rank correlation coefficients (distance = 1−|coefficient|) to parse 54 features into tightly correlated groups (clusters) and selected 19 of them, each representing one such group and having correlations below 0.7 with one another. Notably, considering only the 73 aCFSs, or both the 73 aCFSs and the 124 NFRs, produced similar clustering patterns and led to selecting the same predictors. Such prescreening facilitates subsequent regression model building. It reduces computational time for best subset selection algorithms (see below; since computational time doubles for every additional predictor, excluding ∼30 features reduced the computational burden by a trillion-fold). Moreover, it improves estimation through the model-building process, providing a higher “observations per predictor” ratio. This is especially important for logistic regression, where estimation is performed by numerical maximum likelihood and requires sufficiently large sample sizes to converge. Note that prescreening predictors by clustering mitigates, but does not eliminate, the risk of multicollinearity in our regressions (even though potential predictors are picked to have relatively low pairwise correlations, overall linear associations might still be high). We, therefore, still evaluate multicollinearity using variance inflation factors during model building (see below).

Regression analyses

Two types of regressions were used in our study—logistic and standard multiple linear regression. The former models a binary response (aCFS = “1” vs. NFR = “0”) and the latter an approximately continuous response (breakage frequency of aCFSs). For both regressions, we (1) performed transformations on the 19 potential predictors to approximate Gaussian distributions; for the standard regression, also the response (breakage frequency) was transformed by natural logarithm to regularize its distribution and ensure homoscedasticity in the fits, (2) ran a best subset selection algorithm to select a smaller subset of predictors based on the Akaike information criterion, (3) checked this subset of predictors for autocorrelation using the partial autocorrelation function—no absolute partial autocorrelations above 0.15 were detected in any of the analyses, (4) identified and removed influential data points (outliers), based on Cook's distances computed with the model comprising this subset of predictors (we removed points with Cook's distance larger than 4/[sample size – number of predictors – 1], which corresponded to ∼0.02 and 0.05 for the logistic and standard regression, respectively), (5) further reduced the model iteratively eliminating predictors based on their coefficients' P-values and variance inflation factors; this led to models retaining only predictors significant or marginally significant after Bonferroni correction for multiple testing and with variance inflation factors below 5 (unless noted otherwise), and (6) considered quadratic models comprising square and pairwise product terms obtained from these final sets of predictors—no quadratic terms were found significant in any of the analyses (Fox 2002). Common graphical diagnostics (e.g., residual plots) (Supplemental Fig. S3) were also employed to assess model performance throughout the process. The pipeline of our regression analysis is depicted in Figure 2B.

For both regressions, we evaluated the final models and individual contributions of the predictors retained in them based on explained deviance (logistic regression) or variance (standard regression). For the logistic regression, we calculated the pseudo R-squared of a model using (D_o–D)/D_o, where D_o is the null deviance and D is the residual deviance of the model. We calculated the relative contribution of each predictor to a model using [(D_o–D) − (D_o–D_(−p))]/(D_o–D), where D_(−p) is the deviance of the smaller model obtained removing the predictor of interest. For standard regression, we calculated the R-squared of a model using (TSS – SSE)/SSE, where TSS is the total sum of squares and SSE the residual sum of squares of the model. We calculated the relative contribution of each predictor to a model using the partial R-squared, which is defined as (SSE_(−p) – SSE)/SSE_(−p), where SSE_(−p) is the residual sum of squares of the smaller model obtained removing the predictor of interest.

All regression analyses were implemented in the R statistical package version 2.11.1 (R Development Core Team 2011). All tools developed for this project are freely available at the Galaxy (Blankenberg et al. 2011) website, http://main.g2.bx.psu.edu/. Tools “Logistic Regression” and “Partial R-squared” can be found under “Multiple Regression,” and tool “Assigned Weighted Average Value of Genomic Feature” can be found under “Regional Variation.” The “Standard Multiple Regression” tool used here was already available in Galaxy.

Cloned aCFSs

Eighteen autosomal aCFSs mapped by fluorescence probes (i.e., “cloned”) (Ciullo et al. 2002; Ruiz-Herrera et al. 2006; Fechter et al. 2007; Reshmi et al. 2007; Bosco et al. 2010; Pelliccia et al. 2010; Blumrich et al. 2011) were studied. For analysis, we intersected their cloned and cytogenetically defined coordinates. For four CFSs, we found no intersections, although clonally defined coordinates were adjacent to the cytogenetically defined coordinates. The 14 intersected regions were used to validate our logistic and multiple regression models. We recalculated values for significant predictors using the same method we used with aCFSs defined at the cytogenetic level. Next, we compared breakage frequency and probability to be an aCFS for the intersected regions vs. their cytogenetically defined counterparts.

Mouse fragile sites and genomic contexts

Cytogenetic locations of 24 known APH-induced mouse fragile sites (Elder and Robinson 1989; Helmrich et al. 2006) were converted to mouse genomic coordinates (mm8). For 16 of these sites, breakage frequencies were estimated from 266 mouse cells (Elder and Robinson 1989). Genomic features for each mouse fragile site were calculated similarly as for human aCFSs. We used rodent B1s as an equivalent to Alu repeats in human as both evolved from the 7SL RNA gene (Yang et al. 2004). Mouse fragile sites were used as a test set to validate our multiple logistic regression for aCFSs prediction. We consider 0.5 to be the threshold for a positive call assuming equal probability to observe fragile and nonfragile regions. Breakage frequencies of mouse fragile sites were used to validate our multiple linear regression for breakage frequency.