How networks change with time

Abstract

Motivation: Biological networks change in response to genetic and environmental cues. Changes are reflected in the abundances of biomolecules, the composition of protein complexes and other descriptors of the biological state. Methods to infer the dynamic state of a cell would have great value for understanding how cells change over time to accomplish biological goals.

Results: A new method predicts the dynamic state of protein complexes in a cell, with protein expression inferred from transcription profile time courses and protein complexes inferred by joint analysis of protein co-expression and protein–protein interaction maps. Two algorithmic advances are presented: a new method, DHAC (Dynamical Hierarchical Agglomerative Clustering), for clustering time-evolving networks; and a companion method, MATCH-EM, for matching corresponding clusters across time points. With link prediction as an objective assessment metric, DHAC provides a substantial advance over existing clustering methods. An application to the yeast metabolic cycle demonstrates how waves of gene expression correspond to individual protein complexes. Our results suggest regulatory mechanisms for assembling the mitochondrial ribosome and illustrate dynamic changes in the components of the nuclear pore.

Availability: All source code and data are available under the Boost Software License as supplementary material, at www.baderzone.org, and at sourceforge.net/projects/dhacdist

Contact: joel.bader@jhu.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Current views of biological networks and pathways are primarily static, comprising databases of curated pathways or of pairwise interactions, primarily between proteins. Many methods have been developed to cluster, partition or segment an interaction network into putative complexes. Recent comparisons suggest that hierarchical stochastic block models provide the most accurate reconstruction of real protein complexes from interaction data (Park and Bader, 2011). These static views, however, fail to capture the rich dynamic structure of a cell. Accounting for dynamic changes in protein complexes is crucial to building accurate models of cellular state.

High-throughput measurements of protein abundance are possible through label-free quantitative mass spectrometry (Haqqani et al., 2008; Sardiu and Washburn, 2011; Zhu et al., 2010), but may be limited to the most highly abundant proteins. In contrast, transcript abundance is more readily available and is often used as a proxy for protein abundance. Previous methods combined transcript dynamics with interaction databases to create a moving picture of the cell state under the crude assumption of a fixed number of protein complexes and with ad hoc criteria to match protein complex membership across time points (Park et al., 2010). The problem considered here is also distinct from evolutionary dynamics, where algorithms have been developed to estimate ancestral networks and infer the most likely evolutionary mechanisms (Navlakha and Kingsford, 2011).

This work, in contrast, uses a rigorous probabilistic framework to translate a hierarchical stochastic block model to the dynamic domain. The number of protein complexes can increase or decrease at each time point, and individual complexes can grow, shrink, or swap components with other complexes. The resulting network dynamics reveals the temporal regulation of cell protein state.

The starting point is our previous static clustering method, Hierarchical Agglomerative Clustering, or HAC (Park and Bader, 2011). The HAC method maximizes the likelihood of a hierarchical stochastic block model, also known as the likelihood modularity (Bickel and Chen, 2009). HAC has the appealing features of automatic selection of model size and multi-scale networks views. Furthermore, it out-performs leading methods in the task of link prediction, an objective performance metric when true group assignments are unknown. Extending HAC to dynamic networks requires a solution to the identifiability problem: how complexes inferred at one time point correspond to complexes inferred at other time points. Furthermore, transitions of a protein from one complex to another must be permitted by the model, requiring dynamical coupling between network snapshots.

In this work we address these points. First, we convert likelihood modularity from maximum likelihood to fully Bayesian statistics, which automatically accounts for model complexity and provides well-founded criteria for selecting the correct number of clusters. Second, we ‘kernelize’ the likelihood modularity with an adaptive bandwidth to couple network clusters at nearby time points, similar to methods for regulatory network inference (Song et al., 2009). We term this the Dynamical Hierarchical Agglomerative Clustering (DHAC) method. Finally, we solve the general problem of matching clusters across time points with a new belief propagation method, MATCH-EM, that extends Expectation-Maximization and belief propagation for bipartite matching (Bayati et al., 2008) to consistently match multiple time-evolving clusters. We apply these methods to real biological data to discover the dynamical structure of protein complexes.

2 APPROACH

2.1 Dynamic network clustering

Our approach uses stochastic block models, in which interactions are conditionally independent given group membership. These models can be hierarchical, with larger complexes containing sub-complexes with more fine-grained interaction probabilities. Networks are observed at specific time points, termed ‘snapshots’, and the goal is to infer or estimate the time-dependent block model given the snapshots. The model itself is generative. While others have explored networks generated from a pre-specified model (Leskovec et al., 2005), the focus here is on network inference.

The observed snapshots are a series of T time-ordered graphs, {G^(t): t=1,…, T}. Each single network G^(t)=(V^(t), E^(t)) consists of undirected and unweighted binary edges E^(t) and vertices V^(t). Vertices correspond to proteins, and edges represent possible protein–protein physical interactions (PPI). For an arbitrary pair, t≠t′, G^(t) and G^(t′) can have different vertices and edges. Generalizations to additional vertex classes (transcripts, genes, metabolites) and edge types (directed, weighted, epistatic or regulatory interactions) follow directly but are not considered here.

The goal is to infer a corresponding sequence of time-evolving stochastic block models, {M^(t) : t=1,…, T}, where each M^(t) is a good network−generative model for G^(t). Many methods maximize the model for each snapshot independently, obtaining 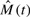as argmax_M P(M|G^(t)), then attempt to stitch together the results. Here, we show that introducing explicit coupling between time points improves dynamic network clustering.

3 METHODS

3.1 DHAC

A stochastic block model M is a generative model for a network G. The number of vertices is V and the number of possible blocks, groups or clusters is K. Typically, indices u, v, w∈1… V denote vertices, and indices i, j, k∈1… K denote clusters. The notation u∈i indicates that vertex u is in cluster i, and n_i is the number of vertices assigned to cluster i.

The probability that a vertex is in cluster k is π_k, the parameter for the k-th cluster in a multinomial distribution, with ∑_k π_k=1. The parameter θ_ij=θ_ji∈[0, 1] gives the probability of an undirected, unweighted edge between any pair of vertices u∈i and v∈j, modeled as independent Bernoulli trials for each pair. This model M generates a network G by first sampling the membership of each vertex u with probability π_k for cluster k, then sampling each edge e_uv=0 or 1 as a Bernoulli trial with success probability θ_ij for u∈i and v∈j.

Edge counts are summarized at the cluster level as n_ij=∑_u∈i,v∈je_uv for i≠j, or ∑_u≤v∈i e_uv for i=j. It is convenient to keep track of the corresponding number of non-edges, or ‘holes’, h_ij, with e_ij+h_ij=t_ij, the total possible number of edges. For i≠j, t_ij=n_in_j. For i=j, t_ii=n_i(n_i±1)/2, with the ‘+’ term for graphs with self-edges and the ‘−’ for graphs without self-edges. Using these sufficient statistics, the probability of a network G given the structural model and parameters is

3.1.1 Maximum likelihood guide tree

Vertices are merged into increasingly large clusters based on the model likelihood with maximum likelihood parameters 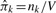and 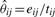. The change in log-likelihood upon merging existing clusters 1 and 2 into a new cluster 1′ is

(1)

where P^ML_ij≡e_ij^e_ijh_ij^h_ij/t_ij^t_ij and the superscript S indicates a single snapshot. The first term, arising from the multinomial cluster membership model and favoring balanced merges, was not included in HAC but is included in DHAC.

3.1.2 Bayesian collapsing criterion

A Bayes factor selects the model complexity (Kass and Raftery, 1995). Integration of parameter θ on a single Bernoulli likelihood with a uniform prior, or Beta(1, 1), results in ∫₀¹ θ^e(1−θ)^h dθ= Beta(e+1, h+1), or e!h!/(e+h+1)! for integer values. Therefore the marginal likelihood is

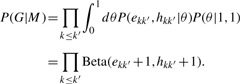A similar procedure integrating out the nuisance parameters π_k with an uninformative prior would yield the additional contribution ∏_kΓ(n_k+1)/Γ(V+K). Alternatively, integrating out the nuisance parameters using a strong prior, P({π_k}) ∝∏_kπ_k^ν with pseudocount ν≫V, yields a contribution that is independent of {n_k}. The Bayesian likelihood for the edge terms provided sufficient collapsing; we did not include the vertex assignment term in the Bayesian likelihood, equivalent to a strong prior. The Bayesian log-likelihood ratio for collapsing groups 1 and 2 into 1′ is

(2)

where the superscript B indicates Bayesian, S indicates a single snapshot, and P^B_ij≡Beta(e_ij+1,h_ij+1). This score is additive, and summing over all ϕ scores from the bottom clusters (individual vertices) upwards is equivalent to the log-likelihood ratio for the model with collapsed versus uncollapsed fine structure, with the collapsed vertices being the top-level groups in a stochastic block model. The guide tree is collapsed from the bottom up, in the order that groups were merged, to identify a local optimum of the cumulative ϕ score.

Our initial methods used the Bayesian likelihood for both the greedy guide tree and the collapsing step. A problem with this approach is that the Bayesian likelihood includes a contribution, asymptotically the Bayes Information Criterion (BIC) correction (Schwarz, 1978), that favors merges of larger clusters with different connectivity patterns over merges of smaller clusters with identical connectivity patterns. Consequently, using the Bayesian likelihood optimized the local Bayes factor but gave a worse global Bayes factor than the maximum likelihood approach, which also has less expensive function evaluations. We therefore used maximum likelihood for the guide tree and Bayesian likelihood for collapsing.

3.1.3 Kernel-reweighted scores

Kernalization of the scores λ and ϕ couples nearby snapshots, also providing noise reduction and smoothing. Merging and collapsing scores were kernelized using Gaussian Radial Basis functions with width parameter τ, w(Δt, τ) ∝exp{−|Δt|/τ}, where for simplicity Δt is the difference in snapshot indices. The kernelized merging score λ^K(t) and collapsing score ϕ^K(t) for the t-th snapshot (K denotes kernelized) are

(3)

(4)

Although the same clustering is used across all T time points, the scores will differ when proteins (or interactions) are present in one time point and absent in another. Kernels are normalized as ∑_s=1^Tw(t−s, τ)=1. As τ→0, λ^K→λ^S and ϕ^K→ϕ^S. Since λ^S is statistically consistent (see Supplementary Material for proof), λ^K is statistically consistent as n_k→∞ and τ→0. Collapsing is then performed as for single snapshots, stopping at the maximum of the bottom-up sum, termed ϕ^K(t; τ)= ∑_{(i,j)∈collapsed} ϕ^K_ij(t; τ). The overall algorithm is summarized in Algorithm 1.

In the DHAC-local method, the bandwidth parameter τ for snapshot t was selected from a grid-search over τ values 0.5, 1.0, 1.5,…, 3.5 to maximize ϕ^K(t; τ), with smaller τ favored when the network changes quickly. For the network considered here, τ ≈ 1 to 2 depending on t. Alternatively, a constant value of τ may be used for all values of t, which we termed DHAC-constant. We set τ=1 for DHAC-constant, although in principle τ could be optimized by maximizing ∑_t ϕ^K(t; τ). In practice, results were very robust to the value of τ, and the performance of DHAC-local was nearly identical to DHAC-constant with τ=1 (see Section 4).

3.2 Cluster matching algorithm

DHAC-constant and DHAC-local output T models, {M₁,…,M_T}, and many groups will change slowly between time points. The total number of groups may differ between time points, however, and even if the number of groups and the group membership are nearly identical, group order may be permuted across time points. Matching similar groups across time points remains a general problem for dynamic networks.

For T=2 groups, reasonable yet ad hoc procedures are to match groups based on shared members, Jaccard correlation of shared neighbors or maximum weighted matching of shared neighbors or other pairwise scores (Bayati et al., 2008). Here, we extend these ideas to multi-partite matching based on a novel probabilistic model that introduces some rigor to the time course matching problem.

The goal is to find most probable mapping of cluster i at time t to a globally consistent index k. Let z_ik^(t)=1 if cluster i of snapshot t is assigned to k, and 0 otherwise, with normalization ∑_k z_ik^(t)=1. Conversely, the sum over local clusters, ∑_i z_ik^(t), is not fixed because the global cluster may be absent at time t (sum = 0) or it may be broken into multiple smaller clusters (sum > 1).

Each cluster i contains original network vertices {u}⊆V, and n_ij^(t) counts the number of shared members between group i at time t and group j at time t+1. The probability that a vertex makes a transition from global state k to state k′ between two snapshots is ψ_kk′, with normalization ∑_k′ ψ_kk′=1. For simplicity, ψ_kk′ is independent of t. When groups do not change over time, ψ_kk′=δ_kk′, 1 if k=k′ else 0. Similarly, the time-independent parameter ν_uk is the probability that vertex u is in global group k, with ∑_k ν_uk=1.

The matching probability under consistent indexing is

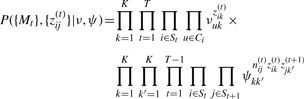(5)

where S_t denotes the set of clusters at snapshot t and C_i the set of vertices in one of these clusters.

We solved the maximum a posteriori (MAP) inference problem using Expectation-Maximization (EM). The M-step updates are

(6)

(7)

The E-step for z_ik(t) is more complicated. If the state at time t is represented as the assignment matrix {z_ik(t)}, then the probability structure is a hidden Markov model (HMM). This state space is large, however, on the order of K^K ~ K!, because each of the approximately K clusters at time t may be assigned to one of K global clusters, and the transition matrix is of order K^2K. Instead, we simplify the state space by considering each z_ik(t) independently and introducing additional couplings that create loops in the corresponding graphical model, no longer permitting a dynamic programming solution. When groups are stable over time, however, the topology is close to a tree structure and belief propagation (BP) works well (Yedidia et al., 2005).

For max-product BP algorithm we reformulate the above Markov Random Field, or joint probability [Equation (5)], constructing a factor graph consisting of factors (hyper-edges) and variables (latent variables). Latent variables z_i^(t) take on values from 1,…, K, or succinctly [K]. In other words, z_i^(t) provides the index k of the global cluster for which z_ik^(t)=1. Parameters {ν} are used to represent singleton factors and {ψ} pairwise factors. A certain latent variable z_i^(t) depends on neighboring pairwise factors N(i, t−1) from the previous snapshot and N(i, t+1) from the subsequent snapshot. MAP inference is carried out by sending messages from i to j via pairwise factor e. The update equations of the message m_i→e from variable i at time t to factor e and then the message m_e→j from e to variable j at time t+1 is

(8)

(9)

For variable j at time t−1, the message m_e→j is

(10)

The belief b_i of a certain variable i at snapshot t is the product of incoming messages,

(11)

normalized as ∑_k b_i(k)=1. To prevent the MLEs and BP steps from overshooting, parameters and messages were updated as 1/10 of the full change, with updates to messages performed on a logarithmic scale (Koller and Friedman, 2009). We call this EM method MATCH-EM (Algorithm 2).

3.3 Dynamic network data generation

Dynamic biological networks were obtained by combining experimental gene expression time series data with static protein interaction networks to project out the consistent edges, both active (two interacting proteins are expressed) and inactive (neither protein is expressed). This method assumes that presence of a protein is related to transcriptional abundance of the corresponding transcript at a nearby time, with possible delays due to translation and protein lifetimes. More realistic models are possible and should yield more accurate results (see Section 5).

Time-series measurements of the expression levels of N genes across T time points generates a N×T matrix X. Each element X_ut corresponds to the expression of gene u at snapshot t. The matrix X is assumed to be preprocessed and normalized, here performed with gcrma quantile-normalization (Wu et al., 2004). Next it is row-standardized to have zero mean, ∑_t X_ut=0, and equal variance, ∑_t X_ut²=T−1, for each gene.

The dynamics of the network were then inferred from X, under the assumption that proteins in a complex have correlated gene expression profiles (Jansen et al., 2002). To account for transient complexes and cases where delays due to translation and protein lifetime are important, correlations were averaged over a bandwidth τ,

with the Gaussian kernel function w(Δt, τ)∝exp(−|Δt|/τ) and normalized to 1. Although this bandwidth τ has a similar role to the bandwidth for likelihood kernelization, it was not optimized but rather set to 1.5. Results were quantitatively similar for τ from 1.2 to 2. Smaller values of τ result in stricter co-expression requirements and result in a sparser network.

Each edge is then declared present or absent based on the value of 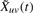: for each snapshot t=1,…, T, a dynamic edge e_uv(t)=1 if and only if 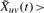and e_uv=1 in static network. This procedure retains edges at time t where both proteins are present (X_us, X_vs>0) or both absent (X_us, X_vs<0) for times s close to time t. We found that using the negative evidence improved the prediction of protein complexes, and that the transcriptional data could then be used to identify which complexes or subunits were present or absent at each time point. Results were stable for less stringent thresholds, 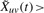. While this method is appropriate for periodic processes, other methods for extracting time-dependent interactions may be more appropriate for more general processes (see Section 5).

3.4 Performance evaluation

3.4.1 Held-out link prediction

Link prediction accuracy for held-out edges provides an objective measure of clustering performance for real-world data where the true group structure is fundamentally unknown (Henderson et al., 2010; Park and Bader, 2011).

At each time point, we randomly select pairs of vertices (u, v), some connected at time t with e_uv(t)=1, and others unconnected with e_uv(t)=0, the relative fraction of connected pairs (edges) and unconnected pairs (holes) matching the network as a whole. These pairs are then a test set, and the remaining edges serve as the training set. After clustering based on the training set, vertex u will be assigned to some group i, and vertex v will be assigned to group j. The maximum likelihood probability of the (u, v) edge, denoted ê_uv^(t), is then ê_ij^(t) = e_ij^(t)/(e_ij^(t)+h_ij^(t)).

Varying a threshold θ for ê_uv^(t), or in practice ranking pairs in decreasing order of ê_uv^(t), the true positive count is TP = I{ê_uv^(t)>θ ∧ e_uv^(t)=1}, the false positive count is FP = I{ê_uv^(t)>θ ∧ e_uv^(t)=0}, the true negative count is TN = I{ê_uv^(t)≤θ ∧ e_uv^(t)=0}, and the false negative count is FN = I{ê_uv^(t)≤θ ∧ e_uv^(t)=1}. A precision–recall curve (PRC) is then created from the precision and recall,

Similarly, a receiver operating characteristic (ROC) curve is generated from the true-positive and false-positive rates,

The dynamic clustering methods are then compared using the area under the PRC (AUPRC) and the area under the ROC (AUROC). The AUPRC measures the average precision for known positives, which is a useful measure for link prediction where classes are skewed with far fewer known positives than known negatives. Interaction data are very skewed, with only about 1% fraction of positives. The AUROC has the theoretical benefit of being invariant to class bias. It is less informative in practice but is included here because its use has become standard.

3.4.2 Competing methods

We compared the following algorithms: DHAC-constant, dynamic clustering with a constant fixed bandwidth (τ=1 for the link prediction experiments); DHAC-local, bandwidths adaptively optimized for each snapshots (τ=0.5, 1.0, 1.5,…, 3); HAC, DHAC with bandwith τ=0, similar to HAC-ML method but using bottom-level clusters for link prediction (Park and Bader, 2011); and CNM, fast modularity optimization (Clauset et al., 2004). We initially considered Variational Bayes Modularity (VBM, Hofman and Wiggins, 2008) but did not include it because it is slower and is often trapped in bad local optima. Initially we attempted to model network dynamics with a Markov model, similar to a Markov chain of static exponential random graph model (Hanneke et al., 2010). We found that kernelization, used previously in the KELLER algorithm for transcriptional networks (Song et al., 2009), provides better performance. In contrast, the Markov chain approach performed worse than DHAC and only slightly better than HAC (results not shown) and is not included in the comparison. For more extensive comparison of other static clustering methods we refer to our previous studies, which identified HAC-ML as the best-performing link-prediction method for large networks, including cluster-free link prediction by graph diffusion kernels (Park and Bader, 2011).

4 RESULTS

4.1 Link prediction performance

4.1.1 Drosophila networks

As a proof of concept we first tested our algorithm on a dynamic network for Drosophila development, for which a gene expression time course is available (Arbeitman et al., 2002). Rather than analyzing the expression data directly, we relied on previous analysis using KELLER to identify time-varying regulatory interactions between genes, yielding a network with 66 time points and 588 gene vertices (Song et al., 2009). Thus, genes u and v are connected at time t∈1… 66 according to these previous results, defining a sparse time-varying network with mean vertex degree ≈6.5. Since gene interactions were generated with time smoothing, DHAC-constant and DHAC-local are expected to outperform static methods.

In extensively cross-validated link prediction performance, DHAC-constant and DHAC-local are seen to be far superior to the next-best method, HAC, which in turn dominates CNM until ~30% of the true edges are removed (Fig. 1). To perform these studies, from 5% to 80% of the known edges were removed; results were averaged over the 66 time points; and the entire procedure was repeated more than 10 times.

Fig. 1.

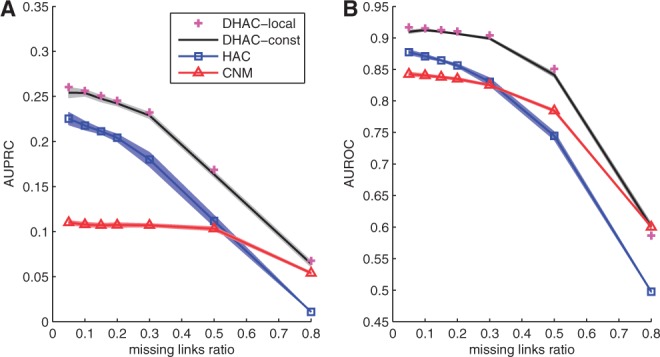
Link prediction results for Drosophila networks. (A) average AUPRC scores for different methods (y-axis) along different missing link ratios (x-axis); (B) AUROC scores for different methods (y-axis) along different missing link ratios (x-axis). Points and lines: averge time-cumulative performance; shaded area: 1-standard error. See Section 3 for details

The similar results of DHAC-constant and DHAC-local point to robust behavior with respect to the kernelization parameter τ. The improved performance of CNM relative to HAC at a high frequency of missing links may be due to the tendency of CNM to generate large clusters and to lose resolution. The resolution limit is usually a drawback, but here is beneficial for link prediction in a sparsified network. Even in this limit, however, DHAC remains superior by drawing information from adjacent timepoints.

4.1.2 Yeast Metabolic Cycle networks

We then tested link prediction accuracy on Yeast Metabolic Cycle (YMC) networks. The YMC networks started with a large-scale protein–protein interaction dataset (BioGrid 3.1.81 with 63 410 physical interactions and 4342 proteins, Stark et al., 2006). Requiring support by two or more publications, a criterion used previously by others (Bandyopadhyay et al., 2010), retained 13 401 interactions and 3248 proteins. This physical network was combined with data from YMC gene expression microarrays over 36 time points showing 3510 significantly periodic genes, of which 2979 occur in the physical network (Tu et al., 2005). We retained edges e_uv^(t) that connected periodic genes and were observed for at least two values of t. Snapshots on average contained 1380 proteins with degree 1.8, sparser than the Drosophila network. The union over all snapshots contained 1575 proteins.

As before, DHAC methods clearly outperform static clustering methods for link prediction on YMC data (Fig. 2). The performance of DHAC-local is slightly better than DHAC-constant. HAC performs better than CNM for AUPRC, but CNM performs better for AUROC. This follows the trend seen with the Drosophila data, where resolution loss improves the relative performance of CNM for sparse networks.

Fig. 2.

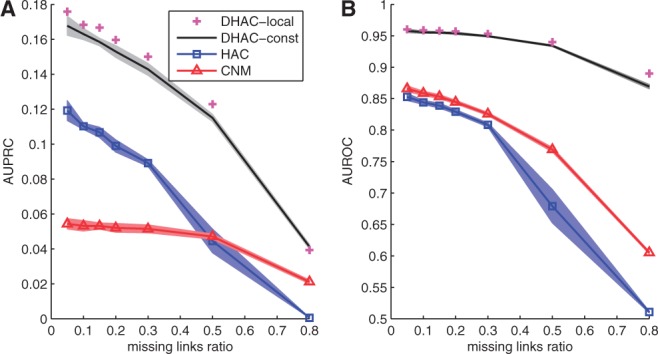
Link prediction results for YMC networks. (A) average AUPRC scores for different methods (y-axis) along different missing link ratios (x-axis); (B) AUROC scores for different methods (y-axis) along different missing link ratios (x-axis). Points and lines: average performance; shaded area: 1-standard error. See Section 3 for details

4.1.3 Static versus dynamic edge removal

The link prediction results described above used a protocol in which the held-out edges were resampled for each snapshot. Thus, noise is uncorrelated between snapshots, and dynamic smoothing suppresses the noise by time-averaging because the full gold standard changes slowly (due to kernelization with KELLER) or not at all (with the yeast physical interaction network). We therefore tested an alternative link prediction scheme for the YMC data in which the held-out edges are systematically removed across all snapshots, eliminating the advantage of time averaging. In this case, dynamic smoothing is not expected to help, and the performance of DHAC indeed fell to the performance of the static HAC algorithm (results not shown).

4.2 YMC dynamics

YMC transcriptional profiling reveals three dominant metabolic states: reductive building (RB, 977 genes); reductive charging (RC, 1510 genes); and oxidative (OX, 1023 genes) (Tu et al., 2005). Almost a half of total genes oscillate along this cycle, indicating that a broad swath of processes are involved but making it difficult to extract specific dynamical modules from expression data alone.

Prior to clustering, the network used for link prediction was made less sparse by applying an iterative degree cutoff (≥3). Combining with the 36 time-varying snapshots, 3 complete cycles of 12 snapshots each, reduced the size of the network from 1380 proteins per snapshot to 480±14 and increased the mean vertex degree from 1.8 to 6.6. Networks were clustered by DHAC-local. Clusters were matched across time points using MATCH-EM to yield 31 complexes with a total of 613 proteins.

We checked robustness using a bootstrapping procedure in which a fraction α of edges are randomly rewired according to the degree-consistent configurational model (Karrer et al., 2008). We used α!=!0.01 and performed 500 bootstraps, with ~80% co-membership conserved across bootstraps at each snapshot.

4.2.1 Macro-view of YMC complexes

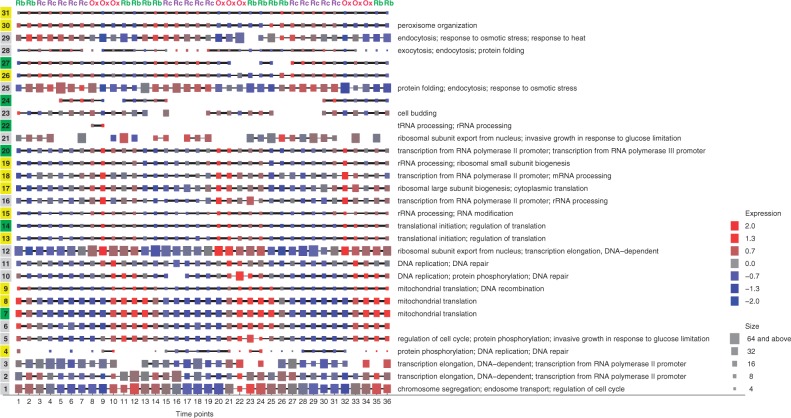
We recovered 31 dynamic complexes with at least 3 proteins and bootstrap co-membership ~80% (Fig. 3). Many of the complexes have cluster-specific gene ontology (GO) keywords with P-value ≤0.05. Organizing clusters by average gene expression at each time point separates those that are active in each phase. RB clusters, #1 to #10, are related to cell cycle checkpoints and mitochondrial translation. OX clusters, #11 to #20, include ribosome metabolism, DNA replication/repair, and translation. RC clusters, #23 to #31, include stress response and transport.

Fig. 3.

Dynamic network clustering reveals a detailed global view of periodic protein complexes during the yeast metabolic cycle. Squared nodes represent clusters matched across time points, showing only clusters having at least three genes/proteins. Cluster order: clusters are organized by peak activity in RB phase (#1 to #10), OX phase (#11 to #20) and RC phase (#23 to #31). (Color code of cluster index: predicted clusters were matched with known complexes (see the text); cluster indexes are differently color-coded by Jaccard correlation; yellow for a good match (Jaccard correlation ≥80%), green for moderate similarity (correlation ≥20% and <80%), and gray for poor overlap (correlation <20%)). Node size: number of genes/proteins contained in this cluster. Node color: average standardized gene expression level at time t. Edge width: Jaccard coefficient (or coherence) between clusters of adjacent snapshots. Gene Ontology: cluster-specific GO keywords were identified by hypergeometric tests. The right panel shows the top three enriched GO categories with P-value ≤0.05

Most of the complexes can be matched across the entire time course, but some disappear then reappear. An example is complex #4, annotated for DNA repair that is most active at the end of each 12-point cycle. This behavior required the MATCH-EM algorithm for globally consistent clusters, and would have been impossible to resolve given matching to nearest neighbors alone.

We ascertained whether the complexes predicted by our methods correspond to known complexes obtained from manual curation, CYC2008, or from high-throughput experiments, YHTP2008 (Pu et al., 2009). The 408 manual and 400 high-throughput complexes were filtered to retain the periodic proteins from YMC data, and then the catalog complex with the best Jaccard correlation was identified for each predicted complex. Of the 31 predicted complexes, 14 are poorly represented in the catalogs (Jaccard correlation <20%), 11 are only moderately similar (correlation ≥20% and <80%) and 6 have a good match (correlation ≥80%). The predicted complexes with poor overlap often recombine subunits from multiple catalog complexes (see #16 below).

To test the effects of the filtering, we also performed clustering using all 63 410 BioGrid interactions and including all genes with YMC data, periodic or non-periodic, yielding a network of 54 758 interactions among 4987 proteins. Clustering this network and retaining complexes with at least three proteins and edge density >0.1 yields 20-−40 clusters at each snapshot with 900±100 proteins included. Most clusters in the unfiltered network contains a high-degree core from the filtered network. Occasionally multiple cores are combined by low-degree connections, making the cluster count smaller than in the filtered network. The overlap with protein complex catalogs is similar to the unfiltered network.

4.2.2 Micro-views of YMC dynamics

The protein complex dynamics provide a rich view of YMC providing new biological insight, as demonstrated by in depth analysis of clusters #7, the mitochondrial ribosome and cluster #16, the nuclear pore.

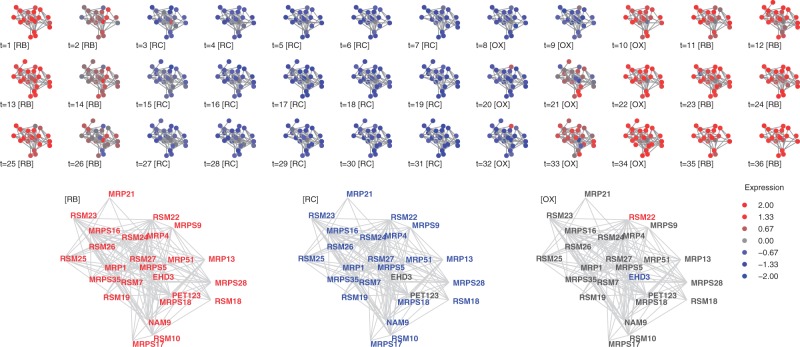
Mitochondrial ribosome complex (#7) The mitochondrial ribosome is generally assumed to be RB-specific, with transcription switched on briefly at the transition from OX to RB (Fig. 4). This complex contains primarily RSMs (ribosomal small subunit of mitochondrias) and MRPs (mitochondrial ribosomal proteins), known components of the mitochondrial ribosome (Saveanu, 2001).

Fig. 4.

Cluster #7, mitochondrial ribosome. Top: cluster members for the 36 gene expression snapshots. Bottom: Average expression for the three YMC phases. Node color: standardized gene expression level. Gene names were colored red or blue if expression values are above 0.5 or −0.5 respectively

Underneath this general pattern, however, RSM22 shows systematic expression ahead of other components. At time points t = 9, t = 20, and t = 32, RSM22 is active whereas other proteins are not transcribed. RSM22 is a nuclear-encoded putative S-adenosylmethionine (SAM) methyltransferase (Petrossian and Clarke, 2009), and methylation of the 3′-end of the rRNA of the small mitochondrial subunit is required for the assembly and stability of the mitochondrial ribosome (Metodiev et al., 2009). Deleting RSM22 yields a viable cell with non-functional mitochondria. Together, these results suggest the hypothesis that early expression of RSM22 may provide the methylation activity necessary for assembly of the mitochondrial ribosome.

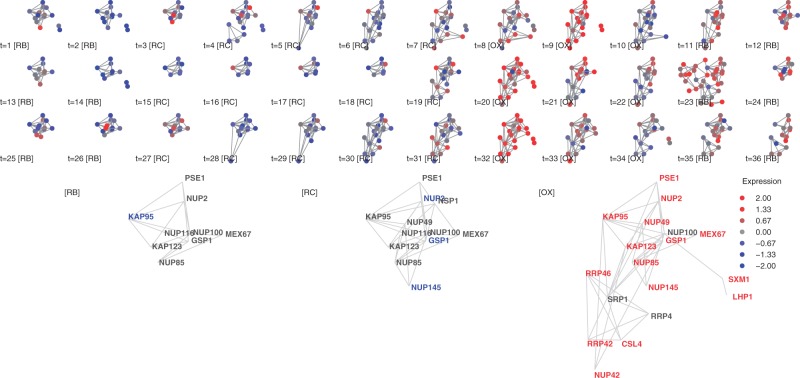
Nuclear pore complex (#16) Most genes in the nuclear pore complex are OX-responsive and the complex is most active at t=9, 20, 32 (Fig. 5). Unlike the mitochondrial ribosome, where the entire complex is generally transcribed in synchrony, this complex shows a smaller co-expressed core that is complemented with transient members during the OX phase. While it combines subunits of several annotated complexes, it has poor overlap with any single complex. Its best overlap is a 15 Jaccard correlation with high-throughput complex CID15 from YHTP2008.

Fig. 5.

Cluster #16, nuclear pore complex. Top: cluster members for the 36 gene expression snapshots. Bottom: Average expression for the three YMC phases. Node color: standardized gene expression level. Gene names were colored red or blue if expression values are above 0.5 or −0.5 respectively

The co-expressed core includes nuclear pore complex (NPC) and Karyopherin (KAP) proteins (Pemberton et al., 1998; Strambio-De-Castillia et al., 2010). The physical structure of the NPC comprises mostly NUP proteins. Among the proteins included in cluster #16, NUP2, NUP100 and NUP116 shape the Phe-Gly passage of the NPC (Strambio-De-Castillia et al., 2010). In contrast, KAP proteins are not considered structural but rather mediate export and import of RNA and proteins (Strambio-De-Castillia et al., 2010; Grünwald et al., 2011). KAP123 and PSE1 specifically transport ribosomal proteins (Schlenstedt et al., 1997). During the OX phases, SRP1 and SXM1 are additionally recruited. These KAP proteins recognize either nuclear localization sequences (NLS) or nuclear export sequences (NES) and direct transport into or out of nucleus (Pemberton et al., 1998).

Other transient memberships suggest additional hypotheses. RRP4 and RRP42 are a part of the exosome that edits RNA molecules 3′→5′ (Mitchell et al., 1997). Our clustering predicts that these proteins transition between the nuclear pore and other complexes during the cycle. CSL4 was recently reported to interact with RNA and is a possible exosome component (Liu et al., 2006). LHP1 is a La protein that binds to RNA polymerase III transcripts and small ribonuclear proteins (snRNPs), working as a molecular chaperone to protect and terminate the 3′-end of transcripts (Yoo and Wolin, 1994). These results are consistent with the hypothesis that RNA processing is tightly coupled to transport through the nuclear pore to the cytoplasm (Strambio-De-Castillia et al., 2010), but also suggest that dynamic reorganization of the nuclear pore occurs during the metabolic cycle. Additional evidence is the appearance of a second expression peak involving a subset of nuclear pore components at the start of the RB phase, which has not been previously described.

5 DISCUSSION

Dynamic network clustering is an increasingly important problem across diverse disciplines. Our algorithm optimizes the likelihood modularity, which is asymptotically consistent (Bickel and Chen, 2009). Other machine learning and physics approaches are based on probabilistic graphical models such as Latent Dirichlet Allocation (LDA, Airoldi et al., 2008; Ball et al., 2011; Blei et al., 2003). Dynamic extensions have been proposed (Fu et al., 2009), but prior to our work have been impractical except for very small networks with around 100 vertices and under 10 latent classes. Even efficient variational methods such as VBM (Hofman and Wiggins, 2008) have scaling that is far worse than a near linear or at least quadratic run time in the number of nodes and edges.

Our DHAC algorithm scales as O(EJln V), the same as HAC (Park and Bader, 2011), with a constant prefactor for the number of time points. This provides an excellent trade-off for genome-scale problems. Networks considered here with 2000 vertices required about 5 min on a single 2 GHz processor. A full-genome network with 10 000 to 100 000 vertices could be analyzed in a day to a week on single processor, but in practice would be much faster because each time point could be run in parallel.

The cluster matching algorithm MATCH-EM is a second contribution that provides a solution to the general problem of tracing the evolution of a set of groups or clusters over time. It generalizes a previous belief propagation method for bipartite matching (Bayati et al., 2006). The bipartite max-product algorithm is exact with a worst-case run-time of O(K³) for K classes. Our generalization has an additional linear factor of the number of time points. While it is no longer guaranteed to converge to the exact solution, for biological networks here it converges rapidly with good results.

Our methods applied to real biological data provide new insight. Many transcription time course experiments reveal waves of correlated gene expression, with no standard methods to parse a large set of correlated genes into well-defined protein complexes. The DHAC method is a general solution to this problem and provides a multi-resolution view of dynamic expression and organization of the proteome. Focusing on specific predicted complexes reveals possible mechanisms of regulation and control. Our analysis of the yeast metabolic cycle identifies protein complexes with asynchronous gene expression, which suggests RSM22 as an RNA methyltransferase whose early expression may be required to assemble and stabilize the mitochondrial ribosome.

Our methods permit proteins to switch between complexes over time, which we see in the dynamics of the nuclear pore. Hierarchical methods like DHAC also provide a natural multi-scale description of complexes, subcomplexes and proteins. A separate challenge is introducing mixed membership, with the same protein serving as a subunit in two distinct protein complexes (Palla et al., 2005).

Several improvements to DHAC are possible. Previous work showed that the hierarchical structure inferred from static networks corresponds to levels of biological organization, pathway to complex to subcomplex and the fine structure underneath a collapsed complex can also be used to improve link prediction (Park and Bader, 2011). In the current work, however, we lacked a method to match the dynamically evolving hierarchical structure across snapshots. Consequently the focus here is on the bottom-level clusters rather than the hierarchical structure.

This work assumes that the population average transcription data is a good representation for the transcriptional state of each cell. In reality, individual cells may differ from the mean. In the yeast metabolic cycle, for example, about half of the cells undergo cell division per metabolic cycle, potentially yielding two distinct cell populations. More advanced methods have been proposed to increase resolution and drive toward single-cell models (Baym et al., 2008).

Direct measurements of protein abundance through quantitative mass spectrometry could improve the analysis and would be intriguing to combine with expression data. For transcription data, protein abundance may be better estimated by a transcription-translation model, 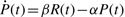, where R(t) is the measured transcriptional abundance, P(t) is the abundance of the corresponding protein and β and α are production and degradation rates. This model generates exponentially weighted smoothing of protein abundance, similar to the exponential kernel we used for smoothing. Since the exponential smoothing kernel already works well, we anticipate that results should be robust to choices of β and α, with the possibility of using consensus values for most proteins.