DACTAL: divide-and-conquer trees (almost) without alignments

Abstract

Motivation: While phylogenetic analyses of datasets containing 1000–5000 sequences are challenging for existing methods, the estimation of substantially larger phylogenies poses a problem of much greater complexity and scale.

Methods: We present DACTAL, a method for phylogeny estimation that produces trees from unaligned sequence datasets without ever needing to estimate an alignment on the entire dataset. DACTAL combines iteration with a novel divide-and-conquer approach, so that each iteration begins with a tree produced in the prior iteration, decomposes the taxon set into overlapping subsets, estimates trees on each subset, and then combines the smaller trees into a tree on the full taxon set using a new supertree method. We prove that DACTAL is guaranteed to produce the true tree under certain conditions. We compare DACTAL to SATé and maximum likelihood trees on estimated alignments using simulated and real datasets with 1000–27 643 taxa.

Results: Our studies show that on average DACTAL yields more accurate trees than the two-phase methods we studied on very large datasets that are difficult to align, and has approximately the same accuracy on the easier datasets. The comparison to SATé shows that both have the same accuracy, but that DACTAL achieves this accuracy in a fraction of the time. Furthermore, DACTAL can analyze larger datasets than SATé, including a dataset with almost 28 000 sequences.

Availability: DACTAL source code and results of dataset analyses are available at www.cs.utexas.edu/users/phylo/software/dactal.

Contact: tandy@cs.utexas.edu

1 INTRODUCTION

Phylogeny estimation methods are used to estimate the true tree from sequences that have evolved down the tree. This estimation is typically performed using two phases: first, a multiple sequence alignment (MSA) is estimated, and then a statistical estimation method [such as maximum likelihood (ML)] is applied to the alignment. Such ‘two-phase’ approaches produce highly accurate trees when the datasets are small enough (under a few hundred sequences) and have evolved without too many insertions and deletions (called ‘indels’) (Liu et al., 2009). Several methods for coestimation of trees and alignments based on statistical models of evolution that include indels as well as substitutions have been developed, including Fleissner et al., 2005; Lunter et al., 2003; Novák et al., 2008; and Redelings and Suchard, 2005. Of these methods, BAli-Phy (Redelings and Suchard, 2005) is the only one that, to our knowledge, has been able to analyze datasets with 100 sequences, but even these analyses can take a week or more. SATé is a new coestimation method, but (unlike the methods discussed earlier) estimates these alignments and trees without reference to a parametric model that includes indels as well as substitutions. Simulations show that SATé produces more accurate trees than two-phase methods on large hard-to-align datasets (Liu et al., 2009), and does so fairly quickly. Because SATé uses RAxML (Stamatakis, 2006), a popular ML heuristic, to produce phylogenies, it is computationally intensive for large datasets; furthermore, SATé's realignment technique can have very large memory requirements on some datasets with >25 000 sequences (Liu et al., 2010). Thus, none of the current methods is able to produce highly accurate phylogenetic estimation on very large sequence datasets, when they are difficult to align. As large phylogenetic studies are increasingly common (Cannone et al., 2002; Smith et al., 2009) (and more will likely arise as a result of next-generation sequencing technologies), this represents a substantial limitation.

An alternative approach to two-phase methods are ‘alignment-free’ methods that estimate trees without performing any MSA at all. Although some of the promising methods have not yet been implemented (e.g. Daskalakis and Roch, 2010), the best of the currently available alignment-free methods, while exhibiting surprising and desirable properties (such as improved accuracy in the presence of among-site rate variation), do not yet produce trees of the same accuracy as two-phase methods that first align and then estimate the tree (Hohl and Ragan, 2007).

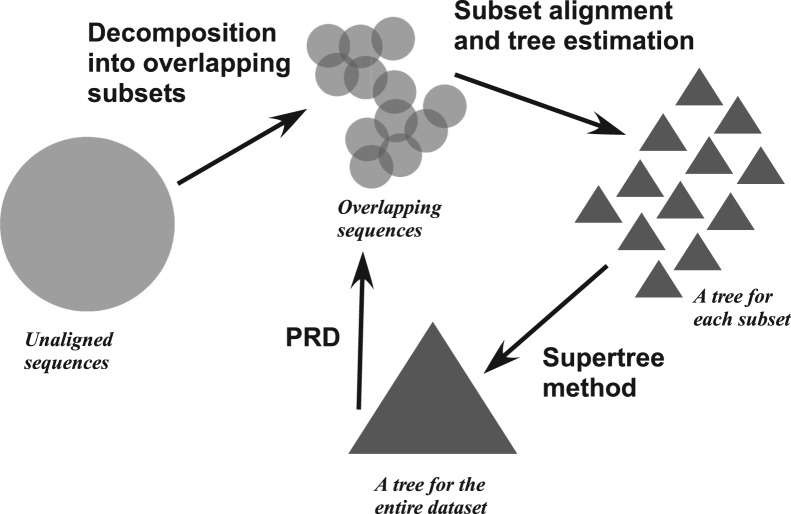
Here, we present DACTAL (‘Divide-And-Conquer Trees (ALmost) without alignments’), a method that is designed to estimate trees, but not a MSA, on large datasets. DACTAL combines iteration with a divide-and-conquer dataset decomposition approach to produce a tree without ever needing to estimate an alignment on the full dataset (Fig. 1). The dataset decomposition technique used in DACTAL is inspired by theoretical results related to supertree estimation methods and observations from extensive experience with phylogenetic analyses of large datasets; the iterative technique, however, is purely empirically motivated. Our study compares DACTAL to several existing methods, including several leading two-phase methods and SATé, on simulated and biological datasets with 1000 to almost 28 000 sequences. We show that:

• DACTAL produced more accurate trees than ML analyses of the alignment methods we studied, when analyzing very large difficult-to-align datasets, and matches accuracy on datasets that are easy to align;

• DACTAL matched the accuracy of SATé but was much faster (about one-tenth the time for each iteration on the largest datasets); and

• DACTAL was able to analyze larger datasets than SATé can, including one dataset with ~28 000 rRNA sequences, for which, SATé's re-alignment technique had excessive memory requirements.

Fig. 1.

DACTAL algorithmic design. DACTAL can begin with an initial tree (bottom triangle), or through a technique that divides the unaligned sequence dataset into overlapping subsets. Each subsequent DACTAL iteration uses a novel decomposition strategy called PRD to divide the dataset into small, overlapping subsets, estimates trees on each subset, and merges the small trees into a tree on the entire dataset.

2 DACTAL

2.1 Theoretical basis

Supertree estimation and the strict consensus merger: Supertree estimation refers to the estimation of a tree on a set S of taxa from trees on subsets of the taxa. However, computing accurate supertrees is computationally challenging. For example, the subtree compatibility problem, which asks whether a tree exists on which a set of unrooted trees agree, is NP-complete (Bodlaender et al., 1992) and so most optimization problems for supertree estimation are also NP-hard (Jiang et al., 2001).

However, some special cases of the subtree compatibility problem are solvable in polynomial time. Here, we present an algorithm called the strict consensus merger (SCM) (originally presented in Huson et al., 1999a but also used in Roshan et al., 2004 and Swenson et al., 2011), and prove that the SCM method solves the subtree compatibility problem when the input satisfies some constraints. Later, we will show that the dataset decomposition technique used in DACTAL is designed to produce inputs to SCM that are likely to satisfy these constraints. The improvement in accuracy then follows from empirical observations made from extensive studies of phylogenetic analyses of large datasets.

The SCM technique takes as input a set of trees on subsets of the full taxon set S, and merges these ‘source trees’ two at a time until a tree on the full set of taxa is computed. Here, we describe how SCM operates when all the input trees are binary (i.e. no nodes of degree greater than three) and compatible, meaning that some tree exists which induces a tree homeomorphic to each input tree when restricted to the leaf set for that input tree.

The SCM of two trees first computes the set of taxa that the two trees share; under the assumption that the two trees are compatible with a tree on the full set of taxa, they will induce the same subtree on that set of common taxa. This common subtree, which can easily be computed in polynomial time, is called the ‘backbone tree’.

We now describe how we insert the remaining taxa into the backbone tree t. First, we define the u-clades (unrooted clades) of an unrooted tree t′ to be those sets X such that for some subset Y of the leafset of t′, X|Y is a bipartition on the leafset of t′ (obtained by deleting some edge in t′). Now, consider an edge e of the backbone tree t, and the bipartition A_e|B_e defined by e. Let A be the (unique) minimal u-clade of t′ containing A_e, and B the (unique) minimal u-clade of t′ containing B_e. We will say that the source tree t′ contributes to the edge e in the backbone tree if, for some subset G of the leafset of t′, A, B, A∪G and B∪G are all u-clades of t′.

Note that when this happens, then A|B∪G and A∪G|B are both bipartitions in t′. Also, t′ will contain a path separating the subtrees on A and B, with one or more subtrees hanging off that path whose leafsets are subsets of G. If there is only one source tree contributing to the edge e, then the subtrees it has on the taxa in G can be attached to the edge e in a unique way: the edge e is subdivided (by adding j additional nodes if there are j subtrees to add), and then attaching each subtree in the correct order. However, if there is more than one source tree contributing to the edge e, then there will not be a unique binary supertree containing the source trees as induced subtrees; this is called a ‘collision’.

In the presence of a collision, the SCM tree is produced by subdividing the edge e once (thus producing a new node v_e) and then attaching all the subtrees that should be attached to e to v_e. In other words, the SCM tree will be incompletely resolved (i.e. will have nodes of degree >3) in the presence of any collision, even if the source trees are compatible. However, under some conditions that relate the source trees to some tree T on the full set of taxa, no collisions will occur, so that there will be a unique way to merge the two trees together, and the SCM method will be guaranteed to return T.

We begin with a definition of a ‘short quartet’. Let the pair (T, w) consist of a binary (fully resolved) tree T on n leaves and with positive edge weights defined by w:E(T)→ℝ⁺. Let e be an internal edge in T, and let A₁, A₂, A₃ and A₄ be the four subtrees of T produced by deleting e and its endpoints. Let a_i be a leaf in A_i (i=1, 2, 3, 4) that is closest to e with respect to the path length (defined by the edge weights). Then {a₁, a₂, a₃, a₄} is a short quartet around e. Letting e range over the internal edges of T, we obtain the set of short quartets of (T, w). Note that this definition depends on the edge-weights, so that different edge weight functions w will produce different short quartets. For all binary trees T, it is possible to reconstruct T given the set of induced four-leaf trees on the short quartets of T (Erdös et al., 1997). We will use this fact to prove the following theorem about the SCM method:

Theorem 1. —

Let t₁, t₂,…, t_k be unrooted binary trees and let S_i be the leafset of t_i. Let T be a tree on ∪_iS_i. Assume that S_i=A_i∪X, with A_i∩A_j=∅ for all i≠j, that t_i=T|S_i (the subtree of T induced by taxon set S_i), and that every short quartet of T is in some S_i. Then SCM applied to {t₁, t₂,…, t_k} returns T, independent of the order in which the trees are merged.

Proof. —

It suffices to show that at most one tree t_i contributes taxa to any edge in the backbone tree, as then the merger of any two trees is uniquely determined. As every two trees agree with T, the backbone tree T₀ on X is fully resolved. Let e be an edge in T₀, and let P be the maximal path in T of edges that define the same bipartition on X as e. Now assume, by way of contradiction, that two or more source trees contribute taxa to e. Then, P has at least one internal node, and so we can write P=v₀, v₁,…, v_k−1, v_k, with k≥2. Thus, we can define rooted trees T₁, T₂,…, T_k−1 of T to be those subtrees of T hanging off the path P, with T_i rooted at v_i. As two or more source trees contribute taxa to edge e, one of two conditions must hold: (i) there must be a tree T_i that has taxa from two or more source trees; or (ii) all trees T_i have taxa from only one source tree and there are two adjacent trees T_i and T_i+1 that have taxa from different source trees. For case (i), as the short quartets define a tree, it follows that there is a short quartet of T containing taxa a∈A_j and b∈A_k, with j≠k. As all short quartets of T are in some S_i, this implies that both a and b are in some common source tree. However, as the sets A_j and A_k are disjoint, this is a contradiction. For case (ii), let e_i be the edge on the path P between the roots of T_i and T_i+1, and let a, b, c, d be a short quartet around e_i, with a∈T_i and b∈T_i+1. Again we derive that a and b are in some source tree together, and obtain a contradiction.

Tree error impacted by evolutionary diameter: Phylogeny estimation is typically studied in the context of a Markov model of sequence evolution; simulations of sequence evolution under these models are used to understand the model conditions that impact accuracy of phylogeny estimation methods, and theoretical results establish conditions under which methods are guaranteed to be accurate. One of the key questions is the sequence length that is required for accuracy with high probability, expressed as a function of the model tree parameters (number n of taxa and parameters f and g, defined to be the minimum and maximum edge lengths, respectively, where the length of an edge is the expected number of substitutions of a random site on that edge). We now know that some methods can recover the true tree with high probability given sequence lengths that grow exponentially with the maximum leaf-to-leaf distance (Atteson, 1999; Erdös et al., 1999a; Lacey and Chang, 2006; St. John et al., 2001). As the maximum leaf-to-leaf distance can be Θ(ng), this result implies that the sequence length that suffices for accuracy with high probability can grow exponentially in the number of leaves, even when the maximum edge length is bounded. These theoretical results are complemented by simulations of sequence evolution that show that error rates of many phylogeny estimation methods (even ML) grow with the maximum evolutionary distance (Liu et al., 2009; Moret et al., 2002; Nakhleh et al., 2002; Wang et al., 2011).

Methods that can be shown to produce accurate trees with high probability from sequences that grow polynomially rather than exponentially in n (once f and g are fixed) are called absolute fast-converging (AFC) (Warnow et al., 2001). The first AFC methods, called the ‘short quartet methods’, used pairwise distances to guess at the set of short quartets, computed trees on each such quartet, and then combined the trees to produce a tree on the full set of taxa (Erdös et al., 1999a, b). Subsequently, other AFC methods were developed (Cryan et al., 1998; Csürős and Kao, 1999; Gronau et al., 2008; Huson et al., 1999a; Nakhleh et al., 2001; Roch, 2010), including the DCM1 method, also known as the first disk covering method (DCM) (Huson et al., 1999a; Warnow et al., 2001). The DCMs, as a class, are dataset decomposition techniques that construct trees on each subset and then combine the trees into a tree on the full set of taxa using the SCM method. Some of these DCMs are useful for large-scale optimization but do not provide any statistical guarantees (Huson et al., 1999b; Roshan et al., 2004).

Key to the empirical and theoretical performance of DCM methods is that the dataset decompositions produce datasets with smaller evolutionary diameters, and so that each short quartet is in some subset. The first of these two properties improves the chances that trees on the subsets will be highly accurate, whereas the second property makes it possible to combine the subset trees into a tree on the full taxon set without loss of accuracy. However, these theoretical guarantees depend on the supertree method used for combining trees on the subsets and not all supertree methods have sufficiently strong theoretical properties.

From an empirical standpoint, DCM-boosting has been shown to improve the topological accuracy of several distance-based methods (Huson et al., 1999a; Moret et al., 2002; Nakhleh et al., 2001; Nakhleh et al., 2002; St. John et al., 2001). However, the impact of DCM-boosting on better distance-based methods, or on heuristics for ML or maximum parsimony, has not been studied. More generally, from an empirical standpoint, because the second step of DCM-boosting (supertree estimation, such as SCM) reduces accuracy, DCM-boosting will only yield empirical benefits to the extent that the phylogeny estimation method improves in accuracy on the taxon subsets compared with its accuracy on the original full set of taxa more than the supertree estimation method reduces accuracy. Thus, although we can improve the accuracy of the final tree using a more accurate supertree estimation method than SCM, DCM-boosting will still fail to yield improvements (and could lead to less accurate trees) unless the phylogeny estimation method is substantially more accurate on the smaller subsets than it is on the full dataset. Therefore, DCM-boosting may not be beneficial when used with methods like ML on datasets that are already aligned, or for which alignment estimation is fairly easy.

However, for sequence datasets that are challenging to align well, DCM-boosting could lead to improved tree estimations. This led us to the design of DACTAL. As empirical results suggest that trees and alignments are more accurately estimated when datasets have small diameter and are densely sampled, decompositions that produce datasets with these properties are likely to yield more accurate trees for each subset. As before, we need to have sufficient overlap between subsets to improve the chances that all short quartets will be in some subtree. Finally, to improve the topological accuracy, we use the SuperFine (Swenson et al., 2011) supertree method rather than SCM to merge the trees together. SuperFine begins by computing the SCM and then refines the resultant unresolved tree in a computationally efficient manner. In practice, SuperFine has much greater accuracy than SCM (Swenson et al., 2011).

2.2 DACTAL design

DACTAL uses an iterative procedure, in which each iteration produces a decomposition of the taxa into four sets of the form S_i=A_i∪X, with A_i∩A_j=∅ for i≠j, recursively computes a tree t_i on each S_i, and then combines the trees t₁, t₂, t₃ and t₄ using the SuperFine (Swenson et al., 2011) method. Because SuperFine begins by computing the SCM tree and then refines it if the SCM tree is not fully resolved, the theoretical guarantees obtained for the SCM method are also ensured when using SuperFine. Therefore, by Theorem 1, if each t_i is correctly computed and every short quartet in the true tree is in some S_i, then the SCM tree is the true tree, and so DACTAL produces the true tree at the end of the iteration.

Because of space limitations, we describe the most important details of DACTAL's design, and direct the interested reader to Nelesen, 2009 (where DACTAL is called BLuTGEN) for additional details. The first iteration begins with a tree estimated either through the use of a fast two-phase method or with a novel BLAST-based (Altschul et al., 1990) method for producing a tree, called ‘BLF’ (BLAST-based Fast). BLF uses BLAST to produce a collection of subsets of sequences, with one such subset computed for each sequence in the dataset. Each subset contains a targeted number of sequences that BLAST selects as highly similar to the seed sequence, and the subsets are ‘padded’ to ensure that they have sufficient overlap with at least one other subset. The user provides two parameters: B, the target size for each subset, and C, the target overlap each subset should have with at least one other subset. Nelesen, 2009 provides more details about BLF, and about related BLAST-based decompositions we evaluated.

Each subsequent DACTAL iteration begins with the tree computed in the previous iteration, and has the following structure. Step 1: Divide the sequence dataset into overlapping subsets using a padded-Recursive-DCM3 decomposition (PRD), with parameters s (the subset size) and p (the overlap size). Step 2: Compute trees on each subset; here, we use RAxML version 7.2.6 in its default setting under GTRCAT, applied to alignments produced using MAFFT version 6.240 in its L-INS-i setting (mafft-localpair-maxiterate 1000). Step 3: Compute a supertree on the subset trees, using SuperFine.

Thus, to define the DACTAL iteration process, we only need to describe the PRD decomposition. This dataset decomposition technique is similar to the Recursive-DCM3 (Roshan et al., 2004) decomposition, modified so that there is more overlap between the subsets. A PRD decomposition takes as input a tree on the full set of taxa, and finds an edge in the tree that splits the tree into two subtrees containing roughly equal numbers of taxa. The removal of this edge and its endpoints divides the tree into four subtrees, A, B,C and D. For each of these four trees, the set of p/4 closest leaves (using topological distance) to the edge e are selected, and put into a set X; thus, X has approximately p taxa. Then, the number of taxa in each of A∪X, B∪X, C∪X and D∪X is computed; if any of these sets is larger than the target size s, then the decomposition is repeated recursively on that set. When each subset is small enough, the decomposition step stops, and the set of subsets is returned. Thus, each subset will contain at most s taxa, and will overlap with some other set by at least p. We used custom software to run the PRD decomposition method to produce subproblems.

Comments: The DACTAL algorithm is designed to allow the user to modify the different steps; thus, although we set certain steps within DACTAL (e.g. how we estimate trees on the subsets, and how we compute a supertree from the trees on each subset), even these techniques can be replaced by other techniques. Overall, the user can specify seven algorithmic parameters: the method for calculating the starting tree, the number of taxa in each subset of a decomposition, the size of the overlap between subsets, the techniques for estimating alignments and trees on each of the small subsets, the supertree method used to construct a tree on the entire set of taxa and the stopping criterion.

We explored settings for these parameters, and selected default settings that worked well across the datasets we explored. As previously noted, we set the technique used to compute trees on each subset to be RAxML on MAFFT (Katoh and Toh, 2008) alignments, and we set the the supertree method used to combine the trees on the subsets to be SuperFine. The remaining parameters (starting trees, PRD decompositions, and number of parameters) are interesting, and different settings have different advantages. In particular, the starting tree and the parameter p within the PRD decomposition impact the probability that every short quartet will be in some subset of the decomposition (larger values for p and more accurate starting trees increase this probability).

However, the starting tree does not need to be completely correct for each short quartet to be in some subset. Instead, two properties are needed. First, the starting tree should not distort evolutionary distances too much (i.e. taxa placed very close together in the starting tree should not be too distant in the true tree, and conversely closely related taxa should not be very distant from each other in the starting tree). Second, the padding parameter p should be large enough that each short quartet (as defined by the true tree) should be in the padded set. When the starting tree does not distort evolutionary distances at all, the padded set should contain all the short quartets (even for fairly small p); thus, small values for p should suffice when the starting tree has only small distortion.

Fortunately, in practice, trees estimated using good techniques (ML analyses of reasonable alignments) do seem to have these properties. The evidence for this assertion is that the Robinson–Foulds (RF) distance, also called the bipartition distance, between true trees and the estimated trees tends to be moderate. For example, in Liu et al., 2009, the better two-phase methods had RF distances to the true tree that were generally <30%, with the exceptions to this being the very hardest model conditions. The RF distance is very sensitive to taxon movements: so that if just one taxon were to move halfway across the tree from its correct location, and otherwise everything remained in place, then the RF distance would be 50%. Thus, empirical evidence suggests that tree estimation errors tend to be relatively local. This implies that starting trees based on reasonable ML analyses of reasonable alignments are likely to have these favorable properties. Therefore, for starting trees that are approximately correct and for large enough p, the subsets that are produced will have the desired properties: smaller evolutionary diameters and all short quartets in some subset.

We studied several settings for these parameters, and determined default settings that worked well across the entire range on the datasets we explored. For the PRD decomposition, we set the subset size to 250 and the overlap size p to 50. For the starting trees, we picked two different two-phase methods: one for datasets with at least 1000 sequences [FastTree (Price et al., 2010) on a MAFFT-PartTree (Katoh and Toh, 2007) alignment], and one for the smaller datasets [RAxML on the L-INS-i MAFFT (Katoh and Toh, 2008) alignment]. To reduce the running time, we set the number of iterations to 5 for the large datasets and 10 iterations for smaller datasets.

3 PERFORMANCE STUDY

We used 180 1000-taxon simulated datasets studied in Liu et al., 2009 and three biological datasets studied in Liu et al., 2010. For each of these datasets, we used reference trees provided in the studies, and the tree error and running time results provided in the studies for SATé analyses and two-phase methods using RAxML. We also attempted to run BAli-Phy (Redelings and Suchard, 2005) and ALIFRITZ (Fleissner et al., 2005), two leading methods that use statistical techniques to estimate trees from unaligned sequences, but these methods failed to finish running (even after many weeks) on even 500-taxon datasets.

The 1000-taxon simulated datasets were analyzed using SATé and RAxML v. 7.0.4 on many alignment methods, including the default and Quicktree versions of ClustalW (Thompson et al., 1994), the L-INS-i and PartTree versions of MAFFT (Katoh and Toh, 2007, 2008), Muscle (Edgar, 2004), Opal (Wheeler and Kececioglu, 2007), and Prank+GT (Liu et al., 2009; Loytynoja and Goldman, 2005). These datasets evolved under GTR+Gamma+indel models, with expected indel lengths that range from short (~2 nt) to long (~9 nt). The simulated datasets range from relatively easy to align to quite difficult and help us characterize the accuracy of DACTAL trees under a wide range of model conditions. We set the reference tree for each alignment to be the model tree that generated the data (known to us because we performed the simulation), with all zero-event branches contracted.

The biological datasets used in the study come from the comparative RNA website (CRW) (Cannone et al., 2002): 16S.B.ALL (27 643 sequences), 16S.T (7350 sequences), and 16S.3 (6323 sequences), modified to remove all taxa with 50% or more unsequenced letters. The CRW datasets were chosen for analysis because they have highly reliable curated alignments based on secondary and higher order structure; to our knowledge, there are no larger biological datasets with alignments of comparable reliability. For each biological dataset, Liu et al., 2010 provided a reference tree, computed using RAxML v. 7.0.4, on the curated alignment, retaining only branches with bootstrap support of 75% or greater (Hillis and Bull, 1993).

We measured topological accuracy in terms of the missing branch rate (also known as the false negative rate), which is the percentage of branches in the reference tree that are missing from the estimated tree. It is worth noting that for the simulated datasets, this is extremely close to the Robinson–Foulds error, as the estimated trees are fully resolved and the reference trees nearly so (only zero-event branches are contracted). However, the reference trees for the biological datasets are highly unresolved, which makes the Robinson–Foulds rate inappropriate.

As noted, the RAxML analyses are computationally intensive, and so we did not rerun the SATé or two-phase methods on the simulated or biological datasets; however, all these analyses were based on RAxML v. 7.0.4, whereas DACTAL uses RAxML v. 7.2.6 to estimate the trees on small subsets. The differences between the two versions are not supposed to affect the accuracy (in terms of ML score or tree error), but we performed a small comparison to verify this. We compared these two versions of RAxML on four alignments of the 16S.3 and 16S.T datasets; these analyses showed that differences in the missing branch rates were at most half a percent, with the newer version worse than the older version as often as it was better. Thus, as expected, the differences in the two versions does not impact the accuracy of the analysis.

4 RESULTS

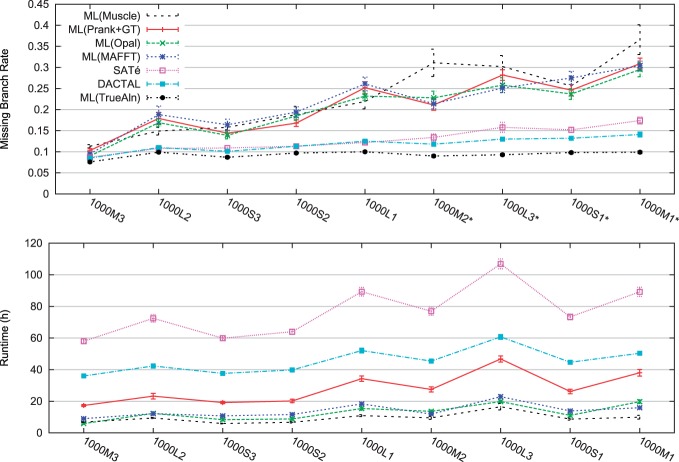
DACTAL, SATé, and other methods on simulated data On simulated datasets (for which we know the true tree), we can compute the accuracy of all estimated trees precisely. Figure 2 shows results comparing DACTAL to the default 24-h analysis using SATé and to two-phase methods (RAxML analyses of leading alignment methods) on the more difficult 1000-taxon model conditions. Note that all methods give the same accuracy on the easy model conditions but can be distinguished on the harder model conditions. For these harder model conditions, DACTAL and SATé both give substantially improved accuracy compared with RAxML on estimated alignments, and DACTAL has a slight advantage over SATé in terms of accuracy on the hardest datasets. DACTAL is faster than SATé on these datasets.

Fig. 2.

Comparisons of 10 iterations of DACTAL to SATé and RAxML trees estimated on different alignments on ‘moderate-to-difficult’ simulated 1000-taxon datasets. We show missing branch rates (top) and runtimes in hours (bottom); n=20 for each model condition, and standard error bars are shown. DACTAL and SATé runtimes include the time to compute RAxML(MAFFT) starting trees. Asterisks (*) denote model conditions for which DACTAL's missing branch rate is a statistically significant improvement over the next best method, according to Benjamini–Hochberg-corrected (Benjamini and Hochberg, 1995) pairwise t-tests (n=40, α=0.05).

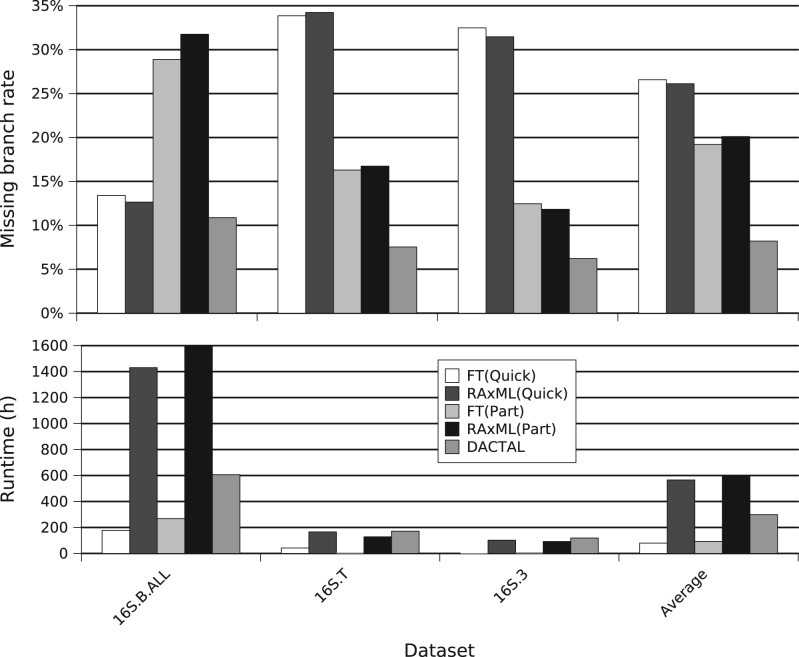
DACTAL, SATé, and other methods on biological datasets The advantage of DACTAL is most evident on the three biological datasets we analyzed, which range from 6323 to 27 643 sequences. First, many two-phase methods (first align, then compute a tree) simply fail to run on very large datasets (Liu et al., 2010), largely because of limitations in the alignment methods. However, SATé also failed to produce its first realignment on the largest of these biological datasets, 16S.B.ALL. In contrast, DACTAL completed five iterations of the 16S.B.ALL dataset in under 400 h, so that each iteration took slightly >3 days. Furthermore, DACTAL achieved a missing branch rate of ~11 on the 16S.B.ALL dataset, which was better than the missing branch rates of the other methods (Fig. 3). Thus, DACTAL can analyze datasets that SATé fails to analyze.

Fig. 3.

DACTAL (based on five iterations) compared with ML trees computed on alignments of three large biological datasets with 6 323–27 643 sequences. We used FastTree (FT) and RAxML to estimate ML trees on the PartTree (Part) and Quicktree (Quick) alignments. The starting tree for DACTAL on each dataset is FT(Part).

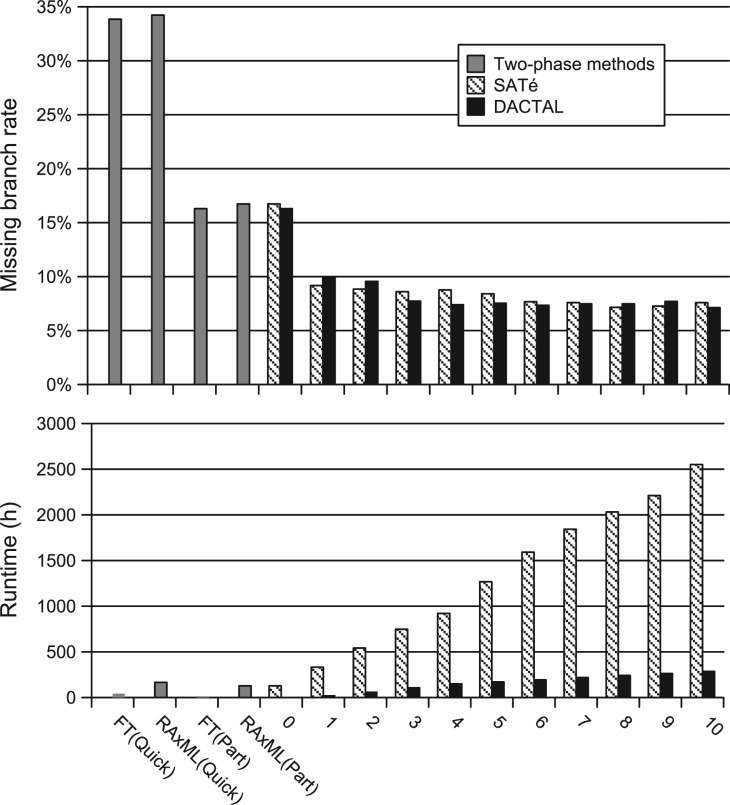
On datasets that both DACTAL and SATé can analyze, they achieve approximately the same accuracy in each iteration, but DACTAL is much faster: on the largest datasets, a single DACTAL iteration takes about 10% of the time of a SATé iteration. Figure 4 shows this for the 16S.T. dataset with 7350 sequences (results on the other datasets show the same trends).

Fig. 4.

Comparisons of DACTAL and SATé iterations with two-phase methods on 16S.T dataset with 7 350 sequences. The starting trees were RAxML(Part) for SATé and FT(Part) for DACTAL. We show missing branch rates (top) and cumulative runtimes in hours (bottom); n=1 for each reported value. Iteration 0 is used to compute the starting tree for DACTAL and SATé.

We now compare DACTAL to two-phase methods. In Liu et al., 2010, we evaluated several two-phase methods on these datasets. Even when run on a dedicated machine with 256 GB, all alignment methods except for MAFFT-PartTree and ClustalW-quicktree failed to align one or more datasets. For example, only ClustalW-Quicktree and MAFFT-PartTree managed to align the largest dataset (16S.B.ALL), whereas Prank and Muscle failed to complete on any of these datasets. The L-INS-i version of MAFFT only succeeded in aligning one of the three datasets (producing segmentation faults on the other two).

A comparison of five iterations of DACTAL to the best result of any of these two-phase methods on each dataset shows that DACTAL produced more accurate trees on the 16S.B.ALL and 16S.3 datasets (by ~2% and 3%, respectively), and that DACTAL was slightly less accurate (by 0.2%) than RAxML(MAFFT L-INS-i) on the 16S.T dataset. In terms of running times, however, DACTAL was much faster than the most accurate two-phase methods on each dataset. For example, on the 16S.T dataset, producing the MAFFT L-INS-i alignment took 615 h and RAxML on this alignment took ~200 h, for a total of >800 h. By comparison, DACTAL completed five iterations in 172 h. Thus, DACTAL took less than a fourth of the time used by RAxML(MAFFT L-INS-i) on this dataset.

We now compare DACTAL to ML trees on the QuickTree and PartTree alignments, as these were the only methods that were able to align all three datasets; see Figure 3. Note that DACTAL was more accurate than trees based on QuickTree or PartTree and had less than half the average error. A comparison of running times shows that DACTAL was slower than FastTree(QuickTree) or FastTree(PartTree), but faster than RAxML(QuickTree) and RAxML(PartTree).

Robustness to using BLF or estimated trees for initialization Of particular importance is the robustness of DACTAL to how it is initiated—with a starting tree or using BLF. We explored DACTAL's performance when it used the BLF decomposition to initialize instead of a starting tree. In some cases, the initial trees obtained using BLF were more accurate than the starting trees we could produce, and in some cases they were less accurate. However, in all cases, within two iterations of DACTAL (from both starting conditions), accuracy levels were approximately the same; Figure 5 shows results for this comparison on one hard model condition.

Fig. 5.

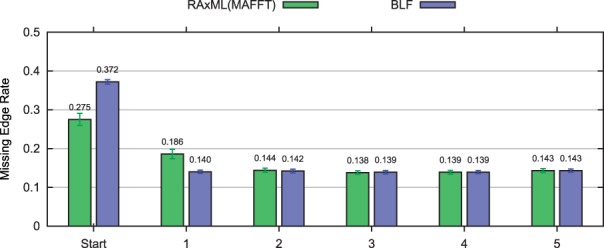
Impact of starting tree on DACTAL iterations for 1000 taxon simulated datasets from 1000S1. The accuracy of each starting tree [the default RAxML(MAFFT) tree and the BLF tree] are shown together with five iterations of DACTAL (PRD decompositions) from each starting tree. Results in green (the left bar within each pair of bars) indicate DACTAL results that start with RAxML(MAFFT) as the starting tree, and results in blue (the right bar) indicate DACTAL results that start with the BLF tree.

We then examined the choice of starting tree, and observed similar results: although the starting trees might differ substantially in terms of accuracy, after a few DACTAL iterations, the accuracy levels were the same. The main issue, therefore, is a matter of running time and using very fast methods to estimate initial trees is sufficient, provided one runs DACTAL for at least a few iterations.

DACTAL's robustness to dataset decompositions We also examined performance under different dataset decomposition strategies, varying the size of the subsets produced by the PRD (padded recursive decomposition) technique. This comparison showed that increasing the subset size could lead to improved estimations of the tree but at a running time cost. Furthermore, within a few iterations, the analyses using different subset sizes had approximately the same accuracy; Figure 6 gives results on the largest biological dataset, and other analyses showed similar results.

Fig. 6.

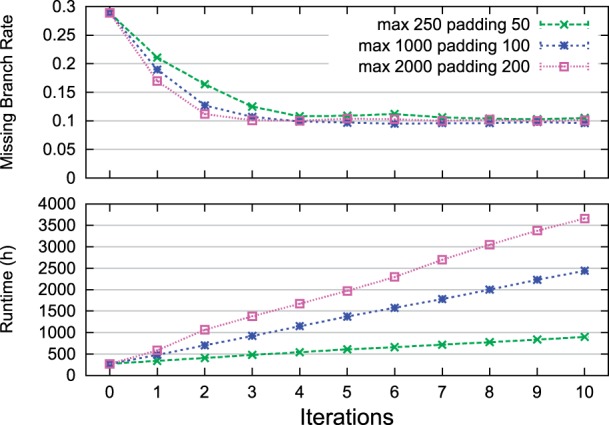
Comparisons of DACTAL iterations using different decomposition sizes on the 16S.B.ALL dataset. DACTAL is run in default mode except for changes in the PRD parameters [maximum subproblem size (‘max’) and the padding size (‘padding’)]. Panels from top to bottom are missing branch rates and runtime (hr); n=1 for each reported value. DACTAL's iteration 0 is used to compute the starting tree. Runtimes are cumulative.

5 DISCUSSION

DACTAL is designed for large datasets that are difficult to align. DACTAL has not been tested on datasets with fewer than 1000 sequences, where we anticipate little advantage in using DACTAL; indeed, it is likely that DACTAL will be less accurate than good two-phase methods on small enough datasets. Furthermore, some large datasets (such as 16S.T) can be fairly accurately aligned using the best alignment methods, and in these cases, DACTAL may also not provide any improvement in topological accuracy (although it may provide a running time advantage for large enough datasets). Thus, DACTAL does not provide advantages for all types of datasets but only for some. However, for those datasets that are large and difficult to align, this performance study demonstrates that DACTAL can provide substantially improved tree estimations and can do so quite quickly.

DACTAL's performance is the result of three algorithmic design techniques that work synergistically. First, because DACTAL's decomposition strategy produces subsets with at most 250 sequences, it is possible to run MAFFT in more accurate ways to align each subset than may be possible on the full taxon set. Second, the divide-and-conquer approach used in DACTAL produces small densely sampled subsets containing sequences that tend to be very similar; these features increase the accuracy of estimated alignments, so that ML trees computed on these subset alignments tend to be more accurate than ML trees computed on alignments estimated on the full dataset. Finally, the SuperFine method produces trees on the full dataset that retain much of the accuracy of the smaller trees (Swenson et al., 2011). A single iteration of DACTAL, therefore, typically produces a tree with greater accuracy than the starting tree, unless the starting tree is itself highly accurate. The next few iterations will often yield further improvements, as the estimated alignments continue to improve in accuracy.

6 FUTURE WORK

This study evaluated DACTAL on datasets ranging from 1000 sequences to almost 28 000 sequences. In this range of dataset sizes, DACTAL yielded improved accuracy compared with the two-phase methods we tested on most of the difficult-to-align datasets, and matched (or came very close to matching) the accuracy on the easy to align datasets. However, because we did not examine larger datasets, we do not know whether DACTAL's approach will continue to provide advantages over two-phase methods as the number of sequences increases; future work will seek to evaluate this possibility.

The results shown here are for a hybrid method in which we combine DACTAL's iterative divide-and-conquer strategy with a highly accurate two-phase method, RAxML on MAFFT alignments. However, DACTAL can be paired with any phylogeny estimation method and any kind of phylogenetic data (gene order data, morphology, distances, etc.) and can also be used with multi-marker data. DACTAL's modular approach also allows us to replace each step (alignment, tree estimation, supertree estimation and even the dataset decomposition) with new approaches. Thus, DACTAL is a very general algorithmic ‘booster’ for phylogeny estimation methods.

DACTAL also has potential advantages for datasets in which model parameters typically held fixed across the tree (such as the GTR matrix) are expected to vary (for example, due to changes in the GC content across the tree). That is, as DACTAL computes trees on each small subset using RAxML, this allows each RAxML analysis to compute a separate GTR matrix for each subset of taxa. Thus, DACTAL analyses may be more robust to model violations than methods that do not have this flexibility.

Despite its good empirical performance, DACTAL provides no statistical guarantees, and it is likely that statistical methods based on models of evolution that treat indels as events, rather than as missing data, would produce more accurate trees (Warnow, 2012). Unfortunately, the statistical methods that properly handle ‘long’ indels are not sufficiently fast on even moderately large datasets. Given the interest in statistical coestimation methods, however, we predict that improved methods with greater scalability are likely to be developed in the coming years.

Finally, we note that some projects are planning to estimate much larger phylogenies than those studied in this article. For example, the iPlant Collaborative will attempt to estimate a species tree on 500 000 plant species. Given the difficulty in estimating highly accurate MSAs for very large datasets, and in likelihood-based analyses of very large alignments, divide-and-conquer approaches (such as DACTAL) might be particularly helpful in ultra-large phylogeny estimation problems.