Abstract
Motivation: The generation of time series transcriptomic datasets collected under multiple experimental conditions has proven to be a powerful approach for disentangling complex biological processes, allowing for the reverse engineering of gene regulatory networks (GRNs). Most methods for reverse engineering GRNs from multiple datasets assume that each of the time series were generated from networks with identical topology. In this study, we outline a hierarchical, non-parametric Bayesian approach for reverse engineering GRNs using multiple time series that can be applied in a number of novel situations including: (i) where different, but overlapping sets of transcription factors are expected to bind in the different experimental conditions; that is, where switching events could potentially arise under the different treatments and (ii) for inference in evolutionary related species in which orthologous GRNs exist. More generally, the method can be used to identify context-specific regulation by leveraging time series gene expression data alongside methods that can identify putative lists of transcription factors or transcription factor targets.
Results: The hierarchical inference outperforms related (but non-hierarchical) approaches when the networks used to generate the data were identical, and performs comparably even when the networks used to generate data were independent. The method was subsequently used alongside yeast one hybrid and microarray time series data to infer potential transcriptional switches in Arabidopsis thaliana response to stress. The results confirm previous biological studies and allow for additional insights into gene regulation under various abiotic stresses.
Availability: The methods outlined in this article have been implemented in Matlab and are available on request.
Contact: d.l.wild@warwick.ac.uk
Supplementary Information: Supplementary data is available for this article.
1 INTRODUCTION
The generation and analysis of highly resolved time series datasets measuring transcriptional change has become an increasingly common and powerful approach for disentangling complex biological processes, with several consortia having generated detailed time series under different experimental conditions/ perturbations, for example, the AtGenExpress consortium (Goda et al., 2011; Kilian et al., 2007) or PRESTA consortium1 (Breeze et al., 2011). A major goal in the analysis of such data is the identification of regulatory relationships by reverse engineering gene regulatory networks (GRNs).
Recent approaches for the reverse engineering of GRNs from time series data make use of nonparametric Bayesian learning strategies that have proven competitive with other state-of-the-art approaches, particularly when learning from multiple datasets (Äijö and Lähdesmäki, 2009; Klemm, 2008; Penfold and Wild, 2011). To be computationally manageable, these methods assume that the number of transcription factor (TF) proteins binding the promoter region of a given gene at any given time are limited, corresponding to a fan-in restriction. Recent studies using yeast one-hybrid screens of Arabidopsis thaliana TFs, however, suggest that large numbers of TFs have the potential to bind any given gene (Mitsuda et al., 2010; Ou et al., 2011). Additionally, in order for these nonparametric methods to learn from multiple datasets, it was assumed that the individual time series were generated from networks with identical topology. In light of the number of TF-binding promoter regions, it is likely that most organisms use a series of transcriptional switches to cope with the variety of stresses and environmental challenges they face, with the TFs binding under a given condition not necessarily the same as those binding in another condition or in different tissues. In these situations, the number of TFs binding under any given condition is likely to be fewer than the total number that can possibly bind. Consequently, it is of interest to identify which subsets of TFs are binding under different conditions, by identifying treatment-specific GRNs which may, or may not share some common structure. In this regard, identifying context-specific regulatory networks represents a useful way of combining time series gene expression data with methods that can identify putative transcriptional regulators, including yeast one-hybrid (Lopato et al., 2006) and multiple ChIP-chip/Seq experiments (Park, 2009).
Alternatively, the GRNs of evolutionarily related species might be expected to share some common structure by virtue of a shared ancestral network. Time series data generated in the two species could therefore be informative of one another. In these cases, it might be of interest to identify the similarities and differences in the GRNs of the two species (Baumbach et al., 2009; Liu et al., 2011). Such an approach could prove immensely useful for leveraging information from simpler, but better understood model systems, into more complex organisms, allowing for useful biological insights, such as addressing why some plants are capable of nodulation while others are not (see e.g. http://www2.warwick.ac.uk/fac/sci/lifesci/research/systemsdev).
Rather than treating different datasets independently, or assuming identical network topologies in the different conditions/species, a more principled strategy is to adopt a hierarchical modelling framework such as that used by Werhli and Husmeier (2008), in which a separate network structure is inferred from each individual dataset, albeit with the network topology constrained via a hypernetwork, as a means of leveraging multiple sources of prior information. The work of Werhli and Husmeier (2008), however, deals with steady state data using Bayesian networks, and consequently is not applicable to time series data. In this study, we combine such a hierarchical framework with the non-parametric causal structure identification (CSI) algorithm (Klemm, 2008; Penfold and Wild, 2011) to allow for network reconstruction when multiple sources of (perturbed) time series data exist.
2 CAUSAL STRUCTURE IDENTIFICATION
The CSI algorithm (Klemm, 2008; Penfold and Wild, 2011) and related approaches (Äijö and Lähdesmäki, 2009) have previously been used to reverse engineer GRNs and shown to perform well against other state-of-the-art algorithms (Äijö and Lähdesmäki, 2009; Penfold and Wild, 2011). The discrete-time version of CSI assumes that the mRNA expression level of a particular gene in a larger set, i∈ , evolves as a nonlinear dynamical system:
, evolves as a nonlinear dynamical system:
| (1) |
where xi(t) represents the expression level of gene i at time t,  a(i)⊆
a(i)⊆ represents the genes encoding for TFs binding the promoter regions of gene i (parents of gene i) with x
represents the genes encoding for TFs binding the promoter regions of gene i (parents of gene i) with x a(i)(t) the vector expression level of those parents at time t, and f(·) represents some unknown (non-linear) function capturing the dynamics of the system. If the parents of gene i were known a priori, the non-linear function in equation (1) could be estimated directly from the data by assigning the function a Gaussian process (GP) prior and assuming Gaussian additive white noise, to yield a posterior GP (Rasmussen and Williams, 2006). The marginal likelihood of a set of N observed expression values for gene i, y=(xi(t1),…, xi(tN))⊤, given the matrix of expression levels X at previous time points (where the column X:,l=(xl(t0),…,xl(tN−1))⊤ represents the vector of expression for gene l at times t0 through tN−1), is, therefore, jointly Gaussian:
a(i)(t) the vector expression level of those parents at time t, and f(·) represents some unknown (non-linear) function capturing the dynamics of the system. If the parents of gene i were known a priori, the non-linear function in equation (1) could be estimated directly from the data by assigning the function a Gaussian process (GP) prior and assuming Gaussian additive white noise, to yield a posterior GP (Rasmussen and Williams, 2006). The marginal likelihood of a set of N observed expression values for gene i, y=(xi(t1),…, xi(tN))⊤, given the matrix of expression levels X at previous time points (where the column X:,l=(xl(t0),…,xl(tN−1))⊤ represents the vector of expression for gene l at times t0 through tN−1), is, therefore, jointly Gaussian:
| (2) |
where 0 represents a vector of zeros of length N and 𝕀 represents an N×N identity matrix. Here, θ represents the hyperparameters of the GP prior, the interpretation of which will depend on the choice of covariance function, Kθ. In this case, the functional form of the covariance function was chosen to be the squared exponential:
| (3) |
and the hyperparameters θ={σn2, σf2, l} therefore represent the variance of the observation noise, variance of the process and characteristic length scale, respectively. Alternatively, related approaches (Äijö and Lähdesmäki, 2009) make use of a Matérn covariance function.
Typically, the parents of a given gene are not known a priori but must additionally be inferred from the data. This may be achieved using Bayes' rule, where the probability of a particular set of parents,  a(i), is given by:
a(i), is given by:
 |
(4) |
Ideally, the summation in the denominator takes place over all possible combination of transcription factors, that is, the power set of  ,
,  (
( ), where
), where  ⊆
⊆ represents the set of all transcription factors and θk the set of hyperparameters for the k-th parental set. For large systems, summation over all possible transcription factor combinations is unfeasible because the number of combinations scales factorially with the number of TFs. To overcome this, the summation may be truncated to include only parental sets of limited in-degree ≤c, pa(i)∈
represents the set of all transcription factors and θk the set of hyperparameters for the k-th parental set. For large systems, summation over all possible transcription factor combinations is unfeasible because the number of combinations scales factorially with the number of TFs. To overcome this, the summation may be truncated to include only parental sets of limited in-degree ≤c, pa(i)∈ c(
c( ), resulting in polynomial scaling.
), resulting in polynomial scaling.
The distribution in equation (4) will, of course, depend on the choice of hyperparameters in the covariance function. Rather than setting these manually, it is preferable to allow the data to determine their value(s), that is, by maximizing the marginal likelihood with respect to the individual hyperparameters for each parental set θk (Äijö and Lähdesmäki, 2009) (see also Supplementary Section 1.1) or jointly constraining θ1=θ2=… and maximizing the marginal likelihood with respect to these parameters using expectation maximisation (Klemm, 2008; Penfold and Wild, 2011) (CSI-EM; Supplementary Section 1.2). Alternatively, a combined Gibbs/Metropolis algorithm can be used to sample parental structure and GP hyperparameters, respectively (CSI-Gibbs; Supplementary Section 1.3). Finally, a distribution over causal network structures, ℙ( ), can be assembled from the distribution over individual parental sets, constituting the CSI algorithm:
), can be assembled from the distribution over individual parental sets, constituting the CSI algorithm:
| (5) |
2.1 Hierarchical modelling for CSI
The CSI framework outlined above can readily be extended to the type of hierarchical learning used by Werhli and Husmeier (2008), with the notable advantage of being able to correctly deal with time series data. In this framework, the joint distribution for all model parameters conditioned on the data is factorised as:
 |
where  ={
={ 1,…,
1,…,  d} represents the d datasets with
d} represents the d datasets with  j={Xj, yj} the input/output mRNA expression level for the jth dataset (defined as for the standard CSI approach),
j={Xj, yj} the input/output mRNA expression level for the jth dataset (defined as for the standard CSI approach),  aj(i) the parents of gene i in dataset j,
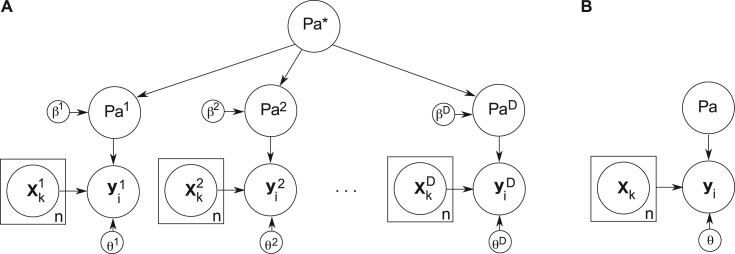
aj(i) the parents of gene i in dataset j,  a*(i) the constraining hyperparents of gene i, Θ={θ1,…, θd} the hyperparameters of the GP priors, and β={β1,…, βd} an additional hyperparameter controlling the influence of the individual parents upon the hyperparents and vice versa. The hierarchical CSI model can be represented graphically in Figure 1A (compare with the graphical model for the standard CSI in Fig. 1B).
a*(i) the constraining hyperparents of gene i, Θ={θ1,…, θd} the hyperparameters of the GP priors, and β={β1,…, βd} an additional hyperparameter controlling the influence of the individual parents upon the hyperparents and vice versa. The hierarchical CSI model can be represented graphically in Figure 1A (compare with the graphical model for the standard CSI in Fig. 1B).
Fig. 1.
Graphical model representation of the CSI framework for node i. (A) In the hierarchical framework, a network structure,  aj, is inferred for each of the D datasets, with each possessing a unique hyperparameter θj for the system dynamics, where j={1,…, D}. The structure of the hypernetwork,
aj, is inferred for each of the D datasets, with each possessing a unique hyperparameter θj for the system dynamics, where j={1,…, D}. The structure of the hypernetwork,  a*, is also inferred along with a set of hyperparameters βj controlling the influence of the individual parents on the hypernetwork. When βi=0 the hypernetwork is independent of the ith network, while βi≫0 induces a strong coupling between the ith parent and hypernetwork. (B) Inference using the standard CSI algorithm identifies a parent structure,
a*, is also inferred along with a set of hyperparameters βj controlling the influence of the individual parents on the hypernetwork. When βi=0 the hypernetwork is independent of the ith network, while βi≫0 induces a strong coupling between the ith parent and hypernetwork. (B) Inference using the standard CSI algorithm identifies a parent structure,  a, for the union of all datasets, as well as the hyperparameter, θ, for the GP model of the system dynamics
a, for the union of all datasets, as well as the hyperparameter, θ, for the GP model of the system dynamics
The conditional distribution ℙ( j|
j| aj(i), θj) represents the probability of the ith gene in the jth dataset, given the parental set
aj(i), θj) represents the probability of the ith gene in the jth dataset, given the parental set  aj:
aj:
| (6) |
and can be calculated using equation (2). The conditional distribution for the parents of gene i in dataset j given the hyperparent is chosen to correspond to a Gibbs distribution:
| (7) |
where ||·|| represents the Hamming distance between parental structures and  represents a normalizing constant:
represents a normalizing constant:
| (8) |
which can be calculated explicitly by summing over all possible parental sets. The parameter βj represents the inverse temperature such that βj=0 allows the parental structure in the jth dataset to be independent of the hyperparent, while βj≫0 induces a strong dependence between the hyperparent and parental structure. Conceptually, the parameter βj can be interpreted differently according to the context of the hierarchical modelling. When looking at different perturbed networks,  a* can be considered as the average parents in the network, with βj representing how different the network is from the average. Likewise, when inferring orthologous networks,
a* can be considered as the average parents in the network, with βj representing how different the network is from the average. Likewise, when inferring orthologous networks,  a* can instead be thought of as the parents in the ancestral network, with βj representing the evolutionary distance of the organism in dataset j from that network.
a* can instead be thought of as the parents in the ancestral network, with βj representing the evolutionary distance of the organism in dataset j from that network.
The distributions ℙ(θj) and ℙ(βj) represent prior distributions over the hyperparameters of the model, and are chosen to correspond to independent Gamma distributions. For the β parameters, distributions peaked about zero represent prior expectations that the network structures are independent, while distributions peaked about large positive values tend to represent prior expectations that the networks are strongly similar. Finally, the distribution ℙ( a*(i)) represents the prior distribution over hyperparent structures, and will generally be unknown and thus set to be uniform over all combinations.
a*(i)) represents the prior distribution over hyperparent structures, and will generally be unknown and thus set to be uniform over all combinations.
Inference within the hCSI model consists of inferring parental structure, hyperparent structure, GP hyperparameters and inverse temperature hyperparameters for each node in the network. Although exact inference is not possible, samples can be generated using using Markov chain Monte Carlo (MCMC) via Gibbs sampling of parents/hyperparents, alongside Metropolis updates of hyperparameters (hCSI-Gibbs; Supplementary Section 2.1), or using Metropolis–Hastings update of parents/hyperparents and Metropolis updates of hyperparameters (hCSI-MH; Supplementary Section 2.2). Again, a network structure can be assembled from the parent distributions for each node, with a hypernetwork assembled from the the distributions over hyperparents:
 |
(9) |
3 RESULTS
Since there is typically no way of knowing a priori how similar or dissimilar two networks might be, we first benchmark the hCSI approach using two extreme cases that could feasibly occur in biological data. In Section 3.1, we gauge the performance of CSI/hCSI in recovering network structures when data was generated from identical networks albeit with perturbed dynamics, as might be encountered when dealing with identical conditions in different individuals, or when observing identical processes over different time scales. In Section 3.2, we benchmark the performance of the algorithm when data is generated from independent networks. Finally, in Section 3.3, we use hCSI and yeast one-hybrid data alongside a variety of time series gene expression datasets to identify potential transcriptional switches in the stress response of A. thaliana.
3.1 Modelling of in silico time series from identical networks
The hCSI algorithm was first benchmarked using the DREAM4 10-gene in silico datasets (Marbach et al., 2009, 2010, Prill et al., 2010). The datasets consist of five independent networks, each of which was used to generate five simulated time series under different initial conditions (hereafter referred to as perturbations), using stochastic differential equations. Since the true network structure was known, the ability of hCSI to recover network topologies could be evaluated using the the receiver operating characteristic curve (ROC) and the precision-recall (PR) curve as used in Penfold and Wild (2011). Specifically, the ROC curve plots the false-positive rate (FP/FP + TN) versus the true positive rate (TP/TP + FN), whereas the precision recall curve plots precision/positive predictive value (TP/TP + FP) versus the true positive rate, where FP, FN, TP and TN refers to the number of false positives, false negatives, true positives and true negatives, respectively. The overall performance of the algorithm could then be gauged using the areas under the ROC and PR curves. Benchmarking of the algorithms proceeded as follows. For a given dataset with five perturbation, a separate GRN was inferred from each of the perturbations using hCSI (hCSI-Gibbs and hCSI-MH), with constraining hyperparents linking the five perturbations. Performance was measured against the standard CSI algorithm [EM (Klemm, 2008), and MCMC implementations] run individually on each of the five perturbations. The results are summarized in Table 1.
Table 1.
Average AUROC and average AUPR with standard deviation shown in brackets to three decimal places for the 10 gene DREAM4 networks with and without a hypernetwork constraints
| Dataset | Pert(s). | AUROC |
AUPR curve |
||||
|---|---|---|---|---|---|---|---|
| hCSI-Gibbs | hCSI-MH | CSI-Gibbs | hCSI-Gibbs | hCSI-MH | CSI-Gibbs | ||
| 1 | 1 | 0.70 (0.014) | 0.70 (0.019) | 0.66 (0.005) | 0.46 (0.019) | 0.44 (0.036) | 0.36 (0.011) |
| 2 | 0.69 (0.023) | 0.69 (0.023) | 0.65 (0.006) | 0.35 (0.020) | 0.34 (0.028) | 0.26 (0.004) | |
| 3 | 0.65 (0.010) | 0.66 (0.016) | 0.64 (0.004) | 0.34 (0.011) | 0.35 (0.030) | 0.27 (0.024) | |
| 4 | 0.58 (0.010) | 0.58 (0.020) | 0.53 (0.004) | 0.21 (0.028) | 0.20 (0.031) | 0.16 (0.002) | |
| 5 | 0.73 (0.013) | 0.73 (0.021) | 0.72 (0.005) | 0.28 (0.024) | 0.30 (0.036) | 0.28 (0.009) | |
| 2 | 1 | 0.72 (0.011) | 0.72 (0.019) | 0.68 (0.006) | 0.44 (0.013) | 0.43 (0.022) | 0.32 (0.006) |
| 2 | 0.72 (0.010) | 0.72 (0.017) | 0.71 (0.003) | 0.46 (0.009) | 0.46 (0.019) | 0.34 (0.016) | |
| 3 | 0.66 (0.010) | 0.66 (0.019) | 0.62 (0.004) | 0.35 (0.014) | 0.35 (0.030) | 0.26 (0.002) | |
| 4 | 0.73 (0.012)}a | 0.73 (0.015) | 0.74 (0.005) | 0.47 (0.011) | 0.46 (0.018) | 0.43 (0.003) | |
| 5 | 0.67 (0.012) | 0.67 (0.018) | 0.61 (0.005) | 0.33 (0.014) | 0.32 (0.024) | 0.24 (0.007) | |
| 3 | 1 | 0.76 (0.012) | 0.75 (0.015) | 0.70 (0.004) | 0.35 (0.027) | 0.35 (0.032) | 0.29 (0.003) |
| 2 | 0.76 (0.012) | 0.75 (0.019) | 0.69 (0.004) | 0.42 (0.015) | 0.40 (0.022) | 0.33 (0.015) | |
| 3 | 0.78 (0.008) | 0.76 (0.016) | 0.72 (0.004) | 0.36 (0.024) | 0.36 (0.034) | 0.26 (0.004) | |
| 4 | 0.75 (0.012) | 0.74 (0.019) | 0.69 (0.007) | 0.34 (0.013) | 0.32 (0.036) | 0.27 (0.005) | |
| 5 | 0.73 (0.010) | 0.72 (0.014) | 0.67 (0.004) | 0.45 (0.019) | 0.43 (0.025) | 0.36 (0.005) | |
| 4 | 1 | 0.75 (0.009) | 0.76 (0.015) | 0.71 (0.005) | 0.48 (0.014) | 0.48 (0.028) | 0.46 (0.015) |
| 2 | 0.74 (0.010) | 0.74 (0.018) | 0.65 (0.005) | 0.45 (0.017) | 0.45 (0.029) | 0.38 (0.008) | |
| 3 | 0.72 (0.011) | 0.72 (0.016) | 0.67 (0.005) | 0.43 (0.015) | 0.42 (0.025) | 0.33 (0.005) | |
| 4 | 0.72 (0.009) | 0.72 (0.015) | 0.64 (0.005) | 0.45 (0.013) | 0.44 (0.019) | 0.37 (0.005) | |
| 5 | 0.80 (0.011) | 0.80 (0.020) | 0.76 (0.006) | 0.52 (0.020) | 0.50 (0.037) | 0.41 (0.017) | |
| 5 | 1 | 0.79 (0.009) | 0.80 (0.014) | 0.74 (0.003) | 0.51 (0.020) | 0.51 (0.030) | 0.33 (0.015) |
| 2 | 0.82 (0.006) | 0.82 (0.014) | 0.79 (0.003) | 0.54 (0.013) | 0.54 (0.025) | 0.42 (0.005) | |
| 3 | 0.84 (0.008) | 0.83 (0.014) | 0.78 (0.003) | 0.43 (0.012) | 0.43 (0.028) | 0.31 (0.006) | |
| 4 | 0.87 (0.005) | 0.88 (0.013) | 0.82 (0.004) | 0.52 (0.029) | 0.53 (0.055) | 0.28 (0.005) | |
| 5 | 0.84 (0.010) | 0.83 (0.021) | 0.75 (0.006) | 0.53 (0.012) | 0.53 (0.034) | 0.37 (0.020) | |
An independent Gamma prior is placed over each of the Gaussian process hyperparameters θ~Γ(10, 0.1). For inference with hypernetworks, an independent Gamma prior is placed over the individual temperature parameters, β~Γ(1, 1). Values in bold indicate the score is both statistically significantly different from that achieved using a standard CSI-Gibbs (third and sixth columns) algorithm according to a Wilcoxon rank-sum test (P<0.01), and shows improved performance.
aCases marked indicate scores that were both statistically significantly different and showed worse performance in the hierarchical modelling compared with the standard implementation.
In all experiments, six chains of 100 000 samples were generated for hCSI-Gibbs and hCSI-MH discarding 10 000 each for burn-in, with three chains of 200 000 generated for CSI-Gibbs, allowing 20 000 steps for burn-in. MCMC chains were binned into groups of 10 000 samples, with AUROC/AUPR scores calculated for each bin, resulting in 54 bootstrapped estimates for the AUROC/AUPR. Significant differences in AUROC/AUPR scores could then be gauged using a Wilcoxon rank-sum test.
As expected, the performance of the hierarchal model, in terms of the area under the ROC (AUROC) curve, and area under the PR (AUPR) curve, appears to be generally better than for the EM or Gibbs implementation of CSI. In 48 out of 50 cases, both hCSI-Gibbs and hCSI-MH had an AUROC statistically significantly different from the standard CSI-Gibbs, according to a Wilcoxon rank-sum test (P<0.01). {For hCSI-Gibbs, only 1 of the 49 statistically significantly different scores showed worse performance than CSI-Gibbs, whereas there were no cases where hCSI-MH performed worse.} Additionally, hCSI-Gibbs has a AUPR score statistically significantly different from CSI-Gibbs in 49 out of 50 cases, whereas hCSI-MH was statistically significantly different in all 50 cases. It should be noted that in all cases where there was a statistically significant difference the mean AUROC/AUPR was greater in the hierarchical modelling. Although these results are perhaps not surprising (the hierarchical implementation was allowed to propagate information between several experimental perturbations via the hyperparents, whereas the standard EM and Gibbs implementation of CSI learnt separately form individual perturbations), they do illustrate that, when the networks used to generate time series datasets are identical, learning jointly from multiple perturbations is preferable to learning individually on each perturbation.
3.2 Modelling of in silico time series from independent networks
The results in Section 3.1 demonstrate that the hCSI framework can prove useful when the individual datasets are generated from identical networks, by allowing propagation of information via the hyperparents. In some situations, however, the generating networks could be dramatically different in the different perturbations. In these cases, it is possible that a constraining hypernetwork could prove detrimental to the accuracy of network reconstruction. A second set of experiments is designed to test whether the presence of a constraining hypernetwork would negatively impact on the accuracy of the algorithm when the generating networks were independent. In this example, two of the (independent) DREAM4 datasets (each using all five perturbations) were used to infer a GRN, with a constraining hypernetwork. Again, the performance in terms of AUROC and AUPR is compared with situations where no constraining hypernetworks exist (Table 2). MCMC samples were again binned into sets of 1000 samples, allowing the distribution of the AUROC/AUPR scores to be compared using a Wilcoxon rank-sum test.
Table 2.
Average AUROC and average AUPR with standard deviation shown in brackets to three decimal places for the 10 gene DREAM4 networks with and without a hypernetwork constraints
| Dataset | Pert(s). |
AUROC |
AUPR curve |
||||
|---|---|---|---|---|---|---|---|
| hCSI-Gibbs | hCSI-MH | CSI-Gibbs | hCSI-Gibbs | hCSI-MH | CSI-Gibbs | ||
| 1 & 2 | 1−5 | 0.77 (0.009) | 0.77 (0.014)a | 0.78 (0.006) | 0.55 (0.008) | 0.55 (0.013) | 0.55 (0.006) |
| 1−5 | 0.77 0.009) | 0.77 (0.015)a | 0.78 (0.008) | 0.60 (0.005) | 0.60 (0.011) | 0.60 (0.007) | |
| 1 & 3 | 1−5 | 0.77 (0.009) | 0.77 (0.015) | 0.78 (0.006) | 0.54 (0.006)a | 0.55 (0.011) | 0.55 (0.006) |
| 1−5 | 0.71 (0.009) | 0.72 (0.019) | 0.70 (0.004) | 0.52 (0.006)a | 0.52 (0.010)a | 0.53 (0.003) | |
| 1 & 4 | 1−5 | 0.78 (0.011) | 0.78 (0.018) | 0.78 (0.006) | 0.55 (0.007) | 0.55 (0.012) | 0.55 (0.006) |
| 1−5 | 0.76 (0.013) | 0.76 (0.020) | 0.76 (0.008) | 0.62 (0.016) | 0.62 (0.035) | 0.62 (0.008) | |
| 1 & 5 | 1−5 | 0.78 (0.011) | 0.77 (0.015) | 0.78 (0.006) | 0.55 (0.008) | 0.55 (0.012) | 0.55 (0.006) |
| 1−5 | 0.87 (0.012) | 0.87 (0.017)a | 0.88 (0.008) | 0.71 (0.018) | 0.72 (0.022) | 0.72 (0.019) | |
| 2 & 3 | 1−5 | 0.78 (0.008) | 0.78 (0.015) | 0.78 (0.008) | 0.60 (0.006) | 0.60 (0.011) | 0.60 (0.007) |
| 1−5 | 0.71 (0.008) | 0.71 (0.016) | 0.70 (0.004) | 0.53 (0.005) | 0.52 (0.011) | 0.53 (0.003) | |
| 2 & 4 | 1−5 | 0.78 (0.009) | 0.78 (0.018) | 0.78 (0.008) | 0.60 (0.007) | 0.60 (0.013) | 0.60 (0.007) |
| 1−5 | 0.76 (0.013) | 0.76 (0.022) | 0.76 (0.008) | 0.62 (0.013) | 0.62 (0.036) | 0.62 (0.008) | |
| 2 & 5 | 1−5 | 0.78 (0.010) | 0.78 (0.017) | 0.78 (0.008) | 0.60 (0.006) | 0.60 (0.010) | 0.60 (0.007) |
| 1−5 | 0.87 (0.013) | 0.87 (0.014)a | 0.88 (0.008) | 0.71 (0.017) | 0.72 (0.021) | 0.72 (0.019) | |
| 3 & 4 | 1−5 | 0.71 (0.010) | 0.72 (0.013) | 0.70 (0.004) | 0.53 (0.008) | 0.52 (0.013)a | 0.53 (0.003) |
| 1−5 | 0.77 (0.014) | 0.76 (0.019) | 0.76 (0.008) | 0.62 (0.015) | 0.62 (0.028) | 0.62 (0.008) | |
| 3 & 5 | 1−5 | 0.70 (0.010) | 0.71 (0.015) | 0.70 (0.004) | 0.53 (0.006) | 0.52 (0.013) | 0.53 (0.003) |
| 1−5 | 0.87 (0.010) | 0.87 (0.014) | 0.88 (0.008) | 0.71 (0.015) | 0.72 (0.021) | 0.72 (0.019) | |
| 4 & 5 | 1−5 | 0.76 (0.014) | 0.75 (0.018)a | 0.76 (0.008) | 0.62 (0.015) | 0.62 (0.028) | 0.62 (0.008) |
| 1−5 | 0.88 (0.013) | 0.87 (0.012) | 0.88 (0.008) | 0.72 (0.016) | 0.72 (0.019) | 0.72 (0.019) | |
An independent Gamma prior is placed over each of the Gaussian process hyperparameters θ~Γ(10, 0.1). For inference with hypernetworks, an independent Gamma prior is placed over the individual temperature parameters, β~Γ(1, 1). Values in bold indicate the score is both statistically significantly different from than that achieved using a standard CSI-Gibbs algorithm (third and sixth columns) according to a Wilcoxon rank-sum test (P<0.01), and shows improved performance.
aCases marked indicate scores that were both statistically significantly different and showed worse performance in the hierarchical modelling compared with the standard implementation.
When networks are independent, the hierarchical modelling still appeared to perform well in reconstructing the network topology, with AUROC/AUPR scores better than expected for randomly generated networks, and with performance competitive with standard CSI approaches using the individual network datasets. In 14 out of 20 cases, the AUROC scores using independent hCSI-Gibbs runs were not statistically significantly different from that achieved using CSI-Gibbs according to a standard Wilcoxon rank-sum test (P<0.01). Of the remaining six cases, three performed marginally better in the hierarchical model and three appeared to be statistically significantly different only due to an increased variance or altered skewness. For hCSI-Gibbs, the AUPR was not statistically different from CSI-Gibbs in 15 cases. In the five remaining cases, the AUPR was worse in the hierarchical modelling in two cases and possessed the same mean value in three, albeit with greater variance. In situations where the distributions were statistically different, the absolute differences tended to be very small. A similar observation seen when comparing CSI-Gibbs with hCSI-Gibbs, where AUROC/AUPR are statistically significantly different in 7 and 13 cases, respectively.
3.3 Combining hierarchical modelling and yeast one-hybrid to identify transcriptional switches in A. thaliana
Yeast one-hybrid (Y1H) screens can be used to identify which TFs in a library are capable of binding the promoter region of a particular gene (Lopato et al., 2006). However, Y1H only identifies which TFs are capable of binding in yeast, and not necessarily those that are binding in a particular condition. Additionally, TFs may be missing from the library, which, combined with false negatives, means that identification of potential upstream TFs is likely to be incomplete. Conversely, false positives will result in spurious connections. In these cases, combining Y1H screens along with time series gene expression data might help determine which particular genes are binding in a given experiment. Since the CSI algorithm infers the upstream connections of a particular gene on a node-by-node basis, we have previously suggested that the method would make an ideal partner to Y1H experiments (Penfold and Wild, 2011).
In this study we use hCSI to identify the role played by the gene RD29A and upstream TFs in abiotic stress responses. RD29A contains both a dehydration-responsive element (DRE) and an ABA-responsive element (ABRE), and has previously shown to be differentially expressed in response to dehydration, low temperature and high salt (Yamaguchi-Shinozaki and Shinozaki, 1994). Y1H screens by Mitsuda et al. (2010) have identified nine proteins capable of binding the promoter region of RD29A, whereas non-Y1H studies by Tsutsui et al. (2009) further suggest that a DREB-family protein, CEJ1/DEAR1, might also be upstream of RD29A. Using hCSI-MH, we infer which genes were upstream of RD29A using time series gene expression data from a variety of experimental conditions, including:
Time series containing six time points (0, 2, 5 15, 30 and 60 min) and two biological replicates detailing A. thaliana response to gravity stimulation via rotation at 135○ (Kimbrough et al., 2004),
The AtGenExpress abiotic datasets, containing nine small timeseries (6–7 time points, 2 replicates, 2 tissue types) in detailing plant responses to cold, drought, wounding, osmotic stress, salt stress, genotoxic and oxidative stress heat stress, and UV-B exposure (Kilian et al., 2007),
An AtGenExpress biotic dataset detailing A.thaliana response to Golvinomyces orontii (8 time points, 3 replicates) available from http://affymetrix.arabidopsis.info/ (NASCARRAYS-169).
In total six chains of 50 000 samples were generated using hCSI-MH, with 10 000 samples discarded for burn-in in each run. In all cases, the hyperparents were fixed, corresponding to the set containing all 9 TFs (CEJ1, DREB1A, DREB1B, DREB1D, HRD, OBP2, At4G16750, At1G71450, At5G52020), representing a prior in which all prospective parents were upstream simultaneously in all datasets. The marginal probabilities of a given parent being upstream of RD29A in a given experiment could be represented in the form of a heat map (Figure 2A).
Fig. 2.
(A). Heat map indicating the probability of TFs influencing RD29A expression. Here, dark blue indicates a low probability of that TF being influential in the time series expression dataset, whereas dark red indicates a high probability of the TF being influential. (B). Inferred temperature parameters for each of the experiments compared with samples generated from the prior distribution of temperature. (C). Unsigned stress signalling network adapted from Tsutsui et al. (2009). Here question marks indicate speculative or indirect links that have not been verified via Y1H
RD29A appeared to be expressed above baseline in all datasets except for the gravity stimulation and G. orontii infection datasets, where expression was flat. Since these datasets were therefore uninformative, we would expect the distribution over parental sets to correspond to the prior distribution, that is, with all parents simultaneously upstream in those two datasets. This was indeed observed, with all prospective TFs showing high probabilities of being upstream in the gravity stimulation and G. orontii datasets (vertical red/orange columns in the colour map). Indeed, for these datasets, the posterior distribution over the temperature parameter appears to be similar to that of the prior distribution over the temperature parameter (Figure 2B).
Of the remaining nine datasets, six showed dynamic RD29A expression in that the expression varied over time (non-flat profiles), but not with respect to the appropriate control experiments (not differentially expressed). Again, for the majority of these conditions, the posterior distribution over the temperature parameter appeared to be similar to that of the prior, suggesting relatively uninformative datasets for that subset of genes. Here, dynamic expression profiles were determined by fitting an independent GP to the expression data and identifying the times at which the gradient was significantly non-zero, that is, the zero point was more than 2 SDs from the posterior GP derivative (Breeze et al., 2011), whereas differential expression was gauged using the GP two-sample method of Stegle et al. (2010). Finally, three datasets, cold, osmotic and salt stress, demonstrated both dynamic behaviour and differential expression of RD29A compared with control. For the cold and osmotic stress datasets, the distribution over the temperature parameter appears to be shifted towards the origin, suggesting that the datasets contain information that differs from the prior hypernetwork.
Under cold stress, RD29A appeared to be primarily influenced by CEJ1/DEAR1 and DREB1A, with lower probabilities of other DREB TFs binding (DREB1B/D), and relatively little evidence of other TFs influencing expression. This observation appears consistent with the network model of Tsutsui et al. (2009), in which freezing tolerance is dependent on RD29A acting downstream of CEJ1 and DREB1 TFs (Figure 2C). It is interesting to note that CEJ1 appears to be less influential in the osmotic stress dataset, with other DREB-family proteins, AT4G16750, DREB1A and HRD, appearing to be drive RD29A expression. Potentially, this group of genes might play an important role in distinguishing between cold and osmotic stress with both common (e.g. RD29A) and stress-specific targets downstream of CEJ1 and AT4G16750/HRD, respectively (Figure 2C).
4 DISCUSSION
Recent approaches for reverse engineering GRNs make use of nonparametric Bayesian methods (Äijö and Lähdesmäki, 2009; Klemm, 2008) and have proven competitive with other approaches (Äijö and Lähdesmäki, 2009; Penfold and Wild, 2011). A key advantage of these nonparametric approaches is their ability to learn from multiple experimental perturbations. To do so, however, these methods must make assumptions about the number of TFs that can bind any given gene, and further assume that each of the time series (perturbations) were generated from an identical network. These assumptions do not appear to hold in vivo, where large numbers of TFs can bind, albeit with different subsets likely acting under different perturbations/conditions. To address these limitations, we have used a hierarchical modelling framework that that should be applicable to a variety of novel situations including:
Modelling GRNs under different experimental conditions, different tissues or ecotypes, where different but overlapping sets of transcription factors are expected to bind in the different treatments, with a limited number of TFs binding under any given condition/tissue/ecotype.
Modelling of orthologous networks in evolutionary-related species, where orthologous genes are expected to form similar (but non-identical) networks. In these situations, the hyperparent can be interpreted as the network structure of a common ancestor, with the individual temperature parameters representing evolutionary distance from the common ancestor.
For leveraging multiple sources of (potentially contradictory) prior information, such as competing network structures, similar to the use in Werhli and Husmeier (2007).
Finally, a particularly promising extension of such hierarchical modelling is to include multiple sources of data besides standard time series microarary expression data. Notable examples could include leveraging next-generation sequencing time series alongside microarray data, or the inclusion of protein/metabolite abundance. Additionally, given appropriate statistical models, this type of learning could readily incorporate promoter sequence information into the network inference.
Benchmarking of the hierarchical method on in silico datasets demonstrates that the method generally outperforms the standard CSI algorithm, by allowing propagation of information via the hypernetwork. Additionally, experiments using data generated from independent networks have shown the hierarchical approach performs no worse than the standard CSI run on the independent datasets, suggesting the temperature hyperparameters correctly distinguish between datasets with similar structure, and those with independent structures. These findings suggest that hierarchical modelling is particularly useful in biological systems where it is not known ahead of time if networks in different conditions/species are identical, and which would previously have to have been treated as independent.
A major limitation with the standard CSI approach lies in its computational scaling, requiring the evaluation of a GP model for each of the parental set combinations, the number of which scales either factorially or polynomially (with fan-in restrictions) with the number of prospective transcription factors. The Gibbs implementation of CSI and Gibbs implementation of hCSI unfortunately inherit these same scaling issues, making them useful for small systems of genes, but less so for much larger systems. To tackle these issues of continuously evaluating GP models for unlikely parental sets, we have additionally implemented a Metropolis–Hastings version of hCSI, that should allow for hierarchical inference in larger systems involving hundreds or thousands of genes. For the small 10 gene DREAM4 networks, inference using the standard CSI-EM approach typically takes less than a minute, whereas 100 000 samples using CSI-Gibbs, hCSI-Gibbs and hCSI-MH takes several hours per node.
Another key benefit of the CSI approach lies in its ability to infer upstream interactions on a node-by-node basis, making it an ideal theoretical method for leveraging Y1H screens. The hierarchical implementation of CSI is similarly amenable to incorporating the results from Y1H screens, and in particular could be of great use in identifying under which conditions a particular TF binds. In this study, we have used a simple A. thaliana stress response network to investigate this possibility. Our results show agreement with literature-based results in identifying genes important for cold tolerance, and have suggested additional genes that might be involved in other abiotic response (with CEJ1 and RD29A at the core). {Besides Y1H, a number of experimental approaches exist for identifying prospective relationships between transcription factors and promoter sequences, including ChIP-chip/Seq (Park, 2009) and bacterial one-hybrid (B1H) systems (Bulyk, 2005), and indirect approaches such as gene knockouts or overexpression. Additionally, TF databases and computational methods can also be used to identify putative TF binding sites (Cooke et al., 2009; Matys et al., 2003; Roth et al., 1998). In light of the increasing availability of such sets of data, the combination of putative TF/promoter interactions and time series gene expression data within a hierarchical modelling framework should prove to be a powerful approach for generating novel biological predictions and hypotheses regarding transcriptional networks, facilitating greater insight into biological responses and more targeted interventions.
ACKNOWLEDGEMENTS
We thank Zoubin Ghahramani for helpful comments and discussion.
Funding: This work was supported by the BBSRC [grant BB/F005806/1] (Elucidating Signalling Networks in Plant Stress Responses); C.A.P., V.B.-W., K.J.D. and D.L.W.) and EPSRC [grant EP/I036575/1] (Advanced Bayesian Computation for Cross-Disciplinary Research; D.L.W.)
Conflict of Interest: none declared.
Footnotes
1Plant response to environmental stress in Arabidopsis thaliana (PRESTA) homepage: http://www2.warwick.ac.uk/fac/sci/lifesci/research/presta
REFERENCES
- Äijö T., Lähdesmäki H. Learning gene regulatory networks from gene expression measurements using non-parametric molecular kinetics. Bioinformatics. 2009;25:2937–2944. doi: 10.1093/bioinformatics/btp511. [DOI] [PubMed] [Google Scholar]
- Baumbach J., et al. Reliable transfer of transcriptional gene regulatory networks between taxanomically related organisms. BMC Bioinformatics. 2009;3 doi: 10.1186/1752-0509-3-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breeze E., et al. High resolution temporal profiling of transcripts during Arabidopsis leaf senescence reveals a distinct chronology of processes and regulation. Plant Cell. 2011;23:873–894. doi: 10.1105/tpc.111.083345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bulyk M.L. Discovering DNA regulatory elements with bacteria. Nat. Biotechnol. 2005;23:942–944. doi: 10.1038/nbt0805-942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooke E., et al. Computational approaches to the integration of gene expression, chip-chip and sequence data in the inference of gene regulatory networks. Semin. Cell Dev. Biol. 2009;20:863–868. doi: 10.1016/j.semcdb.2009.08.004. [DOI] [PubMed] [Google Scholar]
- Goda H., et al. The atgenexpress hormone and chemical treatment data set: experimental design, data evaluation, model data analysis and data access. Plant J. 2011;55:526–542. doi: 10.1111/j.0960-7412.2008.03510.x. [DOI] [PubMed] [Google Scholar]
- Kilian J., et al. The atgenexpress global stress expression data set: protocols, evaluation and model data analysis of uv-b light, drought and cold stress responses. Plant J. 2007;50:347–363. doi: 10.1111/j.1365-313X.2007.03052.x. [DOI] [PubMed] [Google Scholar]
- Kimbrough J.M., et al. The fast and transient transcriptional network of gravity and mechanical stimulation in the arabidopsis root apex. Plant Physiol. 2004;136:2790–2805. doi: 10.1104/pp.104.044594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klemm S.L. Master's thesis. UK: Department of Engineering, University of Cambridge; 2008. Causal Structure Identification in Nonlinear Dynamical Systems. [Google Scholar]
- Liu Y., et al. Temporal graphical models for cross-species gene regulatory network discovery. J. Bioinform. Comput. Biol. 2011;9:231–250. doi: 10.1142/s0219720011005525. [DOI] [PubMed] [Google Scholar]
- Lopato S., et al. Isolation of plant transcription factors using a modified yeast one-hybrid system. Plant Methods. 2006;2 doi: 10.1186/1746-4811-2-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marbach D., et al. Generating realistic in silico gene networks for performance assessment of reverse engineering methods. J. Comput. Biol. 2009;16:229–239. doi: 10.1089/cmb.2008.09TT. [DOI] [PubMed] [Google Scholar]
- Marbach D., et al. Revealing strengths and weaknesses of methods for gene network inference. Proc. Natl. Acad. Sci. USA. 2010;107:6286–6291. doi: 10.1073/pnas.0913357107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matys V., et al. TRANSFAC: transcriptional regulation, from patterns to profiles. Nucleic Acid Res. 2003;31:374–378. doi: 10.1093/nar/gkg108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitsuda N., et al. Efficient yeast one-/two-hybrid screening using a library composed only of transcription factors inArabidopsis thaliana. Plant Cell Physiol. 2010;51:2145–2151. doi: 10.1093/pcp/pcq161. [DOI] [PubMed] [Google Scholar]
- Ou B., et al. A high-throughput screening system for arabidopsis transcription factors and its application to med25-dependent transcriptional regulation. Mol. Plant. 2011;4:546–555. doi: 10.1093/mp/ssr002. [DOI] [PubMed] [Google Scholar]
- Park P.J. Chip-seq: advantages and challenges of a maturing technology. Nat. Rev. Genet. 2009;10:669–680. doi: 10.1038/nrg2641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Penfold C.A., Wild D.L. How to infer gene networks from expression profiles, revisited. J. R. Soc. Interface Focus. 2011;6:857–870. doi: 10.1098/rsfs.2011.0053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prill R.J., et al. Towards a rigorous assessment of systems biology models: The DREAM3 challenges. PLoS One. 2010;5:e9202. doi: 10.1371/journal.pone.0009202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rasmussen C., Williams C.K.I. Gaussian processes for Machine Learning. 2. Cambridge, USA: MIT Press; 2006. [Google Scholar]
- Roth F.P., et al. Finding dna regulatory motifs within unaligned noncoding sequences clustered by whole-genome mrna quantitation. Nat. Biotechnol. 1998;16:939–945. doi: 10.1038/nbt1098-939. [DOI] [PubMed] [Google Scholar]
- Stegle O., et al. A robust Bayesian two-sample test for detecting intervals of differential gene expression in microarray time series. J. Comput. Biol. 2010;17:355–367. doi: 10.1089/cmb.2009.0175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsutsui T., et al. DEAR1, a transcriptional repressor of DREB protein that mediates plant defense and freezing stress responses in Arabidopsis. J. Plant Res. 2009;122:633–643. doi: 10.1007/s10265-009-0252-6. [DOI] [PubMed] [Google Scholar]
- Werhli A.V., Husmeier D. Reconstructing gene regulatory networks with Bayesian networks by combining expression data with multiple sources of prior knowledge. Stat. Appl. Genet. Molec. Biol. 2007;6 doi: 10.2202/1544-6115.1282. Article 15. [DOI] [PubMed] [Google Scholar]
- Werhli A.V., Husmeier D. Gene regulatory network reconstruction by Bayesian integration of prior knowledge and/or different experimental conditions. J. Bioinform. Comput. Biol. 2008;6:543–572. doi: 10.1142/s0219720008003539. [DOI] [PubMed] [Google Scholar]
- Yamaguchi-Shinozaki K., Shinozaki K. A novel cis-acting element in an arabidopsis gene is involved in responsiveness to drought, low-temperature, or high-salt stress. Plant Cell. 1994;6:251–264. doi: 10.1105/tpc.6.2.251. [DOI] [PMC free article] [PubMed] [Google Scholar]