Minimum message length inference of secondary structure from protein coordinate data

Abstract

Motivation: Secondary structure underpins the folding pattern and architecture of most proteins. Accurate assignment of the secondary structure elements is therefore an important problem. Although many approximate solutions of the secondary structure assignment problem exist, the statement of the problem has resisted a consistent and mathematically rigorous definition. A variety of comparative studies have highlighted major disagreements in the way the available methods define and assign secondary structure to coordinate data.

Results: We report a new method to infer secondary structure based on the Bayesian method of minimum message length inference. It treats assignments of secondary structure as hypotheses that explain the given coordinate data. The method seeks to maximize the joint probability of a hypothesis and the data. There is a natural null hypothesis and any assignment that cannot better it is unacceptable. We developed a program SST based on this approach and compared it with popular programs, such as DSSP and STRIDE among others. Our evaluation suggests that SST gives reliable assignments even on low-resolution structures.

Availability: http://www.csse.monash.edu.au/~karun/sst

Contact: arun.konagurthu@monash.edu (or lloyd.allison@monash.edu)

1 INTRODUCTION

Periodic hydrogen-bonding patterns in globular proteins give rise to elements of secondary structure—helices and sheets. The α-helix and β-sheets were among the first structural motifs predicted from first principles of stereochemistry by Pauling and Corey (1951). We now know these specific motifs are almost ubiquitous across the corpus of known structures. Eventually, other repetitive motifs were also identified, and the alphabet of secondary structures was expanded to include 3₁₀-helix, π-helix, β-turn, γ-turn, Ω-turn and β-bulges, among other minor elements. In what follows, we use the term secondary structure to include both the classical helices and sheets, and other common substructural elements.

Accurate assignment of secondary structure of proteins from coordinate data is an important and a challenging problem (Andersen and Rost, 2009). Secondary structure underpins the architectural organization in proteins. It simplifies the complex atom-level description of proteins and is therefore the key to generation of schematic diagrams of their three dimensional (3D) folding patterns (Lesk and Hardman, 1982; Richardson, 1981). They are central in training methods geared for predicting secondary structure from amino acid sequence (Andersen and Rost, 2009). They form a linchpin to efficient methods for structural comparison and analysis (Kamat and Lesk, 2007; Konagurthu et al., 2008).

Over the last 30 years, many programs were developed to address the problem of assigning secondary structure to protein coordinate data. A broad classification can be made of the assignment strategies: (i) methods that use distance and angle profiles of local fragments; (ii) methods that detect hydrogen bonds between backbone atoms; (iii) methods that use 3D geometry of local fragments; and (iv) methods that approximate the backbone trace with a set of straight lines.

The following reviews some of the major earlier contributions to the literature of this problem. Levitt and Greer (1977) were the first to generate an automatic method for secondary structure assignment, based on distance and dihedral angle profiles of C_α atoms over a sliding window of four residues. P-SEA (Labesse et al., 1997) is another method in this category which assigns secondary structural states using a short C_α distance mask and two C_α dihedral angle criteria. PROSS (Srinivasan and Rose, 1999) proposes an assignment based solely on backbone dihedral angles. Xtlsstr (King and Johnson, 1999) calculates backbone dihedral angles and distances and assigns secondary structural types that would be consistent with interactions of amide-amide groups observed from circular dichroism of a protein in ultraviolet range (Andersen and Rost, 2009). More recently, PALSSE (Majumdar et al., 2005) was designed to delineate protein structure into helices and strands, mainly using distance and torsion angle constraints to identify core elements which are later extended to longer segments. KAKSI (Martin et al., 2005) is based on C_α distances and backbone dihedral angles and designed primarily to show concordance with the manual assignments found in the protein data bank (PDB).

The most popular method in this space is ‘Dictionary of Secondary Structure of Proteins’ (DSSP) developed by Kabsch and Sander (1983). DSSP is based on detecting hydrogen bonds between nitrogen and carbonyl groups along the protein polypeptide chain using a Coulomb approximation of the hydrogen-bond energy function (Andersen and Rost, 2009). Many now consider this method a standard for secondary structural assignment (Martin et al., 2005). Since DSSP was published, several methods have been designed that rely on computing the hydrogen-bond energy between backbone atoms. STRIDE (Frishman and Argos, 1995) is among the successful variants of DSSP which uses a modified hydrogen-bond energy function as well as backbone dihedral angles to compute its assignment. SECSTR (Fodje and Al-Karadaghi, 2002) is another variant which improves the detection and assignment of π-helices which both DSSP and STRIDE have difficulty characterizing (Martin et al., 2005).

There are other methods which assign secondary structure using 3D features in a protein structure. Richards and Kundrot (1988) describe a method, DEFINE-S, to assign secondary structure using local geometry of ideal secondary structures. The P-CURVE (Sklenar et al., 1989) algorithm uses an helicoidal axis approach derived from a series of peptide planes to assign secondary structure. The VoTAP (Dupuis et al., 2004) algorithm relies on Voronoi tessellation of a residue contact map and then matching the contact map profiles to a consensus assignment of secondary structures by methods like DSSP and STRIDE.

In the last category are indirect methods, such as STICK (Taylor, 2001) and PMML (Konagurthu et al., 2011) which work by approximating the C_α spatial trace using a set of lines. These methods seek the best approximation of the protein backbone using piecewise lines. Only as a post-process to this approximation, each line segment is indirectly attributed a secondary structural type based on criteria such as the average rise and pitch of the C_α atoms within the segment. These approaches solve a related yet different problem, namely ‘the best line approximation of the protein chain’.

Consistent with this large number of proposed methods, assignment of secondary structure has been recognized to be an ‘inexact process’ (Cuff and Barton, 1999). Previous comparative studies have highlighted the difficulties of existing programs to assign secondary structure consistently (Andersen and Rost, 2009; Colloc'h et al., 1993; Cuff and Barton, 1999; Martin et al., 2005; Zhang et al., 2008). These disagreements can be major as shown by Colloc'h et al. (1993) where the percentage of agreement between DSSP, DEFINE-S and P-CURVE was only 63% on a residue basis. It has been observed that most disagreements arise in the terminal regions of the assigned secondary structural elements. Reflecting on this problem Robson and Garnier (1986) comment [as quoted by Martin et al. (2005)]: ‘In looking at a model of a protein, it is often easy to recognize helix and to a lesser extent sheet strands, but it is not easy to say whether the residues at the ends of these features be included in them or not. In addition, there are many distortions within such structures so that it is difficult to assess whether this represents merely a distortion, or a break in the structure. In fact, the problem is essentially that helices and sheets in globular proteins lack the regularity and clear definition found in the Pauling and Corey models.’

Given the complexity of the details of individual protein structures, it is not surprising that the secondary structure assignment problem has resisted a mathematically rigorous definition. The effect can be seen in the use of a variety of definitions by the existing tools, although all of them are reasonable. In this study, we describe an approach, SST, to the secondary structure assignment problem using minimum message length (MML) inference (Wallace and Boulton, 1968). Linking statistical inference with data compression, the goal is to communicate losslessly the coordinates of a protein using a two-part message. The first part transmits the secondary structure assignment as a hypothesis about the coordinates. The second-part transmits the details of coordinates not explained by the hypothesis. This gives rise to statistically robust objective function to optimize: find the best hypothesis on the coordinate data that minimizes the total two-part message length.

SST assigns secondary structure segments of the following types: α, 3₁₀ and π-helix (including left-handed versions of all these helices when they occur), sharp turns, β-strands and others (coil). SST in a post-processing step merges consecutive structures where appropriate, and groups all strands of a sheet, identifies β-bulges, to convert the results to a molecular biologist's conventional secondary structure description, and produces a PyMol script to visualize the secondary structural assignments. (Fig. 1.)

Fig. 1.

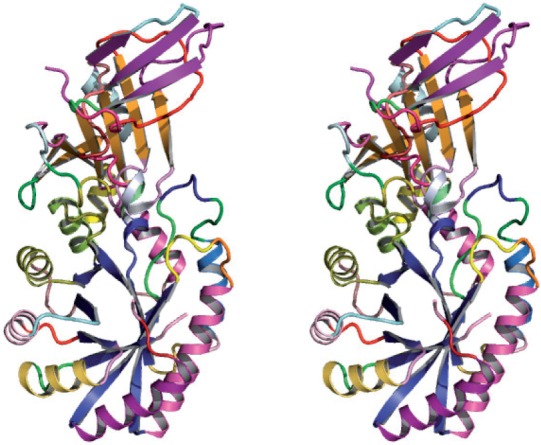
SST assigned secondary structure to coordinates of a 1.6Å crystal structure, Ornithine decarboxylase from mouse.

2 OVERVIEW OF MML CRITERION

The MML criterion provides an information–theoretic objective for problems of inference where the goal is to find the best explanation (or theory, hypothesis, model) for a set of observed data (Wallace and Boulton, 1968). MML relies on quantifying the amount of information required to convey losslessly the observed data in an explanation message. The best hypothesis is the one which can convey the entire data set in the shortest possible explanation message.

More formally, for some observed data D and a hypothesis H that offers an explanation of the data D, Bayes's theorem (Bayes and Price, 1763) gives

where P(H) is the prior probability of hypothesis H, P(D) is the prior probability of data D, P(H|D) is the posterior probability of H given D, and P(D|H) is the likelihood.

Using Shannon's mathematical theory of communication (Shannon, 1948), the amount of information for an explanation of the data D with the hypothesis H is given by

where I(x)=−log₂(P(x)) gives the optimal code length to convey some event x whose probability is P(x).

This immediately gives an objective means to compare competing hypotheses. For hypotheses H₁ and H₂ on the same data D, we have

It follows that the best hypothesis H^* over all competing hypotheses is the one where the expression I(H^*)+I(D|H^*) is minimized.

A concrete realization of the MML framework comes from describing it as a communication process between an imaginary transmitter (Alice) and receiver (Bob) connected over a Shannon channel. Alice's objective is to send the observed data D using an explanation message in a form such that Bob can receive and decode the data D precisely as Alice sees it. Alice and Bob agree on a codebook containing the general rules of communication composed solely of common knowledge about typical, hypothetical data. Anything that is not a part of the codebook must be strictly transmitted as a part of the message. If Alice can find the best hypothesis H^* on the data, Bob will receive a decodable explanation message most economically: The best inference about the data is the hypothesis that minimizes the total message length.

Alice sends the explanation message of D in two parts. In the first part, she transmits the best hypothesis, H^*, she could find on the data D taking I(H^*) bits. In the second, she transmits the details of the observed data D not explained by H^*, taking I(D|H^*) bits (i.e. the deviations from H^*). Notice that MML inference gives a natural trade-off between hypothesis complexity (I(H^*)), and its goodness of fit to the data (I(D|H^*)).

For a comprehensive resource on MML see Wallace (2005).

3 THE DESIGN OF THE COMMUNICATION FRAMEWORK

Protein coordinates for a single-polypeptide chain are represented as an ordered set of 3D points of the form ={p₁,···, p_n}, where any p_i corresponds to the ith C_α coordinate along N- to C-terminus of the protein chain. Each p_i defines a 3D real-valued vector (p_i^x, p_i^y, p_i^z) in Angstrom (Å) units, where each component of the vector comes specified (in the PDB) to three positions after the decimal place. Therefore, in this work, we treat the accuracy of measurement of the data as ϵ=0.001 Å (independent of the actual accuracy of the experimental structure determination). The transmitter (Alice) has to send a message to the receiver (Bob) who will then be able to reconstruct the original data from the encoded explanation message exactly. For coordinate data from the PDB, Bob will reconstruct each coordinate of each atom to the original precision of three digits after the decimal point.

3.1 Null model description of a protein coordinate data

MML gives a natural hypothesis test: The null-model corresponds to transmitting the data raw. If any hypothesis H on the data takes longer than the null model, then clearly H is unacceptable. However, the statement of the raw null model message (without any hypothesis) has to be economical; it must not be willfully inefficient.

The construction of an efficient null model for protein coordinates relies on the observation that the distance between successive C_α atoms in a protein chain is highly constrained at about 3.8Å with only small deviations from this value. The method starts with the transmission of the first C_α coordinate p₁ in any choice of encoding that both transmitter and receiver agree on. (Stating p₁ simply adds a constant overhead to the message length, whether transmitted via a null model message or an explanation using a hypothesis. A simple way to do away with this overhead is for Alice to translate such that p₁ becomes the origin. p₁ then need not be transmitted explicitly in the message and can be treated implicitly a part of the codebook.) Alice then computes the observed distance r between the successive C_α coordinates p₁ and p₂. This distance r can be communicated efficiently using an encoding over a normal distribution 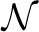(μ, σ) with a certain fixed mean (μ) and a small standard deviation (σ) around it. Based on the prior knowledge of C_α–C_α distances between successive atoms, these values are set to μ=3.8Å and σ=0.4Å and are considered to be part of the codebook.

The probability density of a random variable x over a normal distribution with mean μ and a standard deviation σ is given by:

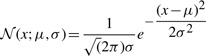Therefore, the probability of stating any distance r to an accuracy of ϵ (given ϵ≪σ) using the above normal distribution is P(r)=ϵ×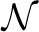(x=r; μ, σ). This implies

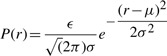The optimal code length to transmit r is given by −log₂(P(r)) bits:

(1)

Note that Bob will not be able to recover p₂ simply from the transmitted information of p₁ and the distance r between p₁ to p₂. p₂ can lie anywhere on the surface of a sphere of radius r centered on p₁. The precise location of p₂ stated to ϵ can be transmitted by first dividing the surface area of this sphere into cells each of area ϵ². This results in 4πr²/ϵ² such cells distributed uniformly on the surface. These cells can be numbered using a convention that Alice and Bob both agree upon (as a part of the codebook). On the basis of this discretization of the sphere's surface area, Alice transmits the cell number c in which the observed p₂ falls within. Assuming uniform probabilities, the probability that the point p₂ falls in a cell number c is given by P(c)=ϵ²/4πr². Following from this, the code length to state the cell number is:

(2)

Bob now has all the information to reconstruct p₂ to the precision of ϵ using the information he has received.

With p₂ known at Bob's end, Alice can proceed to encode in the same fashion p₃ with respect to p₂, then p₄ with respect to p₃ and so on until all the points in are transmitted.

Let r_i (∀1≤i<n) denote the observed distance between any two successive C_α coordinates p_i and p_i+1. Let c_i (∀1≤i<n) denote the cell number on the surface of the sphere of radius r_i centered on the point p_i in which the point p_i+1 falls. The message length to transmit the entire C_α coordinate data in is therefore

(3)

where O(1) denotes the constant number of bits to state p₁ (0 bits if Alice translates the coordinates such that p₁ lies on the origin).

3.2 Models to describe segments of proteins

The secondary structure elements are used as a hypothesis to explain the coordinates. Here, we consider eight models to describe any contiguous stretch of C_α atoms (of arbitrary length) along the protein chain: (i) a right-handed α-helix; (ii) a left-handed α-helix; (iii) a right-handed 3₁₀-helix; (iv) a left-handed 3₁₀-helix; (v) a righ-handed π-helix; (vi) a left-handed π-helix; (vii) an extended β-strand; and (8) coil.

The Helical (1–6) and strand (7) models follow ideal Pauling–Corey geometry (Pauling and Corey, 1951) and are of arbitrary length. We term these seven collectively ideal models. (Pauling–Corey models are common knowledge and taken to be in the codebook.)

The coil model (8) is treated simply as a model that describes a segment of a protein raw, using the null model approach described above in Section 3.1.

3.3 Describing a protein segment using an Ideal model

Assume that at some stage of the transmission Bob has received C_α coordinates up to an intermediate point p_i, that is he has received coordinates (p₁, p₂,···, p_i) (i<n). Alice now will transmit a contiguous segment of coordinates p_i to p_j (1≤i<j≤n) using one of the ideal (helical or strand) models. If it is a good model, then the coordinates can be transmitted cheaply. (The discussion of the optimal choice is given in Section 4.)

The number of points to be transmitted in this segment is j−i since the start point of the segment p_i is already known at the receiver's end. The remaining points p_i+1,···, p_j are transmitted as follows:

3.3.1 Transmitting the end point of the segment

The end point of the segment (p_j) is transmitted using the sphere approach similar to the one described in Section 3.1. Instead of the distance between successive C_α coordinates, Alice transmits the distance d_ij between the start (p_i) and end (p_j) points. This is encoded using a normal distribution where the mean (μ) is taken as the distance (d^*) between the start and end points from the ideal model containing j−i+1 points. The standard deviation σ of the end point is set to min((j−i)×0.2Å, 3Å) based on the length of the segment being transmitted and this rule is taken to be a part of the codebook.

On the basis of Equation 1, the code length to state d_ij to the accuracy of ϵ is given by

(4)

On the basis of equation 2, given the start point of the segment p_i and distance d_ij of the end point p_j, the end point can lie anywhere on a sphere with radius d_ij. p_j can therefore be stated by specifying the cell number c_ij on the surface of this sphere in

(5)

3.3.2 Encoding the interior points

With the start and end points already known, there are j−i−1 interior points of the segment, p_i+1,···, p_j−1, yet to be transmitted. These points can be transmitted cheaply if the chosen ideal model agrees with the observed points in the segment. Alice uses the following procedure to transmit the interior points given a chosen ideal model. (Details of how the optimal choice is made appear in Section 4.)

Consider an ideal model containing l=j−i+1 points, denoted formally as 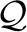={q₁, q₁,···, q_l}. The coordinates in 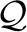are orthogonally transformed to 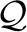^′={q^′₁, q^′₂,···, q^′_l} such that:

1. q^′₁ is same as the start point p_i of the segment;

2. the direction cosines of the vector connecting the start and end points of the ideal model q^′_l−q^′₁ and the direction cosines of the vector connecting the start and end points of the observed segment p_j−p_i are the same; and

3. the sum of the squared error of the (l−2) interior points of the segment with the corresponding interior points of the ideal model is minimized. That is, ∑_{1≤k≤l−2} |p_i+k−q^′_1+k|² is minimized, where |.| denotes the Euclidean vector norm.

Such a spatial transformation is related to the more general superposition problem that minimizes the sum of the squared distance between two corresponding vector sets (Kearsley, 1989). However, the transformation is further constrained such that the first points of the two sets are the same (Constraint 1) and the rotational axis for the ideal model is the vector between the start (p_i) and end (p_j) points of the segment (Constraint 2). The first two constraints can be achieved using elementary translation and rotation of the ideal coordinates.

Once 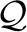is transformed such that the first two constraints are realized, the best rotation θ^* of 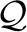about the p_j−p_i axis has to be found so that Constraint 3 is realized. With an approach similar to the generalized superposition problem between two vector sets (Kearsley, 1989), this minimization problem can be solved analytically as an eigenvalue decomposition of a 2×2 square symmetric matrix in quaternion parameters of the corresponding points. (The detailed proof of the analytical method is too long for the main text and hence is provided as Supplementary Material.)

Once the transformation of 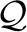to 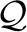^′ is achieved as described above, Alice can transmit the interior points of the segment, p_i+1,···, p_j−1 by:

1. transmitting the best rotation about the p_j−p_i axis of the ideal model. (Note, Bob has already received the start and end points, p_i and p_j.);

2. transmitting the interior points p_i+1··· p_j−1 as spatial deviations from their corresponding transformed interior points of the ideal model. (Bob already knows p_i and the coordinates of 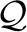of the ideal model from the codebook. After he receives the end point of the segment p_j (using the sphere approach described above), the ideal coordinates can be transformed such that Constraints 1 and 2 of the transformation discussed above are realized. After Bob receives the rotation θ^*, the ideal coordinates are rotated by that angle around the axis p_j−p_i whose information he already has. Once Alice sends the spatial deviations of interior points p_i+1,···, p_j−1 with respect to the transformed ideal coordinates, Bob can reconstruct the observed interior points of the segment.)

3.3.3 Transmitting the rotation

Rotation θ^* is transmitted using a uniform distribution over a circle whose radius r_θ^* is the farthest distance of an interior point of the ideal model from the axis of rotation. Note that r_θ^* need not be transmitted because it is a property of the coordinates of the ideal model which the receiver already knows as a part of the codebook.

The rotation is transmitted by dividing the circumference of a circle of radius r_θ^* into arc segments of length ϵ and stating the segment number in which the rotated coordinate with the farthest radius to the axis falls. Thus, the code length of stating θ^* is

(6)

3.3.4 Transmitting the interior points as spatial deviations

Let any error vector of an interior point of the segment with respect to the corresponding transformed interior point of the ideal model, e_k≡(p_i+k−q^′_1+k), 1≤k≤l−2 have the vector components (Δx_k, Δy_k, Δz_k).

Each Δx, Δy and Δz of an interior point is transmitted using a normal distribution with a μ of 0 and a standard deviation σ set to the sample standard deviation computed from these error components.

Wallace (2005) gives the MML estimate of code length to transmit a set of independent data (Δx₁, Δy₁, Δz₁), (Δx₂, Δy₂, Δz₂), ··· (Δx_l−2, Δy_l−2, Δz_l−1) using a normal distribution as:

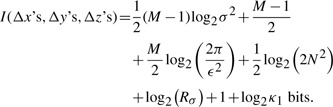(7)

where M=3×(l−2) is the total number of components of the error vectors e_k being transmitted, R_σ gives the prior knowledge of the limits to log₂ σ and κ₁≈1/12 denotes the constant corresponding to quantizing lattices proposed by Conway and Sloane (1984). In this study, we assume that σ is bounded by 3Å because this is consistent with the limits of utility of root-mean-squared-deviation (RMSD) in superposition as a measure to estimate protein structural similarity.

Therefore, combining code lengths from equations 4–7, the code length required to transmit coordinates of a segment of a protein using any ideal model is give by

(8)

3.4 Describing a protein segment using the coil model

When transmitting a segment of a protein p_i,···, p_j as a coil, the coordinates are stated raw in that range using a null model (Section 3.1). Therefore, the code length of stating a segment p_i,··· p_j as a coil is

(9)

where I(r_k) and I(c_k) are code lengths given in equations 1 and 2.

3.5 Describing the protein as a collection of segments

Having laid the foundations of encoding segments of a protein using one of the ideal models or the coil model (Sections 3.3 and 3.4), this section deals with describing the entire protein coordinates as a collection of segments of a model type.

The main idea here is to find the best decomposition of points of a protein into segments where each segment is described using exactly one of eight potential models. Note that the decomposition, with the associated model descriptors, gives a secondary structural hypothesis of a protein.

Formally, a segmentation of ={p₁,···, p_n} gives an ordered subset of points ^′={p^′₁≡p_i1, p^′₂≡p_i2,···, p^′_m≡p_im} where 1=i₁<i₂<···<i_m=n. Each successive pair of points in ^′, 〈p^′₁, p^′₂〉, 〈p^′₂, p^′₃〉,··· 〈p^′_m−1, p^′_m〉, defines the start and end points of a segment. (Notice that ^′ gives m−1 segments of P, where end point of one segment is same as the start point of the next.) Associated with each segment 〈p^′_k, p^′_k+1〉 of length l_k=i_k+1−i_k+1 is a model type t_k, 1≤k≤m−1. A secondary structural assignment of is given by the segmentation {p^′₁,···, p^′_m} and its corresponding model assignment {t₁,···, t_m−1}.

We note that for n points in , there are 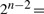possible segmentations – the first and last points of ^′ are the same as those in . Since each segment of any segmentation can be assigned to any of the eight possible model types, the total possible secondary structural assignments is given by the formula: 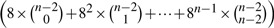. For an average protein, this gives a massive search space. (An efficient dynamic programming method to find the best secondary structural assignment is detailed in Section 4.)

Any given segmentation ^′ of and its associated model types acts as a secondary structural hypothesis of the given coordinate data. Alice can describe and transmit the coordinates in using this hypothesis over a two-part message.

3.5.1 First part of the explanation message

In the first part of the message, Alice communicates the segmentation ^′={p^′₁,···, p^′_m} and its corresponding model assignments {t₁,···, t_m−1} as the hypothesis on the observed coordinate data in . This part of the message will be composed of the following:

1. the number of segments (m−1) in ^′ and

2. for each segment p^′_k (1≤k≤m−1), communicate

   1. the length of the segment l_k=i_k+1−i_k+1 and
   2. the model type t_k to encode the points in that segment.

The number of segments (m−1) is an integer transmitted using a log^* distribution assuming a universal prior on the distribution of numbers. Rissanen (1983) gives the code length of transmitting any integer n>0 as

(10)

where log₂^*(n)=log₂ n+log₂ log₂ n+··· (over all +ve terms).

Next, the lengths of the segments are positive integers. Although these integers can also be transmitted using a log^* distribution, it is rather inefficient because in practice the lengths of helices, strands and coils are constrained. Therefore, in this work, we, encode the lengths of the segments using a Poisson distribution with a predefined mean of λ for each model type: (The parameters λ for each of the eight types of models are treated to be a part of the codebook. In this work we empirically set λ=4 for coil and λ=5 for strands. The lengths of helices are transmitted using a mixture of two Poisson distributions with means 4 and 8.)

The code length to state any integer n>0 using this distribution is:

(11)

Finally, each model type t (encoded as an integer 0≤t≤7) of any segment is stated using a uniform distribution (uniform is the simplest choice. Since some models as more probable than others (e.g. α-helices and strands are significantly more probable than other models), a more elaborate coding scheme can also be considered taking into account the empirical distribution of various models.) in

(12)

In summary, combining equations 10–12, the code length of the first part of the message proposing the secondary structural hypothesis on is

(13)

3.5.2 Second part of the explanation message

In the second part of the message, Alice sends the actual details of the coordinates in economically given the hypothesis ^′.

The procedure to transmit coordinate data of a segment of a protein using the ideal and coil models has been discussed in Sections 3.3 and 3.4.

Using the notations in Section 3.5, the hypothesis received in the first part of the message is of the form 〈p^′_k, p^′_k+1〉, with each segment of some length l_k and type t_k. The message length to transmit the coordinates given the above segmentation is:

(14)

where O(1) is the constant number of bits to state the first C_α coordinate p₁ (Section 3.1), I_model(p^′_k,···, p^′_k+1)=I_ideal(p^′_k,···, p^′_k+1) if 0≤t_k≤6 and I_model=I_coil(p^′_k,···, p^′_k+1) if t_k=7.

The total message length of communicating with ^′ comes from combining equations 13 and 14

(15)

3.6 Problem Statement

From the earlier section, the problem of inferring the best secondary structural assignment can now be stated formally as follows: given containing n points, find the secondary structural segmentation ^′ and its corresponding model assignment such that the total message length to transmit losslessly, I_total (&^′)=I_first(^′)+I_second(|^′) is minimized.

4 INFERENCE OF SECONDARY STRUCTURE

This section describes the search method to find the best MML secondary structural segmentation from given coordinate data.

4.1 Constructing the code length matrices

Equation 15 gives the total message length of communicating coordinates in using a segmentation ^′:

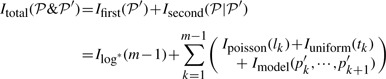For a given protein, any pair of points can potentially be the start and end points of a segment. At the same time, a segment can be described using any of the eight models considered here. Therefore, the procedure to assign secondary structure to C_α coordinates {p₁,···, p_n} in a given protein begins by constructing a set of eight code length matrices, one for each model type t (0≤t≤7):

(16)

where any cell (i, j)_1≤i<j≤n of the matrix for type t gives the code length of stating the segment p_i to p_j using the model t.

4.2 Finding the best secondary structural assigning

The segmentation of using various model types enforces a strict ordering constraint, satisfying the requirements for a solution by dynamic programming, even though the search space is huge as discussed in Section 3.5. Let any D(i) store the optimal message length of transmitting points p₁,···, p_i, for all 1≤i≤n. With the boundary condition of D(1)=0, the dynamic programming recurrence to find the optimal assignment is given by

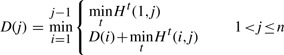The above recurrence is used to fill the array D iteratively from 1 to n. On completion, the best secondary structure assignment can be derived by remembering the index i and type t from which the optimal D(j) is computed.

5 POST-PROCESSING

In the post-processing step, the above-defined successive segments of same type (helical or strand) from the MML inference are examined for moderate curvature. Further, sharp turns are identified and distinguished from coil assignments. Finally, β-sheets are identified by grouping together the assigned strands.

Checking for moderate curvature in helix and strand: The MML inference automatically gives the best (in the information–theoretic sense) piecewise approximation of a curved helix or strand. In a single pass through the secondary structural assignment generated by our method, we check for such curvatures and merge successive segments to form a larger segment.

Each helix (1≤t≤6) and strand (t=7) is represented by a vector. For a helical segment, the vector is the axis of the helix. For the strand segment, the vector is the least-square line fitting its C_α atoms. Two successive segments (of the same model type) are joined to form a single segment if the orientation angle of their vectors is within 30^○. [For a detailed description of the finding the axes and orientation angle, see Konagurthu et al. (2008)]

Identifying sharp turns: sharp turns often have geometries that are conformationally similar to a turn of ideal helical models considered in this work. Any assignment of a helical segment of length less than or equal to four residues that is preceded and succeeded by other assigned segments is relabeled as a sharp turn.

However, α-helices often fray or tighten at their N- or C-terminal ends giving a short stretch of π or 3₁₀ helical segment. In order not to incorrectly assign these ends as sharp turns, the orientation of a candidate segment is checked against the preceding and succeeding segments and only assigned a sharp turn if the segment's orientation exceeds 45^○ relative to its neighbouring segments.

Grouping strands forming β-sheet: all strand segments are extracted from a given assignment. A strand adjacency matrix is computed where two strands are treated to be adjacent if and only if they are in parallel (with orientation angle in the range ± 45^○) or anti-parallel (with orientation angle in the range [135^○ to 180^○] or [−135^○ to −180^○]) orientation and there exist Van der Waals interactions between at least two pairs of atoms from the segment.

Strands from a β-sheet are then identified and grouped using a complete depth-first search on the strand adjacency matrix.

6 RESULTS

Implementation: a program (SST) implementing the method described in the previous section has been developed in C++ programming language. The program accepts protein coordinates in the Brookhaven PDB format and outputs the secondary structure assignment both at a segment level (stating the start and end point of each secondary structural segment) as well as at a residue level. The program also generates a PyMol script, which allows users to visualize the secondary stucture assignment. (Fig. 1).

Datasets and comparison methods: To study the performance of SST, we consider a dataset of 1737 PDB structures. These structures are the same as the dataset considered by Martin et al. (2005), excluding the structures which have been deprecated or those structures that failed running on any one of the considered methods. (See below.) These structures are divided into four datasets: high-resolution (HRes) dataset with 631 crystal structures solved to 1.7 Å or better; medium resolution (MRes) dataset with 582 crystal structures with resolution between 1.7 and 3 Å resolution; low-resolution (LRes) dataset with 306 structures with resolution >3 Å and finally, a dataset of 218 NMR structures.

In this work, we mainly compare SST with DSSP (Kabsch and Sander, 1983) and STRIDE (Frishman and Argos, 1995) exhaustively on the large structural dataset described earlier. Although there are other programs for secondary structure assignment, we had difficulty finding distributions that we could download. For those we managed to download, we could not install the programs due to unresolvable dependencies in their source code. However, we use a web server 2Struct (Klose et al., 2010), which allows manual submission of queries with a single point of access to a variety of secondary structure assignment methods beyond DSSP and STRIDE such as KAKSI (Martin et al., 2005), PALSSE (Majumdar et al., 2005), STICK (Taylor, 2001), XTLSSTR (King and Johnson, 1999) and P-SEA (Labesse et al., 1997). To facilitate comparisons with other methods, we randomly selected 30 low-resolution structures from the LRes dataset and manually collected the secondary structure assignments from the server. The list of structures used in this experiment can be download from http://www.csse.monash.edu.au/~karun/sst.

Comparison: we first assess the composition of the assigned regular secondary structures (helices and strands) using DSSP, STRIDE and SST over the four datasets described earlier. Overall DSSP assigns 34.5% of residues to helices and 19.9 of residues to strands. STRIDE assigns 37.3 and 27.4%, and SST assigns 40.4 and 25.3% of residues to helices and strands, respectively. In general, DSSP is conservative in assigning regular secondary structures resulting in shorter elements compared with output from STRIDE and SST. Examining the lengths of various secondary structural segments, we observe that the average length of a helix and strand segment assigned by SST is 12.1 and 6.1 residues, respectively. Unlike SST, which states the residue start and end points of each segment, computing the lengths of secondary structural elements from DSSP and STRIDE's output is problematic and error-prone (Majumdar et al., 2005).

Table 1 shows the comparison between SST, DSSP and STRIDE over high, medium, low resolution and NMR structures. To undertake this comparison, the assignments of the three programs are grouped into three classes: helix (of all types), strand and other. DSSP and STRIDE use similar methods for assignment based on detecting hydrogen bonds. Therefore, as one would expect, their assignments are highly similar. SST largely agrees with DSSP and STRIDE when assigning helices. Strands, however, show some disagreement. Visually examining several instances, we find that in many cases SST assigns longer strands than the other two methods. Agreement between strand assignments on NMR structures among the three methods is rather poor. Surprisingly, even DSSP and STRIDE differ enormously in this class even though their assignment methods are quite similar.

Table 1.

Performance of SST compared with DSSP and STRIDE on four datasets: HRes, MRes, LRes and NMR

	HRes (% Agreement)			MRes (% Agreement)
	Helix	Strand	Total	Helix	Strand	Total
SST versus DSSP	97.6	81.9	84.1	97.6	83.4	83.9
SST versus STRIDE	97.1	80.8	84.3	97.2	82.3	84.3
STRIDE versus DSSP	99.4	98.5	96.7	99.4	98.9	96.9
	LRes (% Agreement)			NMR (% Agreement)
	Helix	Strand	Total	Helix	Strand	Total
SST versus DSSP	97.7	84.3	82.7	98.4	53.8	51.5
SST versus STRIDE	97.2	82.3	83.8	94.4	78.9	83.9
STRIDE versus DSSP	99.3	98.3	96.0	99.6	64.6	68.7

Columns labelled ‘Helix’ and ‘Strand’ give the percentage agreement of residues assigned as helix and strand, respectively, between the two methods. Column ‘Total’ gives the percentage agreement over three classes: helix, strand and others.

Table 2 extends the comparison of SST with other popular methods for assignment on low-resolution structures. The table shows the percentage agreement of secondary structural assignments between the methods. Consistent with previous comparative studies (Colloc'h et al., 1993; Martin et al., 2005), we see considerable differences in the assignments. In the absence of a universally acknowledged gold standard for assignment, it becomes very difficult (if not impossible) to objectively validate one method to be truly better than the other. The observed differences mainly arise from the different criteria used by the methods. However, manually examining many cases where the methods differ, we find that most disagreements appear at the ends of various (helical or strand) segments. We will use a simple example to highlight the most common type of differences. Figure 2 gives the overall residue-level secondary structure assignment across different methods for a flavodoxin structure from Clostridium beijerinckii (wwPDB ID:5NLL). DSSP and STRIDE assignments are nearly identical to each other. From the figure, small disagreements between methods can be seen around the start and end points of various segments demarcated by SSTs segment view (labelled SST(SEG)). A major difference between DSSP and SST is the region Lys28…Asn34, which SST assigns as a strand. DSSP starts the segment three residues further at Asn31. Inspecting the structure, we find a backbone hydrogen bond between Asp29 and Met1. This might suggest the start of the strand at either Asp29 or one residue upstream at Lys28 as identified by SST. Also, in the region Glu62… Ile73, only SST correctly assigns a π-helical cap (Glu62… Phe66) leading into a α-helix.

Table 2.

Pairwise comparison between secondary structure assignment methods

	DSSP (%)	STRIDE (%)	KAKSI (%)	PALSSE (%)	P-SEA (%)	STICK (%)	XtlSStr (%)
SST	77.4	75.3	74.3	80.7	53.9	69.0	74.9
DSSP		86.1	76.9	76.0	57.1	71.8	77.6
STRIDE			67.8	74.8	48.8	64.5	73.8
KAKSI				75.4	67.4	79.4	72.9
PALSSE					50.9	69.9	70.8
P-SEA						66.6	54.1
STICK							66.7

Each cell in the upper-triangular matrix gives the percentage agreement of the residue-level assignments between a pair of methods indicated in the first row and column. The agreement is measured over all three classes: helix, strand and other.

Fig. 2.

Residue-level secondary structure assignment of a 1.75 Å flavodoxin structure from Clostridium beijerinckii. SST residue-level assignment and the segment boundaries are shown in addition to the assignments across multiple methods. For details of the secondary structure codes, see http://www.csse.monash.edu.au/karun/sst/codes.html

To evaluate the consistency of SSTs secondary structural assignments on coordinates solved at different resolutions, we randomly selected 15 protein structures for which both the superseded low-resolution coordinates and the new high-resolution coordinates were available. Table 3 gives the list of considered structures along with the percentage agreement between SSTs assignment at different resolutions. The results indicate that SST produces consistent results on structures determined at different resolutions. The <10% differences (Table 3, last column) in agreement on the chosen structures may well represent genuine structural differences rather than shortcomings of the algorithm.

Table 3.

SST assignment sensitivity to changes in coordinate resolution. Resolution numbers marked with ^* are taken from the original papers

Structure name	LRes PDB ID	HRes PDB ID	%Agree
Lysozyme	2LZH (6.0 Å)	2ZQ3 (1.6 Å)	95.3
Ferrochelatase	1LD3 (2.6 Å)	1DOZ (1.8 Å)	97.4
Glutamate Dehydrogenase	1AUP (2.5 Å)	1BGV (1.9 Å)	90.6
Pseudomonas Cytochrome	151C (2.0 Å)	351C (1.6 Å)	93.9
Bence-Jones Protein	1BJL (2.9 Å)*	3BJL (2.3 Å)	90.2
Concanavalin A	4CNA (2.9 Å)*	5CNA (2.0 Å)	91.8
Endochitinase	1BAA (2.8 Å)	2BAA (1.8 Å)	95.5
Ferredoxin Reductase	1FNR (2.6 Å)	1FND (1.7 Å)	95.9
Endonuclease III	1ABK (2.0 Å)	2ABK (1.6 Å)	97.6
Myohemerythrin	1MHR (2.9 Å)*	2MHR (1.3 Å)	92.4
Phosphofructokinase	5PFK (7.0 Å)*	6PFK (2.6 Å)	95.3
Serine Protease Inhibitor	1QLP (2.9 Å)	2PSI (2.0 Å)	95.4
Dimeric Hemoglobin	1SDH (2.4 Å)*	3SDH (1.4 Å)	98.4
Glutathione Reductase	1GRS (3.0 Å)*	3GRS (1.5 Å)	94.4
Calmodulin Fragment TR2C	1TRC (3.6 Å)	1FW4 (1.7 Å)	93.9

Further, to illustrate the reliable segmentation produced by SST on structures with long, curved helices and strands, we chose two structures: Leucine zipper protein (wwPDB: 1NKP) composed of very long helices and Sucrose-specific porin protein (wwPDB: 1A0S) composed of long, curved strands forming β-barrels. Although SST initially breaks the curved segments into smaller pieces, the post-processing step explained in Section 5 reconstitutes these pieces back correctly into fuller segments. [Fig. 3 gives SSTs assignment on the porin protein (1A0S). The figure shows that the curved strands of the β-barrels have been reconstituted and grouped reasonably well in the post-processing step.]

Fig. 3.

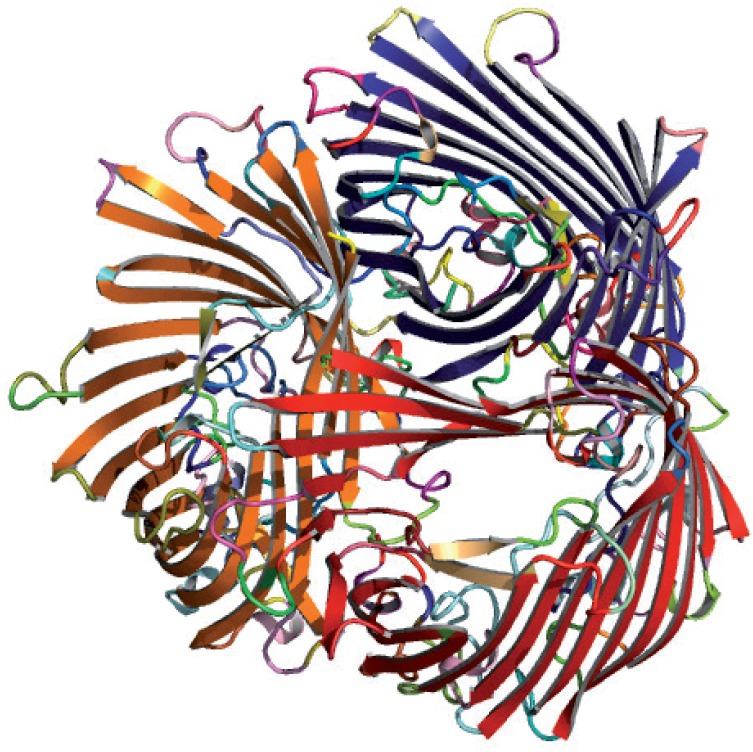
Automatically generated PyMol image of SSTs secondary structural assignment on sucrose-specific porin (ScrY) from Salmonella typhimurium (wwPDB: 1A0S)

Finally, as a difficult case we consider the 10 Å resolution protein coordinates of Elongation Factor Tu (GDB.Kirromycin) from Escherichia coli (wwPDB: 1qzd) solved using Cryo-Electron Microscopy. Its wwPDB file contains only C_α coordinate information. DSSP, STRIDE and P-SEA fail to process such information as the coordinates of other atoms are needed to decipher Hydrogen bonds. KAKSI and XTLSSTR are able to process this structure but assign all residues in the chain to coil. Of the considered methods, only SST, PALSSE and STICK assigned any secondary structure. For lack of space, the overall residue-level assignment across these three methods are presented in Figure 1 of the supplementary text. Examining the structure, PALSSE consistently overestimates the regular secondary structural regions by a large margin. STICK performs well, especially in identifying β-strands. However, it miscalculates several secondary structural elements. In comparison, SST produced the most reasonable segmentation of the three methods on visual inspection of the structure.

7 CONCLUSION

Reliable secondary structure assignment is an important problem. We have developed a novel information theoretic method to address this problem using the Bayesian framework of MML inference. Careful examination of the results over a large number of structures suggests that our method gives consistent assignments even on low-resolution data. We note that our method uses a dictionary of models composed of ideal secondary structural elements. The details of the models are explicit and open to scrutiny. It is likely that these models can be improved. (‘Essentially, all models are wrong, but some are useful.’—George Box.) However, modification to the models is an improvement if, and only if, it yields extra compression.