GraphClust: alignment-free structural clustering of local RNA secondary structures

Abstract

Motivation: Clustering according to sequence–structure similarity has now become a generally accepted scheme for ncRNA annotation. Its application to complete genomic sequences as well as whole transcriptomes is therefore desirable but hindered by extremely high computational costs.

Results: We present a novel linear-time, alignment-free method for comparing and clustering RNAs according to sequence and structure. The approach scales to datasets of hundreds of thousands of sequences. The quality of the retrieved clusters has been benchmarked against known ncRNA datasets and is comparable to state-of-the-art sequence–structure methods although achieving speedups of several orders of magnitude. A selection of applications aiming at the detection of novel structural ncRNAs are presented. Exemplarily, we predicted local structural elements specific to lincRNAs likely functionally associating involved transcripts to vital processes of the human nervous system. In total, we predicted 349 local structural RNA elements.

Availability: The GraphClust pipeline is available on request.

Contact: backofen@informatik.uni-freiburg.de

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

In recent years, tiling arrays and high-throughput sequencing have strikingly driven the discovery of novel transcripts, of which an outstanding amount is not translated into proteins (ENCODE Project Consortium, 2007). These non-protein coding RNAs (ncRNAs) have moved to a key research in molecular biology, fundamentally challenging established paradigms and rapidly transforming our perception of genome complexity. There is mounting evidence that the eukaryotic genome is pervasively transcribed (Clark et al., 2011) and that ncRNAs function at various levels regulating gene expression and cell biology (Amaral et al., 2008; Brosnan and Voinnet, 2009).

Recent advances in the computational de-novo prediction of ncRNAs enabling genome-wide analysis have uncovered a wealth of signals for potentially novel ncRNAs in genomic sequences from basically all kingdoms of life. Examples include metazoans with thousands of predicted ncRNA signals in human, fish or insects (Rose et al., 2007, 2008; Washietl et al., 2005). Consequently, the prediction, comparison and (functional) annotation of ncRNAs are major tasks of current RNA research. Annotation of ncRNAs, however, is still not part of generic annotation pipelines of genome or next-generation sequencing data and precise functional annotations of the majority of predictions remain elusive.

One of the major reasons for the multitude of unannotated ncRNAs is that in contrast to protein-coding genes, ncRNAs belong to a diverse array of classes with vastly different structures, functions, and evolutionary patterns (Bompfünewerer Consortium 2007). Albeit their heterogeneity, ncRNAs can be divided into RNA families according to inherent functional, structural, or compositional similarities. Today, the Rfam 10.1 database already lists 1973 different RNA families (Gardner et al., 2011). In contrast to RNA families, an RNA class groups together ncRNAs whose members have no discernible homology at the sequence level, but still share common structural and functional properties. Prominent examples are the two distinct classes of snoRNAs (box H/ACA and box C/D) and micro RNAs (miRNAs).

Since an RNA-class consists of RNA with similar structure and function, clustering according to sequence–structure similarity has now become a generally accepted scheme for ncRNAs annotation. The quality and complexity of the clusters are however, largely determined by the pairwise sequence comparison method. The most generic methods, as introduced with LocARNA (Will et al., 2007) and FoldAlign (Torarinsson et al., 2007), use derivates of the full Sankoff algorithm (Sankoff, 1985) of simultaneous alignment and folding. They suffer, however, from a very high computational complexity (at least O(n⁴) in time) and are thus limited to relative small sequence sets. As poignantly stated by Gorodkin et al. (2010): ‘Even using substantially more sophisticated techniques, genome-scale ncRNA analyses often consume tens to hundreds of computer years. These high computational costs are one reason why ncRNA gene finding is still in its infancy.’ For this reason, many approaches use different heuristics to achieve a reasonable trade-off between time and quality. Oversimplifying and without completeness, given the variety of approaches present in literature, one can distinguish two main classes of clustering approaches. The first class uses simplifications in the representation of structures. Ritchie et al. (2007) and Khaladkar et al. (2007) use comparison tools that consider single-predicted structures such as RNAforester (Hochsmann et al., 2004) or MARNA (Siebert and Backofen, 2005). These comparison approaches heavily depend on the correctness of the structure, although computational prediction of secondary structures are known to be error prone. Other approaches such as Sato et al. (2008) use simplified structural models. To some extend, the work by Parker et al. (2011) can also be listed under this class as they use an approximate measure between two structural RNAs' SCFG models for clustering hits found by EvoFold (Pedersen et al., 2006).

The second class uses sequence information as prior knowledge to speed up the computation. In the simplest case, sequences are first clustered by sequence-alignment (Kunin et al., 2007; Shi et al., 2009). These alignments are then used to predict conserved consensus structures using approaches such as RNAalifold (Bernhart et al., 2008) or PETfold (Seemann et al., 2008). A similar overall scheme is e.g. applied by (Weinberg et al., 2010), who use CMfinder (Yao et al., 2006) to determine a consensus motif from a cluster of unaligned sequences. Yet, another set of tools uses a sequential encoding of structural information (Tseng et al., 2009). Finally, one can use the information from an ensemble of sequence-alignments to speed up the computation as done by Saito et al. (2011), an approach that is commonly seen in sequence–structure alignment. The major problem, however, is that the sequence of an ncRNA evolves much faster than its structure, which implies that in most of the cases, no homology on the sequence level is detectable. Indeed, it has been shown that family assignments of structured RNAs obtained from sequence alignments at pairwise sequence identities below 60% are often wrong (Gardner et al., 2005).

In this article, we propose an efficient approach for clustering very large sets of RNA sequences according to sequence and structure information. The size of current datasets exclude the use of alignment-based techniques. Hence, to achieve the required efficiency, we propose here an alignment-free hashing technique over a novel encoding for RNA structures. Although there are alignment-free methods for comparison of RNA with respect to sequence and structure (Gan et al., 2003; Liu and Wang, 2006), we are not aware of any alignment-free method capable to perform RNA sequence–structure comparisons on hundred of thousands sequences. In a second phase, we increase the quality of the resulting clusters by employing alignment methods to filter away inconsistent elements. More specifically, we extend a fast graph kernel technique that we have recently developed (Costa and Grave, 2010) for chemoinformatics applications and we adapt it to detect similarities between RNA secondary structures. The key novelty that we introduce lies in an explicit representation of the associated sequence–structure information which we encode as sparse vectors in a very high-dimensional space. This allows us to use efficient locality sensitive hashing methods to accurately retrieve dense data regions with a complexity that is linear in the number of sequences N, rather than quadratic as it would be with both alignment methods or standard kernels that work with implicit representations.

We have integrated the approach in a ready-to-use pipeline for large-scale clustering of putative ncRNA. The method has been evaluated on known ncRNA classes and compared against existing approaches, that is, the complete LocARNA-pipeline and RNAsoup (Kaczkowski et al., 2009). We show that our clustering is of high quality yielding reliable clusters. Due to the algorithmic improvements presented in this contribution, we achieve a striking performance speedup (from years to days for serial computation and even hours when parallelized) outperforming any of the existing approaches. We applied our method to six heterogeneous large-scale datasets containing >220 000 sequence fragments. First, we analyzed computationally derived predictions of short ncRNAs lacking reliable class assignments. Next, we searched for local structural elements specific to experimentally validated lincRNAs. We observed enriched GO-terms for lincRNAs containing predicted local motifs likely functionally ‘linc’-ing these transcripts to vital processes of the human nervous system. In general, both application scenarios aim at the detection of novel structural non-coding RNAs. In total, we predicted 349 local structural RNA classes.

2 APPROACH

We propose to retrieve candidate clusters using an efficient hashing technique over a novel RNA structure representation. To enhance the quality of the results, we filter away inconsistent elements using alignment-based techniques. To increase the recall, we induce covariance models for each cluster and scan the dataset to collect missed sequences. More in details, we propose to sample a small number of probable, but sufficiently different, structures for each RNA sequence. We then encode each structure as a labeled graph preserving all information about the nucleotide type and the bond type (i.e. binding or backbone). In this way, a sequence's structure is represented as a graph with several disconnected components. We could now compute the similarity between the representative graphs using a graph kernel. However, to avoid a quadratic number of comparisons, we first extract an explicit vector representation for each graph, and then build an inverse index on a compressed representation obtained via hashing techniques. This allows us to retrieve in constant time the nearest neighbors sequences for any given query structure. We evaluate each neighborhood and select as candidate clusters those that contain very similar elements. Each (small) candidate cluster is then refined using alignment techniques. Finally, a covariance model is induced for each cluster. The dataset is scanned using these models and before reiterating the procedure, the recognized missing sequences are associated to the corresponding cluster and removed from the set.

2.1 Vector-based representation of RNA structures using explicit graph kernel

Graph encoding for structures. Minimum free energy-based secondary structure prediction has been shown to be error prone. For this reason, we want to use a representation of the entire ensemble of low-energy conformations. Resorting to a complete enumeration of near-optimal structures would yield a tremendously large number of structures. Instead, we opt for abstract shape analysis methods introduced in (Giegerich et al., 2004). Here, one analyzes the complete folding space using the notion of partition function (McCaskill, 1990) but classifies the structures a priori into abstract classes called shapes.

We note, however, that there is an issue regarding the true sequence boundaries: while benchmark test for sequence–structure alignments are usually given as full-length transcripts, this setting is quite unlikely in practical application scenarios, where one often has either a partial transcript (e.g. from RNA-seq data), or just transcripts with wrong boundaries. The fact that secondary structure prediction may change when additional context is considered adds considerable noise to the task of functional families identification. To deal with this issue, we consider several subsequences obtained from the original sequence, as overlapping windows of different sizes (parameterized by a set of values W) and at different starting locations (parameterized by the overlap value O). Note that the window size influences the locality of the structural features that the method is aware of. In the experiments, we chose two window sizes, one of 30 nt and the other of 150 nt to capture both local hairpins and larger multiloop structures. Finally, for each subsequence in each window, we consider the set of l most representative structures obtained by RNAShape and encode them as disconnected components. The vertex set for each of the graph components is derived from the sequence nucleotides, whereas the edge set encodes both the nucleotide sequence adjacency information and the pairwise binding status. In addition, an extra set of vertices (and corresponding edges) is introduced to better match biological knowledge on important RNA motifs, namely, for each stacking base pairs quadruplet, an additional vertex is added (and linked to each of the four nucleotides involved; in this way, the notion of neighborhood subgraph (see next section) coincides with that of a sequence of stacking base pairs (Fig. 1).

Fig. 1.

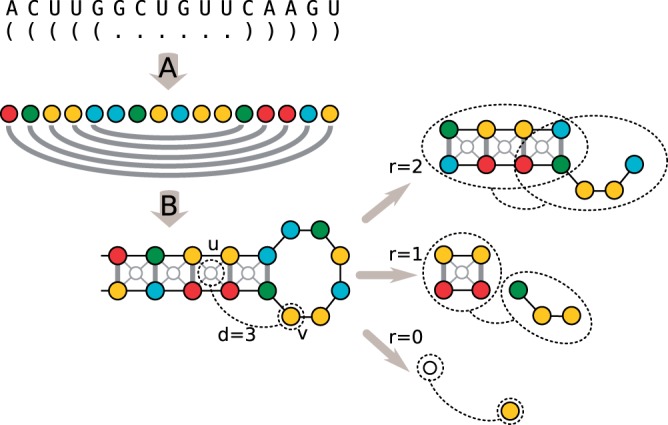
RNA secondary structure encoding and Graph Kernel Features: Top (A) The graph encoding preserves the nucleotide information (vertex labels) and the base pairs (edge labels), here depicted with different colors. (B) Additional vertices are inserted to induce features related to stacking base-pairs quadruplets (thin light gray vertices at the center of each stacking pair). Right: example of features induced by the graph kernel NSPDK for a pair of vertices u, v at distance 3 with radius 0,1,2. Neighborhood graphs are enclosed in dashed ovals

Graph kernel. To deal with entities represented as graphs, graph kernels of several types have been proposed. Graph kernels compute a similarity measure between graphs in terms of a dot product function. We start from the recently introduced (Costa and Grave, 2010) fast kernel called neighborhood subgraph pairwise distance kernel (NSPDK), as this kernel is suitable for large datasets of sparse graphs with discrete vertex and edge labels. However, here we choose to materialize and explicitly list all the features. This will turn out to be key in successive phases, where, for efficiency reasons, we need to build an index over these features.

The NSPDK is an instance of a decomposition kernel (Haussler, 1999), i.e. a composite kernel that operates over all possible ‘parts’ defined by a given relation. In this case, the parts are pairs of special subgraphs, called ‘neighborhood’ subgraphs. More formally, for a given graph G=(V, E), and an integer r≥0, let N_r^v(G) denote the neighborhood subgraph, i.e. the subgraph of G rooted in v induced by the set of vertices at distance (The distance between two vertices v, u is the number of edges of the shortest path between u and v.) not >r. The neighborhood-pair relation R_r,d, is defined to hold when the distance between the roots of two neighborhood subgraphs of radius r is exactly equal to d. The authors define a kernel κ_r,d as the decomposition kernel on the relation R_r,d, that is,

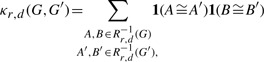(1)

where R_r,d⁻¹ is the inverse of the relation R_r,d and indicates all the possible pairs of neighborhood subgraphs of radius r, whose root vertices are at distance d in the given graph G, 1 denotes the indicator function, and ≅ the isomorphism between rooted graphs. The type of features that the NSPDK is considering, in the specific case of graphs originating from RNA sequences, is depicted in Figure 1. The (non-normalized) NSPDK is finally defined as the sum of all the kernels for all radii and all distances:

(2)

For efficiency reasons, the authors consider the zero extension of K obtained by imposing an upper bound on the radius and the distance parameter: K_r^*,d^*(G, G′)=∑_r=0^r* ∑_d=0^d* κ_r,d(G, G′), i.e., they limit the sum of the κ_r,d kernels for all increasing values of the radius (distance) parameter up to a maximum given value r^* (d^*). Furthermore, a normalized version of κ_r,d is suggested, that is, to ensure that the features induced by all values of radii and distances are equally important regardless of the overall dimensionality of the induced feature space.

As running an exact isomorphism test is computationally expensive, the authors propose to substitute the test with a more efficient graph invariant computation. (Note that in doing so, potential feature ‘collisions’ are introduced (i.e. different subgraphs can induce the same features), although in practice the collision event is negligible.) The core idea is to devise an efficient graph serialization procedure, such that two isomorphic graphs can be reduced to an identical string. The encoding is achieved using a technique based on the distance information between pairs of vertices and can be computed in linear time w.r.t. the vertex size of the component on sparse graphs with bounded degree. Finally, an iterative hashing procedure can map the string encoding into an integer code (Costa and Grave (2010) for further details). The isomorphism test between two graphs is then reduced to the equality test between their integer codes.

Explicit feature representation. The novel idea here is to materialize the implicit feature encoding which is key to obtain sublinear efficiency in the clustering phase. Differently from Costa and Grave (2010), we here make use of the integer code for the invariant graph encoding as a feature indicator. In this way, we can interpret the integer associated to each feature (i.e. each pair or neighborhood subgraphs of radius r whose roots are at distance d) as the feature key and the (normalized) count of occurrences as its value. This allows us to obtain an explicit feature encoding for a given graph G as a sparse vector in ℝ^m (with a very high dimension m). The feasibility of the approach lies in the fact that the encoding does not produce an exponential number of features, as it would happen with most graph kernels that enumerate all possible general subgraphs. Instead, NSPDK limits the number of features to O(r^* d^*|V(G)|²) pairs of neighborhood subgraphs, i.e. one feature for each pair of vertices times each possible combination of values for the radius and the distance. Note that typically r^*∈[0, 5] and d^*∈[0, 10] and hence the multiplicative factor (≈50) is reasonable. Moreover, for sparse graphs, the number of vertices that are reachable within fixed small distance is typically small (depending on the average degree) so that the dependency on the vertex set size can be more tightly approximated by O(|V(G)|). As a result each graph is mapped into a sparse vector that lives in a very high-dimensional feature space but that has a number of non-zero features which is linear in the number of the graph's vertices. As the computation of the encoding for each neighbor subgraph can be cached, the practical complexity for the overall encoding of a graph is linear in its vertex set size with small hidden multiplicative coefficient, making it one of the fastest graph kernels available (Costa and Grave, 2010).

2.2 Efficient candidate cluster determination using locality sensitive hashing

As datasets size increases (i.e. >10⁴), algorithms that directly make use of pairwise distance or similarity information become infeasible as they inevitably exhibit a quadratic complexity. The key idea then is to formulate the clustering problem in terms of approximate nearest neighbors queries which can be answered efficiently (sublinearly). That is, given a set of n instances P={p₁,…, p_n} in a metric space X with a distance function d, a neighborhood query is a procedure that returns the instance in P closest to a query instance q∈X. The nearest neighbor search problem is formulated as a dataset preprocessing that allows nearest neighbors queries to be answered efficiently. For high-dimensional cases, an efficient solution was proposed by Indyk and Motwani (1998). The key idea is to relax the requirements, ask for ϵ–approximate nearest neighbor queries, and use locality-sensitive hashing techniques. The ε−approximate nearest neighbor query returns an instance p for a given query q such that ∀p′∈P, d(p, q)≤(1+ϵ)d(p′, q). A locality sensitive hash function is a hash function such that the probability of collision is higher for objects that are close to each other than for those that are far apart. As locality sensitive hash function, we choose the min-hash function (Broder, 1997) as it approximates the natural similarity notion defined by the Jaccard index. However, these techniques require instances to be represented as sparse binary vectors rather than sparse real vectors. We therefore binarize all instances from ℝ^m↦{0, 1}^m setting to 1 all non-null components. Let x, z∈{0, 1}^m be two instances; the Jaccard similarity between the two instances is defined as s(x, z)=(|x∩z|)/(|x∪z|), that is, the ratio of the number of features that the instances have in common over the overall number of features. We build a min-hash function starting from a set of random hash functions f_i:ℕ↦ℕ, functions that map integers randomly (but consistently) to integers; in our case, the domain/codomain represents feature indicators. These functions must be independent and satisfy: ∀x_j≠x_k, f_i(x_j)≠f_i(x_k), and ∀x_j≠x_k, P(f_i(x_j)≤f_i(x_k))=1/2. The min-hash function derived from f_i is defined as h_i(x)=argmin_xj∈xf_i(x_j), the min-hash returns the first feature indicator under a random permutation of the features order. A rather surprising (and useful) fact is that a min-hash collision is an unbiased estimator of the Jaccard similarity:

i.e. the probability to select as the minimum feature indicator a non-null feature that belongs to both x and z is exactly the fraction of features that x and z have in common over the total number of non-null features of x and z. To decrease the (high) variance of this estimate, one can take N independent min-hash functions and compute the number n of times that h_i(x)=h_i(z). The estimated value n/N is the average of N different 0-1 random variables, which evaluates to one when h_i(x)=h_i(z) and zero in all other cases. The average of these unbiased estimators of s(x, z) is also an unbiased estimator, with an expected error bounded by , or, equivalently, for any constant γ > 0, we can compute a constant N=O(1/γ²) such that the expected error of the estimate is at most γ. For example, with 400 hash functions, the estimate of s(x, z) would have an expected error ≤0.05.

We collect the results of the entire set of min-hash functions in an instance sketch as the tuple 〈h₁(x),…, h_N(x)〉. To obtain an efficient neighbor search procedure, we build an inverse index that returns all instances with the same min-hash value in O(1). More precisely, given the i-th hash function and a value 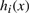, we collect the set of instances . The approximate neighborhood Z of an instance x is then induced from the multiset Z={Z_i}_i=1^N. Note that when γ (or equivalently N) is fixed, the complexity to build a single signature is constant and therefore the complexity for building the index is linear in the size of the dataset. To improve the quality of the returned neighbors, we consider only the most frequent elements in Z and sort them according to their NSPDK similarity to x. The k-neighborhood N_k(x) is finally the set of the k-closest elements. If the size of Z is small and independent of the dataset size |P|, these steps can be performed in constant time.

Given the efficient ϵ-approximate nearest neighbor search procedure offered by the min-hash technique, we can define candidate clusters using the notion of data density. Intuitively, we prefer as a candidate cluster a set of closely related instances. The idea is therefore to rank each instance x according to the density D_k of its k-neighborhood N_k(x), defined as the average pairwise similarity between x and all elements in its k-neighborhood D_k(x)=1/k ∑_z∈Nk(x) K_r^*,d^*(x, z). The candidate clusters are finally obtained from the densest neighborhoods.

2.3 GraphClust pipeline

Details of our clustering pipeline are given in the following (Fig. 2). We distinguish nine phases: initially, near-duplicates are filtered away (1), suboptimal structures for each sequence are computed in parallel (2); the sparse encoding is extracted for each structure (3); the encoding is then used to build the feature index for fast similarity searches; the top dense sets are returned as candidate clusters (4) and subsequently refined using structural alignment procedures (5); the remaining instances are used as high quality seeds to build covariance models (6) with which additional instances are retrieved to further populate the clusters (7); before reiterating starting from Step 4, the clustered elements are eliminated from the working set (8). Finally, redundant clusters are merged and all instances receive a unique cluster assignment (9).

• Phase 1: Preprocessing (sequential). The GraphClust pipeline is able to cluster RNA sequences which originate from different sources such as RNA-seq or computational methods like RNAz (Washietl et al., 2005) or EvoFold (Pedersen et al., 2006). Therefore, a solid preprocessing of the input sequences is essential. We mask repeats to avoid clusters made of genomic repeats. Next, we split long sequences into smaller fragments to enable the detection of local signals. Subtle sequence–structure relationships of near identical sequences were removed using blastclust (Altschul et al., 1997) to prevent a bias toward sequential clusters.

• Phase 2: Structure determination (parallel). In this phase, we extract a set of structures for each sequence employing the RNAShape tool as detailed in Section 2.1. As a rule of thumb, a sequence of 150 nt is encoded in a set of disconnected graphs of ≈2500 vertices and is obtained in 1 se on a Xeon 5160, 3.0 GHz (O=20%, W=30, 150, l=3).

• Phase 3: Encoding (parallel). In this phase, we manipulate the set of structures encoded as graphs in Phase 2 and produce an explicit sparse feature encoding as detailed in Section 2.1. For all experiments, we consider radius r^*=2 and distances between neighborhood pairs d^*=4. For a 150 nt long sequence, this yields a sparse vector with ≈8000 features and is obtained in ~1 S on a Xeon 5160, 3.0 GHz.

• Phase 4: Candidate cluster (sequential). The conversion of the folding structures into sparse vectors (e.g. 10 k sequences of length 150 require ≈1GB RAM) allows us to the efficient ϵ–approximate nearest neighbor search procedure offered by the min-hash technique (see Section 2.2) to define candidate clusters.

  Note that just returning the top ranking dense neighborhoods would produce highly redundant sets as the densest instances are likely to be part of the same cluster. To tackle the redundancy issue, we adopt a simple yet effective strategy: the candidate clusters are chosen as the top ranking neighborhoods provided that the size of their overlap is below a specified threshold th. More specifically, we sort all candidate clusters c_i in decreasing order so that ∀i<j, D(c_i)>D(c_j). We then iteratively build the union of the candidate clusters as 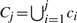, but we greedily discard a candidate cluster c_k if |C_j∩c_k|>th.

  As this phase constitutes the bottleneck of the entire pipeline (as we go from a parallel flow to a sequential one), we use additional procedures to trade-off accuracy with speedup improvements. Specifically, instead of ranking the entire set of sequences according to their approximate density, we work on a smaller sample extracted uniformly at random. The intuition is that the larger the cluster, the higher is the probability that it will be hit by the sample. In this way, samples of 50% or 25 allow a 2–4-fold speedup while having a high probability to identify at least one of the instances of the underlying high density clusters of size >2 or >4, respectively. Note that the neighborhood queries, the density estimates, and the returned neighborhood are computed on the complete dataset, not on the sample.

• Phase 5: Cluster refinement (parallel). Candidate clusters reaching-phase 5 contain sequences (≈15) that are deemed similar under the NSPDK similarity measure. In order to incorporate domain-specific knowledge (consider for example compensatory mutations) and create a high quality model of the cluster, we perform a sequence–structure alignment of the candidate set with the tool LocARNA (Will et al., 2007). A cluster tree is created by applying an average-linkage algorithm (UPGMA) to the pairwise distance matrix induced by the LocARNA alignment score. All subtrees with at least three leafs are then ranked by their quality, which is defined as the average pairwise alignment scores of its leafs. Note that the quality is not necessarily inversely proportional to the subtree size, that is, large subtrees can be ranked higher than smaller ones (Sadreyev and Grishin, 2003). Only the top ranked subtree, which contains the sequences (≈3–7) that exhibit the best quality, is retained.

• Phase 6: Cluster model (parallel). The selected top ranked RNA candidates are realigned with the tool LocARNAp (Will et al., 2012), which allows the computation of an alignment reliability score. The reliability signal can be used to identify a trusted alignment region and estimate the borders of the common local motif. A covariance model (CM) is finally created by applying the Infernal (Nawrocki et al., 2009) tool on the identified subsequences.

• Phase 7: Model scanning (parallel). Each cluster induces a CM model which is used to search the full dataset for residual potential cluster members. The sequence hits that are considered significant on the basis of their bit-score (≈20) or E-value are added to the final cluster. Note that, as every time we perform the search on the entire dataset, a sequence can be assigned to multiple clusters. This ambiguity is allowed in this phase as, until all clusters are available, there is not enough information to decide unambiguously for the best cluster assignment.

• Phase 8: Iteration and removal (sequential). All cluster members found in the previous phase are removed from the dataset and a new iteration starts from Phase 4. The termination condition is given either by a predetermined max number of iterations, a time limit or when the remaining dataset is exhausted. Note that Phases 5 to 7 allow us to go beyond the graph kernel similarity. The instances identified in Phase 4 come from the neighborhood of elements in high density regions. These clusters have a spherical shape in the kernel feature space. By first filtering, the cluster via alignment procedures and then expanding it using the covariance model, we remove this bias and obtain non-spherical clusters. This is one of the main justification for the iterative nature of the pipeline as the iterative removal of the non-spherical clusters alters the density distribution in the kernel feature space and allows novel clusters to emerge.

• Phase 9: Post-processing (sequential). Redundant clusters are merged and instances that belong to multiple clusters are assigned unambiguously. For every pair of clusters, we compute the relative overlap (i.e. the fraction of instances that occur in both clusters) and merge them if the overlap exceeds 50%. Cluster members are finally ranked by their CM bitscore.

Fig. 2.

Complete clustering pipeline diagram. Phases that are executed in parallel are represented in stacked boxes. (1) filter near-duplicates, (2) compute suboptimal structures, (3) compute sparse vector encoding, (4) compute global feature index and return top dense sets, (5) refine clusters with structural alignment procedure, (6) build covariance model with remaining high quality instances, (7) populate each cluster with retrieved instances, (8) remove clustered instances and iterate from Step 4 and (9) merge redundant clusters.

3 METHODS

3.1 Datasets

Benchmarking. We have tested and measured the performance of our method by clustering known ncRNA classes obtained from two different sources. (i) We clustered a set of 503 families obtained from the Rfam database (Gardner et al., 2011) which has previously been successfully used to benchmark LocARNA-based structural clustering (Will et al., 2007). The original set consists of all Rfam seed sequences (v7.1), filtered for 80% sequence similarity and lengths <400 nt. Application of blastclust to remove trivial sequence clusters leaves 3900 sequences. The majority of families (252/503), however, has <3 members. Only 124 families, comprising ~80% (3118) of all sequences, have >5 members. (ii) We collected a comprehensive set of 49 bacterial small ncRNA families (941 sequences) from the NCBI Genome Database. Non-coding RNAs present in at least 10 species were considered. Removing sequences exceeding 400 nt in length and similar sequences using blastclust leaves 363 bacterial ncRNAs. These were randomly embedded in 50 nt genomic context sequence to harden the classification problem. The set contains 6 families with <3 members and 37 families with >3 members. Sequences of both benchmark sets were not split. In addition, intended to recover the structural classes presented in Parker et al. (2011), we clustered 725 EvoFold hits that form 220 EvoFam families (Parker et al., 2011).

Application. We analyzed different sets of predicted ncRNAs: we clustered 37 381 human EvoFold hits, 16 377 RNAz ncRNA candidates of the fruit fly Drosophila melanogaster (Rose et al., 2007), and 11 536 ncRNA candidates of the teleost Takifugu rubripes (Rose et al., 2008). EvoFold predictions are generally short and were not split before clustering. For both RNAz screens, sequences were fragmented into stretches of 150 nt (minimum length 50 nt). Removing nearly similar sequences using blastclust left 17 765 fragments for fruit fly and 11 287 fragments for teleosts. Moreover, we searched for novel local structural motifs in long ncRNAs. (i) We clustered the collection of 8195 human lincRNAs described in (Cabili et al., 2011). Splitting (150 nt windows, minimum length 50 nt) and blastclust filtering resulted in 31 418 fragments. (ii) We clustered the set of 1133 lincRNAs expressed in zebra-fish embryos recently reported in Pauli et al. (2011). Preprocessing yielded 5877 fragments, ready for clustering.

Resulting structural clusters were annotated using Infernal (v.1.0.2) (Nawrocki et al., 2009). Using CMsearch, we compared our clusters with all Rfam seed models (v.10.1) that have an average seed sequence length ≤500 nt. Clusters yielding CMsearch hits with an E-value of E<10⁻⁵ were considered as known, others as novel.

3.2 Evaluation

GraphClust works iteratively and hence, we can measure the clustering quality at the end of each round. We use the F measure and the adjusted Rand index (Hubert and Arabie, 1985) as quality measures. The F measure is the harmonic mean of precision and recall and measures the quality of a single cluster, defined as F=2 (Prec·Recall)/(Prec+Recall). Precision is defined as Prec=TP/(TP+FP), where TP is the number of correct cluster members and FP is the number of wrong cluster members. Recall is defined as the fraction of correctly clustered members over the full family size. To each cluster, we assign the family with the majority of members. We report the average F measure over all clusters at the end of each round. The Rand index compares two clustering hypotheses taking into account all possible pairs of instances. The similarity measure is based on the fraction of times when the two clustering hypothesis agree that the elements in each pair belong to the same or to different clusters. We use the adjusted Rand index, which uses a hypergeomeric model to correct for chance effects, so that the value range is [0, 1], with random partitioning scoring 0 and perfect agreement scoring 1. Note that we measure only the quality of clustered RNA sequences, that is, we skip elements which are not part of any cluster, which is reasonable when dealing with large datasets.

We calculate the quality measures on the basis of different clustering hypotheses, called partition types. The initial clustering resulting from all candidate clusters is called SOFT clustering where a specific RNA candidate could belong to >1 cluster. From this SOFT clustering, we generate two partitions BEST and MERGED. In addition, we consider for evaluation purposes a theoretical ORACLE partition. Partion BEST assigns an RNA candidate to the model with the best score (without any merging). MERGED uses the described merging strategy (see Section 2.3, Phase 9) of overlapping clusters and applies BEST afterward. This clustering hypothesis is used as results for all application scenarios. The ORACLE partition assumes a supervised or perfect merging strategy and shows the maximum theoretical performance. In this case, all initial clusters (SOFT clustering) with the same majority true class were merged, using BEST as final partitioning strategy. The overall running time is an important measure of our pipeline. Here, we measure the time of each phase and provide a total time after each iteration and an average time per predicted cluster.

Furthermore, details on applied parameters are given in the Supplementary Material.

Comparison to other methods. Alignment-based RNA clustering methods which take into account structural properties need to calculate a pairwise distance matrix first. This information can be used to get a clustering hypothesis using different methods, for example, by creating a guide tree. We compare our clustering to a LocARNA-based clustering. The idea of the comparison is to show that our clustering approach achieves similar and high clustering qualities but with the discussed benefits especially in complexity and therefore runtime. We use RNAsoup to partition the LocARNA cluster tree into an optimal number of clusters and evaluate them with the given quality measures. A cluster is reported as optimal cluster if the sum-of-squared error for two clusters is not significantly smaller than expected by chance. The significance level of RNAsoup can be controlled by k and authors give a range 0.8≤k≤1.2 for Rfam sequences. The error of a cluster is determined via the free energy of its consensus structure and the minimum free energies of its individual sequences. Clearly, this procedure gives a full clustering whereas our pipeline only clusters a subset. Therefore, we eliminate all clusters with <3 members from the RNAsoup partition. We also measure the LocARNA runtime as aggregated serial time. We use LocARNA without any speedup heuristics to stress the inherent complexity issue of existing structure-based clustering methods. Using speedup heuristics would give a much lower overall LocARNA runtime, but not in the order of several magnitudes.

4 RESULTS

4.1 Evaluation of the GraphClust pipeline

Rfam benchmark. We run our pipeline for 15 iterations, retrieving 10 candidate clusters at each iteration. Table 2 gives an overview of the result for the clustering of 3901 Rfam sequences. See Supplementary Information Tables S1 and S2 in the Supplementary Material for more details. After 15 iterations, we identified 130 clusters (MERGED partition). The high F measure (0.834) and Rand index (0.984) indicate a correct clustering. The result reflects the fact that only 124 of 502 families have >5 members. Prior to the merging phase, we identified 148 clusters (SOFT clustering) with a quality of F=0.796 (R=0.483). This clearly indicates that the overall cluster quality can be significantly improved employing a merging strategy. Increasing the number of iterations does not produce additional meaningful clusters, resulting rather in a slightly decreased overall quality. We report the aggregated runtimes for all serial and parallel phases. Running the entire pipeline took ~36 h (129 626 s) when viewed as serial process. The parallelized version, however, took ~3 h. Note that the clustering step in Phase 4 took only between 1 and 8 min (serial time), which was the bottleneck in previous approaches. See also Figure S1 for more details. To compare our results to state-of-the-art sequence–structure clustering, we applied RNAsoup to the cluster tree obtained from LocARNA alignment scores. We chose the partition with k=0.8 which gave a quality of F=0.588 (R=0.586) for 160 predicted clusters containing 3569 sequences. We considered only cluster with at least three members for a fair match. Other k values give similar (although slightly worse) results. Clustering 3901 sequences with LocARNA without any speedup heuristics took ~370 days, yielding a theoretical 246-fold speedup for our method. Clearly, it is possible to employ parallelization and effective heuristics also for LocARNA. We also analyzed the impact of using a sample of 50% and 25% in Phase 4 and observe a similar quality (see Supplementary Table S5).

Table 2.

Results for Rfam and small ncRNA benchmark set

			Quality (MERGED)		Time (in s)
i	#Seq	#C	F	Rand	Phase 4	Timei	TimeALL
Rfam benchmark
0						8314	8314
1	271	5	0.882	0.888	458	14 995	23 309
2	629	14	0.834	0.932	416	19 962	43 272
3	1076	23	0.868	0.956	334	15 108	58 380
7	2181	58	0.877	0.985	154	11 964	104 940
15	2821	130	0.834	0.984	77	2491	129 626
Small ncRNA benchmark
0						720	720
1	140	10	0.942	0.945	42	2434	3154
2	232	20	0.926	0.939	27	3395	6549
3	270	26	0.936	0.935	17	7681	14 230
7	329	35	0.890	0.897	5	250	23 186
15	360	43	0.858	0.866	1	92	24 301

Results for each iteration i on the MERGED partition. Clustering quality is given as F measure and Rand index. The total number of clustered sequences is indicated with #Seq. The total number of clusters after merging is given by #C. Time_i denotes the total time for iteration i, Time_ALL is the total serial time up to iteration i.

Small ncRNAs benchmark. We run our pipeline for 15 iterations, retrieving 10 candidate clusters at each iteration. Table 2 gives an overview of the results for the clustering of 363 small ncRNAs (see also Supplementary Tables S3 and S4). After 15 iterations, we identified 43 clusters (MERGED partition) from 38 unique families. The overall clustering quality is high with F=0.858 and R=0.866. The additional flanking sequences do not disturb the quality. LocARNA applied to this set results in a quality of F=0.729 and R=0.88 using RNAsoup with k=0.4 (other k have lower qualities). The serial runtime of the pipeline is ~6.8 h. LocARNA applied to the same dataset takes ~7 days.

EvoFam families. Application of GraphClust (five iterations) to the 725 EvoFam-annotated sequences yielded 37 structural classes. We recovered 14 known families with F≥0.5. In particular, even raising the threshold (F≥0.7), we identified 5 out of 8 families with ≥10 members. Applying GraphClust on all 37 381 human EvoFold hits (20 iterations, see Table 1 for runtimes and Figure S3 for exemplary clusters) recovered the same amount (5/8) of EvoFam families (albeit different in type) having ≥10 members. ∈ fernal annotates ~38% (14/37) of the GraphClust-derived EvoFam clusters as known ncRNA classes. For example, we identified the Histone 3′UTR stem-loop motif and the let-7 miRNA family. The vast majority of clusters (11/14) were known miRNAs. For 10 of the 11 miRNA cluster, the E-value of the best Infernal hit was <10⁻¹⁵ indicating a reliable class annotation. Interestingly, these GraphClust results can also be used to identify novel human miRNA candidates, see Supplementary Figure S4.

Table 1.

Overview

Species	Type	Method	Input	Size (Mb)	Timea	Cluster	MPIavg	SCI>0.5	Reference
Benchmark
Bacteria	Small ncRNAs	Misc	363	0.06	6.8 h	39	0.75	29	NCBI ftpb
Human	Predicted RNA elements	EvoFam	699	0.03	0.3 h	37	0.52	36	Parker et al. (2011)
Misc	Small ncRNAs	Rfam	3900	0.51	36 h	130	0.64	98	Gardner et al. (2011); Will et al. (2007)
De-novo discovery
Fugu	LincRNAs	RNA-seq	5877	0.09	10.3 h	99	0.39	16	Pauli et al. (2011)
Fugu	Predicted RNA elements	RNAz	11 287	1.36	13.3 h	97	0.39	22	Rose et al. (2008)
Fruit fly	Predicted RNA elements	RNAz	17 765	2.15	20.4 h	95	0.34	23	Rose et al. (2007)
Human	LincRNAs	RNA-seq	31 418	5.40	3.6 d	95	0.34	3	Cabili et al. (2011)
Human	Predicted RNA elements	EvoFold	37 258	1.37	5.7 d	117	0.75	109	Pedersen et al. (2006)
Human	3′UTRs	RefSeq	118 514	21.91	12.8 d	106	0.34	13	Pruitt et al. (2009)
∑			227 081	32.88	25.7 d	815	–	349

^aPlease see text for different parameters influencing the run-times.

^bftp://ftp.ncbi.nih.gov/genomes/Bacteria/ The table summarizes the datasets used in this study and gives an overview on GraphClust-detected clusters. For each screen, we provide the number of input instances and the sum of their lengths (size). We denote the required serial running time to process the input and list the number of obtained clusters. Next, we report the mean pairwise identity (MPI) and the number of clusters that have a structure conservation index (SCI) above 0.5. These are prime candidates for structured ncRNA classes.

4.2 GraphClust predicts novel local structural motifs

Most of the known families, including tRNAs, snRNAs (U2, U5), and miRNAs, were recovered in the fruit fly RNAz screen (six annotable clusters). Throughout all de-novo discovery screens, miRNAs were most abundantly detected (four clusters in fugu- and two clusters in the fruit fly-RNAz screen; two clusters in fugu lincRNAs). Clustering the EvoFam dataset has shown that GraphClust can recover known UTR elements. Therefore, we decided to analyze and search for novel cis-regulatory UTR elements on a broader scale by clustering all RefSeq 3′UTRs. Beyond a single box H/ACA snoRNA, this search again returned the Histone 3′UTR stem-loop motif. Furthermore, it resulted in up to 116 candidates for novel cis-regulatory elements. The majority of generated clusters, however, cannot be annotated by existing Rfam models and are candidates for novel ncRNA classes. As depicted in Table 1 (see also Supplementary Figure S2), our obtained motifs have comparably low sequence similarity (measured by MPI). Nevertheless, we predicted 186 novel clusters that have an SCI >0.5 indicating that these are indeed novel structural clusters.

Structural motifs of lincRNAs. We extracted 95 local motifs from the 8195 human lincRNAs recently reported by Cabili et al. (2011). In 55% (52/95), of all cases, the majority of transcripts underlying our structural clusters are consistently expressed in the same tissue. The vast majority of clusters (49/52) contains transcripts specifically expressed in testes. This, however, is expected, since Cabili et al. (2011) have already shown that most of their lincRNAs are expressed in testes. Nevertheless, we also obtained structural motifs from transcripts that are consistently and specifically expressed in either skeletal muscle, kidney and brain. Next, half of our clusters (47/95) contain transcripts for which the studies of Cabili et al. (2011) resulted in enriched GO-FAT (Gene Ontology subset with more specific terms in contrast to GO-SLIM) biological process terms (Huang et al., 2009) and hence are putatively functionally linked to their nearest protein-coding gene. We found 17 clusters that contain at least two different lincRNAs with enriched GO terms. Of these, ~53% (9/17) of structural lincRNA motifs are associated with exactly the same GO term. The actual number of structural motifs with a specific biological function is likely higher, as different GO terms can still convincingly refer to similar biological processes. For example, we obtained clusters whose transcripts are described by the obviously related GO terms ‘neuron differentiation’, ‘regulation of neurogenesis’, ‘regulation of nervous system development’ and others. Manual inspection has shown that most of the cluster-associated GO terms deal with aspects of neuron differentiation and development, neuronal signaling, cognition and related processes. This is in-line with the recent findings that long ncRNAs are functionally linked to the nervous system, neuronal diseases and brain function (Chodroff et al., 2010; Qureshi et al., 2010).

Furthermore, we extracted 99 local motifs from the 1133 teleost lincRNAs recently reported by Pauli et al. (2011). Interestingly, these contain up to five times more novel structural classes than their human counterpart. This might be explained by the fact that teleost fish underwent an additional whole-genome duplication (Christoffels et al., 2004) which increases the likelihood to identify paralogous genes.

5 DISCUSSION

We introduced for the first time an ultra-fast pipeline for large-scale comparison and clustering of RNAs according to sequence and structure, which is key to the functional annotation of ncRNAs. Strikingly, its core steps are alignment-free. As clearly indicated by the result, the approach is linear in time and thus scales to sets of hundreds of thousands of sequences. The largest dataset we considered in this study consists of ~118 thousand sequences, and they can be clustered by the proposed pipeline on a single computer in ~12.8 days. Furthermore, we have parallelized 5/9 phases of the pipeline: this allows to reduce the run-time for clustering the 3901 Rfam seed sequences from 36 to ~3 h. When compared with the time required by an efficient pairwise sequence–structure alignment, namely LocARNA, we observe a ~250-fold speedup. It indeed took us 370 days to perform the clustering based on this state-of-the-art complete all-against-all sequence/structure comparison.

We have integrated the alignment-free clustering approach in a pipeline that uses LocARNA and Infernal to improve the initial clusters found by a neighborhood search. The latter, now allows us for the first time to compile RNA classes of ncRNA and determine associated consensus structures for large-scale datasets without resorting to alignment-based clustering. This is important as it is known that sequence alignments often fail at pairwise sequence identities below ~60%. In addition, our pipeline exhibits an anytime characteristics, as we do not need to produce a complete hierarchical cluster tree, which is a computational bottleneck for large datasets. In contrast, we output as many best clusters as wanted by the user. The overall complexity of our pipeline is to a large extend determined by the number of reported clusters.

We have evaluated the approach on several benchmark sets consisting of Rfam seed alignments, EvoFam families and known bacterial ncRNA. Here, we achieve a high overall clustering quality, even if the known RNA signal is embedded in flanking context. To further elucidate the capacity of our approach, we have also clustered datasets where no clustering approach has been applied so far. By processing the complete dataset to generate its density landscape, our method in particular enables us to likely detect previously missed structural classes.

The screens of this pilot study only consisted of sequences from a single genome. Thus, we can cluster only RNA genes that are present in multiple copies within a genome. This implies that most of the found clusters consist of paralogs, structures from repeat-associated RNAs mobile elements, i.e. transposon-derived ncRNAs and maybe also pseudogenes. Even under this setting, we can show that we find many structured classes, when we use the commonly accepted SCI to determine structuredness of a cluster. This can easily be improved by using additional information on orthologs, as it is for instance done in the EvoFam approach, where a 41-way multiple alignment is used.

Since the lincRNA dataset contains GO annotation, we have used this information for further evaluation. Albeit the GO enrichment analysis is limited by the low number of transcripts that are associated with GO terms [overall, GO terms are only available for 12% (1044/8195) of the Cabili et al. (2011) lincRNAs], we found nevertheless that the GO terms for the majority of clusters (53 but likely more) are consistent and support our clustering approach.

One of our ideas to soon improve our pipeline from an algorithmic point of view is to, instead of relying to fixed parameters, base the parameter optimization onto machine learning techniques, i.e. let a support vector machines select the optimal parameters. This, together with future applications of graph kernel-based alignment-free clustering approaches will likely result in the detection of additional functionally relevant structural ncRNA classes.

Funding: German Federal Ministry of Education and Research (BMBF) [0313921 to R.B. and his lab]; German Research Foundation [BA 2168/3-1 and BA 2168/4-1 to R.B. and his lab].

Conflict of Interest: none declared.