Interfacing with the Computational Brain

Abstract

Neuroscience is just beginning to understand the neural computations that underlie our remarkable capacity to learn new motor tasks. Studies of natural movements have emphasized the importance of concepts such as dimensionality reduction within hierarchical levels of redundancy, optimization of behavior in the presence of sensorimotor noise and internal models for predictive control. These concepts also provide a framework for understanding the improvements in performance seen in myoelectric-controlled interface (MCI) and brain-machine interface (BMI) paradigms. Recent experiments reveal how volitional activity in the motor system combines with sensory feedback to shape neural representations and drives adaptation of behavior. By elucidating these mechanisms, a new generation of intelligent interfaces can be designed to exploit neural plasticity and restore function after neurological injury.

I. Introduction

David Marr famously identified three levels on which to describe information processing in the nervous system: implementation, algorithm and computation [1]. Interfacing with the implementation of the brain, single neurons, is now reliably achieved in invasive BMIs with chronically implanted electrodes, which allow individual action potentials to be recorded from stable populations of 10s to 100s of neurons over period of weeks to years [2]–[5]. Interfacing at the level of algorithm may be considered as a problem of `decoding' the neural representation. Numerous methods have been developed for this purpose, often based on assuming neural encoding schemes for movement parameters determined during off-line analysis [6]–[11]. However, restoring sophisticated sensorimotor function after neurological injury will require BMIs to interface also with high-level, on-line processes that allow the brain to optimize control of complex effectors with multiple, redundant degrees of freedom. These occur over a range of time-scales, and may only become apparent once a BMI is incorporated into the motor system over many days [12]–[14]. With improved stability of chronic electrodes, long-term BMI experiments are revealing plastic changes in neural representations and affording new insights into these complex adaptive processes driven by sensorimotor interactions. In this review, we draw on recent theoretical work in optimal motor control and experimental studies of learning and plasticity in the context of brain- and myoelectric-controlled devices to present a framework for interfacing at the computational level of the brain.

II. The biomimetic decoding approach to BMI

The conventional biomimetic decoding approach to BMI design has its historical roots in neuroscience experiments from the 1960s onwards that attempted to uncover the neural representation of natural movements. In an influential study of center-out reaching, Georgopoulos and colleagues [15] found that activity of individual neurons in primary motor cortex (M1) was modulated with the direction of arm movements. Neuronal firing rates exhibited cosine-shaped tuning functions of direction that were maximal for movements in the cells' preferred direction (PD). By recording the activity of multiple neurons with different PDs, a population vector could be calculated (by a weighted sum of individual vectors) that closely matched the actual direction of movement. One interpretation of these results is that populations of neurons `encode' information about direction, which is `decoded' by downstream circuitry (perhaps located in the spinal cord) in order to execute a movement. Using such logic, the decoding machinery can be replaced by a BMI algorithm to read out movement information for control of an artificial effector, for example a computer cursor or robotic arm [16]–[18]. The advantage of effective biomimetic decoding is the ability to confer immediate intuitive control without undue cognitive load [19].

Since the first demonstrations of biomimetic BMIs, considerable effort has been expended developing decoding algorithms of increasing sophistication [6]–[11]. Typically decoders are trained on neural data recorded during natural movements before `brain control' commences, and this relationship between neural activity and movement parameters (or neuromotor mapping) is preserved for control of the artificial effector. The requirement for a training dataset presents a practical problem for ultimate clinical applications with paralyzed patients, although motor imagery may provide a suitable substitute for actual movement [19]. A more serious problem is that an artificial effector is unlikely ever to reproduce the rich sensory and proprioceptive feedback provided by a real limb which influences the motor system at multiple levels [20–21]. It is therefore unlikely that neuromotor relationships derived from natural movements will be optimal under the deprived sensory conditions afforded by a BMI. This may explain why the quality of off-line decoding performance is rarely matched by on-line performance, which has been likened to the movements made by deafferented patients [22], particularly with regard to the lack of fast, on-line correction of errors. Unlike the smooth, ballistic trajectories of natural limbs, movements of a BMI often comprise discrete segments, with trajectory deviations corrected only after delayed visual feedback [23]. These observations have motivated attempts to restore proprioceptive feedback artificially, for example via microstimulation of sensory cortex or thalamus [22], [24], although such an agenda may present an even greater challenge than efferent decoding. Furthermore, a distinction should be drawn between errors that arise due to external sources of noise (i.e. uncertainty about the state of the limb or the environment it interacts with) and errors arising from internal sources of noise (due to the inadequacy of decoding from a limited population of motor cortex neurons). External sources of noise are fundamentally unpredictable, and therefore generate errors that can only be corrected through appropriate feedback. By contrast, internal sources of noise can in principle be monitored and compensated for on-line even in the absence of feedback.

Another fundamental issue that has received surprisingly little attention within the BMI community is the validity of the primary assumption underlying the biomimetic approach, namely that movement parameters are meaningfully and consistently encoded by the firing rates of M1 neurons at all. Indeed the recent history of movement neuroscience may be viewed as a steady retreat from this idea [25]–[28], from debates over `muscles versus movements' [29]–[33] to the ever expanding range of parameters found to co-vary with neural activity in primary motor cortex [26], [27]. On the one hand, the lack of a specific `encoding' scheme does not render `decoding' impossible. Indeed, over forty years ago Humphrey and colleagues [34] showed that the correct choice of weights allowed them to decode from the same set of neurons either force, displacement or their temporal derivatives during repeated wrist movements (see also [18]). On the other hand, without principled assumptions about what parameters are encoded, there is no reason to expect any decoder to generalize beyond that sub-space of movements sampled within the training set. Thus, we should not be surprised to learn that neuromotor mappings derived from an instructed center-out task do not generalize to freely-made movements [35], [36], or that the distinct neural pathways subserving postural control, goal-directed movements and on-line trajectory corrections may employ different encoding schemes [27], [37], [38]. Therefore, while features of ballistic movements to targets made during training phases can be accurately fitted off-line, these decoders may be inappropriate for fast, on-line corrections of errors arising from central sources of variability in neural command signals.

III. The Biofeedback approach to BMI

An alternative conceptual approach to BMI can be traced from early biofeedback experiments in which subjects were trained to volitionally modulate the firing rate of neurons [39], [40]. Typically, these experiments required subjects to learn arbitrary mappings between neural activity and a feedback signal (visual or auditory) in order to achieve a reward. An important early question was the degree of flexibility to associate or dissociate two signals. Thus, Fetz and Baker [41] showed that monkeys could learn within minutes to differentially activate neighboring motor cortical neurons to drive a biofeedback meter arm to the reinforcement target. Furthermore, the activity of cortical neurons and four groups of forearm muscles could also be readily activated in various combinations [42]. In particular, the activity of neurons and consistently coactivated forearm muscles could be dissociated when the monkey was rewarded for such patterns. More recently bidirectional dissociation has been demonstrated for corticomotoneuronal (CM) cells and their target muscles, which normally have tight correlational linkages [43]. This degree of flexibility indicates that the specific neuromotor mappings that subserve natural movements are unnecessary for learned BMI control. Moreover, volitional control could exploit a larger population of neurons than those identified by traditional biomimetic decoding methods [44].

Recently, Ganguly and Carmena [13] have extended this approach to a two dimensional BMI decoder. Importantly they used a subset of recorded cells which showed stable activity over a period of up to 20 days. This afforded the animal time to practice over several days and consolidate a stable neural representation of a biomimetic BMI. Interestingly, the animal was then able to learn a new, randomized neuromotor mapping based on the same set of neurons, and even to switch readily between the two when required.

While biomimetic and biofeedback BMIs can be seen as contrasting approaches, it should be acknowledged that few BMI groups actually fall into such extreme positions. The pioneering closed-loop decoding studies [16]–[18] already recognized the importance of learning mechanisms to optimize BMI control. Nevertheless, this conceptual distinction is relevant to how BMIs are envisaged to relate to normal motor function. A biomimetic BMI may be conceived of as a `prosthesis' to restore (as seamlessly as possible) function lost through injury, whereas a biofeedback BMI represents a `tool' that the brain has to learn to use in a new way. Although such tools can replace a lost function, they may also have broader applicability in affording new or enhanced abilities to their user, or as a rehabilitation mechanism for training new neural circuits to compensate after injury [12], [45], [46].

IV. Internal models for arm movements and BMIs

To understand how feedback drives learning in the BMI paradigm, it is useful first to consider the computations that must be performed by the motor system during natural movements. Human reaching movements are typically fast, accurate and characterized by stereotyped features such linear trajectories and bell-shaped speed profiles [47]. It is commonly accepted that such movements cannot be generated by simple feedback control, due to delays in sensory information and the need to co-ordinate muscles acting across different joints of the limb [48]. Instead the motor system requires advanced knowledge of the kinematics and dynamics of the limb and environment; this knowledge is often described as an internal model. An `inverse model' describes the transformation from desired states of the environment to motor commands (Figure 1B) and could generate feed-forward, goal-directed movements without the delays incurred by feedback. However, inverse models are in general ill-posed, one-to-many mappings due to multiple levels of redundancy in the motor hierarchy (Figure 1A). Whenever a particular goal is specified (for example an object to reach for), we are confronted with a wealth of potential choices concerning how best to achieve it. There are multiple trajectories that the hand could follow to reach the goal, and any given trajectory could be generated using multiple patterns of joint angles and muscular contractions (due to redundancy in the musculoskeletal system). A further level of redundancy results from the massive convergence and divergence within the corticospinal pathway [49], which allows a particular set of muscle activations to be achieved by many different activity patterns distributed across the population of cortical neurons.

Fig. 1.

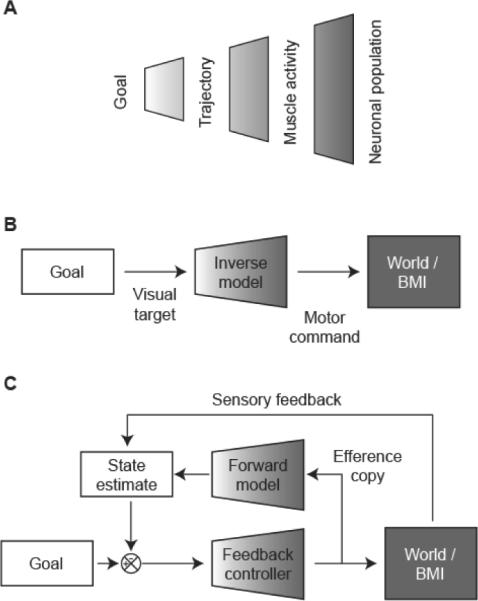
A. Schematic representation of multiple levels of redundancy within the motor system. B. Generating optimal movements requires advance knowledge of the environment. Here an inverse model converts visual target information into a feed-forward motor command to drive a BMI. C. Optimal feed-back control uses a forward model to generate predictions based on a copy of the motor command. This prediction can be combined with sensory feedback to form a state estimate that drives movement through a feedback controller.

By analogy with natural movements, the ability of subjects to learn feed-forward control of a BMI requires the acquisition of an internal model of the neuromotor mapping between a desired goal state (e.g. target location) and the neural control signals required to achieve that state. As with natural movements, in general this inverse problem is ill-posed due to the dimensionality reduction from control to task spaces. If 100 neurons control the position of a cursor in two dimensions then any given target can be reached by a manifold of potential solutions within the space of neural firing rates.

Accurate control either of natural arm movements or a BMI therefore involves two distinct problems: (1) learning the relationship between motor commands and their effect on the world, and (2) choosing from the manifold of all possible acts that could achieve a desired goal the particular solution that is best. These problems are separated explicitly within the framework of optimal feedback control [50]. In this scheme, the motor system learns a `forward' model (which predicts the peripheral state based on a copy of the efference command) and a feedback policy that operates on task-relevant dimensions of the state-space (Figure 1C). Acquiring a forward model is then a well-posed problem that can be achieved by self-supervised mechanisms and may facilitate subsequent optimization of the controller. This theoretical framework has the additional advantage that internal predictions based on efference copy can be combined with available sensory feedback in generating an estimate of the current state. However, while optimal feedback control explains several features of natural movements, distinguishing the relative contributions of inverse models, forward models and sensory feedback remains an unresolved issue.

V. Optimal control of a BMI

Irrespective of how natural movements are controlled, their repeatable kinematic profiles have been interpreted at the computational level as the optimization of behavior within the constraints of the redundant motor system based on some additional criterion, e.g. smoothness [51], torque change [52] or inaccuracy due to motor noise [53], [54]. Optimal control theory can be formulated mathematically by defining a cost function, and selecting a control policy to minimize that function [55], [56]. By analogy, we may suppose that acquiring optimal control of a BMI involves minimizing some cost function within the constraints imposed by the decoding scheme. Experimental studies have described a variety of changes in the tuning functions of individual neurons during brain-control [16], [18], [57], [58]; reviewed in [14]. To what extent can these disparate results be explained by a single cost function? One possibility is that the brain tries to limit the amount of effort required to make BMI movements, for example the metabolic cost of driving neurons to high firing rates. This is consistent with an overall decrease in firing rates with development of BMI control seen in some studies (e.g. [18], [58]). Alternatively, given the limited accuracy of BMI systems, it may be that minimizing the influence of neural noise on effector movements is critical for optimizing performance [59], [60]. The minimization of overall motor error has been used to explain cosine tuning of muscles during natural movements [54], [61]. However the extension of this approach to BMI paradigms is not straightforward since the signal-dependence of neural noise is hard to characterize and unlikely to be statistically independent across the population [61], [62]. In general, it seems likely that the brain attempts to minimize some combination of effort and inaccuracy with the relative contribution of each depending on particular experimental circumstances.

VI. Investigating learning using myoelectric-controlled interfaces

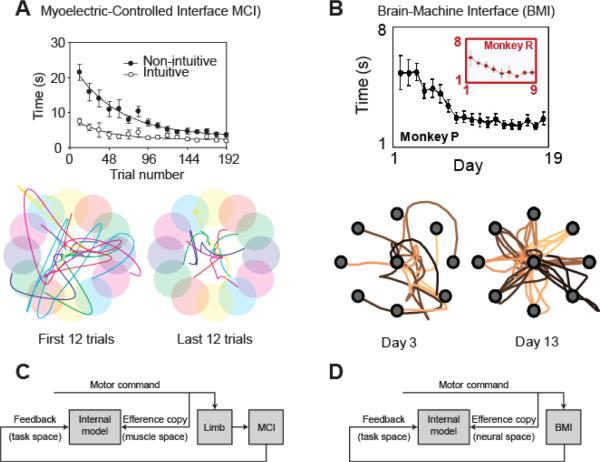
To explore the ease with which the brain optimizes behavior under novel neuromotor mappings, Radhakrishnan and colleagues [63] developed a myoelectric-controlled interface (MCI) mimicking the dimensional reduction problem faced during BMI control. Rectified and smoothed EMG activity from six hand and arm muscles was mapped onto a two-dimensional visual task space through a linear combination of vectors aligned to a direction of action (DoA) for each muscle. In what follows it will be important to distinguish the DoA (also referred to as the `decoded PD' [64]) from the preferred direction (PD) of individual units (neurons in BMI studies, or muscles in MCI studies) defined by the peak of the tuning function of activity with respect to actual cursor movements. The DoA is determined by the particular decoding algorithm chosen by the experimenter, while the PD is measured experimentally from the subjects behavior. In the case of biomimetic decoding, the DoA is chosen to be the same as the PD during natural hand movements in space, but this does not have to be the case. Reference [63] compared such intuitive, biomimetic control (in which DoAs were aligned with the action of each muscle on the hand), with `nonintuitive' control in which DoAs were assigned randomly. Although performance was initially poorer under nonintuitive arrangements, after 200 practice trials (~ 30min) performance reached a plateau comparable to control under the intuitive mapping (Figure 2A). After training, tuning functions (muscle activity as a function of cursor movement) were cosine-shaped with a PD that aligned to the DoA in cursor space. Such broad tuning functions are consistent with the minimization of position error in the presence of signal-dependent muscle noise [54], [61]. Further experiments that manipulated the noise level in a subset of muscles showed a relative decrease in use of those muscles, again suggesting an accuracy constraint [63]. Importantly, after training these tuning functions emerged early in the movement, indicative of feed-forward control based on an appropriate predictive internal model.

Fig. 2.

A. Learning curves for MCI performance. Average trial time reaches a comparable level irrespective of whether the decoding algorithm is intuitive (muscles act on the cursor in directions that are consistent with their action on the limb) or non-intuitive (muscles act in random directions). By the end of a single training session, subjects make fast, straight movements to the target. Adapted from [63]. B. Learning curves for BMI performance with the same neural population. Average trial time decreases over successive days for two monkeys. In this case the decoding algorithm was biomimetic (intuitive). Subsequent training on a randomized (non-intuitive) decoder required several more days to be optimized (not shown; see Fig. 6 in [13]). Adapted from [13]. C, D. Proposed model for learning MCI and BMI control involves acquiring the mapping between a copy of the efferent command signal and task-space feedback provided by the interface.

The apparent ease with which subjects could learn this task is in contrast to the longer time-frame (days) required to learn BMI control in animal studies [13] (Figure 2B). One explanation could be the presence of proprioceptive information about the limb in an MCI setting, even though the arm is restrained and actual movement is minimal. However degrading sensory signals with randomly amplitude- and frequency-modulated vibration of the hand and arm did not affect the rate at which MCI learning progressed [63]. We suggest that proprioception is unnecessary for MCI tasks since the brain has access to information about the motor command via efference copy. Acquiring an internal model of the MCI is then equivalent to learning the mapping between the efferent command and its consequence in the task space (Figure 2C). A similar process may underlie learning in BMI contexts when proprioceptive feedback is unavailable (Figure 2D). In principle, feedback about the task space may be provided in any modality and exploiting relatively direct proprioceptive channels into the motor system may be advantageous [65]. However, the key difference between MCI and BMI tasks is the level of efference copy onto which this maps. For an MCI task, the mapping is at the level of muscle activity, whereas in a BMI the task space maps onto the activity of individual neurons, which is lower in the hierarchical representation of Figure 1A.

VII. Hierarchical remapping: a unifying framework for MCI and BMI experiments

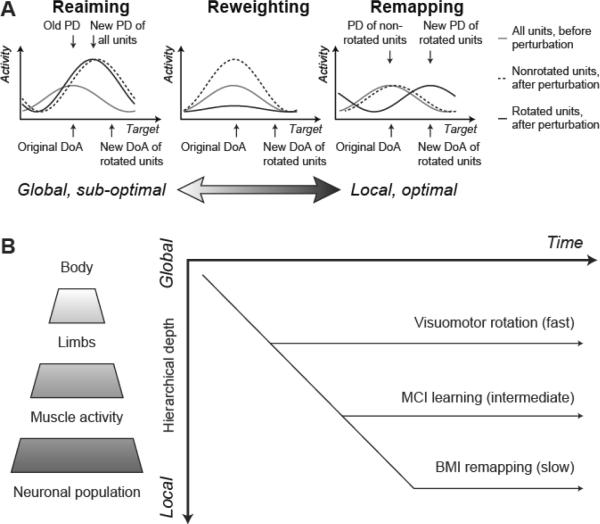
Further insight into the mechanisms of internal model acquisition comes from experiments in which a previously learned BMI or MCI decoder is subject to specific perturbations [64], [66]. These experiments deliberately decouple the DoA of units (neurons or muscles) from their preferred direction with respect to arm movements. Again, the DoA is determined by the experimenter, while the PD (with respect to movements of the cursor) is measured empirically. Since the mapping from units to cursor space is redundant, multiple different strategies can compensate for any perturbation so subjects' particular choice is informative of their expectations about the causes of errors. Jarosiewicz and colleagues [64] examined three such strategies in response to rotational perturbation of the DoAs of 25% or 50% of cortical units: reaiming, reweighting and remapping (Figure 3A). Reaiming may be described as aiming for an imaginary target repositioned in the task space so as to compensate for the overall rotation, although this strategy need not be explicit [67]. In any case, when the activity of units is plotted as a function of the direction of cursor movement towards the actual target, reaiming appears as a consistent rotation of the PD of all units relative to their old DoA as if the perturbation were a global visuomotor rotation (note that since this applies to all the units, the magnitude of this rotation is less than the actual rotation applied to the perturbed units). However, this strategy requires an overall increase in activity (effort) since the new PD of units is inappropriate for the direction they actually act on the cursor (the perturbation in fact only affects some of the units). Reweighting is a local strategy in which the activity of perturbed units is selectively reduced. However, this strategy is also sub-optimal since subsequent control uses only the unperturbed subset of units and will therefore be less accurate. Local remapping describes the selectively rotation of the PDs of rotated units to reflect their new DoA; the tuning functions of remaining units are unchanged. This strategy minimizes both effort and inaccuracy since all units continue to contribute to control and are maximally active for movements aligned to the new direction they act on the cursor. Reaiming and remapping therefore reflect extremes of a spectrum ranging from global, sub-optimal to local, optimal strategies. While [64] found some evidence of local remapping, the observed PD changes for unperturbed units also indicated a large contribution of global, sub-optimal reaiming to the adaptation process.

Fig. 3.

A. Three (out of many) strategies that can be used to compensate for local rotational perturbation to a MCI or BMI mapping. The plots show the activity of representative units as a function of target direction relative to the original DoA (before a perturbation occurs). Tuning functions are assumed to be cosine-shaped, initially peaked at the DoA (gray line). Plots show predictions of three strategies (reaiming, reweighting and remapping) after a local perturbation in which the DoA of a subset of units rotates (indicated by arrows beneath the abscissa). Tuning functions for rotated units (solid line) and non-rotated units (dashed line) are shown following perturbation. B. Schematic of the hierarchical remapping framework. Remapping progresses from global to local levels of the redundant motor hierarchy. Therefore optimal adaptation to perturbations at a high level (e.g. visuomotor rotation) occurs before adaptation at lower levels (e.g. after local perturbation of BMI decoders).

We have recently applied similar perturbations in the MCI setting by rotating the DoA of a subset of muscles [66]. In contrast to BMI experiments, we saw rapid remapping at the level of muscles, with PDs evolving to reflect the new DoAs within about 30 min while the PD of unperturbed muscles was unchanged. We suggest the difference in these results may be resolved by considering the motor hierarchy represented in Figure 3B. Since there is redundancy at each level, remapping at any one level may be achieved by a strategy that is either global or local at the level beneath. We propose that remapping is hierarchical such that control is optimized at progressively lower levels with time (Figure 3B). Therefore the time required to adapt to a perturbation will depend on the level within the hierarchy at which it acts. A globally-consistent perturbation such as visuomotor rotation is learned quickly (typically around 20–50 trials). This would correspond to a prior expectation that environmental changes act on the body as a whole. In response to a perturbation of individual muscle DoAs in an MCI task, subjects' behavior approaches optimality at the level of muscles after about 100 trials [66]. This hierarchical scheme can be extended to incorporate remapping at the neural level; the results of [64] suggest that such a process is incomplete within a single session. Transient increases in tuning depth reported early in brain control [60] may also reflect sub-optimal, global reaiming or reweighting at the neural level. The results of Ganguly and Carmena [13], however, suggest that after sufficient practice over several sessions, optimal remapping at the level of individual neurons is possible.

The hierarchical remapping framework may also help explain why some BMI experiments report spontaneous changes or cessation of overt arm movements after extended periods of brain control [16], [18], [57]. Since only a small proportion of motor cortex neurons will contribute to any decoder, activation of the remaining population may be unnecessary for control. Recently, a reduction in the tuning depth of neurons that did not contribute to a BMI decoder has been reported [58], consistent with local remapping, but this occurred only late in the learning process after the monkey achieved proficiency. As cortical activity is optimized to the level of the individual neurons controlling a BMI, the population signal controlling activity at the level of muscles may no longer be appropriate or sufficient to move the limb. This is particularly advantageous if the motor system aims to minimize the overall effort. Note however that if accuracy is the more important factor, there may be no penalty for concurrent modulation of neurons that are not associated with brain control, which may explain the persistence of residual limb movements reported in other experiments [23].

The hypothesis of hierarchical remapping requires further experimental testing to establish its validity. Nevertheless, theoretical considerations of redundancy suggest some such process must occur for the brain to be able to learn anything. In response to a global error signal, the brain is faced with a multitude of possible sources at the neural level. An unstructured search through this high-dimensional space would be impossibly inefficient. BMI remapping experiments like those in [13], [58] and [64] reveal the route by the brain eventually finds optimal solutions to these neuronal `credit assignment' problems.

VIII. Role of Hebbian plasticity in neural remapping

Developing successful neuroprostheses will require interfacing with the brain on all three of Marr's levels. Here we have suggested that concepts derived from computational level descriptions of natural movements such as dimensionality reduction, cost functions, internal models and optimal feedback control may be usefully applied to the problem of learning to control a BMI. But because BMIs also interface directly with the implementation of the brain (individual neurons) they afford new possibilities for bridging these levels by relating neural activity during learning with the changes in neural connectivity and subsequent behavioural improvement.

Donald Hebb [68] proposed that the efficacy of neural connections is enhanced when there is a persistent causal relationship between pre- and post-synaptic activity. We demonstrated such plasticity with a recurrent BMI that used endogenous activity recorded from M1 in a freely-behaving monkey to control intracortical microstimulation (ICMS) of a second site [12]. Continuous pairing of action potentials recorded at one site with stimuli delivered to a second electrode caused changes in the motor representation at the recording site consistent with a strengthening of connections to those cortical or downstream sites activated by stimulation. Plasticity could only be induced when stimuli were delivered within ~50 ms of the triggering spike, consistent with a mechanism of spike-timing dependent plasticity [69]. Similar Hebbian plasticity has now been demonstrated more directly for primate corticospinal connections. Using action potentials of CM cells to trigger intraspinal stimuli near the terminals of these cells during 20+ hours of free behavior led to clear increases in the sizes of post-spike effects obtained in spike-triggered averages of EMG activity [70]. These plastic changes also depended on the interval between spikes and stimuli, consistent with spike-timing dependent plasticity. A third example of such plasticity has been reported for spike-triggered stimulation of cortical sites in freely behaving rats [71].

Can the associative plasticity mechanisms revealed by these recurrent BMIs help to understand remapping observed in biofeedback BMI experiments? In a recurrent BMI, neural recordings cause electrical stimulation of a second site, whereas in biofeedback BMIs, neural recordings cause resultant sensory feedback. If associative plasticity occurs as a result of consistent causal relationships, then plasticity may occur at any sites receiving convergent input from both an efference copy of the command signals and resultant sensory representations. In simplistic terms, this may be precisely what is required in order to learn an internal model of the neuromotor mapping (Figure 2D).

If activity-dependent plasticity underlies changes in behavior during learning then plasticity induced artificially should also have behavioral consequences. Reference [72] provides one recent demonstration of this in rats, by examining the perceptual threshold for detecting ICMS after pairing with another site. Reference [73] used a non-invasive paired-stimulation protocol in humans to induce corticospinal plasticity and produce a mismatch between subjects' perceived and actual force production. These studies provide a small glimpse of the future possibilities afforded by BMI technologies. Long-term, recurrent interfaces between neuronal populations and sophisticated BMI decoding algorithms provide an unprecedented opportunity to shape neural representations and connectivity through activity-dependent mechanisms. In combination with a computational-level description of motor learning, these technologies may allow the formation of new hybrid circuits to replace or enhance damaged pathways and restore function following neurological injury.

Biographies

Andrew Jackson received a MPhys degree in physics from the University of Oxford, UK in 1998 and a PhD in Neuroscience from University College, London UK in 2002.

He is currently a Wellcome Trust Research Career Development Fellow at the Institute of Neuroscience, Newcastle University, UK. His scientific interests include the neural mechanisms of motor control, cortical plasticity and spinal cord physiology. This basic research informs the development of neural prosthetics technology to restore motor function to the injured nervous system.

Dr. Jackson is a graduate member of the Institute of Physics and a member of the Society for Neuroscience.

Eberhard E. Fetz received a BS degree in physics from the Rensselaer Polytechnic Institute, Troy, NY in 1961, and a PhD in physics from the Massachusetts Institute of Technology, Cambridge, MA, in 1966.

He is currently Professor of Physiology and Biophysics and Adjunct Professor of Bioengineering at the University of Washington, Seattle, WA. He is also a Core Staff member of the Washington National Primate Research Center in Seattle. His primary research interest is neural mechanisms of volitional control of limb movements in behaving primates. His current research is focused on applications of implantable bidirectional brain-computer interfaces.

Dr. Fetz is a member of the Society for Neuroscience and the AAAS. He received the New York Academy of Sciences and Aspen Brain Forum first Prize in Neurotechnology In 2010.