A Method for the Control of Multigrasp Myoelectric Prosthetic Hands

Abstract

This paper presents the design and preliminary experimental validation of a multigrasp myoelectric controller. The described method enables direct and proportional control of multigrasp prosthetic hand motion among nine characteristic postures using two surface electromyography electrodes. To assess the efficacy of the control method, five nonamputee subjects utilized the multigrasp myoelectric controller to command the motion of a virtual prosthesis between random sequences of target hand postures in a series of experimental trials. For comparison, the same subjects also utilized a data glove, worn on their native hand, to command the motion of the virtual prosthesis for similar sequences of target postures during each trial. The time required to transition from posture to posture and the percentage of correctly completed transitions were evaluated to characterize the ability to control the virtual prosthesis using each method. The average overall transition times across all subjects were found to be 1.49 and 0.81 s for the multigrasp myoelectric controller and the native hand, respectively. The average transition completion rates for both were found to be the same (99.2%). Supplemental videos demonstrate the virtual prosthesis experiments, as well as a preliminary hardware implementation.

I. Introduction

The Human hand is extensively articulated, possessing approximately 20 major degrees-of-freedom (DoF) which allow it to execute a wide variety of grasps and postures. Movement of the hand is dictated by the action of an even greater number of muscles, which are concerted by a multitude of efferent and afferent neural signals. This stands in contrast to traditional, commercially available, myoelectric hand prostheses. Until recently, these devices have been restricted to a single DoF, driven by a single actuator and commanded by a single electromyogram (EMG) input (two EMG electrodes placed on antagonistic muscle pairs of the residual forearm). Although such prostheses have far fewer DoFs than the native hand, there are several advantages related to this approach. Primarily, the control of these devices requires little cognitive effort due to the one-to-one mapping between the actuator and EMG input. Also, traditional myoelectric prostheses can provide direct, proportional control of motion. Because they only require a single pair of EMG electrodes the interface is manageable and is easily incorporated into a socket. Furthermore, the control method is not computationally demanding and can occur with minimal delay. A modern version of a single grasp myoelectric prosthesis is the MyoHand VariPlus Speed (Otto Bock, Germany).

Despite these advantages, it has also been noted that single grasp devices have limited grasping capability (because they cannot conform to objects and there is little contact area) and unnatural appearance of motion (mainly due to their low level of articulation) [1]. This is supported by patient surveys which indicate that greater functionality [2] and increased articulation [3] are among their top design priorities. In response to these limitations, and facilitated greatly by recent technological advances (such as improved batteries, actuators, and microelectronics), several multigrasp prosthetic hands have been developed [4]–[13]. These multigrasp hands are highly articulated (containing 8 to 16 joints), are driven by a plurality of actuators (ranging from 2 to 6), and hold the potential for improved grasping, manipulation, and fidelity of motion. However, the full realization of this potential requires the development of an effective multigrasp control interface, as noted in [14].

An effective multigrasp interface must enable the user to access the multifunctional capability of the prosthetic hand accurately and dependably. The control approach should be direct and intuitive, offering continuous and proportional control of motion with negligible latency. This remains a challenging area in upper extremity prosthetics research, although several significant strides have been made. Prevalent approaches to multigrasp control thus far include pattern recognition [14]–[19] and event driven finite-state control [20]–[27]. Pattern recognition for multigrasp hands involves determining user intent (i.e., selecting postures and grasps) based on the observation (of typically a plurality) of EMG inputs, which are observed in a series of moving windows in time (frames). In this approach, a classifier is trained which associates EMG input patterns with intended postures and grasps. During operation, the classifier examines each frame of EMG data and makes a decision (or classification) about which movement is being commanded.

In event driven finite-state (EDFS) approaches, the controller consists of a series of interconnected states. For each state the control action is uniquely defined. Transitions among the respective states are based on predefined events or conditions which depend on sensory inputs. The overall behavior of an EDFS controller is therefore a function of the structure and interconnectedness of the states, the device behavior within each state, and the events and conditions required to transition among states (all of which are interdependent). This approach was initially developed and applied to myoelectric prosthetic hand control in the 1960s ([20], [21]), followed by the more recent work described in [22]–[27]. In [22]–[24], EDFS control approaches were used to modulate grasp within a preselected hand posture based on measured EMG amplitudes. In these works, posture preselection depended on the activation of contact switches located on the prosthesis. Later in [25] and [26], a control approach was proposed which also utilized EDFS for grasp modulation, but where EMG pattern recognition, rather than contact switches, was utilized for posture preselection. Alternatively, in [27], an EDFS control approach was described in which an EMG-amplitude-based algorithm was used to preselect a given posture, but where the grasping process was automated by the controller to differing degrees. Specifically, after posture preselection, an automated grasping action was initiated by the controller or by the user (depending on controller variation). Grasping was then either terminated automatically, based on measured grasp force, or manually via a subsequent EMG command (depending again on controller variation).

This paper presents the design and preliminary experimental validation of a myoelectric control methodology for multigrasp transradial hand prostheses. Like the approaches presented in [22]–[27], the control approach involves event-driven finite-state methods. Unlike these approaches, however, the controller allows for selection of a given posture based on continuous movement through the finite-state control structure. This provides access to any one of nine possible hand postures, in addition to the continuum of configurations between them. In this way, posture selection and grasp modulation within that posture may occur simultaneously.

This approach to multigrasp myoelectric control is described in detail in Section II. To assess the efficacy of the proposed method in obtaining the nine different hand postures, relative to the ability to obtain the same set of postures with the native hand, the control approach was implemented on a virtual multigrasp prosthesis and experiments were conducted with nonamputee subjects. These experiments are described in Section III of the paper, and the results are discussed in Section IV. A video is included in the supplemental material that depicts the virtual prosthesis experiments and demonstrates preliminary use of the multigrasp myoelectric controller with hardware.

II. Description of Multigrasp Myoelectric Control Structure

Theoretically, a multigrasp prosthesis should enable amputees to better perform the activities of daily living, primarily by providing a set of hand postures and grasps which better span the prehensile forms employed during them. As studied in [28] and reported in [29], there are six grasps (i.e., tip, lateral, tripod, cylindrical, spherical, and hook) which constitute approximately 85% of those used in the activities of daily living. In addition to this set of grasps, two postures, a pointing posture and a platform (open-palm) posture, are also useful for interaction with the environment. The Multigrasp Myoelectric Controller (MMC) was therefore designed to enable the attainment of these grasps and postures utilizing a standard, two-electrode EMG interface as user input.

To allow for this, it was assumed that the hardware (the hand prosthesis) to be controlled could at minimum provide digit I (thumb) flexion and extension, digit I opposition and reposition, digit II (index) flexion and extension, and simultaneous flexion and extension of digits III through V (middle, ring, and little finger). It was also assumed that the respective digit displacement (i.e., position) and digit grasping forces are measureable or known. The proposed method is applicable to any multigrasp prosthesis with the aforementioned minimum requirements. Examples of multigrasp prostheses that meet these criteria are those described in [6]–[13].

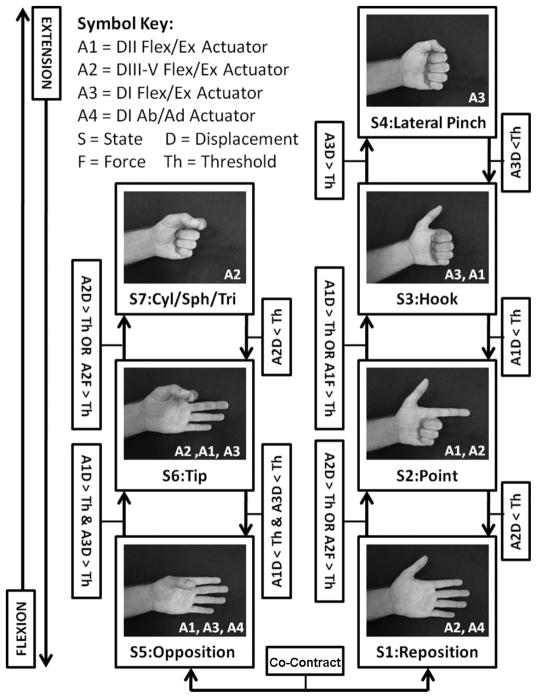
To coordinate the motion of the digits, the MMC incorporates an event driven finite-state control structure. The topography of this structure is depicted in Fig. 1. The states of the MMC consist of the postures and grasps which multigrasp hands, such as those mentioned above, are capable of providing. These include the thumb reposition (platform), point, hook, lateral pinch, thumb opposition, tip, and combined cylindrical/spherical/tripod postures. Note that the latter state includes three postures, as the determination of posture in this state depends also on the shape of the object being grasped. There are thus seven states, and nine possible grasps/postures. The future state of the prosthesis is determined as a function of the current state and the inputs to the finite-state controller, which include EMG signals, hand configuration information, and grasp force information. It is important to note that the topography of the state chart, where the states have been arranged progressively according to the degree of hand closure and where postures and grasps have been grouped specifically based on the position of the thumb, is unique to the work presented here. This arrangement is intended to provide streamlined access to the enhanced functionality of a multigrasp hand and lends itself to navigation of multiple postures using a traditional myoelectric interface.

Fig. 1.

The structure of the MMC finite-state machine. The states are comprised of different hand postures. The active actuators are indicated for each state. Transitions from state to state depend on actuator displacement, actuator forces, and co-contraction detection logic. In general, the actuator displacement and force thresholds for each transition are unique. Contraction of the forearm flexors is associated with upward movement in the state chart. Contraction of the forearm extensors is associated with downward movement in the state chart. Co-contraction initiates an automated toggling motion between the opposition and reposition states.

The user navigates the state chart by four essential inputs which are standard in current clinical devices and are indicated by measured EMG at two electrode sites: flexion, extension, co-contraction, and rest. Flexion involves the contraction of the anterior musculature of the forearm and is associated with closing of the prosthesis (upward movement through the state chart in Fig. 1). Extension involves the contraction of the posterior musculature of the forearm and is associated with opening of the prosthesis (downward movement through the state chart in Fig. 1). Note that the speed with which the prosthesis closes or opens is proportional to the strength of muscular contraction. Co-contraction involves simultaneous contraction of the antagonistic flexion/extension muscle groups and occurs when both EMG channels concurrently exceed their respective thresholds (the determination of these thresholds is described below). Co-contraction toggles between the opposition and reposition states, causing automated positioning of the thumb. Because the state chart has been arranged such that all states in which the thumb are opposed stem from the opposition state (the left side of the state chart) and all states in which the thumb are reposed stem from the reposition state (the right side of the state chart) co-contraction effectively selects which branch of the state chart the user may navigate by virtue of flexion or extension. The position of the thumb therefore provides an important visual indication to the user regarding which portion of the state chart the prosthesis is operating in. Note that the opposition and reposition states are the only states in which co-contraction has effect. Co-contraction in any other state will not elicit toggling of the thumb or additional control action. Because the effects of co-contraction are restricted to the opposition and reposition postures in which grasping and manipulation generally do not occur, an unintended co-contraction should not have an effect on grasping capability or robustness. Finally, relaxation of the forearm musculature (resting) halts movement within the state chart (i.e., the prosthesis remains stationary).

Transitions within the state chart are based on logical conditions that operate on measured digit displacements (e.g., joint angles), measured digit forces, and/or measured EMG levels (i.e., detection of co-contractions). The behavior of the hand within each state is determined by a coordination controller that governs which subset of actuators is active in the hand at any given time. If a transition occurs, the current state of the hand changes, and a new subset of actuators become activated by the coordination controller. The actuators which are active are always those associated with transitions to adjacent states.

For example, and with reference to Fig. 1, assume the hand is in the platform posture (State 1). In this posture, the actuator(s) responsible for the flexion and extension of the third, fourth and fifth digits, is (are) active (A2). Contraction of the forearm flexors (Electrode 1) generates a velocity level signal which is integrated and added to the current position reference for the active actuator(s). Consequently, the third, fourth and fifth digits begin to flex. If the digit flexion or force exceeds a certain threshold (i.e., if these digits either nearly close or come into contact with an object) a state transition will occur, and the hand will transition to the point posture (State 2). In the point posture the actuator(s) responsible for the movement of the second digit (A2), as well as the actuator(s) responsible for flexion of digits three through five, are active. If flexion continues, the position references for these digits will increase. Because digits three through five are almost fully closed upon entering the point posture, their position reference will quickly saturate. However, the position reference for digit II will continue to increase until its displacement or force exceeds a certain threshold, at which point the hand will transition to the hook posture (State 3). Alternatively, if contraction of the forearm extensors (Electrode 2) had occurred after entering the point posture (State 2), a velocity level signal would have been generated, integrated and subtracted from the current position references for the active actuators corresponding to digits two and three through five. In this scenario, since the second digit is almost fully open upon entering the point posture, its position reference will quickly saturate. However, the position reference for digits three through five will continue to diminish until the third, fourth and fifth digits are fully extended, at which point the hand will be in the reposition posture (State 1) once again. The user may toggle from the reposition posture (State 1) to the opposition posture (State 5) by co-contraction. When a desired posture or grasp is obtained, the user relaxes the flexors and extensors of the forearm. This causes the velocity-level references to fall to zero. As these signals are then integrated, the position references for all actuators remain constant (i.e., the digits remains stationary). The user may relax at any time during transitions, and therefore has access to all of the intermediate positions between the idealized states.

In summary the MMC consists primarily of a uniquely structured finite-state machine and a coordination controller. The output of the finite-state machine, the current hand state (posture), dictates which subset of actuators is active in the hand at any given time. The position references for these actuators are driven by proportional signals arising from a standard two-channel EMG interface. Changes in digit position or digit grasping force trigger transitions in the state chart based on pre-established position and force thresholds. Co-contraction commands cause transitions between the reposition (platform) and opposition postures. When a state transition occurs a new subset of motors becomes activated by the coordination controller. The active motors are always those associated with transitions to adjacent states. This, in conjunction with the controller structure, provides access to any one of nine possible hand postures, in addition to a continuum of configurations among adjacent postures. In this way, posture selection and grasp modulation within a posture may occur simultaneously.

III. Experimental Methods

A. Subject Information and Testing Overview

Experiments were conducted to assess the ability of the MMC to control hand posture. Five healthy, nonamputee subjects aged 22–44 participated in the experiments. Of these subjects, four were right handed and one was left handed. Each subject participated in six trials. Each trial involved performing postural transitions with both the data glove and MMC, and each of the five subjects attempted each transition type three times during each experimental task. This resulted in 45 data points for each transition type for both the data glove and the MMC. The time between trials ranged from one day to three weeks and all subjects completed the six experimental trials within a time frame of approximately one month. All experiments were conducted on the right hand and forearm. The experimental protocol for this study was approved by the Vanderbilt University Institutional Review Board.

B. Data Acquisition With Data Glove

A custom data glove was constructed to track the movement of the native hand (See Fig. 2). This was accomplished using variable resistance flex sensors (Spectra Symbol) attached to a lightweight, highly flexible, slip-on glove (Fox Head, Inc.). The flex sensors were inserted into elastic sleeves which had been stitched onto the glove. The sensors were allowed to translate within the sleeve to accommodate for stretching of the glove over the joints. Four flex sensors were used to capture the flexion and extension of digits I–III (digits IV and V of the virtual prosthesis tracked digit III) as well as abduction and adduction of digit I. This allowed for the detection of the postures attainable with the configuration of the MMC described in this paper. The variable resistance flex sensors were incorporated into a voltage divider circuit whose output was amplified, adjusted, and buffered before being acquired using an MF624 data acquisition card (Humusoft) and accessed at a sampling rate of 1 kHz using Simulink Real Time Windows Target (The Mathworks). These signals were then low-pass filtered at 2 Hz and normalized in Simulink to be used as position references for control of the virtual prosthesis. Each subject was allowed to manipulate the virtual prosthesis using the data glove to gain familiarity with the interface before starting the experimental trials.

Fig. 2.

The data glove used to capture motion of the native hand. Four sensors are used to capture flexion and extension of digits I–III, as well as abduction and adduction of the thumb. An individual flex sensor is also shown.

C. Data Acquisition With EMG

Two self-adhesive, Ag/AgCl snap bipolar electrodes with a spacing of 22 mm (Myotronics, Inc.) were used for EMG data acquisition. The electrodes were placed on the anterior and posterior surfaces of each subject’s forearm in the approximate vicinity of the flexor carpi radialis (Electrode 1) and extensor carpi radialis muscles (Electrode 2). These muscles were chosen due to their proximity to the skin, proximal location on the forearm, and because of their role in flexion and extension of the hand at the wrist. Additionally, because these muscles are located in close proximity to the flexor digitorum superficialis and extensor digitorum muscles respectively, flexion or extension of the digits, along with the hand about the wrist, was seen to produce strong EMG signals. An alcohol pad was used to clean the electrode sites before electrode placement. The analog EMG signals detected by the electrodes were differentially preamplified with a gain of 100 and low pass filtered at a cutoff frequency of 500 Hz using custom analog circuitry at the electrode site. This information was sampled at 1 kHz using the MF624 data acquisition card and accessed using Simulink Real Time Windows Target. The signals were then digitally high-pass filtered at 50 Hz, rectified, and low pass filtered again at 2 Hz for use as velocity references.

The EMG signals of each subject were calibrated by establishing normalization parameters and co-contraction threshold levels before the experimental trials. The mean EMG values during Flex and Rest (Electrode 1) and Extend and Rest (Electrode 2) were established as upper and lower bounds for each signal, respectively. A dead band of 10% of full range was utilized for both channels to avoid spurious motion. To enable real-time co-contraction detection, thresholds were established for each EMG channel based on an exhaustive search. The thresholds which maximized the number of correctly detected co-contractions, and minimized the number of incorrectly detected co-contractions during the calibration session were selected. As noted above, a co-contraction was assumed to have occurred if both signals concurrently exceeded their respective thresholds. This process transformed the two EMG signals into two normalized, proportional signals which were used to provide velocity references and co-contraction events for multigrasp prosthesis control. Once established, this calibration was not repeated for the remainder of all experiments (for a given subject). The resulting normalization parameters and co-contraction thresholds were maintained for the duration of the multi-week experimental sessions. Subjects were allowed to operate the virtual prosthesis using EMG signals until they were familiar with the structure and operation of the multigrasp myoelectric control scheme before starting the experimental trials.

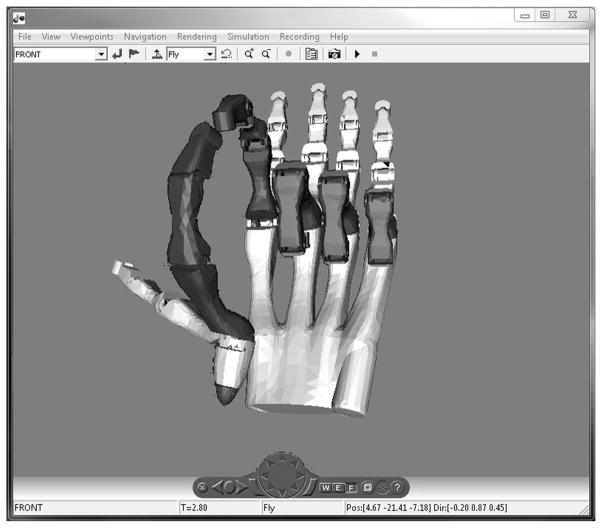
D. Virtual Prosthesis

To create the virtual prosthesis (see Fig. 3), solid model part and assembly files of the hand prosthesis described in [12] were exported from Pro/Engineer (PTC) to a virtual reality modeling language (.vrml) file. The virtual reality model was then animated using signals generated in Simulink (The Math-works). The virtual ghost was created by inserting another, darkly shaded copy of the virtual prosthesis into the virtual environment. The virtual prosthesis was controlled by the user via signals emanating from either the data glove or MMC. The virtual ghost was controlled automatically by the computer and served as a postural reference for the user. For the experiments described here, the MMC was modified to control the virtual prosthesis. Because the virtual environment did not allow for interaction with objects, force dependent transitions were not invoked in the state chart. Instead, state chart transitions were strictly position dependent. The velocity gains in the MMC were set so that the virtual prosthesis moved with speeds reflective of the capabilities of a multigrasp prosthetic hand (i.e., the maximum speeds, as described in [12]).

Fig. 3.

The virtual prosthesis (light) and virtual ghost (dark). The virtual ghost is controlled automatically by the computer, and serves as a postural reference for the user. When the user brings the virtual prosthesis sufficiently close to the virtual ghost, the ghost is no longer displayed, indicating to the user that they have acquired the desired target posture.

E. Experimental Procedure

Each trial consisted of two experimental tasks which involved the acquisition of target postures. In the first task, the data glove was used to control the movement of the virtual prosthesis with the native hand. In the second task, EMG signals were used to control the movement of the virtual prosthesis with the MMC. Note that the first task (data glove) was intended to characterize the performance of the native hand and thereby establish a performance benchmark for the MMC. In both tasks, seven target postures (e.g., the reposition, point, hook, lateral pinch, opposition, tip, and cylindrical postures displayed in Fig. 1) were presented randomly. Because differentiation of the cylindrical, spherical, and tripod grasps is dependent upon the grasped object, and as grasping was not involved in the virtual environment, the cylindrical/spherical/tripod grasp was reduced to only the cylindrical grasp in the virtual experiments. Thus, there were seven unique postures to be obtained with the virtual prosthesis in the experiments, and from these, 42 unique transitions, each of which was presented three times per task. This resulted in 126 movements per task, with each of the seven postures being presented 18 times.

Each target posture was displayed visually on a computer monitor by the virtual ghost. When a subject brought the virtual prosthesis to the target posture the virtual ghost was no longer displayed, indicating that the user had sufficiently achieved the desired pose. For a movement to be considered successful, and before a new target posture was displayed, it was required that the target posture be held for 3 s without excessive deviation (within 25% of the total range of motion for each digit). This was done both to deter overshoot and to allow subjects to rest between subsequent postures. If a transition was not acquired within 5 s, it was considered unsuccessful and a new target posture was presented.

The operation of the data glove and MMC were explained before the trials to prepare subjects for the above procedure. In addition, each subject was allowed to use the data glove and the MMC interface to control the virtual prosthesis until they were comfortable with each. In either case, and for all subjects, these familiarization periods required less than 5 min. A video which includes footage of an experimental trial is available in the supplemental material.

F. Performance Metrics

The time required for each transition, starting at the instant when the target posture was initially displayed and ending when the target posture was successfully acquired, was recorded. This was defined as the transition time. The number of successfully completed transitions (those completed within 5 s) over the total number of attempted transitions was defined as the transition completion rate. These metrics are similar to the real-time performance metrics used in [19] to quantify pattern recognition based myoelectric control. Note, however, that the transition time as defined in this study includes visual, cognitive, neural, and muscular delay, in addition to joint angular velocity limits (representative of a physical prosthesis), which were imposed on the virtual prosthesis.

IV. Experimental Results and Discussion

A. Performance Trends

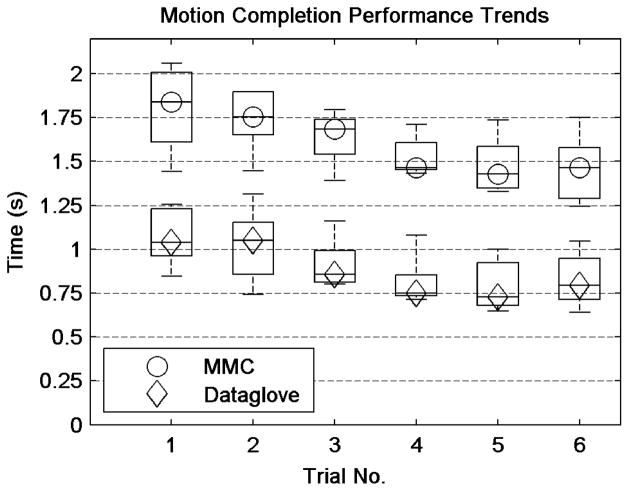
The median overall transition times for both the data glove and MMC decreased with essentially every subsequent trial (see Fig. 4). (The second data glove trial was an exception to this decreasing trend.) After the third trial, the median transition times for both the data glove and MMC fell within 10% of their collective means. Specifically, the median times for data glove trials 4, 5, and 6 were within 6% of their mean, and the median times for MMC trials 4, 5, and 6 were within 2% of their mean. This was considered to be indicative of a performance plateau and the final three trials were utilized to obtain the results reported here. These trends also imply that the MMC approach is intuitive, as both data glove and MMC transition times displayed similar trends and reached a plateau during the same trial. Additionally, in all cases familiarization periods were brief (< 5 min). It is also important to note that only a single calibration was used over the one month trial period. In contrast, it has been noted that pattern recognition approaches can require retraining on a more frequent basis due to various sensitivities [30], [31]. Because inter-trial variation existed in electrode placement over the course of these experiments, the MMC approach appears to be robust with respect to some degree of spatial and temporal variation in EMG measurement. This is similar to single DoF commercial myoelectric hand prostheses, in which two-site, direct, EMG velocity control is known to provide a degree of robustness relative to variations in electrode placement. This is due in part to the significant degree of physical separation between electrodes, the significant degree of muscular decoupling between the anterior and posterior forearm musculature, and due to the fact that velocity control integrates the EMG, which decreases sensitivity to noise and gain in the EMG measurement. In this way, the MMC approach leverages the benefits of traditional methods (e.g., direct mapping of input, simplified interface, robustness), while enabling the control of a multigrasp hand.

Fig. 4.

Plot of average motion completion times for each subject for each of six trials. The central mark for each box denotes the median motion completion time and each box encompasses the 25th to 75th percentiles for that trial and control methodology. Whiskers extend to the maximum and minimum times recorded.

B. Transition Times

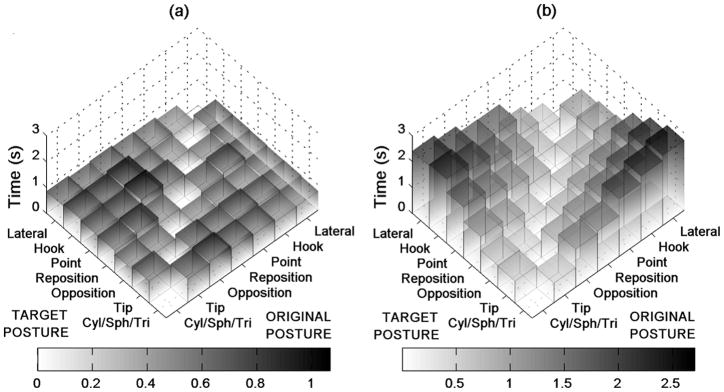
The average transition times for each transition type are given for the native hand and the MMC in Tables I and II, respectively. The same information is displayed graphically in Fig. 5. As can be seen in Tables I and II, and Fig. 5, transition times for the native hand are relatively uniform (standard deviation of 0.10 s) when compared to the MMC (standard deviation of 0.58 s). The distribution of transition times for the MMC may be attributed to the distance between the original and target postures on the state chart as depicted in Fig. 5. That is, transition times between adjacent postures are relatively short (average of 0.87 s), whereas transition times between states which lie at the far ends of the state chart (e.g., the lateral pinch and cylinder/sphere/tripod grasps) are longer (average of 2.55 s). The structure of the state machine imposes this distribution.

TABLE I.

Average Transition Times of All Subjects Between Different Grasps and Postures for the Native Hand^*

		Target Posture
		Lateral	Hook	Point	Reposition	Opposition	Tip	Cyl/Sph/Tri
Original Posture	Lateral		0.81 (0.36)	0.81 (0.36)	0.79 (0.36)	0.76 (0.50)	0.78 (0.25)	0.74(0.21)
	Hook	0.59 (0.12)		0.69 (0.25)	0.90 (0.65)	0.67 (0.19)	0.80 (0.28)	0.72 (0.19)
	Point	0.72 (0.31)	0.62 (0.15)		0.81 (0.60)	0.73 (0.19)	0.88 (0.26)	0.82 (0.28)
	Reposition	0.76 (0.25)	0.72 (0.18)	0.86 (0.48)		0.65 (0.28)	0.82 (0.50)	0.86 (0.22)
	Opposition	0.82 (0.30)	1.02 (0.48)	1.06 (0.53)	0.71 (0.19)		0.89 (0.30)	0.97 (0.38)
	Tip	0.77 (0.12)	0.94 (0.47)	0.90 (0.33)	0.96 (0.33)	0.71 (0.23)		0.91 (0.39)
	Cyl/Sph/Tri	0.85 (0.42)	0.92 (0.33)	0.86 (0.31)	0.86 (0.27)	0.72 (0.15)	0.84 (0.24)

^*Standard deviations are displayed in parenthesis.

TABLE II.

Average Transition Times of All Subjects Between Different Grasps and Postures for Multigrasp Myoelectric Control^*

		Target Posture
		Lateral	Hook	Point	Reposition	Opposition	Tip	Cyl/Sph/Tri
Original Posture	Lateral		1.20 (0.63)	1.32 (0.53)	1.37 (0.21)	2.02 (0.70)	2.43 (0.68)	2.70 (0.69)
	Hook	0.67 (0.14)		0.89 (0.29)	1.05 (0.14)	1.60 (0.39)	2.03 (0.51)	2.50 (0.95)
	Point	1.12 (0.35)	0.84 (0.22)		0.81 (0.43)	1.25 (0.36)	1.67 (0.32)	2.21 (0.50)
	Reposition	1.82 (0.96)	1.34 (0.36)	1.02 (0.31)		0.92 (0.51)	1.36 (0.51)	1.57 (0.56)
	Opposition	1.84 (0.44)	1.79 (0.56)	1.38 (0.43)	0.75 (0.26)		1.11 (0.43)	1.47 (0.88)
	Tip	2.16 (0.44)	2.18 (0.56)	1.68 (0.38)	1.15 (0.44)	0.61 (0.13)		0.75 (0.10)
	Cyl/Sph/Tri	2.40 (0.40)	2.46 (0.61)	1.97 (0.55)	1.40 (0.37)	0.88 (0.17)	0.85 (0.22)

^*Standard deviations are displayed in parenthesis.

Fig. 5.

Average transition times for: (a) the native hand (using the data glove) and (b) multigrasp myoelectric control (using electrodes). Note that the grayscale duration bars are scaled differently for (a) and (b). It can be seen that the transition times are relatively uniform for the native hand while for MMC they are dependent on distance between the original and target posture in the state chart. Note that transition times for adjacent postures with MMC are similar to the average transition time for the native hand.

To provide a measure of overall performance, the overall transition times were calculated for the native hand and MMC. This is the average time required to get to any given posture from any other. The overall transition time for each subject, and the average overall transition time over all subjects are given in Table III. For the native hand, the average overall transition time was 0.81 s with a standard deviation of 0.14 s. For the MMC the average overall transition time was 1.49 s with a standard deviation of 0.15 s. These data suggest that the MMC performs similarly to the native hand when transitioning between adjacent states, but is slower when transitioning among states that are nonadjacent.

TABLE III.

Overall Transition Times and Transition Rates^*

Subject	Criteria	Data glove	MMC
HS1 (RH)	Transition Time	0.74	1.48
	Transition Rate	99.2	99.7
HS2 (LH)	Transition Time	1.04	1.73
	Transition Rate	99.2	98.1
HS3 (RH)	Transition Time	0.84	1.50
	Transition Rate	99.2	99.7
HS4 (RH)	Transition Time	0.75	1.33
	Transition Rate	99.2	99.2
HS5 (RH)	Transition Time	0.68	1.40
	Transition Rate	99.2	99.5
Average	Transition Time	0.81 (0.14)	1.49 (0.15)
	Transition Rate	99.2 (0.00)	99.2 (0.67)

^*RH and LH are abbreviations for right-handed and left-handed, respectively. The standard deviations are given in parentheses.

C. Transition Completion Rate

Transition completion rates for each subject, as well as the average transition completion rates for both the data glove and MMC, are given in Table III. The average transition completion rate for the data glove was 99.2% with a standard deviation of 0.00% (coincidentally, all subjects had exactly three failed attempts when using the data glove). The average transition completion rate for the MMC was also 99.2%, but with a standard deviation of 0.67% (subjects had from one to seven failed attempts using the MMC). Qualitative feedback from subjects indicated that causes for missed transitions were misinterpretation of reference postures (data glove and MMC), accidental excessive deviation from the target posture (data glove and MMC), and the inability to switch between thumb opposition and reposition as a result of an insufficient co-contraction effort (MMC). The latter could have likely been mitigated by retraining the controller, but as previously stated, the authors chose instead to train the controller a single time at the outset, and not retrain during the course of these experiments.

These data indicate that transitions were completed as often with the MMC as with the native hand and that, in either case, transitions were completed (in under 5 s) nearly 100% of the time. Because of this, the average transition times reported in the previous section are representative of typical performance, whether or not the 5-s time limit is considered. These results indicate that the experimental subjects were able to reliably adopt target postures using the MMC.

D. Real-Time Control

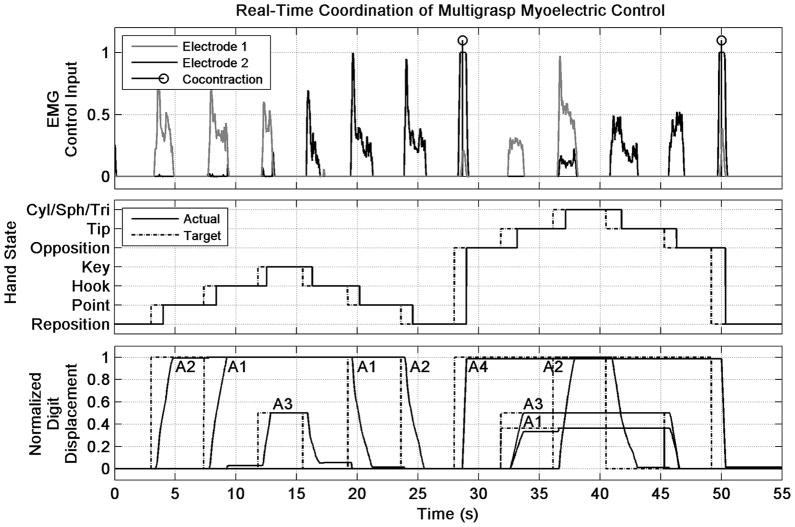
In order to demonstrate real-time control commands, the minimal hardware configuration (for the MMC) was assumed, in which one actuator (A3) provides digit I flexion and extension, a second actuator (A4) provides digit I opposition and reposition, a third actuator (A1) provides digit II flexion, and a fourth actuator (A2) provides coupled flexion for digits III–V. Given such a hardware configuration (implemented virtually), Fig. 6 shows the EMG inputs, hand state, and normalized digit displacement (where unity corresponds to the fully flexed position and zero corresponds to the fully extended position) for a 55 s session using MMC. During this session the user was sequentially prompted through the full range of hand postures. The figure demonstrates several important characteristics of MMC. First, the same EMG input can affect positional references for different actuators based on the current state of the hand. For instance, EMG input coming from the forearm flexors (Electrode 1) generates references for A2 around the point state, and generates references for A1 around hook state (between t = 0 and t = 10 s). Second, a single EMG input may govern multiple actuators, such as Electrode 1 simultaneously controlling actuators A1 and A3 between transitions from opposition to tip states around t = 33 and t = 46 s. Third, a high intensity co-contraction of flexor and extensor muscles results in a co-contraction event a t = 28 and t = 50 s. The co-contraction event causes automated opposition and reposition of the thumb. As can also be seen in Fig. 6, response to user intent is immediate. That is, movement occurs as soon as elevated EMG signal levels are detected.

Fig. 6.

Plot of EMG Input, Hand State, and Normalized Digit Displacement as a user is prompted through a series of Target Postures. Here, actuator A1 provides digit II flexion and extension, actuator A2 provides coupled flexion and extension of digits III–V, actuator A3 provides digit I flexion and extension, and actuator A4 provides digit I abduction and adduction.

E. Continuous and Proportional Motion

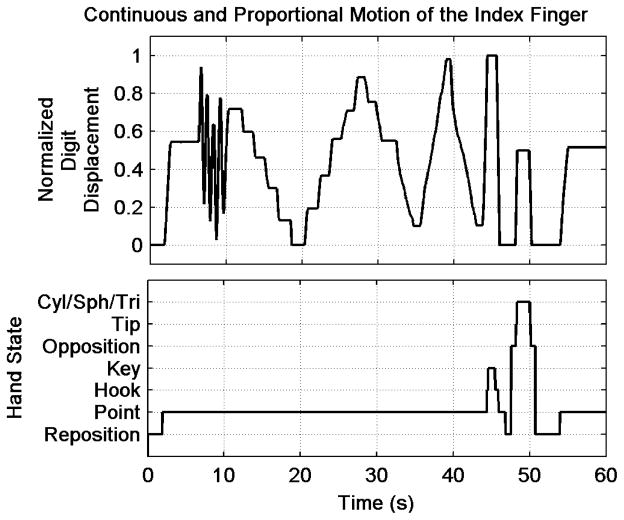
The continuous and proportional motion allowed by the MMC is illustrated in Fig. 7 and shown in the accompanying video. This was done using the second digit in the point state. After displacing the second digit to approximately half of its full range, high frequency motion was produced by rapid alternating contractions of the forearm flexors and extensors (t = 7 – 11 s). This was followed by periods of intermittent flexion and extension, punctuated by brief periods of rest, causing graded, step-like motion (t = 11 – 32 s). Next, slow, low frequency motion was produced with low-level EMG input (t = 32 – 44 s). Finally, the virtual prosthesis was taken through all of the states to show that continuous motion amongst the idealized states was possible within the state chart (t = 44 – 54 s). The demonstration ended with the second digit back in its middle position.

Fig. 7.

Plot of normalized digit displacement and hand state during continuous and graded motion of the index finger. High frequency motion, graded motion, low frequency motion, and motion of the index finger during transitions through the state chart are displayed. A video taken during these activities is included in the supplemental materials.

F. Physical Interaction

The virtual experimental paradigm utilized in this paper enables characterization of the ability of several subjects to transition from a given posture to all other (randomly presented) given postures (within a desired set of hand postures). Despite this, in many activities of daily living, the use of a hand prosthesis fundamentally entails interaction with the environment, which introduces physical forces on the prosthesis and limb, and can correspondingly modify EMG patterns. As indicated elsewhere in this paper, the standard, two-site EMG approach was incorporated into the MMC structure because of its proven history of efficacy in the control of myoelectric prostheses. Since the EMG interface with single-grasp myoelectric hands is not substantially altered by interaction with the environment, and since the nature of the traditional EMG interface is essentially intact in the MMC method, the authors expect that physical interaction with the environment will not significantly alter the ability of the user to obtain hand postures and grasps. This assertion, however, cannot be confirmed without performing a set of appropriate experiments incorporating the controller described herein with an appropriate multigrasp hand prosthesis, and assessing the ability of the user to obtain a set of desired grasps, or perform a set of desired tasks. The investigators hope to conduct such experiments in future work. As a preliminary step toward this goal, and to demonstrate the efficacy of the controller in physical hardware, the MMC has been implemented on the multigrasp prosthesis prototype described in [12]. A video demonstrating the implementation of the multigrasp controller on this prosthesis prototype is included in the accompanying supplemental material.

V. Conclusion

This paper presents a multigrasp myoelectric control interface that enables coordinated control of a multigrasp hand prosthesis using a standard EMG electrode interface. Specifically, the use of two EMG electrodes (on the anterior and posterior aspects of the forearm), along with position and force information from sensors in the hand, enables a user to navigate through a finite state control structure, and in doing so, to achieve one of nine possible hand postures, in addition to a continuum of configurations between adjacent postures. Experiments were conducted on five nonamputee subjects, in which the subjects utilized the myoelectric controller to command the motion of a virtual prosthesis between random sequences of target hand postures to assess the efficacy of the controller with respect to controlling hand posture. The results of these experiments were compared to the same subjects’ ability to achieve similar random sequences of target postures with their native hand, as measured by a data glove. The average time (across all subjects) to transition from one posture to another was 1.49 s for the myoelectric controller, and 0.81 s for the native hand, while the average completion rates were the same for both (99.2%). As such, the experimental results presented here indicate that the multigrasp myoelectric control approach enables (nonamputee) subjects to effectively obtain target postures within a virtual environment.

Biographies

Skyler Ashton Dalley (M’09) was born in Omaha, NE, in 1985. He received the B.E. degree in mechanical engineering, in 2007, from Vanderbilt University, Nashville, TN, where he is currently a Ph.D. student in the Department of Mechanical Engineering.

He works as a Research Assistant in the Center for Intelligent Mechatronics at Vanderbilt University. His research interests include the design and control of electromechanical devices for medical applications and, in particular, the development of prosthetic devices for the upper extremity and spine.

Huseyin Atakan Varol (M’01) received the B.S. degree in mechatronics engineering from Sabanci University, Istanbul, Turkey, in 2005. He received the M.S. and Ph.D. degrees both in electrical engineering from Vanderbilt University, Nashville, TN, in 2007 and 2009, respectively.

He is currently an Associate Professor at the Robotics and Mechatronics Department of Nazarbayev University, Astana, Kazakhstan. His current research interests include biomechatronics with an emphasis on upper and lower-limb prostheses, control, signal processing, machine learning, and embedded systems.

Michael Goldfarb (M’93) received the B.S. degree in mechanical engineering from the University of Arizona, Tucson, in 1988, and the S.M. and Ph.D. degrees in mechanical engineering from Massachusetts Institute of Technology, Cambridge, in 1992 and 1994, respectively.

Since 1994, he has been with the Department of Mechanical Engineering, Vanderbilt University, Nashville, TN, where he is currently the H. Fort Flowers Professor of Mechanical Engineering. His research interests include the design and control of assistive devices for disabled persons, including upper and lower extremity prostheses, and powered lower limb orthoses for gait restoration for spinal cord injured individuals.