Automatic Motion Compensation of Free Breathing acquired Myocardial Perfusion Data by using Independent Component Analysis

Abstract

Images acquired during free breathing using first-pass gadolinium-enhanced myocardial perfusion magnetic resonance imaging (MRI) exhibit a quasiperiodic motion pattern that needs to be compensated for if a further automatic analysis of the perfusion is to be executed. In this work, we present a method to compensate this movement by combining independent component analysis (ICA) and image registration: First, we use ICA and a time-frequency analysis to identify the motion and separate it from the intensity change induced by the contrast agent. Then, synthetic reference images are created by recombining all the independent components but the one related to the motion. Therefore, the resulting image series does not exhibit motion and its images have intensities similar to those of their original counterparts. Motion compensation is then achieved by using a multi-pass image registration procedure. We tested our method on 39 image series acquired from 13 patients, covering the basal, mid and apical areas of the left heart ventricle and consisting of 58 perfusion images each. We validated our method by comparing manually tracked intensity profiles of the myocardial sections to automatically generated ones before and after registration of 13 patient data sets (39 distinct slices). We compared linear, non-linear, and combined ICA based registration approaches and previously published motion compensation schemes. Considering run-time and accuracy, a two-step ICA based motion compensation scheme that first optimizes a translation and then for non-linear transformation performed best and achieves registration of the whole series in 32 ± 12s on a recent workstation. The proposed scheme improves the Pearsons correlation coefficient between manually and automatically obtained times-intensity curves from .84 ± .19 before registration to .96 ± .06 after registration.

1. Introduction

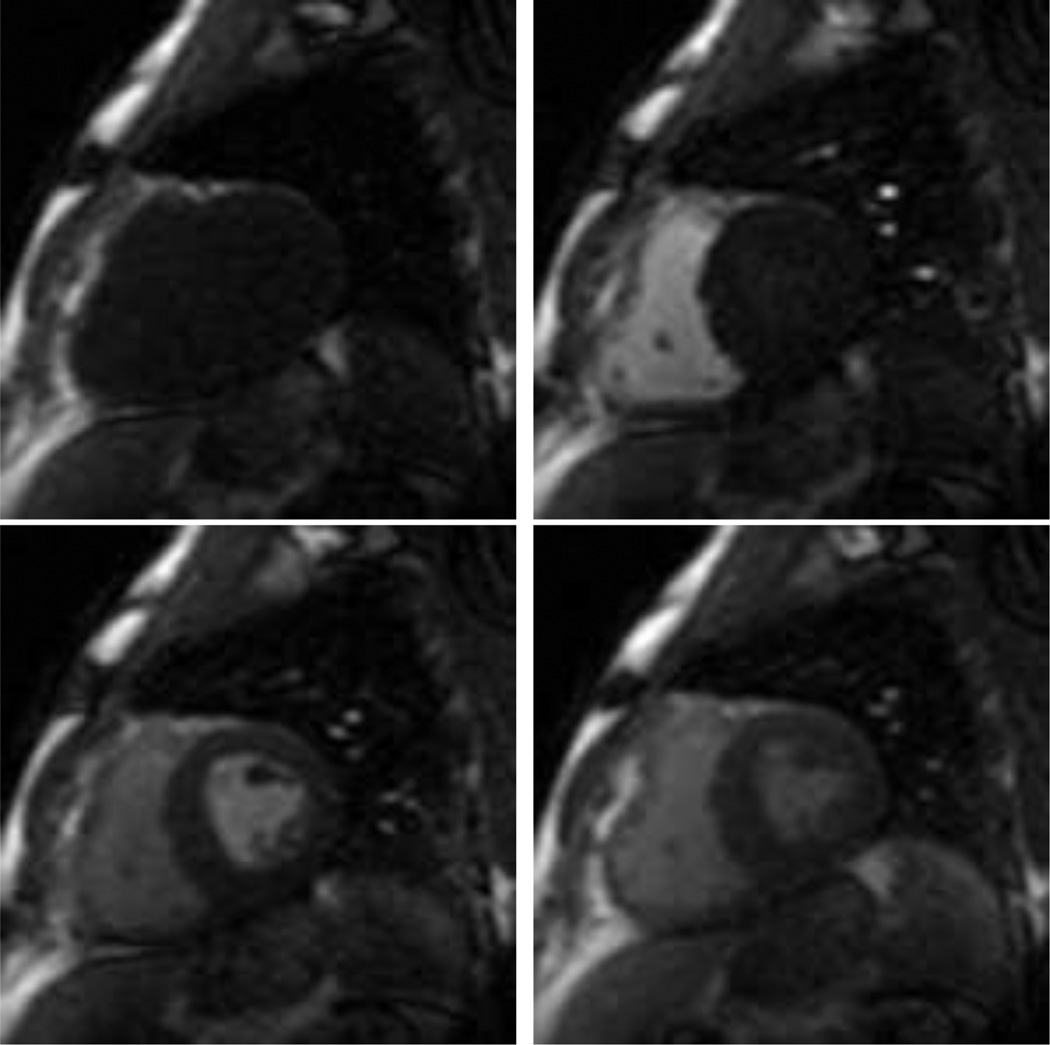
Perfusion quantification by using first-pass gadolinium-enhanced myocardial perfusion magnetic resonance imaging (MRI) has proved to be a reliable tool for the assessment of myocardial blood flow that ultimately can be used for the diagnosis of coronary artery disease that leads to reduced blood supply to the myocardium. In a typical imaging protocol, images are acquired over 60 seconds to cover some pre-contrast baseline images and the full cycle of contrast agent first entering the right ventricle (RV), then the left ventricle (LV), and finally, the agent perfusing the LV myocardium (Fig. 1). Then, to measure the blood flow, the image intensity of areas in the myocardium is tracked over time (cf. Jerosch-Herold (2010)).

Figure 1.

Images from a first-pass gadolinium-enhanced myocardial perfusion MRI study. From left to right: pre-contrast, RV-peak, LV peak, and myocardial perfusion.

In order to perform an automatic assessment of the intensity change over time, it is desired that no movement occurs in the images taken at different time points and that the heart is always imaged at the same contraction phase. While the latter can be achieved by ECG based triggering, the 60 seconds acquisition time span is too long for average people to hold their breath, and therefore, breathing movement is normally present in the image series. An additional challenge to motion compensation is posed by the contrast agent passing through the heart that results in a strong intensity change over time.

To acquire images that exhibit little motion, it is possible to ask the patients to breath shallow which results in a breathing pattern that exhibits only a low amplitude but the movement is rather irregular and no movement pattern exists that could be exploited for motion compensation.

It is also possible to ask the patients to hold their breath, but here, when a patient cannot hold it anymore a deep gasp occurs that results in a high amplitude motion that requires the accommodation of larger deformations for motion compensation, and it also results in a large through-plane motion which can not be dealt with by a 2D in-plane registration. The large gasp may also lead to image artifacts associated with parallel imaging, and it may occur during a critical phase of myocardial enhancement, particularly for patients with slow myocardial perfusion.

These problems can be avoided by letting the patient breathe normal, which results in a regular, almost periodic breathing movement of low amplitude with highly reduced through-plane motion when compared to the deep gasps that may occur for breath-held studies. Acquisition during normal free breathing also reduces incidence of missed ECG triggers or breath-hold induced arrhythmias, it improves patient comfort, simplifies the acquisition workflow, and the acquisition time is no longer limited by breath-held duration. Finally, the quasi-periodicity of the breathing can be exploited when the motion is compensated for to enable a later automatic analysis of the myocardial perfusion.

1.1. State of the art

Various image registration methods have been proposed to automatically compensate breathing movement in series of perfusion images in general.

All these methods have to deal with two challenges: The motion to be compensated, and the rather strong intensity change that are induced by the contrast agent. Some approaches rely on linear registration only and to overcome the problem of intensity change, they optimize similarity measures drawn from information theory, e.g., (normalized) mutual information (MI), as used by Wong et al. (2008), or (normalized) cross correlation (CC) as used by Breeuwer et al. (2001) or Gupta et al. (2003). Other options include the use of contour masks obtained from gradient images and potential maps (Delzescaux et al. (2003)) or the removal of the area of high intensity change by masking (Dornier et al. (2003)), or employing independent component analysis (ICA) to create synthetic images that are then used as references for image registration (Milles et al. (2007)). However, since the breathing movement results in the heart moving within the barely moving chest, the all-over movement pattern is highly non-linear, and masking is needed to extract a region of interest (ROI) around the heart that must be small enough to not contain non-moving body parts but big enough to accommodate the full movement range of the heart itself. In addition, linear registration does not account for the non-linear deformations of the myocardium itself.

Employing non-linear registration can compensate for the non-linear deformations and it doesn’t require the extraction of a bounding box. Yet, employing straightforward approaches that require the registration of images from different perfusion phases still have to deal with the additional challenge of changing intensities. For example Xue et al. (2009) relied on CC, and MI was employed by Ólafsdóttir (2005) to compensate breathing movement in myocardial perfusion series. However, both MI and CC are global measure in the sense that they rely on a consistent material-intensity mapping over the whole image domain and do not account for the local intensity change as it can be seen in perfusion series. For MI Likar and Pernus (2001) and Studholme et al. (2006) proposed methods to minimize the effects of these local intensity variations during registration, but these methods are tailored only to accommodate slowly varying intensities that may result from field inhomogeneities or tissue degeneration. They are not well suited for the strong local changes resulting from a contrast agent passing through the heart ventricles and the myocardium. Also, non-linear registration is already an ill-posed problem that has many local minima, and the complexity of the above criterions may add even more local minima. In addition, these measures are usually computationally demanding.

As an alternative to these global image similarity measures, a highly local similarity measure based on normalized gradient fields (NGF) has been proposed by Haber and Modersitzki (2005) and used for motion compensation in myocardial perfusion in Wollny et al. (2010b,a). However, as NGF is a highly local measure, it can hardly be used to register images with large movements that would require to correct for large deformations. Consequently, in Wollny et al. (2010b) NFG was combined with the sum of squared differences (SSD) and only images in temporal succession were registered so that only relatively small changes had to be accommodated, and in Wollny et al. (2010a) the measure was used to register images that were already identified as being closely aligned.

Because of the complications of non-linear registration that result from the intensity change over time it is desirable to reduce the need for the registration of images of different perfusion phases or to avoid it altogether.

One method to achieve this is to register only images in direct temporal succession, and align all images to one reference by accumulating the obtained transformations (see, e.g., Xue et al. (2009), Tautz et al. (2010), and Wollny et al. (2010b)). However, this accumulation of transformation may also result in the accumulation of small registration errors and may, therefore, result in considerable large errors in the overall alignment for frames that are “far away” from the common reference.

In Wollny et al. (2010a), the quasi-periodicity of free breathing was used to identify key frames that are already closely aligned, and registered using NGF. Then synthetic references were created by linearly combining images from the registered key frames and used for the registration of the remaining images. Yet, at the beginning of the series when the contrast agent passes through the right and left heart ventricle, the linear combination of images failed to model the fast change of intensities properly in some cases, resulting in bad motion compensation for this early phase of the perfusion sequence.

To completely eliminate the need for the registration of images from different perfusion phases, Li and Sun (2009) used prior knowledge to first obtain an approximation of ground truth and then used this pseudo ground truth (PGT) as reference for non-linear registration to reduce motion. Running this two-step scheme in a multi-pass fashion will eventually lead to full motion compensation. Li et al. (2011) later extend the method to be based on an initial semi-automatic segmentation of the heart ventricles and enhanced optimization methods.

Milles et al. (2007), and in its extension Milles et al. (2008), and Gupta et al. (2010) also completely eliminated the need to register images from different perfusion phases by employing ICA to identify three feature images (baseline, peak RV enhancement, peak LV enhancement) and combine these to create synthetic references. Then linear registration was used to compensate for breathing motion, hence the extraction of a ROI around the heart was required and done based on the identified RV and LV enhancement peaks. However, Gupta et al. (2010) reported that the method failed to properly identify the feature images if large movement was present. Also, in Wollny et al. (2010a) it was reported that this approach failed for perfusion series acquired free breathing, and in Wollny et al. (2011) an extension to the method was given to enable its application to free breathing acquired data. Since the approach we present in this article builds on the idea of using ICA to create reference images, we will discuss the method in section 2 in more detail.

Finally, learning based methods can be used for motion compensation, e.g. Stegmann et al. (2005). However, these methods usually need large training sets to generate the model that is later used for registration.

1.2. Our contribution

First, we will give a detailed review of the ICA based analysis and motion compensation method presented by Milles et al. (2006, 2007, 2008), and Gupta et al. (2010), discuss its advantages and where it fails. Then, we will present enhancements to these methods by replacing the ranking scheme for the IC labeling presented by Milles et al. (2006) by a more robust approach that is based on wavelet analysis to identify the independent component (IC) related to motion and select the optimal number of ICs. In order to enable linear registration and/or to speed up computation in the non-linear registration we provide a alternative approach to segment a bounding box around the LV myocardium that is based on the IC feature images. We follow Gupta et al. (2010) by creating synthetic reference images based on the ICA, and omitting the identified motion component when combining the ICs to create reference images that are free of motion. Instead of compensation for translation only, we either employ non-linear registration only, or as refinement step after linear registration. Some of these enhancements were sketched in Wollny et al. (2011) and will be presented here in more detail. Experiments on clinical data and a validation and comparison to other methods conclude the article.

2. ICA based motion compensation revisited

Using ICA in order to analyze myocardial perfusion series has been first proposed by Milles et al. (2006). The method presented there did not target motion compensation but a direct analysis of the perfusion process by identifying key components of the perfusion series - baseline, peak RV enhancement, peak LV enhancement, myocardial perfusion, and outliers - and reconstructing the series from these components. Further perfusion analysis was then directly executed at this reconstructed data set. In order to label the components, a ranking for a voting system was presented and is replicated in Table 1. With this ranking scheme, Milles et al. (2006) reported success rates for labeling of real data of 87.8% for LV and RV, 98.0% for Baseline and 65.3% for Myocardium.

Table 1.

Criteria used for automated labeling and corresponding IC ranking, 1 being most probable and 5 least probable as presented in Milles et al. (2006).

Sorting Criterion	Ordering	1	2	3	4	5
Mean weight value	Descending	Baseline	RV	LV	Myocardium, Outliers
Maximum weight value	Descending	Baseline	RV	LV	Myocardium, Outliers
Time point of maximum	Ascending	Baseline	RV	LV	Myocardium, Outliers
Maximum time derivative	Descending	RV, LV, Outliers			Myocardium	Baseline
Histogram symmetry of IC	Descending	Outliers	Myocardium	RV, LV, Baseline

Unfortunately, Milles et al. (2006) did not give a clear indication on how this voting is actually applied, nor any explanation why for the outliers the histogram symmetry of IC should be high, why the maximum weight value for the outliers should be smaller for outliers than for all the other components, or why the time point of the maximum of LV and RV should be before the time point of the maximum of the outlier component. Especially the latter two properties do not hold in a free breathing setting.

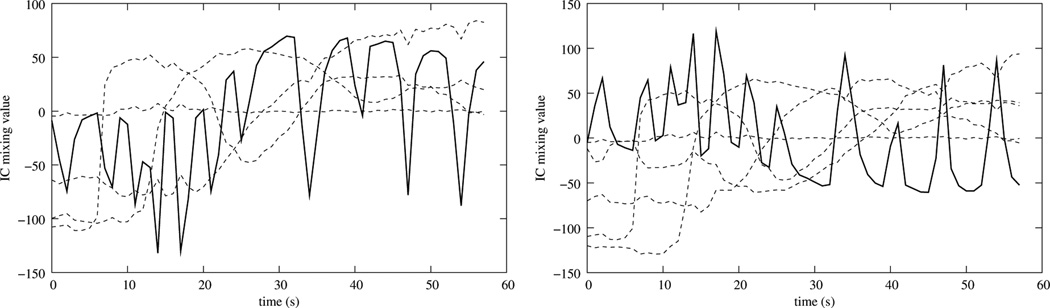
In Milles et al. (2007) (and in extension in Milles et al. (2008)) a linear registration scheme was proposed that used a three-component ICA, identifies Baseline, RV and LV enhancement by using the first three rows of Table 1, and uses these components to create synthetic references that are free of motion. The linear registration allowed only translational movement and optimized cross correlation in a two-pass registration scheme that uses a sub-sampled version of the images in the first pass and full resolution images in the second pass. However, for data sets that are acquired free breathing, a three component ICA will not properly separate RV and LV. Instead, the motion and one of the two ventricle cavity enhancements may be merged into one component, making proper identification of the RV and LV impossible (Fig. 3). In addition, images created from these components retain most of the motion and can, therefore, not be used as reference images to compensate for the motion.

Figure 3.

Time curve representation of the mixing matrix for ICAs with three numbers of retained components and the corresponding ICs.

In a further extension to Milles et al. (2008), Gupta et al. (2010) suggested to use a five component ICA to run the motion compensation algorithm using the ranking proposed above to identify the ICs corresponding to LV, RV, baseline, myocardial perfusion and motion. Since the identification and labeling of the component related to myocardial perfusion proved to be difficult only the components related to LV, RV, and baseline were used for reference image creation, and the motion component was explicitly dropped. It is not clear from the text, however, whether this implies that in the end only a four component ICA was applied, or a five component ICA was run and both the motion component and the myocardial component were discarded. Finally, to achieve motion compensation the same linear registration was applied that was used in Milles et al. (2008), with an additional final registration pass at the full image resolution. Gupta et al. (2010) noted that for series containing large movements the algorithm failed.

To summarize: ICA provides an elegant way to create motion free synthetic reference images for motion compensation in myocardial perfusion images, yet for a successful application of the method, a proper labeling of the components is imperative. The labeling approach proposed by Milles et al. (2006, 2008) doesn’t provide such labeling in a free breathing setting or when strong motion is present.

In Wollny et al. (2011) we proposed a method to overcome some of these difficulties by using non-linear registration to eliminate the need to segment a bounding box around the LV, and by using a heuristic based on mixing weight curve length to select an optimal number of ICs, to identify the motion related IC, and drop it from reference image creation. The drawback of this method is that it can not be applied to perfusion series that were acquired with initial breath-holding.

3. Method

In the following, our main focus will be on free breathing acquired perfusion series. Nevertheless, most assumptions also hold for data sets that were acquired with initial breath holding, and we will discuss differences when applicable.

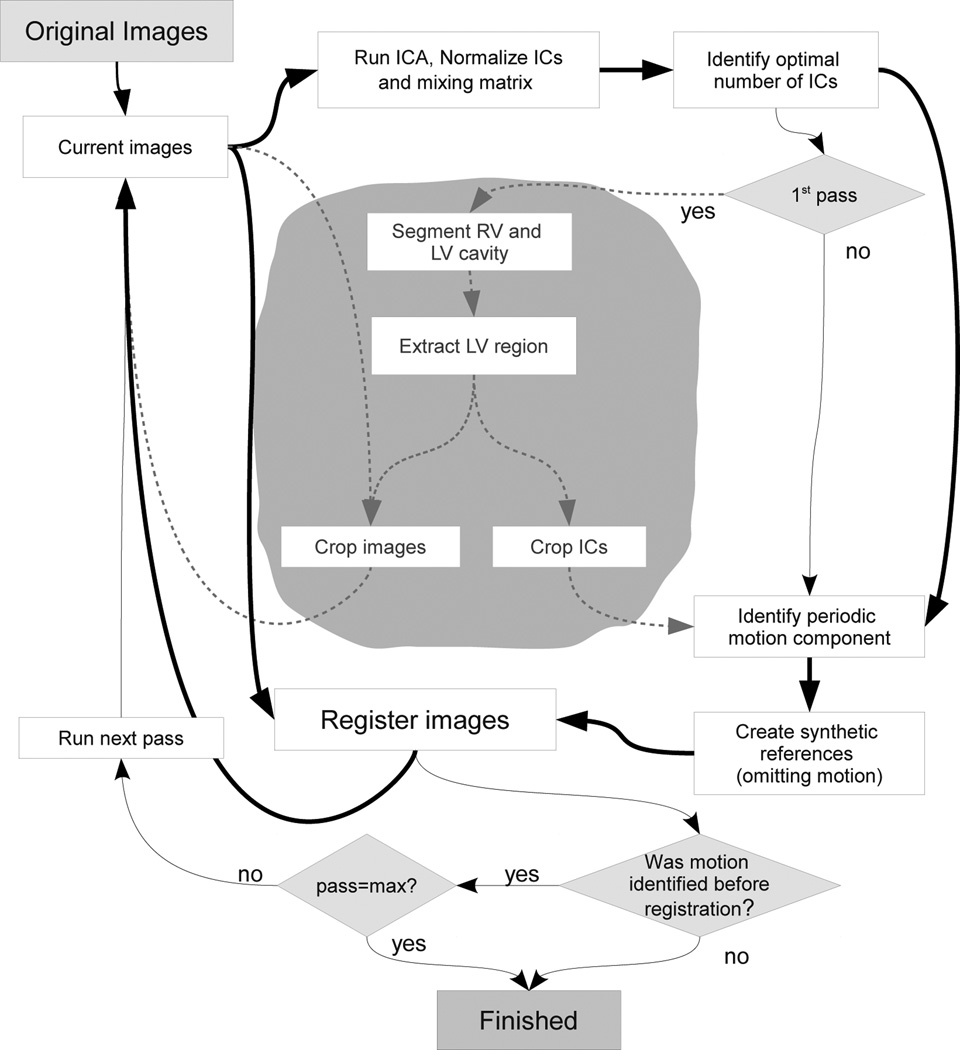
We propose a new motion compensation method that is run in a multi-pass scheme and composed of the following steps (Fig. 4): First, an ICA is run for various numbers of ICs. For each number, the components related to motion are identified, and that number of ICs is used for further processing that results in the lowest non-zero number of motion components. If no motion component could be identified, one last registration pass will be run using reference images created from all ICs and the multi pass scheme stops. If more than one motion component was identified the component with the highest signal energy in the mixing weight curve will be labeled as major motion component. Then, motion-free reference images are created from the ICs leaving out the major motion component, and the original images are registered to the synthetic references. If a predefined maximum number of registration passes is run then the motion compensation algorithm stops here. Otherwise the next pass is started by running ICA using the registered images as input.

Figure 4.

Scheme of the registration algorithm. The bold lines indicate the data flow and the thin lines represent the logical flow. The grayed texts in the gray area and dashed lines represent the additional steps for bounding box creation that are not a requirement for a non-linear motion compensation scheme. These steps may be executed to accelerate the registration and are required if linear registration is to be run.

If one desires to run linear registration, or in order to speed up non-linear registration by restricting it to the region around the heart, a bounding box estimation may be run in the first pass, after the labeling of the motion component.

3.1. ICA and motion component labeling

As the first step of the algorithm an ICA is run. ICA decomposes measured mixed signals X into a set of statistical independent sources S and their corresponding weights W (Comon (1994)). Given a domain Ω := [1, n] × [1,m] ⊂ ℤ², and an Image I : Ω → ℝ of dimension n × m, with I_i,j := I(i, j) the intensity of the pixel at (i, j) ∈ ℤ², image I can be written as a vector x := (I_1,1, I_2,1, …, I_n,1, …, I_n,m). Furthermore, given N images {I^(k)|k = 1, …, N} an image series can be written as X := (x₁, x₂, …x_N)^T. With x̄ := [x̄₁, x̄₂, …, x̄_N], and x̄_k the average image intensity of image I^(k) an ICA model of such a data set is formulated as:

$$\mathbf{X}\approx \mathbf{x̄}+\mathbf{\text{SW}}.$$ (1)

With C the number of retained components, the matrix S ∈ ℝ^{mn × C} defines the ICs, and W ∈ ℝ^{C × N} the mixing matrix. S can also be written as a vector (s₁, s₂, …, s_C)^T of row vectors s_i ∈ ℝ^mn and W as a vector (w₁, w₂, …, w_C) of column vectors w_c ∈ ℝ^N. The rows s_i of S can be interpreted as feature images and the columns w_c ∈ ℝ^N of W are the mixing weight curves of the individual ICs (Fig. 3).

3.1.1. On the optimal number of ICs

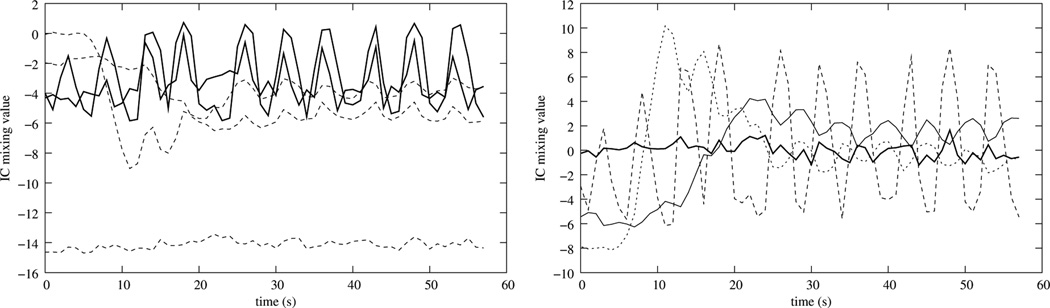
As suggested by Milles et al. (2006), a perfusion series is actually composed of five major components: the baseline, the LV cavity enhancement, the RV cavity enhancement, the myocardial perfusion, and the movement component. In a free breathing setting, this movement is quasiperiodic over the whole acquisition time, and in a series acquired with initial breath holding, the movement is quasiperiodic after the onset of the breathing motion. Hence, a separation into five components should be the optimal approach for the application of ICA. However, as Gupta et al. (2010) noted and as we confirmed in experiments, sometimes the perfusion component can not be separated well, and instead the movement component is split into two different ICs which results in more than one mixing curve exhibiting periodic behavior (Fig. 5 (left), solid lines). Here, reducing the number of components can result in an unambiguous separation of the motion component (Fig. 5 (right)).

Figure 5.

Left: Mixing matrix obtained using a five component ICA. Note, that the quasiperiodic movement component is actually split into two components. Using a four component ICA results in better separation (right).

In other cases, intensity change patterns resulting from the imaging process or the perfusion of additional tissue create more components that can be identified without introducing ambiguity for the motion related component, resulting in a better separation of the movement if more than five components are used (Fig. 6).

Figure 6.

Left: Mixing matrix obtained using a five component ICA. Note, that the shape of the quasiperiodic movement component indicates that it is not completely separated from the perfusion component. With a six component ICA this effect is reduced significantly (right).

To ensure the best separation of the movement from the other components we target to find the highest number of ICs that result in the lowest positive number of motion components.

3.1.2. Normalization

As a result of ICA the ICs are already normalized to have a unit variance. Additionally, we normalize the mixing matrix W like follows: First, we shift the values of the mixing curves ${\mathbf{w}}_c^{*}$ to have a zero mean ${\mathbf{w}}_c^{\prime }≔{\mathbf{w}}_c^{*}-{{\mathbf{w̄}}^{*}}_c\text{ with }{{\mathbf{w̄}}^{*}}_c=\frac{1}{N}{\displaystyle {\sum }_{i=1}^N}{w}_{c,i}^{*}$, and we create the mean image $\mathbf{X̄}\prime ≔{\displaystyle {\sum }_{c=1}^C}{{\mathbf{w̄}}^{*}}_c{\mathbf{s}}_c$ that retains the extracted information. Then, all ICs s are sign corrected so that the mixing curves ${\mathbf{w}}_c^{\prime }$ start with a negative value. As a result eq. (1) reads now

$$\mathbf{X}\approx \mathbf{x̄}+\mathbf{W}\prime \mathbf{S}\prime +\mathbf{X̄}\prime .$$ (2)

with the primed quantities being the corrected versions of the originals.

A typical representation of the resulting mixing matrix is shown in Fig. 7. Specifically, in the feature images related to RV and LV enhancement, the corresponding cavities are represented with high intensities (Fig. 7 (right)), and the RV and LV peak enhancements correspond to the first large maximums in the corresponding mixing weight curves (Fig. 7 (left), solid lines). Often this maximum is also the global maximum, but this is not guarantied.

Figure 7.

Time curve representation of the mixing matrix for ICAs with four components after normalization and sign correction (left), and corresponding RV (right, upper), and LV (right, lower) components.

3.1.3. Considerations on the time-frequency behavior of IC mixing curves

In order to properly identify the ICs as belonging to motion, we use a component-wise wavelet based time-frequency analysis of the IC mixing matrix W (Mallat (1999)). Compared to a Fourier analysis, a wavelet based analysis provides not only a frequency spectrum, but also time-based information, which makes it possible to apply the method not only to completely free breathing data, but also data that starts with breath-holding.

The time-frequency analysis is based on applying a discrete wavelet transform (DWT) individually to the mixing curves resulting from the ICA. The result of the DWT is a series wavelet coefficients that are attributed to frequency bands or levels, and time ranges - the higher the frequencies are that are covered by certain band, the higher is the time resolution of the analysis - which is expressed by more coefficients being attributed to the according frequency band.

For practical purposes, the size of the input vector to a DWT needs to be of power of two, and with a complete DWT, the number of wavelet levels is L := log₂(N). For further explanation we will assume that the acquired series consists of 64 images. This is a little more than the size of the series that usually result from a 60s acquisition sequence and the input data needs to be padded with zeros to achieve the required size.

With 64 images that are acquired triggered at the heart beats, a DWT of the mixing weight curves results in log(64) = 6 wavelet levels. These levels correspond to the following frequency ranges (given in events per heart beat (EPH)):

$$\left\{\left[\frac{1}{4},\frac{1}{2}\right),\left[\frac{1}{8},\frac{1}{4}\right),\left[\frac{1}{16},\frac{1}{8}\right),\left[\frac{1}{32},\frac{1}{16}\right),\left[\frac{1}{64},\frac{1}{32}\right),\left[\alpha ,\frac{1}{64}\right)\right\},$$ (3)

with α referring to the scaling function that is used to cutoff the analysis for low frequencies (Mallat (1989)). The number of coefficients per level N_l are {32, 16, 8, 4, 2, 1} respectively. Note, that the standard notation for wavelet coefficients the counting of the levels starts at the highest frequency range.

Our main purpose for using DWT is to select the best number of ICs and to identify the component related to motion properly. Therefore, consider that the resting heart rate is about 75 heart beats per minute and a healthy respiratory rest breathing rate is about 12 per minute (Tortora and J-Grabowski (2002)). Hence, a breathing cycle amounts to about six frames in the heart-beat triggered image acquisition, and the significant coefficients representing this movement should be found in the second wavelet frequency level l_mov = 2. Since the movement pattern also includes higher frequency components, the coefficients of the first wavelet level will also be significant. However, since signal separation in ICA is not perfect, the higher level wavelet coefficients may also be non-zero, but usually not significantly larger than the low level coefficients (Fig. 8 (f)).

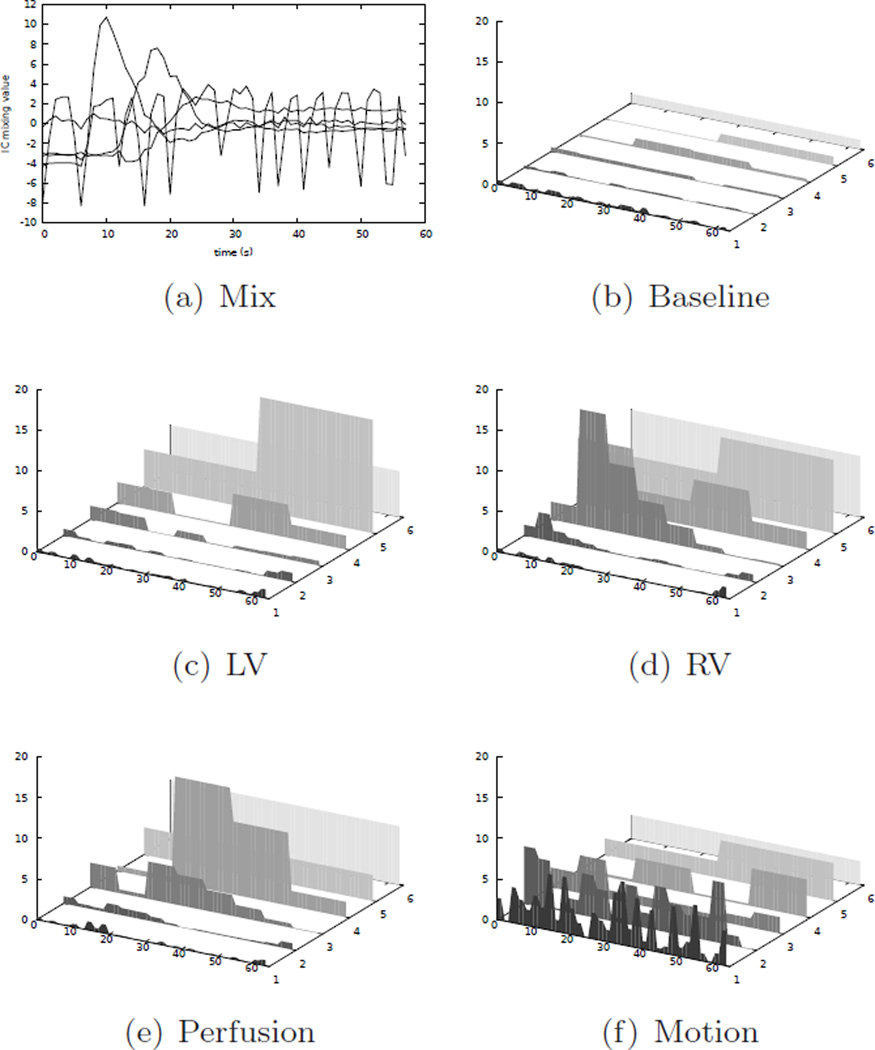
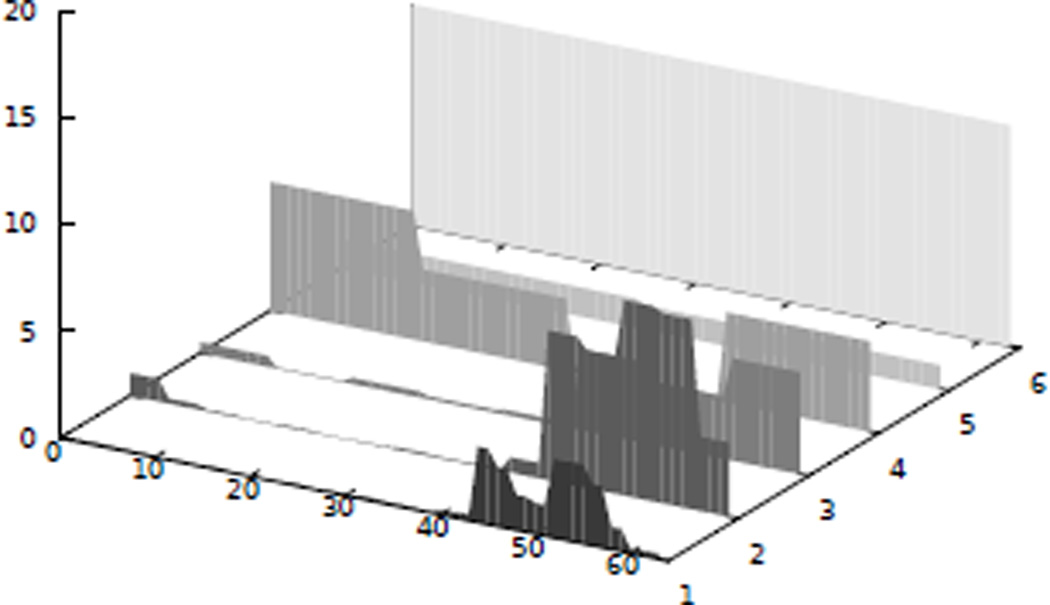
Figure 8.

Visualization of the absolute values (vertical axis) of the wavelet coefficients (b–f) over time (horizontal axis given in frames/heartbeats) of the mixing curves (a) of the perfusion series features obtained by an optimal five component ICA. Note, how the movement component (f) exhibits larger coefficients in the lower wavelet levels (depth axis), while the signal energy for the LV (c), RV (d) and perfusion component (e) is located in the higher wavelet levels.

The myocardial perfusion, LV and RV enhancement, are, on the other hand, processes that require more time, and the significant wavelet coefficients corresponding to these processes can be found in the higher wavelet levels, i.e. in the four levels that cover the frequency range $(\alpha ,\frac{1}{8}]$ EPH (Fig. 8(c,d,e)). Note, however, that the fast increase of the RV enhancement curve also results in notable coefficients at the beginning of the second wavelet level (Fig. 8(d)).

Finally, the baseline component has generally small coefficients (Fig. 8 (b)) and they are distributed over all wavelet levels.

In images series acquired free breathing, for the component(s) attributed to motion the wavelet coefficients in the motion related levels will be evenly distributed among the time indices. In the case of breath holding followed by breathing, these coefficients will be close to zero for low time indices and high for later indices. In addition, the coefficient in the highest wavelet level will also be large, representing the constant value of the mixing curve during the breath-holding phase of the image acquisition (Fig. 9).

Figure 9.

Wavelet spectrum corresponding to the movement IC for a perfusion series that starts with breath holding. Note, that the coefficients related to motion are close to zero at the beginning, and that coefficient related to the highest wavelet level is also large.

3.1.4. Labeling of components and identification of the optimal number of ICs

Based on above observations, the following procedure can be formulated to label the motion components:

First, we evaluate the DWT for all mixing curves ${\mathbf{w}}_c^{\prime }$

$${\mathbf{f}}^{(c)}≔\mathit{\text{DWT}}({\mathbf{w}}_c^{\prime })$$ (4)

resulting in the wavelet coefficients

$$\mathbf{f}≔\{f_{l,k}|l≔1,2,\dots ,L;k≔1,2,\dots ,2^l\}.$$ (5)

Based on the temporal distribution of the coefficient of the motion related wavelet level we decide now whether the perfusion sequence was acquired free breathing or with initial breath holding (for details see Appendix A).

For further component labeling we then evaluate for all coefficient series f^(c)

$$S_l^{(c)}≔{\displaystyle \sum _{i=1}^{2^l}}|f_{l,i}^{(c)}|.$$ (6)

Now we base the proper labeling of the movement component(s) on the sum of the low frequency coefficients

$$S_{\mathit{\text{LF}}}^{(c)}≔{\displaystyle \sum _{k=3}^{L-1}}{S}_k^{(c)},$$ (7)

and the sum of the high frequency coefficients

$$S_{\mathit{\text{HF}}}^{(c)}≔S_1^{(c)}+S_2^{(c)}.$$ (8)

In $S_{\mathit{\text{LF}}}^{(c)}$ we ignore the coefficient $S_L^{(c)}=f_{L,1}$, since for acquisition patterns that includes breath holding this coefficient will also be high.

Now, if $S_{\mathit{\text{LF}}}^{(c)}<S_{\mathit{\text{HF}}}^{(c)}$, then the component c will be labeled as motion with two exceptions: If c is the component with the lowest mixing value range it will be labeled as baseline, and if a free breathing acquisition pattern was estimated, but the component was labeled to exhibit motion at the beginning of the series according to (A.1), it is not labeled as motion, since in this case, the high values of the coefficients stem from the steep RV enhancement curve.

As a result of this labeling process, we obtain a set C_mov of movement components, a set C_rem of remaining components, and most of the time one component c_b labeled as baseline.

Based on the number of components that have been labeled as to contain motion, we proceed like follows: If no component was labeled as containing motion, then the series is considered to be free of motion. If one or more ICs were labeled as related to motion, we label this component as the main motion component that exhibits the largest value $E_{\mathit{\text{mov}}}≔{\text{max}}_{c\in C_{\text{mov }}}{S}_{l_{\text{mov}}}^{(c)}$. If this value E_mov is smaller than the value $S_{l_{\text{mov}}}^{(c_b)}$ of the base line component, then the series is also considered to be free of motion.

To rate the quality of the signal separation obtained by the ICA, we use the number of identified motion components: a lower positive number is better.

In order to obtain the optimal number of ICs, we run the ICA followed by the wavelet analysis described above for various numbers of components C. The number of components C that results in the lowest positive number of motion components is used for further processing.

Finally, out of the remaining components C_rem we label he ICs related to RV and LV enhancement based on the maximum mixing curve gradient and the time point of this maximum. Since the motion components were already labeled, only slowly changing components are left. For these, RV enhancement comes first and has the steepest enhancement, then comes LV enhancement, and finally perfusion. To compose the steepness and the time point of the enhancements into one value, we evaluate $t_{\text{grad},c}≔\mathit{\text{arg }}({\text{max}}_{i=1,2,\dots ,N}\frac{1}{i}\frac{\mathrm{d}}{\mathrm{d}t}{a}_{c,i})$ which weights the mixing curve gradient value against its time index and, hence, gives a preference to local gradient maxima that occur earlier. Then, the RV and LV ICs can be labeled based on

$$t_{\text{grad},c}(\mathit{\text{RV}})<t_{\text{grad},c}(\mathit{\text{LV}})<\dots$$ (9)

However, if the RV cavity is very small, as it may happen at the apical level, the LV enhancement curve may actually be a lot more prominent and steeper than the RV enhancement curve. Therefore, in a final step we test if the maximum mixing curve gradient of the supposed RV enhancement curve comes indeed before the one attributed to LV enhancement, and switch labeling of this is not the case.

For this labeling to succeed, the set of remaining components C_rem must contain at least two components. If this is not the case, we consider the ICA to be of low quality, since LV enhancement and RV enhancement should both be separated as well, unless RV cavity can be identified at all as it may be the case at the apical level. The result of such an ICA can not be used for an LV bounding box estimation, and hence it can only be used if non-linear registration is to be applied, or a registration scheme using linear registration is running in the second or later pass, when the region of interest was already segmented and cropped.

3.2. LV bounding box estimation

Given the properly labeled RV and LV enhancement components one can segment a region of interest around the LV myocardium. This segmentation is required, if linear registration is to be executed, and it also can be used to speed up non-linear registration by restricting image processing to this region of interest.

We base our segmentation on the difference of the RV and LV feature images that result from the preceding ICA instead of using the original images related to peak enhancement as proposed by Milles et al. (2008), and instead of using thresh-holding, we base the segmentation on a k-means classification (see Appendix B for a detailed description).

Given that the segmentation succeeded, we define the LV bounding box as squared and centered around the geometric center of the LV, c_LV and the length of its sides is set to 2s|c_RV − c_LV| with s being a scaling parameter. Because the breathing movement results in highly non-linear deformations of the interior of the chest, using linear registration requires a very accurate estimation of this bounding box and hence of the parameter s. In non-linear registration, a bounding box is only useful to speed up computations and it is better to set the scaling parameter to a larger value in order give enough freedom to the non-linear registration.

If the segmentation failed, then linear registration can not be run, but non-linear registration can still be achieved.

3.3. Image registration

In order to register the perfusion series, we create synthetic reference images for each time point by linearly combining all ICs and the mean image X̄′ that resulted from the normalization of the mixing curves, but we exclude the IC labeled as main motion component. By this method, the movement is removed from the reference image series, but the intensity change is preserved, resulting in reference images that exhibit the same intensity distributions as their original counterparts. Therefore, the sum of squared differences can be used as registration criterion.

Because initially, the feature images and the mean image retain a blurriness that results from the breathing motion, the reference images created by above method are also quite blurry (Fig. 10(left)). Therefore, in order to achieve good registration results it is better to use a multi-pass registration scheme.

Figure 10.

Example synthetic references, note the blurriness of the reference in the first pass (left) and the improved representation of features in the third pass (right).

Based on the freedom given to the transformation T_reg that is used to achieve registration a variety of registration approaches can be applied to achieve motion compensation. In the simplest case, one may compensate only for translation as do Milles et al. (2008). However, the accuracy of this linear registration approach is limited since it does not compensate for the local deformations of the heart.

Alternatively, one can employ non-linear registration, and, thereby, avoid the burden of optimal bounding box creation, and also aim at achieving higher accuracy by compensation for non-linear deformation of the heart. Our non-linear registration approach utilizes a B-Spline model for the transformation (Kybic and Unser (2003)), and a regularization that is based on the separate norms of the second derivative of each of the deformation components (Rohlfing et al. (2003)) weighted by a factor κ. In the first pass, we restrict the freedom of the non-linear registration by employing a high weight on the regularization, and by using a large knot spacing for the B-spline based transformation. In the subsequent passes, when the reference images are a lot less blurred (Fig. 10(right)), we employ a lower weight for regularization and a smaller B-spline knot spacing.

Finally, it is also possible to first run linear registration followed by non-linear registration to refine the initial alignment.

4. Experiments and Validation

4.1. Image data

13 first-pass contrast-enhanced myocardial perfusion imaging data sets were acquired and processed under clinical research protocols and all subjects provided written informed consent. Six data sets are rest studies, five data sets are stress studies, and for the remaining two sequences this information was lost due to too aggressive anonymization. Two distinct pulse sequences were used for image acquisition: a hybrid GRE-EPI sequence and a true-FISP sequence. Both sequences were ECG-triggered and used 90-degree-saturation recovery imaging of several slices per R-R interval acquired for 60 heartbeats. The pulse sequence parameters for the true-FISP sequence were 50-degree readout flip angle, 975 Hz/pixel bandwidth, TE/TR/TI = 1.3/2.8/90 ms, 128 × 88 matrix, 6 mm slice thickness. The GRE-EPI sequence parameters were 25-degree readout flip angle, echo train length = 4, 1500 Hz/pixel bandwidth, TE/TR/TI = 1.1/6.5/70 ms, 128 × 96 matrix, 8 mm slice thickness. The spatial resolution was about 2.8 mm × 3.5 mm. Parallel imaging using the TSENSE (Kellman et al. (2001)) method with acceleration factor = 2 was used to improve temporal resolution and spatial coverage.

For all but one patient, a half dose of contrast agent (Gd-DTPA, 0.1 mmol/kg) was administered at 2.5 ml/s, followed by saline flush. For one patient the dose was administered at a higher rate which resulted in a significantly higher contrast. For 12 patient data sets the images series were reconstructed to a final matrix size of 256 × 192 (3/4 phase FOV) using zero filling for interpolation, and for one patient the final matrix size was 128 × 128 instead. This low resolution series and the series with a higher contrast resulted from acquisition protocols that are no longer in use. Nevertheless, we include this data here to test the robustness of the algorithm with respect to varying input. All data sets were acquired using a free breathing protocol, still, one rest study and one stress study exhibited a somewhat erratic breathing pattern while the others showed the expected quasiperiodic motion, and in all data sets the RV and LV cavity could be identified visually. Motion correction was performed for three short-axis slices of these 13 patients covering different levels of the LV myocardium (basal, mid, and apical levels) totaling in 39 slice sequences. Out of the 60 images per slice sequence, the first two frames were acquired as proton density weighted images for use in correcting the surface coil intensity variation. These frames were acquired at a lower excitation flip angle and without the saturation recovery preparation, and were omitted from the motion compensation resulting in 58 perfusion images per slice sequence.

In order to also test our method on perfusion series that were acquired breath holding, we replaced approximately the first 40 frames of some of the original series with the registered images thereby simulating perfusion series with initial breath holding followed by normal breathing. Our main purpose for these series was to test the IC labeling scheme in a breath-holding setting, therefore, we did not run an additional segmentation based validations for these simulated breath holding series.

4.2. Methods implemented and tested

We run our motion compensation experiments by using a variety of methods. Firstly, we run tests by using the ICA based method described above executing (1) non-linear registration only (ICA-SP), (2) linear registration by optimizing a translation (ICA-T), which is similar to Gupta et al. (2010) but employs the new labeling scheme. Then, we will run (3) ICA-T followed by at least one pass of spline based non-linear registration (ICA-T+SP).

In addition to these methods, we will compare to methods presented elsewhere. Specifically, we will compare to (4) motion compensation exploiting the quasiperiodicy of the breathing movement (QUASI-P), Wollny et al. (2010a), (5) serial registration with the accumulation of transformations (SERIAL), Wollny et al. (2010b), and (6) pseudo-ground-truth based registration (PGT) Li and Sun (2009) with some variations: Since this approach requires already linearly aligned input images, we used the output of ICA-T as input images, we replace the demons based non-linear registration by the same spline based approach that is used for ICA-SP, and instead of using Gaussian elimination to solve the PGT estimation problem, we used the L-BFGS algorithm (Fletcher (2000)).

4.3. Software and Parameters

All methods have been implemented using the same image processing software and made available (Wollny (2010)). For the independent component analysis the FastICA algorithm was used (Hyvarinen (1999)) as implemented in Ottosson et al. (2009). The FastICA algorithm was first run in deflation mode, if this didn’t result in a usable signal separation, symmetric mode was run and the provided result was used regardless of the convergence of the algorithm. The maximum of iterations was set to 400.

For the discrete wavelet transform we relied on the implementation in Galassi et al. (2009) and used the centered Daubechies wavelet family of maximum phase with five vanishing moments (Daubechies (1988)). For the ICA based methods the optimization of the objective function was achieved using the rank-1 method of the shifted limited-memory variable metric algorithm (VAR1) by Vlcek and Luksan (2006) as implemented in Johnson (2011) when running non-linear registration (breaking conditions: maximum of 300 iterations, or 0.001 absolute x-tolerance, or 0.001 relative objective function value), and the simplex algorithm of Nelder and Mead (1965) implemented in Galassi et al. (2009) when running linear registration (breaking condition for the simplex algorithm was set to 0.01, and its start step size to 0.001).

For QUASI-P a gradient decent provided significantly better results than VAR1 and we used the method implemented in Galassi et al. (2009), a start step size of 0.01, and a stopping condition of 0.001.

The parameters used to run the non-linear registrations are given in Table 2. In addition, SERIAL used a weighted sum of normalized gradient fields (NGF) (1.0) and the sum of squared differences (SSD) (1.0) as registration criteria.

Table 2.

Registration parameters used in the schemes that include non-linear registration. “scale” refers to the value used to scale the according parameter with each new registration pass.

Method	SERIAL	QUASI-P	ICA-SP/PGT-SP	ICA-T
regularization weight κ/scale	100	10 / −	105 / 0.5	-
knot spacing/scale	16	10 / −	16 / 0.5	-
multi-resolution-levels	3	3	3	3
passes	1	1	≤ 3	≤ 2

Li and Sun (2009) does requires three parameters for ground truth estimation that are not given in the article. After conversation with the authors, we set these parameters to α = 0.1, β = 4, and ρ = 0.85.

If linear registration was to be run - stand alone or followed by non-linear registration — then the bounding box amplification parameter was set to s = 1.3, and if only non-linear registration was to be run it was set to s = 2.0. For all additional parameters that are not given here, the default values as implemented in the respective software libraries were used.

All experiments and timings were run on a AMD Phenom II X6 1035T processor (2.6GHz), Gentoo/Linux 64 bit. The software was compiled with GNU g++ (Gentoo 4.5.3-r1), and optimization flags −O2 −march=native −mtune=native −funroll-loops - ftree-vectorize.

4.4. Validation

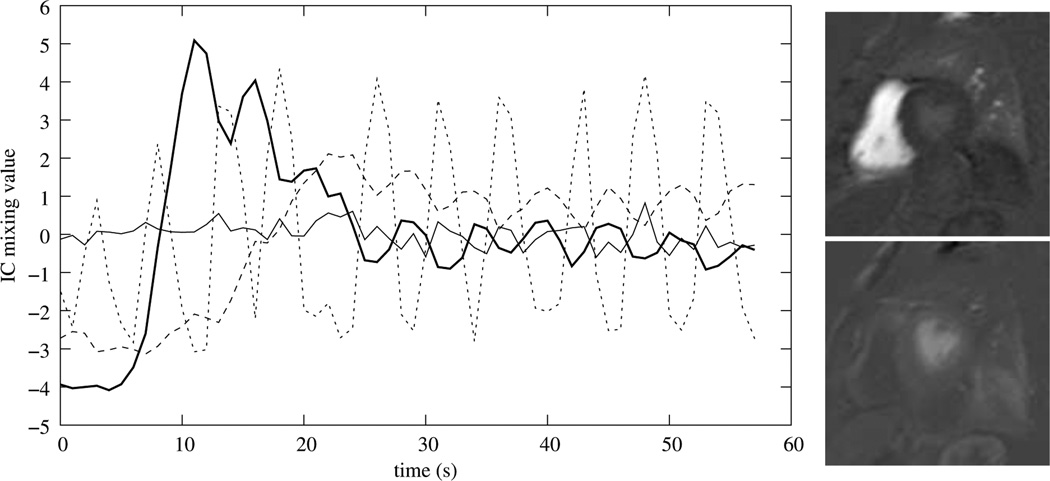
Time-intensity curves of sections of the myocardium are the prominent feature on which a medical indication would be based. Therefore, we will base our validation on the comparison of manually acquired time-intensity curves ${\mathit{K̂}}_{\text{ref}}^{(s)}$ of 12 sections s ∈ 𝕊 of the myocardium compared to automatically obtained ones before ${\mathit{K̂}}_{\text{orig}}^{(s)}$ and after ${\mathit{K̂}}_{\text{reg}}^{(s)}$ registration (Fig. 11). For a better comparison the time-intensity curves were normalized linearly so that the manual obtained series ${\mathit{K̂}}_{\text{ref}}^{(s)}$ cover an intensity range of [0,1].

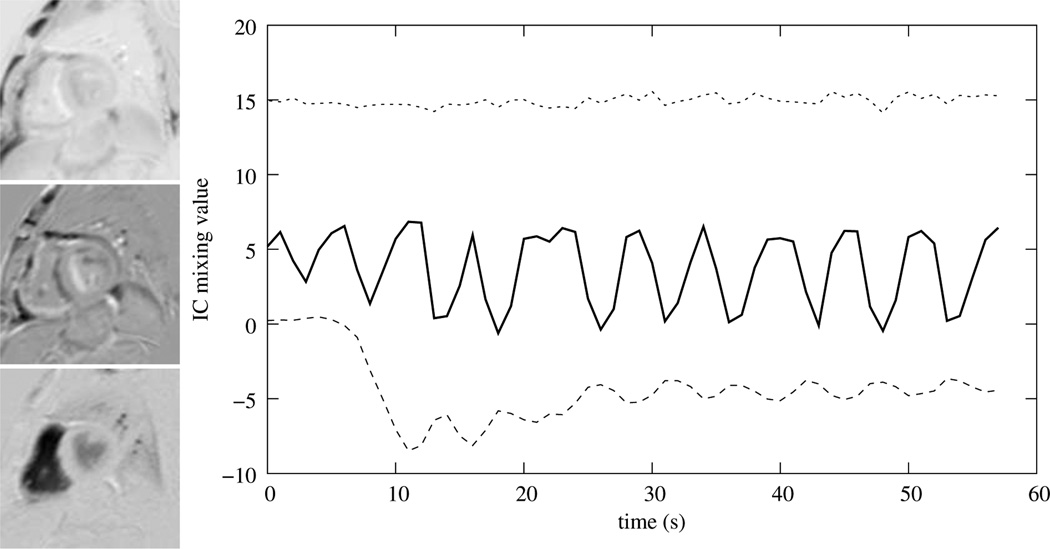
Figure 11.

Example segmentation of a slice of the myocardium (left). The RV insertion point is indicated by a circle and based on its location and the center of the LV the myocardium is segmented clock-wise into 12 segments that enclose equal angles. An example of the time-intensity curves before and after registration as well as the corresponding manually obtained curve is given on the right.

In order to estimate these time-intensity curves, for all data sets in each slice the LV-myocardium was segmented and the center of the LV as well as the RV insertion point from the short-axis images were identified. Since it is difficult to identify the LV center directly, we selected three points on the outer wall of the LV myocardium, evaluate the circle passing through these points and use the center of this circle as LV center. Using the LV center as angular point and beginning at the RV insertion point, the myocardium was segmented clock-wise into 12 segments enclosing equal angles (Fig. 11, left). Finally, time-intensity curves were evaluated based on the average pixel intensities of these segments (Fig. 11, right).

For comparison of the curves before and after registration we evaluated Pearsons correlation coefficient R² between the manually obtained time intensity curves and the time intensity curves that were obtained by using the segmentation of one reference slice as mask for all frames. Here, higher correlation indicates a better registration.

Secondly, the Normalized Mean Squared Error (NMSE)

$$\text{NMSE}({\mathit{K̂}}^{(s)})≔\frac{1}{N}\frac{{\displaystyle {\sum }_{t\in \mathrm{\Theta }}}{({\mathit{K̂}}^{(s)}(t)-{\mathit{K̂}}_{\text{ref}}^{(s)}(t))}^2}{\overline{{\mathit{K̂}}^{(s)}}·\overline{{\mathit{K̂}}_{\text{ref}}^{(s)}}},$$ (10)

is used as a quality measure, and it is evaluated before $(\text{NMSE}({\mathit{K̂}}_{\text{orig}}^{(s)}))$ and after $(\text{NMSE}({\mathit{K̂}}_{\text{reg}}^{(s)}))$ registration; smaller values indicate better motion compensation.

Finally, we consider the average standard deviation of the intensity in the 12 segments s_i of the myocardium σ_si,t:= Σ_t∈Θ σ(s_i) as obtained by using the myocardial mask of one reference frame of the motion-corrected sequence. Here, smaller values also indicate a better registration.

For the automatic extraction of the time-intensity curves, we choose the reference frame 30, since it lies in the middle of the series and should reduce the effect of accumulating errors when applying SERIAL, without having any specific influence on the other methods. Because all segmentations were done before the image registration was executed, the masks for the myocardium within the reference frame have to be transformed using the registration transformation. Only for SERIAL the original mask can be used for the automatic analysis. Therefore, for all other algorithms it also has to be considered that the masks for automatic intensity-time curve extraction are subject to registration errors.

Other measures have been presented in the literature that quantify the registration quality based on comparing manual segmentations features before and after registration, see e.g. Milles et al. (2008); Xue et al. (2008). As discussed in Wollny et al. (2010a), a validation based on comparing manually segmented shapes is not a reliable option for our target application. Specifically, the accurate tracking of the myocardium through time in perfusion studies is not an easy and repeatable task because it is difficult to track inner boundary of the ventricle properly: on one hand, at the beginning of the series the myocardium and the left ventricular cavity exhibit the same intensities, and on the other hand the papillary muscles and the myocardium often also exhibit the same intensities throughout the series. Segmentation errors, however, will show up in any segmentation based quality assessment, but may have no influence on the tracking of the time-intensity curves, the feature the final analysis of the perfusion series is based on. For the sake of completeness we will provide two measures that rate the registration accuracy based on segmentations, the dice index (DI) between the manually obtained myocardial shape and the reference shape that is propagated through the series (higher values are better), and the boundary root mean square error (BRMSE) of the according myocardial contours and the propagated reference contour (smaller values are better).

All measures given here will be evaluated for all 58 frames of each series, and the means are evaluated over all sections of all slices of all data sets. Since the samples can be matched based on section, frame, slice, and data set the one-sided t-test for paired samples is used to test the significance improvements of the observed validation measures (Sokal and Rohlf (1995)).

5. Results

Using the parameters given above, we were able to achieve a significant reduction of motion with all tested methods for all slices, including the data sets with a more erratic breathing pattern. For all cases, the RV and LV labeling scheme was successful as was the segmentation of the LV bounding box. The quantification of the registration quality by the measures given above is summarized in Table 3. The full results of the significance tests for the differences between the methods are given in the accompanying material.

Table 3.

Results for the validation measures given in the text. ICA-T+SP provides the best motion compensation results for all validation measures. The significance of the difference of ICA-T+SP when compared to the other motion compensation methods is given in Table 4.

	R2 ↑	NMSE ↓	σ ↓	BRMSE↓	DI ↑	$\frac{\mathit{\text{time}}}{s}$
manual	–	–	.204±.084	–	–	–
unregistered	.838±.185	.529±.482	.346±.178	1.66±.424	.703±.162	–
ICA-SP	.959±.076	.287±.333	.254±.150	1.16±.366	.818±.087	47 ± 19
ICA-T	.928±.135	.327±.384	.274±.146	1.25±.358	.794±.114	9 ± 3
ICA-T+SP	.963±.058	.259±.261	.249±.131	1.10±.234	.826±.085	17 ± 9
SERIAL	.942±.116	.336±.373	.266±.146	1.43±.359	.768±.133	846 ±157
QUASI-P	.942±.089	.305±.280	.272±.147	1.29±.263	.790±.121	400 ± 76
ICA-T+PGT	.955±.085	.282±.302	.259±.138	1.15±.258	.815±.092	18 ± 9

With the automatic ICA based mask creation the size of the region to be processed was reduced to an average of 90 × 90 pixel for non-linear registration only, and 58×58 for all approaches that include linear registration.

The best motion compensation results were obtained by running ICA-T+SP, i.e. by running an initial ICA-based two-pass linear registration optimizing a translation only, followed by an at-most three-pass non-linear registration. This approach performed best across all measures resulting in consistently better validation measures as compared to the remaining methods across all validation measures (Table 4). Only for Pearsons correlation coefficient R² and BRMSE and when comparing to ICA-SP, the difference in the results is of only low significance.

Table 4.

Results of the significance test of ICA-T-SP method compared to the other methods using the one-sided paired t-test. The improvement is highly significant (p < 0.05) for all validations measures and tested methods but Pearsons correlation coefficient R² and BRMSE when compared with ICA-SP. In these two cases the improvement is of a low significance (p < 0.1).

		SERIAL		QUASI-P		ICA-T		ICA-T-PGT		ICA-SP
	df	t	p	t	p	t	p	t	p	t	p
R2	467	4.14	2e-05	5.37	6.3e-08	7.19	1.3e-12	3.10	0.001	1.42	0.078
MNSE	467	−6.72	2.7e-11	−6.11	1e-09	−6.87	1e-11	−4.29	1.1e-05	−2.81	0.0026
σ	467	−3.60	0.00018	−6.17	7.6e-10	−8.79	2.2e-16	−4.99	4.3e-07	−1.37	0.085
BRMSE	38	−6.90	1.7e-08	−8.55	1.1e-10	−3.74	0.00031	−3.67	0.00037	−2.04	0.024
DICE	2261	29.50	2.2e-16	20.52	2.2e-16	20.53	2.2e-16	14.53	2.2e-16	7.82	4.1e-15

As second best methods, ICA-SP and ICA-T-PGT perform equally well and result in better motion compensation than the remaining three tested methods SERIAL, QUASI-P, and ICA-T. These three methods give a mixed picture regarding the validation measures and no clear ranking can be given.

In addition we tried to run PGT without initial linear registration, but this generally doesn’t result in proper motion compensation proofing that this algorithm indeed requires initial linear registration.

The run-times of the linear registration scheme are very low - as it can be expected. Motion compensation that first utilizes linear registration still have a very low run-time and even ICA-SP achieves the registration at a rate below one frame per second, despite the multi-pass scheme. This low run-time can be attributed to the automatic extraction of a region of interest around the LV that is used to reduce the computational load during registration and to the use of the shifted limited-memory variable metric algorithm used for optimization. However, for SERIAL and QUASI-P this optimization algorithm did not yield as good results as using gradient decent which is known for its slow convergence. In addition, SERIAL and QUASI-P, both always run at the full image resolution, since both methods don’t offer any means to automatically extract regions of interest.

Running the ICA based motion compensation algorithm for the simulated breath-holding data also resulted in a proper identification of the ICs related to motion and RV/LV and proper motion compensation, showing that this method is also applicable to data that was acquired with initial breath holding.

Finally, no significant differences of the performance of the motion compensation algorithms could be observed between rest and stress studies.

6. Discussion

Image registration is an established method to compensate for breathing motion in myocardial perfusion data sets, and the use of ICA as proposed in Milles et al. (2008) provides an elegant way to create synthetic reference images for such a registration that exhibit intensity distributions that are close to counterparts from the original series thereby simplifying image registration.

Milles et al. (2008) focused on identifying the features that need to be retained, i.e. RV/LV enhancement and baseline, However, for sequences that were acquired free breathing, the labeling scheme sketched by Milles et al. (2006) and used by Gupta et al. (2010) is not suitable, because its presumptions about the maximum weight values and its time point do not generally hold. Also, Gupta et al. (2010) reported that the labeling method fails if strong motion is present.

Still, ICA is well suited to separate a quasiperiodic motion component from the other features of myocardial perfusion series, namely LV/RV enhancement, perfusion, and baseline — regardless whether this motion takes place during the whole image acquisition sequence (free breathing), or only at the end of the acquisition sequence (initial breath holding). However, to properly identify the ICs in such a setting it is better to shift the focus to the feature that needs to be removed — the motion.

Therefore, we presented a new labeling scheme based on a discrete wavelet analysis of the mixing value curves that first focuses on the identification of the motion component(s) and the number of ICs the results in the best separation of signals. By identifying the IC(s) corresponding to the breathing motion that is quasiperiodic over the whole acquisition time or part of the series and then eliminating it from the reference image creation, we were able to create series of reference images that are free of motion. Note, that Gupta et al. (2010) did not normalize the mixing curves to have a zero mean. Therefore, by leaving out one component in the reference image creation, an intensity bias is introduced into the synthetic reference image and consequently they had to use a more complex registration criterion, namely cross correlation. Since we normalize the mixing value curves to have a zero mean and create an additional feature image that retains the extracted information, we avoid the introduction of this intensity bias in the synthetic reference images when the motion component is dropped from the mix. As a result we obtain synthetic references that truly exhibit similar intensity distributions like the original images, and we can use the sum of squared differences as registration criterion.

To label the components related to RV and LV enhancement we proposed an approach that lowered the requirements for the RV and LV mixing value curves as compared to the ranking proposed by Milles et al. (2006). They base the labeling on the global maximum of these curves, and assume that the global maximum of the enhancement curves always coincides with the enhancement peak, an assumption that does not hold if strong or free breathing movement is present. Our approach identifies the maximum gradient weighted by its time-position and only after the identification of motion related components and a possible baseline component, thereby making RV and LV enhancement component labeling more robust. With our labeling approach, motion and RV and LV enhancement components were properly identified in all 39 free breathing image series as well as the data sets simulating initial breath holding.

Our primary focus was to apply non-linear registration to achieve motion compensation, therefore, the proper labeling of the RV and LV components and the segmentation of a region of interest (ROI) around the LV based on the corresponding feature images comes as a bonus that makes it possible to speed up registration by either restricting the registration to this ROI, and/or by first running a linear registration algorithm. Other than Milles et al. (2008), who based a bounding box creation on the RV/LV peak enhancement images that may picture the cavities at extremal points of the breathing motion, we used the corresponding IC feature images, since here the cavities are located at their average position. We based the segmentation of the RV/LV cavities on a k-means classification instead of thresholding so that we don’t have to make any assumptions about the intensities that are required when setting a threshold. With this alternative labeling and segmentation scheme we were able to successful identify motion and RV/LV enhancement and automatically segment a LV bounding in all 39 slices of the 13 patient data sets that were acquired free breathing and included rest and stress studies.

If only linear registration is to be run, the selection of a proper bounding box scaling parameter s to set the size of the ROI becomes a delicate task: A small value may result in the ROI not covering the LV myocardium completely, and a large value will result in a ROI that contains non-moving body parts that hinder a proper linear alignment. If the linear registration is followed by non-linear registration, then it is best to select a larger s to make sure that the whole LV myocardium with its whole movement range is covered.

Our results show, that the results of motion compensation by applying linear registration can be improved by running an additional non-linear registration. Also running the ICA based motion compensation by only applying non-linear registration performs better then employing linear registration only.

Because initially, the synthetic references created by the ICA based motion compensation scheme are quite blurry, it is best to apply the motion compensation algorithm in a the multi-pass fashion. To achieve full registration employing non-linear based registration, it is best to put a high penalty on the nonlinear transformations in the first registration pass, and give more freedom to the transformation in subsequent passes, when the newly created reference images are less blurry.

Running one of the proposed ICA based registration schemes has its advantage over running QUASI-P. On one hand, with QUASI-P the final registration is dependent on the initial registration phase: A failed registration here results in various badly created synthetic references that result in a final bad registration. On the other hand, as reported in Wollny et al. (2010a), since the reference image creation is based on the linear interpolation the references may not model well the fast enhancement of RV and LV, resulting in bad synthetic references and hence in a bad registration in this part of the series. Because in this study we used more data sets, the latter problem of QUASI-P became more evident, resulting in notable worse performance of the algorithm as compared to the results presented in Wollny et al. (2010a). Also QUASI-P doesn’t provide automatic means to speed up registration, like the ICA based approach does, which results in a relatively large run-times.

Since with the ICA based motion compensation scheme, for each original image of a perfusion sequence a corresponding synthetic reference image is create, registration errors in one frame have no influence on the performance of the motion compensation for the reminder of the sequence. Hence an accumulation of errors, as it can be seen in SERIAL is not possible and consequently the ICA based methods provide better motion compensation.

The pseudo-ground-truth (PGT) based registration scheme provides results that are of a similar quality as the ICA-SP registration scheme. However, in the estimation of PGT it is assumed that the pixel-wise second order derivative of the intensity change over time is low, yet image acquisition itself may introduce intensity variations over time that don’t result from the breathing movement (see, e.g., Fig. 11, right, manually obtained curve) Therefore, the generation of a pseudo ground truth by also smoothing over time may overcompensate. In addition, PGT requires an initial linear registration that in turns requires the proper identification of a ROI around the LV myocardium. If no such region can be identified automatically, a PGT based approach will require manual interaction or it will fail. In such a case the purely non-linear motion compensation approach ICA-SP can still successfully be applied on the full image scale.

Since the ICA based methods provide a simple way to automatically define a region of interest around the LV myocardium, registration can be speed up significantly, and as a result all ICA based methods are computationally less demanding than SERIAL and QUASI-P. Given a successful estimation of such a region of interest an additional speedup can be achieved by preceding the non-linear registration by linear registration.

We also tested our algorithm on simulated breath holding data which is still widely used in the clinical routine. Here the wavelet based labeling scheme was also able to properly identify the ICs resulting in successful bounding box creation and identification of the motion component. With these prerequisite in tact, it was possible to run the motion compensation scheme and achieve full motion compensation. This is an advantage over the heuristic curve length based scheme presented in Wollny et al. (2011) that can only be applied to free breathing acquired data.

7. Conclusion

We presented a motion compensation scheme that loosely follows the approach presented by Milles et al. (2008) in using an ICA to identify main features of the perfusion series and create synthetic references from these features in order to achieve motion compensation by image registration. Since Milles et al. (2008) IC labeling approach is not suitable for perfusion sequences that were acquired free breathing, and tends to fail for sequences that exhibit strong motion (Gupta et al. (2010)), we replaced their labeling scheme by a new, more robust approach, that is based on an initial time-frequency analysis and first focuses an the identification of motion that is then omitted in the creation of synthetic references.

Which this new labeling scheme we were able to identify the IC component related to motion successfully in all free breathing acquired sequences and all simulated breath holding sequences. Since we employ non-linear registration, this was sufficient to achieve full motion compensation in all cases.

Nevertheless, our enhanced labeling scheme also made it possible to properly identify the ICs related to RV and LV enhancement, and with the segmentation approach based on k-means classification the LV and RV cavities could be segmented successfully and a bounding box enclosing the LV myocardium could be created in all cases. Hence, it was possible to speed up non-linear registration by restricting registration to the region of interest around the LV myocardium (ICA-SP) or by preceding it with linear registration (ICA-T+SP).

Our validation showed that the latter approach performed best for all considered validation measures as compared to methods published elsewhere (Wollny et al. (2010a,b); Li and Sun (2009)) and also required the lowest run-time of all methods implemented and tested here that include non-linear registration.

Our proposed method works best with perfusion sequences that were acquired free breathing, but it can also be applied to data that was acquired with initial breath-holding, which is still the standard in most clinical applications.

Finally, ICA provides additional information about the perfusion cycle, like the time points for RV and LV peak enhancement than may be of use in the further automatic analysis of the perfusion data.

• *ICA based non-rigid motion compensation scheme for free breathing and breath holding acquired perfusion data
• *validation based on the clinically relevant time-intensity curves
• *performs comparable to or better than previously published approaches
• *runs fully automated
• *an implementation of the presented algorithm is available as free software

Figure 2.

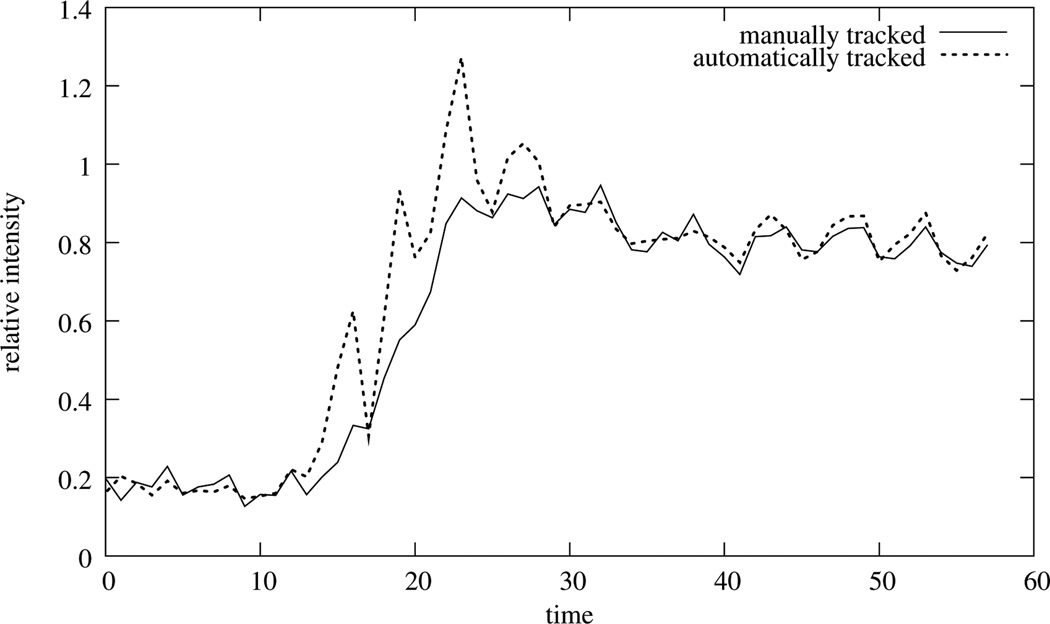
Manually tracked intensity change of a myocardial segment versus an automatically obtained time-intensity curve of a free breathingly acquired data set. Note, that not even the average of the automatically obtained time-intensity curve would result in a proper assessment of the blood flow. Also note, that the manually tracked curve is not smooth in itself - an effect that is the result of the image acquisition process.

Glossary

CC

cross correlation

DWT

discrete wavelet transform

ECG

electrocardiogram

IC

independent component

ICA

independent component analysis

MRI

magnetic resonance imaging

MI

mutual information

NGF

normalized gradient fields

LV

left ventricle

RV

right ventricle

ROI

region of interest

SSD

sum of squared differences

Appendix

Appendix A. Estimation of breathing pattern

First, for all f_c we evaluate the mean time index for the breathing motion related wavelet coefficient level l_mov according to

$$t_{\text{mean},l_{\text{mov}}}^{(c)}≔\frac{{\displaystyle {\sum }_{t=0}^{N_{l_{\text{mov}}}}}t*|f_t^{(c)}|}{{\displaystyle {\sum }_{t=0}^{N_{l_{\text{mov}}}}}|f_{c,t}^{(c)}|}$$ (A.1)

Based on in which interval out of $\{[0,\frac{1}{3}),[\frac{1}{3},\frac{2}{3}),[\frac{2}{3},1]\}$ this value falls, the component is labeled as either to exhibit movement at the beginning, at the end, or continuously over time.

Then, we accumulate the coefficients sums $S_{l_{\text{mov}}}^{(c)}$ of the movement related frequency levels according to their movement time frame label obtaining sums S_begin, S_cont, S_end. Based on which is the maximum of these sums it is decided whether the breathing movement was only at the beginning, continuous, or only at the end of the acquisition series, and hence which breathing pattern was used during acquisition time. Hereby we assume, that the acquisition patterns breath holding - free breathing - breath holding and free breathing - breath holding - free breathing are not used.

Appendix B. RV and LV cavity segmentation

The segmentation of the RV and LV cavities is based on the difference w_LV − w_RV of the RV and LV feature images. In this difference image, the RV cavity has a low intensity and the LV cavity a high intensity.

In order to segment both objects, we first use morphological gray scale opening and closing of radius 2 pixels to remove small holes and connections, then classify the intensities using k-means of initially 7 classes. To segment the RV cavity we select the k-means class corresponding to the lowest intensity label connected components and identify the largest connected component as RV cavity.

For LV cavity segmentation we select the k-means class corresponding to the highest intensity, also run a connected component labeling. Depending on the contrast agent dose and timing of the imaging, more than one large connected component may result from this labeling. Therefore, to identify the LV cavity, we do not only use the area of the connected component to identify it, but also its distance to the already segmented RV cavity, i.e. given the geometric center c_RV of the RV cavity and the centers c_L of the LV cavity candidates as well as their areas A_L, we use the quotient $\frac{\mathit{\text{dist}}({\mathbf{c}}_{\text{RV}},{\mathbf{c}}_L)}{A_L}$ as the distant measure to be minimized.

Segmentation may fail, either because of a wrong identification of the LV/RV components, or because k-means classification did not sufficiently separate the intensity ranges, which usually results in very large segmented regions. Therefore, as an heuristic to judge success of the segmentation, we measure if the area of the estimated cavity is below $\frac{1}{10}$ of the whole image area. If this is not the case then we retry segmentation using more classes in the k-means algorithm. If the maximum of 13 classes is exhausted without proper segmentation result, the segmentation is considered to have failed.