Bayes Factor based on the Trend Test Incorporating Hardy-Weinberg Disequilibrium: More Powerful to Detect Genetic Association

Summary

In the analysis of case-control genetic association, the trend test and Pearson’s test are the two most commonly used tests. In genome-wide association studies (GWAS), Bayes factor is a useful tool to support significant p-values, and a better measure than p-value when results are compared across studies with different sample sizes. When reporting the p-value of the trend test, we propose a Bayes factor directly based on the trend test. To improve the power to detect association under recessive or dominant genetic models, we propose a Bayes factor based on the trend test and incorporating Hardy-Weinberg disequilibrium in cases. When the true model is unknown, or both the trend test and Pearson’s test or other robust tests are applied in genome-wide scans, we propose a joint Bayes factor, combining the previous two Bayes factors. All three Bayes factors studied in this paper have closed forms and are easy to compute without integrations, so they can be reported along with p-values, especially in GWAS. We discuss how to use each of them and how to specify priors. Simulation studies and applications to three GWAS are provided to illustrate their usefulness to detect non-additive gene susceptibility in practice.

Introduction

Although p-value is a main tool in the analysis of case-control genetic association studies, Bayes factor (BF) is an important measure of association to be reported, especially in genome-wide association studies (GWAS) (Stephens & Balding 2009; Sawcer 2010). Because BFs incorporate both significance (p-value) and power (sample size) to detect association, they are used to support significant associations identified by small p-values, and preferred to p-values when the significant results are compared across studies with different sample sizes. Hence p-value and BF can be both reported in GWAS, e.g., WTCCC (2007) and Yasuno et al. (2010).

In this paper, we propose a BF, denoted as BFA, for case-control association studies directly based on the trend test. Hence BFA can be directly linked to the p-value of the trend test. The trend test and Pearson’s test are the two most commonly used statistics for testing case-control genetic associations. The former is more powerful under additive or multiplicative models, while the latter is more powerful under recessive or dominant models. Thus, the trend test may fail to detect associated markers with recessive or dominant models. Definitions of genetic models will be given later. To enhance the power under non-additive or non-multiplicative models, we further propose a BF, denoted as BFAD, based on the trend test as well as deviation from Hardy-Weinberg equilibrium (HWE) in cases. It is known that deviation from HWE may indicate association when the true genetic model is neither multiplicative nor additive (Nielsen et al. 1998; Song & Elston 2006; Zheng & Ng 2008). Therefore, we expect BFAD would have better power to detect association when the genetic model is recessive or dominant.

The true modes of inheritance of disease loci are rarely known for many complex traits, although genetic models at marker loci (SNPs), which are in linkage disequilibrium with the disease loci, tend to be close to the additive model (Zheng et al., 2009). That is why both the trend test and Pearson’s test or other robust tests have been used for genome-wide scans. Specifically, WTCCC (2007) used a more significant p-value based on the p-values of the trend test and Pearson’s test, and Sladek et al. (2007) and Li et al. (2008) used a robust test, MAX (or MAX3), for genome-wide scans. Analogous to these robust frequentist approaches, we propose a third BF, denoted as JBF, that jointly combines BFA and BFAD. All the three BFs (BFA, BFAD and JBF) have closed forms and are easy to compute although they need specifications of priors. We give guidelines how to determine subjective and objective priors under practical settings and also provide typical objective priors to use in applications.

We conduct extensive simulation studies to examine performances of the proposed methods under different practical situations. Applications to real GWAS data from Klein et al. (2005), the WTCCC (2007) and Sladek et al. (2007) are reported to illustrate the usefulness of the proposed methods and demonstrate why BF is more suitable than p-value when comparing results across GWAS with different sample sizes, and how the use of proposed BFs enhances the power to detect markers with recessive or dominant effect. Summary of the proposed methods and discussion of applying both Bayesian and frequentist methods for genetic association studies are given at the end.

Methods

Three GWAS Datasets

Klein et al. (2005) reported perhaps the first successful GWAS using 100,000 SNPs, in which they identified a major risk variant within the gene, CFH, for age-related macular degeneration (AMD). The sample size in Klein et al. (2005) was about 150 (about 100 controls and 50 cases). The WTCCC (2007) studied GWAS using 500,000 SNPs for seven common diseases and had about 5000 samples for each disease (about 2,000 cases and 3,000 controls). For this paper, we only consider two of them, rheumatoid arthritis (RA) and type 2 diabetes (T2D), of the WTCCC (2007). Sladek et al. (2007) conducted a GWAS for T2D using 500,000 SNPs with about 1,300 samples. They identified and replicated 8 SNPs. The sample size for replication was about 5,500.

We consider these three GWAS because the AMD study has a very small sample size relative to the other two, so we can see the impact of the sample size on the p-value and BF. Klein et al. (2005) used a test similar to the trend test for genome-wide scans, while the WTCCC (2007) and Sladek et al. (2007) employed robust tests. Hence, we can compare the three proposed BFs when the trend test or robust tests are applied in the analysis of GWAS. Using the data in Sladek et al. (2007), we can also demonstrate how to report a combined analysis of initial data and replication data using a proposed BF.

Notation and Bayes Factor

Assume a marker of interest has alleles A and B with three genotypes (G₀, G₁, G₂) = (AA, AB, BB) and the genotype counts (r₀, r₁, r₂) among r cases and (s₀, s₁, s₂) among s controls. Let n = r + s. Denote the genotype frequencies in cases and controls as p_i = Pr(G_i∣case) and q_i = Pr(G_i∣control), respectively and their estimators as p̂_i = r_i/r and q̂_i = s_i/s (i = 0, 1, 2). Let p_B = Pr(B) = p₂ + p₁/2 be the population frequency of B, and ψ = r/n. The normal distribution with mean μ and variance σ² is denoted as N(μ, σ²) and “T ~ N(μ, σ²)” is used for a test statistic T to have an approximate or asymptotic normal distribution. The distribution function of N(0, 1) is denoted as Φ. H₀ and H₁ stand for the null and alternative hypotheses, respectively, where the null hypothesis is no association can be written as H₀ : p_i = q_i for i = 0, 1, 2.

Genetic models are defined using the penetrances f_i = Pr(case∣G_i) (i = 0, 1, 2). Without loss of generality, let B be the risk allele. Then a genetic model is recessive (REC), additive (ADD), multiplicative (MUL), or dominant (DOM) when f₀ = f₁, f₁ = (f₀ + f₂)/2, $f_1^2=f_0{f}_2$, or f₁ = f₂, respectively. It has been shown in the simulations that association tests perform similarly under the ADD and MUL models (Freidlin et al., 2002). In fact, under local alternatives (f_i ≈ 1 for i = 0, 1, 2), by the Taylor expansions around the null point f_i = 1, we have f₀f₂ ≈ 1+(f₀ − 1)+(f₂ − 1) = f₀ + f₂ − 1 and $f_1^2\approx 1+2(f_1-1)=2f_1-1$. Hence, the ADD model 2f₁ = f₀ + f₂ implies the MUL model $f_1^2\approx 2f_1-1\approx f_0{f}_2$. Thus, we mostly focus on the ADD model in the simulation although the ADD and MUL models are different. The genotype relative risks (GRRs) are defined as f_i/f₀ (i = 0, 1).

A Bayes factor (BF) studied by Johnson (2005) can be written as

$$\mathrm{BF}=\frac{\mathrm{Pr}(T\mid H_1)}{\mathrm{Pr}(T\mid H_0)}=\frac{\int \mathrm{Pr}(T\mid \theta ,H_1){\prod }_1(\theta )d\theta }{\int \mathrm{Pr}(T\mid \theta ,H_0){\prod }_0(\theta )d\theta },$$ (1)

where T is a test statistic for H₀ of no association, θ is the unknown parameter, Pr(T∣θ, H_i) is the asymptotic distribution of T under H_i, and Π_i(θ) is the prior density function of θ under H_i (i = 0, 1). A larger value of the above BF provides stronger evidence to support H₁.

If a prior odds (PO) of association is given, the posterior probability of association (PPA) can be obtained as PPA = PO × BF/(1 + PO × BF). Bayesian power is defined as Pr(PPA > t) for some threshold t. For example, if the prior probability of association is 0.01, PO ≈ 0.01. Then the Bayesian power for t = 0.2 is the probability that the PPA is at least 20 times that of the prior probability of association due to the influence from the data through the test T. Given the same PO, two SNPs that have the same BF would have the same PPA. Thus, in general, we can only report BF (in a log₁₀ scale). We also report Pr(PPA > t) under H₀ with various thresholds t in simulations to examine the performance of the proposed BFs under H₀.

Bayes Factor for Association (BFA)

First, we propose a BF by applying (1) with T replaced by the trend test Z_TT, given by (Zheng & Gastwirth, 2006),

$$Z_{\mathrm{TT}}=\frac{\sqrt{n}\{({\widehat{p}}_1+2{\widehat{p}}_2)-({\widehat{q}}_1+2{\widehat{q}}_2)\}}{{\left[{\psi }^{-1}\{({\widehat{p}}_1+4{\widehat{p}}_2)-{({\widehat{p}}_1+2{\widehat{p}}_2)}^2\}+{(1-\psi )}^{-1}\{({\widehat{q}}_1+4{\widehat{q}}_2)-{({\widehat{q}}_1+2{\widehat{q}}_2)}^2\}\right]}^{1/2}}.$$ (2)

Under H₀, Z_TT ~ N(0, 1) and under H₁, $Z_{\mathrm{TT}}~N\left(\sqrt{n}\beta ,1\right)$ where β is the genetic effect > 0 (or < 0) when B (or A) is the risk allele, which is the unknown parameter like θ in (1). An expression of β is given in the technical details of the online supplementary material. Note that nβ² can be regarded as the non-central parameter of a one-degree-of-freedom chi-squared distribution, $F_{{\chi }_1^2}$, for $Z_{\mathrm{TT}}^2$ under H₁. A natural prior for β is $\beta ~N\left(0,W_{\beta }^2\right)$ under H₀ and H₁ with a user-specified $W_{\beta }^2$. Then the BF in (1) can be written as (see the online technical details)

$$\mathrm{BFA}={\left(\frac{1}{n{W}_{\beta }^2+1}\right)}^{1/2}\exp \left(\frac{Z_{\mathrm{TT}}^2}{2}\frac{n{W}_{\beta }^2}{n{W}_{\beta }^2+1}\right).$$ (3)

When the trend test is applied, its p-value can be written as $p=1-F_{{\chi }_1^2}(Z_{\mathrm{TT}}^2)$ or $Z_{\mathrm{TT}}^2=F_{{\chi }_1^2}^{-1}(1-p)$. Thus, BFA directly relates to the p-value of the trend test. Given Z_TT, BFA depends on the sample size n (and, thus, the power) but p-value does not (which depends on n only through the test statistic Z_TT), which is an important difference between BF and p-value. From (3), BFA → 0 as n → ∞ under H₀ and BFA → ∞ as n → ∞ under H₁. Note that, when n → ∞, Z_TT → ∞, so the p-value goes to 0 too. Hence, under H₁ when n is large enough, using either BFA or p-value would lead to rejection of H₀. However, there is no clear cut how large n should be because BF directly involves n while p-values does not. On the other hand, when both BFs and p-values are reported, we would have similar conclusions if n is large enough regardless of choices of priors. But if the p-values and BFs give contradictory conclusions, further investigations are required before one reaches any conclusion, including computing the conditional power for the test used. This is one of the motivations why BFs are still useful after reporting p-values even though the sample size is large. For example, WTCCC (2007) reported both p-values and BFs with n = 5, 000. The above arguments are made based on BFA, which can be applied to the two other BFs given below.

Bayes Factor (BFAD) for REC or DOM Models

We first study a BF based on a statistic for deviation from HWE. Denote the Hardy-Weinberg disequilibrium (HWD) coefficient among cases as $\mathrm{\Delta }=p_2-p_B^2$, which is estimated by Δ̂ = p̂₂ − (p̂₂ + p̂₁/2)². E(Δ̂) = Δ when r is large enough and $\mathrm{Var}(\widehat{\mathrm{\Delta }})=\{p_B^2{(1-p_B)}^2+{(1-2p_B)}^2\mathrm{\Delta }-{\mathrm{\Delta }}^2\}/r$ (Weir 1996). Denote V_Δ = rVar(Δ̂). Define a test statistic $Z_{\mathrm{HWD}}=\sqrt{r}\widehat{\mathrm{\Delta }}/{\widehat{V}}_{\mathrm{\Delta }}^{1/2}=\sqrt{n\psi }\widehat{\mathrm{\Delta }}/{\widehat{V}}_{\mathrm{\Delta }}^{1/2}~N(0,1)$ under H₀ and $~N\left(\sqrt{n}\delta ,1\right)$ under H₁, where δ is the unknown parameter whose expression is given in the online technical details. A natural prior for δ is $\delta ~N(0,W_{\delta }^2)$ under H₀ and H₁ with a user-specified $W_{\delta }^2$. Applying (1) with T = Z_HWD and like the derivation for (3), we obtain the BF for the deviation from HWE as

$$\mathrm{BFD}={\left(\frac{1}{n{W}_{\delta }^2+1}\right)}^{1/2}\exp \left(\frac{Z_{\mathrm{HWD}}^2}{2}\frac{n{W}_{\delta }^2}{n{W}_{\delta }^2+1}\right).$$ (4)

When a mixture of normal prior is used for δ, as we will suggest later, the BF can be calculated as a mixture of BFs as follows. Denote BFD in (4) with prior $\delta ~N\left(0,W_{\delta }^2\right)$ as $\mathrm{BFD}(W_{\delta }^2)$. Then, with $\delta ~\pi N(0,W_{{\delta }_1}^2)+(1-\pi )N(0,W_{{\delta }_2}^2),\mathrm{BFD}=\pi \mathrm{BFD}(W_{{\delta }_1}^2)+(1-\pi )\mathrm{BFD}(W_{{\delta }_2}^2)$, where π is user-specified.

There is no (or little) information of association in Δ̂ under the MUL (or ADD) model (Nielsen et al., 1998). But BFD would be useful in detecting association under REC or DOM models. For better power to detect association under these two models than BFA, we propose a simple linear combination of the two test statistics Z_TT and Z_HWD, like in a meta-analysis. In this case, we require both tests have the same sign. This can be easily achieved when the true genetic model is known. It is known (Zheng & Ng 2008) that Z_TT and Z_HWD have the same sign (βδ > 0) under the REC model and different sign (βδ < 0) under the DOM model, while the two tests are nearly independent under the ADD model (and independent under the MUL model). In order to accommodate unknown model situations, we propose a new test Z = wZ_TT + (1 − w)Z_HWD if Z_TTZ_HWD > 0 and Z = wZ_TT − (1 − w)Z_HWD if Z_TTZ_HWD ≤ 0 with w to be specified later. Denote the probability Z_TTZ_HWD > 0 as μ and w₁ = w, w₂ = 1 − w. The distribution for Z is N(0, 1) under H₀, and a mixture of normals $\mu N\left(\sqrt{n}{z}_{+},{\sigma }_{+}^2\right)+(1-\mu )N\left(\sqrt{n}{z}_{-},{\sigma }_{-}^2\right)$ under H₁, where z_± = w₁β ± w₂δ, ${\sigma }_{\pm }^2=w_1^2+w_2^2\pm 2w_1{w}_2\rho$, and ρ is the correlation of Z_TT and Z_HWD, given in the online technical details, where we also show that μ → 1 as n → ∞ if βδ > 0 and 0 if βδ < 0 (i.e., 1 − μ → 1). That is, the asymptotic distribution for Z is approximately a single normal $N\left(\sqrt{n}{z}_{+},{\sigma }_{+}^2\right)$ if Z_TTZ_HWD > 0 or $N\left(\sqrt{n}{z}_{-},{\sigma }_{-}^2\right)$ otherwise. To unify the notation, we denote $Z~N\left(\sqrt{n}{z}_{\pm },{\sigma }_{\pm }^2\right)$ asymptotically under H₁.

Applying (1) with T replaced by Z and the prior z_± ~ N(0, W²) with $W^2=w_1^2{W}_{\beta }^2+w_2^2{W}_{\delta }^2+2w_1{w}_2{\rho }_0{W}_{\beta }{W}_{\delta }$ and user-specified correlation ρ₀, which takes care of the signs (see the section of choices of priors presented later), and $\left(W_{\beta }^2,W_{\delta }^2\right)$, we obtain the BF given by

$$\mathrm{BFAD}={\left(\frac{{\sigma }_{\pm }^2}{n{W}^2+{\sigma }_{\pm }^2}\right)}^{1/2}\exp \left\{\frac{Z^2}{2}\frac{n{W}^2}{{\sigma }_{\pm }^2(n{W}^2+{\sigma }_{\pm }^2)}\right\},$$ (5)

where ${\sigma }_{\pm }^2$ is replaced with ${\widehat{\sigma }}_{\pm }^2=w_1^2+w_2^2+2w_1{w}_2\widehat{\rho }$ when z_TTz_HWD > 0 and ${\widehat{\sigma }}_{\pm }^2=w_1^2+w_2^2-2w_1{w}_2\widehat{\rho }$ otherwise and ρ̂ is an estimator of ρ given in online supplementary material. The derivation of (5) is similar to those of (3) and (4). Note that BFA and BFD are special cases of BFAD with (w₁, w₂) = (1, 0) and (w₁, w₂) = (0, 1), respectively, under which ρ₀ is not required to specify.

Although incorporating information of deviation from HWE has not been seen in BF in the literature, it has been done in frequentist hypothesis testing to detect genetic association. For example, Song & Elston (2006) considered a linear combination of Z_TT and a similar Z_HWD. Hence, BFAD can be regarded as a Bayesian counterpart of the frequentist combination test of Song & Elston (2006). As the deviation statistic Δ̂ has an expected value approximately 0 under the MUL model, BFAD is not ideal under this model. Instead, BFA should be applied under the MUL model.

Joint Bayes Factor (JBF)

As expected, the simulation results presented later show that BFAD is more powerful than BFA under the REC or DOM models, while BFA is more powerful under the ADD model. Hence there is a trade-off between BFA and BFAD with respect to the underlying genetic model. We therefore propose JBF to borrow strength from both BFA and BFAD. We simply set JBF = BFA if the p-value of the trend test is no more than that of Pearson’s test and JBF = BFAD otherwise. That is, JBF is a BF stratified by the p-values of the two most commonly used association tests. The idea behind this simple decision rule is this: if the p-value of the trend test is smaller, it indicates an ADD model. On the other hand, the p-value of Pearson’s test is smaller under the REC or DOM models. The same idea can be used to motivate the use of the more significant p-value of the trend test and Pearson’s test in the WTCCC (2007). Note that, as n is large enough, since both BFA and BFAD go to 0 under H₀ and go to infinity under H₁, JBF also converges to 0 and infinity under H₀ and H₁, respectively. Note that JBF depends on BFA and BFAD as well as their priors. Hence there is no need to specify additional priors to apply JBF.

Choosing Priors

One important difference between Bayesian and frequentist methods is the specification of priors when applying Bayesian methods. Using priors is one of the advantages of Bayesian analysis, but it is also one of the main reasons why Bayesian method is not widely used in genetic association studies (Stephens & Balding 2009). We explain how to determine priors to apply the proposed BFs and give typical priors to use in applications. To apply BFA and BFD, we have to determine priors for β and δ, respectively, and to apply BFAD, we need to determine prior for z_±. Given the values of BFA and BFAD, there is no extra prior to specify to apply JBF. These hyper parameters are often determined based on prior scientific knowledge of a disease and markers, including allele frequencies and modes of inheritance, etc. When such information is available, an informative (subjective) prior may be used, and when such information is not available, a non-informative (objective) prior can be used. We discuss how to determine informative and non-informative priors separately.

To obtain an informative prior, we need to know, based on prior studies, (i) the frequency of the allele of interest, (ii) the genetic model, (iii) a targeted GRR such that the GRRs of associated SNPs are likely no more than that targeted one, and (iv) the disease prevalence in the study population. We illustrate the procedure with an example. Suppose, based on prior studies, we expect the allele frequency of the marker of interest is about 0.30, with probability 95% that the GRR is not greater than 2.0 with the disease prevalence in the population 0.1, and that the mode of inheritance is REC. Then we can calculate β and δ values using the formulas given in the online technical details and obtain β = 0.094 and δ = 0.113. Since $\beta ~N\left(0,W_{\beta }^2\right)$, we have 0.975 = Pr(β < 0.094) = Φ(0.094/W_β). Hence, $W_{\beta }^2=0.0023$. A similar idea to derive priors for odds ratio was considered by Wakefield (2007). We consider a two-sided probability as we may not know the risk allele. If we know the risk allele, a one-sided probability can be used. Likewise, for a two-sided probability, we obtain $W_{\delta }^2=0.0033$. Thus, informative priors, β ~ N(0, 0.0023) and δ ~ N(0, 0.0033), can be determined for this candidate marker. Detailed formulas to calculate $W_{\beta }^2$ and $W_{\delta }^2$ are given in the online supplementary material.

In practice, we may not know much about markers, e.g., conditions (i)-(iv) given above, that are potentially associated with a disease or we may want to apply the same prior to all markers in GWAS. In this case, we can determine non-informative priors. Table S1 (online supplementary material) reports values of β, δ, ρ, $W_{\beta }^2$ and $W_{\delta }^2$ with different minor allele frequencies (MAFs) and with REC, ADD, MUL, or DOM models by assuming a prevalence of 0.1 and with 95% probability that the GRR would be less than 2.0. The table helps understand sensitivities of these values under various practical situations. Based on the results, we see $W_{\beta }^2$ is consistent about 0.005, so we use β ~ N(0, 0.005) to apply BFA. To determine prior when applying BFD, $W_{\delta }^2$ depends on the genetic model. If the true model is ADD, then $W_{\delta }^2\approx 0.0001$, and otherwise $W_{\delta }^2$ is between 0.001 and 0.003. Note that, under the MUL model, δ = 0 and $W_{\delta }^2=0$. Hence, as we mentioned before, only BFA can be applied under the MUL model. Since we do not know the model, we choose a mixture of two normals as the prior for δ: δ ~ πN(0, 0.0001) + (1 − π)N(0, 0.003) with π = 0.8. However, if we know the genetic model is neither ADD nor MUL, we choose δ ~ πN(0, 0.001) + (1 − π)N(0, 0.003) with π = 0.1. If the genetic model is ADD, we also choose δ ~ πN(0, 0.001) + (1 − π)N(0, 0.003) but with π = 0.9. To apply BFAD, we also need to choose ρ₀ based on ρ. When the model is unknown, we choose ρ₀ = 0. When the model is neither ADD nor MUL, we choose ρ₀ = 0.1 for the REC model and -0.1 for the DOM model. Therefore, ρ₀ incorporates the signs in Z used in BFAD. To calculate W² in z_± ~ N(0, W²), we choose $W_{\beta }^2=0.005$ and $W_{\delta }^2=0.003$ with w = 0.8 for the ADD model and w = 0.5 for the REC or DOM models. To help apply the proposed BFs, summary for the priors for BFA, BFD and BFAD is given in Table 1 depending on whether or not the underlying genetic model is known (see also Table S2 online material for a summary for the choices of parameter values for BFAD). These priors can be generally used regardless of MAFs, preferably for the GRR likely to be less than 2.0. Given BFA and BFAD, no additional priors are required to apply JBF.

Table 1.

Choices of non-informative priors depending on whether or not the true genetic model is known with common variants and GRR likely no more than 2.0: $\beta \sim N\left(0,W_{\beta }^2\right)$ for applying BFA, $\delta \sim \pi N\left(0,W_{{\delta }_1}^2\right)+\left(1-\pi \right)N\left(0,W_{{\delta }_2}^2\right)$ for applying BFD, and z_± ~ N(0, W²) for applying BFAD.

Genetic model	BF	Priors
Unknown	BFA	β ~ N(0, 0.005)
	BFD	δ ~ 0.8N(0, 0.0001) + 0.2N(0, 0.003)
	BFAD	z± ~ N(0, 0.0020)
REC	BFA	β ~ N(0, 0.005)
	BFD	δ ~ 0.1N(0, 0.001) + 0.9N(0, 0.003)
	BFAD	z± ~ N(0, 0.0022)
ADD	BFA	β ~ N(0, 0.005)
	BFD	δ ~ 0.9N(0, 0.001) + 0.1N(0, 0.003)
	BFAD	z± ~ N(0, 0.0033)
MUL	BFA	β ~ N(0, 0.005)
	BFD	Not applicable
	BFAD	Not applicable
DOM	BFA	β ~ N(0, 0.005)
	BFD	δ ~ 0.1N(0, 0.001) + 0.9N(0, 0.003)
	BFAD	z± ~ N(0, 0.0018)

Note that the prior $\beta \sim N\left(0,W_{\beta }^2\right)$ for applying BFA does not depend on the genetic model. However, in the prior for BFD, when the genetic model is unknown, we place more weight (π = 0.8) on $W_{\delta }^2=0.0001$ corresponding to the ADD model because, in practice, the model for associated markers is more likely the ADD model (Zheng et al. 2009). For the same reason, applying BFAD, we set 80% weight on the ADD model when it is true and still 50% weight on the ADD model when it is not true. The priors in Table 1 are regarded as non-informative. We can use the priors with unknown genetic model in Table 1 for genome-wide scans. If we want to detect candidate-gene with known models, we can use other specified priors under those models.

Results

Simulation Studies

All MAFs were generated from a uniform distribution U(0.1, 0.5) and HWE held in the general population. Under H₁, the genetic model is REC, ADD or DOM; either known or unknown. The disease prevalence was fixed at 0.1. We used the priors outlined in Table 1. The sample sizes were 1,000 cases and 1,000 controls (n = 2, 000) with 1,000 or 10,000 replicates. When interpreting the results in the figures, we use (i,j) to indicate the panel in row i and column j.

Figure 1 presents plots under H₀. Panel (1,1) reflects the functional relationship (3) between Z_TT and the BFA. In panels (1,2) and (1,3), the relationship is slightly affected due to the deviation from HWE. The second row of Figure 1 shows that BFA, BFAD and JBF are not that correlated. In frequentist hypothesis testing, type I error rates of test statistics are reported in simulations, which are probabilities to reject H₀ when the data are generated under H₀. For Bayesian hypothesis testing, we report the probabilities that PPAs of BFA, BFAD and JBF are respectively greater than a given threshold under H₀. We chose the prior odds of H₁ as PO = 0.01. Then the thresholds of PPA, 0.01, 0.03, 0.10, 0.20 and 0.50, correspond to BF 1, 3.0, 10, 30 and 100, respectively. These thresholds are often interpreted as the evidence of H₁ in the data that is barely worth mentioning, substantial, strong, very strong and decisive (Kass & Raftery, 1995). The results are reported in Table 2, which show that the above probabilities of BFAD and JBF are comparable and slightly greater than those of BFA. Further, for both BFAD and JBF, the probabilities are less than 0.25 when the outcomes are at least barely worth mentioning under H₀ and less than about 0.055 when they are at least substantial under H₀.

Figure 1.

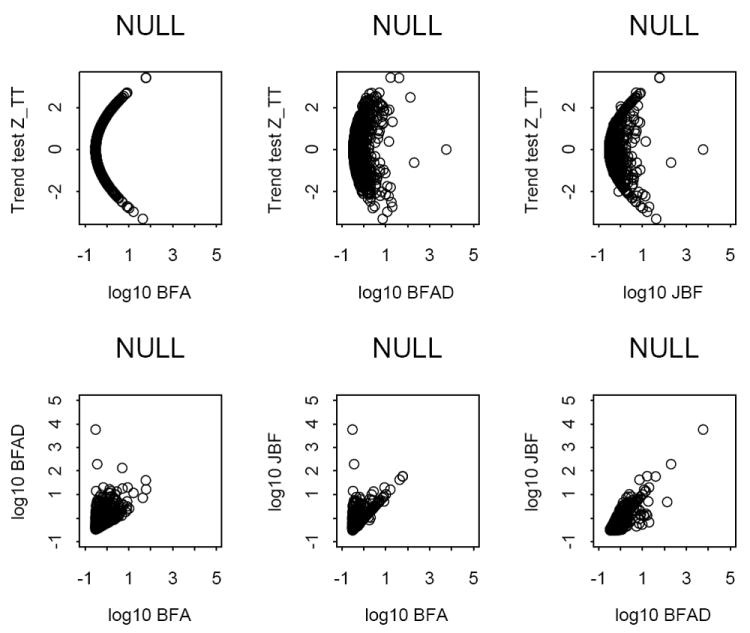
Under H₀: plots of the trend test vs. log₁₀ BFA, log₁₀ BFAD and log₁₀ JBF (row 1), and plots among log₁₀ BFA, log₁₀ BFAD and log₁₀ JBF (row 2). The number of replicates is 1,000.

Table 2.

Probabilities that PPA are at least barely worth mentioning (t = 0.01), substantial (t = 0.03), strong (t = 0.1), very strong (t = 0.2) and decisive (t = 0.5) based on BFA, BFD, BFAD and JBF under H₀ when the PO is about 0.01. The priors are given in Table 1 depending on the genetic model assumed (unknown, REC, ADD or DOM). The number of replicates is 10,000.

Model	t	Pr(PPA ≥ t) under H0
		BFA	BFD	BFAD	JBF
Unknown	0.01	0.107	0.194	0.222	0.180
	0.03	0.024	0.001	0.055	0.046
	0.10	0.004	0.000	0.015	0.013
	0.20	0.002	0.000	0.006	0.006
	0.50	0.000	0.000	0.002	0.002
REC	0.01	0.106	0.168	0.207	0.173
	0.03	0.022	0.027	0.051	0.043
	0.10	0.004	0.005	0.011	0.010
	0.20	0.002	0.002	0.004	0.005
	0.50	0.000	0.000	0.001	0.001
ADD	0.01	0.097	0.226	0.142	0.113
	0.03	0.023	0.018	0.034	0.027
	0.10	0.004	0.002	0.008	0.005
	0.20	0.002	0.001	0.003	0.002
	0.50	0.001	0.000	0.001	0.001
DOM	0.01	0.100	0.179	0.226	0.175
	0.03	0.020	0.029	0.053	0.043
	0.10	0.003	0.005	0.012	0.010
	0.20	0.001	0.002	0.006	0.004
	0.50	0.000	0.001	0.001	0.001

Plots under H₁ are reported in Figure 2 (rows 1 and 2 for unknown genetic models and rows 3 and 4 for known models). We summarize Figure 2 here. (i) When the model is unknown, BFAD and JBF have similar values and both are greater than BFA under the REC or DOM models, while JBF and BFA have similar values and both are greater than BFAD under the ADD model. That is, although JBF is stratified by the trend test and Pearson’s test, JBF always has similar performances to the larger BF of BFA and BFAD. (ii) When the model is known (REC, ADD or DOM), the conclusions in (i) still hold except that, under the ADD model, BFAD and BFA have similar values. (iii) In panels (1,1), (1,3), (3,1) and (3,3), more dots (corresponding to log₁₀ BF < 20) tend to be above the diagonal, indicating that BFAD tends to be slightly larger than JBF under the REC or DOM models.

Figure 2.

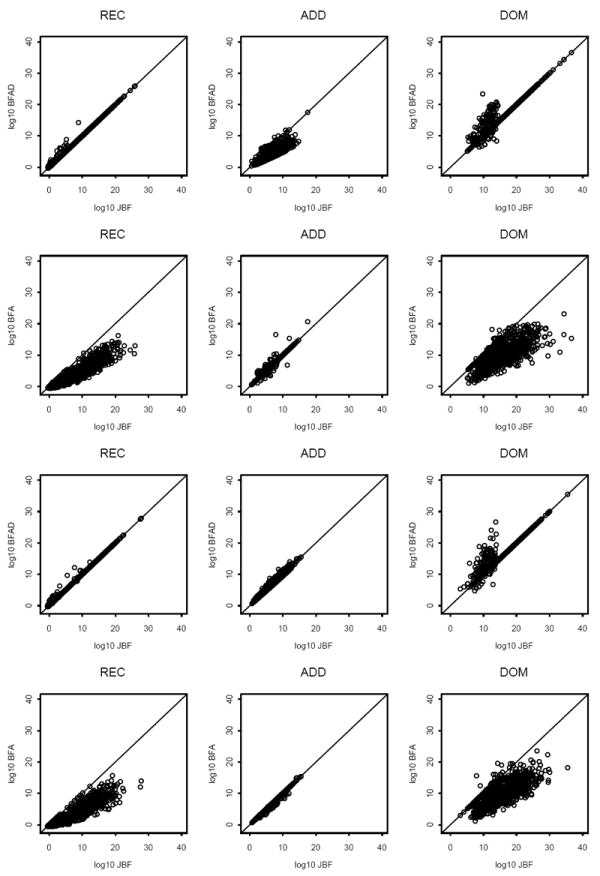
Under H₁: plots of log₁₀ BFAD vs. log₁₀ JBF (rows 1 and 3) and log₁₀ BFA vs. log₁₀ JBF (rows 2 and 4) when the genetic model is unknown (rows 1 and 2) and known (rows 3 and 4). The GRR is 2.0. The number of replicates is 1,000.

To further compare the BFs, we also simulated their Bayesian power with t = 0.2, which is reported in online Figure S1 when the genetic model is unknown (row 1) and when the model is known (row 2). Figure S1 is another way to look at the performance of the three BFs in Figure 2. We can see from Figure S1 that there is a trade-off between BFAD and BFA due to whether or not the genetic model is known. However, JBF is more robust to the genetic model uncertainty. It has nearly best performance across the three models regardless of whether or they are known.

Sensitivity Analysis

BFs are sensitive to the priors used. Sensitivity analysis with different priors is helpful, especially when BFs are reported alone in the analysis of genetic association studies. We conduct simulations for BFA with three different priors. $W_{\beta }^2=0.005$ was used in the simulations before. From Table S1 online material, the range of $W_{\beta }^2$ is 0.0004 to 0.0082. Hence we consider three priors β ~ N(0, 0.0004), N(0, 0.005) and N(0, 0.0082) for BFA under H₀. Like before, we consider the threshold t = 0.03, 0.10, 0.20 and 0.50 for PPA of BFA with PO=0.01. Three sample sizes n = 500, 2, 000 and 10, 000 are also used. The results are reported in Table 3. Although using different priors would have different PPAs as expected, the false positive rates, measured with Pr(PPA ≥ t), with three different priors are all small (< 0.03 with any substantial or stronger evidence of H₁ in the null data).

Table 3.

Sensitivity of BFA under H₀ with three different priors: β ~ N(0, 0.0004), N(0, 0.005) and N(0, 0.0082). The entries are the probabilities of PPA greater than a threshold t corresponding to substantial (t = 0.03), strong (t = 0.1), very strong (t = 0.2) and decisive (t = 0.5) evidence of H₁ in the data with PO 0.01 and sample size n. The number of replicates is 10,000.

n	t	Pr(PPA ≥ t) under H0
		β ~ N(0, 0.0004)	β ~ N(0, 0.005)	β ~ N(0, 0.0082)
500	0.03	0.0002	0.0272	0.0281
	0.10	0.0000	0.0028	0.0037
	0.20	0.0000	0.0009	0.0013
	0.50	0.0000	0.0000	0.0002
2,000	0.03	0.0118	0.0226	0.0191
	0.10	0.0004	0.0048	0.0039
	0.20	0.0001	0.0025	0.0022
	0.50	0.0000	0.0003	0.0003
10,000	0.03	0.0269	0.0120	0.0093
	0.10	0.0041	0.0022	0.0016
	0.20	0.0018	0.0016	0.0014
	0.50	0.0003	0.0003	0.0003

Applications to Three Real GWAS

We first discuss which BFs should be used in practice. BFs are reported to support p-values of a test statistic. Hence, if the trend test is applied, BFA should be reported, although it may not detect some markers with REC or DOM models. If BFA is primarily reported, BFAD can also be reported to provide insight of the results with BFA, although it is expected that BFAD is not powerful under the MUL model. For example, a strong association based on the p-value of the trend test and a large BFA with a small BFAD is different from a similar association with similar p-value of BFA but with a large BFAD. In GWAS, using a single trend test is not efficiency robust (WTCCC, 2007; Li et al. 2008; Zheng et al. 2009), other robust tests have been applied in genome-wide scans. Although they have different forms, they have the same goal to detect associated markers with different genetic models. JBF is a more robust BF to report if a robust test and its p-value are used.

In the applications, the priors in Table 1 were used. Klein et al. (2005) applied an allelic test for genome-wide scans and detected two SNPs. Their test is equivalent to the trend test. Thus, we focus on the p-value of the trend test and BFA, both are in bold in Table 4 for the top two SNPs reported in Klein et al. (2005). The WTCCC (2007) applied the more significant p-value of the trend test and Pearson’s test. They reported 11 SNPs (12 SNPs) with moderate or strong associations with RA (T2D). We then focus on JBFs, both the more significant p-values (or the robust p-values) and the JBFs are in bold for these SNPs in Table 4. The results show that BFA is comparable well to the p-value of the trend test for all three diseases. However, it is not so well (with the BFAs in italic) when the robust p-value is used, especially for the SNPs with non-ADD or non-MUL models. Overall, JBF performs well with the robust p-values. It also often takes the larger of BFA and BFAD regardless of the genetic models. The sample sizes for AMD and RA/T2D are about 150 and 4800, respectively. Although the p-values of the two SNPs for AMD often indicate stronger significance than those for RA and T2D, the associated SNPs for RA and T2D often have larger BFs than those of AMD. This is because p-value only measures the significance not the power, while BF measures both. Hence, BF is more favored for measuring the strength of association than p-value and for comparing results across GWAS with different sample size.

Table 4.

SNPs along with p-values and BFs associated with AMD (Klein et al. 2005) and RA and T2D (WTCCC 2007). The p-values in bold are equivalent to those used in Klein et al. (2005) and the WTCCC (2007). The BFs in bold are the ones to be reported with the p-values in bold. The sample size is about 150 for AMD and about 4,800 for RA and T2D.

Study	SNP	chrom	ZTT	Pearson’s	log10 of
					BFA	BFAD	JBF
AMD	rs380390	1	1.01E-08	1.72E-06	2.91	1.37	2.91
	rs1329428	1	4.21E-07	4.31E-06	2.21	1.43	2.21
RA	rs6684865	1	4.18E-06	3.14E-05	3.71	2.58	3.71
	rs11162922	1	6.11E-07	1.02E-05	4.48	2.07	4.48
	rs6679677	1	2.71E-24	5.55E-25	20.85	14.48	14.48
	rs3816587	4	8.55E-03	9.25E-06	0.74	3.42	3.42
	rs6457617	6	7.63E-85	5.18E-75	78.71	39.63	78.71
	rs6920220	6	6.70E-06	1.57E-05	3.52	1.59	3.52
	rs11761231	7	1.19E-06	2.65E-06	4.21	2.83	4.21
	rs2104286	10	4.86E-06	2.52E-05	3.65	2.47	3.65
	rs9550642	13	1.47E-05	3.90E-05	3.21	1.47	3.21
	rs2837960	21	3.90E-02	1.67E-06	0.19	2.17	2.17
	rs743777	22	1.07E-05	1.15E-06	3.33	2.67	2.67
T2D	rs4655595	1	4.91E-06	1.33E-05	3.65	1.59	3.65
	rs6718526	2	1.47E-06	1.15E-05	4.13	3.26	4.13
	rs358806	3	4.84E-01	3.05E-06	-0.59	2.25	2.25
	rs7659604	4	1.95E-02	9.41E-06	0.43	2.96	2.96
	rs9465871	6	1.66E-06	3.34E-07	4.08	3.22	3.22
	rs9326506	10	6.90E-06	2.98E-05	3.51	2.33	3.51
	rs4506565	10	7.00E-13	5.04E-12	10.04	5.78	10.04
	rs12304921	12	5.23E-02	7.06E-06	0.08	4.04	4.04
	rs1495377	12	1.14E-06	6.51E-06	4.23	2.98	4.23
	rs2930291	15	6.39E-06	4.39E-05	3.54	2.06	3.54
	rs2903265	15	7.54E-06	4.97E-05	3.48	2.45	3.48
	rs9939609	16	4.72E-08	1.90E-07	5.51	4.65	5.51

In our last application, we demonstrate that JBF can be used when other robust tests are applied, and show that JBF can also be reported for a combined analysis of initial and replication data. The results are reported in Table 5 for the 8 replicated SNPs in Sladek et al. (2007). Note that, a smaller p-value always corresponds to a smaller JBF in the initial, replication and combined studies. In the combined analysis, not only the p-values become more significant, the JBFs become much larger than those in either the initial or the replication studies.

Table 5.

SNPs detected and replicated in Sladek et al. (2007) with association of T2D. The p-values reported are the more significant ones of the trend test and Pearson’s test. JBFs are all in log₁₀ scale.

	Initial		Replication		Combined
SNP	P-value	JBF	P-value	JBF	P-value	JBF
rs1103790	4.23E-05	2.43	1.73E-04	2.22	2.14E-06	3.81
rs1111875	2.22E-06	3.79	2.76E-06	3.87	2.35E-10	7.69
rs1113132	9.09E-05	2.27	3.20E-04	1.98	7.05E-06	3.48
rs1326663	1.94E-05	3.54	5.23E-08	5.48	8.15E-11	8.13
rs3740878	4.22E-05	2.37	1.10E-04	2.40	1.93E-06	3.85
rs7480010	1.86E-05	3.02	1.12E-04	2.39	1.61E-07	5.01
rs7903146	2.67E-20	15.66	3.73E-35	31.31	4.85E-53	48.78
rs7923837	7.30E-07	4.19	6.913-06	3.51	3.85E-10	7.49

Discussion

In this paper, we proposed three simple BFs that are based on the trend tests, the deviation from HWE in cases and a combined BF. These BFs have closed forms and are simple to compute. When the trend test is applied, the proposed BF, BFA, can be reported along with the p-value of the trend test. When other robust tests, e.g. MAX (MAX3) and the minimum of the p-values of the trend test and Pearson’s test, are used for genome-wide scans, the joint BF, JBF, can be reported. Our applications show that reporting BFA based on the trend test alone may be misleading when p-values of robust tests are applied.

Instead of reporting BFs alone, we recommend reporting BFs along with p-values as in WTCCC (2007). Given the test statistic, p-values only measure significance and is independent of the sample size of the study while BFs integrate both the significance and the sample size (power) to detect associations. Hence, reporting BFs along with p-values is always a helpful strategy even though the sample size is large, especially in GWAS where small p-values are always observed due to testing a large number of null hypotheses. Moreover, because many GWAS results have been published for common diseases, BFs can effectively incorporate these results in the priors to improve the power to detect associations or to help identify some associated markers that p-values fail to detect.

Another benefit of reporting BFs is that they are more appropriate measures than p-values when one compares results across GWAS with different sample sizes. Impact of different sample sizes on the results, although they may be both large, is not known when p-values are reported. Another advantage of BFs over p-values is that there is no need to adjust for multiple testing using BFs using conservative Bonferroni correction, which can be controlled by specifying the prior of association and reporting PPA (Stephens & Balding 2009; Sawcer 2010).

Specifying priors is an essential part in Bayesian analysis. Typical priors for the genetic effect is a normal or a mixture of normals (WTCCC, 2007; Stephens & Balding 2009). In this paper, the variances of the normal priors were derived for the BFs based on the trend test and/or HWD. A simple normal prior was also given for applying JBF. We discussed how to determine informative and non-informative priors for genetic association studies. The non-informative priors that we gave can be generally applied when the targeted GRR is likely no more than 2.0, which fits the situation of GWAS for common variants with small to moderate genetic effects.

The purpose of this paper is to illustrate how to develop BFs directly based on frequentist trend test and test for HWD and their p-values. In situations when the trend test is not a powerful tool, the corresponding BF would not be useful either. One such application is rare variants, which have smaller MAFs (< 0.5%) and large genetic effects. In the online supplementary material, we also computed the values of β , δ, $W_{\beta }^2$, $W_{\delta }^2$, and ρ for rare variants with large effects using the trend test and HWD. Table S3 reports the values of the above parameters with MAFs equal to 0.001, 0.003 and 0.005 and GRR 5.0. The results show that under the REC model, $W_{\beta }^2$ and $W_{\delta }^2$ are both nearly 0, while are slightly greater than 0 under the DOM model. The BF would be about 1 (i.e., H₁ is not worthy mentioning when testing a single SNP) if the variance in the prior is very close to 0. This indicates that the trend test, useful for GWAS, is not a good test statistic for rare variants, in particular for REC diseases, nor does its Bayesian counterpart. In fact, many test statistics have been recently developed for rare variants. If rare variants are detected by a newly developed test statistic, then the corresponding BF based on that test statistic can be derived, which is a new topic that needs further research.

If BFs are reported alone without reporting p-values and BFs do not indicate decisive evidence of association in the data, sensitivity analysis with different choices of priors for detected SNPs, as we did in the simulation section, is important and necessary. However, when BFs are reported along with p-values, as in the WTCCC (2007) and Yasuno et al. (2010), and/or when BFs show decisive evidence, sensitivity analysis becomes less critical.

One advantage of our proposed robust JBF is its simplicity. More complicated BF may also be considered. For example, one can consider a BF directly based on the robust test (the minimum p-value or MAX). This requires derive the asymptotic or approximate distributions of the robust tests under both the null and alternative hypotheses. The asymptotic distributions of robust tests under the null hypothesis are not simple at all (Zang et al., 2010), let alone those under the alternative hypothesis. But, mathematically, BFs directly based on robust tests may achieve more efficiency robustness. We focused on a binary trait in this paper. Similar methods can be developed for a quantitative trait with comparison to Bayes factors based on some robust tests (So & Sham, 2011).