Differential recruitment of the sensorimotor putamen and frontoparietal cortex during motor chunking in humans

Abstract

Motor chunking facilitates movement production by combining motor elements into integrated units of behavior. Previous research suggests that chunking involves two processes: concatenation, aimed at the formation of motor-motor associations between elements or sets of elements; and segmentation, aimed at the parsing of multiple contiguous elements into shorter action sets. We used fMRI to measure the trial-wise recruitment of brain regions associated with these chunking processes as healthy subjects performed a cued sequence production task. A novel dynamic network analysis identified chunking structure for a set of motor sequences acquired during fMRI and collected on three days of training. Activity in the bilateral sensorimotor putamen positively correlated with chunk concatenation, whereas a left hemisphere frontoparietal network was correlated with chunk segmentation. Across subjects, there was an aggregate increase in chunk strength (concatenation) with training, suggesting that subcortical circuits play a direct role in the creation of fluid transitions across chunks.

Introduction

Motor sequence learning refers to the process by which temporally ordered movements are prepared and executed with increasing speed and accuracy (Willingham, 1998). To do so, the processing demands associated with the rapid planning of multiple serial movements within a sequence must be reconciled. The traditional notion is that the individual motor commands that constitute new sequences become temporally integrated into elementary memory structures or chunks (Gallistel, 1980; Lashley, 1951; Book, 1908). Chunking in motor sequencing allows groups of individual movements to be prepared and executed as a single motor program facilitating the performance of complex and extended sets of sequences at lower cost (Halford et al., 1998). The grouping of distinct elements into a single unit is a general performance strategy that is also observed in non-motor tasks (Gobet and Simon, 1998; Ericsson et al., 1980).

A host of behavioral studies of sequence learning support a hierarchical model of sequencing, in which long sequences of finger movements are segmented into shorter chunks (Verwey et al., 2009; Bo and Seidler, 2009; Kennerley et al., 2004; Verwey and Eikelboom, 2003; Sakai et al., 2003). The temporal pattern commonly observed is the production of one slow key press that is followed by several key presses produced in quick succession (Sakai et al., 2003; Verwey and Eikelboom, 2003). Recent studies suggest that individuals will spontaneously segment sequences into a set of subject-specific chunks (Verwey et al., 2009; Bo and Seidler, 2009; Kennerley et al., 2004; Sakai et al., 2003; Verwey and Eikelboom, 2003). The benefit of such segmentation is that it reduces memory load during ongoing performance (Bo and Seidler, 2009; Ericsson et al., 1980). With extended practice, short chunk segments can be concatenated into longer segments (Sakai et al., 2003; Verwey, 1996), suggesting that concatenation can operate on pairs of individual motor elements or between two sets of motor elements.

The aforementioned findings suggest that two chunking processes are at play during sequence learning. One process concatenates adjacent motor elements so that sequences can be expressed as a unified action, and the other process parses sequences into shorter groups. Both processes could lead to the pattern observed in chunking. In concert, they impart competing strategies for enhancing performance in the production of long motor sequences, presumably driven by the formation of motor-motor associations and the strategic control over sequence segmentation (e.g., Verwey, 2001).

Evidence suggests that the basal ganglia support the concatenation of multiple motor elements of a sequence. Studies from individuals with Parkinson’s disease (Trembley et al., 2010) and stroke patients (Boyd et al., 2009) found that damage to the basal ganglia impairs one’s ability to integrate motor elements into chunks. Further support comes from rodent and nonhuman primate research (Graybiel, 2008; Yin and Knowlton, 2006). As rats learn to navigate a T-maze for reward, neurons in the nigrostriatal circuit gradually represent motor sequences as chunks by firing preferentially at the beginning and end of action sequences, yielding concurrent improvements in performance (Thorn and Graybiel, 2010; Barnes at al., 2005). The disruption of this phasic nigrostriatal activity also leads to the impairment of sequence learning in mice (Jin and Costa, 2010). Similarly, subcutaneous injections of raclopride, a dopamine antagonist of the D2 receptor, disrupt sequence consolidation and chunking behavior in cebus monkeys (Levesque et al., 2007), which can be reversed by administration of a dopamine agonist (Trembley et al., 2009).

Several recent studies have argued that a frontoparietal network is critical for the segmentation of long sequences into multiple chunks (Pammi et al., 2012; Verwey et al., 2011; Verwey, 2010). The ability to segment long sequences into chunks is greatly diminished in older adults (Verwey et al., 2011; Verwey, 2010), possibly due to decreasing cortical capacity (Raz et al., 2005; Resnick et al., 2003). Moreover, a frontoparietal network was recruited when subjects produced long sequences that could be segmented into chunks relative to those that could not (Pammi et al., 2012). Further, transcranial magnetic stimulation (TMS) of the pre-supplementary motor area (preSMA), a part of the prefrontal cortex, disrupts the selection of chunks that are held in memory during the production of newly learned sequences (Kennerley et al., 2004).

Critically, the aforementioned experiments examined either the concatenation or the parsing process of chunking but not both processes simultaneously. By contrast, the following experiment that we report investigated the dynamics of both aspects of chunking over the course of extensive motor sequence learning. Our goal was to examine if both of these chunking processes enhance performance and to identify the underlying neural activity. To achieve this, it was critical to establish a method that overcame some of the limitations of existing methods for chunk identification.

When subjects retrieve chunks from memory, it is common to observe a non-random subset of prolonged inter-key intervals (IKIs) that are assumed to represent boundaries between separable chunks (Sakai et al., 2003; Verwey and Eikelboom, 2003). A common test for determining chunk boundaries is to compare response times at a subjectively identified pause relative to the IKIs between these pauses (Kennerley et al., 2004; Verwey and Eikelboom, 2003). This technique facilitates the extraction of putative sequence segments but relies on assumptions that during training (1) chunk boundaries are static and (2) short chunks are not combined into larger chunks. Further, this approach averages IKIs over multiple elements within each sequence, obscuring movement-by-movement contributions to chunking. Thus, this approach is not sensitive enough to measure the chunking structure that unfolds with training. These limitations underscore the need to develop a more flexible method for the identification of chunking structure, so that no constraints are made as to where or when chunks occur, and further, that it allows for changes to occur in the degree of parsing, where parsing occurs, and the strength of motor-motor associations of adjacent elements.

To model chunking behavior, we modified a network-based community detection algorithm (Bassett et al., 2011; Mucha et al., 2010). We modeled each trial as a network with nodes representing individual IKIs in a simple chain structure connecting neighboring IKIs with weights indicating their similarity (see Experimental Procedures). The networks were constrained to this simple chain structure to allow only interactions between adjacent movements within a sequence. To identify chunks, we performed community detection (a form of data clustering) using a multi-trial extension (Mucha et al. 2010) of the modularity-optimization approach (Fortunato, 2010; Porter et al., 2009; Newman, 2004). Modularity-optimization algorithms seek groups of nodes that are more tightly connected to each other relative to connections to nodes in other groups, and the multi-trial extension allowed us to consider both intra-trial and inter-trial relationships between nodes. We then quantified the strength of trial-specific network modularity (Q_{single–trial}, see Experimental Procedures). Network modularity (Q) can be conceptualized as the ease that a network can be divided into smaller communities. We define chunk magnitude as 1/Q_{single–trial}, which we denote by ϕ. To determine the relative strength of ϕ for a given trial, we normalized ϕ with respect to ϕ̄ for each participant and sequence. Thus, for trials with a high ϕ, it was computationally more difficult to parse the entire sequence into smaller groups (i.e., chunks). Conversely, trials with a low ϕ corresponded to sequences that were more easily divisible into chunks. We chose model parameters such that trials had between two and four chunks over each sequence. Our method is flexible in the sense that it imposes no constraints on where or when these chunk boundaries occur in a given trial. Furthermore, it allows for the identification of different chunking patterns in each individual and the identification of changes in chunking patterns over the course of training.

To measure the trial-by-trial contributions of the brain to chunking during sequence learning, we correlated blood oxygenated level dependent (BOLD) estimates with ϕ. Subjects learned a set of 12-element explicitly cued sequences using the four fingers of the left hand during the collection of functional magnetic resonance imaging (fMRI) data on three days of scanning. The aim of the fMRI experiment was to determine which brain regions support trials characterized by concatenation or by parsing. We used normalized values of ϕ as weights in a parametric analysis correlating ϕ with the regional change of the BOLD signal on a trial-by-trial basis. We predicted that trials with low ϕ and thus having easily separable chunks would correlate with activity in a frontoparietal network previously shown to be sensitive to sequence segmentation (Pammi et al., 2012; Kennerley et al., 2004). Conversely, trials with high ϕ, or those dominated by the concatenation process, would correlate with the sensorimotor striatum. Lastly, we tested if ϕ would increase with sequence learning and if this change was independent of conventional measures such as the time needed to complete a sequence. If true, ϕ could serve as a measure of sequence learning based on the strength of motor-motor associations that emerge with training.

Experimental Procedures

The data presented in this paper were collected in an experiment previously described by Bassett et al. (2011). Twenty-five right-handed subjects (16 female, average age ≈ 24 years, range ≈ 19–30 years), as confirmed by the Edinburgh Handedness Inventory, volunteered with informed consent in accordance with the Institutional Review Board/Human Subjects Committee, University of California, Santa Barbara. All subjects had less than 4 years of experience with any musical instrument, had normal vision, and had no history of neurological disease or psychiatric disorders. All completed three training sessions and one follow-up test session within 2 weeks. All training sessions were completed during the first 5 days, and the test session was completed 5 - 7 days after the final training session. All training and test sessions were performed during the acquisition of BOLD. In the following discussion, we focus on the data collected from the training sessions.

Experiment setup and procedure

Subjects lay supine in the MRI scanner and padding was placed under the left forearm to minimize muscle strain during the task. Subjects performed a cued sequence production (CSP) task by responding to visually cued sequences on a response box using their left hand. Responses were made using the 4 fingers of the left hand. Sequences were presented as a static series of musical notes on a 4-line staff (Figure 1A). Subjects reported the note configurations from left to right. The top line mapped onto the leftmost key using the leftmost finger and the bottom line was mapped onto the rightmost key using the rightmost finger. Each 12-element sequence contained 3 notes per line. The notes were randomly ordered without repetition and were free of regularities such as runs (123) and trills (121) with the exception of one frequently trained sequence (see below) that contained a trill. The number and order of sequence trials was identical for all subjects, with the exception of two who each missed one run of training due to technical difficulties.

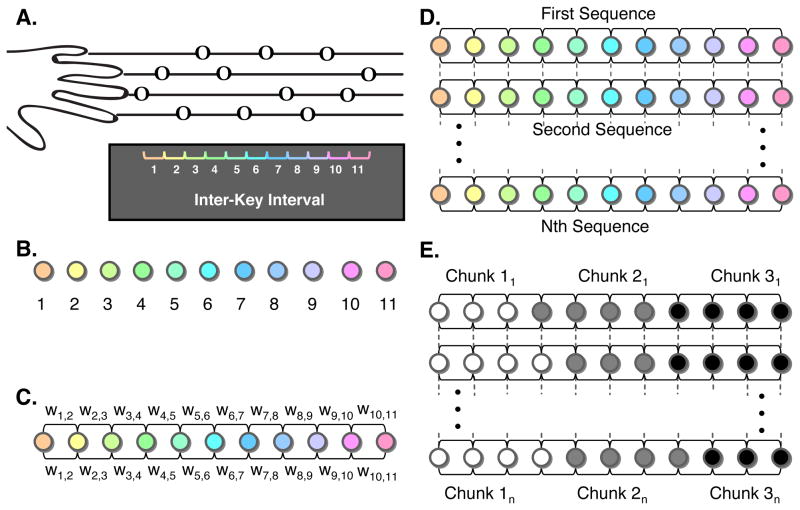
Figure 1.

(A) A trial started with the onset of a static image depicting a sequence of 12 notes arranged in the style of sheet music. Presentation served as the signal to report the sequence of notes, which were read left to right proceeding one note to the next. Subjects reported the sequences using their non-dominant left hand, with the leftmost finger corresponding to notes on the top line and the rightmost finger corresponding to notes on the bottom line. Construction of a trial-by-trial sequence network for multi-trial community detection: Using the inter-key interval (IKI) between button presses, we constructed single-trial sequence networks by converting each IKI into a node (B), which are linked to each other using undirected edges. The weight (C) of an edge is defined as the normalized absolute value of the difference between the 2 IKIs that it connects (see Experimental Procedures). We applied multi-trial community detection to these sequence networks, and incorporated information between consecutive trials by linking each node in one trial network to itself in contiguous trials (D). Utilizing information from linked nodes in consecutive trials, we partitioned IKIs into chunks using a multi-trial community detection (D) that grouped nodes that were strongly connected to one another.

A trial began with a fixation signal, which was displayed for 2 s. The complete sequence was presented immediately after and subjects responded as quickly as possible. They had 8 s to type each sequence correctly. The sequence was present for the entire duration that subjects typed. If a sequence was reported correctly, the notes were replaced with a fixation signal until the trial duration was reached. If a participant responded incorrectly, the verbal cue ‘INCORRECT’ appeared and the participant waited for the next trial. Trials not finished within the time limit were counted as incorrect.

Subjects trained on 16 different sequences at 3 different levels of training exposure. Three sequences were trained frequently; with 189 trials for each sequence and uniformly distributed across the training sessions. These ‘frequent sequences’ are the focus of the present manuscript. The following frequent sequences were presented: s1: ‘324124134132’; s2: ‘342142134312’; s3: ‘231431241342’. These numbers indicate the placement of the musical note on the staff: notes on the top line are represented by a ‘1’ while notes on the bottom line are represented by a ‘4’. Additionally, a second set of three sequences were each presented for 30 trials and a third set of ten sequences were each presented between 4 - 8 trials during training. For the remainder of this paper, we report the results for the three frequent sequences.

Frequent sequences were practiced in blocks of 10 trials, with 9 out of 10 being the same frequent sequence, and the other a rare sequence. Trials were separated by an inter-stimulus interval (ISI) between 0 s and 20 s, not including time remaining from the previous trial. Following the completion of each block, and in order to motivate subjects, feedback was presented that detailed the number of correct trials and the mean time needed to complete a sequence for the block. Training epochs contained 40 trials (i.e., 4 blocks) and lasted 345 scans. Each training session contained 6 scan epochs and lasted a total of 2070 scans.

Behavioral apparatus

Stimulus presentation was controlled with a laptop computer running MATLAB 7.1 (Mathworks, Natick, MA) in conjunction with Cogent 2000 (FIL, 2000). Key-press responses and response times were collected using a button box connected to a digital response card (DAQCard-6024e; National Instruments, Austin, TX).

Imaging procedures

Functional MRI recordings were conducted using a 3.0 T Siemens Trio with a 12-channel phased-array head coil. For each epoch, a single-shot echo planar imaging sequence that is sensitive to BOLD contrast was used to acquire 33 slices per repetition time (TR = 2000 ms, 3 mm thickness, 0.5 mm gap), echo time (TE) of 30 ms, flip angle of 90 degrees, field of view (FOV) of 192 mm, and 64 × 64 acquisition matrix. Before the collection of the first epoch, a high-resolution T1-weighted sagittal image of the whole brain was acquired (TR =15.0 ms; TE = 4.2 ms; flip angle = 9 degrees, 3D acquisition, FOV = 256 mm; slice thickness = 0.89 mm, acquisition matrix = 256 × 256).

Data analysis: behavior

We collected three behavioral variables during training: the time between key presses (i.e., the vector of inter-key intervals), movement time (MT), and error. MT is the time elapsed from the initial to final key press. Error was scored as any trial not produced in the correct order as well as those trials not completed within the 8 s time limit. To test for learning, we entered the MT data for each subject, sequence, and session into a repeated-measures ANOVA (with subject treated as a random factor). To test for differences in error over training, we combined error for each frequent sequence and entered them for each subject and session using a repeated-measures ANOVA. For all statistical tests, we set a probability threshold of P < 0.05 for the rejection of the null hypothesis.

Sequence network construction

We collected inter-key interval (IKI) data for all correct frequent sequence trials. Each trial consisted of 11 IKI data points (Figure 1A). We excluded the first key press in the sequence from the IKIs because it contained the time elapsed from initial cue presentation to the completion of the first button press. We calculated the mean for each frequent sequence IKI (giving a total of 11 mean IKIs/sequence) for each participant. We then excluded trials containing IKIs greater than 3 standard deviations from each mean IKI. To facilitate the examination of chunking behavior, we constructed a sequence network to encode the relationship between IKIs for each trial. We defined the nodes for each sequence network as the 11 IKIs for a trial (Figure 1B). We defined motor chunks as specific groups of movements that occur serially in time. Consecutive nodes are therefore connected to one another using undirected edges; the node representing IKI₁ is connected to the node representing IKI₂ and the node representing IKI₂ is also connected to the node representing IKI₁ (Figure 1C). Furthermore, intra-chunk movements occur in rapid succession relative to inter-chunk movements. We therefore defined the similarity in IKIs as (d̄_ij − d_ij)/d̄_ij, where d_ij is defined as the absolute difference in IKIs, (i.e., d_ij =|IKIi − IKI_j|) and d̄_ij is defined as the maximum of d_ij over the entire trial. In each sequence network, these similarity scores weight the connecting edges between neighboring nodes only: the weight w₁₂ between nodes 1 and 2 is equal to the similarity s₁₂ between nodes 1 and 2 (Figure 1C). We define the weight matrix w to be the 11×11 matrix whose elements w_ij represent the pairwise connectivities of the sequence network. Importantly, consecutive IKIs (e.g., IKI₁ and IKI₂, IKI₂ and IKI₃, etc. located along the |1|-diagonal of w) are linked by the nonzero weights s_ij but non-consecutive IKIs (e.g., IKI₁ and IKI₃, IKI₁ and IKI₄, etc. located in the, |2|- to |11|-diagonals of w) are linked by zero-valued weights to hard-code the fact that only sequential movements are related. This process creates the chain topology shown in Figure 1C.

Multi-trial sequence network construction

One can investigate chunking behavior in the individual sequence networks for each trial by using an algorithm for community detection (Fortunato, 2010; Porter et al., 2009). However, this treats the movements in each sequence as if they were independent of other trials and ignores the information available in consecutive trials. This would imply that chunking could be based on outlier behavior of single trials. To prevent this, we used information from multiple adjacent trials to determine chunking structure, based on a multilayer approach (Bassett et al. 2011; Mucha et al. 2010). To do this, we linked the sequence network from a single trial to the sequence network of the subsequent trial by connecting each node in the first network with itself in the second network (Figure 1D) with weight equal to the selected inter-trial coupling parameter (see below). Thus each trial defines a layer in the multilayer structure. We constructed separate multilayer sequence networks by combining all trials for each of the three frequent sequences for each participant.

Chunk detection

After constructing a multilayer sequence network, we identified chunks by performing community detection using a multilayer extension (Mucha et al. 2010) of the popular modularity-optimization approach (Fortunato, 2010; Newman, 2010; Porter et al., 2009; Newman, 2004). Communities in sequence networks represent movement chunks. Modularity-optimization algorithms applied to individual networks seek groups of nodes that are more strongly connected to one another than they are to other groups of nodes. In a multilayer community-detection algorithm, one performs a similar optimization procedure that simultaneously utilizes information from consecutive layers. This allows chunks to be identified within a sequence based on evidence across adjacent trials. The result is a partitioning of the IKIs in each sequence into chunks (Figure 1E). Importantly, these partitions can vary between sequences and within sequences over training.

Parameter selection

Multi-trial community detection requires the selection of two resolution parameters (Mucha et al. 2010; Porter et al. 2009): one determines the relative weights between intra-trial IKIs and the other determines the relative weights between inter-trial IKIs. The intra-trial resolution parameter (γ), which determines the sensitivity of multi-layer modularity to the size of chunks, was set to 0.9. The inter-trial coupling parameter (C), which determines the sensitivity of multi-layer modularity to variability across trials, was set to 0.03. We selected these two parameters based on the following. Previous chunking studies suggest that sequences are separable into chunks containing 3 - 5 elements (Bo and Seidler, 2009; Verwey, 2001). We expected to find sequences that contained between 2 and 4 chunks and selected γ accordingly. Second, longer sequences that contain multiple chunks have slower IKIs at the boundaries of a chunk relative to the other IKIs found within a chunk (Sakai, et al., 2003; Verwey, 2001). We selected C and γ so that slow IKIs for a trial marked the transition between serial chunks. Third, chunking patterns are not constant, but are plastic over the course of learning (Sakai et al., 2003; Verwey, 1996). Accordingly, we selected a value of C that allows for realistic plasticity in chunk boundaries over training.

Diagnostics

We studied chunking characteristics in terms of the segregation of a sequence trial into chunks (Q_{single–trial}), and its multiplicative inverse, chunk magnitude ϕ, which measures the aggregate strength of chunking for a given trial. Both the segregation and aggregation single-trial diagnostics were based on the maximization of the multi-layer modularity quality function (Q), which provided the best partitioning of the multilayer sequence networks into chunks. The identification of the optimal partition is NP-hard and here we employ a generalization of the Louvain approach (Blondel et al. 2008). The modularity of a partition of a sequence network is defined in terms of the weight matrix w. In the simplest case of computing the modularity for a single trial, we suppose that IKI_i is assigned to chunk g_i and IKI_j is assigned to chunk g_j. Then the network modularity Q (Newman and Girvan, 2004) is then defined as

$$Q={\sum }_{ij}[w_{ij}-P_{ij}]\delta (g_i,g_j),$$ (1)

where δ(g_i, g_j) = 1 if g_i = g_j and it equals 0 otherwise, and P_ij is the expected weight of the edge connecting IKI_i and IKI_j under a specified null model (Fortunato, 2010; Porter et al., 2009). In the multi-trial network case, we use a more complicated formula developed in Mucha et al. 2010 for a broad class of time-dependent and multiplex networks. In this case, the quality function to be maximized is given by

$$Q_{\mathit{multi}-\mathit{trial}}=\frac{1}{2\mu }{\sum }_{\mathit{ijlr}}[(A_{\mathit{ijl}}-{\gamma }_l\frac{k_{il}{k}_{jl}}{2m_l}){\delta }_{lr}+{\delta }_{ij}{C}_{\mathit{jlr}}]\delta (g_{il},g_{jr}),$$ (2)

where the adjacency matrix of trial l has components A_ijl, γ_l is the resolution parameter of trial l, g_il, gives the community assignment of node i in layer l, g_jr gives the community assignment of node j in layer r, C_jlr is the connection strength between node j in layer r and node j in layer l, k_il is the strength of node i in layer l, 2μ = Σ_jr κ_jr, κ_jl = k_jl + c_jl, and c_jl = Σ_r C_jlr. In optimizing Q_{multi–trial}, we attained optimal partitions for all trials simultaneously using the constant values γ_t = 0.9 and for neighboring layers l and r, C_jlr = 0.03. To determine the modularity of each trial separately (Q_{single–trial}) we computed the modularity function Q given in Equation (1) using the partition assigned to that trial by Q_{multi–trial}.

Chunk magnitude (ϕ) is defined as 1/Q_{single–trial}. Low values of ϕ correspond to trials with greater segmentation, which are computationally easier to split into chunks and high values of ϕ correspond to trials with greater chunk concatenation, which contain chunks that are more difficult to computationally isolate. We normalized the values of ϕ across correct trials for each frequent sequence:

$$\varphi =[({\varphi }^t-\overline{\varphi })/\overline{\varphi }],$$ (3)

where ϕ^t is the chunk magnitude for a single trial and ϕ̄ is the mean chunk magnitude.

Statistical validation

An important caveat of modularity-optimization algorithms is that they provide a partition for any network under study whether or not that network has significant community structure (Fortunato, 2010). It is therefore imperative to compare results obtained from empirical networks to random null models in which the empirical network structure has been destroyed. We constructed a random null model by randomly shuffling the temporal placement of IKIs within the network for each trial. By contrasting the optimal modularity Q_{multi–trial} of the empirical network to that of this null model network, the amount of modular structure (i.e., the amount of chunking) observed in the real data can be tested.

Statistical sampling

As described in Good et al. (2010), modularity-optimization algorithms can yield numerous partitions near the optimum solution for the same network. The number of near-degenerate solutions increases significantly with network size and when the distribution of edge weights approaches a bimodal distribution (i.e., when the networks are unweighted). In the current application, our use of small networks (11 nodes in each layer and approximately 150 layers in a multilayer sequence network) with weighted connections minimizes the risk of near-degeneracy. In addition, we sampled the optimization landscape 100 times for each network, albeit with the same computational heuristic (different results occur because of pseudo random ordering of nodes in the algorithm). We report the mean and standard deviation from those 100 samples. The mean results are expected to be representative of the system structure, and such a procedure has been used for other networks (Bassett et al., 2011).

fMRI data analysis

We executed the preprocessing and analysis of the functional imaging data in Statistical Parametric Mapping (SPM5, Wellcome Department of Cognitive Neurology, London, UK). Raw functional data were realigned, coregistered to the native T1, normalized to the MNI-152 template with a resolution of 3 × 3 × 3 mm and a smoothing kernel of 8 mm full-width at half-maximum. To control for potential fluctuations in intensity across the training sessions and the test session, we normalized global intensity across all functional volumes by scaling each volume by the aggregate voxel mean.

The design matrix included all trial types as well as the blocking variables for run epochs. We determined relative differences in the BOLD signal by using a general linear model (GLM) for event-related functional data. We created first-level designs with stimulus onset timing vectors for each frequent sequence. To isolate brain regions that are involved in chunking the frequent sequences, we included an additional covariate vector that contained the normalized ϕ values based on the segmentation patterns attained from community detection. Differences in brain activity due to MT were accounted for by using MT as the modeled duration for corresponding events. MT is a direct measure of time spent on the task rather than the magnitude of a behavior, thus it is logical to model this temporal measure in terms of duration. This approach leads to accurate modeling of the BOLD response in the GLM (Grinband et al., 2008). We convolved events using the canonical hemodynamic response function (HRF) and temporal derivative of the BOLD signal. Using freely available software (Steffener et al., 2009), we combined beta image pairs for each event type (HRF and temporal derivative) at the voxel level to form a magnitude image (Calhoun et al., 2004)

$$H=\mathit{sign}({\widehat{B}}_1)\ast \sqrt{{\widehat{B}}_1+{\widehat{B}}_2},$$ (4)

where H is the combined amplitude of both the estimation of BOLD (B̂₁) and its temporal derivative (B̂₂). We performed mixed-effects group analysis using a full-factorial design, with chunking as the factor (3 levels: one for each frequent sequence). We minimized detection of false-positives (type II error) by using cluster-corrected family-wise error rate correction at P < 0.05. We evaluated results pertaining to hypothesis-driven contrasts that failed to survive this corrected threshold at uncorrected P < 0.001 with a 10-voxel cluster threshold.

The aim of this investigation was to identify which regions are involved in motor sequence chunking based on the correlation of the BOLD response with ϕ. Both negative and positive correlations might be present: positive correlations indicate the regions that support the concatenation of chunks within a sequence, and negative correlations indicate the regions that support the segmentation of sequences into separable chunks.

Results

Behavior effects of sequence learning

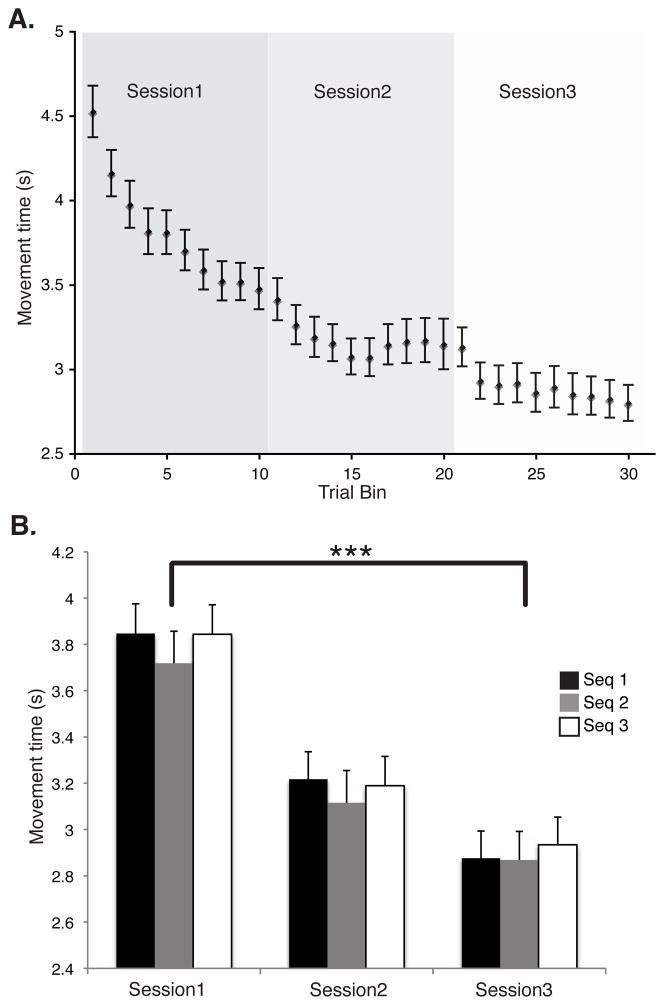
We evaluated practice-related change in movement time (MT) over the course of training using a 2-way (sequence × session) repeated-measures ANOVA. This revealed a main effect for session [F(2,21) ≈ 92.13, P < 0.00001]. This finding confirms that subjects learned the sequences during training. There was no significant effect of sequence type or interaction, confirming that the three sequences were learned similarly and with similar speed (Figure 2). The mean percent error (+/− SD) across the training sessions was 12.8 +/− 7.5. We found no significant effect of error over session, indicating that there was no change in the speed/accuracy tradeoff even though MT values decreased with training.

Figure 2.

The time needed to complete each frequently trained sequence, or movement time (MT), decreased over the course of training that was performed inside the scanner during the simultaneous acquisition of BOLD images. The upper image (A) depicts the decreasing group MT pattern, collapsed across the three frequently trained sequences. We combined trials for each participant separately for each scan session into 10 equally sized trial bins (preserving temporal order) and then averaged within each bin. The lower image (B) depicts group MT change during each scan session; each sequence is shown separately. Using an ANOVA, we found a significant effect of session (P < 0.00001) but did not find any significant effect of sequence or interaction. This result confirms that performance was substantially improved over the 3 scan sessions, and that all three frequent sequences were learned equally well. Error bars give the standard error of the mean (SEM).

We quantified chunking within each sequence by the optimized modularity Q_{multi–trial} of the sequence networks. Modularity in this case measures the separability between clusters of IKIs. Higher values of Q indicate a greater ease in separating chunks. The average modularity was 0.54 +/− 0.007, which was significantly greater than that expected in a random null model network (P < 0.000000001, T ≈ 8.44, DF = 42). This demonstrates that significant chunking exists in the data.

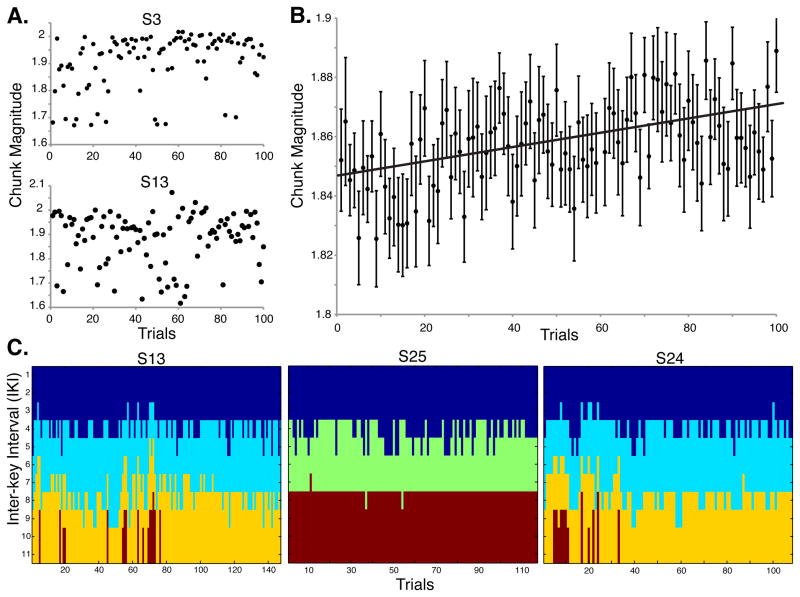
We predicted ϕ would increase with learning, reflecting stronger associations across adjacent chunks. Subjects demonstrated considerable variability of ϕ (Figure 3A). To test for increasing ϕ over time at the group level, we correlated group ϕ̄ to a linear slope. We first calculated group ϕ̄ by taking a random sample of 100 values of ϕ ordered in time for each participant. To control for the random selection of trials, we performed and then pooled 100 instances of the correlation between the group ϕ̄ and the linear slope (Figure 3B). Confirming our prediction, group ϕ̄ increased significantly over the course of training (R > 0.40, P ≈ 0.0002).

Figure 3.

The dynamics of chunking behavior. (A) Normalized chunk magnitude (ϕ) for each trial for two representative subjects. High values of ϕ reflect greater chunk concatenation and low values reflect greater chunk segmentation (see Experimental Procedures). There was a substantial amount of variability in ϕ across trials and among individual subjects over training. Some had a robust increase (top) and others had modest change (bottom). (B) Group mean ϕ increased significantly over training, reflecting the tendency at the population level for training to induce greater concatenation and formation of unified actions. (C) Multi-trial community detection of chunks for one of the sequences, plotted for three subjects. Some individuals show considerable trial-wise variability in segmentation boundaries over the course of training (S13, S24), whereas others show less (S25). Colors indicate separate chunks among the IKIs.

Because ϕ and MT both change over time, it is critical to evaluate their relationship. We correlated trial-wise ϕ and MT for each participant and then pooled (averaged) the R values and resultant p values over subjects, revealing that the two measures are independent (R ≈ 0.13, P > 0.20). This suggests that brain regions correlated with ϕ reflect a novel performance diagnostic related to sequence learning.

Although we found ϕ had no significant relationship to MT, the two performance diagnostics could still be related to individual differences. An important question to ask is whether “good learners” are also “good chunkers”? In this sense, “good learners” can be defined as those with the greatest improvement in MT over training (e.g., Crossman, 1959), and “good chunkers” can be defined similarly, as those with the greatest increase in ϕ over training. We divided the ϕ and MTs for each participant and sequence into three bins that preserved temporal order and averaged over sequences. A correlation between ϕ and MT difference scores (given by a subtraction between the first and third bins) revealed that there was no significant relationship (R ≈ 0.17, P > 0.44) between those with the largest improvements in MT and those with the largest improvements in ϕ.

We carried out several tests to determine the robustness of our model to adhere to the behavioral features of chunking. Previous accounts suggest that IKIs at the start of chunks are slower and reflect retrieval (Kennerley et al., 2004, Sakai et al., 2003; Verwey, 2001). To test whether our model and its parameters specified chunks that were consistent with this, we first determined the boundaries for each chunk. Using a repeated-measures ANOVA with sequence as the repeated measure and type of IKI as the categorical factor (border IKI or other IKI in a chunk), we found that the border IKIs are significantly slower than the IKIs taken from the middle of chunks [F(1, 21) ≈ 11.686, P≈ 0.003]. Thus, our model identified chunks in a reproducible manner and the elements at the chunk borders show the expected increase of retrieval time relative to other elements within the same chunk.

In addition, we confirmed that the number of chunks identified for a given trial using community detection at the selected resolution parameters was consistent with previous behavioral accounts (e.g., Sakai et al., 2003). We expected the sequences to be segmented into approximately 2 - 4 chunks and found that the mean number of chunks per sequence was 3.06 +/− 0.06. Figure 3C shows examples from representative subjects (each showing 2 - 4 chunks per sequence). Critically, the patterns of chunks are not static but instead fluctuate (as do the numbers of elements contained within chunks) over training.

Neural correlates of motor chunking

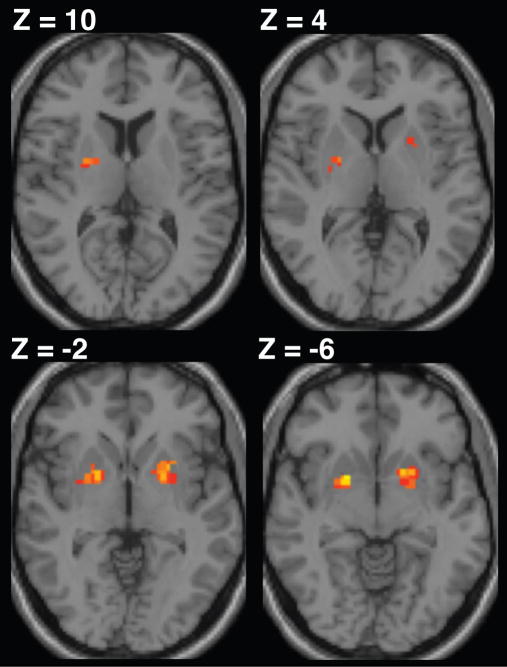
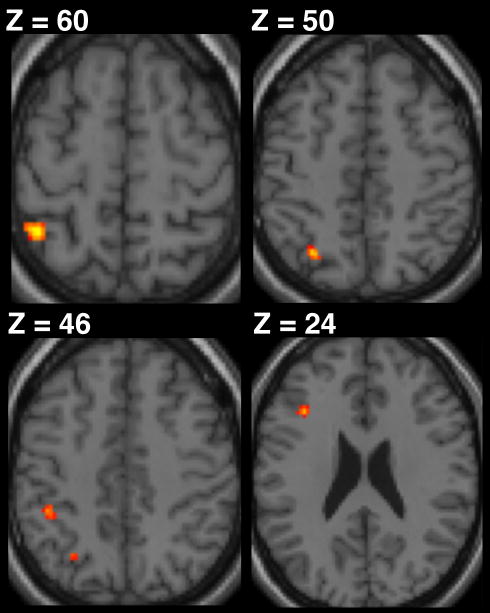
Based on previous studies of motor chunking (e.g., Pammi et al., 2012; Trembley et al., 2010; Boyd et al., 2009; Kennerley et al., 2004) we hypothesized that ϕ would isolate distinct brain regions that support the concatenation and segmentation chunking processes on a trial-by-trial basis. Confirming our prediction that the basal ganglia is involved in binding sequential motor elements, we observed a positive correlation between ϕ and fMRI BOLD activity within the bilateral putamen. The pattern of activation within the contralateral putamen extended ventrally from the dorsal posterior sensorimotor territory alongside the border with the external globus pallidus. We found activation of the ipsilateral putamen to be distinct from that in the contralateral cluster, extending ventrally from a more intermediate locus (rostral to y = 0, ventral to z = 4) (Figure 4 and Table 1). Further, consistent with our prediction that segmentation involves the recruitment of frontoparietal regions, we found a negative correlation between ϕ and BOLD in left hemisphere cortical regions including the mid-dorsolateral prefrontal cortex (mid-DLPFC) and foci along the intraparietal sulcus (IPS). Activation in the mid-DLPFC was rostral to the premotor cortex and deep within the inferior frontal sulcus (IFS). In addition, we found three separate voxel clusters along the IPS. Two of these clusters were located next to the supramarginal gyrus and an additional cluster was located at the posterior aspect of the IPS (Figure 5 and Table 2). These regions are presented at a hypothesis-directed uncorrected threshold of P < 0.001 with an activation cluster threshold of 10 contiguous voxels.

Figure 4.

BOLD activation in the putamen was positively correlated with normalized ϕ, reflecting increased involvement during the concatenation of sets of adjacent motor elements. Results are shown at a cluster-level corrected threshold of P < 0.05 (FWE), with the voxel resolution set to 2 × 2 × 2 mm.

Table 1.

Brain regions positively correlated with chunking magnitude

Region	Side	MNI coordinates			Voxels	Peak t-value
		x	y	z
Putamen	R	21	6	−6	42	5.07
		27	−3	9		4.05
		30	−9	3		3.34
Occipital Pole	L	−21	−93	25	56	4.91
		−12	−93	28		4.90
Posterior cingulate gyrus	R/L	9	−18	45	54	4.67
		−3	−21	42		4.50
		−3	−12	39		4.06
Putamen	L	−15	9	−6	47	4.58
		−24	9	−3		4.49

Significance for all voxels were tested with a group mixed-effects analysis, cluster-level familywise error rate corrected, P < 0.05.

Figure 5.

BOLD activation of the intraparietal sulcus (IPS) and the mid-dorsolateral prefrontal cortex (mid-DLPFC) was negatively correlated with normalized ϕ, reflecting increased involvement during the segmentation of sets of motor elements. Results are shown at P < 0.001 (uncorrected with a cluster threshold of 10 voxels) with voxel resolution set to 2 × 2 × 2 mm.

Table 2.

Brain regions negatively correlated with chunking magnitude

Region	Side	MNI coordinates			Voxels	Peak t-value
		x	y	z
Intraparietal sulcus (middle)	L	−42	−47	57	18	4.31
Intraparietal sulcus (posterior)	L	−27	−2	52	12	4.23
Inferior frontal sulcus	L	−36	21	24	19	4.18
Intraparietal sulcus (anterior)	L	−42	−39	45	12	4.12

Significance for all voxels were tested with a group mixed-effects analysis, P < 0.001, uncorrected with a cluster threshold of 10 voxels.

Discussion

Chunking is a performance strategy that supports increasing speed and accuracy through the formation of hierarchical memory structures. Two separable processes drive the formation of temporal structures: one parses long sequences into shorter groups to be handled more easily in memory, and the other concatenates pairs of adjacent motor elements or sets of elements to express a long sequence as a unified action. Because chunking is not static during learning (e.g., Sakai et al., 2003) and is variable across subjects (e.g., Kennerley et al., 2004; Verwey and Eikelboom, 2003), it has been challenging to quantify these two concurrently active processes and to use them as a description of performance. To address this, we identified chunks on a trial-by-trial basis using a novel multi-trial network analysis for community detection (Bassett et al., 2011; Mucha et al., 2010) that takes into account both intra-trial information and the interaction between neighboring trials for chunk identification. Our approach is based on multi-trial network linkages and imposes no constraints on where or when chunking ought to occur. This led to the identification of chunks that were different across subjects and sequences, but also could be different from one trial to the next. We found a range in chunking over training, as some subjects had variable segmentation patterns (S13, S24 in Figure 3C), while others changed very little (S25 in Figure 3C). Further, we measured how trial-wise chunk magnitude (ϕ) changed over training, with higher values reflecting greater concatenation and lower values reflecting greater segmentation. Some subjects were highly variable (S13 in Figure 3A) relative to others (S3 in Figure 3A). Critically, at the group level, ϕ increased over training (Figure 3B) suggesting that the structure of a sequence was strengthened and individual chunks became more difficult to isolate.

Using normalized ϕ as a covariate provided for the trial-wise assessment of the neural activity related to both the concatenation and the parsing processes during sequence learning. This led to the identification of two activation patterns. First, trials that were computationally difficult to divide into chunks due to stronger motor-motor associations correlated with an increase in activation of the bilateral putamen. Second, trials that were easily separable into chunks, a characteristic of increased hierarchical parsing, led to increased activation of a frontoparietal network isolated to the left hemisphere.

Recent evidence from patient populations suggests that chunking motor sequences is supported by the basal ganglia (Trembley et al., 2010; Boyd et al., 2009), consistent with a dopamine-dependent mechanism that is reliant on the sensorimotor putamen. Parkinson disease (PD) patients are known to be impaired in generating previously automatic movements due to lesions of sensorimotor dopaminergic nuclei in the basal ganglia. Chunking, which emerges as a feature of practiced movements, is blocked in unmedicated patients while performing a sequencing task, relative to both age-matched controls and PD patients on L-DOPA (Trembley et al., 2010). Critically, all groups were able to demonstrate learning, but only patients without medication were unable to translate single motor responses into chunks. In other words, the absence of chunking does not necessarily restrict all potential avenues for sequence learning, such as cortically based associative learning, which elderly subjects were likely using despite their lack of chunking during sequence learning (Verwey, 2010). Similarly, Boyd et al. (2009) found that chunking was impaired in patients with chronic middle cerebral artery (MCA) stroke involving the basal ganglia when they used their non-hemiparetic arm.

The involvement of the sensorimotor striatum in the expression of chunking through well-practiced procedures has been studied extensively in both rats and nonhuman primates (Graybiel, 2008; Yin and Knowlton, 2006). Neural firing patterns recorded in the rat dorsolateral caudoputamen display a task-bracketing distribution, with phasic firing at the start and finish of T-maze navigation (Barnes et al., 2005; Jog et al., 1999). Further, the expression of these phasic patterns in the dorsolateral caudoputamen is linked to learning motor components of navigation behavior (Thorn et al., 2010). Task-bracketing activity sharpens throughout early learning and occurs in parallel with phasic patterns in the associative dorsomedial caudoputamen. Critically, once cue-based associations are learned, dorsomedial firing wanes and performance is correlated with the ongoing phasic dorsolateral activity. This suggests that firing in the dorsolateral caudoputamen supports the expression of habitual actions (Thorn et al., 2010). Our finding that ϕ increases with sequence learning is consistent with these results, suggesting that increased activation from the bilateral putamen is necessary for strengthening motor-motor associations associated with fluid sequential behavior. Growing evidence suggests that a frontoparietal network also supports chunking but in a fundamentally different way (Pammi et al., 2012; Verwey et al., 2011; Verwey, 2010; Bo and Seidler, 2009; Bo et al., 2009). Consistent with our observation that a frontoparietal network was preferentially activated on trials that could be more readily divided into segments, Pammi et al. (2012) found a substantial increase in activation of the mid-DLPFC and the parietal cortex when subjects were able to spontaneously segment long sequences into chunks. These activation foci were consistent with the locations of the left mid-DLPFC and IPS clusters that we observed to represent segmentation. Pammi et al. (2012) required subjects to perform an m × n visuospatial sequencing task involving the maintenance of several “sets” of button presses in memory. They found that set size load facilitated chunking, with subjects able to spontaneously segment a sequence that required only 2 button presses to be remembered at a time but not in another sequence that required 4 button presses to be remembered. Hence, the reduction in set size facilitated segmentation, which was associated with frontoparietal recruitment.

Other recent studies have shown aging to have a substantial effect on one’s ability to segment sequences into chunks. It was found that older adults are unable to employ a segmentation strategy when learning simple yet unstructured sequences (Verwey et al., 2011; Verwey, 2010). This finding was observed when subjects performed a discrete sequence production (DSP) task in which they responded to sequential spatially ordered stimuli such that the next stimulus was immediately presented after a response was made to the previous stimulus. Following brief practice on the DSP task, young adults are able to transition from reacting to each successive stimulus to the execution of the entire sequence as a whole (Rhodes et al., 2004; Verwey et al., 2002). In contrast, these studies revealed that older adults could still learn sequences but were unlikely to employ strategic control to process sequential elements (Verwey et al., 2011; Verwey, 2010). Interestingly, these effects could be driven by known frontoparietal structural changes in grey matter and white matter that emerge during aging (Madden et al., 2009; Perry et al., 2009; Raz et al., 2005; Resnick et al., 2003).

Segmentation during chunking reflects the formation of temporally ordered action boundaries. Consistent with this interpretation, there is growing evidence that suggests goal-oriented actions are represented hierarchically in both the lateral prefrontal cortex (Badre et al., 2009; Shima et al., 2007; Koechlin and Jubault, 2006) and along the IPS (Hamilton and Grafton, 2008, 2006; Jubault et al., 2007). For instance, Koechlin and Jubault (2006) found that the selection of learned key press movements followed a gradient of increasing abstraction extending from the dorsal premotor cortex for the selection of a simple button press to a set of increasingly rostral mid-DLPFC regions first for the selection of a simple sequence (Brodmann Area 44) and for the selection of a superordinate set of contextually selected simple sequences or chunks (Brodmann Area 45). Similarly, we found that trials with increased behavioral evidence of segmentation were associated with increased activation of the mid-DLPFC and within the IFS. Moreover, in a related investigation, Jubault et al. (2007) observed that distinct regions within the parietal cortex were involved in the sequential organization of action. They found the left IPS was involved at different levels of sequence organization, including phasic activation patterns for separate anterior and posterior regions in left IPS (signifying the updating of action sets). Our results reflect a similar pattern, with separate anterior and posterior activation IPS foci correlated with sequence segmentation. Across these experiments, the common temporal pattern of slow and fast elements during sequencing might reflect the increased involvement of cognitive processes for the selection and temporal organization of high-level action representations.

The quantity ϕ represents a novel performance diagnostic for sequence behavior. How does ϕ relate to learning? For individual subjects, on a trial-by-trial basis, this measure was largely independent of traditional measures of performance, such sequence completion time (MT). Furthermore, we found no significant relationship between those who could be considered “good chunkers” (i.e., those who increased their ϕ the most over training) with those who might be considered “good learners” based on the reduction of MT with practice. Nevertheless, when averaged over subjects, we found that ϕ progressively increased over training. This suggests that there is a general tendency for greater concatenation of chunks with enough practice. This in turn highlights the role of practice in the formation of longer, unified sequences of actions irrespective of movement speed. It is important to emphasize that the 12-element sequence in our study was long relative to typical sequencing tasks such as the DSP task (Rhodes et al., 2004). Additionally, subjects were required to learn three frequent sequences, which might require persistent use of segmentation - even after three days of practice - explaining the slow change in ϕ with training. Other levels of sequence length, difficulty, or number of sequences might lead to different trade-offs between the concatenation or segmentation processes used to maintain performance of motor sequences.

Our approach to chunking is notably different from models of sequence learning that focus on rates of change in behavior that might underlie “stages” of learning (Doyon and Benali, 2005; Doyon and Ungerleider, 2002). Our findings suggest that chunking is strongly engaged throughout the three days of practice, and is unlikely to be a predictor for the rapid rate of improvement seen during this period. Our results also provide a novel conceptualization of how dual processing might be used in sequence planning - one that is different but not mutually exclusive of previous dual models. For instance, Verwey (2001) proposed a dual processor model containing parallel cognitive and motor processors to account for the temporal pauses observed in chunking. According to this model, a motor processor rapidly executes the tightly coupled elements within each chunk, and the cognitive processor prepares each chunk for the motor processor. In this case, the pauses are due to planning at a supraordinate cognitive level. Our results, however, suggest that the cognitive processor is not causing delays due to planning. Instead, the delays are a direct result of frontoparietal circuits segmenting long sequential structures into shorter ones. This strategic parsing is countered by another subcortical process concatenating these same groups of motor elements into longer sequences. In our view, activity of both processes occurs in parallel to enhance performance of long sequences. In another dual model, Hikosaka et al. (2002, 1999) proposed a hierarchical structure to account for the challenge of capacity limitations in planning large motor sequences. In this model, processing limitations are overcome by the activation of two parallel loops, each of which is supraordinate to the planning of individual stimulus response maps. One loop codes for spatial features of sequences and the other loop codes for motor features of sequences. In contrast, our results highlight two loops that parse and concatenate a sequence. It remains to be tested if there is a correspondence between these views, and it would be of interest to see if they can be reconciled. For example, spatial loops - as defined by Hikosaka et al. (2002, 1999) - might be more associated with parsing, whereas motor loops might be linked more closely with concatenation.

• Chunk concatenation is correlated with activity of the putamen.

• Chunk segmentation is correlated with activity of a left frontoparietal network.

• Multi-trial community detection is a reliable estimator of chunk structure.

• Multi-trial community detection is sensitive to both subject and sequence variability.