Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2013 Jun 1.
Published in final edited form as: Spat Spatiotemporal Epidemiol. 2012 Apr 21;3(2):163–171. doi: 10.1016/j.sste.2012.04.009

Spatial-temporal analysis of non-Hodgkin lymphoma risk using multiple residential locations

David C Wheeler a,§, Lance A Waller b, Wendy Cozen c, Mary H Ward d
PMCID: PMC3372929  NIHMSID: NIHMS372233  PMID: 22682442

Abstract

Exploring spatial-temporal patterns of disease incidence and mortality can identify areas of significantly elevated or decreased risk, providing potential etiologic clues. Several methodological issues arise in spatial-temporal analysis of cancer, including population mobility, disease latency, and confounding, but applying modern statistical methods to case-control studies with residential histories can address these issues. As an example, we present a spatial-temporal analysis of non-Hodgkin lymphoma (NHL) risk using data from Los Angeles County, one of four centers in a population-based case-control study. Using residential histories, we fitted generalized additive models (GAMs) adjusted for known risk factors to model spatially the probability that an individual had NHL and identify areas of significantly elevated NHL risk. In previous analyses using models with single lag times, the lag time of 20 years yielded the most significant decrease in model deviance. To better assess cumulative effects of unmeasured environmental exposures over space and time, we considered models that allowed for multiple residences per subject through spatial smoothing functions of residential location at different times. We found that the model with the best goodness-of-fit included components for residential change and residential duration, although the model that included residential duration was not meaningfully better than the model that included only residential change. The estimated cumulative spatial risk surface from the model with residential change amplified the risk surface in some areas compared with the surface based on the model with a single component for the most significant time lag.

Keywords: cancer, generalized additive model, spatial risk, latency, exposure

Introduction

Many cancers have risk factors that are distributed unevenly in the environment. Examples include bladder cancer and arsenic (Silverman et al., 2006), lung cancer and radon (Spitz et al., 2006), and leukemia and benzene (Linet et al., 2006). It is reasonable, therefore, to expect spatial pattern in cancer risk, which may be explained by the uneven distribution of risk factors that may be known or unknown. When risk factors are unknown, studying spatial-temporal patterns in risk may reveal clues about disease etiology. There are numerous examples in the literature of spatial analyses to study patterns in cancers, including childhood leukemia (Alexander, 1993; Bithell and Vincent, 2000; Wheeler, 2007) and bladder cancer (Jacquez et al., 2006).

In spatial analyses of cancer risk, the residence at diagnosis is typically used as a surrogate for unknown environmental exposures, defined broadly to include lifestyle factors as well as pollutants. However, due to the long latency, or lag time, between exposure to a relevant risk factor and diagnosis of cancer, and due to residential mobility, it is reasonable to believe that residential locations many years before cancer diagnosis are potentially more relevant for cancer risk. Researchers in geography (Bentham, 1988; Han et al., 2004; Sabel et al., 2009) and public health (Jacquez et al., 2005; Paulu et al., 2002; Vieira et al., 2005) have recognized the importance of population mobility when studying disease patterns. Ignoring migration when studying health outcomes with long latencies can lead to exposure misclassification, biased risk estimates, and diminished study power (Tong, 2000).

When analyzing cancer risk in epidemiologic studies which include data on residential histories, one may use historic residential locations for individuals to study spatial risk over time. Residential histories can be informative for both the location and the timing of potential environmental exposures associated with residential locations, which is especially useful when the average latency for a cancer with suspected environmental causes is unknown. In such an analysis, one can adjust for known or suspected risk factors that are typically collected in epidemiologic studies and then examine the unexplained risk for spatial-temporal patterns (Kelsall and Diggle, 1998). Researchers have conducted this type of research using generalized additive models (GAMs) and residential histories for several cancers (Vieira et al., 2005; Webster et al., 2006; Wheeler et al., 2011). Researchers have either used all the residential locations available for each subject to estimate one risk surface without modeling lag times (Vieira et al., 2005; Webster et al., 2006) or have estimated a spatial risk surface for one time period or lag time in a model for several time periods of interest, yielding a different risk surface for each model (Vieira et al., 2008; Wheeler et al., 2011). Using residential histories, it should be possible to model spatial risk surfaces at several different times together in one model. Such an approach can be thought of as providing an estimate of unmeasured life-course environmental exposures, which is in concordance with the increasing popular vision in epidemiology of the “exposome” that seeks to characterize the totality of environmental exposures for disease risk (Rappaport and Smith, 2010; Wild, 2005). The rationale is that relevant cumulative environmental exposures could occur over multiple residential locations across time and models should attempt to encompass such life-course environmental exposures.

The research presented in this paper extends earlier work (Wheeler et al., 2011) to include multiple residential locations per subject in one model of the spatial variation of non-Hodgkin lymphoma risk in a population-based case-control study with residential histories. The objective of this research was to consider different approaches to modeling spatial variation in cancer risk using multiple residential locations per subject and assess the impact of allowing for a more cumulative measure of spatial risk. We used an analysis approach based on generalized additive models with several spatial smoothing functions to model residual spatial variation in cancer risk at multiple exposure times jointly after adjusting for known risk factors. We analyzed the cumulative spatial risk of NHL in one of the four study centers, Los Angeles, of the case-control study.

Methods

Study population

The National Cancer Institute (NCI)-Surveillance, Epidemiology and End Results (SEER) NHL study is a case-control study of 1,321 cases aged 20 to 74 years that were diagnosed between July 1, 1998 and June 30, 2000 in four SEER cancer registries, including Detroit, Iowa, Seattle, and Los Angeles County. The study has been described previously (Chatterjee et al., 2004; Morton et al., 2008; Wheeler et al., 2011). Briefly, population controls (1,057) were selected from residents of the SEER areas using random digit dialing (<65 years of age) or Medicare eligibility files (65 and over) and were frequency matched to cases by age (within 5-year groups), sex, race, and SEER area. Among eligible subjects contacted for an interview, 76% of cases and 52% of controls participated in the study. Cases and controls with a history of NHL or known HIV infection were not included in the study. The goal of the NCI-SEER NHL study was to investigate potential environmental and genetic risk factors for NHL.

Computer-assisted personal interviews were conducted during a visit to each subject’s home to obtain lifetime residential and occupational histories, medical history, and other information including date of birth, gender, race, education, and pest treatments including home treatment for termites before 1988 (a surrogate for the insecticide chlordane). Written informed consent was obtained during the home visit and human subjects review boards approved the study at the NCI and at all participating institutions. Historic addresses were collected in a residential history section of an interviewer-administered questionnaire. Participants were mailed a residential calendar in advance of the interview and were requested to provide the complete address of every home in which they lived from birth to the current year, listing the years they moved in and out (De Roos et al., 2010). Interviewers reviewed the residential calendar with respondents and probed to obtain missing address information. Residential addresses were matched to geographic address databases to yield geographic coordinates that were used in this analysis.

Our previous analysis of spatial risk in NHL in the four study centers found that the lag time with the most significant association with risk overall was 20 years before diagnosis. Among the four study areas, this lag period was most statistically significant for the Los Angeles study center (Wheeler et al., 2011). Therefore, we have focused our analysis on this lag time in the Los Angeles study area (Figure 1). In previous work, we limited the analysis to subjects residing in one of the study areas for at least 20 years prior to study enrollment to maximize the power to detect local variation in spatial risk within each center at different lag times. Retaining this selection criterion for consistency, we analyzed 190 cases and 161 controls in the Los Angeles study area.

Figure 1.

Figure 1

Open in a new tab

The study area of Los Angeles County.

Statistical analysis

Single lag

Our main interest in this research is modeling the spatial variation in disease risk, or the spatial risk function, after adjusting for known risk factors. Risk can be estimated for a rare disease in a case-control study through the odds ratio. There are several useful references for modeling spatial variation in risk based on spatial point pattern theory (Diggle, 2003; Kelsall and Diggle, 1995; Kelsall and Diggle, 1998), and we refer readers to those references for more details. Our discussion focuses on a GAM-based approach to model spatial variation on in risk. Consider i = 1,…, n subjects located within a region A, each with known residential location sit at a particular lag time t and a binary label Yi for NHL case status. Defining the spatial risk function as r(s), equal to the probability that a person at location s will be a case, we can define the general spatial log-odds function as l(s) = log[r(s)/{1−r(s)}] and model the log-odds of disease through a crude generalized additive model as

log[P(Yi=1)/P(Yi=0)]=α+lt(sit), (1)

or an adjusted model

log[P(Yi=1)/P(Yi=0)]=α+Xiβ+lt(sit), (2)

which adjusts for covariates Xi parametrically and includes a nonparametric term for the spatial log-odds using residential locations at lag time t. The spatial log-odds is a function of spatial coordinates, eastings and northings, and models residual spatial variation in risk. The residential locations at only one time are used in this spatial log-odds specification. The residual odds ratio surface can be calculated through the spatial log-odds and the mean of the spatial log-odds by exp[l(s)-l̄]

We chose to use two different forms of the spatial log-odds function: a locally weighted scatterplot smoother (LOESS; Cleveland and Devlin, 1988) and a thin plate regression spline (TPRS) smoother (Wood, 2006). A LOESS smoother has been used previously in a GAM to model spatial variation in risk (Vieira et al., 2005; Webster et al., 2006; Wheeler et al., 2011), and the thin plate regression spline is a computationally efficient alternative. A GAM with a bivariate LOESS smoother has been found to have greater power and sensitivity to detect areas of elevated risk when compared with the popular local spatial scan statistic (Young et al., 2010). There is a spatial span parameter to estimate in LOESS and several smoothing parameters to estimate in a thin plate regression spline. We selected the span parameter in LOESS by minimizing the Akaike Information Criterion (AIC; Akaike, 1973) and estimated the smoothing parameters in the thin plate regression spline by minimizing the un-biased risk estimator (UBRE; Craven and Wahba, 1979), which is effectively a linear transformation of the AIC (Wood, 2006). We used the R (R Development Core Team 2010) packages gam version 1.04.1 (http://cran.r-project.org/web/packages/gam) and mgcv version 1.7-6 (http://cran.r-project.org/web/packages/mgcv) to fit the LOESS and the thin plate regression spline approaches, respectively.

For the parametric part of the log-odds in equation (2), we included the following covariates: age at enrollment, gender (male versus female), race (nonwhite versus white), education (<12 years [referent level], 12-15 years, >15 years), and home termite treatment before 1988 (surrogate for chlordane use). These covariates did not vary over time in the models. In addition to adjusted models, we estimated crude spatial models as a comparison.

A null hypothesis of primary interest in this setting is that the risk is constant over space, r (s) = r. One can evaluate the significance of the overall spatial variation in risk at a particular lag time for the LOESS or thin plate regression spline smoothers using a p-value from an analysis of deviance of nested models, where the test is approximately chi-square distributed (Hastie and Tibshirani, 1990). For the thin plate regression spline, another option is to use the p-value from an approximate chi-square test of the smoothing parameters being equal to zero, although the p-values are typically underestimated with penalized splines when the smoothing parameters are estimated (Wood, 2006). Alternatively, for both smoothing functions, one could use a permutation test based on repeated randomization of the case labels to evaluate both the overall and local significance of the spatial log-odds (Waller and Gotway, 2004). Random labeling of subjects as cases or controls is equivalent to the null hypothesis of constant risk over space (Diggle, 2003). The local log-odds or odds ratio, calculated at each data point or predicted for each cell of an overlaid grid, are regarded as statistically significant if they are outside the 2.5% and 97.5% ranked values from the local permutation distribution built from a large number of Monte Carlo randomizations of case labels and re-estimation of model parameters.

The overall p-values from permutation tests have been shown to be less biased than those based on analysis of deviance (Young et al., 2011). Among the different types of permutation tests, the unconditional permutation test has been shown to be unbiased, whereas the conditional permutation test has an inflated type I error (Young et al., 2011). In an unconditional permutation test, the smoothing parameters are estimated for each Monte Carlo randomization of the data, but in a conditional permutation test the smoothing parameters estimated from the observed data are applied in the smoothing of the randomized data. We used the unconditional permutation test in this analysis. We found the unconditional permutation test with the thin plate regression spline to be considerably more computationally efficient than with LOESS.

Multiple lags

In a previous study, we used a GAM with a LOESS and a conditional permutation test to select the most significant (smallest overall analysis of deviance p-value) time lag in equations (1) and (2) from among residential locations 5, 10, 15, and 20 years before diagnosis, with these times chosen a priori as potentially etiologically relevant latencies for NHL. We found that a time lag of 20 years best explained NHL risk overall in the SEER centers (Wheeler et al., 2011). To better model cumulative unmeasured environmental exposures, here we treated the time lag of 20 years as the base spatial risk component and included additional spatial risk components for other time lags. We considered three approaches. The simplest approach was to add a smoothing function for each time lag of interest in the model for log-odds

g(μi)=α+Xiβ+f1(ut1i,vt1i)+f2(ut2i,vt2i)+…+f5(ut5i,vt5i), (3)

where f1 is the bivariate smoothing function of residential locations at lag 20 years, f2 is the smoother for lag 15 years, f5 is the smoother for time at diagnosis, and g is the logit link function. Given that the majority of study subjects did not move over the span of 20 years (Figure 2), there would be potentially strong correlation between spatial log-odds surfaces at different lags. We addressed this issue by using for the smoothing function a thin plate regression spline with a ridge-type shrinkage penalty, which can shrink some terms to zero (Wood, 2006). The ridge penalty effectively adds a small multiple of the identity matrix to the penalty matrix of the smooth.

Figure 2.

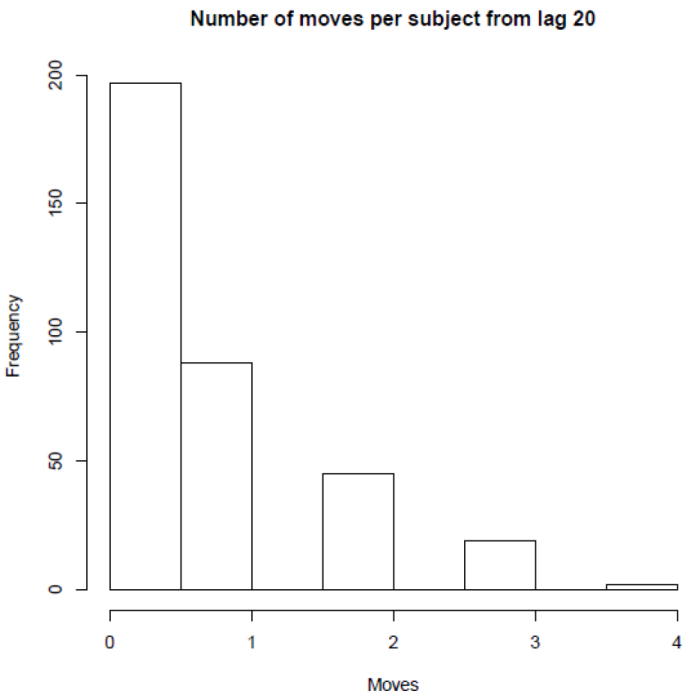
Figure 2

Open in a new tab

Number of residential changes per subject in a time span of 20 years before study enrollment in Los Angeles, starting at a time lag of 20 years before diagnosis and evaluating change of residence at five-year increments.

Alternatively, we specified a model that included only the residences that changed over time for each subject from the base time of 20 years before diagnosis in the additional smoothing terms. We used an indicator variable zti for each spatial term and subject that equaled 1 if a subject changed residence from the previous lag time and 0 otherwise. This is similar to a variable coefficient model (Hastie and Tibshirani, 1993), where smooths are multiplied by a known covariate. The log-odds model is then

g(μi)=α+Xiβ+f1(ut1i,vt1i)+f2(ut2i,vt2i)z2i+…+f5(ut5i,vt5i)z5i, (4)

where the smoothing functions are defined for the same times as in equation (3) and z2i indicates a change in residential location from lag 20 years to lag 15 years, etc. We call this the residential change model.

Another approach is to weight each residential location by residential duration using wti, which equals the duration spent by each subject at the residential location at lag t divided by the total time in the study area. This results in log-odds model

g(μi)=α+Xiβ+f1(ut1i,vt1i)w1i+f2(ut2i,vt2i)w2iz2i+…+f5(ut5i,vt5i)w5iz5i, (5)

where w1i is the proportion of time spent at the residence at lag 20 years for the ith subject, and all other terms are as previously defined. We call this the duration-weighted residential change model.

The significance of individual or groups of spline-smoothed lag functions can be evaluated with the approximately chi-square p-value from an analysis of deviance of nested models. For individual functions one may also use the approximately chi-square p-value from a test of the smoothing parameters equal to zero. However, confidence intervals for the linear predictor and model component functions from simulation studies show that it is easier to estimate the overall smoothing correctly than it is the smoothing parameters for individual model components (Wood, 2006). In addition, these approximate chi-square p-values are known to be biased (Wood, 2006; Young et al., 2011). Therefore, a permutation-based p-value would be preferred to evaluate the overall and local significance of individual and groups of spatial log-odds components. The goodness-of-fit of models with different specifications of spatial risk can be compared using the AIC, and we use this criterion.

Results and Discussion

As an initial comparison, we calculated the p-values from an analysis of deviance and an unconditional permutation test for the deviance for crude and adjusted GAMs with LOESS or TPRS smoothers for the four lags of interest and at the time of diagnosis of NHL in Los Angeles (Table 1). Overall, the lag time of 20 years yielded the most significant decrease in model deviance. For the crude models, lag 20 was the only lag significant at the traditional 0.05 level with both types of test and with both smoothing functions. In the adjusted models, only lag 20 was significant in both tests with the TPRS smoother. Lag 20 was marginally significant with the LOESS GAM. The result of lag 20 years as the most significant is consistent with previous findings using only a LOESS model with an earlier version of the gam package (Wheeler et al., 2011). The p-values were generally substantially larger in the adjusted models compared with the crude models, suggesting that the risk factors explained a substantial amount of the spatial variation in NHL risk. However, the significance of the lag 20 spatial smooth suggests there is local residual variation that is not fully accounted for by the risk factors in the model. P-values were also larger with the unconditional permutation test than with the chi-square test, as expected given the bias in the chi-square p-values.

Table 1.

Approximate chi-square or unconditional permutation test p-values for crude or adjusted GAMS with LOESS or thin plate regression spline smoothers for the spatial log-odds.

Lag Crude Adjusted
LOESS TPRS LOESS TPRS
Chi-sq Perm Chi-sq Perm Chi-sq Perm Chi-sq Perm
20 0.005 0.048 0.001 0.002 0.057 0.084 0.009 0.026
15 0.021 0.075 0.017 0.075 0.376 0.648 0.189 0.511
10 0.017 0.030 0.072 0.155 0.460 0.684 0.268 0.564
5 0.138 0.207 0.180 0.275 0.672 0.865 0.613 0.770
0 0.166 0.256 0.080 0.164 0.712 0.880 0.570 0.749
Open in a new tab

Chi-sq = approximate chi-square test; Perm = unconditional permutation test; LOESS = locally weighted scatterplot smoother; TPRS = thin plate regression spline.

Adjusted models include age at enrollment, gender, race, education, and home termite treatment before 1988.

Both the TPRS and LOESS crude and adjusted models detected local areas of significantly elevated risk in a large northwestern portion of Los Angeles County including Santa Clarita and a smaller area southwest of the city of Los Angeles at a lag of 20 years. The spatial log-odds from the LOESS and TPRS adjusted models are shown in Figure 3. The gaps in the spatial log-odds surface occur in areas without data, and model predictions were not calculated in these areas. In addition to areas of elevated risk, there was one area of significantly lowered risk detected just east of Los Angeles by both the LOESS and TPRS models and several others detected by the TPRS model in the eastern half of the county. A finding of elevated risk in areas west and northwest of the city of Los Angeles is consistent with results from a previous study of NHL cases from the Los Angeles SEER registry from 1972 to 1998 by census tract (Mack, 2004). No areas of significantly elevated residual risk were found in shorter time lags. Comparing the goodness-of-fit of the smoothing models for the most significant lag of 20 years, the AIC for the TPRS model was meaningfully lower than for the LOESS model in both crude (478.2 versus 481.8) and adjusted (487.4 versus 491.0) models. Therefore, we favored the TPRS GAM in this case and used it exclusively in the multiple lag models.

Figure 3.

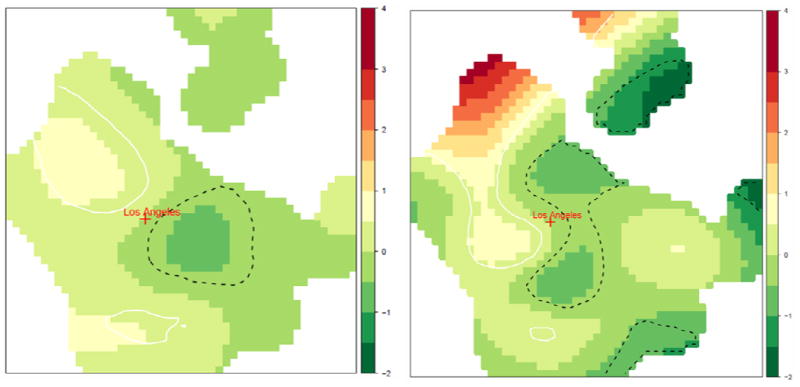
Figure 3

Open in a new tab

Spatial log-odds from the LOESS adjusted (left) and TPRS adjusted (right) models of non-Hodgkin lymphoma risk 20 years before diagnosis in Los Angeles County. Areas of significantly elevated (lowered) residual log-odds are outlined with light solid (dark dashed) lines.

The AIC values for different specifications of the spatial log-odds using a TPRS smoother, including multiple lags, revealed significant differences in goodness-of-fit between adjusted models (Table 2). A model with all lags of interest included with a ridge penalty (equation 3), a full residential change model (equation 4), and a full duration-weighted residential change model (equation 5) all had significantly better goodness-of-fit than a model with only a lag of 20 years. The duration-weighted lag 20 model also improved upon the fit of the lag 20 model, but less substantially. The full duration-weighted residential change model had the best goodness-of-fit, followed closely by the residential change model; there was not a meaningful difference in goodness-of-fit between these two models. The biggest difference in AIC values (>12) was between models that specified residential change and those that did not, indicating that attempting to better model cumulative environmental exposures while reducing redundancy in data best explained variation in NHL risk. According to the analysis of deviance p-values for these models (Table 2), the model with each spatial smoothing function or set of functions significantly lowered the deviance of the model without the smoothing term(s). This is particularly true for the residential change and duration-weighted residential change models with multiple lags, which had the lowest p-values.

Table 2.

AIC values and analysis of deviance p-values for adjusted models with different specifications of the spatial log-odds. Analysis of deviance is between models with and without the terms of interest.

Model AIC p-value
Lag 20 487.4 0.0086
Duration-weighted lag 20 485.3 0.0057
All lags 482.3 0.0109
Full residential change 469.9 <0.0001
Full duration-weighted residential change 468.3 <0.0001
Open in a new tab

Models are adjusted for age at enrollment, gender, race, education, and home termite treatment before 1988.

While improving the goodness-of-fit of the lag 20 model, the residential change model augmented the estimated spatial variation in risk, as evidenced in maps of the estimated spatial log-odds (Figure 4). The spatial log-odds were larger in magnitude in some areas with the residential change model, compared with the lag 20 model. This is especially clear in the northwest part of the county, where spatial risk was highest. This is an area with relatively few subjects at lag 20, and including residential change in the model allowed more cases to appear over time and strengthened the association between place and risk of NHL. This result could indicate a persistent environmental risk factor in this particular area. The value of the spatial log-odds was decreased in the northeast part of the county, where risk was low. Risk was also decreased in small areas south of the city of Los Angeles and in an area well east of the city when using the residential change model. Overall, the residential change model reinforced the pattern of most elevated and lowered risk shown at a lag time of 20 years, but also allowed very localized increases or decreases in the odds of NHL to appear over time in this case.

Figure 4.

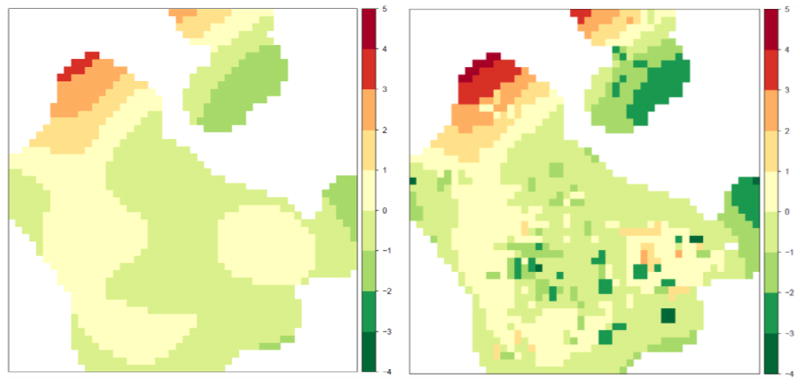
Figure 4

Open in a new tab

Spatial log-odds for a spline smooth at time lag 20 years from an adjusted model (left) and spatial log-odds from an adjusted residential change model with time lags of 20, 15, 10, and 5 years and at time of enrollment (right).

Though we were focused on the cumulative spatial log-odds, it is interesting to visualize the individual spatial log-odds components for the residential change model at several lags of interest. The spatial smooths for lags 20, 15, and 10 years and at time of diagnosis show different spatial patterns amongst themselves (Figure 5). The spatial smooth for lag 20 looks familiar, showing the same general pattern as in Figure 3, but the smooths for the other three times show deviations from the lag 20 pattern. The lag 15 spatial component demonstrates a trend of increasing log-odds increasing east to west. These components overall exhibit more spatial pattern than the components from the penalized all-lags model (results not shown), where the component for lag 10 years was zeroed out through the ridge penalty in the TPRS.

Figure 5.

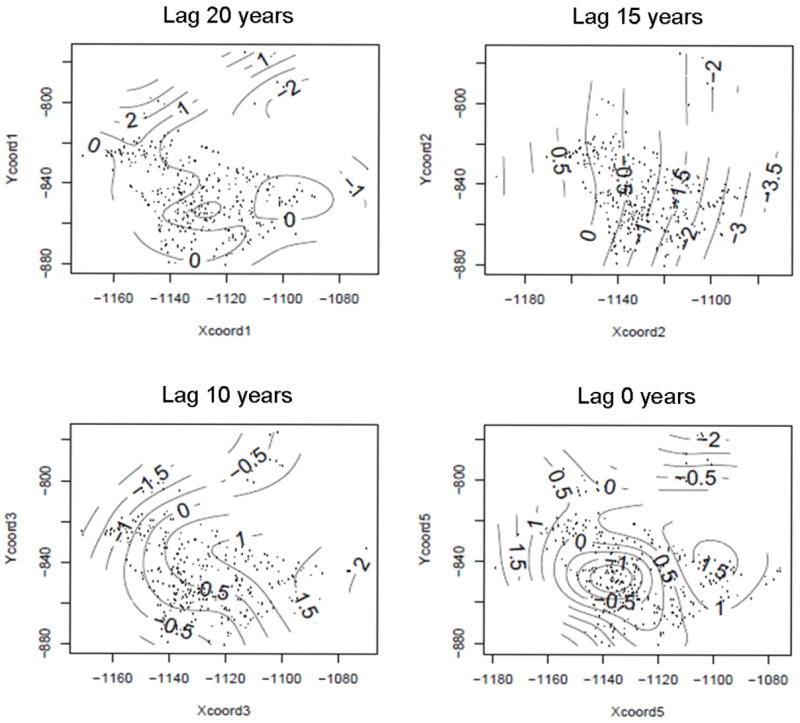
Figure 5

Open in a new tab

Individual spatial smooths of residential locations at time lags 20, 15, and 10 years before diagnosis and at time of enrollment from an adjusted residential change model with all smoothing components included.

Strengths of our study include using a population-based case control study with residential histories and drawing on the residential histories to consider multiple locations of potential environmental exposures per subject in models with different specifications of the spatial log-odds function. A limitation of our analysis is the constraint on long-term residential status within the study area, which originated from the motivation to investigate potential environmental exposures specific to the study area over time. Findings will not necessarily generalize when including all subjects, some of which would have resided in the study area only a short time. We will consider loosening this constraint to include shorter-term residents in future work; the residential change model provides the means to do so. A potential limitation of our analysis is possible differential recall bias among cases and controls, although it seems unlikely that cases and controls recalled previous addresses differentially. Another limitation is potential selection bias due to low response rates. However, our previous comparative spatial analysis of study participants and all eligible cases and controls at the time of study enrollment suggested that response bias was not responsible for areas of significantly elevated risk detected among study participants (Wheeler et al., 2011). We also note that the factors that may explain areas identified as elevated risk may be behavioral/lifestyle or demographic and not related to environmental pollutants.

While we found that the TPRS smoother provided better goodness-of-fit than LOESS, this will likely not always be the case. We plan to perform a simulation study of these smoothing approaches to compare their performance. Other areas for future research include conducting a simulation study for multiple comparisons in GAMs and developing a randomization procedure to evaluate the significance of multiple spatial log-odds components.

Conclusions

We used generalized additive regression models with two nonparametric smoothers of historic residential locations to explore spatial-temporal patterns in NHL risk in Los Angeles County. The results verified earlier results that a time lag of 20 years before diagnosis best explained variation in NHL risk and that there were areas of significantly elevated and lowered risk in Los Angeles County. Also, the thin plate regression spline generalized additive model had better goodness-of-fit than the LOESS model. In addition to the improved goodness-of-fit in this case, the thin plate regression spline approach offers the flexibility to model risk cumulatively over space and time by including multiple lags in the model. This recognizes the possibility that environmental exposures occur at more than one residential location. A ridge-type shrinkage penalty can be added to the smoothing function to reduce the effect of correlation in smoothed terms due to subjects who exhibit low mobility. Alternatively, and yielding better goodness-of-fit in this case, one can include only the residences that changed from the previous residence lag time using an indicator variable. Using this approach should enable researchers to explore more cumulative spatial variation in cancer risk over time while adjusting for known risk factors and allowing for population mobility.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Akaike H. Information theory and an extension of the maximum likelihood principle. In: Petrow B, Csake F, editors. Second international symposium on information theory. Budapest, Hungary: Akademiai Kiado; 1973. pp. 267–281. [Google Scholar]
  2. Alexander F. Viruses, clusters, and clustering of childhood leukaemia: a new perspective? European Journal of Cancer. 1993;29A:1424–43. doi: 10.1016/0959-8049(93)90016-9. [DOI] [PubMed] [Google Scholar]
  3. Bentham G. Migration and morbidity: implications for geographical studies of disease. Soc Sci Med. 1988;26:49–54. doi: 10.1016/0277-9536(88)90044-5. [DOI] [PubMed] [Google Scholar]
  4. Bithell JF, Vincent TJ. Geographical variations in childhood leukaemia incidence. In: Elliot P, Wakefield JC, Best NG, Briggs DJ, editors. Spatial epidemiology: methods and applications. New York: Oxford University Press; 2000. pp. 317–332. [Google Scholar]
  5. Chatterjee N, Hartge P, Cerhan JR, Cozen W, Davis S, Ishibe N, et al. Risk of non-Hodgkin’s lymphoma and family history of lymphatic, hematologic, and other cancers. Cancer Epidemiol Biomarkers Prev. 2004;13(9) [PubMed] [Google Scholar]
  6. Cleveland WS, Devlin S. Locally-weighted regression: an approach to regression analysis by local fitting. JASA. 1988;83:596–610. [Google Scholar]
  7. Craven P, Wahba G. Smoothing noisy data with spline functions. Numerische Mathematik. 1979;31:377–403. [Google Scholar]
  8. De Roos AJ, Davis S, Colt JS, Blair A, Airola M, Severson RK, et al. Residential proximity to industrial facilities and risk of non-Hodgkin lymphoma. Environ Res. 2010;110:70–8. doi: 10.1016/j.envres.2009.09.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Diggle PJ. Statistical analysis of spatial point patterns. second edition. London: Edward Arnold; 2003. [Google Scholar]
  10. Han D, Rogerson PA, Nie J, Bonner MR, Vena JE, Vito D, et al. Geographic clustering of residence in early life and subsequent risk of breast cancer (United States) Cancer Causes and Control. 2004;15:921–9. doi: 10.1007/s10552-004-1675-y. [DOI] [PubMed] [Google Scholar]
  11. Hastie TJ, Tibshirani R. Generalized additive models. London: Chapman & Hall; 1990. [Google Scholar]
  12. Hastie TJ, Tibshirani R. Varying-coefficient models (with discussion) JRSSB. 1993;55:757–96. [Google Scholar]
  13. Jacquez GM, Meliker JR, AvRuskin GA, Goovaerts P, Kaufmann A, Wilson ML, et al. Case-control geographic clustering for residential histories accounting for risk factors and covariates. Int J Health Geogr. 2006;5(32) doi: 10.1186/1476-072X-5-32. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Jacquez GM, Kaufmann A, Meliker JR, Goovaerts P, AvRuskin GA, Nriagu J. Global, local and focused geographic clustering for case-control data with residential histories. Environmental Health. 2005;4:4. doi: 10.1186/1476-069X-4-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Kelsall JE, Diggle PJ. Non-parametric estimation of spatial variation in relative risk. Statistics in Medicine. 1995;14:2335–42. doi: 10.1002/sim.4780142106. [DOI] [PubMed] [Google Scholar]
  16. Kelsall JE, Diggle PJ. Spatial variation in risk of disease: A nonparametric binary regression approach. Applied Statistics. 1998;47:559–73. [Google Scholar]
  17. Linet MS, Devesa SS, Morgan GJ. The leukemias. In: Schottenfeld D, Fraumeni JF Jr, editors. Cancer epidemiology and prevention. third edition. New York: Oxford University Press; 2006. pp. 841–871. [Google Scholar]
  18. Mack TM. Cancers in the urban environment. San Diego: Elsevier Academic Press; 2004. [Google Scholar]
  19. Morton LM, Wang SS, Cozen W, Linet MS, Chatterjee N, Davis S, et al. Etiologic heterogeneity among non-Hodgkin lymphoma subtypes. Blood. 2008;112(13):5150–60. doi: 10.1182/blood-2008-01-133587. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Paulu C, Aschengrau A, Ozonoff D. Exploring associations between residential location and breast cancer incidence in a case-control study. Environmental Health Perspectives. 2002;110:471–8. doi: 10.1289/ehp.02110471. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. R Development Core Team. R: A language and environment for statistical computing. R Foundation for Statistical Computing; Vienna, Austria: 2010. [Google Scholar]
  22. Rappaport SM, Smith MT. Environment and disease risks. Science. 2010;330:460–1. doi: 10.1126/science.1192603. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Sabel CE, Boyle PJ, Raab G, Loytonen M, Maasilta P. Modelling individual space-time exposure opportunities: a novel approach to unravelling the genetic or environmental disease causation debate. Spatial and Spatio-temporal Epidemiology. 2009;1:85–94. doi: 10.1016/j.sste.2009.07.002. [DOI] [PubMed] [Google Scholar]
  24. Silverman DT, Devesa SS, Moore LE, Rothman N. Bladder cancer. In: Schottenfeld D, Fraumeni JF Jr, editors. Cancer epidemiology and prevention. third edition. New York: Oxford University Press; 2006. pp. 1101–27. [Google Scholar]
  25. Spitz MR, Wu X, Wilkinson A, Wei Q. Cancer of the lung. In: Schottenfeld D, Fraumeni JF Jr, editors. Cancer epidemiology and prevention. third edition. New York: Oxford University Press; 2006. pp. 638–58. [Google Scholar]
  26. Tong S. Migration bias in ecologic studies. European Journal of Epidemiology. 2000;16:365–9. doi: 10.1023/a:1007698700119. [DOI] [PubMed] [Google Scholar]
  27. Vieira V, Webster T, Weinberg J, Aschengrau A, Ozonoff D. Spatial analysis of lung, colorectal, and breast cancer on Cape Cod: an application of generalized additive models to case-control data. Environmental Health. 2005;4:11. doi: 10.1186/1476-069X-4-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Vieira VM, Webster TF, Weinberg JM, Aschengrau A. Spatial-temporal analysis of breast cancer in upper Cape Cod. Vol. 7. Massachusetts: 2008. p. 46. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Waller LA, Gotway CA. Applied spatial statistics for public health data. New York: John Wiley; 2004. [Google Scholar]
  30. Webster T, Vieira V, Weinberg J, Aschengrau A. Method for mapping population-based case-controls studies: an application using generalized additive models. International Journal of Health Geographics. 2006;5:26. doi: 10.1186/1476-072X-5-26. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Wheeler DC. A comparison of spatial clustering and cluster detection techniques for child-hood leukemia incidence in Ohio, 1996-2003. Int J Health Geogr. 2007;6(13) doi: 10.1186/1476-072X-6-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Wheeler DC, De Roos AJ, Cerhan JR, Morton LM, Severson R, Cozen W, et al. Spatial-temporal cluster analysis of non-Hodgkin lymphoma in the NCI-SEER NHL Study. Environ Health. 2011;10:63. doi: 10.1186/1476-069X-10-63. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Wild CP. Complementing the genome with an “exposome”: the outstanding challenge of environmental exposure measurement in molecular epidemiology. Cancer Epidemiol Biomarkers Prev. 2005;14(8):1847–50. doi: 10.1158/1055-9965.EPI-05-0456. [DOI] [PubMed] [Google Scholar]
  34. Wood SN. Generalized additive models: an introduction with R. Boca Raton, FL: Chapman & Hall/CRC; 2006. [Google Scholar]
  35. Young RL, Weinberg J, Vieira V, Ozonoff A, Webster TF. A power comparison of generalized additive models and the spatial scan statistic in a case-control setting. Int J Health Geogr. 2010;9:37. doi: 10.1186/1476-072X-9-37. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Young RL, Weinberg J, Vieira V, Ozonoff A, Webster TF. Genealized additive models and inflated type I error rates of smoother significance tests. Computational Statistics and Data Analysis. 2011;55:366–74. doi: 10.1016/j.csda.2010.05.004. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES