Delay Discounting in Lewis and Fischer 344 Rats: Steady-state and Rapid-determination Adjusting-amount Procedures

Abstract

Lewis rats have been shown to make more impulsive choices than Fischer 344 rats in discrete-trial choice procedures that arrange fixed (i.e., nontitrating) reinforcement parameters. However, nontitrating procedures yield only gross estimates of preference, as choice measures in animal subjects are rarely graded at the level of the individual subject. The present study was designed to examine potential strain differences in delay discounting using an adjusting-amount procedure, in which distributed (rather than exclusive) choice is observed due to dynamic titration of reinforcer magnitude across trials. Using a steady-state version of the adjusting-amount procedure in which delay was manipulated between experimental conditions, steeper delay discounting was observed in Lewis rats compared to Fischer 344 rats; further, delay discounting in both strains was well described by the traditional hyperbolic discounting model. However, upon partial completion of the present study, a study published elsewhere (Wilhelm & Mitchell, 2009) demonstrated no difference in delay discounting between these strains with the use of a more rapid version of the adjusting-amount procedure (i.e., in which delay is manipulated daily). Thus, following completion of the steady-state assessment in the present study, all surviving Lewis and Fischer 344 rats completed an approximation of this rapid-determination procedure in which no strain difference in delay discounting was observed.

Delay discounting describes the systematic decrease in reinforcer value with increasing delay (for a review, see Madden & Johnson, 2010). Here, value is operationalized simply as the efficacy of a delayed reinforcer when a smaller, immediate reinforcer is available. Steep declines in reinforcer value reflect a strong preference for smaller, immediate reinforcers over larger, delayed reinforcers—a pattern of choice widely described as “impulsivity” (Ainslie, 1975; Rachlin & Green, 1972). In all species tested thus far, the extent to which reinforcer value is discounted as a function of delay is well-described by the hyperbolic function:

in which V is reinforcer value, A is reinforcer amount, D is reinforcer delay, and the free parameter k provides an index of the degree of discounting (Mazur, 1987).

In humans, steep delay discounting covaries with a wide range of addictive behavior, including substance dependence and pathological gambling (for a review, see MacKillop et al., 2011). In rats, degree of delay discounting predicts greater self-administration of methylphenidate and alcohol (Marusich & Bardo, 2009; Poulos, Le, & Parker, 1995), more rapid response acquisition and escalation of cocaine self-administration (e.g., Anker, Perry, Glidden, & Carroll, 2009; Perry, Larson, German, Madden, & Carroll, 2005; Perry, Nelson, & Carroll, 2008), and higher progressive-ratio breakpoints for self-administered nicotine (Diergaarde et al., 2008). Steep delay discounting also predicts greater locomotoric sensitization—a potential marker of abuse vulnerability (Robinson & Berridge, 1993)—to d-amphetamine in rats (reported in Perry & Carroll, 2008) and ethanol in mice (Mitchell, Reeves, Li, & Phillips, 2006).

Because a complete account of behavior requires knowledge of the role played by biological variables in environment–behavior relations (Skinner, 1981), understanding the relation between delay discounting and the problem clinical behavior with which it covaries requires further investigation of the biological determinants of delay discounting. In this regard, behavioral comparisons between two or more inbred rat strains that differ along specific neurochemical dimensions provides one method for studying such biological determinants. At least five previous studies have shown that Lewis rats make more impulsive choices than Fischer 344 rats in discrete-trial choice procedures (Anderson & Diller, 2010; Anderson & Woolverton, 2005; García-Lecumberri et al., 2010; Huskinson, Krebs, & Anderson, 2012; Madden, Smith, Brewer, Pinkston, & Johnson, 2008).

These strain differences are consistent with the hypothesis that dopamine (DA) or serotonin (5-hydroxytryptamine, 5-HT) function mediates delay discounting (for a review, see Winstanley, 2010) because Lewis rats, compared to Fischer 344 rats, exhibit deficits in several brain regions thought to govern reinforcement. For example, Lewis rats have fewer DA transporters in the nucleus accumbens core (e.g., Flores, Wood, Barbeau, Quirion, & Srivastava, 1998), fewer DA D₂ and D₃ receptors in the nucleus accumbens shell (e.g., Flores et al., 1998), and lower levels of tyrosine hydroxylase (a protein responsible for the synthesis of DOPA) in the nucleus accumbens (Beitner-Johnson, Guitart, & Nestler, 1991). Lewis rats also exhibit lower levels of 5-HT and fewer accumbal 5-HT receptors in the nucleus accumbens (Selim & Bradberry, 1996), lower levels of 5-HT binding in the frontal cortex and hippocampus, and lower levels of tryptophan hydroxylase (the rate-limiting enzyme for 5-HT production) in the hippocampus (Chaouloff, Kulikov, Sarrieau, Castanon, & Mormede, 1995).

Taken together, the strain-related behavioral and neurochemical differences between Lewis and Fischer 344 rats further implicate DA and 5-HT as contributors to delay discounting. However, extant studies demonstrating a difference in impulsive choice between these strains have featured assessment procedures that generate near-exclusive choice for the more highly valued of two choice alternatives. In all such studies, repeated choices between smaller, immediate and larger, delayed food reinforcers were arranged (e.g., one food pellet immediately vs. three food pellets after a delay). In four of these five studies (Anderson & Diller, 2010; Anderson & Woolverton, 2005; García-Lecumberri et al., 2010; Huskinson et al., 2012), choice was assessed with a procedure developed by Evenden and Ryan (1996), in which delay to the larger reinforcer increases monotonically across trial blocks within a session. In the fifth study, Madden et al. (2008) used a procedure in which delay is manipulated between discrete experimental conditions following satisfaction of stability criteria. Because the use of fixed reinforcement parameters in such procedures most often results in near-exclusive preference for the more highly valued alternative at each delay (Mazur, 1987, 2010), choice measures from individual subjects approximate a binomial distribution and have relatively few degrees of freedom. Thus, graded preference often emerges only at the group level when data are averaged across multiple subjects. Further, precise quantification of reinforcer value (as in Equation 1), and hence the form of the discounting function, is not possible.

Precise quantification of delay discounting requires a more dynamic procedure that arranges titrating reinforcement parameters between choice alternatives. For example, adjusting-amount procedures arrange repeated choices between smaller, immediate and larger, delayed food reinforcement. Across trials, the immediate reinforcer's magnitude is titrated until indifference is observed (i.e., approximately 50% choice for either alternative). The average titrated reinforcer magnitude at this indifference point provides an index of the value of the larger, delayed reinforcer.

In the steady-state version of the adjusting-amount procedure (Mazur, 2000), delay is manipulated between experimental conditions following a minimum number of sessions and satisfaction of stability criteria. Once choice stabilizes, indifference points are calculated as the average titrated reinforcer magnitude across several stable sessions. The primary purpose of the present study was to determine whether strain differences in impulsive choice between Lewis and Fischer 344 rats would be reproduced using this steady-state adjusting procedure. However, while we were conducting the present study, Wilhelm and Mitchell (2009) reported no significant strain differences in delay discounting between Lewis and Fischer 344 rats using an abbreviated version of an adjusting-amount procedure. Under this rapid-determination procedure (Richards, Mitchell, de Wit, and Seiden, 1997), delay is manipulated pseudorandomly between every session (in the absence of stability criteria), and indifference points are calculated as the average titrated reinforcer magnitude over the final 30 trials (i.e., half session) of the final five sessions at each delay exposure. In the most commonly used version of the rapid-determination procedure, rats typically complete 10-15 training sessions at each delay prior to the final five sessions from which data are obtained (e.g., Kieres et al., 2004; Reynolds, de Wit, & Richards, 2002; Richards et al., 1997; Wade, de Wit, &Richards, 2000). Thus, full discounting functions may be obtained in approximately 75–100 sessions. However, Wilhelm and Mitchell's rats completed just one training session at each delay prior to the final five sessions, yielding full discounting functions in 30 sessions.

Thus, a secondary purpose of the present study was to re-quantify delay discounting in the Lewis and Fischer 344 rats which completed the steady-state adjusting procedure, using an approximation of the rapid-determination procedure (comparable to that used by Wilhelm & Mitchell, 2009). Further, we sought to determine whether the rapid-determination procedure would yield measures of delay discounting that agree with those of the steady-state procedure.

METHOD

Subjects

Steady-state assessment

Experimentally naïve, male Lewis (n  =  8) and Fischer 344 (n  =  8) rats served as subjects. All rats were approximately 90 days old at the start of the experiment. Rats were weighed daily and maintained at approximately 85% free-feeding weight via supplemental feeding approximately 2 hr postsession. Between sessions, rats were housed individually in plastic cages in a temperature- and humidity-controlled environment on a 12-hr light cycle (lights on at 6:00 a.m.). Water was available continuously in the home cages. One Lewis rat died early in assessment and did not contribute to subsequent analyses.

Rapid-determination assessment

Eleven of the rats used in the steady-state assessment (Lewis: n  =  6; Fischer 344: n  =  5) served as subjects in the rapid-determination assessment. All other rats from the steady-state assessment had been euthanized before publication of Wilhelm and Mitchell's (2009) study. Rats were approximately 17 months old at the start of this assessment. All food restriction, supplemental feeding, and housing arrangements were identical to those described for the steady-state assessment.

Apparatus

Six identical operant chambers (Med Associates, St. Albans, VT; Model ENV-001) were used. Each chamber measured 24.1 cm wide, 30.5 cm long, and 21 cm high. One wall of the chamber was an intelligence panel equipped with a center nose-poke operandum (11 cm above the floor) and two nonretractable side levers (2 cm long, 6.5 cm above the floor, 2 cm from each side wall, and horizontally aligned 11 cm apart). The nose-poke aperture was equipped with an infrared beam to detect responses and a 2-W yellow stimulus light. Above each lever was a white 28-volt DC cue light. Chambers were equipped with a 2.5 kHz Sonalert® tone generator mounted on the outside wall of the intelligence panel. Two separate feeders (Coulbourn, Allentown, PA) equipped with infrared pellet detectors (Pinkston, Ratzlaff, Madden, & Fowler, 2008) arranged delivery of 20-mg, grain-based pellets (Bioserv, Frenchtown, NJ) into two separate food receptacles in the center of the intelligence panel (4.5 cm wide, 2.5 cm deep, and 4 cm high; horizontally aligned 0.5 cm apart and 1 cm above the floor). In all phases of the present experiment, each feeder and receptacle arranged pellet deliveries for responses on its associated lever (e.g., left feeder and receptacle, left lever). Each chamber was enclosed within a light- and sound-attenuating cubicle (Med Associates, St. Albans, VT) equipped with a ceiling-mounted ventilation fan and 28-volt house light. A Med Associates® IV interface system with a temporal resolution of 0.01 s controlled the sessions and collected data.

Procedures

Autoshaping and initial training

An autoshaping procedure was used to establish reliable responding on the nose poke and side levers. A different operandum was active during each autoshaping session. Pressing on left and right levers was trained first (order counterbalanced within and between strains), followed by the nose poke. During each session, the light associated with the active operandum was illuminated every 60 s. Following 5 s of illumination, the light was extinguished and one response-independent food pellet was delivered following the minimum delay the software allowed (0.01 s; henceforth referred to as 0 s). During nose-poke sessions, pellets were delivered to both left and right receptacles, strictly alternating between autoshaping trials. Prior to delivery of the response-independent food pellet, rats could earn the reinforcer at any time by responding on the active operandum. In this and all subsequent phases, responses on the inactive operandum provided no consequences. Sessions terminated following 100 food-pellet deliveries. Autoshaping continued until rats earned all 100 reinforcers (i.e., by making an operant response) for two consecutive sessions. Supplemental hand-shaping was used for five Fischer 344 rats and three Lewis rats that did not acquire lever responding within 10 sessions.

Following autoshaping, rats completed five additional 60-trial training sessions. In these sessions, the nose-poke was illuminated every 60 s. A single nose-poke response extinguished the nose-poke light, activated either the right or left lever (strictly alternating between trials), and illuminated its associated cue light. A response on the active lever extinguished the cue light and resulted in the immediate delivery of one food pellet into its associated receptacle (e.g., left lever, left receptacle).

Delay discounting (steady-state assessment)

Delay discounting was assessed using a steady-state adjusting-amount procedure (Mazur, 2000). One session was completed each day, 7 days a week. Each session consisted of 40 choice trials and a variable number of forced-exposure trials, depending on previous choices. The session was terminated after 105 min if all choice trials had not yet been completed. Each choice trial began with the illumination of the house light and nose-poke light; a single nose-poke response extinguished the nose-poke light, activated both side levers, and illuminated their associated cue lights. A single response on either lever extinguished both cue lights, inactivated both levers, and resulted in pellet delivery. Responses on the left lever resulted in the delivery of ten 20-mg food pellets following a delay that varied between conditions. A continuous tone was presented throughout the delay. Responses on the right lever resulted in the immediate delivery of X pellets; X was adjusted between trials depending on previous choices. Selecting the delayed alternative increased X by one pellet on the next trial, whereas selecting the immediate alternative decreased X by one pellet on the next trial. Adjustments occurred with no upper limit and a lower limit of one pellet. A limited-hold 15-s schedule was in effect during each choice trial, such that if a nose-poke response was not made within 15 s of trial onset, the trial terminated and was counted as an omission. Pellet deliveries on all trials were followed by an intertrial interval (ITI) in which no lights or tones were presented. The ITI ensured that the presentation of the next trial always occurred 120 s after the beginning of the previous trial.

Following two consecutive choices of the same lever, a forced-exposure trial was programmed on the opposite lever on the subsequent trial (Richards et al., 1997). This was done to ensure regular contact with the consequences arranged on both levers. Sequence of stimuli presentation on forced-exposure trials was otherwise identical to that described above, with the following exceptions: only one lever and its associated cue light were active, pellet adjustments did not occur, and the limited-hold omission criterion was not in effect. Responses on the inactive lever during forced-choice trials, or during the ITI, were not recorded.

Discounting was assessed at five delays to food reinforcement, manipulated between conditions. All rats were exposed to the same sequence of delays (0, 10, 5, 2.5, and 1.25 s). At the beginning of the first session in each delay condition, the amount initially available on the immediate alternative was six pellets. In all subsequent sessions in that condition, the amount initially available on this alternative was carried over from the last choice trial of the preceding session. Each delay condition lasted a minimum of 400 choice trials (approximately 10 sessions) and until choice met quantitative and visual stability criteria. The final 100 choice trials, divided into ten 10-trial blocks, were used in determining stability. Data were judged stable when (a) the mean adjusted amount in each trial block did not deviate from the grand mean by more than two pellets and (b) there was no visually apparent, monotonic trend. Indifference points for each rat were then calculated as the mean titrated reinforcer magnitude across the final 100 trials of each delay condition.

Delay discounting (rapid-determination assessment)

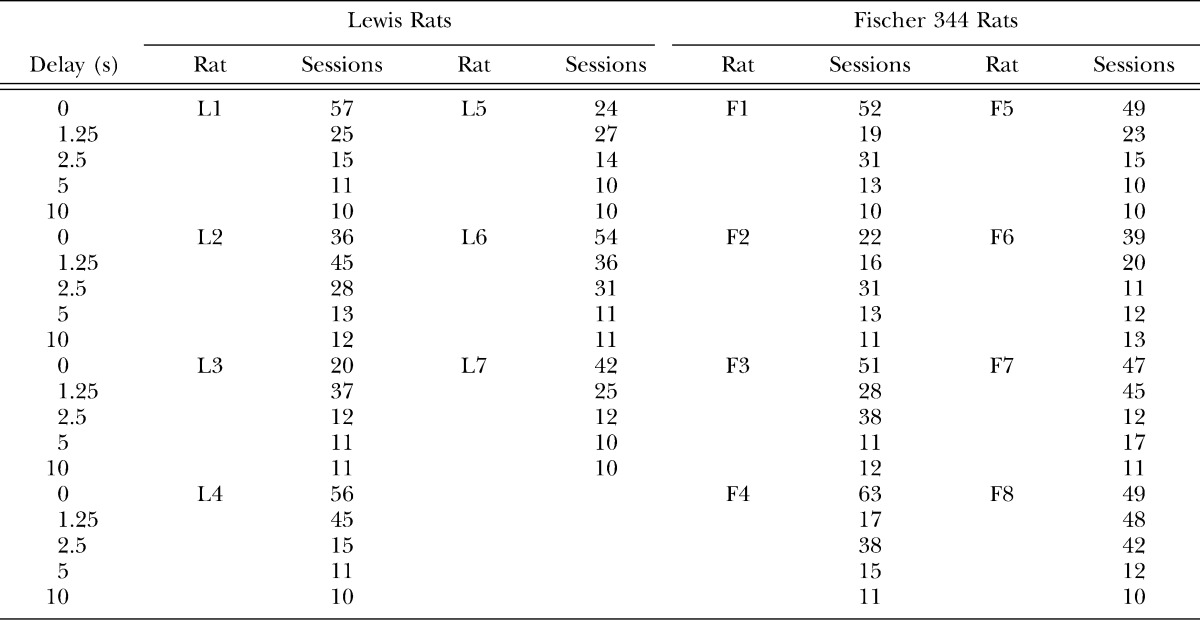
Delay discounting was assessed using a rapid-determination adjusting-amount procedure adapted from the one used by Wilhelm and Mitchell (2009). The procedures were identical to those in the steady-state assessment (above) with the following exceptions. Delays were manipulated daily between sessions, with each delay appearing once in every series of five sessions (order shown in Table 1). Thus, rats were exposed to each delay a total of six times across 30 consecutive days. At the beginning of each of these sessions, the number of pellets available from the immediate alternative was reset to six. Consistent with Wilhelm and Mitchell's study, data from the first series were excluded and only the last five series were analyzed.

Table 1.

Sequence of delays (s) investigated across sessions in the rapid-determination assessment.

By calculating the mean adjustment at each delay over the final five sessions at each delay, Richards et al. (1997) reported that choice approximates indifference during the last half session (Trials 31–60) of their rapid-determination procedure. However, in order to hold constant the number of trials (per session) to which rats were exposed between assessments in the present experiment, we used only 40 trials. Thus, indifference points were calculated as the mean adjusted amount over Trials 31–40 of the last five exposures to a given delay value.

Statistical Analysis

All statistical tests and curve fitting were conducted using GraphPad Prism (version 5.0). For both steady-state and rapid-determination assessments, Equation 1 was fitted to each rat's obtained indifference points, yielding estimates of k that served as our main dependent measure. High k values indicate steeper delay discounting (i.e., reinforcer value is lost more quickly with delay).

To further quantify delay discounting, we calculated area under the empirical discounting curve (AUC) for individual rats within each strain (Myerson, Green & Warusawitharana, 2001). AUC is a theory-free measure of delay discounting that may be interpreted without the need for a priori assumptions regarding the specific form of the discounting function (e.g., hyperbolic, as in Equation 1). This measure, expressed as a proportion of the maximum AUC, can vary from .1 (maximum discounting) to 1.0 (no discounting). Note that AUC is bound in the present data by .1, and not 0, because the amount available on the immediate lever could not be adjusted below one pellet.

In both assessments, unless otherwise noted, nonparametric statistical methods were used either because indifference points, k values, and response latencies did not satisfy assumptions of parametric methods (i.e., normality, equal error variance) or because limited sample sizes did not permit confident assertions that these assumptions had been met. We used Mann-Whitney U tests to examine strain differences in k and AUC in both assessments. In order to examine the potential for systematic choice bias, we used one-sample Wilcoxon signed-rank tests to determine whether indifference points at the 0-s delay differed significantly from the delayed amount (i.e., 10 pellets) in either strain. Indifference points above 10 pellets would reflect bias toward the standard alternative, whereas indifference points below 10 pellets would reflect bias toward the adjusting alternative. We used Wilcoxon signed-rank tests to examine within-strain differences in dependent measures between steady-state and rapid-determination assessments. To examine further the level of agreement in measures of discounting, we used Spearman ρ correlations to compare indifference points, k, and AUC between assessments.

Previous researchers have reported potential motoric differences in Fischer 344 compared to Lewis rats (e.g., Kosten, Zhang, & Haile, 2007; Madden et al., 2008). This is of particular concern because the less active Fischer 344 rats may be more likely to continually select the lever most recently presented on a forced-exposure trial (defined here as a “stay” response). As a result, these rats may reach indifference in fewer sessions and display indifference points closer to the initial pellet value at all delays—an outcome that may be mistaken for more shallow delay discounting. To address this, we used Mann-Whitney U tests in both assessments to compare response latencies and the number of sessions required to meet stability criteria between strains; we also used one-sample Wilcoxon signed-rank tests to examine whether the conditional probability of a stay response following forced-exposure trials in both assessments differed significantly from .5. Conditional probabilities greater than .5 would indicate a perseverative response pattern.

In all tests of statistical significance examining direct measures of delay discounting (i.e., k and AUC values), we used one-tailed tests because several studies in the extant literature (Anderson & Diller, 2010; Anderson & Woolverton, 2005; García-Lecumberri et al., 2010; Huskinson et al., 2012; Madden et al., 2008) allowed us to hypothesize a priori the direction of the expected strain difference in delay discounting. However, in tests of all other measures for which less data were available (e.g., response latencies, conditional probabilities, etc.), we used two-tailed tests. In all tests, the alpha level was .05.

RESULTS

Autoshaping and Initial Training

Because a large proportion of rats within each strain required supplemental hand-shaping in order to acquire lever pressing (Lewis, n  =  3; Fischer 344, n  =  5), potential strain differences in the number of sessions to reach the acquisition criterion through autoshaping could not be analyzed. However, considering that a comparable number of rats within each strain required hand-shaping, no strain differences in acquisition were apparent.

During initial training, all rats in both strains completed all training trials. Mean nose-poke latencies were 1.94 s and 2.46 s for Lewis and Fischer 344 rats, respectively (U  =  20.5, p  =  .25). Mean left-lever response latencies were 0.86 s and 1 s (U  =  22.5, p  =  .34) and mean right-lever response latencies were 0.87 s and 1.02 s (U  =  20.5, p  =  .24) for Lewis and Fischer 344 rats, respectively.

Steady-state Adjusting-amount Procedure

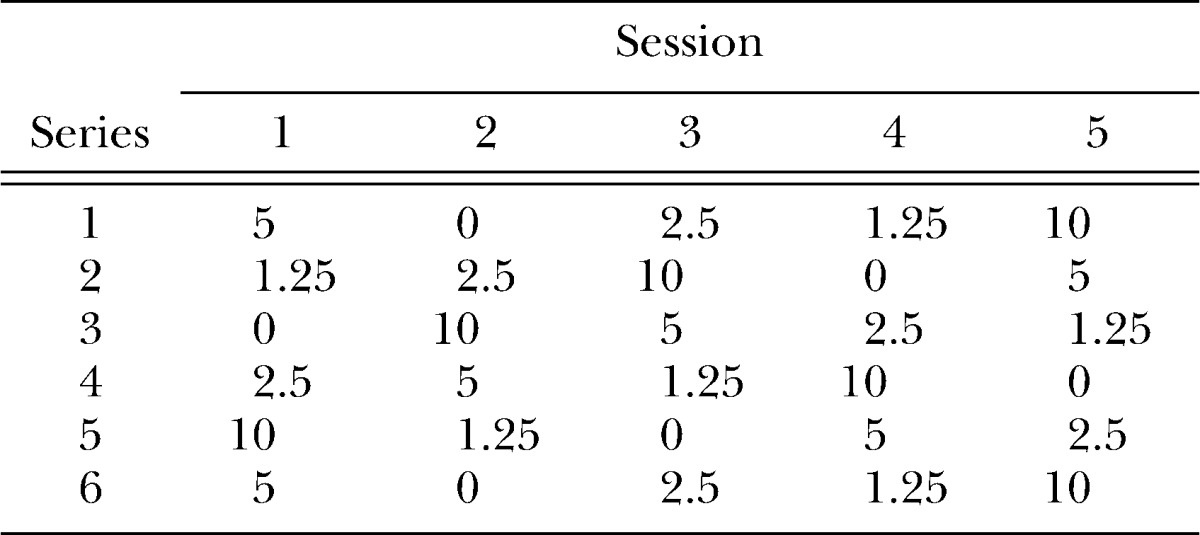
Table 2 provides the number of sessions each rat required to meet stability criteria during the steady-state assessment. No strain differences were observed in the number of sessions required to meet the stability criteria at any delay (U > 12; p >.05 in all cases). Figures 1 and 2A (top panel) show individual-subject and strain-mean stable indifference points across delays, respectively, for Lewis (closed triangles) and Fischer 344 (closed circles) rats in the steady-state assessment. Both individual-subject and strain-mean indifference points decreased as a function of delay for both Lewis and Fischer 344 rats. Discounting in both strains was well described by Equation 1, with individual-subject R² values (also reported in Figure 1) exceeding .90 for all but one Lewis rat (L1) and two Fischer 344 (F7, F8) rats. Mean R² values were .93 for both Lewis and Fischer 344 rats (U  =  23, p  = .61).

Table 2.

Number of sessions Lewis and Fischer 344 rats completed at each delay in the steady-state assessment.

Fig 1.

Indifference points for individual Lewis and Fischer 344 rats in steady-state (SS; closed symbols) and rapid-determination (RD; open symbols) assessments. Curves represent the best fitting functions according to Equation 1. Individual rats' values of k (R²) and AUC are also featured in each panel.

Fig 2.

Mean indifference points (± SEM), values of k, and AUC for Lewis (triangles) and Fischer 344 (circles) rats in steady-state (Panel A; closed symbols) and rapid-determination (Panel B; open symbols) assessments. Curves represent the best fitting functions according to Equation 1. *p < .05.

Also in Figure 1, note that indifference points at the 0-s delay differed substantially from 10 pellets for an approximately equal number of rats within each strain, suggesting the presence of choice bias in these rats. However, bias appeared unsystematic because mean indifference points at the 0-s delay (top panel of Figure 2A) did not differ significantly from 10 pellets in either Lewis rats (mean indifference point  =  10.02; W  =  0, p  = 1.0) or Fischer 344 rats (mean indifference point: 10.12; W  =  4, p  = .84).

As shown in the bottom panel of Figure 2A, the distribution of k values among Lewis rats (mean k  =  1.03) was significantly higher than Fischer 344 rats (mean k  =  0.59; U  =  8, p  = .01; one-tailed test). Also depicted in the bottom panel of Figure 2A, Lewis rats' AUC values (mean AUC  =  .20) were significantly lower than those of Fischer 344 rats (mean AUC  =  .25; U  =  10.5; p  = .04; one-tailed test).

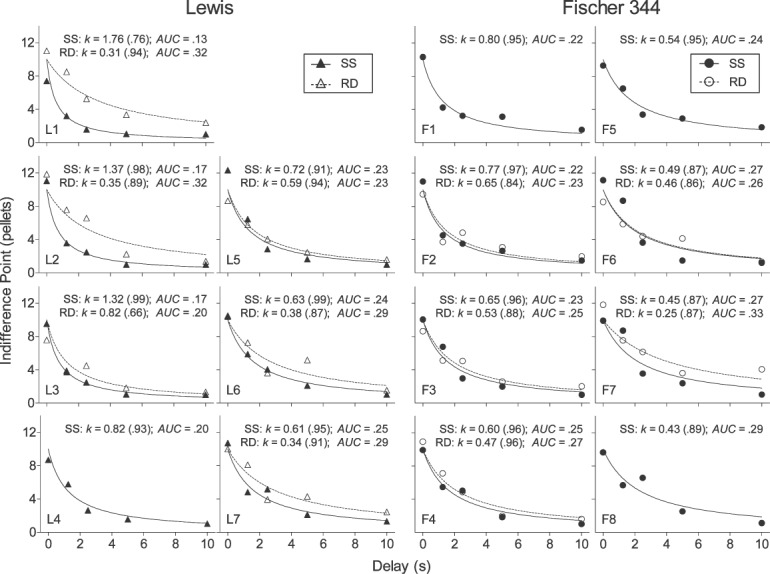
Response latencies were calculated as time from trial onset to a nose-poke response (trial-initiation latency) or from nose-poke response to side-lever response (i.e., choice latencies). Between strains, no significant differences were observed in trial-initiation latencies (U  =  4; p  =  .10; data not shown). Figures 3 and 4A, respectively, show individual-subject and strain-median choice latencies for the delayed and immediate alternatives for Lewis and Fischer 344 rats in the steady-state assessment (closed symbols). Within each strain, no significant differences emerged between latencies on forced-exposure and choice-trial latencies, so we have collapsed data across trial type at each delay. With the exception of 3 rats (L3, F5, and F8), individual-subject choice latencies for the delayed alternative (Figure 3) increased as a function of delay to at least some extent; however, there was no visually apparent difference in the magnitude of this effect between strains. In contrast, latencies for the immediate alternative in both strains remained relatively unaffected by increases in delay. Collapsed across delay, no significant strain difference was observed in latencies for the delayed alternative (U  =  4; p  =  .10); however, shorter latencies for the immediate alternative were observed in Lewis rats compared to Fischer 344 rats (U  =  0, p < .01).

Fig 3.

Median latencies to respond on the delayed (circles) and immediate (squares) alternatives for individual Lewis and Fischer 344 rats in the steady-state (SS; closed symbols) and rapid-determination (RD; open symbols) assessments. Note that the symbols are displaced slightly on the axis for clarity.

Fig 4.

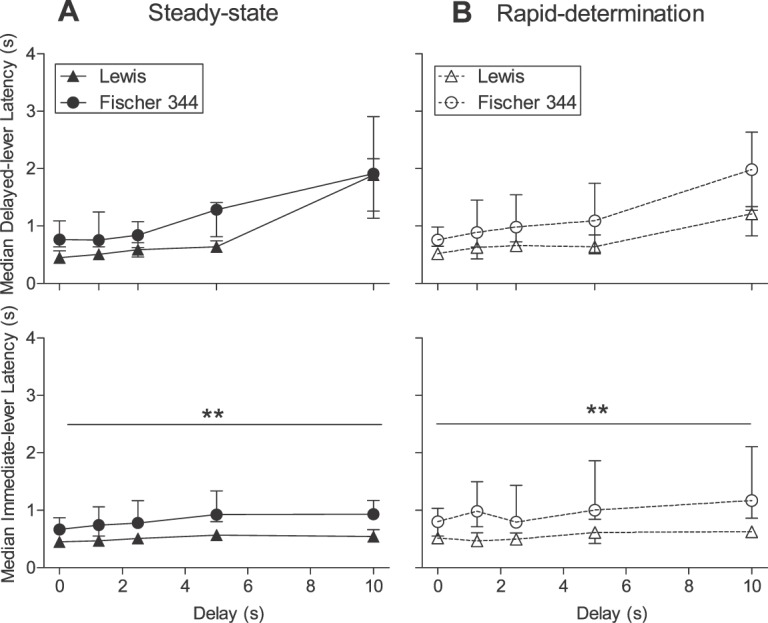
Median latencies (± interquartile range) to respond on the delayed (top panel) and immediate (bottom panel) alternatives in the steady-state (Panel A) and rapid-determination (Panel B) assessments for Lewis (triangles) and Fischer 344 (circles) rats. **p < .01.

Figures 5 and 6, respectively, show individual-subject and strain-mean conditional probabilities of a “stay” response following a forced-exposure trial for Lewis and Fischer 344 rats in the steady-state assessment (closed symbols). Recall that if rats perseverated on the forced-exposure lever (conditional probability significantly greater than .5), then the stability criteria would be more quickly met and obtained indifference points may not have adequately represented the degree of delay discounting. Conditional probabilities in both strains rarely exceeded .5 in the steady-state assessment for individual subjects (Figure 5). Rather, conditional probabilities generally decreased with increases in delay for rats in both strains. The strain-mean conditional probability of staying was not significantly greater than .5 for either strain at any delay (Figure 6). However, the probability of staying was significantly lower than .5 for Lewis rats at the 5-s and 10-s delays (W  =  −28; p  = .02 in both cases) and for Fischer 344 rats at the 0-s (W  =  −36; p  = .01), 5-s (W  =  −34; p  = .02), and 10-s delays (W  =  −36; p  = .01).

Fig 5.

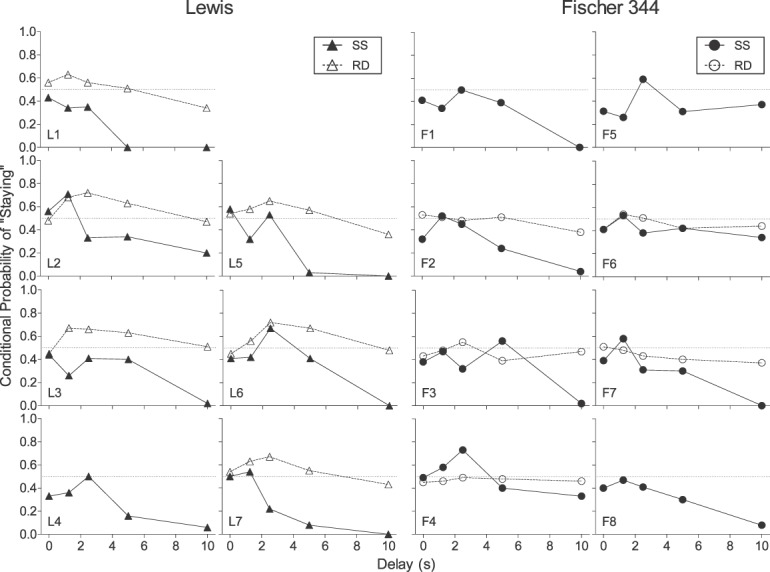
Conditional probabilities of a “stay” response following a forced-exposure trial for individual Lewis and Fischer 344 rats in the steady-state (SS; closed symbols) and rapid-determination (RD; open symbols) assessments.

Fig 6.

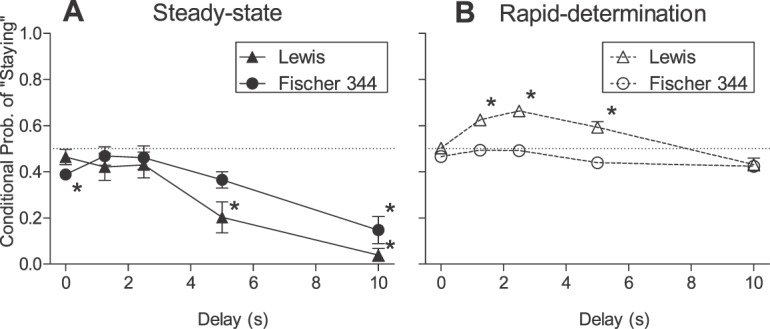
Mean conditional probabilities of a “stay” response following a forced-exposure trial in the steady-state (Panel A) and rapid-determination (Panel B) assessments for Lewis (triangles) and Fischer 344 (circles) rats. *p < .05 denotes conditional probabilities significantly different than .5.

Rapid-determination Adjusting-amount Procedure

Figure 7 shows the mean within-session adjusted amount of pellets across trials in the rapid-determination assessment. Data are separated by strain and are averaged across the final five sessions completed at each delay. Similar to other studies using a comparable procedure (e.g., Reynolds et al., 2002; Richards et al., 1997), visual analysis reveals that group-averaged indifference points were stable following the 30^th trial. Percent choice of the immediate alternative over the last 10 trials of this assessment was 45.6% for Lewis rats and 45.5% for Fischer 344 rats.

Fig 7.

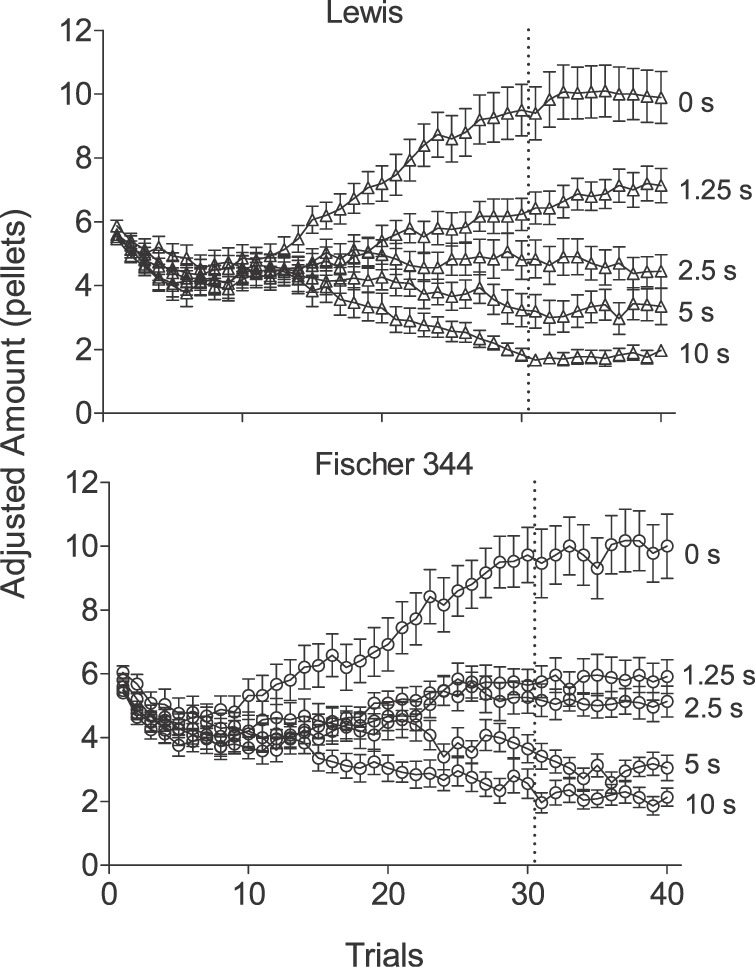
Mean within-session adjusted amount (± SEM) across sessions at all delays for Lewis rats (top panel) and Fischer 344 rats (bottom panel). Dashed lines precede the last ten trials used in analysis.

Figures 1 and 2B (top panel) show individual-subject and strain-mean indifference points across delays, respectively, for Lewis (open triangles) and Fischer 344 (open circles) rats in the rapid-determination assessment. Individual-subject and strain-mean indifference points decreased as a function of delay for both strains. Examining individual indifference points reveals that discounting in individual rats of both strains was reasonably well-described by Equation 1. The mean R² values were .88 for both Lewis and Fischer 344 rats (U  =  12, p  = .66).

Indifference points at the 0-s delay in Figure 1 differed substantially from 10 pellets for an approximately equal number of rats within each strain. However, these deviations again appeared unsystematic because, considered as a group, indifference points at the 0-s delay (top panel of Figure 2B) did not differ significantly from 10 pellets in Lewis or Fischer 344 rats (W  =  −1, p  =  1 in both strains).

The bottom panels of Figure 2B depict the mean k and AUC values in Lewis and Fischer 344 rats. No significant differences in either k (U  =  13, p  = .40) or AUC (U  =  12; p  = .32; one-tailed tests) were observed between strains.

Response latencies were calculated as described above for the steady-state assessment. Because no significant differences emerged between latencies on forced-exposure and choice trial latencies, we again collapsed data across trial type at each delay. Figures 3 and 4B, respectively, show individual-subject and strain-median choice latencies for Lewis and Fischer 344 rats in the rapid-determination assessment (open symbols). With the exception of 3 rats (L2, L3, and F7), individual-subject choice latencies for the delayed alternative (Figure 3) increased as a function of delay to at least some extent; however, there was no visually apparent difference in the magnitude of this effect between strains. In contrast, latencies for the immediate alternative in both strains remained relatively unaffected by increases in delay. Collapsed across delay, Lewis rats again showed shorter latencies for the immediate alternative (U  =  0, p < .01) than Fischer 344 rats. However, no significant strain differences were observed in either trial-initiation latencies (U  =  4; p  =  .12; data not shown) or latencies for the delayed alternative (U  =  3; p  =  .06).

Figures 5 and 6 depict individual-subject and strain-mean conditional probabilities of “stay” responses following a forced-exposure trial in the rapid-determination assessment (open symbols). Conditional probabilities for individual Lewis rats (Figure 5) was an approximate bitonic function of delay, with probabilities above .5 observed at all intermediate delays (i.e., 1.25–5s). However, no systematic effect of delay on conditional probabilities was observed in Fischer 344 rats. In Lewis rats, conditional probabilities were significantly greater than .5 at all intermediate delays (W  =  21; p  = .03 in all cases). In contrast, Fischer 344 rats' conditional probabilities did not differ significantly from .5 at any delay (W < −3; p > .05 in all cases).

Comparing Steady-state and Rapid-determination Assessments

Due to subject attrition between assessments, comparisons between steady-state and rapid-determination assessments are constrained to those Lewis (n  =  6) and Fischer 344 (n  =  5) rats that served in both assessments. With this smaller sample size, Lewis rats' steady-state k values (mean k  =  1.07) were still significantly higher than Fischer 344 rats' (mean k  =  0.59; U  =  5; p  = .04). The difference in AUC, however, was not significant (U  =  6; p  =  .06).

Comparing between assessments, further examination of Figure 1 reveals that for individual rats in both strains, indifference points were generally higher at all delays in the rapid-determination assessment than in the steady-state assessment. However, the magnitude of this difference appeared more pronounced for Lewis than Fischer 344 rats. This is supported statistically, as only Lewis rats' rapid-determination k values were significantly lower (W  =  21; p  = .03), and AUC values significantly higher (W  =  −21; p  = .03), when compared to these values obtained in the steady-state assessment. Fischer 344 rats' values of k (W  =  9; p  = .31) and AUC (W  =  −13; p  = .13) did not differ between assessments.

At the level of individual subjects, Figure 1 also reveals that R² values were generally lower for the rapid-determination compared to the steady-state assessment. However, differences in R² values between assessments were not significant in either Lewis rats (W  =  19; p  = .06) or Fischer 344 rats (W  =  15, p  = .06).

Further inspection of choice latencies in Figure 3 (delayed and immediate alternatives) for both assessments reveals no systematic difference in latency duration between steady-state and rapid-determination assessments. That is, for some rats, rapid-determination latencies were longer than steady-state latencies, and in an approximately equal number of rats, the opposite was true. This is supported statistically, as no significant difference in latencies for the delayed alternative (again, collapsed across delay) between assessments was observed in either Lewis (U  =  9; p  =  .18) or Fischer 344 rats (U  =  12, p  =  1.0). The same was true for latencies for the immediate alternative in both Lewis (U  =  13; p  =  .49) and Fischer 344 rats (U  =  5; p  =  .15).

Table 3 provides Spearman ρ correlation coefficients for indifference points obtained at each delay under steady-state and rapid-determination assessments. Positive correlations indicate that indifference points were comparable across assessments. Only one positive correlation was significant and this was observed in Lewis rats at the 10-s delay (ρ  =  .79). For Lewis rats, two correlations were significantly negative (1.25- and 2.5-s delays; ρ  =  −.89 and −.83, respectively; p < .03 in both cases). In Fischer 344 rats, no correlations were significant, although strong negative (−0.80) and positive (0.70) ρ values were observed, respectively, at the 0- and 1.25-s delays. No significant positive or negative correlations were observed at any delay when indifference points were collapsed across strain (N  =  11).

Table 3.

Spearman ρ correlation coefficients for indifference points between steady-state and rapid-determination assessments in Lewis (n = 6) and Fischer 344 (n = 5) rats. *p < .05.

Values of k and AUC obtained under the steady-state and rapid-determination assessments were unrelated in Lewis rats (k: ρ  =  −.20, p  = .36; AUC: ρ  =  −.31, p  = .28). The primary reason for a lack of a positive relation was that the lowest rapid-determination k values were observed in those Lewis rats with the highest k values in the steady-state assessment (L1 and L2; see Figure 1). In contrast, in Fischer 344 rats, k values were positively correlated (ρ  =  1.0, p < .01); however, the correlation in AUC between assessments was not significant (ρ  =  .82, p  = .07). When data were collapsed across strain, no significant correlations emerged.

DISCUSSION

The present study is the first to our knowledge to demonstrate that delay discounting in both Lewis and Fischer 344 rats is well described by Equation 1. Further, steeper delay discounting for food reinforcers was observed in Lewis rats compared to Fischer 344 rats when a steady-state adjusting-amount procedure was used. Mean k and AUC values differed by less than a factor of 1.5 between strains, with a number of Lewis rats achieving stable k and AUC values in the range of Fischer 344 rats. Visual inspection of individual-subject k and AUC values in the steady-state assessment reveals three conspicuous outliers in Lewis rats (bottom panels of Figure 2A). Although one may be tempted to attribute the significant strain difference in delay discounting in the present study solely to these three observations, our use of a rank-based test (Mann-Whitney U) minimized their parametric influence on our conclusions.

The difference in delay discounting observed under steady-state conditions was unlikely due to a motoric difference between strains because Fischer 344 rats were not more likely than Lewis rats to perseverate on a lever following a forced-exposure trial. Instead, rats in both strains were more likely to switch back to the preferred lever following a forced-exposure trial at the longest delays (i.e., 5 and 10 s for Lewis rats; 10 s for Fischer 344 rats).

Contrasted with the steady-state assessment (and consistent with the findings reported by Wilhelm & Mitchell, 2009), no significant difference between strains in delay discounting was detected when the rapid-determination adjusting-amount procedure was used. Lewis rats' choices were most affected by the procedure change as their k values were not correlated between procedures. Although these findings suggest that the steady-state adjusting-amount procedure is more likely than the rapid-determination procedure to detect strain-related differences in delay discounting between Lewis and Fischer 344 rats, this conclusion is compromised by the quasiexperimental design used. At least two other factors could explain the difference across assessment procedures. First, both rat strains were older in the rapid-determination assessment and some evidence suggests that discounting rates decline with age in mice and rats (Pinkston & Lamb, 2011; Simon et al., 2010). If this effect is more pronounced in Lewis than Fischer 344 rats, then the strain difference observed under steady-state conditions may have abated at the start of the rapid-determination assessment. However, when we compared stable indifference points obtained at the final delay assessed in the steady-state procedure (1.25 s) to those obtained at the same delay under the rapid-determination procedure, there was still a significant effect of strain under the steady-state (U  =  5; p  = .04; one-tailed test) but not the rapid-determination procedure (U  =  8; p  =  .12; one-tailed test). Because only 30 days separated these measures, aging unlikely accounted for the rapid-determination procedure failing to reveal a difference in delay discounting.

Second, the rats completing the rapid determination assessment were those that completed the steady-state assessment more slowly and had not been euthanized by Wilhelm and Mitchell's (2009) publication date. Perhaps the rats that remained were those least sensitive to the amount and delay variables. Evidence against this possibility is that total number of sessions required to complete the steady-state assessment was uncorrelated with either k values (Lewis: ρ  =  0.0, p  = 1.0; Fischer 344: ρ  =  −.29, p  = .5) or AUC (Lewis: ρ  =  .05, p  = .91; Fischer 344: ρ  =  .42, p  = .30). Nonetheless, no strong statements may be made about the relative sensitivity of the steady-state and rapid-determination procedures investigated here.

These data emphasize the need for systematic comparisons of delay-discounting measures that are produced by the large variety of procedures used in the nonhuman discounting literature (see Green, Myerson, Shah, Estle, & Holt, 2007 for one of the few comparisons conducted thus far). We defer direct comparisons between the dependent measures (i.e., k and AUC) yielded by such procedures to future research designed to explicitly provide such comparisons. Comparison between studies can be problematic, particularly because dependent measures like AUC can vary as a function of many factors, including type of dependent measure used in its calculation (i.e., indifference point vs. percent choice), as well as the range and number of delays examined in the assessment. Nonetheless, because steep delay discounting appears to predict translationally important behavior in nonhuman models of drug abuse (e.g., acquisition of cocaine self-administration; Perry et al., 2005; Perry, Nelson, et al., 2008), future inquiry in this area is warranted.

Relation Between Strain-related Biological Differences and Delay Discounting

As reviewed earlier, the role of biology in delay discounting is not well understood, with many researchers reporting mixed or contradictory findings. Echoing a point just made, the effects of experimental manipulation of 5-HT via administration of a 5-HT-selective neurotoxin (5, 7-DHT) in the rat forebrain appears to depend on the procedure used to measure delay discounting. For instance, Mobini, Chiang, Ho, Bradshaw, and Szabadi (2000) reported that 5, 7-DHT increased impulsive choice in rats when delay was manipulated between conditions, although other researchers report no effects of 5, 7-DHT using within-session delay manipulation (Winstanley, Dalley, Theobald, & Robbins, 2003, 2004). Further, when researchers have used both within-session delay manipulation, as well as the rapid-determination procedure, to examine the effects of excitotoxic lesions of the nucleus accumbens, data are difficult to interpret because choice often trends toward indifference at all delays following the lesion (e.g., Acheson et al., 2006; Cardinal, Pennicott, Sugathapala, Robbins, & Everitt, 2001). This trend toward indifference suggests that lesions may not have affected delay discounting, but rather disrupted stimulus control. Further, the mixed results reviewed above suggest that even modest strain differences in the present study, when replicable across experiments, serve to unify the literature regarding the role of DA and 5-HT in delay discounting.

Note, however, that the differences in DA and 5-HT between Lewis and Fischer 344 rats do not represent true independent variables due to other neurobiological differences between these strains. Such differences include lower corticosterone levels, lower basal glutamate levels, and lower μ-opioid receptor binding in several brain regions in Lewis rats compared to Fischer 344 rats (Kosten & Ambrosio, 2002). Corticosterone function in particular has been shown to interact with, and regulate, DA (e.g., Ortiz, DeCaprio, Kosten, & Nestler, 1995; Saal, Dong, Bonci, & Malenka, 2003), although a complete understanding of the effects of this and other strain-related biological differences on delay discounting has yet to be determined. Thus, the extent to which differences in delay discounting between Lewis and Fischer 344 rats reflect the contribution of any one variable of interest is unclear. Future research may attempt to further isolate the effects on delay discounting of DA or 5-HT by examining biological differences within a single rat strain. For example, researchers may examine individual differences in accumbal DA activity in awake, behaving rats using fast-scan cyclic voltammetry to determine if observed differences predict subsequent degree of delay discounting.

In conclusion, the present study further supports a strain-related difference in delay discounting between Lewis and Fischer 344 rats. Significant findings may depend on the use of steady-state methodology, although further experimentation is clearly necessary. Such strain-related differences are important in understanding biological variables that predispose organisms toward steep delay discounting; however, the extent to which the environment may modify the role of biology has yet to be fully explored. Some preliminary evidence from the animal laboratory suggests that training variables (e.g., delay fading; Logue, Rodriguez, Peña-Correal, & Mauro, 1984; Mazur & Logue, 1978) or environmental enrichment (e.g. Perry, Stairs, & Bardo, 2008) attenuates degree of delay discounting in animals. Thus, future researchers may profitably investigate the extent to which biology and environment interact in delay discounting by examining the relative efficacy of such methods in Lewis compared to Fischer 344 rats.