Abstract
We present an approach for the calculation of spin density distributions for molecules that require very large active spaces for a qualitatively correct description of their electronic structure. Our approach is based on the density-matrix renormalization group (DMRG) algorithm to calculate the spin density matrix elements as a basic quantity for the spatially resolved spin density distribution. The spin density matrix elements are directly determined from the second-quantized elementary operators optimized by the DMRG algorithm. As an analytic convergence criterion for the spin density distribution, we employ our recently developed sampling-reconstruction scheme [J. Chem. Phys.2011, 134, 224101] to build an accurate complete-active-space configuration-interaction (CASCI) wave function from the optimized matrix product states. The spin density matrix elements can then also be determined as an expectation value employing the reconstructed wave function expansion. Furthermore, the explicit reconstruction of a CASCI-type wave function provides insight into chemically interesting features of the molecule under study such as the distribution of α and β electrons in terms of Slater determinants, CI coefficients, and natural orbitals. The methodology is applied to an iron nitrosyl complex which we have identified as a challenging system for standard approaches [J. Chem. Theory Comput.2011, 7, 2740].
1. Introduction
In quantum chemistry, the electronic structure of molecules is described by either ab initio wave function methods or density-functional theory (DFT). For large molecular systems such as transition metal complexes, however, wave function based methods are rarely employed due to the corresponding high computational cost (for counterexamples, see refs (1−5)). Hence, the application of DFT became instrumental in theoretical studies of mechanisms in metal-mediated catalysis.6−14 Yet, the treatment of open-shell systems16,18,19 and (near-)degenerate states remains a challenge for DFT.15 Failures of approximate exchange–correlation density functionals in predicting properties of open-shell systems have been traced to the delocalization error and static correlation error,17,20 which are rooted in an inappropriate behavior of the energy with respect to fractional charges and fractional spins.21 In addition to the difficult prediction of ground states from states of different spin,18,22−30 spin density distributions considerably depend on the approximate exchange–correlation density functional if transition metal complexes containing noninnocent ligands are considered.31 Qualitatively correct spin density distributions are difficult to obtain within the standard Kohn–Sham formalism that has not been formulated to also produce accurate spin densities.32
However, accurate spin densities are desirable for various reasons. (1) In electron paramagnetic resonance spectroscopy (EPR),33 the spin density is the central quantity on which EPR parameters explicitly depend.34 Obviously, reliable spin density distributions are important for an accurate calculation of EPR properties, but this remains a difficult task to achieve for theoretical chemistry.35−39 (2) The question of which approximate exchange–correlation density functional yields sufficiently accurate spin densities remains inconclusive.31,40 If accurate reference spin density distributions were available, a more detailed analysis of the spin density distribution in terms of spin density difference plots could be used as a qualitative and quantitative benchmark for the validation of approximate exchange–correlation density functionals. (3) According to the Hohenberg–Kohn theorem,41 the spin density is not needed to calculate the electronic energy or any other expectation value. However, in open-shell systems, it is often introduced as an additional variable which leads to a spin-DFT formalism42 first introduced by von Barth and Hedin.43 In spin-DFT, the spin density becomes a fundamental quantity, and reliable reference spin densities could be used to construct proper approximations to the exact exchange–correlation density functional.
For accurate spin densities in cases for which a DFT description fails, ab initio electron correlation methods need to be applied. Pierloot et al. presented complete-active-space self-consistent-field (CASSCF) studies for large transition metal complexes which provided deeper insights into the quality of DFT spin density distributions.2,44 The large molecular size of these systems requires large active orbital spaces, but the standard CASSCF approach restricts their dimension, which represents the most crucial approximation in such calculations.40 It is therefore important to understand whether the spin density is converged with respect to the dimension of the active orbital spaces used so far. This is a task that is difficult to study within a standard CAS-type approach.
In general, up to about 18 electrons correlated in 18 spatial orbitals are computationally feasible for standard CASSCF. These limitations may restrict the accurate description of electronic structures which could be approved only by enlarging the dimension of the active orbital space. Reliable reference spin density distributions for complicated open-shell structures as found, for instance, in iron complexes with noninnocent ligands require capabilities beyond those of standard correlation methods.
A different approach for the calculation of correlated ab initio spin densities for large molecules was recently presented by Kossmann and Neese45 who discussed the performance of orbital-optimized Mo̷ller–Plesset perturbation theory in calculating hyperfine coupling constants for atoms and small molecules. In this approach, isotropic hyperfine constants of coupled-cluster singles-doubles quality could be obtained, which could be further improved by applying spin-component scaling.
Here, we pursue a different route for the calculation of ab initio spin densities by applying the density-matrix renormalization group (DMRG) algorithm. With the DMRG algorithm, introduced by White46,47 in 1992, much larger active orbital spaces can be considered beyond the limit of, say, 18 electrons correlated in 18 molecular orbitals. It was shown that DMRG is capable of providing accurate wave functions and energies, even for complicated electronic structures (see refs (48−51) for reviews). Moreover, we first showed that the DMRG algorithm yields reliable relative electronic energies between different spin states or isomers of transition metal complexes and clusters for which DMRG was not meant to work and which are a very challenging task for any other multireference quantum chemical method52 (see also ref (53) for latest results and further references). We shall demonstrate in this work that also accurate DMRG spin density distributions can be determined for very large active orbital spaces.
Recently, we presented a convergence analysis of the spin density distribution for a small iron nitrosyl model complex [Fe(NO)]2+ in a field of point charges, which demonstrated that medium-sized active orbital spaces are sufficient for quantitatively correct spin densities.40 However, a quantitative analysis that can explore truly large active spaces is still lacking for this complex, which shall therefore be the target system in this work. In such cases, DMRG spin densities can be considered as reliable references which can serve as benchmark results for approximate exchange–correlation density functionals.
This work is organized as follows. In section 2, we discuss the spin density matrix and its spatially resolved counterpart, the spin density distribution, employing the formalism of second quantization. Then, we continue with the introduction of DMRG spin densities. In section 2.2, we present our approach of approximating the DMRG spin density distribution via one from a complete-active-space configuration-interaction(CASCI)-type wave function which allows us to compare DMRG spin densities from calculations with different DMRG parameter sets. In order to validate our approach, we study the spin densities of a medium-sized active orbital space in section 3. This is then extended by considering up to 29 active orbitals in section 4. Finally, a summary and concluding remarks are given in section 5.
2. Spatially Resolved, Nonrelativistic Spin Densities
Since DMRG is based on the second quantized formalism, we briefly discuss how the spin density in spatial coordinates can be written in second quantization. In first quantization, the operator for the spin density reads
| 1 |
where ŝz,i is the z component of the one-electron spin operator, ri is the spatial coordinate of electron i, and N is the total number of electrons in the system. Applying an orbital basis, the corresponding operator expression in second quantization is given by
 |
2 |
where p,q run over the total orbital basis {ϕi} with ϕi(r) representing the spatial part of a spin orbital. The operators aiσ† and aiσ are the creation and annihilation operators, respectively, for an electron of spin σ in orbital i. In eq 2, the spin density operator δ̂spin(r) is defined in terms of the spin tensor excitation operators
| 3 |
in the orbital basis (see ref (54) for details). The spatially resolved spin density ρspin(r) is calculated as the expectation value of δ̂spin(r):
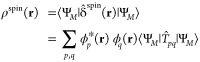 |
4 |
where |ΨM⟩ represents some normalized reference state
| 5 |
|n⟩ = |n1n2...nk⟩ is an occupation number vector with elements np ∈ {0,1}. {n} represents the set of all occupation number vectors constructed from k one-particle states. The expectation value on the right-hand side of eq 4 is a spin density matrix element Tpq(M):
| 6 |
2.1. DMRG Spin Densities from Second-Quantized Elementary Operators
If the reference state |ΨM⟩ is a DMRG wave function in eq 6, the corresponding DMRG spin density matrix elements Tpq(M[DMRG]) are obtained. The matrix representations of the creation and annihilation operators are available in every step of the DMRG algorithm, and each spin density matrix element can thus be easily determined.
The operator apσ†aqσ in its matrix representation is calculated as a tensor product for which we have to distinguish two different cases. The molecular orbitals p and q are defined either (i) on the same or (ii) on different subsystems of the DMRG partitioning of the active orbital space into the active (sub)system, its environment (the complementary subsystem), and one or two explicitly treated orbitals in between. While the former case is straightforward to handle, for an operator expression in the latter case, however, we need to build operators for the superblock where all three subsystems, i.e., the active subsystem, the exactly represented sites, and the environment, are combined as tensor products.
To illustrate this concept, let us consider
two operators a1 and a2 defined
on three different subspaces 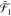 ,
, 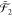 , and
, and 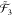 . Then, the combined subspace
. Then, the combined subspace 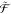 is defined as
is defined as 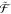 =
=  ⊗
⊗ 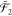 ⊗
⊗  , where
, where  as well as
as well as  ,
,  , and
, and 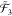 are all subspaces of the N-particle Fock space
are all subspaces of the N-particle Fock space  . For instance, the operator expressions
for the combined subspace are given by
. For instance, the operator expressions
for the combined subspace are given by
| 7 |
| 8 |
where 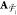 is the anticommutation matrix of the corresponding
subspace
is the anticommutation matrix of the corresponding
subspace  . For the product of two operators, we obtain
. For the product of two operators, we obtain
| 9 |
where we have used the mixed-product property for the right-hand side of the above equation, which mixes the ordinary matrix product with the tensor product. All remaining operator products can be derived in a similar way. After the spin density matrix is determined, the spatially resolved spin density distribution can be calculated from eq 4. If the wave function is real, the spin density matrix is symmetric and the calculation can be speed up by calculating the upper triangular part of the spin density matrix only.
2.2. Spin Density from a Reduced Dimensional CASCI-Type Wave Function
Since CI vectors are in general sparse55−57—if contributions below a predefined threshold are neglected—CASCI-type wave functions can be efficiently and accurately projected onto a smaller set of Slater determinants, which only represent the most important contributions to the wave function expansion. We recently reported the sampling-reconstruction algorithm for CASCI-type wave functions defined in a complete active orbital space from a previously optimized DMRG wave function (SRCAS algorithm).57 An approximate CASCI-type expansion |Ψ̃M⟩ for any wave function |ΨM⟩ consisting of k one-particle states can thus be written as
| 10 |
where the sum runs over all occupation number vectors ñ living in the sampled subspace of the total many-particle Hilbert space. Using eq 6, we can calculate the spin density matrix by substituting the reference state |ΨM⟩ with the approximate state |Ψ̃M⟩:
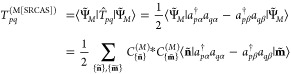 |
11 |
Since the occupation number vectors are orthonormal to each other, the expectation value on the right-hand side of eq 11 can be easily evaluated, and we obtain
| 12 |
where  represents the occupation number vector
where orbital p lacks one electron with σ spin.
Furthermore, we introduced a phase factor εσ to account for the annihilation operations of apσ† acting on the bra-state and aqσ acting on the ket-state.
represents the occupation number vector
where orbital p lacks one electron with σ spin.
Furthermore, we introduced a phase factor εσ to account for the annihilation operations of apσ† acting on the bra-state and aqσ acting on the ket-state.
On the basis of this approximate expression for the spin density matrix, we can determine spin density distributions for subspaces of the many-particle Hilbert space of different dimensions and study the sensitivity of the spin density distribution to the number of active-system states in DMRG calculations.
2.3. Measures for Spin Density Comparisons
For various reasons, we need suitable measures to assess the similarity of different spin densities. For instance, such a measure would be required to assess the accuracy of a given spin density compared to a reference spin density.
Monitoring the evolution of the spin density for an increasing number of active-system states58 can illustrate the convergence behavior of the spin density distribution with respect to the number of active-system states m. Isosurface plots of the difference in spin density distributions for calculations with different m values can only serve as a qualitative convergence measure. As quantitative measures, however, we introduce two distances which quantify how far two spin densities are apart from each other. Both distance measures are defined with the absolute error in the spin density difference distribution. The accumulated absolute error Δabs is given by
| 13 |
and the root-square error Δrs reads
| 14 |
where ρispin(r) refers to the spin density distribution corresponding to some calculation i, e.g., to a CASSCF or DMRG spin density when different chemical methods are compared, or to some parameter sets if different spin densities are determined with the same method. If two spin densities ρi(r) and ρjspin(r) are similar, both Δabs and Δrs approach zero. For accurate ab initio spin densities, we shall require both error measures to be smaller than 0.005 (Δabs) or 0.001 (Δrs), respectively (in view of the results discussed in section 3.1).
A different similarity measure can be applied by employing directly the knowledge of the reconstructed CASCI-type wave function expansion. This procedure relies on the closeness measure of two quantum states, namely the quantum fidelity.59,60 The importance and potential application of the quantum fidelity within the DMRG framework was first discussed by some of us61 in the context of quantum error correction and was also utilized in our SRCAS approach.57 Two CASCI-type wave function expansions reconstructed for different numbers of DMRG active-system states, m1 and m2, can be explicitly compared by calculating their quantum fidelity
| 15 |
as an overlap measure.
3. A Noninnocent Model System
In a previous study, we reported DFT and CASSCF spin density distributions in iron nitrosyl complexes as well as for the [Fe(NO)]2+ molecule embedded in a square-planar field of point-charges to emulate the one-electron states of the full complexes.40 Since DFT spin densities of iron nitrosyl complexes remain ambiguous, we choose the small [Fe(NO)]2+ molecule in its doublet state for our analysis here. The point charges facilitate a dynamic change of the character of the electronic wave function by shortening the distances dpc of the point charges to the metal center. Depending on this distance dpc, both single-reference and multireference situations can be created for [Fe(NO)]2+. When the four point charges are located at a distance of 1.131 Å from the iron atom, the electronic structure of the [Fe(NO)]2+ molecule represents a single-reference problem, while for dpc = 0.598 Å, a multireference case is generated.
The [Fe(NO)]2+ structure features a Fe–N bond length of 1.707 Å and a N–O bond distance of 1.177 Å with a Fe–N–O angle of 146°. The four negative point charges of −0.5e each are located as depicted in Figure 1e. Due to the small size of the [Fe(NO)]2+ molecule, we can efficiently study the dependence of the spin density distribution on different DMRG parameter sets such as the number of DMRG active-system states m. Thereby, we are able to define appropriate convergence measures for the spin density in order to reach a predefined accuracy.
Figure 1.
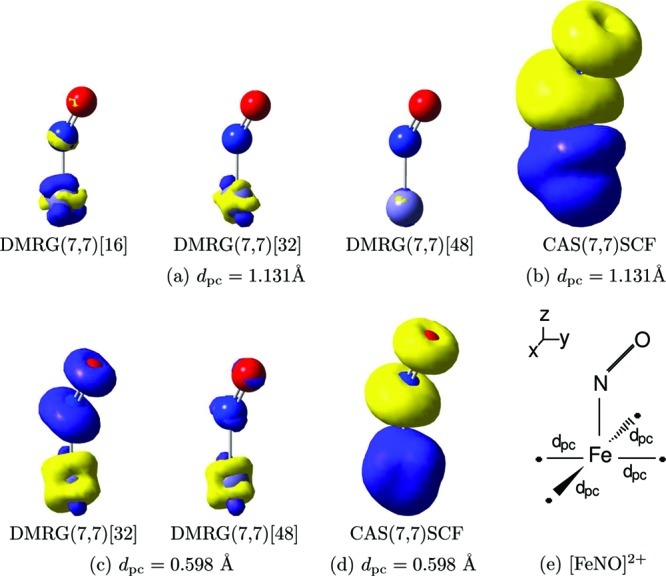
(a and c) Spin density difference plots for DMRG(7,7)[m] spin densities calculated for a different number of DMRG active-system states m with respect to the CAS(7,7)SCF reference spin densities shown in (b) and (d), respectively, for [Fe(NO)]2+ in a quadratic-planar point-charge field. Two different distances are considered, namely, dpc = 1.131 Å (a and b) and dpc = 0.598 Å (c and d). For both distances, the spin density could be perfectly reproduced in a DMRG(7,7)[64] calculation and is therefore not depicted here. An isosurface value of 0.0003 in (a) and (b) and 0.003 in (c) and (d), respectively, is chosen. (e) Structure of [Fe(NO)]2+ with the four point charges of −0.5e. In this and in the following figures, the blue (yellow) color denotes an excess of α-electron density, while yellow (blue) represents an excess of β-electron density in the spin density (difference) plots.
3.1. The Single-Reference Case
As already discussed in great detail in ref (40), the minimal active orbital space for [Fe(NO)]2+ with dpc = 1.131 Å comprises seven electrons correlated in seven orbitals for qualitatively reliable spin density distributions. It consists of Fe 3d (dxy, dyz, dxz, dx2–y2 and dz2) and both NO π* orbitals. As an orbital basis in our DMRG calculations, the natural orbitals from a CAS(7,7)SCF calculation performed with the Molpro program package62 using Dunning’s cc-pVTZ basis set for all atoms63,64 were taken. The one-electron and two-electron integrals in the natural orbital basis were also calculated with the Molpro program package.62 All DMRG calculations reported in this section were carried out with the Zurich DMRG program.65 Random noise was added to the density matrix in order to force the mixing of configurations that would have not been captured otherwise if the number of active-system states m was too small.66,67
We performed DMRG calculations for different numbers of DMRG active-system states m abbreviated as DMRG(x,y)[m], where x corresponds to the number of active electrons and y is the number of active orbitals for m renormalized active-system states. Starting with m = 16, m is further increased to 32 and 48 until the CAS(7,7)SCF reference energy is reproduced for m = 64 active-system states (see Table 1). Note that the number of active-system states needed to reproduce the CASSCF result is very small in this case. This can be explained employing concepts of quantum information theory illustrated in section 4. The DMRG calculations reported in this section do not employ these concepts to enforce better convergence. This decision is deliberately made in order to produce nonconverged low-m results to compare with the m = 64 calculation. We should note that this artifact could be cured by the dynamical block state selection (DBSS) procedure,68,69 while the strong dependence on small m values and the convergence to local minima can be overcome by applying the configuration interaction-based dynamically extended active space (CI-DEAS) procedure.61
Table 1. Ground State Energy for [FeNO]2+ Surrounded by Four Point Charges at Two Different Distance Sets dpc in Hartree Atomic Units for CAS(7,7)SCF and DMRG(7,7)[m] Calculations for Different Numbers of DMRG Active-System States m.
|
dpc = 1.131 Å |
dpc = 0.598 Å |
||
|---|---|---|---|
| method | E/Hartree | method | E/Hartree |
| HF | –1392.844043 | HF | –1396.821220 |
| CAS(7,7)SCF | –1392.887247 | CAS(7,7)SCF | –1396.858313 |
| DMRG(7,7)[16] | –1392.881067 | DMRG(7,7)[16] | –1396.762709 |
| DMRG(7,7)[32] | –1392.885462 | DMRG(7,7)[32] | –1396.818651 |
| DMRG(7,7)[48] | –1392.886893 | DMRG(7,7)[48] | –1396.840018 |
| DMRG(7,7)[64] | –1392.887247 | DMRG(7,7)[64] | –1396.858313 |
The spin density distributions for our four DMRG calculations (m = 16, 32, 48, 64) are shown in Figure 1a and were determined as discussed in section 2.1. To emphasize the dependence on m, the corresponding spin density difference plots with respect to the CAS(7,7)SCF reference spin density distribution (shown in Figure 1b) are displayed. Note that all isosurface plots are shown for the same isosurface value of 0.0003, where a blue surface corresponds to an excess of α-electron density, while a yellow surface corresponds to an excess of β-electron density for all spin density isosurface plots shown. All DMRG calculations yield qualitatively similar spin density distributions; only minor quantitative differences can be observed. The CAS(7,7)SCF reference spin density can be perfectly well reproduced for m = 64 DMRG active-system states and is, hence, not shown in Figure 1a.
To calculate approximate spin density distributions from reconstructed CASCI-type wave functions, we first have to sample the most important configurations of the N-particle Hilbert space. For this purpose, we applied our SRCAS method.57 Due to the small size of the active space, the N-particle Hilbert space is spanned by only 1225 Slater determinants, and all corresponding CI coefficients can be determined directly from the CASSCF reference calculation. In general, similar CI coefficients are obtained for all DMRG calculations and the CASSCF reference; i.e., similar wave functions are converged, resulting in small differences in the spin density distributions. The distribution of the CI coefficients is depicted in Figure 1 of the Supporting Information.
Spin density distributions determined for different sampled subspaces of the N-particle Hilbert space are in good agreement with the corresponding DMRG spin density. Note that the sampled subspaces are defined by the threshold value of the completeness measure (COM) introduced in ref (57) with COM = (1 – ΣICI2), where I runs over all sampled configurations with CI coefficients CI. In general, threshold values of 0.01 to 0.001 turned out to be sufficient for obtaining quantitatively reliable spin densities in this single-reference case. The corresponding isosurface plots and excitation histograms with respect to the COM are summarized in the Supporting Information.
The spin density difference plots in Figure 1a illustrate the convergence of the spin density distribution with respect to the number of DMRG active-system states m. The absolute error Δabs and the root-square error Δrs of the spin density difference distributions provide a quantitive measure for the accuracy (see Table 2). The differences in the spin densities calculated for m = 48 DMRG active-system states is small compared to the CAS(7,7)SCF reference. For 48 active-system states upward, both Δabs and Δrs are below their threshold values, given in section 2.3. The set of quantum fidelity measures Fmi,mi+1 for our four DMRG calculations with mi ∈ {16, 32, 48, 64} is {0.980000, 0.994395, 0.999012}. Increasing m from 48 to 64 DMRG active-system states corresponds to F48,64 = 0.999012, which illustrates the similarity of both DMRG wave functions and results in reliable spin density distributions for m ≥ 48.
Table 2. The Absolute Error Δabs and the Root-Square Error Δrs of the DMRG(7,7)[m] Spin Densities with Respect to the CAS(7,7)SCF Reference for [FeNO]2+ Surrounded by Four Point Charges at Two Different Distance Sets dpc Employing Different Numbers of DMRG Active-System States m.
|
dpc = 1.131 Å |
dpc = 0.598 Å |
|||
|---|---|---|---|---|
| method | Δabs | Δrs | Δabs | Δrs |
| DMRG(7,7)[16] | 0.007678 | 0.002147 | 0.213543 | 0.052168 |
| DMRG(7,7)[32] | 0.004392 | 0.001285 | 0.221198 | 0.052144 |
| DMRG(7,7)[48] | 0.001397 | 0.000412 | 0.081631 | 0.020418 |
| DMRG(7,7)[64] | 1.34 × 10–5 | 5.40 × 10–6 | 9.69 × 10–6 | 3.66 × 10–6 |
3.2. The Multireference Case
A multireference character of the [Fe(NO)]2+ molecule can be induced by decreasing the distances of the point charges to the iron atom. In the squeezed model complex, the point charges are placed at a distance of dpc = 0.598 Å from the iron center in the same configuration as before. Similar to the single-reference problem, the minimum active orbital space considered here comprises seven electrons correlated in seven orbitals. Yet, it consists of four Fe dxy, dyz, dxz, and dz2 (dx2–y2 is excluded due to the compressed point charge environment), two NO π*, and one NO σ orbital which interacts with the Fe dz2 orbital. Again, the natural orbitals from a CAS(7,7)SCF calculation were taken as orbital bases in our DMRG calculations and determined with the Molpro program package62 using Dunning’s cc-pVTZ basis set for all atoms63,64 The calculation of the one-electron and two-electron integrals in this natural orbital basis was also performed with the Molpro program package.62 All DMRG calculations were carried out with the Zurich DMRG program.65 As before, we performed DMRG calculations for four different numbers of DMRG active-system states m. Starting with m = 16, m is further increased to 32 and 48 until the CAS(7,7)SCF reference energy is obtained for m = 64 active-system states (see Table 1). The small-m calculations are designed not to reproduce the CAS(7,7)SCF reference for this analysis. Note, however, that a small number of active-system states was sufficient to reproduce the CASSCF result as observed in the single-reference problem.
In Figure 1d, the CAS(7,7)SCF spin density distribution is shown, which is taken as the reference distribution, while Figure 1c illustrates the spatially resolved differences in the DMRG(7,7)[m] and CAS(7,7)SCF spin density distributions. Note that the same isosurface value of 0.003 was chosen for all spin densities shown. For small m values, qualitatively different spin density distributions are obtained. The β-electron density around the nitrosyl ligand is underestimated and a dumbbell-shaped β-electron density is obtained in contrast to the cylindric shape of the reference β-electron density. The α-electron density around the Fe atom is underestimated. Increasing m to 48 results in a cylindric β-electron density around the NO ligand which differs only little from the reference spin density. The spin density can be exactly reproduced for m = 64 active-system state for which also the CAS(7,7)SCF reference energy is obtained. The convergence properties of the DMRG(7,7)[m] spin density with respect to m can be quantified by the Δabs and Δrs values where significantly large values (>0.005 and >0.001, respectively) are obtained for spin density distributions determined in small-m calculations (see Table 2).
In Figure 2, the distribution of CI coefficients for the DMRG and CASSCF wave functions is shown. Since only the position of the point charges has been modified, the N-particle Hilbert space remains spanned by 1225 Slater determinants, and all corresponding CI coefficients can be determined directly from the CASSCF reference calculation as in the single-reference case. Similar CI coefficients are obtained for the DMRG(7,7)[64] calculation and the CAS(7,7)SCF reference; i.e., similar wave functions are converged. However, significantly different CI coefficients are obtained—as expected—for smaller m values. In particular, the deviations are most significant for configurations corresponding to the largest (absolute) CI weights. Additional information on the distribution of CI coefficients can be found in the Supporting Information.
Figure 2.
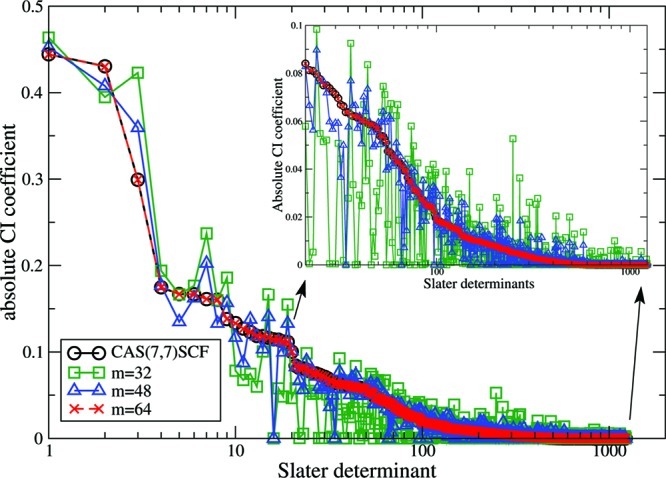
Distribution of the absolute value of the CI coefficients corresponding to the Slater determinants in the DMRG(7,7)[m] calculations with different renormalized active-system states m and in the CAS(7,7)SCF reference calculation for [Fe(NO)]2+ surrounded by four point charges at a distance of dpc = 0.598 Å from the iron atom. All Slater determinants are ordered according to the CI weights of the CAS(7,7)SCF calculation.
Similarly to the single-reference problem discussed above, reliable spin densities obtained from reduced dimensional CASCI-type wave function expansions can be determined for a COM ≥ 0.001 independent of m. A complete collection of spin density distributions for different CASCI-type wave function expansions and DMRG parameter sets can be found in the Supporting Information. Figure 3 shows the ratio of Slater determinants with respect to the complete N-particle Hilbert space which have been picked up in the sampling procedure and sorted by their corresponding CI weights for the DMRG(7,7)[32] and DMRG(7,7)[64] calculation. For COM ≥ 0.001, the reconstructed CASCI-type wave function contains the major part of the important Slater determinants, while for a further decreased threshold value of 10–5 almost all significant Slater determinants have been picked up. Note that the sampling procedure was restricted to accept only configurations with (absolute) CI coefficients larger than the threshold value for COM. Although all possible excitations are included in the CASCI-type wave function in the limit of COM → 0 (see also Figure 4 of the Supporting Information), the pattern of the CI coefficients of the DMRG(7,7)[64] calculation is different from the CI pattern of the CAS(7,7)SCF reference. While large CI coefficients (|CI | > 0.0001) are reproduced within sufficient accuracy, smaller CI weights are underestimated. The maximum of the curve is shifted toward smaller CI weights <10–7. Hence, the DMRG algorithm disregards an exact weighting of unimportant configurations with small CI coefficients, which is a feature of matrix product and tensor network states where large CI coefficients should be reproduced and unimportant configurations are neglected70,71 A complete collection of excitation histograms for different CASCI-type wave functions can be found in the Supporting Information. To quantify the differences in the underlying wave functions for our four DMRG calculations employing mi ∈ {16, 32, 48, 64} active-system states, we calculated the quantum fidelity Fmi,mi+1, which forms in this case a set of overlap measures of {0.831887, 0.897445, 0.955669}.
Figure 3.
CI histogram of the absolute values of the CI coefficients for the Slater determinants for reconstructed CASCI-type wave function expansions from the DMRG(7,7)[m] calculations with different renormalized active-system states m for the [Fe(NO)]2+ molecule surrounded by four point charges at a distance of dpc = 0.598 Å from the iron atom. The CAS(7,7)SCF reference calculation is also shown for comparison. thr corresponds to the threshold value of COM in the sampling-reconstruction procedure and denotes the accuracy of the reconstructed CASCI-type wave function. All Slater determinants with CI coefficients in an interval as indicated on the abscissa are grouped together.
Figure 4.
Mutual information and single orbital entropies s(1) for the DMRG(13,y)[64] calculations determined for different numbers of active orbitals in the [Fe(NO)]2+ molecule surrounded by four point charges at a distance of dpc = 1.131 Å from the iron center.
We conclude that reliable spin density distributions can be calculated either from converged DMRG ground state wave functions or from the reconstructed CASCI-type wave function expansions. In particular, a fully converged DMRG wave function is not mandatory to obtain qualitatively correct spin density distributions if the CI weights of the most important configurations are well reproduced for a given m value. This holds for both the single-reference and the multireference case. A representative set of Slater determinants, i.e., the most important ones (|CI| > 0.001), is sufficient for a qualitatively correct spin density distribution.
4. Spin Density Distributions for Large Active Spaces
While we have studied the convergence features of DMRG calculations for small active spaces, for which we could obtain an exact CASSCF reference result, we shall now proceed to explore territory with DMRG that is not accessible to the CASSCF approach. In our recent analysis of CASSCF spin densities for the [Fe(NO)]2+ molecule,40 the spin density distribution was qualitatively converged with respect to the dimension of the active orbital space. For quantitatively accurate spin densities, we need to increase the dimension of the active orbital space so that important iron and ligand orbitals which are missing in the standard CASSCF calculations, e.g., the Fe dx2–y2 double-shell orbital, could also be included in the active orbital space. Here, we extend the convergence series presented in ref (40) by considering active orbital spaces containing up to 29 active orbitals. Starting with an active orbital space comprising 13 active electrons correlated in 20 active orbitals, the number of active orbitals is further increased to 24 and 29, respectively. The two largest active orbital spaces do also contain the fifth dx2–y2-double-shell orbital which could not be included in all CASSCF calculations presented in ref (40). The [Fe(NO)]2+ molecular structure features the same bond distances and angles as presented in section 3. The four point charges of −0.5e are located at a distance of 1.131 Å from the metal center in order to properly model the square-planar ligand field of the full-fledged complexes in a doublet spin state.
For all DMRG calculations, the natural orbitals from a CAS(11,14)SCF calculation are employed as orbital bases.72−74 Similarly, the CASSCF calculation as well as the calculations of the one-electron and two-electron integrals in the natural orbital basis were performed with the Molpro program package62 using Dunning’s cc-pVTZ basis set for all atoms,63,64 while the DMRG calculations are performed with the Budapest DMRG program.75 In addition, the DMRG orbital orderings were optimized for all three active orbital spaces, and the CI-DEAS starting guess was performed. Figure 4 displays the corresponding single orbital entropies given by
| 16 |
and mutual information determined by
| 17 |
where i = 1...k is the orbital index and runs over all k one-particle states and ωα,i is the α eigenvalue of the reduced density matrix of orbital i,61 while s(2)i,j is the two-orbital entropy between a pair (i,j) of sites introduced by Rissler et al. to the quantum chemical DMRG algorithm.76 Note that the mutual information and single orbital entropies are confined to the first 10 natural orbitals for all considered dimensions of the active orbital space. These natural orbitals are highly entangled and represent the most important orbitals comprised in the active orbital space. Therefore, accurate DMRG spin densities can be obtained already for a reasonably small number of active-system states. Similar entropy profiles can be obtained for smaller dimensions of the active orbital space.
The number of DMRG active-system states m was set to 128, 256, 512, 1024, and 2048, respectively. The ground state energies for all DMRG calculations are summarized in Table 3. Considering the DMRG(13,20)[m] calculations, an energy convergence of 0.135 mH (0.4 kJ/mol) is reached with respect to m. For the largest active orbital space, the DMRG(13,29)[1024] energy is converged to 1.195 mH (3.1 kJ/mol) when compared to the DMRG(13,29)[2048] reference.
Table 3. Ground State Energy for [Fe(NO)]2+ Surrounded by Four Point Charges at a Distance of dpc = 1.131 Å from the Iron Center in Hartree Atomic Units for Our DMRG(x,y)[m] Calculations Employing Different Numbers of DMRG Active-System States ma.
|
E/Hartree | |||
|---|---|---|---|
| method | DMRG(13,20) | DMRG(13,24) | DMRG(13,29) |
| m = 128 | –1393.014662 | –1392.991085 | –1393.014010 |
| m = 256 | –1393.018626 | –1393.019309 | –1393.024883 |
| m = 512 | –1393.020065 | –1393.021876 | –1393.030374 |
| m = 1024 | –1393.020511 | –1393.022946 | –1393.033001 |
| m = 2048 | –1393.020646 | –1393.023294 | –1393.034196 |
The CAS(11,14)SCF energy is −1393.013 396 Hartree.
4.1. Convergence of DMRG Spin Densities
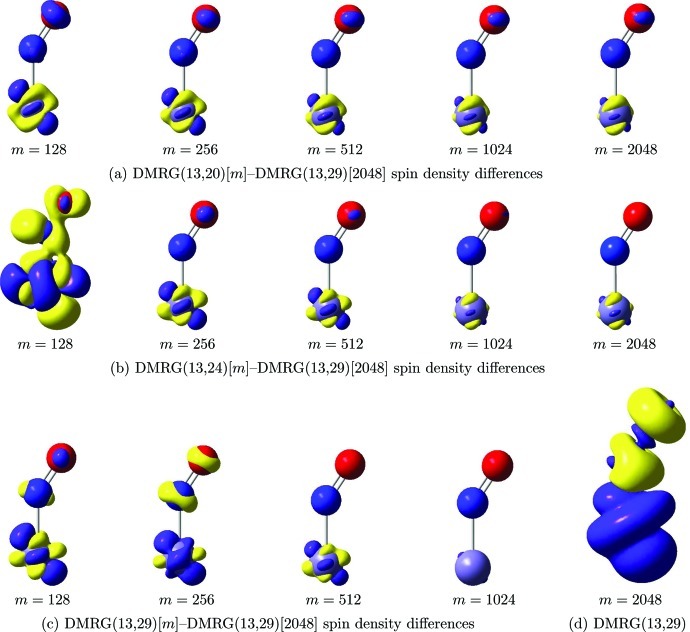
The dependence of the spin density distribution on the number of DMRG active-system states m is shown in Figure 5 where the differences in spin density distribution are plotted for DMRG(13,y)[m] calculations with respect to the converged DMRG(13,29)[2048] reference calculation. For increasing m values, the differences in the spin density distribution decrease (see each row in Figure 5 from the left to the right). Similarly, we observe that the spin density gradually converges with respect to the dimension of the active orbital space (see last column from the top to the bottom of Figure 5). In particular, changes in the spin density are negligible when m is increased from 1024 to 2048, and hence, reliable spin density distributions can be obtained even if the total energy is not yet converged with respect to m (the difference is 1.195 mH, see above).
Figure 5.
DMRG(13,y)[m] and CAS(x,y)SCF spin density difference plots with respect to the DMRG(13,29)[2048] spin density distribution (d) for [FeNO]2+ surrounded by four point charges at a distance of dpc = 1.131 Å from the iron center. All spin densities are displayed for an isosurface value of 0.001. (a) DMRG(13,20)[m]–DMRG(13,29)[2048] spin density difference plots. (b) DMRG(13,24)[m]–DMRG(13,29)[2048] spin density difference plots. (c) DMRG(13,29)[m]–DMRG(13,29)[2048] spin density difference plots. (d) The DMRG(13,29)[2048] reference spin density distribution.
Furthermore, the Δabs and Δrs values quantify the convergence series of the determined DMRG spin density distributions. In Table 4, both error quantities are listed for each DMRG(x,y)[m] spin density with respect to the DMRG(13,29)[2048] reference spin density. In general, the absolute error Δabs and the root-square error Δrs decrease for increasing m, keeping the dimension of the active orbital space fixed. Note that larger active orbital spaces require a larger m value to obtain the same accuracy as achieved in smaller active space calculations. This is not immediately evident from the error data presented in Table 4 since different dimensions of the active orbital space are compared, which result in nonzero error values, while error values determined for different parameter sets, but the same dimension of the active orbital space, could vanish. The large error values for the DMRG(13,24)[128] calculation indicate that important states were not picked up by the DMRG algorithm, resulting in the large differences in the spin density distribution displayed in Figure 5. Furthermore, since both error values determined for the DMRG(13,29)[1024] calculation are below the threshold values, no considerable improvement in the accuracy of the spin density distribution can be expected when m is further increased to more than 2048 active-system states.
Table 4. The Absolute Error Δabs and the Root-Square Error Δrs of the DMRG(13,y)[m] Spin Densities with Respect to the Converged DMRG(13,29)[2048] Reference Spin Density for a Different Number of Normalized Active-System States m for [FeNO]2+ Surrounded by Four Point Charges at a Distance of dpc = 1.131 Å from the Iron Centera.
| method | Δabs | Δrs |
|---|---|---|
| DMRG(13,20)[128] | 0.030642 | 0.008660 |
| DMRG(13,20)[256] | 0.020088 | 0.004930 |
| DMRG(13,20)[512] | 0.016415 | 0.003564 |
| DMRG(13,20)[1024] | 0.015028 | 0.003162 |
| DMRG(13,20)[2048] | 0.014528 | 0.003028 |
| DMRG(13,24)[128] | 0.590022 | 0.235922 |
| DMRG(13,24)[256] | 0.020993 | 0.003245 |
| DMRG(13,24)[512] | 0.014045 | 0.003633 |
| DMRG(13,24)[1024] | 0.011622 | 0.002668 |
| DMRG(13,24)[2048] | 0.010731 | 0.002361 |
| DMRG(13,29)[128] | 0.032171 | 0.010677 |
| DMRG(13,29)[256] | 0.026005 | 0.006790 |
| DMRG(13,29)[512] | 0.010826 | 0.003406 |
| DMRG(13,29)[1024] | 0.003381 | 0.000975 |
| CAS(11,11)SCF | 0.086658 | 0.024495 |
| CAS(11,12)SCF | 0.080249 | 0.020591 |
| CAS(11,13)SCF | 0.046303 | 0.011402 |
| CAS(11,14)SCF | 0.042544 | 0.010954 |
| CAS(13,13)SCF | 0.052239 | 0.012124 |
| CAS(13,14)SCF | 0.073400 | 0.019850 |
| CAS(13,15)SCF | 0.053157 | 0.011180 |
| CAS(13,16)SCF | 0.104928 | 0.031922 |
The Δabs and Δrs values of the CAS(x,y)SCF calculations of ref (40) with respect to the DMRG(13,29)[2048] reference spin density are also listed.
In order to demonstrate the convergence of the DMRG(13,29) wave function with respect to m (and thus the convergence of the obtained DMRG(13,29)[2048] reference spin density distribution), the CASCI-type wave function expansions are reconstructed and compared for all m values. In particular, the influence of the missing dx2–y2-double-shell orbital can be assessed by examining the CI coefficients corresponding to Slater determinants with an occupied dx2–y2-double-shell orbital. Following the conclusions of a benchmark study for intermediate CAS sizes (see Supporting Information), only the most important configurations (|CI| ≥ 0.00001) are necessary to obtain an accurate wave function expansion. As the convergence threshold for the sampling procedure, a value of 0.001 is sufficient. With this threshold, similar CASCI-type wave function expansions are obtained for a quantum fidelity measure close to 0.998. The set of quantum fidelity measures Fmi,mi+1 for our five DMRG calculations with mi ∈ {128, 256, 512, 1024, 2048} is {0.991800, 0.995510, 0.996983, 0.997639}. As the number of DMRG active-system states is enlarged, the CI coefficients of the reconstructed wave function expansion converge gradually, which is indicated by the increasing quantum fidelity measure. Note that Fm1,m2 is close to the ideal value of 0.998 already for a small number of DMRG active-system states m, and hence, only minor variations in the large CI coefficients occur when m is increased, which explains the slight differences in the spin density distributions displayed in Figure 5c.
To demonstrate that this is indeed the case, the CI coefficients of the most important Slater determinants (|CI| > 0.0001) corresponding to the m = 128 and m = 1024 calculations are shown in Figure 6. Slater determinants with large CI weights (|CI| > 0.05) are similar for both DMRG parameter sets; only minor deviations can be observed. Note that all of these Slater determinants have been incorporated in the DMRG wave function already for m = 128. Considerable differences in CI weights are present for Slater determinants corresponding to small-valued CI coefficients (|CI| < 0.015), while some Slater determinants with |CI| < 0.01 have not been incorporated in the DMRG wave function for m = 128. These off-size or missing configurations lead to the different spin density distributions for small m values.
Figure 6.

Distribution of the absolute value of the CI coefficients for the DMRG(13,29)[m] calculations with m = 128 and 1024, respectively, for [FeNO]2+ surrounded by four point charges at a distance of dpc = 1.131 Å from the iron center. The CI coefficients reconstructed for both DMRG calculations are always printed for the same Slater determinants. The determinants are ordered according to the CI weight of the DMRG(13,29)[2048] reference calculation.
From the reconstructed CASCI-type wave function, the influence of the dx2–y2-double-shell orbital as well as of the empty ligand orbitals on the spin density distribution can be analyzed. In the upper part of Table 5, configurations containing an occupied dx2–y2-double-shell orbital and corresponding to the largest CI coefficients are presented. In the lower part of Table 5, some selected configurations with large CI coefficients carrying excitations to empty ligand orbitals that cannot be included in standard CASSCF calculations are presented and compared for the DMRG(13,29)[128] and DMRG(13,29)[1024] calculations. In general, Slater determinants with an occupied dx2–y2-double-shell orbital feature small CI weights (|CI| ≤ 0.003) and are hence of minor importance, while Slater determinants bearing occupied ligand orbitals feature large CI coefficients. Configurations containing occupied ligand orbitals that are only included in the DMRG(13,29)[m] calculations (marked in bold face in Table 5) possess considerably large CI weights. All other Slater determinants with excitations to different empty ligand orbitals have smaller CI coefficients. Hence, those ligand orbitals pose a significant contribution in obtaining accurate spin density distributions for the small model complex and cannot be neglected from the active orbital space.
Table 5. Some Important Occupation Number Vectors (ONV) with the Corresponding CI Weights from DMRG(13,29)[m] Calculations for [FeNO]2+ Surrounded by Four Point Charges at a Distance of dpc = 1.131 Å from the Iron Centera.
| CI weight |
||
|---|---|---|
| Slater determinant | m = 128 | m = 1024 |
| b2b222a0a0000000 0000000 a 00000 | 0.003252 | 0.003991 |
| bb2222aa00000000 0000000 a 00000 | –0.003226 | –0.003611 |
| 222220ab00000000 0000000 a 00000 | –0.002762 | –0.003328 |
| ba2222ab00000000 0000000 a 00000 | 0.002573 | 0.003022 |
| b2a222a0b0000000 0000000 a 00000 | –0.002487 | –0.003017 |
| 202222ab00000000 0000000 a 00000 | 0.002405 | 0.002716 |
| b222a2a0b0000000 0000000 0 0000a | 0.010360 | 0.011558 |
| 22b2a2a0a0000000 0000000 0 b0000 | 0.009849 | 0.011366 |
| 22b2a2a0b0000000 0000000 0 a0000 | –0.009532 | –0.011457 |
| b2222aab00000000 0000000 0 0000a | –0.009490 | –0.010991 |
| a2222baa00000000 0000000 0 0000b | –0.009014 | –0.010017 |
| b2b222a0a0000000 0000000 0 0a000 | 0.008820 | 0.010327 |
| b2222aab00000000 00a0000 0 00000 | –0.004277 | –0.005436 |
| 22b2a2a0b0000000 a000000 0 00000 | –0.004224 | –0.006852 |
Upper part: ONVs containing an occupied dx2–y2 double-shell orbital (marked in bold face). Bottom part: additional selected important configurations with occupied natural orbitals that cannot be included in the active orbital space in CASSCF calculations (marked in bold face), for the same DMRG(13,29)[m] calculations. 2: doubly occupied natural orbital. a: natural orbital occupied by an α electron. b: natural orbital occupied by a β electron. 0: empty natural orbital.
4.2. Assessment of CASSCF Spin Densities
The converged DMRG(13,29)[2048] reference spin density can be used to assess the accuracy of CASSCF spin density distributions and benchmark the quality of the (restricted) active orbital spaces in standard CASSCF calculations (see Figure 7a). Note that the same isosurface value has been taken to display the DMRG(13,y)[m]–DMRG(13,29)[2048] and CAS(x,y)SCF–DMRG(13,29)[2048] spin density difference plots. The CASSCF spin density distributions determined for medium-sized active orbital spaces oscillate around the converged DMRG spin density. Depending on which double-d-shell orbital is included in the active orbital space, the β-electron density around the NO ligand is either overestimated or underestimated. This results either in pure spin-polarized cases with β-electron density found only around the nitrosyl ligand for CAS(11,11), CAS(11,14), CAS(13,13), and CAS(13,14) or some additional α-electron density present around the NO ligand associated with a simultaneous decrease in the β-electron density for CAS(11,12), CAS(11,13), CAS(13,15), and CAS(13,16).
Figure 7.

(a) CAS(x,y)SCF and (b) DFT spin density difference plots with respect to the DMRG(13,29)[2048] spin density distribution for [FeNO]2+ surrounded by four point charges at a distance of dpc = 1.131 Å from the iron center. All spin densities are displayed for an isosurface value of 0.001.
Similarly, the large Δabs and Δrs values stress the differences in the spin density distributions which are considerably larger than those from the DMRG(13,y)[m]–DMRG(13,29)[2048] difference analysis (Table 4). Furthermore, Table 4 indicates that the CAS(11,11)SCF and CAS(11,12)SCF calculations and the CAS(11,13)SCF and CAS(11,14)SCF calculations, respectively, are of similar accuracy, as they have similar error values, but the spin density difference plots emphasize the qualitatively different spin density distributions. Increasing the dimension of the active orbital space results in even larger deviations from the DMRG reference spin density because the active space is not stable and important orbitals are rotated out of the CAS. Note that all DMRG calculations—except DMRG(13,24)[128]—yield smaller error values and smaller differences in the spin density difference plots.
Although the CASSCF spin densities are quantitatively converged with respect to the active orbital space, significant qualitative—but also non-negligible quantitative—differences to the DMRG(13,29)[2048] reference spin density can be observed. The extension of the active orbital space by including an additional shell of d orbitals only is not sufficient to obtain a qualitatively accurate spin density distribution for the small iron nitrosyl molecule. Our analysis indicates that empty ligand orbitals are essential for calculating reliable reference spin densities. This may have severe implications for the standard CASSCF approach that require further analysis in future work.
4.3. Comparison to DFT Spin Densities
A comparison of DFT and CASSCF spin density distributions for medium-sized active orbital spaces for the [FeNO]2+ molecule has already been discussed in our previous work (see ref (40) for more details). For an unambiguous benchmark of approximate exchange–correlation density functionals, the DFT spin densities of ref (40) can be compared to the DMRG reference distribution. The qualitative analysis of the DFT–DMRG(13,29)[2048] spin density difference distributions is shown in Figure 7b. When comparing to the results obtained in ref (40), similar conclusions concerning the performance of approximate exchange–correlation density functionals can be drawn. The best agreement is found for BP86, BLYP, and TPSS, while the remaining approximate exchange–correlation density functionals yield larger deviations and result in too large spin polarization. We should note that BP86, BLYP, and TPSS correctly predict the distribution of the α-electron density around the nitrosyl ligand, although it is overemphasized. In general, nonhybrid functionals yield spin densities which are in closest agreement with the DMRG reference distributions. This observation is supported by both error measures which are smallest for BP86, BLYP, and TPSS (see Table 1 in the Supporting Information).
5. Conclusions and Outlook
In this work, we have demonstrated how reliable ab initio spin density distributions can be calculated for very large active spaces. Our procedure is based on the DMRG algorithm and on two different approaches to obtain spin density matrix elements: (i) on-the-fly directly from the second-quantized DMRG elementary operators or (ii) from an approximate CASCI-type wave function expansion which is determined by our SRCAS algorithm.57 The reconstructed CASCI-type wave function can also be used as a means to compare a series of DMRG calculations employing a different number of DMRG active-system states m.
The small noninnocent molecule [FeNO]2+ surrounded by four point charges represents a suitable system to validate our approach. The spin density distributions are highly sensitive to the nature of the converged state. We deliberately converged DMRG wave functions that correspond to local minima in the electronic energy in order to compare with qualitatively wrong wave functions. The possibility of convergence into local minima is shown by examining the (largest) CI coefficients of the SRCAS-reconstructed CASCI-type wave function. Strong deviations with respect to the absolute value of the CI coefficients indicate that the number of DMRG active-system states m is chosen too small, and hence important states have not been incorporated by the DMRG algorithm. Spin densities corresponding to such local minima deviate considerably from the ground state spin density.
The convergence analysis of the spin density distribution for the [FeNO]2+ molecule considered active orbital spaces comprising up to 29 active orbitals. Difference plots of the spin density distribution for different active orbital spaces as well as the absolute error and the root-square error in the spin density difference distribution indicate a quantitatively converged spin density with respect to the dimension of the active orbital space and the number of active-system states m (which was as large as m = 2048). The DMRG reference spin density has been used to validate CASSCF spin densities resulting in significant quantitative and even qualitative differences. Considering an additional shell of d orbitals is not sufficient to obtain reliable spin densities for the small model system, and the active orbital space must be extended by additional unoccupied ligand orbitals. Similar difficulties are likely to be present for larger iron nitrosyl complexes where the point charges are replaced by different ligands, and hence additional ligand and iron orbitals must be included in the active orbital space. The DMRG study of larger {FeNO}7 complexes is now pursued in our laboratory.
A convergence analysis of the spin density in terms of spin density difference plots with respect to the number of DMRG active-system states indicates that reliable reference spin densities can be obtained even if total energies are not converged with respect to m. A similar conclusion was found in our previous work regarding the energy splittings of states of different spin multiplicity.50,52,53 Comparison of CI weights corresponding to the most important configurations of the reconstructed CASCI-type wave functions for different m values furthermore ensures that reliable spin densities are obtained. The similarities in DMRG wave functions can be quantified by the quantum fidelity measure, which can be used as an additional convergence criterion for spin density distributions in a sequence of DMRG calculations.
Spin densities calculated from approximate CASCI-type wave functions are in good agreement with the DMRG reference spin density. Qualitatively reliable spin densities can be obtained even for large thresholds of COM (0.001) when the most important configurations have been picked up in the wave function expansion. For this threshold, the CASCI-type wave function contains Slater determinants with absolute CI weights larger than 0.00001 which are important for the spin density.
The comparison of DFT spin densities with the DMRG reference distributions allows us to benchmark approximate exchange–correlation density functionals. Although nonhybrid functionals yield spin density distributions closest to the DMRG reference, significant qualitative and quantitative differences to the DMRG reference distributions could be observed for all investigated density functionals. Similar conclusions were drawn in our previous study, where DFT spin densities were assessed against CASSCF spin densities,40 entailing that none of the investigated exchange–correlation density functionals yields sufficiently accurate spin density distributions for the [FeNO]2+ molecule.
Acknowledgments
We gratefully acknowledge financial support by a TH-Grant (TH-26 07-3) from ETH Zurich, by a grant from the Swiss National Science Foundation SNF (project 200020-132542/1), and from the Hungarian Research Fund (OTKA) under Grant Nos. K73455 and K100908. K.B. thanks the Fonds der Chemischen Industrie for a Chemiefonds scholarship. Ö.L. acknowledges support from the Alexander von Humboldt foundation and from ETH Zurich during his time as a visiting professor.
Supporting Information Available
Additional details, distributions of CI coefficients, excitation patterns and spin density distributions are available. This information is available free of charge via the Internet at http://pubs.acs.org/.
The authors declare no competing financial interest.
Supplementary Material
References
- Radon M.; Broclawik E. J. Chem. Theory Comput. 2007, 3, 728–734. [DOI] [PubMed] [Google Scholar]
- Radon M.; Pierloot K. J. Phys. Chem. A 2008, 112, 11824–11832. [DOI] [PubMed] [Google Scholar]
- Roos B. O.; Veryazov V.; Conradie J.; Taylor P. R.; Ghosh A. J. Phys. Chem. B 2008, 112, 14099–14102. [DOI] [PubMed] [Google Scholar]
- Sala X.; Ertem M. Z.; Vigara L.; Todorova T. K.; Chen W.; Rocha R. C.; Aquilante F.; Cramer C. J.; Gagliardi L.; Llobet A. Angew. Chem., Int. Ed. 2010, 49, 7745–7747. [DOI] [PubMed] [Google Scholar]
- Planas N.; Vigara L.; Cady C.; Miró P.; Huang P.; Hammarström L.; Styring S.; Leidel N.; Dau H.; Haumann M.; Gagliardi L.; Cramer C. J.; Llobet A. Inorg. Chem. 2011, 50, 11134–11142. [DOI] [PubMed] [Google Scholar]
- Frenking G.; Fröhlich N. Chem. Rev. 2000, 100, 717–774. [DOI] [PubMed] [Google Scholar]
- Ziegler T.; Autschbach J. Chem. Rev. 2005, 105, 2695–2722. [DOI] [PubMed] [Google Scholar]
- Neese F. Coord. Chem. Rev. 2009, 253, 526–563. [Google Scholar]
- Rozanska X.; Sauer J. J. Phys. Chem. A 2009, 113, 11586–11594. [DOI] [PubMed] [Google Scholar]
- Sillar K.; Hofmann A.; Sauer J. J. Am. Chem. Soc. 2009, 131, 4143–4150. [DOI] [PubMed] [Google Scholar]
- Trinh C.; Timoshkin A. Y.; Frenking G. J. Phys. Chem. A 2009, 113, 3420–3426. [DOI] [PubMed] [Google Scholar]
- Duarte F. J. S.; Cabrita E. J.; Frenking G.; Santos A. G. Chem.—Eur. J. 2009, 15, 1734–1746. [DOI] [PubMed] [Google Scholar]
- Fan J.; Autschbach J.; Ziegler T. Inorg. Chem. 2010, 49, 1355–1362. [DOI] [PubMed] [Google Scholar]
- Podewitz M.; Reiher M. Adv. Inorg. Chem. 2010, 62, 177–230. [Google Scholar]
- Savin A.On degeneracy, neardegenaracy and density functional theory. In Recent Developments and Applications of Modern Density Functional Theory, 1st ed.; Seminario J. M., Ed.; Elsevier Science B.V.: Amsterdam, The Netherlands, 1996; Vol. 4, pp 327–358. [Google Scholar]
- Reiher M. Faraday Discuss. 2007, 135, 97–124. [DOI] [PubMed] [Google Scholar]
- Cohen A. J.; Mori-Sánchez P.; Yang W. Science 2008, 321, 792–794. [DOI] [PubMed] [Google Scholar]
- Reiher M. Chimia 2009, 63, 140–145. [Google Scholar]
- Podewitz M.; Weymuth T.; Reiher M.. Density Functional Theory for Transition Metal Chemistry: The Case of a Water Splitting Ruthenium Cluster. In Modeling of Molecular Properties; Comba P., Ed.; Wiley-VCH: Weinheim, Germany, 2011; pp 139–163. [Google Scholar]
- Cohen A. J.; Mori-Sánchez P.; Yang W. Chem. Rev. 2012, 112, 289–320. [DOI] [PubMed] [Google Scholar]
- Cohen A. J.; Mori-Sanchez P.; Yang W. J. Chem. Phys. 2008, 129, 121104. [DOI] [PubMed] [Google Scholar]
- Reiher M.; Sellmann D.; Hess B. A. Theor. Chem. Acc. 2001, 106, 379–392. [Google Scholar]
- Reiher M.; Salomon O.; Hess B. A. Theor. Chem. Acc. 2001, 107, 48–55. [Google Scholar]
- Reiher M. Inorg. Chem. 2002, 41, 6928–6935. [DOI] [PubMed] [Google Scholar]
- Paulsen H.; Trautwein A. X. Top. Curr. Chem. 2004, 235, 197–219. [Google Scholar]
- Ganzenmüller G.; Berkaine N.; Fouqueau A.; Casida M. E.; Reiher M. J. Chem. Phys. 2005, 122, 234321. [DOI] [PubMed] [Google Scholar]
- Herrmann C.; Yu L.; Reiher M. J. Comput. Chem. 2006, 27, 1223–1239. [DOI] [PubMed] [Google Scholar]
- Zein S.; Borshch S. A.; Fleurat-Lessard P.; Casida M. E.; Chermette H. J. Chem. Phys. 2007, 126, 014105. [DOI] [PubMed] [Google Scholar]
- Swart M. J. Chem. Theory Comput. 2008, 4, 2057–2066. [DOI] [PubMed] [Google Scholar]
- Ye S.; Neese F. Inorg. Chem. 2010, 49, 772–774. [DOI] [PubMed] [Google Scholar]
- Conradie J.; Ghosh A. J. Phys. Chem. B 2007, 111, 12621–12624. [DOI] [PubMed] [Google Scholar]
- Jacob C. R.; Reiher M. In preparation.
- Schweiger A.; Jeschke G.. Principles of Pulse Electron Paramagnetic Resonance; Oxford University Press: Oxford, England, 2001. [Google Scholar]
- Munzarová M. L.; Engels B.; Rassolov V. A.; Chipman D. M.; Patchkovskii, Schreckenbach S., Lushington G., Neese G. H. . EPR Parameters, Methodological Aspects. In Calculation of NMR and EPR Parameters. Theory and Applications, 1st ed.; Kaupp M., Bühl M., Malkin V. G., Eds.; Wiley-VCH: Weinheim, Germany, 2004; pp 461–564. [Google Scholar]
- Munzarová M. L.; Kubáček P.; Kaupp M. J. Am. Chem. Soc. 2000, 122, 11900–11913. [Google Scholar]
- van Lenthe E.; van der Avoird A.; Wormer P. E. S. J. Comput. Chem. 1998, 108, 4783–4796. [Google Scholar]
- Neese F. J. Chem. Phys. 2003, 118, 3939–3948. [Google Scholar]
- Szilagyi R. K.; Metz M.; Solomon E. I. J. Phys. Chem. A 2002, 106, 2994–3007. [Google Scholar]
- Kossmann S.; Kirchner B.; Neese F. Mol. Phys. 2007, 105, 2049–2071. [Google Scholar]
- Boguslawski K.; Jacob C. R.; Reiher M. J. Chem. Theory Comput. 2011, 7, 2740–2752. [DOI] [PubMed] [Google Scholar]
- Hohenberg P.; Kohn W. Phys. Rev. 1964, 136, B864–B871. [Google Scholar]
- Parr R. G.; Yang W.. Spin-density-functional theory. In Density-Functional Theory of Atoms and Molecules, 1st ed.; Breslow R., Goodenough J. B., Halpern J., Rowlinson J. S., Eds.; Oxford University Press, Inc.: New York, 1989; pp 169–174. [Google Scholar]
- von Barth U.; Hedin L. J. Phys. C 1972, 5, 1629–1642. [Google Scholar]
- Radon M.; Broclawik E.; Pierloot K. J. Phys. Chem. B 2010, 114, 1518–1528. [DOI] [PubMed] [Google Scholar]
- Kossmann S.; Neese F. J. Phys. Chem. A 2010, 114, 11768–11781. [DOI] [PubMed] [Google Scholar]
- White S. R. Phys. Rev. Lett. 1992, 69, 2863–2866. [DOI] [PubMed] [Google Scholar]
- White S. R.; Noack R. M. Phys. Rev. Lett. 1992, 68, 3487–3490. [DOI] [PubMed] [Google Scholar]
- Legeza Ö.; Noack R.; Sólyom J.; Tincani L.. Applications of Quantum Information in the Density-Matrix Renormalization Group. In Computational Many-Particle Physics; Fehske H., Schneider R., Weie A., Eds.; Springer: Berlin/Heidelerg, 2008; Vol. 739, pp 653–664. [Google Scholar]
- Chan G. K.-L.; Dorando J. J.; Ghosh D.; Hachmann J.; Neuscamman E.; Wang H.; Yanai T.. An Introduction to the Density Matrix Renormalization Group Ansatz in Quantum Chemistry. In Frontiers in Quantum Systems in Chemistry and Physics, 1st ed.; Wilson S., Grout P. J., Maruani J., Delgado-Barrio G., Piecuch P., Eds.; Springer: Dordrecht, The Netherlands, 2008; Vol. 18, pp 49–65. arXiv:0711.1398v1 [cond-mat.str-el]. [Google Scholar]
- Marti K. H.; Reiher M. Z. Phys. Chem. 2010, 224, 583–599. [Google Scholar]
- Chan G. K.-L.; Sharma S. Annu. Rev. Phys. Chem. 2011, 62, 465–481. [DOI] [PubMed] [Google Scholar]
- Marti K. H.; Malkin Ondìk I.; Moritz G.; Reiher M. J. Chem. Phys. 2008, 128, 014104. [DOI] [PubMed] [Google Scholar]
- Barcza G.; Legeza Ö.; Marti K. H.; Reiher M. Phys. Rev. A 2011, 83, 012508. [Google Scholar]
- Helgaker T.; Jørgensen P.; Olsen J.. Spin in second qunatization. In Molecular Electronic-Structure Theory; Wiley: Chinester, England, 2000; pp 34–79. [Google Scholar]
- Greer J. C. J. Chem. Phys. 1995, 103, 1821–1828. [Google Scholar]
- Mitrushenkov A. O. Chem. Phys. Lett. 1994, 217, 559–565. [Google Scholar]
- Boguslawski K.; Marti K. H.; Reiher M. J. Chem. Phys. 2011, 134, 224101. [DOI] [PubMed] [Google Scholar]
- Moritz G.; Reiher M. J. Chem. Phys. 2007, 126, 244109. [DOI] [PubMed] [Google Scholar]
- Peres A. Phys. Rev. A 1984, 30, 1610–1615. [Google Scholar]
- Zhou H.-Q.; Orús R.; Vidal G. Phys. Rev. Lett. 2008, 100, 080601. [DOI] [PubMed] [Google Scholar]
- Legeza Ö.; Sólyom J. Phys. Rev. B 2003, 68, 195116. [Google Scholar]
- Werner H.-J.; Knowles P. J.; Lindh R.; Manby F. R.; Schütz M.; Celani P.; Korona T.; Mitrushenkov A.; Rauhut G.; Adler T. B.; Amos R. D.; Bernhardsson A.; Berning A; Cooper D. L.; Deegan M. J. O.; Dobbyn A. J.; Eckert F.; Goll E.; Hampel C.; Hetzer G.; Hrenar T.; Knizia G.; Köppl C.; Liu Y.; Lloyd A. W.; Mata R. A.; May A. J.; McNicholas S. J.; Meyer W.; Mura M. E.; Nicklass A.; Palmieri P.; Pflüger K.; Pitzer R.; Reiher M.; Schumann U.; Stoll H.; Stone A. J.; Tarroni R.; Thorsteinsson T.; Wang M.; Wolf A.. MOLPRO, version 2009.1; Cardiff University: Cardiff, United Kingdom; University of Stuttgart: Stuttgart, Germany, 2008. [Google Scholar]
- Dunning T. H. Jr. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar]
- Balabanov N. B.; Peterson K. A. J. Chem. Phys. 2005, 123, 064107. [DOI] [PubMed] [Google Scholar]
- Moritz G.; Marti K. H.; Boguslawski K.; Reiher M.. Qc-Dmrg-ETH; ETH Zürich: Zürich, Switzerland, 2011. [Google Scholar]
- Chan G. K.-L.; Head-Gordon M. J. Chem. Phys. 2002, 116, 4462–4476. [Google Scholar]
- Dorando J. J.; Hachmann J.; Chan G. K.-L. J. Chem. Phys. 2007, 127, 084109. [DOI] [PubMed] [Google Scholar]
- Legeza Ö.; Röder J.; Hess B. A. Phys. Rev. B 2003, 67, 125114. [Google Scholar]
- Legeza Ö.; Sólyom J. Phys. Rev. B 2004, 70, 205118. [Google Scholar]
- Marti K. H.; Bauer B.; Reiher M.; Troyer M.; Verstraete F. New J. Phys. 2010, 12, 103008. [Google Scholar]
- Marti K. H.; Reiher M. Phys. Chem. Chem. Phys. 2011, 13, 6750–6759. [DOI] [PubMed] [Google Scholar]
- Werner H.-J.; Meyer W. J. Chem. Phys. 1981, 74, 5794–5801. [Google Scholar]
- Werner H.-J.; Knowles P. J. J. Chem. Phys. 1985, 82, 5053–5063. [Google Scholar]
- Knowles P. J.; Werner H.-J. Chem. Phys. Lett. 1985, 115, 259–267. [Google Scholar]
- Legeza Ö.QC-DMRG-Budapest; HAS RISSPO: Budapest, Hungary, 2011.
- Rissler J.; Noack R. M.; White S. R. Chem. Phys. 2006, 323, 519–531. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.