Retrospective Distortion Correction for 3D MR Diffusion Tensor Microscopy using Mutual Information and Fourier Deformations

Abstract

Magnetic resonance diffusion tensor imaging (DTI) can be complicated by distortions that contribute to errors in tissue characterization and loss of fine structures. This work presents a correction scheme based on retrospective registration via mutual information (MI), using Fourier transform (FT)-based deformations to enhance the reliability of the entropy-based image registration. The registration methodology is applied to correcting distortions in 3D high-resolution DTI datasets, incorporating a complete set of affine deformations. Results demonstrate that the proposed methodology can consistently and significantly reduce the number of mis-registered pixels, leading to marked improvement in the visualization of internal brain white matter structure via DTI. Post-registration analysis reveals that eddy current effects cannot fully account for the observed image distortions. Combined, these findings are supportive of the non-model-based, post-processing approach for correcting the distortions, and demonstrate the advantages of combining FT-based deformations and MI registration in enhancing the practical utility of DTI.

I. Introduction

Magnetic resonance diffusion tensor imaging (DTI) (1) is a valuable tool for characterizing the microstructure and studying the structure-function relationships of ordered tissues, such as the brain white matter (2,3) and myocardium (4,5). The principle of DTI is based on probing the anisotropy of water diffusion exerted by the tissue microstructure, measuring the molecular translational motion on a pixel-by-pixel basis in terms of a 3 × 3-tensor model. Strong evidence exists to support that the eigenvector of the largest diffusion tensor eigenvalue (i.e., direction of fastest diffusion) parallels the local tissue fiber orientation (4). DTI has been applied to render and visualize large brain white matter tracks (6,7), and used in monitoring changes of brain tissue properties associated with clinical conditions such as ischemia (8), acute stroke (9), multiple sclerosis (10), and schizophrenia (11).

The typical DTI experiment necessitates diffusion to be quantified along a minimum of 6 non-collinear directions, which are determined by the relative amplitudes of the encoding laboratory x, y, and z gradients. However, in addition to enhanced sensitivity to bulk motion, the large gradients required for adequate diffusion weighting make DTI particularly prone to image distortions arising from instrument imperfections, most notably eddy currents. Although the correction would be simple if the distortions are identical in all images, this is often not the case in DTI when different images are encoded with different diffusion gradient magnitudes and directions. The dissimilar distortions are a primary cause of erroneous estimates of tissue fiber orientations and diffusion anisotropy indices (12), particularly for tissue borders and fine structures. Therefore, a key to improve the quality of DTI is to eliminate these image-to-image variations in distortion.

Distortion corrections in DTI, especially for eddy current effects (13-20), have generally relied on a priori modeling and characterizing of the effects of the individual gradients on the image formation process (e.g., contributions to translation, scaling and shearing in the phase-encoding axis by gradient amplitudes experiencing finite exponential decay) and correcting for an arbitrary diffusion encoding gradient direction via the principle of superposition. Although relatively easy to perform once the initial modeling is done, these correction techniques are most suitable only when the image distortions are both predictable and confined to the specific modes of deformations represented.

An adjunct or alternative approach to model-based image distortion correction is via retrospective image registration (21), which involves iterative image deformation and comparison against a common, preferably distortion-free, reference image in terms of some similarity metric (i.e., objective or cost function). Image cross-correlation is an obvious choice and has been previously used as the objective function in registration (13,20), but its utility in DTI is hampered by the dissimilar image contrast among diffusion-weighted images encoded in different directions. A more robust metric (i.e., not directly dependent on one-to-one matching of the image intensity) is the entropy-based mutual information (MI) function, which has been shown useful in cross-modality registration (22,23), and recently extended to DTI distortion correction (24,25).

Because image deformation unavoidably results in non-integral pixel coordinates, a significant challenge in MI image registration is that the objective function is often made artificially rugged by image interpolation, giving rise to local maxima that complicate the registration optimization process (26,27). To alleviate the problem, sophisticated interpolation and MI computation schemes have been proposed (22,28,29). However, most schemes are fundamentally constrained by employing a finite interpolation kernel (i.e., the neighborhood of pixels used in estimating the value of a given location) (28,30). Although desirable for computation time considerations, the low-pass filtering nature of finite kernels is a key factor contributing to the bumpiness of the objective function.

The goal of the present study is to develop a robust distortion correction technique to enhance the accuracy and utility of DTI. To accommodate distortions that need not be predictable, and images of varying contrast, the approach of retrospective image registration via mutual information is taken. In contrast to recent reports on the same subject (24,25), the current registration methodology (a) does not presume the distortions to be caused by eddy current effects or patient motion, which has implications for the DTI post-processing, and (b) incorporates in the MI computation the use of Fourier transformation (FT) operations to achieve image deformation. The latter is expected to be advantageous because it not only takes advantage of the nature of the MRI k-space data, but also conveniently circumvents much of the interpolation-related difficulties. The proposed methodology is demonstrated on 3D fixed mouse brain DTI datasets, with a post-registration analysis performed to validate the approach of non-model-based, retrospective distortion correction.

II. Theory

For the sake of completeness of the discussion, included here is a brief review of the image processing theories underlying the proposed DTI registration technique. In this paper, the source image refers to the distorted image requiring correction. For registration, an entropy-based objective function (e.g., MI) is computed with respect to the reference image (assuming to be distortion-free) for each successive intermediate tentative pose image obtained by applying corrective deformations to the source image, and is used to predict the deformation parameters for the next iteration (22). The steps are repeated until the registration metric, and hence the correction for distortion, are optimized. Treating the images as random variables, the mutual information between images I₁ and I₂ is defined as

$$\mathit{MI}(I_1,I_2)=H\left(I_1\right)+H\left(I_2\right)-H(I_1,I_2),$$ (1)

where H(•) and H(•,•) denote the marginal and joint entropy of images, respectively, estimated from the corresponding image intensity histograms (31). Several variants of MI have been introduced over the years, for example, normalized mutual information (28), which has been shown to be less prone to higher values at decreasing overlaps, or rather increasing mis-registration. Other variants of mutual information include combining MI with spatial gradients that define the edges in an image (29). Including edge information has been shown to improve the smoothness of the objective function for image registration.

Despite the robustness of entropy-based registration techniques, image interpolation presents a significant source of complication, especially for registering relatively noisy and low-resolution images, including DTI. Most notable in conventional (e.g., linear and cubic) interpolation techniques, the abrupt changes in the objective function at grid-aligning transformations not only make the multi-dimensional optimization process challenging, but also make sub-pixel accuracy difficult, if not impossible (26). From a signal and image processing perspective, the finite kernels employed in most interpolation schemes are in effect low-pass filters, which cause both blurring and uneven suppression of noise, resulting in biased frequency response and image histogram. The obvious solution is to employ larger-size interpolation kernels, albeit at the cost of increased computation time.

Fortunately, the inherent discrete FT nature of MRI data (i.e., k-space) offers convenient ways to perform image deformations via properties of FT without interpolation. Denoting the acquired k-space data by S, the FT shift theorem states that translation by the amount of T in the image I spanned by r = (x, y,z)^T is given by

$$\mathit{I}(\mathbf{r}+\Delta )={\Im }^{-1}\left\{S\right(\mathbf{k})\cdot e^{i2\pi (\mathbf{k}\cdot \Delta )}\},$$ (2)

where ℑ is the Fourier transform and k = (kx,ky,kz)^T is the k-space coordinate. Similarly, a shear deformation corresponds to single-dimensional translations whose magnitudes vary linearly as a function of the dimensional position. As such, for example, shear in the x direction along the y-axis and the k-space data are related by

$$I_{\Psi xy}\left(\mathbf{r}\right)={\Im }_x^{-1}\left\{{\Im }_{yz}^{-1}\left\{S\left(\mathbf{k}\right)\right\}{e}^{i2\pi \cdot \Psi xy\cdot kx\cdot y}\right\},$$ (3)

where Ψxy is the magnitude of shear and I_Ψxy(x, y) is the resultant image. (A shear deformation that tilts the y-axis by the angle θ while leaving the x-axis unaffected corresponds to Ψxy ≅ tanθ.)

The basic premise of the current study is that FT-based deformations can be incorporated to improve the reliability of entropy-based image registrations. Because each point of the deformed image is computed from the entire image, the FT deformations are, procedurally, equivalent to sinc-interpolation using the maximally allowable kernel (32), which has been deemed ideal but impractical (when implemented via kernel convolution) for entropy-based registration (33). Although FT image transformations have been previously used in image registration (34), they were used only to realize the deformations of the final solution. Moreover, FT-based deformations have also been used in non-iterative algorithms for motion correction in MRI (35). Consequently, the suitability of FT deformations for iterative, entropy-based registration until now remains largely uninvestigated.

Because DTI relies on the physical representations (i.e., measured attenuations along the diffusion encoding directions) of the image intensity, depending on the nature of the distortions, the registered individual diffusion-weighted images may not be directly usable for DTI postprocessing without appropriate additional steps being taken. For example, corrections for eddy current-induced size-scaling distortions require proportional rescaling of the image intensity prior to diffusion tensor computation (25). In contrast, compensating for image-to-image rotational motion necessitates re-orientation of the corresponding diffusion-encoding direction. Since in the present study neither eddy current effects nor motion is presumed to be the source of the distortions, no additional manipulations were applied to the corrected images and the gradient directions during DTI post-processing.

III. Methods

A. DTI datasets

Retrospective computational experiments were performed using a modest platform that consisted of MATLAB (Version 6.5, The Mathworks, Inc., Natwick, MA) on a 3.06 GHz Xeon IV dual-processor computer. Three-dimensional, high-resolution DTI datasets (N = 6) of fixed mouse brains were obtained from a separate study. Briefly, each DTI dataset consists of a non-weighted (b0) and diffusion-weighted (b ≈ 1200 s/mm²) images (256 × 128 × 128 matrix size, 100 μm isotropic resolution) encoded in an optimized set of 12 gradient directions (36) acquired using a standard spin echo sequence on a 9.4 T instrument. Because it was acquired using spin echo and no diffusion-encoding gradient, the b0 image can reasonably be presumed to be distortion-free and thus used as the registration reference image.

B. Distortion correction via registration

The overall strategy in distortion correction was to separately register each diffusion-weighted image to the b0 image. Without loss of generality, distortions represented by only affine transformations, but all modes of the transformations, were incorporated in the correction. The deformations corrected consisted of translation Δx, Δy and Δz (x, y and z denote the frequency, phase, and “slice” encoding axes, respectively), shearing Ψxy, Ψyx, Ψxz, Ψzx, Ψyz, and Ψzy, and scaling operations Γx, Γy, and Γz. (Note that a rigid-body rotation can be realized by a pair of opposing shear operations; however, the latter implementation does not require the deforming body to be rigid.) as Unless otherwise specified, MI was employed as the objective function and FT deformations were used to perform translation and shear. Because the corresponding FT method requires interpolation of frequency-domain (or k-space) data and thus no advantage was anticipated, image scaling was implemented using image-domain cubic interpolation

For registration, MI between each intermediate tentative pose image and the reference image was computed from their image histograms. Each histogram was divided into 81 bins, based on the cubic root of the number of image pixel elements, primarily to have sufficient number of samples in each bin (27). A coarse search was performed over the individual dimensions of the deformation space (within the range of ±10 pixels in steps of 0.5 pixels for translation, ±10° in steps of 0.5° for shear, and unity scaling) to obtain the initial input for optimization. Subsequently, the Levenberg-Marquardt (LM) algorithm (37) was utilized to search for the MI maximum in the multi-dimensional parameter space, with search increments computed adaptively using finite differences (for calculating the gradient of the registration metric) during the optimization process. The solution to the optimization procedure was applied to correct distortions in the source images.

C. Comparisons of interpolation schemes

To demonstrate the advantages of FT-based deformations for image registration, MI profiles were computed from deliberately distorted diffusion-weighted images and their corresponding b0 images. The MI functions graphed against individual dimensions of translation (with range of ±3 pixels in increments of 0.25 pixels) and shear (up to ±3° in increments of 0.25°) were compared among linear and cubic interpolations, and FT-based deformations.

D. Application to 3D DTI

The proposed registration technique was applied to correcting 3D fixed mouse brain DTI datasets, and the results were evaluated against uncorrected datasets. To evaluate the degree of original distortion and the effectiveness of the distortion correction, the uncorrected and registered diffusion-weighted images were overlaid with the boundary of the brain obtained from the undistorted b0 reference image.

The effectiveness of the registration was also evaluated quantitatively by tallying the number of mis-registered pixels within each uncorrected and registered DTI datasets. To this end, morphological templates for the mouse brain were obtained for each image of the DTI dataset by applying intensity thresholds, determined based on visual inspection of the intensity histogram, to the b0 image. The number of mis-registered pixels (i.e., output of the Boolean exclusive-or operation against the undistorted b0 template) of each diffusion-weighted image were counted, and expressed as a percentage of the brain volume in the b0 image. The mean and standard deviation of mis-registered pixels among all diffusion-weighted images were used as a measure of the consistency of registration for each DTI dataset.

The above pixel count included only mis-registered pixels at the brain periphery. To demonstrate the practical utility of registration in enhancing DTI visualization of the brain internal structure, diffusion tensors were estimated on a pixel-by-pixel basis via multivariate nonlinear least-squares curve-fitting, and diagonalized. The fractional anisotropy (FA) index (12) was computed from the diffusion tensor eigenvalues. Subsequently, the brain white matter fiber structure was visualized as FA-weighted, red-green-blue (RBG) color-coded orientation maps (38) of the eigenvectors of the largest diffusion tensor eigenvalues.

E. Registration post-analysis

To investigate the nature and potential source of the image distortions seen in the current 3D DTI datasets, linear correlation coefficients r were computed between each deformation parameter and each Gx, Gy and Gz components of the diffusion sensitization gradient among the 12 diffusion-weighted images in each DTI dataset. A basic premise is that distortions due to, for example, eddy currents are proportional to the amplitudes of the individual diffusion encoding gradient pulses, which are represented by the Gx, Gy and Gz gradient components when the encoding directions are oblique. Linearity, and thus predictability, of the image distortion with respect to the gradient amplitudes would manifest in high correlation coefficients.

IV. Results

Figure 1 shows the computed MI functions obtained using linear and cubic interpolations, and FT-based implementations for the Δy and Ψxy deformations, which are representative for the results obtained for other parameters of translation and shear distortions and for other diffusion-weighted images examined. The MI profiles for the translation using linear and, to a lesser extent, cubic interpolations exhibit conspicuous false maxima at non-integral amounts of shift. The plots for shear using these interpolation schemes contain a local minimum near the zero-deformation center. In contrast, the corresponding FT cases reveal smooth and unimodal profiles, absent of local extrema that would likely complicate the registration optimization process. These results demonstrate the advantages and validate the choice of FT-based deformations in registration.

Figure 1.

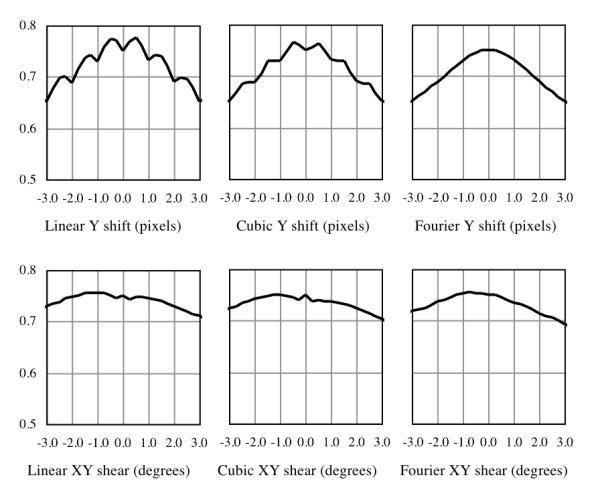
Comparison of mutual information as functions of deformations by different interpolation techniques. In contrast to linear and cubic interpolations, the smoothened profile and unique maximum of the Fourier transform-based deformations are expected to be advantageous for the MI optimization.

Combining FT-based deformations and MI registration in distortion correction of 3D fixed mouse brain DTI datasets, Fig. 2 shows mid-brain coronal slices of corresponding original and post-registration diffusion-weighted images of a representative specimen. Using the overlaid brain boundary from the b0 image (i.e., registration reference) as a guide, the uncorrected image contains conspicuous of distortions (e.g., horizontal shift). In contrast, the retrospective distortion correction yielded a registered image that closely matches the reference brain. For the retrospective 3D registration, the solution was reached typically within 200 iteration steps in about 1.0 hr on the current computation platform.

Figure 2.

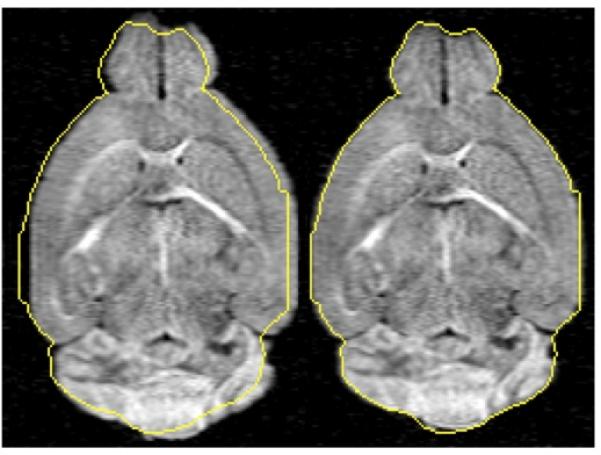
Distortion correction for a representative diffusion-weighted mouse brain MR image. A single coronal slice of the 3D volume is shown, superimposed with the outline (gold solid line) of the registration reference (b0) image. Although the brain structure is relatively symmetrical, anisotropic diffusion in the brain white matter yielded asymmetrical contrast. The uncorrected image (left) exhibits conspicuous misregistration. The image distortion is markedly improved via FT-based deformation (right).

Table 1 lists the intra-dataset means and standard deviations of mis-registered pixel counts before and after correction as a percentage of the total brain volume obtained for the individual DTI datasets. As a group, registration yielded significant reductions of the mean and standard deviation in the amounts of 40% (2.85% to 1.70%, N = 6, paired Student t-test P < 0.008), and 22% (0.57% to 0.44%, P < 0.001), respectively. The reductions indicate that registration lowers not only the overall number of mis-registered pixels, but also the variability among the diffusion-weighted images in each DTI dataset. Due to the inherent inaccuracy in defining morphological templates based on intensity thresholds, these pixel counts represent only a first approximation quantitative measurement of the registration improvement.

Table 1.

Pre- and post-correction intra-dataset mis-registered pixel counts

	Uncorrected		Registered
Specimen	Mean*	Stdev*	Mean*	Stdev*
1	2.85%	0.29%	1.24%	0.08%
2	2.11%	0.37%	1.48%	0.21%
3	3.70%	0.65%	1.77%	0.56%
4	1.72%	0.23%	1.39%	0.12%
5	4.60%	1.61%	2.94%	1.50%
6	2.15%	0.29%	1.39%	0.19%
Mean	2.85%	0.57%	1.70%	0.44%

^*Entries correspond to statistics based on the 12 diffusion-weighted images in each DTI dataset, expressed as percentages of the brain volume in the b0 image. Paired Student t-tests between the uncorrected and registered datasets indicate P<0.01 and P<0.001 for the voxel count means and standard deviations, respectively.

Visualization of the brain internal structure, especially the white matter, is a key goal of DTI. Figure 3 shows before and after-correction coronal and axial slices of RGB color-coded fiber orientation renderings of a representative specimen. Compared to the uncorrected case, registration of the DTI dataset leads to improved visualization manifested in brighter (due to elevated FA) as well as more sharply defined brain white matter. Importantly, the coloring of the white matter appeared more uniform, indicating that the measured orientation of the tissue contained less variability. Specific white matter structures that had markedly better visualization include the genu of the corpus callosum and stria medullaris thalami. Moreover, the fasciculus retroflexus, which was extremely difficult, if not impossible, to demarcate otherwise, becomes conspicuous after registration.

Figure 3.

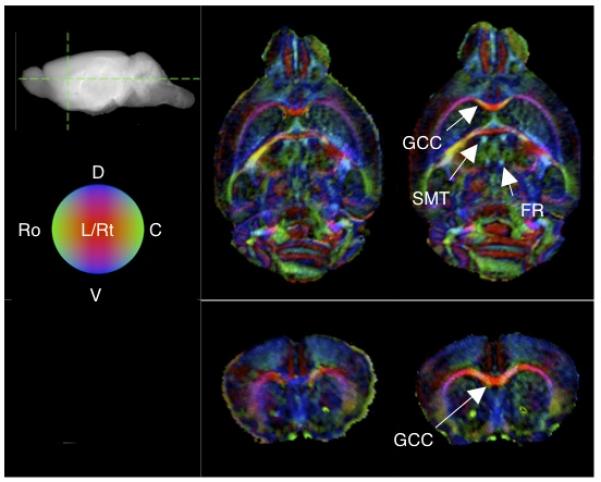
DTI visualization of mouse brain white matter structures. Slices displayed correspond to RGB-coded coronal and axial sections (locations shown on the sagital projection of the brain) obtained for uncorrected (left) and registered (right) DTI datasets from a representative specimen. The brightness is weighted by the FA anisotropy index, and the red, green and blue colors respectively represent orientation components in the left-right (L-Rt), rostral-caudal (Ro-C), and ventral-dorsal (V-D) axes, as indicated by the legend sphere. Compared to the unregistered case (top), the registered dataset (bottom) shows overall visibly sharper, brighter and more uniformly oriented white matter structures. The labeled white matter structures are the genu of the corpus callosum (GCC), stria medullaris thalami (SMT) and fasciculus retroflexus (FR).

Table 2 tabulates the correlation coefficients r between the individual registration deformation parameters and the diffusion encoding gradient amplitudes Gx, Gy and Gz. Most of the 36 relationships tested have relatively small coefficient values, indicating that the gradient amplitudes alone are poor predictors of the image distortions observed in the current study. Only two relationships, Γy-Gx and Ψyz-Gz, have mean r-values greater than 1/√2 (or r² > 0.50), meaning that more than half of the variability in the deformation was accountable by the variability of the gradient amplitude.

Table 2.

Correlations of deformation parameters and diffusion encoding gradients

Parameter	GX	GY	GZ
ΔX	0.00 ± 0.34	−0.07 ± 0.34	−0.03 ± 0.38
ΔY	0.38 ± 0.15	0.46 ± 0.08	0.38 ± 0.08
ΔZ	−0.24 ± 0.18	0.18 ± 0.38	0.23 ± 0.27
Γ X	−0.14 ± 0.24	−0.27 ± 0.23	−0.19 ± 0.19
Γ Y	−0.80 ± 0.06	0.11 ± 0.17	−0.00 ± 0.24
Γ Z	−0.28 ± 0.34	−0.33 ± 0.28	−0.47 ± 0.18
Ψ XY	0.18 ± 0.18	0.26 ± 0.34	0.25 ± 0.28
Ψ XZ	−0.25 ± 0.30	−0.54 ± 0.24	−0.23 ± 0.24
Ψ YZ	0.36 ± 0.17	0.24 ± 0.14	0.72 ± 0.09
Ψ YX	−0.11 ± 0.13	0.57 ± 0.38	0.18 ± 0.26
Ψ ZX	−0.27 ± 0.36	0.11 ± 0.30	0.08 ± 0.31
Ψ ZY	0.13 ± 0.18	−0.09 ± 0.39	−0.29 ± 0.27

Δ: shift; Γ: scaling; Ψ: shear; X: readout; Y: phase; Z slice. Entries represent means and standard deviations (among N = 6 datasets) of cross-correlations between registration parameters and encoding gradient components for the 12 diffusion-weighted images in each DTI dataset.

V. Discussion

The above results demonstrate that retrospective image distortion correction combining FT-based deformations and the MI objective function can significantly and reliably reduce the number of mis-registered pixels in the dataset (Fig. 2 and Table 1), and yield markedly improved DTI-based visualization of the brain white matter (Fig. 3). As a whole, the generally weak correlations observed between individual deformation parameters and diffusion-encoding gradient amplitudes (Table 2) suggest that the eddy current effects are unlikely to be responsible for the image distortions in the DTI dataset. Although more experimentation and analysis are needed to pinpoint the exact cause of the distortion, and the source and nature of distortion may depend on the MR instrument and pulse sequence employed, the finding is supportive of the current heuristic approach (i.e., without relying on identification of the source and predictability of its effects) toward distortion correction.

In entropy-based image registration, the complications imposed by image interpolation have long been recognized. A key underlying factor is the inadvertent noise suppression effect of most interpolation schemes. For DTI, the impact is amplified due to the inherently low signal-to-noise ratio (SNR) of the diffusion-weighted images. While pre-filtering the source images with smoothing operations (e.g., downsampling) is an intuitive solution (39), the associated spatial blurring may lower the accuracy of registration and be ineffective in recovering hidden fine (i.e., high spatial-frequency) tissue structures. Past efforts to enhance the reliability of entropy-based registration have included better interpolation schemes (e.g., partial-volume approximation (22)), variants of entropy-based similarity metric (29), and alternative optimization strategies (e.g., multi-resolution optimization (33)), each of which has its unique advantages and tradeoffs. Although the specific performances remain to be compared, the current FT methodology can be advantageous by its direct approach and computational simplicity.

Because the diffusion-weighted image intensity is defined with respect to the sensitizing gradient direction, one potential concern in performing DTI transformations, especially shear (or rotation) and scaling operations, is the need for gradient direction re-orientation (or equivalent modification in the b matrix) (40). In general, gradient direction re-orientation is required when images are transformed (globally or locally) within the reference frame in which they are acquired. However, in image distortion correction, the image formation process that generated the distortion would also distort the reference frame. Provided that the misregistration is not caused by physical motion of the imaged object, the distortion correction process would preserve the correspondence between the gradient directions and the reference frame. In the present study, the image distortion is assumed to be an imaging artifact, and gradient direction re-orientation is thus not performed.

Being based on FT-based affine deformations, the present registration technique may be limited in two aspects. First, as the registration is confined to the deformations corrected, the current technique compensates for only affine deformations, which may or may not be sufficient in characterizing more complicated distortions. Inclusion of higher-order deformations in the registration may improve the accuracy; however, the technical difficulty of multi-parametric optimization will likely also increase. Second, not all deformations can be computationally implemented via Fourier transform, hence taking advantage of the available k-space data. In the current work, spatial-domain cubic interpolation instead of FT is used to realize the scaling deformations. These limitations may have contributed in part to the residual errors seen in the registered dataset (e.g., in Table 1). Nevertheless, compared to the conspicuous improvements shown in the results, these limitations do not detract from the overall validity of employing FT-based deformations to enhance entropy-based image registration, and to improve DTI characterization of ordered tissues.

VI. Conclusions

Diffusion-weighted image distortions cause errors in the tissue characterization and loss of fine tissue structures in DTI. Retrospective registration using mutual information has been hampered by complications of image interpolation. In the current study, exploiting the available k-space (i.e., frequency-domain) data in MRI, FT-based deformations were employed in MI registration. Results show that incorporation of FT deformations can effectively eliminate the false extrema in the MI function often found in conventional interpolations. Moreover, the proposed registration methodology can significantly and reliably reduce the number of mis-registered pixels in 3D DTI datasets, and lead to marked improvement in visualizing the internal brain white matter structure, including recovering fine structures that were otherwise difficult to detect. These findings demonstrate the advantages of FT deformations in MI registration, and suggest a role of the retrospective distortion correction technique in enhancing the practical utility of DTI.

List of Symbols

I₁ , I₂

Upper case “eye” sub 1 (one) , 2 (two)

MI

Upper case M – upper case “eye”

H(•)

Upper case H, with a dot

S

Upper case S

Δx, Δy, Δz

Greek upper case delta of x, y, and z.

Δ = (Δx,Δy,Δz)^T

Greek upper case delta is a vector; “T” for transpose

r = (x, y,z)^T

Lower case bold r is a vector

ℑ⁻¹

Italic F; “-1” is for inverse

k = (kx,ky,kz)^T

Lower case bold k is a vector

Ψxy

Greek upper case psi Similar symbols with yx, xz, zx, yz, zy

Γz

Greek upper case gamma Similar symbols with x, y

b0

Lower case “bee” followed by a zero

s/mm²

Lower case s, divided by two m (mm), squared

μm

Greek lower case mu- lower case m

±10°

plus or minus, 10 (ten, for example), degrees

Gx, Gy, Gz

Upper case G with subscripts x, y, and z

r

Lowe case italic r

r²

Lower case italic r, squared