Abstract
New evidence from the Utah Population Database (UPDB) reveals that at the onset of the fertility transition, reproductive behavior was transmitted across generations--between women and their mothers, as well as between women and their husbands' family of origin. Age at marriage, age at last birth, and the number of children ever born are positively correlated in the data, most strongly among first-born daughters and among cohorts born later in the fertility transition. Intergenerational ties, including the presence of mothers and mothers-in-law, influenced the hazard of progressing to a next birth. The findings suggest that the practice of parity-dependent marital fertility control and inter-birth spacing behavior derived in part from the previous generation and that the potential for mothers and mothers-in-law to help in the rearing of children encouraged higher marital fertility.
Is fertility between parents and their children positively correlated? Although the first study of intergenerational fertility was conducted more than a century ago, the number of studies remains few. Most investigators report a positive correlation between the fertility of mothers and that of their daughters, but results vary widely. The mechanism linking fertility across generations is also unclear. Early research that advanced the genetic inheritance of fecundity has given way to studies emphasizing a wide range of possible linkages, including the importance of socialization within the family, the transmission of cultural practices and socioeconomic status across generations, and the inheritance of such psychological and biological characteristics as sex drive, fecundity, and health. New research has also extended the earlier focus on correlations in children ever born to include intermediate reproductive indicators and multivariate models of birth spacing.1
In a useful survey of the literature, Murphy concluded that the relationship between the fertility of parents and that of their children has become much more substantial over time. Indeed, most studies of natural-fertility populations suggest the correlation between mothers' and daughters' fertility is probably close to zero. If further research supports this conclusion, the fertility transition was a key moment in the emergence of intergenerational transmission of fertility. In an analysis of genealogies compiled by the Utah Genealogical Society, Anderton et al. reported that daughters' fertility levels were responsive to their mothers' relative fertility and age at marriage during the U.S. fertility transition. More recently, Reher, Ortega, and Sanz-Gimeno reported a substantial increase in the strength of intergenerational effects over the course of the fertility transition in twentieth-century Spain, suggesting the growing importance of the transmission of values and attitudes relative to biological dimensions of reproduction.2
This article takes a new look at intergenerational fertility transmission using the Utah Genealogical Dataset obtained from the Utah Resource for Genetic and Epidemiologic Research. The Utah Population Database (UPDB) includes nearly complete birth, death, and marriage data for multiple generations of the descendants of the Utah pioneers. We extend the earlier study by Anderton at al. in three ways. First, whereas the earlier study limited analysis to the transmission of reproductive behavior between index women and their mothers, the analysis herein also examines the possible transmission between an index woman and her husband's family of origin (index woman/mother-in-law correlations). An examination of the gender pattern of transmission is critical during the fertility transition in the United States, when most effective methods of marital fertility control—periodic abstinence, withdrawal, and reduced coital frequency—were subject to male agency. Although previous studies found a stronger effect for mother's than for mother-in-law's fertility, few of them were conducted in settings where power relations in the family favored male dominance over fertility decisions and where contraceptive technology required male cooperation.
Second, we investigate the possible increasing strength of intergenerational transmission throughout the course of the fertility transition. Third, we make several enhancements to the event-history analysis of birth spacing, including the addition of covariates to test new theories and increase comparability with more recent studies. For example, drawing from recent studies of fertility differentials in developing countries that suggest the importance of kin in childbearing decisions, we test whether the vital status of women's mothers and mothers-in-law affected the timing and probability of subsequent births.3
Background
Although scholars continue to debate the existence and the degree of fertility control in pre-transition populations, there is little evidence to suggest that parity-dependent fertility control was common before the mid-nineteenth century. It is therefore unlikely that intergenerational transmission of attitudes and values about a targeted norm number of children—and effective efforts to stop childbearing after reaching the targeted parity—played a significant role in the intergenerational transmission of fertility. Instead, parents' and children's fertility in “natural fertility” populations could be linked in three possible ways. One mechanism is via positive correlations between environment and socioeconomic status and their possible correlation with fecundity. As a case in point, parents and children sharing low-nutritional status or poor health due to economic stress or residence in a deleterious environment might have suffered lower fecundity relative to their better-fed and healthier peers. Shared socioeconomic status across generations might also be correlated with marriage timing and thus exposure to the risk of pregnancy. Another possible mechanism is genetic transmission. Although most population geneticists believe that large systematic genetic differences in fecundity are unlikely, studies of twins suggest that genetic inheritance plays a significant role in the transmission of fertility behavior in modern populations. Finally, non–parity-dependent behavioral practices that influence fertility and infant mortality, particularly breast-feeding practices, might have been transmitted between generations.4
Most studies of pre-transition populations, however, report no significant correlations in fertility across generations. Langford and Wilson, for example, found no evidence for the transmission of fertility across generations in their study of seven British parishes between the sixteenth and nineteenth century. Desjardins et al. found no relationship between mothers' and their daughters' interval between marriage and first birth in pre-transition Quebec. Similarly, Gagnon and Heyer discovered no relationship between parents' fertility and that of their children for the seventeenth- and eighteenth-century French Canadian population.5
The demographic transition from high birth and death rates to low birth and death rates required a substantial increase in, and perhaps even the innovation of, conscious control of marital fertility. Although the fertility transition can be explained in part by increased costs of children in a modernizing economy—particularly costs associated with urbanization, industrialization, and increased schooling of children—most historical demographers acknowledge a substantial role for ideational factors in explaining the onset and pace of fertility decline. The desire, ability, and cultural acceptability of effectively controlling fertility diffused through populations unevenly. The fertility transition increased the role of choice in fertility outcomes and the potential for fertility behaviors to be transmitted across generations. Parents were one of the most important sources for learning the ideas, norms, and behaviors that affect fertility. The economic modernization accompanying the demographic transition also increased the potential role of socioeconomic factors in differential fertility. Thus, the emergence of intergenerational fertility correlations during the demographic transition can be explained to some extent by the intergenerational transmission of socioeconomic status (SES).6
Anderton et al.'s study of Utah's genealogical records conceded the probable transmission of SES determinants of fertility across generations, but it also argued that the family was the primary locus for the transmission of attitudes and behaviors, such as marriage timing and contraceptive practices, which more directly influence fertility. Their analysis included several innovations, including a reliance on relative-fertility measures, incorporation of intermediate fertility variables, and use of event-history methods. Relative-fertility measures estimate women's fertility level vis-à-vis their age-graded peers. Women whose fertility was low relative to other women in their birth cohort might be expected to have transmitted fertility-reducing behaviors to their daughters. That approach was needed to control for the fact that fertility fell steadily during the study period, potentially biasing mother–daughter correlations. The second innovation brought such intermediate determinants of fertility as age at first marriage, length of inter-birth intervals, and age at last birth to the fore. The third innovation, the reliance on event-history methods, permitted analysis of the timing of births by parity.
Three major findings emerged from the study. First, cohort-specific influences were substantial. Associations between mothers' relative fertility and various measures of their daughters' fertility were greater than associations with mothers' absolute fertility level. Second, analysis of the intermediate determinants of fertility indicated that the indirect relationship of age at marriage was responsible for a large portion of the intergenerational correlation between mothers' relative fertility and their daughters' fertility. Finally, birth order proved to be a significant factor in the timing of births. Daughters exposed to a larger number of younger siblings exhibited a slower pace of childbearing at lower parities, suggesting that women from larger families “were in no haste to replicate their recent exposure to younger children.”7
Reher, Ortega, and Sanz-Gimeno's more recent study of intergenerational fertility during the demographic transition in the Spanish town of Aranjuez documented a considerable increase in intergenerational effects during the course of fertility transition. In contrast to Anderton et al.'s identification of the age at first marriage and the pace of childbearing as the most important intermediate variables affecting intergenerational correlations in fertility, Reher, Ortega, and Sanz-Gimeno observed that the effects were most visible in the age at last birth and duration of childbearing. Although they do not speculate on the difference, it may be due to the greater reliance on “stopping” behavior that appears to have characterized most of the fertility transition in Europe and the importance of birth “spacing” in fertility decline on the Utah frontier. Although parity-dependent control was present in the Utah fertility decline, increased spacing played a much greater role than in the European decline.8
Reher, Ortega, and Sanz-Gimeno also reported much stronger effects for first-born daughters than for later-born siblings, as well as significant effects coming from the families of index women's husbands, although those effects were much smaller than between index women and their mothers. These results closely correspond with those reported in prior studies of post-transition societies. Johnson and Stokes' follow-up study of women graduating from high schools in rural Pennsylvania in 1947 reported that fertility correlations between first-born daughters and their mothers were twice as large as correlations between later-born daughters and their mothers, suggesting either greater conformity associated with first-born children or greater socialization of eldest daughters in their roles as secondary mothers for younger siblings. Studies comparing the strength of the links between an index couple and the husband's and wife's family of origin tend to report stronger mother–daughter links, suggestive of both genetic and cultural mechanisms. Although early studies emphasized the importance of biological factors as an explanation for the stronger effects working through the family of the mother, later research has emphasized stronger mother–daughter links and the role of socialization.9
A related literature in anthropology and evolutionary biology suggests another possible mechanism through which an index woman's family or her husband's family might have affected fertility decisions. In contrast to other mammalian mothers, human mothers receive significant help in child rearing from members of their social group, particularly from spouses and grandmothers. This assistance probably explains the short birth intervals of natural-fertility human populations relative to those of great apes who are similar in body size. Because this help is critical for the health and welfare of children and mothers, humans have adapted by becoming “cooperative breeders.” Group members tell women when it is socially acceptable to have children, how many children to have, and the appropriate pace of childbearing. Postmenopausal grandmothers without significant child-rearing responsibilities of their own are particularly important in providing child-rearing and household help to mothers and in advising about subsequent fertility decisions. Researchers have shown that the presence of kin, particularly a woman's mother and mother-in-law, typically has a positive influence on fertility. Women are more likely to have children, or an additional child, when they are surrounded by supportive kin networks and perceive that the costs of childbearing are manageable.10
With a few exceptions, historical demographers have ignored the potential role of kin in reproductive decisions. Skinner's report of the positive reproductive effect of co-resident mothers and mothers-in-law in his study of Tokugawa Japanese village populations suggests an understanding that the older generation was available to help with child care. More recently, a comparative study of eighteenth- and early nineteenth-century rural populations in five European and Asian populations by Feng et al. found that the presence of a mother or mother-in-law in a household had a significant pro-natal effect only in certain contexts. In the Japanese villages of Shimomoriya and Niita, the presence of a mother or mother-in-law increased the likelihood of female births at parities larger than one but not the likelihood of male births. In the Chinese village of Liaodong, women with co-resident mothers-in-law were more likely to register a first female birth than women without co-resident mothers-in-law. The gender-specific results suggest that older women may have influenced mothers to avoid infanticide. Results for the European study populations tended to be insignificant.11
Data And Methods
The UPDB database on which this study relies includes nearly complete genealogical information for several hundred thousand individuals in families descended from the Utah pioneers of the mid-nineteenth century. The family and other relationships identified in the dataset link mothers to their own children and facilitate the linking of multiple generations.12
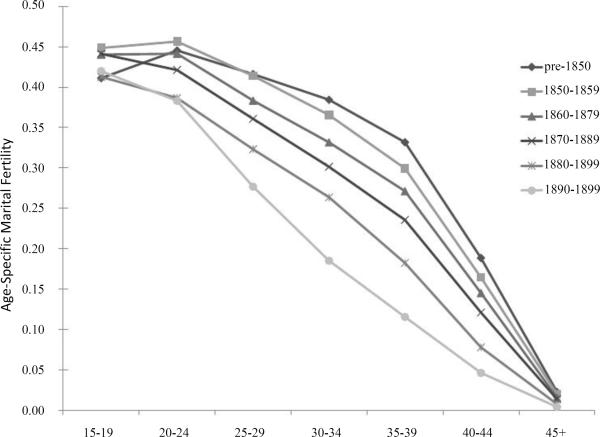
Figure 1 shows age-specific marital fertility rates for selected birth cohorts of women in the dataset. Total marital fertility (ages twenty to forty-nine) fell from 11.0 in the pre-1850 birth cohort to 7.2 in the 1890 to 1899 birth cohort. Marital fertility decline was modest through the 1870 to 1879 birth cohort but accelerated thereafter. Although marital fertility rates fell for all age groups, the faster decline for that of older age groups suggests the importance of both spacing and stopping behaviors. The marital fertility decline documented by the UPDB lagged behind that of the overall white population of the United States by several decades. Period estimates show that the total marital fertility of white women in the United States was 6.9 in 1880--a level that the women in the UPDB did not reach until c. 1905 to 1910. Ewbank's state-level estimates of marital fertility using the Public Use Sample of the 1910 census indicate that Utah was one of only two states in the nation with m values less than 0.2 in the period from 1905 to 1910. Evidently, Utah couples were relatively late to adopt parity-dependent fertility control.13
We begin with an examination of simple bivariate correlations of children ever born and intermediate reproductive indicators between index women, their mothers, and mothers-in-law. Results are shown by birth cohort to determine whether the strength of intergenerational relationships changed during the course of the fertility transition. We then proceed to an event-history analysis of birth spacing by parity. Time-dependent and time-invariant variables are introduced to test various premises.
Bivariate Correlations
Table 1 shows bivariate correlations of reproductive indicators between women in the UPDB and their mothers and mothers-in-law. The results are limited to cases in which index women, their mothers, and mothers-in-law survived to age forty-five, had nonpolygamous husbands, and remained married to first husbands beyond age forty-five. Most reproductive indicators were positively associated between generations. The correlation coefficient between index women and their mother's completed fertility (0.085) was on the low side of those typically reported. The correlation improved slightly when comparing index women and their mother's fertility relative to other women in a nine-year moving birth cohort centered on their respective years of birth (the definition of relative fertility being “women's number of children ever born minus her birth cohort's mean number”).14
Table 1.
Intergenerational Correlation Coefficients of Reproduction Indicators
| INDICATOR | INDEX WOMEN/MOTHERS |
INDEX WOMEN/MOTHERS-IN-LAW |
||||
|---|---|---|---|---|---|---|
| COEFFICIENTa | SIG. | N | COEFFICIENTa | SIG. | N | |
| All Index Women | ||||||
| Fundamental Fertility Links | ||||||
| Children ever born (CEB) | 0.085 *** | 19,938 | 0.055 *** | 19,938 | ||
| Relative no. of children ever born | 0.092 *** | 19,938 | 0.062 *** | 19,938 | ||
| Other Indicators | ||||||
| Age at first marriage | 0.121 *** | 18,468 | 0.056 *** | 18,323 | ||
| Age at first childbirth | 0.090 *** | 18,589 | 0.034 *** | 18,502 | ||
| Age at last childbirth | 0.069 *** | 19,169 | 0.047 *** | 19,169 | ||
| Duration of reproductive period | 0.051 *** | 18,033 | 0.021 ** | 17,949 | ||
| Relative duration of fertile period | 0.063 *** | 18,033 | 0.039 *** | 17,949 | ||
| Intensity of fertility | 0.010 | 18,033 | −0.010 | 17,949 | ||
| Relative intensity of fertility | 0.011 | 18,033 | −0.010 | 17,949 | ||
| First-Born Index Women or Spouseb | ||||||
| Fundamental Fertility Links | ||||||
| Children ever born (CEB) | 0.115 *** | 5,812 | 0.094 *** | 6,026 | ||
| Relative no. of children ever born | 0.091 *** | 5,812 | 0.074 *** | 6,026 | ||
| Other Indicators | ||||||
| Age at first marriage | 0.144 *** | 5,340 | 0.063 *** | 5,461 | ||
| Age at first childbirth | 0.105 *** | 5,422 | 0.043 ** | 5,532 | ||
| Age at last childbirth | 0.084 *** | 5,592 | 0.044 *** | 5,804 | ||
| Duration of reproductive period | 0.072 *** | 5,266 | 0.035 ** | 5,371 | ||
| Relative duration of fertile period | 0.057 *** | 5,266 | 0.031 * | 5,371 | ||
| Intensity of fertility | 0.009 | 5,266 | −0.017 | 5,371 | ||
| Relative intensity of fertility | 0.008 | 5,266 | −0.019 | 5,371 | ||
| Second and Higher-Sibling-Order Index Women and Spouseb | ||||||
| Fundamental Fertility Links | ||||||
| Children ever born (CEB) | 0.080 *** | 14,126 | 0.041 *** | 13,912 | ||
| Relative no. of children ever born | 0.095 *** | 14,126 | 0.055 *** | 13,912 | ||
| Other Indicators | ||||||
| Age at first marriage | 0.111 *** | 13,128 | 0.051 *** | 12,862 | ||
| Age at first childbirth | 0.083 *** | 13,167 | 0.027 ** | 12,970 | ||
| Age at last childbirth | 0.064 *** | 13,577 | 0.051 *** | 13,365 | ||
| Duration of reproductive period | 0.043 *** | 12,767 | 0.012 | 12,578 | ||
| Relative duration of fertile period | 0.066 *** | 12,767 | 0.035 *** | 12,578 | ||
| Intensity of fertility | 0.013 | 12,767 | −0.004 | 12,578 | ||
| Relative intensity of fertility | 0.013 | 12,767 | −0.004 | 12,578 | ||
Pearson correlation coefficients.
Birth order for index women/mothers-in-law correlations refers to the birth order of the index woman's spouse.
p<0.001
p<0.01
p<0.05
Other indicators of reproduction--age at first marriage, age at first childbirth, age at last childbirth, duration of fertile period, and relative duration of the reproduction period--were positively correlated across generations. The intergenerational correlation in age of first marriage was particularly strong, likely playing a large role in the correlation in children ever born. We should be cautious, however, about assuming that the relatively strong correlation in age at first marriage and its likely contribution to children ever born resulted from an intergenerational transmission in the use of marriage as a strategy to control family size. If fathers' and husbands' occupations were correlated (which seems likely), the correlation in age at first marriage between mothers and their daughters may simply reflect the effect of occupation and SES on the feasibility and desirability of marriage. Although weaker, the correlation in age at last birth is better evidence that values and attitudes about family limitation were transmitted across generations. Index women with a young age at last birth were more likely to have mothers with a young age at last birth. The association may have been due to intergenerational correlations in the practice of effective parity-dependent fertility control (that is, “stopping” behavior) or to correlations in the practice of effective inter-birth spacing, which can also lower the age at last birth. Despite the emphasis in earlier studies on the conscious strategy of spacing of births to limit family size by women in the UPDB, however, the bivariate correlations show no intergenerational relationship in the intensity of fertility—defined as the number of children born divided by the duration of the childbearing period—or the relative intensity of fertility.15
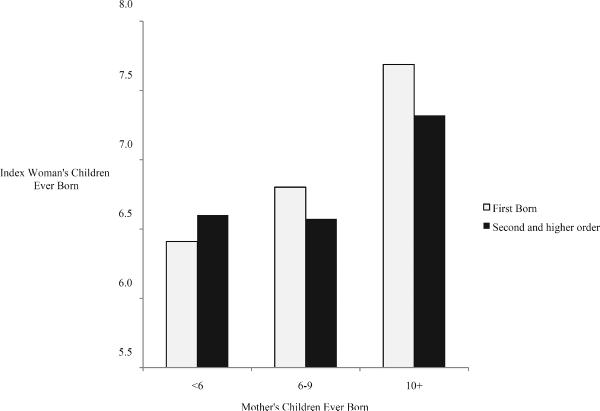
Figure 2 illustrates two findings consistent with other studies. First, although index women with fewer siblings tended to have smaller families of their own, and index women with more siblings tended to have larger families, the relationship was not linear. Index women whose mothers had ten or more children averaged between seven and eight children of their own. Yet, index women whose mothers had fewer than six children averaged more than six children. Second, the relationship between index women and their mothers' children ever born was more responsive for first-born daughters than for second and higher-order-born daughters. Table 1 shows that correlation coefficients for first-born index women were typically greater than correlation coefficients for second- and higher-order-birth women. The differential in the strength of the relationship between children ever born by birth order, however, is largely eliminated by comparing relative fertility across generations, suggesting that much of the birth-order effects were due to cohort effects. Necessarily, first-born daughters were born closer to their mother's cohort than their younger siblings, who were born later in the fertility transition.
Our expectation that correlations through the family of the index woman's husband would rival the size and statistical significance of correlations between the index woman and her mother received weak support. In general, the size of the correlation coefficients between index women and their mothers-in-law were noticeably weaker than correlations between index women and their mothers. The correlation coefficients between the children ever born and the relative number of children ever born of index women and of their mothers-in-law, for example, were approximately two-thirds of those observed between index women and their mothers.
Correlations in other reproductive indicators between index women and their mothers-in-law were even weaker, ranging from about one-third to two-thirds of the size of the coefficients between index women and their mothers. Although more modest than the intergenerational correlation between index women and their mothers' age at first marriage, the correlation between the marriage age of index women and that of their mothers-in-law was statistically significant, indicating the possibility of assortive marriage patterns by occupation, ethnicity, or location. The correlation likely played some role in the correlation in children ever born. Nevertheless, the statistically significant results for most reproductive indicators, including age at last birth, suggests that reproductive behaviors were transmitted from the husband's family of origin.
Table 2 examines correlations between index women and their mothers and mothers-in-law by birth cohort. For the most part, the results confirmed our expectation about the growing importance of intergenerational transmission throughout the course of the fertility transition. Although mostly positive, correlation coefficients between index women and their mothers in birth cohorts before 1870 were not significantly different from zero for most reproductive indicators. This finding is consistent with the literature on pre-transition populations that found little or no intergenerational correlation in fertility. Thereafter, with the exception of the intensity of fertility measures—which remained statistically insignificant throughout the study period— correlation coefficients were positive and statistically significant.
Table 2.
Inter generational Correlation Coefficients of Reproductive Indicators by Birth Cohort
| BIRTH COHORT OF INDEX WOMEN | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| INDEX WOMEN/MOTHERS | 1840–49 | 1850–59 | 1860–69 | 1870–79 | 1880–89 | 1890–99 | ||||||
| INDICATOR | COEF. | SIG. | COEF. | SIG. | COEF. | SIG. | COEF. | SIG. | COEF. | SIG. | COEF. | SIG. |
| Children ever born (CEB) | 0.063 | 0.051 | 0.047 | 0.088 *** | 0.106 *** | 0.092 *** | ||||||
| Relative children ever born | 0.068 | 0.048 | 0.048 * | 0.090 *** | 0.111 *** | 0.097 *** | ||||||
| Age at first marriage | −0.033 | 0.089 ** | 0.072 ** | 0.108 *** | 0.198 *** | 0.160 *** | ||||||
| Age at first childbirth | −0.014 | 0.072 * | 0.050 * | 0.104 *** | 0149 *** | 0.131 *** | ||||||
| Age at last childbirth | 0.034 | 0.016 | 0.059 ** | 0.057 * | 0.068 *** | 0.049 *** | ||||||
| Duration of reproductive period | 0.049 | −0.030 | 0.000 | 0.081 *** | 0.089 *** | 0.061 *** | ||||||
| Relative duration of reproductive period | 0.054 | −0.040 | 0.003 | 0.080 *** | 0.089 *** | 0.064 *** | ||||||
| Intensity of fertility | −0.050 | 0.032 | 0.014 | 0.002 | 0.013 | 0.014 | ||||||
| Relative intensity of fertility | −0.049 | 0.036 | 0.016 | −0.001 | 0.014 | 0.013 | ||||||
| Number of cases (N) | 250 | 781 | 1,723 | 2,996 | 4,930 | 7,661 | ||||||
| BIRTH COHORT OF INDEX WOMEN | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| INDEX WOMEN/MOTHERS-IN-LAW | 1840–49 | 1850–59 | 1860–69 | 1870–79 | 1880–89 | 1890–99 | ||||||
| INDICATOR | COEF. | SIG. | COEF. | SIG. | COEF. | SIG. | COEF. | SIG. | COEF. | SIG. | COEF. | SIG. |
| Children ever born (CEB) | 0.051 | −0.014 | −0.001 | 0.018 | 0.080 *** | 0.101 *** | ||||||
| Relative children ever born | 0.040 | −0.021 | 0.012 | 0.026 | 0.072 *** | 0.097 *** | ||||||
| Age at first marriage | 0.138 * | 0.024 | 0.038 | 0.047 ** | 0.080 *** | 0.091 *** | ||||||
| Age at first childbirth | 0.063 | 0.056 | 0.020 | 0.023 | 0.051 *** | 0.089 *** | ||||||
| Age at last childbirth | 0.079 | −0.011 | 0.048 * | 0.017 | 0.020 | 0.030 * | ||||||
| Duration of reproductive period | 0.097 | −0.002 | −0.013 | 0.017 | 0.030 | 0.062 *** | ||||||
| Relative duration of reproductive period | 0.107 | −0.004 | 0.009 | 0.026 | 0.026 | 0.058 *** | ||||||
| Intensity of fertility | −0.044 | −0.024 | 0.017 | −0.021 | −0.014 | −0.004 | ||||||
| Relative intensity of fertility | −0.028 | −0.014 | 0.020 | −0.023 | −0.013 | −0.008 | ||||||
| Number of cases (N) | 259 | 794 | 1,706 | 2,956 | 4,909 | 7,555 | ||||||
p<0.001
p<0.001
p<0.005
NOTE Person correlation coefficients.
As was true for the overall analysis, age at first marriage had the strongest correlation between index women and their mothers. The size of the coefficient was significantly different from zero for index women in the 1850 to 1859 birth cohort and was larger in subsequent birth cohorts, reaching 0.198 in the 1880 to 1889 birth cohort. Our expectation that marital fertility decline would allow more room for conscious family-limiting behaviors to be passed across generations received support from the age at last childbirth correlations. Although the coefficient was about one-third the size of the correlation for age at first marriage, it was statistically significant for index women in birth cohorts after 1850, suggesting the increasing importance of the transmission of stopping behavior between index women and their mothers.
Correlation coefficients for index women and their mothers-in-law also increased from statistically insignificant levels in early cohorts to positive and statistically significant levels in later cohorts. Once again, the correlation coefficients between index women and their mothers-in-law were noticeably weaker than those between index women and their mothers. As a result, some of the variables were not statistically significant until relatively later-born cohorts of index women. The correlation between the age at last birth of index women and that of their mothers-in-law, for example, was roughly about one-half the size of the correlation in age at last birth between index women and their mothers. Although positive and significant in the 1850 to 1859 and 1890 to 1899 birth cohorts, the correlation was not statistically significant for index women in the 1870 to 1879 and 1880 to 1889 birth cohorts. Nevertheless, the positive correlation between index women and their mothers-in-law in two of the four cohorts suggests the transmission of stopping behavior across families was not limited to transmission between mothers and their daughters. In some small part, stopping behavior, which likely required significant male cooperation, was transmitted from the husband's family of origin.
The bivariate regression results shown in Tables 1 and 2 are in mixed agreement with the results from Reher, Ortega, and Sanz-Gimeno's study of the fertility transition in the Spanish town of Aranjuez. Their results indicated stronger intergenerational correlations between the duration of reproduction and the age at last birth and no correlation in age at first childbirth, which served as a proxy in their study for age at first marriage. Both studies, however, document stronger correlations between index women and their mothers than between index women and their mothers-in-law and increasing strength in correlation coefficients throughout the course of their respective fertility transitions.16
Multivariate Analysis
Although valuable, bivariate correlations are limited. Selection restrictions to index women, mothers, and mothers-in-law whose marriages remained intact beyond their childbearing years result in limited use of the data available in the UPDB. Analyses that examine only bivariate correlations in children ever born also fail to consider that couples' reproductive decisions were part of a sequential process. Although some couples might have commenced childbearing with a desired number (and timing) of children in mind, might never have adjusted their target during their childbearing years, might never have suffered any unexpected losses of children in infancy and childhood, and might have effectively stopped their childbearing after meeting their target number, such couples most likely constituted a small minority. Most couples continually re-evaluated their reproductive goals and adjusted their behavior, whether to accelerate or postpone a birth or to cease childbearing altogether, in response to current conditions and future prospects. Important factors might have included their current number of surviving children, the mother's health, the family's economic condition, and the ability of older children and kin to assist in child rearing and household duties.
In recent years, the study of fertility has moved from reliance on cross-sectional aggregate data to longitudinal microdata and from analyses of the number of births to the timing and likelihood of the next birth. The shift in focus was made possible with advances in event-history methods, which allow the modeling of repeated events. Although the methods require longitudinal data, which are relatively rare for historical populations, the benefits are considerable. First, the ability to include censored observations allows much more of the available data to be analyzed. Women whose childbearing was interrupted by death or divorce, for example, can be included in the analysis. Second, the ability to include time-dependent variables allows researchers to examine the relevance of a wider variety of biological, demographic, and socioeconomic variables on couples' reproductive behavior in a multivariate framework that treats fertility as a dynamic, sequential process.
We rely on event-history methods to examine the intergenerational transmission of reproductive behavior in the UPDB. Because we know the precise timing of demographic events—including the exact date of births, marriages, and deaths across multiple generations— we construct a Cox continuous-time proportional-hazard model. The model assumes that the effects of covariates are proportional to the baseline hazard--the hazard of a woman giving birth since her marriage or last birth. We model each birth interval separately. The approach thus estimates the influence of independent covariates on the relative risk of an index woman giving birth in the interval.
Covariates from the index woman's mother and mother-in-law include their relative fertility, relative age at marriage, length of first birth interval, and a time-dependent covariate for vital status (0=dead, 1=living). For index women, fixed covariates include birth cohort, age at marriage, age differential from spouse, and whether a member of the LDS. Time-dependent variables include the index woman's five-year age group and whether her previous child died before the age of two in the interval. The latter variable is an attempt to control for the effect of differential breast-feeding. The premature death of an infant terminates breast-feeding, which results in a shortened duration of postpartum amenorrhea. Women whose previous child died before the age of two are expected to have shorter birth intervals and are more likely to progress to the next birth, all else being equal.
The model universe includes all index women married to nonpolygamous males linked to mothers and mothers-in-law married to nonpolygamous males. Because we rely on the relative fertility of mothers and mothers-in-law, we exclude index women with mothers or mothers-in-law whose first marriage ended before age forty-five. Most mothers and mothers-in-law still living when their daughters or daughters-in-law began childbearing were either no longer bearing children of their own or would soon be finished. Assuming that they lived in proximity to their daughters or daughters-in-law, most of them would have been able to help with the raising of their grandchildren or with other household duties.17
Hazard ratios for attributes of index women, their mothers, and mothers-in-law are shown in Table 3. Values greater than one indicate a greater hazard of birth (implying a shorter interval to next birth and a greater likelihood of having another child). With the exception of the interval between marriage and first birth, the hazard ratio for the relative fertility of index women's mothers is greater than one and statistically significant in all birth intervals, indicating that index women whose mothers achieved higher fertility than other women in their cohort were more likely to have another child and progress faster to the next birth, all else being equal. Index women whose mothers had one child more than the average for their cohort had, on average, a 1.9 percent increased hazard of having a child in birth intervals between one and nine. The hazard ratio remained at the same approximate level in higher birth intervals, despite the attrition of women with low fertility from the analysis.18
Table 3.
Proportional Model of Fertility Timing by Birth Interval and Family History (Hazard Ratios)
| BIRTH INTERVAL | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0–1 | 1–2 | 2–3 | 3–4 | 4–5 | 5–6 | 6–7 | 7–8 | 8–9 | 9+ | |
| Mother's attributes | ||||||||||
| Relative fertility (CEB--cohort mean CEB) | 1.006 | 1.014 *** | 1.027 *** | 1.025 *** | 1.018 *** | 1.016 *** | 1.014 ** | 1.019 ** | 1.016 * | 1.004 |
| Relative age at marriage (age--cohort mean) | 1.002 | 1.007 * | 1.014 *** | 1.011 *** | 1.003 | 1.011 ** | 1.008 | 1.008 | 1.008 | 1.016 * |
| Interval to first birth (months) | n.a. | 1.000 | 1.001 | 1.000 | 1.000 | 1.000 | 1.001 * | 1.002 * | 1.001 | 0.999 |
| Vital status (dead=0; living=1) | 1.165 *** | 1 172 *** | 1.154 *** | 1.207 *** | 1.206 *** | 1.214 *** | 1.182 *** | 1 173 *** | 1.314 *** | 1 222 *** |
| Mother-in-law's attributes | ||||||||||
| Relative fertility (CEB--cohort mean CEB) | 1.010 * | 1.008 * | 1.015 *** | 1.016 *** | 1.011 ** | 1.015 *** | 1.018 ** | 1.019 ** | 1.013 * | 1.003 |
| Relative age at marriage (age--cohort mean) | 1.006 | 1.005 | 1.005 | 1.003 | 1.002 | 1.002 | 1.002 | 1.002 | 1.007 | 0.992 |
| Interval to first birth (months) | 1.000 | 1.001 | 1.001 * | 1.000 | 1.000 | 1.000 | 1.001 | 1.000 | 0.999 | |
| Vital status (dead=0; living=1) | 0.976 | 1.124 *** | 1.012 | 1 092 *** | 1.059 * | 1 121 *** | 1 129 *** | 1.141 *** | 1.216 *** | 1.118 * |
| Index woman's (daughter's) attributes | ||||||||||
| Age Group | ||||||||||
| 15–19 | 0.277 *** | 0.816 *** | 1.554 *** | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. |
| 20–24 | 0.156 *** | 0.989 | 1111 *** | 1.123 ** | 1.094 | 1.758 *** | n.a. | n.a. | n.a. | n.a. |
| 25–29 | ref. | ref. | ref. | ref. | ref. | ref. | ref. | ref. | ref. | ref. |
| 30–34 | 7.204 *** | 0.596 *** | 0.613 *** | 0.680 *** | 0.866 *** | 0.877 *** | 0.761 *** | 0.776 *** | 0.607 *** | 0.457 *** |
| 35–39 | n.a. | 0.286 *** | 0 339 *** | 0.372 *** | 0.550 *** | 0.558 *** | 0491 *** | 0.577 *** | 0 579 *** | 0.416 *** |
| 40–44 | n.a. | 0.115 *** | 0.084 *** | 0.126 *** | 0197 *** | 0.222 *** | 0.200 *** | 0.271 *** | 0.310 *** | 0.240 *** |
| 45–49 | n.a. | 0.007 *** | 0.011 *** | 0.007 *** | 0.015 *** | 0.019 *** | 0.021 *** | 0.026 *** | 0.041 *** | 0.036 *** |
| Birth Cohort | ||||||||||
| Pre-1850 | ref. | ref. | ref. | ref. | ref. | ref. | ref. | ref. | ref. | ref. |
| 1850–1859 | 1.215 * | 0.908 | 0.972 | 0.992 | 0.926 | 0.928 | 0.830 * | 0.907 | 0.816 ** | 0.820 * |
| 1860–1869 | 1.042 | 0795 *** | 0.863 * | 0.923 | 0.798 *** | 0794 *** | 0742 *** | 0.824 * | 0.788 ** | 0.713 *** |
| 1870–1879 | 0.914 | 0.695 *** | 0.771 *** | 0.840 * | 0.751 *** | 0.758 *** | 0.711 *** | 0.786 ** | 0.701 *** | 0.756 ** |
| 1880–1889 | 0.857 | 0.600 *** | 0.644 *** | 0.705 *** | 0.664 *** | 0.646 *** | 0599 *** | 0.656 *** | 0.644 *** | 0.673 *** |
| 1890–1899 | 0.975 | 0.496 *** | 0.502 *** | 0.540 *** | 0.460 *** | 0.483 *** | 0.453 *** | 0.537 *** | 0.468 *** | 0.532 *** |
| Age at marriage | 0.832 *** | 1.036 *** | 1.047 *** | 1.051 *** | 1.038 *** | 1.044 *** | 1.050 *** | 1.041 *** | 1.032 *** | 1.006 |
| LDS church membership | 1.086 ** | 1.166 *** | 1.182 *** | 1.176 *** | 1.090 *** | 1.108 *** | 1.076 * | 1.125 ** | 1.080 | 1.113 * |
| Age differential from spouse | 1.001 | 0 991 *** | 0.989 *** | 0.994 * | 0.995 | 0.992 ** | 0.997 | 1.000 | 0.998 | 1.005 |
| First-born daughter | 0.981 | 0.987 | 1.029 | 1.014 | 0.979 | 1.023 | 1.004 | 1.046 | 1.026 | 1.045 |
| Infant (previous child's) death in interval | n.a. | 1.264 *** | 1 277 *** | 1.023 | 1.066 * | 1.090 * | 1.114 * | 1.074 | 1.157 ** | 1.130 |
| Time to first birth (months) | n.a. | 0.9891 *** | 0.9947 *** | 0.9982 ** | 0.9976 *** | 0.9990 | 1.0025 ** | 1.0005 | 0.9994 | 0.9973 |
| Spouses' attributes | ||||||||||
| First-born son | 1.013 | 1.000 | 1.023 | 1.022 | 0.968 | 0.993 | 0.951 | 0.965 | 1.052 | 0.989 |
p<.05
p<.01
p<.001
NOTES ref. = reference category; n.a. = not applicable or too few cases for analysis.
Index women whose mothers were still living had a significantly higher hazard rate of giving birth in all intervals, indicating that living mothers exerted a significant pronatal affect on their daughter's fertility. Coefficients ranged between 1.154 and 1.314; index women with living mothers experienced a 15 to 31 percent higher hazard rate of birth (the average for intervals between one and nine was 1.203, or a 20.3 percent increased hazard). The relative fertility and vital status of mothers-in-law of index women exerted similar, albeit slightly less, influence on the hazard ratio of giving birth. With the exception of birth intervals above nine, the relative fertility of mothers-in-law was positive and statistically significant in all birth intervals. Index women whose mothers-in-law had one child more than the average for women in their cohorts had, on average, a 1.4 percent increased hazard of having a child in birth intervals between one and nine (78 percent of the increased hazard associated with the relative fertility of index women's mothers). Index women with living mothers-in-law experienced an approximately 11 percent higher hazard of giving birth (55 percent of the increased hazard associated with the vital status of index women's mothers).
Although the results support the evolutionary biology literature stressing the roles of grandmothers in providing mothers with assistance in child rearing and the pronatal consequences of that care, the lesser influence of mothers-in-law relative to mothers is slightly at odds with a recent literature review of the extent to which kin affect fertility in modern pre-transitional populations. Although many studies report that the presence of maternal grandmothers has a pro-natal effect, Sear and Matthews' systematic literature review found a more consistent pronatal effect from paternal grandmothers, who might on the whole be less concerned about the effect of childbearing on the health of the mother.19
Covariates associated with index women were also significant. Age made the largest difference. That index women with membership in LDS had higher hazard ratios than non-Church women means a positive relationship between membership in the church and marital fertility. With a few exceptions, index women whose previous child died in the interval had higher hazard rates of giving birth. The result suggests either a shortened period of postpartum amenorrhea related to a shortened period of breast-feeding or an attempt on the part of couples to replace the lost child.
Bivariate correlations in children ever born and other indicators of reproduction between index women and their mothers in the UPDB signal the intergenerational transmission of reproductive behaviors in birth cohorts beginning in the late nineteenth century. Although modest, correlations in children ever born between index women and their mothers were statistically significant for index women in birth cohorts after 1860. Among other reproductive indicators, age at marriage had the strongest association across generations and was significantly correlated in birth cohorts after 1850. The statistically significant bivariate correlations in age at last childbirth in birth cohorts after 1860 suggest that the practice of parity-dependent marital-fertility control, or possibly inter-birth spacing behavior, was transmitted between mothers and daughters. Correlations between first-born index women and their mothers were stronger than correlations between second- and higher-birth-order index women and their mothers, suggestive of first-born daughters' greater socialization and greater identification with their mothers.20
This study also found modest bivariate correlations between children ever born and other indicators of reproduction between index women and their mothers-in-law, including correlations in age at last childbirth. Although the correlations were smaller than those between index women and their mothers, the results confirm the existence of significant intergenerational transmission of reproductive behavior from husbands' families; husbands (and mothers-in-law) probably played a significant role in determining reproductive behavior. The result is not unexpected, given the need for men's cooperation in most of the effective means of birth control during the fertility transition in the United States.
Results of the event-history analysis further confirm that reproductive behavior was transmitted across generations. Although hazard ratios associated with the relative fertility of mothers and mothers-in-law appear modest—averaging 1.019 for mother's fertility relative to other women in her birth cohort and 1.014 for that of mothers-in-law—the hazard ratio shown was for a one-child change in relative fertility. The standard deviation for the relative fertility of both mothers and mothers-in-law was 2.9 children throughout the period. Thus, index women whose mother's relative fertility was one standard deviation above the mean had a hazard ratio approximately 11 percent higher than that of index women whose mother's relative fertility was one standard deviation below the mean. For index women with mothers-in-law whose relative fertility was one standard deviation above the mean, the hazard rate was approximately 8 percent higher than for women with mothers in-law whose relative fertility was one standard deviation below the mean. Moreover, index women's increased hazard of birth was repeated in each birth interval.
The event-history analysis also confirms that the vital status of index women's mothers and mothers-in-law was strongly associated with the hazard of giving birth in each birth interval. Index women with living mothers and mothers-in-law were much more likely to progress to the next birth, all else being equal. Although we lack detailed residence information for index women and their mothers, the result supports the hypothesis that close kin, particularly mothers and mothers-in-law, represented critical help in the rearing of children. As “cooperative breeders,” Utah women born in the nineteenth century were not only influenced by the past example of the fertility of their mothers and mothers-in-law; they also adjusted the quantum and tempo of their childbearing in response to the presence of these relations.
Fig. 1.
Age-Specific Marital Fertility Rates by Birth Cohort
Fig. 2.
Index Women's Mean Children Ever Born by Birth Order and Mother's Children Ever Born
Acknowledgments
This work was supported by National Institutes of Health grant AG022095 (The Utah Study of Fertility, Longevity and Aging). The authors thank the Huntsman Cancer Foundation (HCI) for database support provided to the Pedigree and Population Resource of the HCI, University of Utah. They also thank Dr. Geraldine Mineau, Alison Fraser, Diana Lane Reed, and Heidi Hanson at the HCI for valuable assistance in managing the data. Partial support for all datasets within the UPDB was provided by the University of Utah HCI and the HCI Cancer Centre Support Grant, P30 CA42014 from National Cancer Institute. Myron Gutmann, George Alter, Ken Smith, Susan Hautaniemi Leonard, Emily Merchant, and other instructors at the “Longitudinal Methods in Historical Demographic Data” course offered by the Interuniversity Consortium for Political and Social Research (ICPSR) in its summer program (NICHD grant R25HD049479) were instrumental in the publication of this article. Fabian Drixler assisted with the initial analysis. J. David Hacker's research is supported in part by NIHCD grant 1 K01-HD052617-01. Julia Jennings is supported in part by NICHD grants T32 HD007514 (The Pennsylvania State University Population Research Institute) and T32 HD07168 (Carolina Population Center, University of North Carolina, Chapel Hill).
Footnotes
Karl Pearson, Alice Lee, and Leslie Bramley-Moore, “Mathematical Contributions to the Theory of Evolution: VI. Genetic (Reproductive) Selection: Inheritance of Fertility in Man, and of Fecundity in Thoroughbred Racehorses,” in Philosophical Transactions of the Royal Society of London, A192 (1899), 2838-2843; Hans-Peter Kohler, Joseph L. Rodgers, and Kaare Christensen, “Between Nurture and Nature: The Shifting Determinants of Female Fertility in Danish Twin Cohorts,” Social Biology, XLIX (2002), 218-248; idem, “Is Fertility Behavior in Our Genes? Findings from a Danish Twin Study,” Population and Development Review, XXV (1999), 253-288; David Sven Reher, Jose Antonio Ortega, and Alberton Sanz-Gimeno, “Intergenerational Transmission of Reproductive Traits in Spain during the Demographic Transition,” Human Nature, XIX (2008), 23-43.
Michael Murphy, “Is the Relationship between Fertility of Parents and Children Really Weak?” Social Biology, XLVI (1999), 122-145; Douglas L. Anderton et al., “Intergenerational Transmission of Relative Fertility and Life Course Patterns,” Demography, XXIV (1987), 467-480; Reher, Ortega, and Sanz-Gimeno, “Intergenerational Transmission of Reproductive Traits.”
Anderton et al., “Intergenerational Transmission of Relative Fertility”; Murphy, “Is the Relationship between Fertility of Parents and Children Really Weak?”
For a convincing demonstration that European couples consciously delayed childbearing during times of economic stress, see Tommy Bengtsson and Martin Dribe, “Deliberate Control in a Natural Fertility Population: Southern Sweden, 1766-1864,” Demography, XLIII (2006), 727-746. Katherine M. Kirk et al. estimate that 30% of the variance in the fertility of Australian women is attributable to genetic effects (“Natural Selection and Quantitative Genetics of Life-History Traits in Western Women: A Twin Study,” Evolution, LV [2001], 423-435. Kohler, Rodgers, and Christensen, “Is Fertility Behavior in Our Genes?” According to evolutionary models based on Ronald A. Fisher's fundamental theorem of natural selection in The Genetical Theory of Natural Selection (Oxford, 1930), fertility and other traits subject to Darwinian selection should exhibit little standing genetic variation. Put another way, genetic variations in traits subject to strong natural selection will be eroded quickly.
Christopher M. Langford and Christopher Wilson, “Is There a Connection between a Woman's Fecundity and That of Her Mother?” Journal of Biosocial Science, XVII (1985), 437-443; Bertrand Desjardins, Alain Bideau, Evelyne Heyer, and Guy Brunet, “Intervals between Marriage and 1st Birth in Mothers and Daughters,” ibid., XXIII (1991), 49-54; Alain Gagnon and Evelyne Heyer, “Intergenerational Correlation of Effective Family Size in Early Quebec (Canada),” American Journal of Human Biology, XIII (2001), 645-659. Can they pl supply first names?
John Cleland and Christopher Wilson, “Demand Theories of the Fertility Transition: An Iconoclastic View,” Population Studies, XLI (1987), 5-30; John E. Knodel and Etienne van de Walle, “Lessons from the Past: Policy Implications of Historical Fertility Studies,” Population and Development Review, V (1979), 217-245.
Anderton et al., “Intergenerational Transmission of Relative Fertility,” 477.
Reher, Ortega, and Sanz-Gimeno, “Intergenerational Transmission of Reproductive Traits”; Anderton and Lee L. Bean, “Birth Spacing and Fertility Limitation: A Behavioral Analysis of a 19th-Century Frontier Population,” Demography, XXII (1985), 169-183. For Europe, see Knodel, “Starting, Stopping, and Spacing during the Early Stages of Fertility Transition: The Experience of German Village Populations in the 18th and 19th Centuries,” ibid., XXIV (1987), 143-162. Recently, Gloria L. Main has argued that increased birth spacing played an important role in reducing the fertility of New England women between the late eighteenth and early nineteenth centuries (“Rocking the Cradle: Downsizing the New England Family,” Journal of Interdisciplinary History, XXXVII [2003], 35-58).
Reher, Ortega, and Sanz-Gimeno, “Intergenerational Transmission of Reproductive Traits”; Nan E. Johnson and C. Shannon Stokes, “Family Size in Successive Generations: The Effects of Birth Order, Intergenerational Change in Lifestyle, and Familial Satisfaction,” Demography, XIII (1976), 175-187; Frank J. Sulloway, Born to Rebel: Birth Order, Family Dynamics, and Creative Lives (New York, 1996); Anderton et al., “Intergenerational Transmission of Relative Fertility”; Murphy, “Is the Relationship between Fertility of Parents and Children Really Weak?”; Pearson, Lee, and Bramley-Moore, “Mathematical Contributions.” For the emphasis in earlier studies, see Michael Dunlop Young and Peter Willmott, Family and Kinship in East London (London, 1957).
K. Hawkes et al., “Grandmothering, Menopause, and the Evolution of Human Life Histories,” Proceedings of the National Academy of Sciences of the United States of America, XCV (1998), 1336-1339; Ruth Mace and Rebecca Sear, “Are Humans Cooperative Breeders?” in Eckart Voland, Athanasios Chasiotis, and Wulf Schiefenhoevel (eds.), Grandmotherhood: The Evolutionary Significance of the Second Half of Female Life (Piscataway, 2005), 143-159; Sear, Mace, and Ian A. McGregor, “The Effects of Kin on Female Fertility in Rural Gambia,” Evolution and Human Behavior, XXIV (2003), 25-42; Sear and Paul Matthews, “The Impact of Kin on Female Fertility: A Systematic Review,” paper presented at the meeting of the International Union for the Scientific Study of Population (Marrakesh, Morroco, 2009). Evolutionary biologists have argued that changing patterns of kin availability may be a significant factor in fertility transitions. Lesley Newson et al., “Why Are Modern Families Small? Toward an Evolutionary and Cultural Explanation for the Demographic Transition,” Social Psychology Review, IV (2005), 360-375. On the declining level of family help during the Fertility Decline in the United States, see Susan E. Short, Frances K. Goldscheider, and Berna M. Torr, “Less Help for Mother: The Decline in Coresidential Female Support for the Mothers of Young Children, 1880-2000,” Demography, XLIII (2006), 617-629. In a valuable review of thirty-nine studies examining the influence of kin on fertility, Sear and David Coall note that paternal kin have a more consistent pro-natal effect on fertility than maternal kin do; their findings suggest that maternal kin can act at times to protect women from maternal depletion (“How Much Does Family Matter? Cooperative Breeding and the Demographic Transition,” Population and Development Review, XXXVII [2011], 81-112).
G. William Skinner, “Conjugal Power in Tokugawa Japanese Families: A Matter of Life or Death,” in Barbara Diane Miller (ed.), Sex and Gender Hierarchies (New York, 1993), 236-270; Wang Feng et al., “Household Organization, Co-Resident Kin, and Reproduction,” in Noriko O. Tsuya et al. (eds.), Prudence and Pressure: Reproduction and Human Agency in Europe and Asia, 1700-1900 (Cambridge, Mass., 2010), 67-96. Patrilocal marriage rules prevalent in East Asia dictated that women were much more likely to have lived with their parents-in-law than with their parents. The neolocal family-formation pattern characteristic of West European populations limits the potential for studies based on co-residence to find a significant effect of kin on fertility. Nonresident kin residing in the same village or area, however, might have played a significant role in child care, economic assistance, and reproductive decisions. Although the results reported by Feng et al. for Sart, Belgium, in “Household Organization,” indicated a positive relationship between fertility at higher order births and the presence of both parents, Sart women spent their reproductive lives “almost exclusively in simple family households” (71).
Bean, Dean L. May, and Mark Skolnick, “The Mormon Historical Demography Project,” Historical Methods, XI (1978), 45-53; Bean, Geradline P. Mineau, and Anderton, Fertility Change on the American Frontier: Adaptation and Innovation (Berkeley, 1990), 69-106; Bean et al., “The Geneaological Society of Utah as A Data Source for Historical Demography,” Population Index, XLVI (1980), 6-19.
Bean, Mineau, and Anderton, Fertility Change on the American Frontier, report similar trends but slightly different estimates. Coale and Trussell's m parameter was negative or zero in all birth cohorts before 1855, and it did not exceed 0.2—typically considered the threshold of the onset of parity-dependent control in the population as a whole—until the 1875 to 1879 birth cohort. Although the population included in the UPDB had a few unusual features—including its frontier location, high levels of membership in the LDS, and relatively late adoption of parity-dependent fertility control—the benefits of the UPDB data outweigh concerns about the population's representativeness. Precise data on birth spacing by parity in the early United States are rare. No other datasets document birth intervals throughout the decades of most rapid fertility decline. Some researchers, however, have used genealogical data to study birth spacing in the early stages of the decline. Main's “Rocking the Cradle” may well be the most significant effort to date. Other significant research includes Robert V. Wells, “Family Size and Fertility Control in Eighteenth-Century America: A study of Quaker families,” Population Studies, XLVI (1971), 85-102; Daniel Scott Smith, “Population, Family and Society in Hingham, Massachusetts, 1635-1880,” unpub. Ph.D. diss (University of California, Berkeley, 1973). These studies demonstrate the importance of increased birth spacing at the onset of the U.S. fertility decline, suggesting that the strategies of UPDB couples were not unique to LDS members on the Utah frontier. Douglas C. Ewbank, “The Marital Fertility of American Whites before 1920,” Historical Methods, XXIV (1991), 141-170. Ansley J. Coale and James T. Trussell, “Model Fertility Schedules: Variations in the Age Structure of Childbearing in Human Populations,” Population Index, XL (1974), 185-258.
The selection criteria favor fertile women from comparatively healthy families. Given the assumptions that a woman's health affected her fecundity and that mothers' and daughters' health were correlated, the intergenerational correlation coefficients shown in Tables 1 and 2 are biased downward. Unfortunately, even greater bias would result from reliance on women with incomplete reproductive histories. Event-history analysis, applied in the latter part of the article, allows us to rely on daughters with incomplete birth histories. In “Intergenerational Transmission of Reproductive Traits,” Reher, Ortega, and Sanz-Gimeno reported a correlation coefficient of 0.115 in children ever born and noted that typical estimates in most studies fell in the range 0.060 to 0.200.
Langford and Wilson in “Is There a Connection?” reported a 0.097 correlation coefficient between mothers' and daughters' age of marriage. For occupational differentials in nuptiality during the late nineteenth and early twentieth centuries, see Catherine A. Fitch, “Transitions to Marriage in the United States, 1850-2000,” unpub. Ph.D. diss. (University of Minnesota, 2005), and Hacker, “Economic, Demographic, and Anthropometric Correlates of First Marriage in the mid Nineteenth-Century United States,” Social Science History, XXXII (2008), 307-345. The bivariate correlation between index women and their mothers' age at last birth could have been due to a genetic similarity in the age at menopause. The cohort results shown in Table 2, however--which indicate no significant mother-daughter correlations in age at last birth among early, natural-fertility birth cohorts and significant correlations in later birth cohorts known to be practicing parity-dependent control--strongly suggests that the correlation in age at last birth was related to the intergenerational transmission of behavioral practices. On the importance of birth spacing in the Utah population, see Anderton, “Starting, Stopping, and Spacing during the Early Stages of Fertility Transition--Comment,” Demography, XXVI (1989), 467-470; idem and Bean, “Birth Spacing And Fertility Limitation” Bean, Mineau, and idem, Fertility Change on the American Frontier.
Reher, Ortega, and Sanz-Gimeno, “Intergenerational Transmission of Reproductive Traits.”
Index women who died before age forty-five or whose husbands died before index women reached that age were censored at the date of either the index woman's or her husband's death. A small proportion of mothers and mothers-in-law may well have had to take care of young children of their own, especially in the case of first-born index women, born relatively early in their mothers' childbearing years. We might expect, therefore, that first-born index women received relatively less help from their living mothers than higher-birth-order index women. Although less restrictive than the selection criteria used for the bivariate correlations above, the model universe remains biased toward women in healthier families. The likely result is to understate the significance of intergenerational transmission of fertility.
The interaction of the relative fertility of mothers (and of mothers-in-law) and the index woman's birth order were tested, since higher-birth-order women tend to come from mothers with higher relative fertility. The interaction terms were not significant, and model fit did not improve in terms of the Bayesian Information Criterion (BIC).
The interactions between living mothers (and mothers-in-law) and the index women's birth cohort were tested to explore the potential role of increasing longevity over time. The interaction terms for mothers-in-law were not significant, and model fit did not improve in terms of the BIC. The interaction terms for mothers were significant for most birth intervals, but the size of the coefficient was small. Since the model fit did not improve in terms of the BIC, the interaction terms were not included in the models presented herein. The interactions between living mothers (and mothers-in-law) and index women's birth order were also tested, since higher-birth-order women are less likely to have a living mother than lower-birth-order women. The interaction terms were not significant, and the model fit did not improve in terms of the BIC. Sear and Matthews, “The Impact of Kin on Female Fertility.”
Some exploratory analyses using sibling shared frailty terms (with reduced sample sizes and Weibull models) suggest that this transmission extends to sisters as well. However, computational constraints involved with the estimation of these models using the full dataset prevent direct comparison with the Cox models presented herein. The investigation of shared effects within sibling sets remains a topic for future analysis.