Conformational relaxation and water penetration coupled to ionization of internal groups in proteins

Abstract

Molecular dynamics simulations were used to examine the effects of ionization of internal groups on the structures of eighteen variants of staphylococcal nuclease (SNase) with internal Lys, Asp, or Glu. In most cases the RMSD values of internal ionizable side chains were larger when the ionizable moieties were charged than when they were neutral. Calculations of solvent-accessible surface area showed that the internal ionizable side chains were buried in the protein interior when they were neutral, and moved towards crevices and the protein-water interface when they were charged. The only exceptions are Lys-36, Lys-62, Lys-92 and Lys-103, which remained buried even after charging. With the exception of Lys-38, the number of internal water molecules surrounding the ionizable group increased upon charging: the average number of water oxygen atoms within the first hydration shell increased by 1.7 for Lys residues, by 5.2 for Asp residues, and by 3.2 for Glu residues. The polarity of the micro environment of the ionizable group also increased when the groups were charged: the average number of polar atoms of any kind within the first hydration shell increased by 2.7 for Lys residues, by 4.8 for Asp residues, and by 4.0 for Glu residues. An unexpected linear relationship was observed between the absolute value of the shifts in pK_a values measured experimentally, and structural relaxation as described in terms of the net difference in the polarity of the micro environment of the charged and neutral forms of the ionizable groups, and of the RMSD values of the charged side chains. The effects of ionization of internal groups on the conformation of the backbone were noticeable but mostly small and localized to the area immediately next to the internal ionizable moiety. Some variants did exhibit local unfolding.

Introduction

Internal ionizable groups in proteins are essential for many fundamental biochemical processes. They are necessary for enzyme catalysis,¹ for H⁺ transport and e⁻ transfer in proteins such as ATP synthase,^2,3 bacteriorhodopsin,^4–6 the photosynthetic reaction center,⁷ cytochrome c oxidase,⁸ and the bc1 complex.⁹ To understand the relationship between structure and function of these proteins it is necessary to identify and understand the factors that govern the pK_a values of internal ionizable groups.

Sequestering of ionizable groups from bulk water by burial in the interior of proteins can induce large shifts in pK_a values relative to the normal values in water. If the protein environment is relatively apolar, the shifts will be in a direction that promotes the neutral state.^10,11 The molecular determinants of these functionally essential shifts in pK_a values are not known in detail, but it is clear that they can be modulated additionally through water penetration,^12–15 and through interactions between the ionizable moieties and polar and other internal or surface charges.^16,17 Conformational changes coupled to the ionization of an internal ionizable group will also be reflected in its pK_a.^18–20 Partly for this reason, it is of special interest to understand conformational reorganization coupled to the ionization of internal groups in proteins.

Many proteins harness structural relaxation coupled to protonation/deprotonation of internal groups for function. Prominent examples include H⁺ pumps such as ATP synthase,^2,3 bacteriorhodopsin^4–6 or cytochrome c oxidase.⁸ The photoactive yellow protein is another excellent example of a protein that depends on the presence of internal charge for function. The internal charge triggers a conformational transition required for activation of a signaling cascade.^21–23 Conformational responses to the ionization of an internal group can be local, such as in bacteriorhodopin, or more global, such as in the photoactive yellow protein. Despite the wealth of experimental methods that have been applied to examine the structural basis of conformational transitions coupled to the ionization of internal groups, the detailed mechanisms of protein relaxation in the presence of an internal charge remain elusive. Carefully calibrated computational methods will be invaluable to examine mechanisms of structural relaxation at the microscopic level. This level of understanding will be necessary to elucidate the structural and energetic basis of function governed by the ionization of internal groups.

The calculation of electrostatic properties of internal ionizable groups buried in a protein is challenging, for several reasons. The dielectric properties of proteins are not well understood primarily because in terms of chemistry and dynamics, proteins are heterogeneous and anisotropic. A protein’s response to the ionization of an internal group may depend on the chemical nature of the group and on its location inside the protein.^10,17 Continuum models in which the dielectric properties of a protein are represented with a single valued dielectric constant are usually unable to reproduce pK_a values of internal groups self-consistently when the calculations are performed with static structures.^11,13,24,25 Attempts to improve structure-based pK_a calculations with methods that account for multiple structures are promising.^26–28 One of the problems with these approaches is that contributions related to conformational relaxation (including backbone relaxation) associated with charging or uncharging of the internal groups, is not accounted for properly. Methods based on free energy simulations^29–31 as well as molecular dynamics simulations at constant pH^32–38 are being developed to circumvent the problems inherent to internal ionizable groups.

To examine systematically the effects of internal charges on conformation, we studied some proteins from a family of variants of staphylococcal nuclease (SNase) in which 25 internal positions were replaced with Lys, Arg, Asp or Glu, one at a time.^10,11 The pK_a values of these proteins have been determined experimentally.^{10,11,24,39–43} The extent of structural response to the ionization of internal groups has been examined experimentally with Trp-fluorescence and CD spectroscopy. The crystallographic structures of many of these variants are available.^{16,17,20,44,45} Furthermore, the 25 variants with internal Lys residues and the variants with Asp and Glu at positions 38 and 66 have been characterized with NMR spectroscopy.^{12,13,16,17,20,45} The pK_a values of the majority of the internal ionizable groups in SNase are very different from the normal pK_a values in water. Some are shifted by as many as 5 pK_a units. These shifts are in the direction that favors the neutral form of the ionizable group, clear evidence that the interior of SNase is not as good a solvent for charges as water.¹⁰ In only a couple of cases the ionization of the internal group unfolds the protein globally.¹⁰ In a few more cases the ionization of the internal groups has a small but detectable effect on the conformation of the protein.^{10,11,20,42,43,45} What was more surprising is that in the majority of cases the ionization of the internal group triggers no detectable changes by Trp fluorescence or CD spectroscopy.^10,11,43 We are interested in rationalizing these findings and understanding the structural consequences of the ionization of internal groups in molecular detail.

The large collection of variants of SNase with internal Lys, Arg, Asp and Glu will enable unprecedented, systematic, stringent benchmarking of computational methods for structure-based pK_a calculations. They offer opportunities to examine in detail the molecular determinants of pK_a values of internal groups. In this study we have applied molecular dynamics (MD) simulations to examine the range of conformational relaxation coupled to the ionization of internal groups. Previous MD studies of five of these variants of SNase suggested that water penetration, side chain relaxation and relaxation of the backbone could affect the pK_a values of the internal groups.^{14,15,30,46–48} Here we have performed a systematic comparison of the response of 18 variants to the ionization of Lys, Asp, or Glu with the purpose of identifying general trends in the response of proteins to internal charges.

Methods

Simulated systems

The 18 starting structures used in the simulations were obtained from the Protein Data Bank (Table 1). Variants of three different forms of SNase were studied: (1) WT (the true wild type), PHS (a highly stable variant with three substitutions: P117G, H124L, S128A), and Δ+PHS (an even more stable variant of SNase that consists of the PHS protein with additional substitutions G50F, V51N, and a 44–49 deletion).

Table 1.

Simulation setup

Proteina	PDB codeb	Backgroundc	Neutrald				Chargedd
			DOWSER	Na+	Cl−	tot wat	Na+	Cl−	tot wat
L25E	3EVQ	Δ+PHS	1	7	13	5228	8	13	5240
L25K	3ERQ	Δ+PHS	2	7	13	5230	7	14	5216
L36K	3EJI	Δ+PHS	1	7	14	5213	6	14	5216
L38E	3D6C	PHS	1	6	15	5182	6	14	5179
L38K	2RKS	PHS	2	5	14	5179	5	15	5174
T62K	3DMU	PHS	2	5	14	5175	5	15	5168
V66D	2OXP	PHS	2	6	15	5168	6	14	5167
V66E	1U9R	PHS	3	6	15	5151	6	14	5153
V66K	2SNM	WT	2	5	14	5214	5	15	5209
I72E	3ERO	Δ+PHS	0	7	13	5241	8	13	5237
I72K	2RBM	Δ+PHS	0	7	14	5198	6	14	5199
Y91E	3D4D	Δ+PHS	1	7	13	5232	8	13	5229
I92D	2OEO	Δ+PHS	3	7	14	5215	7	13	5210
I92E	1TR5	Δ+PHS	4	7	14	5189	7	13	5188
I92K	1TT2	Δ+PHS	6	7	14	5181	6	14	5187
L103K	3E5S	Δ+PHS	0	7	13	5225	7	14	5219
V104K	3C1F	Δ+PHS	1	7	13	5235	7	14	5223
L125K	3C1E	Δ+PHS	0	7	13	5205	7	14	5205

^aSubstitution used to make the variant protein;

^bPDB accession code of simulated protein;

^cbackground form of SNase in which the substitution was engineered;

^dnumber of DOWSER water molecules, Na⁺ and Cl⁻ ions, and total number of water molecules included in the simulations.

A previous study of hydration of internal polar groups in SNase showed that molecular dynamics simulations started from the structures in which internal cavities were initially soaked with water molecules using the program DOWSER⁴⁹ usually converged to the same hydration state as simulations that initially had crystallographic or no water molecules at all.¹⁵ For the sake of faster convergence, the DOWSER algorithm was used to hydrate the protein interior artificially. Internal water molecules identified with DOWSER that were found within a 6 Å radius around the ionizable moieties of interest were included in the molecular dynamics simulation. The number of DOWSER water molecules found for each simulation is listed in Table 1. These DOWSER water molecules were included only in the simulations in which the internal group was treated as neutral. In simulations in which the internal ionizable group was charged water penetration was fast, obviating the need for artificial hydration of internal cavities with DOWSER.

Histidine residues were treated as neutral and protonated at the N_ε atom in all simulations. All other surface ionizable groups were assumed to be charged. After 500 steps of minimization with the steepest descent method the proteins were embedded in a box of TIP3 water molecules. The program CHARMM was used for setting up the system, for minimizations and for all subsequent MD simulations.^50,51 The CHARMM force field, version 27 with the phi, psi cross term map (CMAP) correction was employed.⁵² The force field contained the patches to construct the topologies for neutral Asp, Glu and Lys residues. Water molecules within 2.5 Å of the protein or crystallographic or DOWSER water molecules were removed. The protein was centered at the origin and all water molecules further than 36 Å from the origin were removed. The total number of water molecules and ions for the simulated systems are listed in Table 1. The final systems were subjected to minimizations under rhombic dodecahedral symmetry.

Molecular dynamics simulations

Each system was heated up in steps of 2 K, from 100 to 300 K. Equilibration for 100 ps in an NPT ensemble followed. The extended system formalism was used to maintain constant pressure and temperature with the Hoover thermostat⁵³ with a thermostat coupling constant of 1,000 kcal/mol/ps², while the normal pressure was maintained with a barostat with a piston mass of 500 amu, and piston collision frequency of 20/ps.⁵⁴ Rhombic dodecahedral periodic boundary conditions and the particle mesh Ewald (PME) method⁵⁵ for electrostatic interactions were employed, with the following parameters for Ewald simulations: κ=0.45, interpolation order of 6, grid spacing of approximately 1 Å, and real space interaction cutoff of 10 Å. Lennard-Jones interactions were shifted to zero after 10 Å. The leapfrog Verlet algorithm was used with a timestep of 1 fs. Five different heating and equilibration runs were initiated for each protein, with five different seed numbers for the random number generator used for assigning initial velocities.

Convergence of simulations

Simulations were performed in blocks of 5 ns. Convergence was examined after each block using criteria described ahead. If convergence was achieved at the end of a block, the simulations were stopped. Otherwise, another 5 ns block of simulations was performed.

The largest perturbation to the system originated from the charging of the internal ionizable group of interest. Therefore, structural convergence of that side chain and of its immediate vicinity was taken into consideration when examining the overall convergence. The average values of the following side chain attributes were examined to assess the convergence: RMSD values, state of hydration, and polarity of its environment. The state of hydration of the side chain (n_wat) was assessed by counting water oxygen atoms within a 3.5 Å radius of the polar atoms of the internal ionizable side chain. The polarity of the side chain environment (n) was determined by counting all polar atoms (including water) within a 3.5 Å radius of the polar atoms of the side chain. The backbone RMSD values of every protein residue, except for the residues belonging to the N-terminus (residues 6 or 7–9) and two large loops (residues 37–54 and 77–87), were also used as criteria for establishing convergence. The N-terminus and the two loops were highly mobile and have considerable structural fluctuations, which is why their structural convergence was not used to judge convergence of the simulations overall. For each ns of simulations the average values of all the convergence parameters were determined based on the snapshots that were recorded every 10 ps. Averaging over the 5 simulations started with different initial velocities was also performed.

The convergence criteria of side chain hydration and polarity were met when the difference of the average values calculated for the last and the first ns of the simulated block was less than 0.5. If the difference in average side chain RMSD values (only non hydrogen atoms were considered) between the last and the first ns of the simulated block was less than 0.5 Å, side chain RMSD values were considered converged. If the average backbone RMSD values between the last and the first ns of the simulated block of each considered residue was smaller than 0.75 Å, the backbone RMSD convergence criterion was deemed satisfied. The overall convergence was met when all four criteria were met in a same block of simulations. Note that in reality, proteins that continue to undergo large conformational changes on slow timescales may appear locally converged under this criterion but without actually being fully converged. However, the definition of convergence that was employed was practical and relevant to the problem under study given that the perturbations of the system involved alterations of the side chains.

Data analysis

GNUplot⁵⁶ was used for least squares fitting. RMSD values were determined with CHARMM.^50,51 Solvent accessible surface area (SASA) of the side chains was calculated with VMD.⁵⁷ The secondary structure content (i.e., α-helical and β-strand composition) of the proteins was determined with DSSP.⁵⁸

Results and Discussion

Convergence of simulations

Convergence in the simulations with the internal side chain in both the charged and the neutral state was established using four criteria: side chain hydration, side chain RMSD, polarity of the side chain environment, and backbone RMSD (Table 2). For the majority of variants the simulations performed with the internal group in the neutral form took less or equal time to converge than those in which the internal group was charged. For simulations with the internal ionizable group in the neutral state convergence was achieved in 5 to 15 ns whereas in the cases with charged internal groups it took between 5 and 45ns for the simulations to converge.

Table 2.

Convergence of 5 ns long blocks of simulations; + identifies converged, and − identifes non-converged simulations.

Protein	Neutral			Charged
	5 ns	10 ns	15 ns	5 ns	10 ns	15 ns	20 ns	25 ns	30 ns	45 ns
Δ+PHS/L25E	++++			++−	++++
Δ+PHS/L25K	++++			−+−	++++
Δ+PHS/L36K	−+++	++++		−++−	−+++	−+++	++++
PHS/L38E	++++			−+−	−+−	++++
PHS/L38K	++++			++++
PHS/T62K	++++			++++
PHS/V66D	−+−+	++++		++++
PHS/V66E	++++			−+	++++
V66K	+++−	+−+−	++++	++++
Δ+PHS/I72E	++++			++−+	+++−	++++
Δ+PHS/I72K	++++			+++−	++++
Δ+PHS/Y91E	−−−	++++		−+−	+++−	+++−	++++
Δ+PHS/I92D	+++−	++++		+−−	++−+	−+−+	−−−	−−+	+++−	++++
Δ+PHS/I92E	++++			−+−	−++−	+++−	+++−	+++−	++++
Δ+PHS/I92K	+++−	++++		−++−	−+++	−+−	+++−	++++
Δ+PHS/L103K	+−+−	++++		+++−	−+++	++++
Δ+PHS/V104K	++++			+++−	++++
Δ+PHS/L125K	++++			−+−	+−+−	+−+−	++++

The different markings refer to convergence of four different criteria, in this order (left to right): hydration of the side chain, RMSD values of the side chain, number of polar contacts of the side chain, and backbone RMSD values.

The variants with Lys-92, Asp-92 or Glu-92 are known to undergo global unfolding when these ionizable groups, which have highly perturbed pK_a values, are charged.^11,42,43 These were the variants that were the slowest to converge in our simulations (25–45ns). Large conformational changes consistent with global unfolding are expected to occur on timescales longer than tens of ns. A previous study of the I92D variant that used the self-guided Langevin dynamics method (SGLD) to enhance sampling recorded conformations in which the protein interior was filled with water and had several β-strands and the N-terminus of helix α₁ unfolded.¹⁵ The MD simulations in the present study also showed increased hydration of the protein interior, and some unfolding of those elements of secondary structure, but nothing comparable to what was observed in the SGLD simulations. The fact that the convergence criteria were met for this problem (Table 2) means that the additional conformational changes observed in the SGLD simulations are occurring either very gradually or infrequently, i.e., on a timescale longer than tens of ns. The MD simulations of variants with L25K, L25E, I92E, I92K, and L125K also showed evidence of changes in the secondary structure (described ahead). It is possible that the MD simulations of these variants do not represent a fully converged ensemble, and that the conformational changes upon ionization of these internal groups are somewhat underestimated in this study.

Water and polar atoms near internal groups

All simulations, except those of the L38K variant, showed that the hydration of the internal ionizable moieties increased with their ionization (Table 3). The number of water molecules near the ionizable moiety of the ionizable group of Glu residues increased by 2.7 to 3.5 water molecules, with an average of 3.2. For the two internal Asp residues that were studied the increase in the number of water molecules near the ionizable group was of 5.5 and 4.8 water molecules. The increase for Lys residues ranged from −0.1 to 3.5 with an average of 1.7 more water molecules when the internal Lys side chain was charged than when it was neutral. The only variant that experienced a minor decrease in its state of hydration was Lys-38. Notably, this is the only variant studied that does not have a depressed pK_a.¹⁶

Table 3.

Microenvironments of internal ionizable moieties.

Protein	Watera		Polarb		Δnwatc	Δnd	|ΔpKa|e
	Neutral	Charged	Neutral	Charged
L25E	0.2±0.4	3.4±0.7	0.4±0.6	6.1±1.0	3.2	5.7	3.0
L25K	0.0±0.0	3.4±0.9	0.0±0.1	4.1±0.8	3.4	4.1	4.1
L36K	0.0±0.2	1.9±1.0	1.1±1.0	4.0±1.1	1.9	2.9	3.2
L38E	0.4±0.6	3.9±1.2	2.5±1.4	6.1±1.0	3.5	3.6	2.3
L38K	1.7±0.7	1.6±0.9	2.9±1.0	4.1±0.8	−0.1	1.2	n/a
T62K	1.0±0.6	1.8±1.5	2.4±0.9	4.7±0.8	0.8	2.3	2.3
V66D	0.4±0.5	5.9±1.7	2.4±0.7	7.3±1.6	5.6	4.9	4.0
V66E	1.6±0.7	5.0±1.8	2.2±0.9	6.7±1.2	3.4	4.5	4.5
V66K	0.5±0.6	2.9±1.0	0.7±0.8	4.2±0.6	2.4	3.5	4.0
I72E	1.5±1.3	4.3±1.0	3.6±2.1	6.4±0.9	2.8	2.8	2.8
I72K	1.7±1.0	3.7±0.9	2.8±1.0	4.8±0.8	2.0	2.0	1.8
Y91E	1.7±1.2	4.3±1.0	3.7±1.2	6.7±1.1	2.6	3.0	2.6
I92D	1.1±0.7	5.9±0.8	2.4±1.1	7.1±1.0	4.8	4.7	4.1
I92E	1.1±0.6	4.9±0.8	1.1±0.6	5.7±1.1	3.8	4.6	4.5
I92K	0.6±0.6	1.9±1.4	0.7±0.6	3.6±0.7	1.3	2.9	5.1
L103K	0.8±0.7	1.1±0.3	2.0±0.8	4.2±0.6	0.3	2.2	2.2
V104K	0.5±0.6	3.0±0.9	1.5±0.7	4.5±0.9	2.5	3.0	2.7
L125K	0.0±0.0	2.9±0.8	1.1±0.7	3.8±0.8	2.9	2.7	4.2

^aNumber of oxygen atoms of water molecules within a 3.5 Å radius around the polar atoms of the internal ionizable side chains.

^bNumber of total polar atoms (water and protein) within a 3.5 Å radius around the polar atoms of the internal ionizable side chains.

^cDifference in the number of water atoms with 3.5 Å of the ionizable groups in the charged and neutral states obtained as an average over the last ns of simulations.

^dDifferences in the total number of polar atoms with 3.5 Å of the ionizable groups in the charged and neutral states obtained as an average over the last ns of simulations.

^eExperimentally measured pK_a value shift.^{11,20,40,42,43}

The total number of protein polar atoms within 3.5 Å of the internal ionizable atoms was always higher when this moiety was charged. For the internal Glu residues the increase in the number of polar atoms ranged from 2.8 to 5.7 with an average of 4.0. For the two internal Asp residues the increase was 4.9 and 4.7, and for the internal Lys residues it ranged from 1.2 to 4.1 with an average of 2.7.

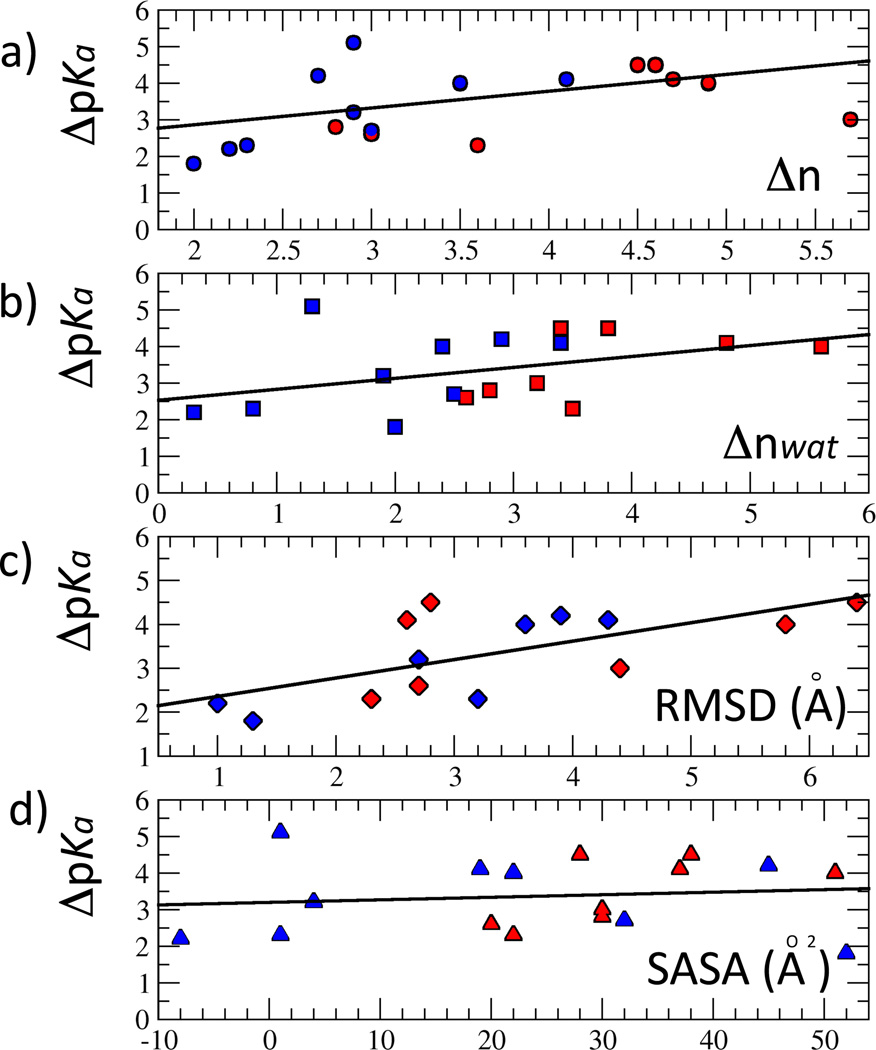
An interesting and unexpected correlation was observed between the absolute value of the shift in the experimental pK_a values (|ΔpK_a|), calculated as the difference between the measured pK_a ^{11,20,40,42,43} and the normal pK_a values (4.0, 4.5 and 10.4 for Asp, Glu and Lys in water, respectively), and the total difference in neighboring polar atoms Δn between the charged and the neutral species. The data in Table 3 show that with exception of the two Asp variants, the range of n, which refers the total number of polar atoms (from protein, water, and electrolyte counterions) around the internal ionizable group, is larger when the side chain is neutral than when the side chain is charged. For example, for Glu residues n for the neutral species ranged between 0.4 and 3.7 whereas for the charged species n ranged from 5.7 to 6.7. For Asp residues n was 2.4 for both Asp residues when they were neutral, and 7.1 and 7.3 when they were charged, and for Lys n ranged between 0 and 2.9 when the side chain was neutral and from 3.6 and 4.8 when Lys was charged. This suggests that differences in Δn are dominated by the differences of the polarity of environment when the internal ionizable groups are neutral. The correlation between the difference in n between charged and neutral forms and the experimental |ΔpK_a| thus shows that the variants whose internal ionizable side chains in their neutral form are in a more polar environment exhibit a smaller pK_a value shifts than those whose side chains are in a less polar environment.

Δn is a sum of three contributions, Δn_wat (contributions arising from contact with internal water molecules that penetrate into the protein in response to the ionization of the internal group), Δn_prot (contributions from contacts with polar and ionizable groups of the protein), and Δn_ion (contributions from interactions with counterions). To rationalize the linear relationship between |ΔpK_a| and Δn it is necessary to assume that each polar contact acquired upon charging of the internal ionizable group (Δn in Table 3) scales equally with |ΔpK_a|. This approximation is quite extreme, especially if some of those polar atoms that contribute to n are charged. The fit of the linear function |ΔpK_a| =a₁ Δn + a₂ yielded coefficients a₁ = 0.46 and a₁ = 1.93. (Figure 1). The RMS of the fit is 0.89. When fitting the |ΔpK_a| vs Δn data no distinctions were made between Lys residues and Asp and Glu residues. The linear relationship between |ΔpK_a| vs Δn would hold regardless of how ionizable residues are grouped.

Figure 1.

Correlation between experimental shifts in pK_a values and structural parameters. |ΔpK_a| refers to the difference in pK_a values of the internal ionizable groups in the protein and the normal values in water. Solid lines represent a fit of the data. (A) Correlation between |ΔpK_a| and Δn (difference in total number of polar atoms neighboring the charged and the neutral forms of the ionizable moiety). (B) Correlation between |ΔpK_a| and Δn_wat (difference in number of water atoms neighboring the charged and the neutral forms of the ionizable moiety). (C) Correlation between |ΔpK_a| and RMSD values of the charged side chain. (D) Correlation between |ΔpK_a| and ΔSASA (difference in solvent accessible surface area of the ionizable moiety when it iss neutral and when it is charged. In all plots, variants with Lys residues are colored blue, and variants with carboxylic residues are colored red.

Only 5 out of 17 variants studied deviated significantly from the linear correlation between |ΔpK_a| and Δn: L25E, L38E, V66K, I92K and L125K (Figure 1A and Table 3). Insufficient sampling might be one reason why these variants are different from the rest in this respect. For example, the variants with L25E and L38E substitutions exhibited unusually low hydration of the internal ionizable group when it was neutral (0.2 and 0.4 respectively). Such sparse interactions with internal water molecules appear to be quite common for the Lys side chains, but are rather unusual for the Glu side chains. If the number of water molecules in contact with the internal ionizable group in the neutral state was larger, n for these cases would be smaller. The most likely reason that variants with V66K, I92K and L125K substitutions are outliers is that sampling is probably insufficient in the simulations performed with these internal ionizable group in the charged state. Experiments with Trp fluorescence and CD and NMR spectroscopy suggest that the V66K and L125K variants undergo local unfolding upon ionization of the internal Lys residues, and that the variant I92K undergoes global unfolding.^10,45 This is why we speculate that sampling was insufficient in the MD simulations performed with these variants with Lys in the charged state. The consequence of limited convergence is that the change in the number of polar atoms in contact with the charged internal amino groups has most likely been underestimated.

For the majority of the variants the main contribution to Δn stems from Δn_wat, which reflects water penetration in response to the presence of a charge buried inside the protein (Table 3). When it was assumed that internal water molecules were solely responsible for stabilization of the internal groups in the charged state, the fit of the function |ΔpK_a| =a₁ Δn_wat + a₂ yielded a₁ = 0.30, a₂ = 2.53, with an rms of 0.94 (Figure 1B). This is not as good a fit as when the full Δn was used, indicating that contributions to Δn from contacts between the internal ionizable moieties and polar atoms from the protein or with ions are significant.

To gain more insight into factors that contribute to n, the average number of polar atoms within 3.5 Å of the ionizable moiety (n) was broken down into contributions from water molecules, counterions, backbone N and O atoms, side chain polar atoms, and side chain charged atoms (Table 4). According to these data a Na⁺ ion was associated with the charged carboxylate form of three internal groups. Binding of ions to the neutral side chain was not observed, and neither was the binding of a chloride ion. Although it is not clear whether the force field is sufficiently accurate to be useful to detect specific ion effects, the simulations suggest that the pK_a values of internal carboxylic side chains might, in some cases, exhibit detectable salt dependence.

Table 4.

Average number of atoms of a particular kind within a 3.5 Å radius of the polar atoms of the ionizable side chain.

Protein	Wata		Na+b	Nc		Od		Polare		Chargedf
	N	C	C	N	C	N	C	N	C	N	C
L25E	0.2	3.4	0	0	2.5	0.1	0	0	0	0	0
L38E	0.4	3.9	0	0.7	1.3	0.6	0	0.7	0.7	0	0
V66E	1.6	5.0	0	0	0.6	0.5	0.4	0	0	0	0.6
I72E	1.5	4.2	0.2	0.9	1.3	1.2	0.2	0	0.5	0	0
Y91E	1.7	4.2	0.8	0.2	0	0.3	0	1.3	1.1	0.1	0.5
I92E	1.1	4.9	0	0	0.5	0	0.2	0	0	0	0
Average E	1.1	4.3	0.2	0.3	1.0	0.9	0.1	0.3	0.4	0	0.2
V66D	0.4	5.9	0.4	1.0	0.1	0.8	0.8	0.2	0	0	0
I92D	1.1	5.9	0	0.8	0.7	0.4	0.2	0	0	0	0
Average D	0.8	5.9	0.2	0.9	0.4	0.6	0.5	0.1	0	0	0
L25K	0	3.4	0	0	0	0	0.6	0	0	0	0
L36K	0	1.9	0	0	0	0.6	1.4	0.5	0.3	0	0.4
L38K	1.7	1.6	0	0	0	0.9	1.2	0	0	0.2	1.0
T62K	1.0	1.8	0	0.3	0	1.1	2.5	0	0.4	0	0
V66K	0.5	3.0	0	0	0	0.4	0.7	0	0.6	0	0
I72K	1.7	3.7	0	0	0.2	1.2	0	0	0	0	0
I92K	0.6	1.9	0	0	0	0	1.5	0	0	0	0.2
L103K	0.6	1.1	0	0	0	0.4	1.0	0.6	1.7	0	0.3
V104K	0.5	3.0	0	0	0	0.9	0.2	0	0	0	1.2
L125K	0	2.9	0	0	0	0.7	0.4	0.2	0	0	0.5
Average K	0.7	2.4	0	0	0	0.6	1.0	0.1	0.3	0	0.4

^aWater oxygen atoms,

^bsodium ions,

^cbackbone nitrogen atoms (N),

^dbackbone oxygen atoms (O),

^eside chain polar atoms of any type,

^fside chain charged atoms of any type.

All numbers were obtained as an average over the last ns of simulations. Contributions smaller than 0.1 are not shown. N means neutral, and C means charged. For Glu, Asp and Lys side chains we show averages over all simulated side chains of a certain type (rows Average E, Average D and Average K respectively).

Internal Lys side chains in either the neutral or the charged form had no or very few backbone N atoms in its vicinity (Table 4). In contrast, the internal Glu side chain in the neutral state had both N and O backbone atoms in its immediate environment, with a preference for O atoms. The internal Glu side chains, when charged, had a clear preference for N backbone atoms. Surprisingly, the Asp side chains did not follow the trends of the Glu side chains; they displayed interactions with both types of backbone atoms in both the neutral and the charged states. The pronounced difference in preference for N and O backbone atoms between the neutral and charged Glu residues, and to a lesser extent between the neutral and charged forms of internal Lys residues, suggests that backbone conformational change can be expected upon ionization of these side chains. One interesting pattern observed when the identity of polar or charged side chain residues that interact with the internal ionizable moiety was tracked in detail¹ was that the majority of the ion pairs that are made were only temporarily (Table 4). The two strongest ion pairs made were between Lys-104 and Glu-129 and between Lys-38 and Glu-122. This latter interaction has been shown to be negligible with NMR spectroscopy.¹⁶

Side chain relaxation

Average side chain RMSD values of the the internal ionizable side chains were calculated for all simulations with the internal ionizable groups in both the charged or the neutral state (Table 5). In three variants (I72E, I92K, V104K) the internal ionizable group has two distinct conformations in the crystal structure. The conformation labeled B was used in the starting structure of all simulations, and the values reported in Table 5 correspond to RMSD values relative to the B conformation. The average RMSD values from the A conformations were also calculated and are (in Å): 2.5±0.8 for neutral Lys-72, 1.6±0.3 for charged Lys-72, 2.0±0.7 for neutral Lys-92, 3.1±1.2 for charged Lys-92, 2.0±0.5 for neutral Lys-104, 1.1±0.1 for charged Lys-104.

Table 5.

RMSD values and solvent accessible surface area.

Protein	Sidechain RMSDa		Backbone RMSDb		SASA, Neutralc		SASA, Chargedd
	Neutral	Charged	Neutral	Charged	R=1.4Å	R=2.0Å	R=1.4Å	R=2.0Å
L25E	1.5±0.3	4.4±1.3	0.8±0.6	1.2±0.9	0	0	30	8
L25K	1.5±0.4	4.3±0.9	0.8±0.6	1.2±1.7	0	0	19	7
L36K	1.2±0.4	2.7±0.7	0.8±0.6	1.2±0.8	1	0	5	0
L38E	1.6±0.3	2.3±1.7	1.1±0.9	1.4±1.0	0	0	22	7
L38K	1.7±0.4	1.9±0.6	1.1±0.9	1.2±1.1	6	1	20	5
T62K	1.6±1.0	3.2±0.9	1.3±1.3	1.6±1.7	7	2	8	1
V66D	0.8±0.3	5.8±1.1	1.1±0.9	1.3±1.0	1	0	52	35
V66E	1.7±0.3	6.4±0.6	1.1±0.9	1.1±0.9	2	0	40	26
V66K	1.4±0.4	3.6±2.0	1.2±1.1	1.2±0.9	5	0	27	23
I72E	2.0±0.4	3.1±0.5	0.8±0.5	1.0±0.7	3	1	33	20
I72K	1.6±0.3	1.3±0.3	1.0±0.7	1.0±0.7	12	6	64	54
Y91E	1.8±0.5	2.7±0.7	1.0±0.8	1.4±1.2	7	0	27	3
I92D	1.3±0.6	2.6±1.3	1.0±0.8	1.4±0.8	3	0	37	4
I92E	1.4±0.6	2.8±0.6	0.7±0.5	1.6±1.6	2	0	30	6
I92K	2.1±0.8	1.7±0.9	1.2±1.4	1.2±1.0	4	0	5	0
L103K	1.6±0.3	1.0±0.7	1.1±1.0	0.9±0.7	8	0	0	0
V104K	1.3±0.4	2.2±0.3	1.0±0.6	1.1±0.9	8	1	40	10
L125K	1.2±0.2	3.9±1.3	0.8±0.7	1.1±1.0	0	0	45	33

^aSidechain RMSD values (in Å).

^bTotal backbone RMSD values (in Å).

^cSolvent accessible surface area (SASA) of the ionizable moiety relative to the SASA of a model coumpound (in %), calculated with a probe radius of 1.4 Å and 2 Å.

The side chain RMSD values in simulations with the internal ionizable group in the neutral state were in most cases smaller that those in the charged state. This indicates that, and it might also suggest that in the crystal structure the internal ionizable groups are neutral and that the neutral side chains are more easily tolerated in the apolar interior of the protein. Specifically, the side chain RMSD values suggest that for the variants with substitutions at L25E, L25K, L36K, T62K, V66D, V66E, V66K, I92D, I92E, and L125K the internal ionizable group is neutral in the crystal structure. The difference between RMSD values of the neutral and charged side chains of variants with L38K, I72K, Y91E and L103K substitutions was less than 1 Å (with the RMSD values of charged species being larger in cases of I72K and L103K), which might indicate that in the crystal the internal ionizable moiety in these variants is charged.

For the variants with I72E and V104K substitutions, in which the internal ionizable side chain is found in two different conformations in the crystal structure, the average position of the side chain in the neutral form is closer to the B conformation in both cases, and the charged form is closer to the A conformation. It is possible that the crystal structures of these proteins reflects a mixture of charged and neutral side chains. The RMSD values of the side chain of Lys-92 in the neutral state are about equal relative to the A and B conformations. Close inspection of Figure 3 reveals that the side chain of Lys-92 samples both A and B conformations during the simulations, as well as conformations in between A and B. The RMSD values of the Lys-92 side chain in the charged state are closer to the B conformation.

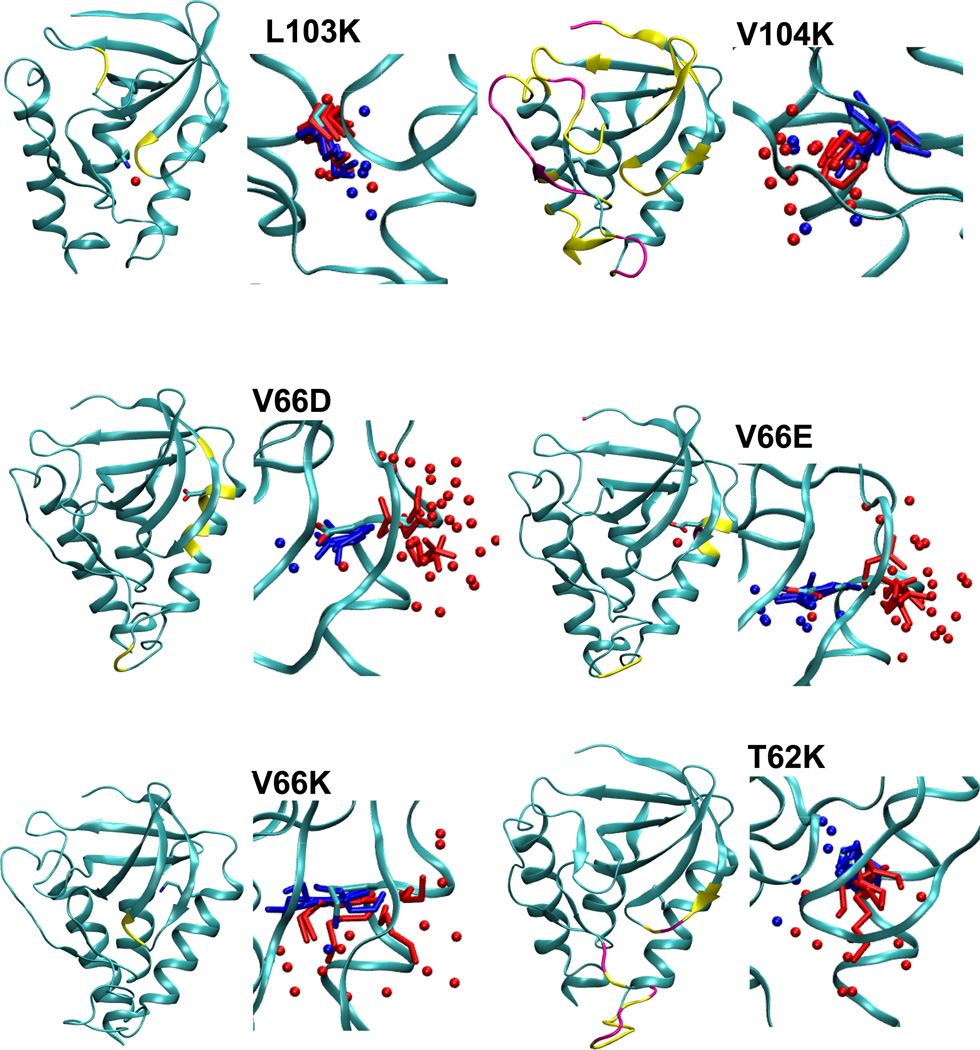
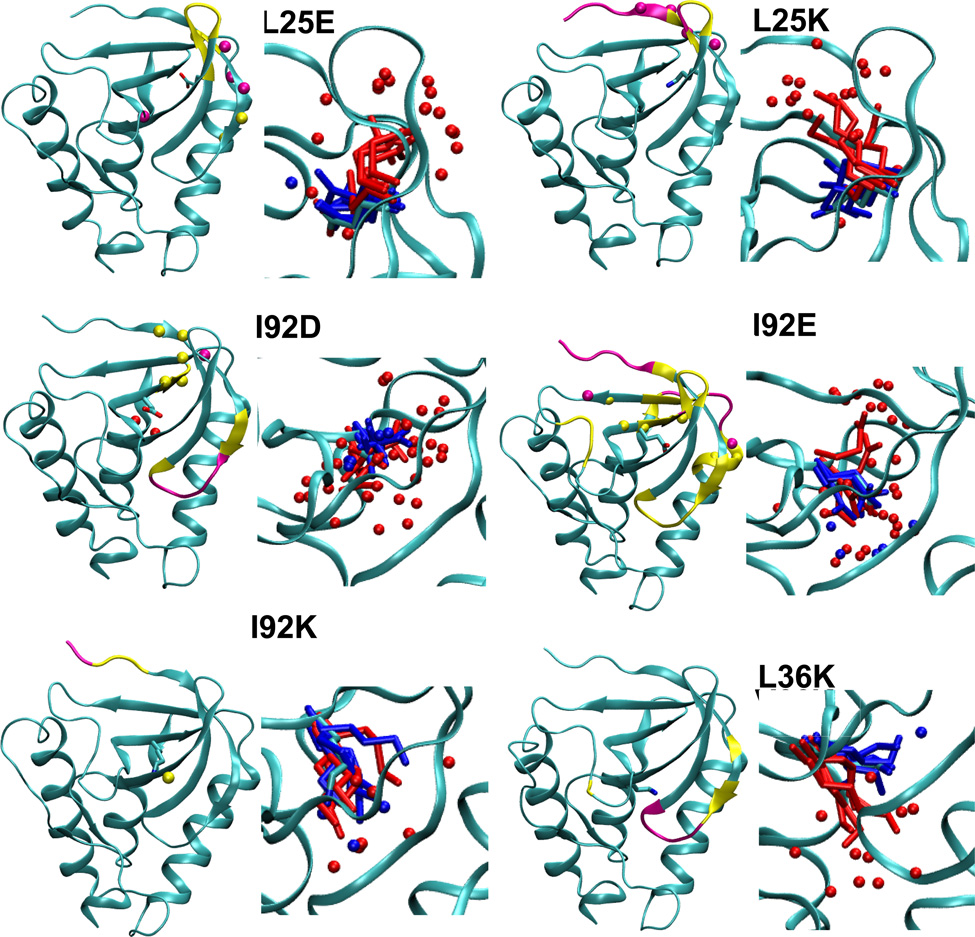
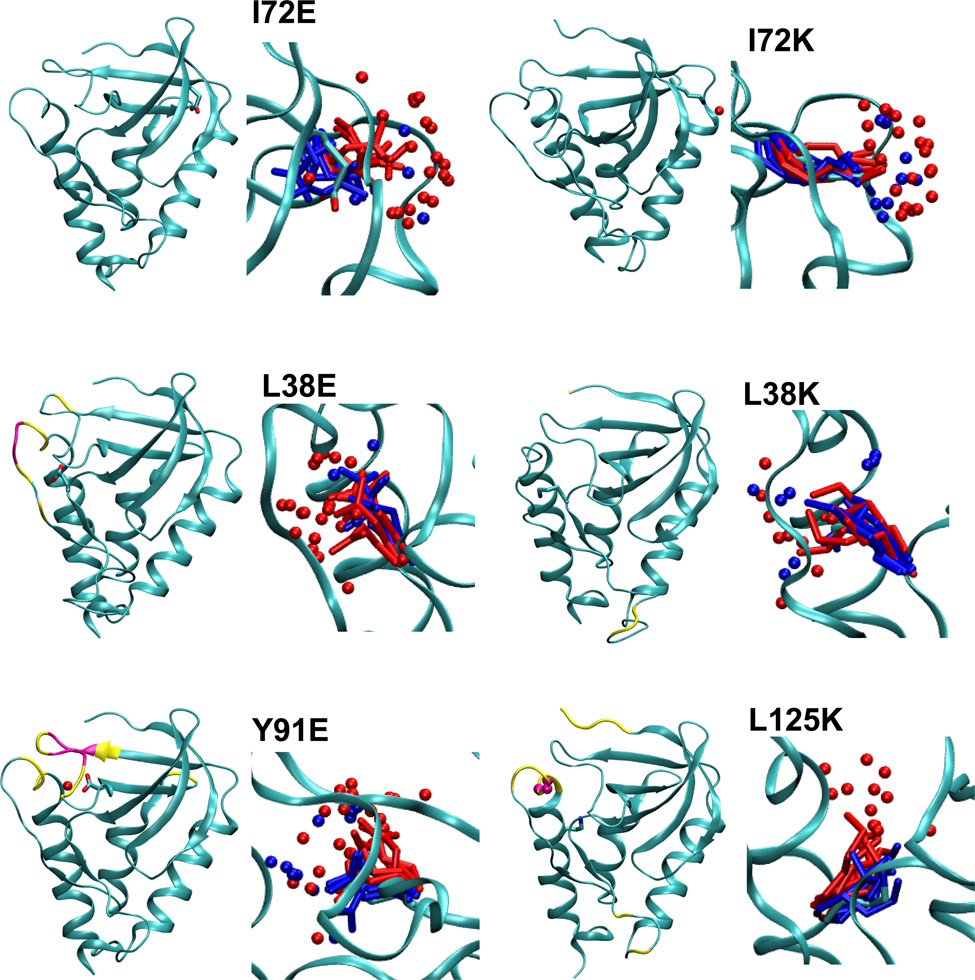
Figure 3.

Summary of structural consequences of ionization of internal groups in 18 variants of SNase. For each variant: (LEFT) Difference in backbone RMSD values between the simulations with internal ionizable groups in the charged and in the neutral states. Yellow and magenta identify residues that display a difference larger than 1 and 2 Å, respectively. Yellow and magental spheres identify residues that are unfolded in simulations with the internal ionizable group in the charged state in more than 25% and 50% of simulations, respectively. (RIGHT) Snapshot from the last ns of simulations showing the conformation and state of hydration of the internal ionizable side chains in the charged (red) and the neutral (blue) state. Spheres identify water molecules near the ionizable moiety. Figure made with VMD.⁵⁷

Final snapshots from simulations with each protein, five performed with the internal ionizable side chain in the neutral state, and five in the charged state, are shown in Figure 3. The range of conformations sampled by the internal ionizable side chains in the simulations are illustrated in this figure. The figure shows that for the variants in which the crystal structure is thought to have the internal side chain in the neutral state (L25E, L25K, L36K, T62K, V66D, V66E, V66K, I92E, and L125K), the conformations sampled by the internal ionizable side chain in the charged state are different from those found in the crystal structure. This further supports the suggestion that in these cases the ionizable group is indeed neutral in the crystal structure.

The side chain RMSD values were plotted against experimental |ΔpK_a| to determine if the magnitude of the conformational response of the side chains in the charged state was correlated with the experimental shift in pK_a (Figure 1C). Indeed, these two quantities appear to be correlated: the fit of the linear function |ΔpK_a| = a₁ * RMSD + a₂ yields a₁ = 0.42, a₂ = 1.94 and an rms of 0.75. This linear fit is higher than the one between |ΔpK_a| and Δn.

Solvent accessible surface area (SASA) of the polar atoms of each internal ionizable side chain was calculated to determine whether the ionizable moiety was internal or external, before and after ionization. Average values were determined for the last ns of simulations based on snapshots recorded every 10 ps. SASA was determined with probe radii of 1.4 Å and 2 Å. Small cavities and narrow crevices can be identified with a 1.4 Å probe radius, whereas it is likely that they will be missed with a 2.0 Å probe (i.e., a SASA of 0 will be reported). A SASA value that is close to zero with both probes indicates a buried residue. A residue located in a crevice or in a small cavity will have a non-zero SASA calculated with a probe radius of 1.4 Å and a negligible SASA calculated with a probe radius of 2 Å. Residues located on the protein surface will have large SASA with both probes.

To determine relative SASA, the areas calculated for an internal residue was divided by the SASA calculated for a model compound. The average SASA of a model compound was determined based on snapshots of a simulation run for a single Lys, Asp or Glu residue (in protonated or deprotonated forms) with methylated C-terminus and acetylated N-terminus inserted in a box of water. The relative SASA values (Table 5) show that most ionizable side chains are buried and have a negligible or small SASA (less than 8% with a 1.4 Å probe, and less than 2% with a 2 Å probe) in the neutral state. The only exception is the Lys-72 side chain which has a relative exposure of 12% calculated with a 1.4 Å probe and of 6% calculated with a 2 Å A probe.

The side chains of the majority of variants showed an increase in SASA when the side chains were charged, consistent with the ionizable moiety being able to access crevices or the protein/water interface. The exceptions were the side chains of Lys-36, Lys-62, Lys-92 and Lys-103, which showed no or rather small increase in SASA upon charging, consistent with them being fairly buried even after ionization. The charged Asp, Glu and Lys side chains at positions 66, 72 and 125 appear to have relatively large SASA, even with a 2.0 Å probe. These should be labeled as interfacial residues.

The difference in SASA between the charged and neutral side chain and |ΔpK_a| was examined by fitting the linear function |ΔpK_a| = a₁ * ΔSASA + a₂. This yielded coefficients a₁ = 0.007, a₂ = 3.20 with an rms of 1.02. This linear fit is not as good as the one between |ΔpK_a| and side chain RMSD values in the charged state, and between |ΔpK_a| and Δn.

Backbone relaxation

The average backbone RMSD values of all residues were determined for all simulations (Figure 3). The only variants that did not exhibit noticeable differences in backbone RMSD values anywhere in the protein were variants with I72E and I72K substitutions, consistent with the observation that the side chains of Glu-72 and Lys-72 are quite exposed to water when they are charged. The side chain of Lys-72 is exposed to water even when it is neutral as it appears to be at the protein-water interface rather than being buried in the interior of the protein. For the L38K variant the differences in backbone RMSD values were found only in flexible loops and N and C-terminal areas, far from the site of the L38K substitution proper. In most cases the response of the backbone to the ionization of the internal ionizable group was limited to the vicinity of the site of substitution. Only the variant with the V104K substitution exhibited a more global response.

The average secondary structure content of the proteins was calculated for simulation snapshots recorded every 10 ps. Only simulations with the charged side chain were analyzed for secondary structure content as the RMSD values suggested that under these conditions the proteins experienced larger conformational changes than in the simulations performed with the internal ionizable groups in the neutral state.

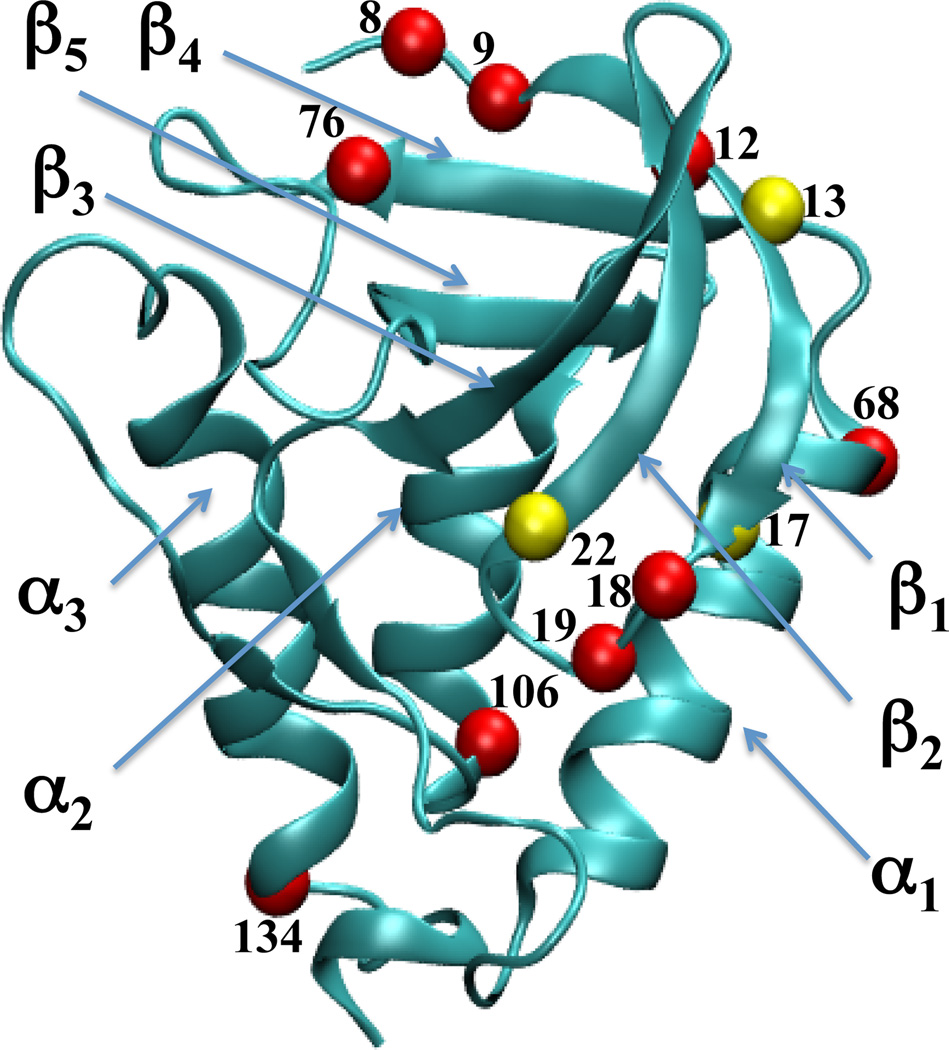
Identification of termini of elements of secondary structure may depend on the method used to identify secondary structure. The standard programs for secondary structure assignment, such as DSSP⁵⁸ used in this study, use criteria based on hydrogen bond patterns. Others, such as STRIDE,⁵⁹ use a combination of hydrogen-bond patterns and phi/psi angles, and others, such as KAKSI,⁶⁰ use C_α distances and phi/psi angles. Residues for which secondary structure assignment depends on the method used may often exhibit a partially unfolded secondary structure content. This means that the average over secondary structure assignments based on simulation snapshots ranges from 0 and 100%. For practical purposes, if the calculated average secondary structure content of a residue ranged from 10% and 75% the residue was considered to be partially unfolded. The following secondary structure elements were unfolded in simulations of at least 12 variants: residue 12 in the middle of strand β1, C-terminus of β1 (residues 18 and 19), C-terminus of β4 (residue 76), C-terminus of α1 (residue 68), C-terminus of α2 (residue 106), and the C-terminus of α3 (residue 134). In addition, the N-terminus of β1 (residues 8 and 9) was unfolded in at least 7 simulations. The partially unfolded residues listed above were recorded in simulations of several variants and their partially unfolded character is thus most likely unrelated to ionization of the internal group. The C_α atoms of those residues are shown as red spheres in Figure 2.

Figure 2.

Secondary structure of staphylococcal nuclease.⁴⁰ Colored spheres identify residues that display partial secondary structure content (i.e., average α-helical or β-strand content between 10% and 75 %) in simulations of more than 6 variants (red), and in simulations of less than 6 and more than 2 variants (yellow). Figure made with VMD.⁵⁷

The following residues (shown in yellow in Figure 2) appear to be partially unfolded in simulations of at least three variants: residue 13 located in the middle of β1 is unfolded in simulations of variants L25E, L25K, I72E, I72K, L38E; residues 17 located at the C-terminus of β1 is unfolded in simulations of variants L25E, L36K, I72E, I92E, and T62K; and residue 22 located at the N- terminus of β1 is unfolded in simulations of variants L36K, V66K and T62K. With the exception of the unfolding of residue 13 in simulations of the L38E variant, all of the unfolding in positions 13, 17 and 22 occurs in variants in which the substituted side chain is either near the unfolding residue or is pointing into the small cavity located in the β-barrel of the protein. In a previous MD study of water penetration in SNase⁶¹ we showed that the unfolding residues 13, 17 and 22 are all involved in formation of passages for penetration of water into this small cavity. Thus the backbone atoms of the unfolding residues might be interacting with either the ionizable side chain, or with water molecules that penetrate into the cavity to hydrate the ionizable side chain. Since the DSSP software employed here to determine secondary structure uses hydrogen bonding patterns, we speculate that the apparent unfolding of these residue may simply be a signature of the perturbed hydrogen bonding networks involving these residues and not of the unfolding events.

Several other local unfolding events are most likely related to the ionization of internal groups since they are specific for particular variants and mostly limited to the vicinity of the site of substitution (yellow and magenta backbone in Figure 3): (1) In simulations with the L25E variant unfolding of several residues of β1 was observed, and a residue at the N-terminus of β4 was added. (2) In simulations with the L25K variant unfolding of the N-terminus of β1 was observed. (3) In simulations with the I92K variant, a residue in β3 undergoes local unfolding. (4) In simulations with the I92D variant, local unfolding of the N-termini of β1 and β4, and C-terminus of β5 were observed. (5) In simulations of the I92E variant, unfolding of the C-termini of β4 and α1 and several residues in β5 was. (6) In the L125K variant the N-termini of β2 and α3 undergo local unfolding.

The changes in the backbone in response to the ionization of internal groups observed in the MD simulations are consistent with what was observed in pH titrations of these variants, monitored with Trp fluorescence and far-UV CD. For example, these experiments showed that the I92K, I92E and I92D variants are globally unfolded when the internal ionizable groups are charged.^10,42 The pH titrations of variants with L25E, V66K, V66E, V104K and L125K substitutions suggested the presence of sub-global conformational reorganization coupled to the ionization of the internal group.¹⁰ The spectroscopic studies revealed no details about the nature of these conformational changes. The variants that show evidence of global or sub global unfolding in the experiments show unfolding of secondary structure or changes in backbone RMSD values in the MD simulations (Figure 3). There are cases, such as the variant with the L25K substitutions, where the experiments did not detect conformational reorganization coupled to the ionization of the internal ionizable group, but for which the MD simulations recorded local unfolding (at the N-terminus of β1). However, in crystallographic structures the N-terminus of β1 is not always assigned a β-strand character, suggesting that the simulations are in fact in agreement with experimental data.

One of the general features identified with the MD simulations and consistent with what was observed experimentally is that for the majority of variants most of the backbone remained largely intact following the ionization of the internal group. According to the simulations, relatively minor conformational rearrangements of the backbone are needed for the internal charged moieties to increase contact with water or with protein polar atoms upon ionization. This is fully consistent with the absence of large changes in spectroscopic signals upon pH titrations.^{10–13,16,19,43} In the case of variants with V66D, V66E and V66K substitutions, NMR experiments have shown that the ionization of the internal groups leads to increased dynamics or fluctuations in the region immediately adjacent to the internal ionizable moiety (i.e. the N-terminus of helix α1⁴⁵). The MD simulations do not show unfolding in this region - that might require much longer simulations. However they show clear evidence of increased RMSD values of the backbone in the case of variants V66D and V66E, but missed this in the case of the V66K variant. Another case where the results of MD simulations can be compared directly with experimental observations is for variants L38K and L38E.^16,17 The differences in the effects of L38E and L38K substitutions and ionization of these groups on the backbone, as observed with NMR spectroscopy, is comparable to what was observed in the MD simulations, which showed that the L38E substitution increased RMSD values in the vicinity of the site of substitution more than the L38K variant. NMR spectroscopy studies are underway in our laboratory to examine detailed molecular effects of the ionization of internal Lys side chains in SNase. The results of the present MD simulations will be useful for structural interpretation of the NMR spectroscopy data.

Summary and conclusions

Multiple molecular dynamics simulations were performed with crystal structures of eighteen variants of staphylococcal nuclease with Lys, Asp or Glu residues lodged in the interior of the protein. The goal was to examine patterns of conformational reorganization triggered by the ionization of internal groups in the protein interior. Simulations performed with the ionizable groups in the charged and in the neutral states were compared. For most variants the RMSD values of the side chains and the total backbone RMSD values were smaller when the internal ionizable groups were neutral than when they were charged. This suggests that these crystal structures describe internal side chain in the neutral state. It also reflects the structural reorganization of the internal side chains when charged in search of new micro environments with more polar contacts. Indeed, the polarity of the micro evnvironment of the charged side chain was higher than that of the neutral side chain for all simulated variants. Solvent accessible surface areas calculations showed that with one exception (I72K), all internal ionizable side chains and their ionizable moieties are buried when they are in the neutral state. With the exception of L36K, T62K, I92K and L103K variants the ionization of the internal side chain leads to increase in the solvent accessibility of the side chain either through opening of small crevices that connect the side chain to bulk water, or through the exposure of the side chain to the protein-water interface. The ionization of the internal side chain led to an increase in its hydration for all variants except for I72K.

For most variants the ionization of internal groups triggered some degree of backbone relaxation. This reorganization of the backbone was, for the most part, modest, consistent with local unfolding reactions localized to the region where the internal ionizable group was located. Only three of the simulated variants are known to unfold globally. Although the simulations were too short to show large unfolding events, some aspects of what was observed (e.g. small amounts of unfolding of several residues, as well as large increase in the number of internal water molecules) was consistent with the incipient global unfolding that is observed experimentally with these proteins.

Analysis of the correlation between the shifts in the pK_a values of the internal ionizable groups measured experimentally, and different factors that contribute towards structural relaxation in response to the presence of an internal charge, revealed an unexpected and interesting correlation between the absolute value of the shifts in |ΔpK_a| values and the differences between the total number of water and polar groups, Δn, surrounding the ionizable moiety in the charged and in the neutral state. The major contribution to the variability in n comes from the variability in the polarity of the environment of the side chain when in neutral state, which is fully consistent with the idea that the side chains that are in more polar environments in the neutral state experience smaller shifts in the pK_a values than those that are in a less polar environment in their neutral states. This also suggests that the contributions from water penetration and protein polar atoms are approximately of the same magnitude. The correlation between the pK_a and the RMSD values of the side chain in the charged state was even better than the correlation between |ΔpK_a| and Δn. The correlation between |ΔpK_a| and the difference in water-accessible surface area between charged and neutral states for each internal side chain was not as good. The observed linear correlation between |ΔpK_a| and net differences in polarity between neutral and charged forms, as well as side chain RMSD values suggests that, after proper benchmarking, an empirical method based solely on MD simulations could be used for the difficult task of predicting the pK_a values of internal ionizable groups in proteins.

The results of these MD simulations have other interesting implications for structure based calculations of pK_a values of internal ionizable groups. They suggest that in addition to the relaxation of side chains, which is done explicitly in methods such as the MCCE continuum electrostatics algorithm,²⁸ water penetration and relaxation of the backbone concomitant with ionization of internal side chains also have to be taken into account.^30,31,47 Owing to the important roles of internal water molecule that penetrate into the protein interior in response to the ionization of the internal group, constant pH MD methods^33,37,38 that consider protein relaxation explicitly should be performed with explicit water molecules.

The results of these simulations also have interesting implications for interpretation of the properties of internal ionizable groups in proteins involved in biological energy transduction, where internal ionizable groups are the recurring and fundamental structural motif. They suggest that some degree of conformational relaxation accompanying slow charge transfer reactions may be expected, and that the types of conformational relaxation may involve formation of crevices in the protein to connect the charged group with bulk water molecules. Even subtle structural reorganization of the type that has been observed in all the proteins that we studied could have a very large influence on the kinetic and thermodynamic properties of H⁺ transport mechanisms.