Bayesian Inference of the Fully Specified Subdistribution Model for Survival Data with Competing Risks

Abstract

Competing risks data are routinely encountered in various medical applications due to the fact that patients may die from different causes. Recently, several models have been proposed for fitting such survival data. In this paper, we develop a fully specified subdistribution model for survival data in the presence of competing risks via a subdistribution model for the primary cause of death and conditional distributions for other causes of death. Various properties of this fully specified subdistribution model have been examined. An efficient Gibbs sampling algorithm via latent variables is developed to carry out posterior computations. Deviance Information Criterion (DIC) and Logarithm of the Pseudomarginal Likelihood (LPML) are used for model comparison. An extensive simulation study is carried out to examine the performance of DIC and LPML in comparing the cause-specific hazards model, the mixture model, and the fully specified subdistribution model. The proposed methodology is applied to analyze a real dataset from a prostate cancer study in detail.

1 Introduction

Competing risks data are frequently encountered in various medical applications due to the fact that patients may die from different causes. Studies on this topic have been active and productive. Gail (1975) proposed a multivariate model of failure times due to different causes. Tsiatis (1975) showed that for any joint distribution of n failure times there exists a joint distribution of n independent failure times such that the marginal cause-specific cumulative incident functions from the two joint distributions coincide, which implies that the correlations between the failure times are not identifiable in the multivariate failure time model. Prentice et al. (1978) introduced a cause-specific hazards model. Larson and Dinse (1985) established a mixture model with hazards function conditional on failure from a specific cause. Fine and Gray (1999) discussed the subdistribution model with proportional hazards assumption to assess the covariates effect on the cumulative incidence function of the cause of interest. Recently, Fan (2008) introduced a Bayesian nonparametric methodology based on the full likelihood for the proportional subdistribution hazards model. Elashoff et al. (2007, 2008) jointly modeled the longitudinal measurements and survival data with competing risks, where they extended respectively the cause-specific hazards model and the mixture model for survival data, and used latent random variables to link together the sub-models for longitudinal measurements and survival data.

The Bayesian literature on competing risks analysis is still sparse. Fan (2008) developed Bayesian methods by extending the subdistribution model of Fine and Gray (1999) for each cause-specific risk. More recently, Hu et al. (2009) and Huang et al. (2011) developed the Bayesian methods for a joint analysis of longitudinal measurements and survival data with competing risks, in which cause-specific hazards sub-models were considered for modeling survival times. As pointed out in Fine and Gray (1999), one of the nice properties of the subdistribution model is that the effect of a covariate on the marginal probability function can be directly assessed. However, the subdistribution model proposed by Fine and Gray (1999) cannot be compared to two other established models as the competing risks for other causes are not specified in their model. Due to this reason, we develop a fully specified subdistribution model with subdistribution hazard for the primary cause of death and conditional hazards for other causes of death. Under this fully specified subdistribution model, we are able to establish a theoretical connection between the partial likelihood of Fine and Gray (1999) and the one under the fully specified subdistribution model for the cause of primary interest when all failure times are observed. We notice that this connection may not be established under the models discussed in Fan (2008). With this new development, formal model comparisons between the fully specified subdistribution model and two other established models, namely, the cause-specific hazards model (Prentice et al., 1978) and the mixture model (Larson and Dinse, 1985), can be carried out via Bayesian Deviance Information Criterion (DIC) and logarithm of the Pseudomarginal likelihood (LPML). Furthermore, the fully specified subdistribution model also facilitates an efficient implementation of the Gibbs sampling algorithm.

The rest of the article is organized as follows. In Section 2, we present a detailed development of the fully specified subdistribution model and examine various properties of it. The prior and posterior are discussed and an efficient Gibbs sampling algorithm via a set of latent variables is developed in Section 3. In Section 4, we briefly review the cause-specific hazards model (Prentice et al., 1978) and the mixture model (Larson and Dinse, 1985), and provide necessary mathematical formulations for DIC and LPML under these two models and the fully specified subdistribution model. In Section 5, we present the design of a simulation study and the simulation algorithms for generating the data under the three competing risk models. We notice that these three competing risk models have never been formally compared based on our best knowledge. In Section 6, we analyze a real data from a prostate cancer study in detail. We conclude the paper with brief discussion and some extensions of the proposed model in Section 7.

2 Subdistribution Based Models for Competing Risks

2.1 Preliminary

We consider two competing risks throughout the paper and the extension to more than two competing risks will be discussed in Section 7. Let T_j be the time to failure due to cause j for j = 1, 2 and δ be the index of cause of death. Also let T = min{T₁, T₂}. Assume cause 1 is the cause of primary interest. The subdistribution hazard for cause 1 defined in Gray (1988) is given as follows:

$$h_1(t)=\underset{\mathrm{\Delta }t\to 0}{\text{lim}}\left\{\frac{\mathit{\text{Pr}}(t\le T\le t+\mathrm{\Delta }t,\delta =1|T\ge t\cup (T\le t\cap \delta \ne 1))}{\mathrm{\Delta }t}\right\}=\frac{\partial F_1(t)/\partial t}{1-F_1(t)},$$ (2.1)

where F₁(t) = Pr(T ≤ t, δ = 1). As discussed in Fine and Gray (1999), to develop the regression model of (2.1) with the proportional hazards assumption, h₁(t|x) = h₁₀(t) exp(x′β₁) and $F_1(t|\mathit{x})=1-\text{exp}\{-{\displaystyle {\int }_0^t}{h}_{10}(u)\text{ exp }(\mathit{x}\prime {\mathit{\beta }}_1)\mathit{\text{ du}}\}$, where x is a vector of covariates and β₁ is a vector of the corresponding regression coefficients. As pointed out in Fine and Gray (1999), the covariate effects can be directly assessed on the cumulative incidence function for primary cause under the subdistribution model. However, the distributions for failure times due to other causes are never specified in Fine and Gray (1999).

2.2 A Fully Specified Subdistribution Model for Two Competing Risks

Let $T_j^{*}=T_j\times I(\delta =j)+\mathrm{\infty }\times I(\delta \ne j)$, j = 1, 2, where we define ∞ × 0 = 0. Write $T^{*}=\text{min}\{T_1^{*},T_2^{*}\}$ as the observed time to failure. We propose the cause-specific cumulative incidence functions for both causes as follows:

$$\begin{array}{c}{F}_1(t)=\mathit{\text{Pr}}(T^{*}\le t,\delta =1)=\mathit{\text{Pr}}(T_1\le t,\delta =1),\hfill \\ F_2(t)=\mathit{\text{Pr}}(T^{*}\le t,\delta =2)=M_2(t)\mathit{\text{Pr}}(\delta =2),\hfill \end{array}$$ (2.2)

where M₂(t) is the cumulative incidence function conditional on cause 2. The fact that $\underset{t\to \mathrm{\infty }}{\text{lim}}{F}_j(t)=\mathit{\text{Pr}}(\delta =j)<1$ implies that F_j(t) is improper. Yet M₂(t) is proper due to $\underset{t\to \mathrm{\infty }}{\text{lim}}{M}_2(t)=\underset{t\to \mathrm{\infty }}{\text{lim}}[F_2(t)/\mathit{\text{Pr}}(\delta =2)]=1$. Note that in (2.2), we do not directly model the correlation between T₁ and T₂, which is not identifiable as shown in Tsiatis (1975). Instead, F₁(t) and F₂(t) are related to each other via Pr(δ = 2) = 1 − Pr(δ = 1) = 1 − F₁(∞).

We apply the definition of subdistribution hazard in Fine and Gray (1999) for cause 1 by $h_1(t)=\frac{\partial F_1(t)}{\partial t}\times \frac{1}{1-F_1(t)}$. Then H₁(t) is improper because $\underset{t\to \mathrm{\infty }}{\text{lim}}{H}_1(t)=-\text{log}[1-\underset{t\to \mathrm{\infty }}{\text{lim}}{F}_1(t)]<\mathrm{\infty }$. We specify a proportional hazards model with an improper baseline hazard function for F₁(t|x) as

$$F_1(t|\mathit{x})=1-\text{exp }\{-H_{10}(t)\text{ exp}(\mathit{x}\prime {\mathit{\beta }}_1)\}.$$ (2.3)

For cause 2, we propose a proportional hazards model for M₂(t|x) as

$$M_2(t|\mathit{x})=1-\text{exp }\{-H_{20}(t)\text{ exp}(\mathit{x}\prime {\mathit{\beta }}_2)\}.$$ (2.4)

The model defined by (2.3) and (2.4) is thus called the fully specified subdistribution (FS) model. Under the FS model, Pr(δ = 2|x) = 1 − Pr(δ = 1|x) = exp{−H₁₀(∞) exp(x′β₁)}.

Assume there are n observations with the vector of observed time t = (t₁, t₂, … , t_n)′, the matrix of covariates X = (x₁, x₂, … , x_n)′, and the vector of cause indicator δ = (δ₁, δ₂, … , δ_n)′, where δ_i takes possible values of 0, 1, and 2, corresponding to “censored”, “died due to cause 1”, and “died due to cause 2” for the i^th subject, respectively. Under the model defined in (2.3) and (2.4), the likelihood function is given by

$$L({\mathit{\beta }}_1,{\mathit{\beta }}_2,h_{10},h_{20}|\mathit{t},X,\mathit{\delta })={\displaystyle \prod _{i=1}^n}{[h_{10}(t_i)\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\text{ exp }\{-H_{10}(t_i)\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\left\}\right]}^{I({\delta }_i=1)}\times {[h_{20}(t_i)\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_2)\text{ exp }\{-H_{20}(t_i)\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_2)-H_{10}(\mathrm{\infty })\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\left\}\right]}^{I({\delta }_i=2)}\times {\left[\text{exp }\right\{-H_{10}(t_i)\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\}-(1-\text{exp }\{-H_{20}(t_i)\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_2)\})\times \text{exp }\{-H_{10}(\mathrm{\infty })\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\left\}\right]}^{I({\delta }_i=0)}.$$ (2.5)

2.3 Justification of Fine and Gray’s Partial Likelihood

The FS model is not only a natural expansion of the subdistribution model of Fine and Gray (1999) but also provides novel justifications of Fine and Gray’s partial likelihood under certain conditions. Assume there are n complete observations with the vector of observed time t = (t₁, t₂, … , t_n)′, the matrix of covariates X = (x₁, x₂, … , x_n)′, and the vector of cause indicator δ = (δ₁, δ₂, … , δ_n)′. The partial likelihood of β₁ for cause 1 given in Fine and Gray (1999) is of the form

$$L_p({\mathit{\beta }}_1|\mathit{t},X,\mathit{\delta })={\displaystyle \prod _{i=1}^n}{\left[\frac{\text{exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)}{{\displaystyle {\sum }_{j\in R_i^{*}}}\text{exp}\{{\mathit{x}}_j^{\prime }{\mathit{\beta }}_1\}}\right]}^{I({\delta }_i=1)},$$ (2.6)

where $R_i^{*}$ is defined as a special risk set at failure time t_i given by

$$R_i^{*}=\{j:(t_j\ge t_i)\cup (t_j\le t_i\cap {\delta }_j\ne 1)\}.$$ (2.7)

Note that the risk set $R_i^{*}$ is quite different than the risk set in Cox’s partial likelihood (Cox, 1972, 1975) as the patients who died from cause 2 before t_i are also included in $R_i^{*}$.

Three theorems are established below to show that the partial likelihood (2.6) can be obtained under the FS regression model via three different approaches with detailed proofs given in Appendix B. Denote D₁ as the number of deaths due to cause 1. Let y_i = t_i when δ_i = 1, and y_i = ∞ when δ_i ≠ 1. Write y = (y₍₁₎, y₍₂₎, … , y_(n))′, where 0 = y₍₀₎ < y₍₁₎ < ⋯ < y_(D1) < y_(D1+1) = ⋯ = y_(n) = ∞. Since all observations are failure times, the likelihood function of β₁ for cause 1 given the n complete observations is the part of the likelihood function in (2.5) involving β₁:

$$L({\mathit{\beta }}_1,h_{10}|\mathit{y},X,\mathit{\delta })={\displaystyle \prod _{i=1}^n}[h_{10}(y_{(i)})\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)]\times \text{exp }\{-H_{10}(y_{(i)})\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\}.$$ (2.8)

Theorem 1 With n complete observations, assume that in the FS model the baseline hazard rate h₁₀ is zero after the last failure time due to cause 1. The partial likelihood function (2.6) can be attained by the profile likelihood approach, which is to plug in the profile maximum likelihood estimator of h₁₀ in the likelihood function L(β₁, h₁₀|y, X, δ).

Theorem 2 With n complete observations, assume that in the FS model the baseline hazard rate h₁₀(t) is zero after the last failure time due to cause 1 and the prior of h₁₀(t) is degenerate at 0 everywhere except at y_i’s when δ_i = 1. Let h₁₀(y_i) = λ_i when δ_i = 1 and λ = (λ₁, … , λ_D1)′. We further assume independent Jeffreys-type priors for the λ_i’s, i.e., $\pi (\mathit{\lambda })\propto {\displaystyle {\prod }_{i=1}^{D_1}}1/{\lambda }_i$. Then, the partial likelihood function (2.6) is obtained by

$$L_p({\mathit{\beta }}_1|\mathit{y},X,\mathit{\delta })\propto {\displaystyle \int }L({\mathit{\beta }}_1,h_{10}|\mathit{y},X,\mathit{\delta })\pi (\mathit{\lambda })d{\lambda }_1\dots d{\lambda }_{D_1},$$

where L(β₁, h₁₀|y, X, δ) is defined in (2.8).

Theorem 3 With n complete observations, assume that in the FS model the baseline hazard rate h₁₀(t) is zero after the last failure time due to cause 1 and that H₁₀(t) has a Gamma process prior, i.e., h_1i ~ Gamma(c₀h_0i, c₀), where c₀ > 0, h_1i = H₁₀(y_(i)) − H₁₀(y_(i−1)) for i = 1, 2, … , D₁, h_{1, D1+1} = ⋯ = h_1n = 0, h_0i = H₀(y_(i)) − H₀(y_(i−1)), H₀(y) is increasing and differentiable at y₁, … , y_D1 with H₀(0) = 0, and the h_1i are independent of each other. Then the partial likelihood function (2.6) can be approximated by

$$L_p({\mathit{\beta }}_1|\mathit{y},X,\mathit{\delta })\approx \underset{c_0\downarrow 0}{\text{lim}}g(c_0)E^{h_{10}}[L({\mathit{\beta }}_1,h_{10}|\mathit{y},X,\mathit{\delta })],$$

where g(c₀) is a function of c₀, which is free from β₁.

Fine and Gray (1999) also showed that the partial likelihood arises from complete data using a certain reduced data structure, without any assumptions on the models for the subdistribution for other causes. The results established in the above theorems give insight into Fine and Gray’s partial likelihood.

3 Prior, Posterior, and Computational Development

3.1 Prior and Posterior

For the sake of simpler calculation, a special case of the gamma process prior for the cumulative baseline hazard function assumed in Theorem 3 is considered here for the FS model. Assume the baseline hazard functions respectively have piecewise constant forms, which are, with K_j + 1 partitions of the time axis, 0 = s_j0 < s_j1 < s_j2 < ⋯ < s_jKj < ∞,

$$\{\begin{array}{cc}{h}_{10}(t)=\hfill & {\lambda }_{1k},s_{1,k-1}<t\le s_{1k},k=1,2,\dots ,K_1;\hfill \\ h_{10}(t)=\hfill & {\lambda }_{1,K_1+1}\text{ exp}\{-(t-s_{1K_1})\},t>s_{1K_1};\hfill \\ h_{20}(t)=\hfill & {\lambda }_{2k},s_{2,k-1}<t\le s_{2k},k=1,2,\dots ,K_2;\hfill \\ h_{20}(t)=\hfill & {\lambda }_{2K_2,}t>s_{1K_2}.\hfill \end{array}$$ (3.1)

To construct posterior distributions for the unknown parameters, we assume β_j follows an improper uniform prior, λ_jk follows a Jeffreys-type prior, and λ_1,K1+1 follows a gamma prior. We further assume that β_j, λ_jk, and λ_1,K1+1 are independent for k = 1, … , K_j and j = 1, 2. Let λ₁ = (λ₁₁, λ₁₂, … , λ_1,K1+1)′ and λ₂ = (λ₂₁, λ₂₂, … , λ_2K2)′, then the joint prior of (β₁, β₂, λ₁, λ₂) is specified as follows

$$\pi ({\mathit{\beta }}_1,{\mathit{\beta }}_2,{\mathit{\lambda }}_1,{\mathit{\lambda }}_2)=\pi ({\mathit{\beta }}_1)\pi ({\mathit{\beta }}_2)\pi ({\mathit{\lambda }}_1)\pi ({\mathit{\lambda }}_2)\propto \left[{\displaystyle \prod _{j=1}^2}{\displaystyle \prod _{k=1}^{K_1}}\frac{1}{{\lambda }_{\mathit{\text{jk}}}}\right]\pi ({\lambda }_{1,K_1+1}),$$ (3.2)

where $\pi ({\lambda }_{1,K_1+1})\propto {\lambda }_{1,K_1+1}^{a-1}\text{exp}(-b{\lambda }_{1,K_1+1})$ with a > 0 and b > 0, which are prespecified hyperparameters. The joint posterior distribution is given by

$$\pi ({\mathit{\beta }}_1,{\mathit{\beta }}_2,{\mathit{\lambda }}_1,{\mathit{\lambda }}_2|\mathit{t},X,\mathit{\delta })\propto {\pi }^{*}({\mathit{\beta }}_1,{\mathit{\beta }}_2,{\mathit{\lambda }}_1,{\mathit{\lambda }}_2|\mathit{t},X,\mathit{\delta })\equiv L({\mathit{\beta }}_1,{\mathit{\beta }}_2,{\mathit{\lambda }}_1,{\mathit{\lambda }}_2|\mathit{t},X,\mathit{\delta })\pi ({\mathit{\beta }}_1,{\mathit{\beta }}_2,{\mathit{\lambda }}_1,{\mathit{\lambda }}_2),$$ (3.3)

where L(β₁, β₂, λ₁, λ₂|t, X, δ) is given by (2.5) with h₁₀(t) and h₂₀(t) defined in (3.1). Recently, Wang et al. (2012) established a theoretical connection between the gamma process prior specified for the cumulative baseline function and the independent gamma priors for the λ_jk for the interval-censored survival data. Also, the independent gamma priors assumed for the baseline hazard function approximate the gamma process prior when c₀ → 0+. Thus, the priors in (3.2) for the λ_jk can be considered as a special case of the gamma process priors specified for the cumulative baseline function in this sense.

Let ν_jik = 1 if the i^th subject failed or was censored in the k^th interval (s_j,k−1, s_jk], and 0 otherwise for k = 1, 2, … , K_j +1, and i = 1, 2, … , n, where s_j,Kj+1 = ∞, for j = 1, 2. Also let X_j be a matrix with its i^th row equal to $I({\delta }_i=j)({\nu }_{\mathit{\text{ji}}1},\dots ,{\nu }_{{\mathit{\text{jiK}}}_j},{\mathit{x}}_i^{\prime })$ for j = 1, 2. Then, we are led to the following theorem regarding the the propriety of the posterior distribution of (β₁, β₂, λ₁, λ₂) with an improper prior given by (3.2).

Theorem 4 Assume that (i) when δ_i > 0, t_i > 0 and for k = 1, 2, … , K_j for j = 1, 2, and (ii) X₁ and X₂ are of full rank. Then, the posterior distribution π(β₁, β₂, λ₁, λ₂|t, X, δ) in (3.3) with the prior specified in (3.2) is proper.

A proof of Theorem 4 is given in Appendix B. Theorem 4 gives very mild conditions for ensuring propriety of the joint posterior distribution of (β₁, β₂, λ₁, λ₂) under the fully specified subdistribution model. The conditions (i) and (ii) essentially require that all event times are strictly positive, at least one event occurs in each chosen interval (s_j,k−1, s_jk], and the corresponding covariate matrix is of full rank. Notice that we do not require any events for the last interval (s_1K1, ∞) for the primary cause as we specify a proper prior for λ_1,K1+1. These conditions are easily satisfied in most applications and are quite easy-to-check. Under certain additional conditions, we can also show that when π(λ_1,K1+1) ∝ 1 in (3.2), the resulting posterior of (β₁, β₂, λ₁, λ₂) is still proper. We also notice that following Chen et al (2006), the posterior propriety by assuming full gamma process priors on H₁₀ and H₂₀ for c₀ > 0 can be established and, however, stronger propriety conditions are required in this case.

3.2 Computational Development

Due to the complexity of the likelihood structure of the FS model, an analytical evaluation of the posterior distribution does not appear to be possible. In order to carry out posterior inference, we adopt Markov chain Monte Carlo (MCMC) methods and develop a computationally efficient Gibbs sampling algorithm to sample from the posterior distribution in (3.3).

In order to avoid the complicated form in the censored part of the likelihood function, we introduce a latent variable η_i to indicate whether or not subject i would eventually fail from cause 1 or 2 and another latent variable u_i to be the failure time such that u_i ≥ t_i when subject i was censored at t_i and η_i = 1. Then the complete likelihood is constructed as

$$L({\mathit{\beta }}_1,{\mathit{\beta }}_2,h_{10},h_{20}|\mathit{t},X,\mathit{\delta },\mathit{\eta },\mathit{u})={\displaystyle \prod _{i=1}^n}{[h_{10}(t_i)\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\text{ exp }\{-H_{10}(t_i)\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\left\}\right]}^{I({\delta }_i=1)}\times {[h_{20}(t_i)\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_2)\text{ exp }\{-H_{20}(t_i)\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_2)-H_{10}(\mathrm{\infty })\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\left\}\right]}^{I({\delta }_i=2)}\times {[h_{10}(u_i)\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\text{ exp }\{-H_{10}(u_i)\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\left\}\right]}^{I({\delta }_i=0,{\eta }_i=1)}\times {\left[\text{exp }\right\{-H_{20}(t_i)\text{ exp }({\mathit{x}}_i^{\prime }{\mathit{\beta }}_2)-H_{10}(\mathrm{\infty })\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\left\}\right]}^{I({\delta }_i=0,{\eta }_i=2)},$$ (3.4)

where η = (η_i : δ_i = 0, 1 ≤ i ≤ n) and u = (u_i : δ_i = 0, η_i = 1, 1 ≤ i ≤ n). Based on the complete data likelihood, the augmented posterior of (β₁, β₂, λ₁, λ₂, η, u) is given by

$$\pi ({\mathit{\beta }}_1,{\mathit{\beta }}_2,{\mathit{\lambda }}_1,{\mathit{\lambda }}_2,\mathit{\eta },\mathit{u}|\mathit{t},X,\mathit{\delta })\propto L({\mathit{\beta }}_1,{\mathit{\beta }}_2,h_{10},h_{20}|\mathit{t},X,\mathit{\delta },\mathit{\eta },\mathit{u})\pi ({\mathit{\beta }}_1,{\mathit{\beta }}_2,{\mathit{\lambda }}_1,{\mathit{\lambda }}_2),$$ (3.5)

where h₁₀(t) and h₂₀(t) are defined in (3.1). It is easy to show that

$${\displaystyle \sum _{\eta }}{\displaystyle \int }\pi ({\mathit{\beta }}_1,{\mathit{\beta }}_2,{\mathit{\lambda }}_1,{\mathit{\lambda }}_2,\mathit{\eta },\mathit{u}|\mathit{t},X,\mathit{\delta })d\mathit{u}=\pi ({\mathit{\beta }}_1,{\mathit{\beta }}_2,{\mathit{\lambda }}_1,{\mathit{\lambda }}_2|\mathit{t},X,\mathit{\delta }),$$

where π(β₁, β₂, λ₁, λ₂|t, X, δ) is the posterior given in (3.3). This result ensures that whenever (β₁, β₂, λ₁, λ₂, η, u) ~ π(β₁, β₂, λ₁, λ₂, η, u|t, X, δ), then (β₁, β₂, λ₁, λ₂) ~ π(β₁, β₂, λ₁, λ₂|t, X, δ).

The introduction of the latent variables η and u greatly facilitates a convenient implementation of the Gibbs sampling algorithm. To develop an efficient Gibbs sampling algorithm, we use the collapsed Gibbs method of Liu (1994). First, we group (β₂, λ₂, η, u) together. Then, the Gibbs sampling algorithm requires to sample from the following conditional posterior distributions in turn: (i) [β₁|λ₁, β₂, λ₂, η, u, t, X, δ]; (ii) [λ₁|β₁, β₂, λ₂, η, u, t, X, δ]; and (iii) [β₂, λ₂, η, u|β₁, λ₁, t, X, δ]. For (i), the conditional posterior density of β₁ given (λ₁, β₂, λ₂, η, u, t, X, δ) is log-concave in each component of β₁. Thus, we can use the adaptive rejection algorithm of Gilks and Wild (1992) to sample β₁. For (ii), it can be shown that given (β₁, β₂, λ₂, η, u, t, X, δ), the λ_1k’s are conditionally independent and each of them follows a gamma distribution. Thus, sampling λ₁ is straightforward. For (iii), it is easy to see that

$$[{\mathit{\beta }}_2,{\mathit{\lambda }}_2,\mathit{\eta },\mathit{u}|{\mathit{\beta }}_1,{\mathit{\lambda }}_1,\mathit{t},X,\mathit{\delta }]=[{\mathit{\beta }}_2,{\mathit{\lambda }}_2,\mathit{\eta }|{\mathit{\beta }}_1,{\mathit{\lambda }}_1,\mathit{t},X,\mathit{\delta }][\mathit{u}|{\mathit{\beta }}_1,{\mathit{\lambda }}_1,{\mathit{\lambda }}_2,\mathit{\eta },\mathit{t},X,\mathit{\delta }].$$ (3.6)

In (3.6), we collapse out u in the conditional distribution [β₂, λ₂, η|β₁, λ₁, t, X, δ]. However, jointly sampling (β₂, λ₂, η) from their conditional distribution is not possible. Thus, we need to run a sub-Gibbs sampling algorithm to sample (β₂, λ₂, η) from this conditional posterior distribution. The approach is called the modified collapsed Gibbs sampling algorithm. As shown in Chen et al. (2000), the modified collapsed Gibbs sampling algorithm yields the target posterior as its stationary distribution. The sub-Gibbs sampling algorithm requires to sample from the following three additional conditional posterior distributions in turns: (iiia) [β₂|β₁, λ₁, λ₂, η, t, X, δ]; (iiib) [λ₂|β₁, λ₁, β₂, η, t, X, δ]; and (iiic) [η|β₁, λ₁, β₂, λ₂, t, X, δ]. For (iiia) the conditional posterior density of β₂ is log-concave in each component of β₂ and we again use adaptive rejection algorithm of Gilks and Wild (1992) to sample β₂. For (iiib), the λ_1k’s are conditionally independent and each of them follows a gamma distribution. Finally, for (iiic), η_i’s are conditionally independent and each η_i follows a Bernoulli distribution. The technical detail of sampling η from [η|β₁, λ₁, β₂, λ₂, t, X, δ] and sampling u from [u|β₁, λ₁, λ₂, η, t, X, δ] is given in Appendix C.

4 Model Comparison

The cause-specific hazards model and the mixture model are two well-established models for competing risks survival data. We discuss details of these two models and compare them with the FS model both theoretically, in simulation, and in an analysis of a real dataset.

4.1 Other Models for Comparison

Cause-specific Hazards Model

As discussed in Gaynor et al. (1993), the cause-specific hazard function is denoted by

$$h_{\mathit{\text{Cj}}}(t)=\underset{\Delta t\to 0}{\text{lim}}\left\{\frac{\mathit{\text{Pr}}(t\le T<t+\Delta t,\delta =j|T\ge t)}{\Delta t}\right\},j=1,2.$$

Under the proportional hazards assumption, h_Cj(t|x) = h_Cj0(t) exp(x′β_j) and the cumulative incidence function of cause j is given by

$$F_j(t|\mathit{x})=\mathit{\text{Pr}}(T\le t,\delta =j)={\displaystyle {\int }_0^t}{h}_{\mathit{\text{Cj}}0}(u)\text{ exp}(\mathit{x}\prime {\mathit{\beta }}_j)\text{ exp }\{-{\displaystyle \sum _{j=1}^2}{H}_{\mathit{\text{Cj}}0}(u)\text{ exp}(\mathit{x}\prime {\mathit{\beta }}_j)\}\mathit{\text{du}}.$$

The covariate effects can be directly assessed on the cause-specific hazard functions. But they cannot be directly estimated by β_j alone on the cause-specific cumulative incidence function of cause j, as the cause-specific cumulative incidence function of cause 1 also depends on regression coefficients β₂ for cause 2.

Mixture Model

Larson and Dinse (1985) discussed the mixture model. Assume the types of cause-specific failures follow a multinomial distribution. Define the probability of failing from cause j as p_j = Pr(δ = j) for j = 1, 2, where p₁ + p₂ = 1. Define h_Mj(t) as the hazard function conditional on failure from cause j,

$$h_{\mathit{\text{Mj}}}(t)=\underset{\Delta t\to 0}{\text{lim}}\left\{\frac{\mathit{\text{Pr}}(t\le T<t+\Delta t|\delta =j,T\ge t)}{\Delta t}\right\}.$$

Under the proportional hazards assumption, h_Mj(t|x) = h_Mj0(t) exp(x′β_j) and the cause-specific cumulative incidence function is given by

$$F_j(t|\mathit{x})=\mathit{\text{Pr}}(T\le t,\delta =j|\mathit{x})=p_j(1-\text{exp }\{-H_{\mathit{\text{Mj}}0}(t)\text{ exp}(\mathit{x}\prime {\mathit{\beta }}_j)\left\}\right).$$

It is observed that both cause-specific hazard functions and cause-specific cumulative incidence functions depend on regression coefficients of the corresponding cause as well as the probability of failing from that cause.

Notice that the definition of the subdistribution hazard is different than the definition of the cause-specific hazard function or the definition of the conditional hazard function in the mixture model. Thus, if the proportional structure on the hazard function of one model is true, the hazard functions of other two models could never achieve the Cox proportional hazards assumption.

4.2 Model Comparison Measures

Deviance Information Criterion (DIC) (Spiegelhalter et al., 2002) and Logarithm of the Pseudomarginal Likelihood (LPML) (Ibrahim et al., 2001) are used here to compare the cause-specific hazards model, the mixture model, and the FS model. Let θ denote a collection of model parameters. DIC is defined as DIC = D(θ̂) + 2p_D, where D(θ) is a deviance function, p_D = D̄ − D(θ̂), D̄ and θ̂ are the posterior means of D(θ) and θ. The formula of LPML is given by $\text{LPML}={\displaystyle {\sum }_{i=1}^n}\text{log}({\text{CPO}}_i)$, where the Conditional Predictive Ordinate (CPO), CPO_i = f(t_i|x_i,D⁽ⁱ⁾) = ∫ f(t_i|θ, x_i)π(θ|D⁽ⁱ⁾), D⁽ⁱ⁾ is the data with the i^th observation deleted, and π(θ|D⁽ⁱ⁾) is the posterior distribution based on the data D⁽ⁱ⁾. According to Gelfand and Dey (1994), LPML implicitly includes a similar dimensional penalty as AIC asymptotically.

For the proposed FS model, θ = (β₁, λ₁, β₂, λ₂), and the deviance function D(θ) is given by D(θ) = −2 log L(β₁, β₂, h₁₀, h₂₀|t, X, δ), where L(β₁, β₂, h₁₀, h₂₀|t, X, δ) is given by (2.5) and h₁₀(t) and h₂₀(t) are defined in (3.1).

For the cause-specific hazards model, suppose the piecewise exponential models for h_Cj0(t), j = 1, 2. The deviance function is defined by

$$D(\mathit{\theta })=-2\text{ log }{L}_C({\mathit{\beta }}_1,{\mathit{\beta }}_2,h_{C10},h_{C20}|\mathit{t},X,\mathit{\delta }),$$

where

$$L_C({\mathit{\beta }}_1,{\mathit{\beta }}_2,h_{C10},h_{C20}|\mathit{t},X,\mathit{\delta })={\displaystyle \prod _{i=1}^n}{\{h_{C10}(t_i)\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\}}^{I({\delta }_i=1)}\times {\{h_{C20}(t_i)\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_2)\}}^{I({\delta }_i=2)}\times \text{ exp }\{-H_{C10}(t_i)\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)-H_{C20}(t_i)\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_2)\}.$$

From the above likelihood function, it is easy to see that under the cause-specific hazards model, DIC=DIC₁+DIC₂, where DIC_j is the DIC of the survival model with single cause j by treating other causes of death as censored.

For the mixture model, let p_1i denote the probability of death due to cause 1 for the i^th subject, p₁ = (p₁₁, p₁₂, … , p_1n)′. The likelihood function is

$$L_M({\mathit{\beta }}_1,{\mathit{\beta }}_2,h_{M10},h_{M20},{\mathit{p}}_1|\mathit{t},X,\mathit{\delta })={\displaystyle \prod _{i=1}^n}{[p_{1i}{h}_{M10}(t_i)\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\text{ exp }\{-H_{M10}(t_i)\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\left\}\right]}^{I({\delta }_i=1)}\times {[(1-p_{1i})h_{M20}(t_i)\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_2\}\text{ exp }\{-H_{M20}(t_i)\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_2)\left\}\right]}^{I({\delta }_i=2)}\times {\left[p_{1i}\text{ exp }\right\{-H_{M10}(t_i)\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\}+(1-p_{i1})\text{ exp }\{-H_{M20}(t_i)\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_2)\left\}\right]}^{I({\delta }_i=0)}.$$

Assume $p_{1i}=\frac{\text{exp}\{{\mathit{z}}_i^{\prime }\mathit{\varphi }\}}{1+\text{exp}\{{\mathit{z}}_i^{\prime }\mathit{\varphi }\}}$, where z_i is a vector of covariates, which may be a subset of x_i.

For the cause-specific hazards model and mixture model, the form of the baseline hazard functions h_Cj0 and h_Mj0 and the prior of (β₁, β₂, λ₁, λ₂) are assumed in the same way as those in the FS model excluding the last piece h₁₀(t) when t ≥ s_1,K1. Similar to the FS model, the propriety of the joint posterior distribution of (β₁, β₂, λ₁, λ₂) can also be established under an improper joint prior π(β₁, β₂, λ₁, λ₂), which is similar to (3.2).

5 A Simulation Study

In this section, we carry out a simulation study to compare the cause-specific hazards model, mixture model, and fully specified subdistribution model via DIC and LPML. To generate data from the FS model, we assume there are two causes with cause 1 to be the cause of interest, and there are two covariates with true parameters β₁ = (β₁₁, β₁₂)′ and β₂ = (β₂₁, β₂₂)′, which are chosen such that Pr(δ = 1) is around 1/3. Covariates x_i1 are generated from N(0, 1) and x_i2 given x_i1 are generated from Bernoulli(p(x_i1)), where $p(x_{i1})=\frac{\text{exp}\{0.5+0.3x_{i1}\}}{1+\text{exp}\{0.5+0.3x_{i1}\}}$. Assume the failure times of two causes follow distinct piecewise exponential distributions, where for cause 1 the time is partitioned as s₁₀ = 0, s₁₁ = 8, s₁₂ = 12, s₁₃ = 15, s₁₄ = 16, and s₁₅ = 17 with corresponding λ₁ = (0.001, 0.01, 0.03, 0.02, 0.3)′, and for cause 2 the time is partitioned as s₂₀ = 0, s₂₁ = 3, s₂₂ = 5, s₂₃ = 8, s₂₄ = 10, s₂₅ = 11, s₂₆ = 12, s₂₇ = 13, s₂₈ = 15, s₂₉ = 17, and s₂₁₀ = 18 with corresponding λ₂ = (0.001, 0.005, 0.01, 0.02, 0.04, 0.07, 0.1, 0.15, 0.2, 1.0)′. Generate r_i from U(0, 1). If r_i < Pr(δ_i = 1|x_i), then generate $t_i^{*}$ of cause 1 from a piecewise exponential distribution

$$f_1(t_i^{*}|{\mathit{x}}_i)=\frac{h_{10}(t_i^{*})\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\text{ exp }\{-H_{10}(t_i^{*})\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\}}{1-\text{exp }\{-H_{10}(\mathrm{\infty })\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\}}.$$

If r_i ≥ Pr(δ_i = 1|x_i), then generate $t_i^{*}$ of cause 2 from a piecewise exponential distribution

$$f_2(t_i^{*}|{\mathit{x}}_i)=\frac{h_{20}(t_i^{*})\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_2)\text{ exp }\{-H_{20}(t_i^{*})\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_2)-H_{10}(\mathrm{\infty })\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\}}{\text{exp }\{-H_{10}(\mathrm{\infty })\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\}[1-\text{exp }\{-H_{20}(\mathrm{\infty })\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_2)\left\}\right]}.$$

The censoring time c_i is generated from a uniform distribution, U(a_c, b_c), where 0 < a_c < b_c are chosen so that the proportion of death is around 2/5, and then t_i is taken to be $t_i=\text{min}\{t_i^{*},c_i\}$. Note that under the FS model, $\mathit{\text{Pr}}({\delta }_i=1|{\mathit{x}}_i)=F_1(\mathrm{\infty }|{\mathit{x}}_i)=1-\left\{-H_{10}(\mathrm{\infty })\text{exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\right\}$.

For the mixture model, the settings of model parameters and covariates are similar to those for the FS model, while Pr(δ = 1) is calculated by $p_1=\frac{\text{exp}(\mathit{z}\prime \mathit{\varphi })}{1+\text{exp}(\mathit{z}\prime \mathit{\varphi })}$, where ϕ = (ϕ₁, ϕ₂)′ is chosen such that p₁ is around 1/3. If r_i from U(0, 1) falls in (0, Pr(δ = 1)), then $t_i^{*}$ of cause 1 is generated from a piecewise exponential distribution

$$f_1(t_i^{*}|{\mathit{x}}_i)=h_{10}(t_i^{*})\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\text{ exp }\{-H_{10}(t_i^{*})\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\}.$$

Otherwise, $t_i^{*}$ of cause 2 is generated from a piecewise exponential distribution

$$f_2(t_i^{*}|{\mathit{x}}_i)=h_{20}(t_i^{*})\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_2)\text{ exp }\{-H_{20}(t_i^{*})\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_2)\}.$$

For the cause-specific hazards model, the parameter and covariates settings are also similar as above. According to Lu and Tsiatis (2001), t_i is generated by t_i = min{t_1i, t_2i, c_i}, where t_1i, t_2i, and c_i are generated independently, respectively, from a piecewise exponential distribution

$$f_1(t_{1i}|{\mathit{x}}_i)=h_{10}(t_{1i})\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\text{ exp }\{-H_{10}(t_{1i})\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\},$$

a piecewise exponential distribution

$$f_2(t_{2i}|{\mathit{x}}_i)=h_{20}(t_{2i})\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_2)\text{ exp }\{-H_{20}(t_{2i})\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_2)\},$$

and a uniform distribution, U(a_c, b_c), such that the proportion of death is around 2/5.

500 data sets with n = 500 observations in each dataset were generated from each of the three models, respectively, as described above. Each simulated dataset was fitted by all three models and the corresponding DICs and LPMLs were calculated. From Table 1, we see that the best model chosen by DIC and LPML is always consistent with the true model where the data were simulated. The mean DIC and mean LPML under each model and scenario are shown in Table 4 of Appendix A. The true value, estimate, standard deviation, mean square error, and coverage probability of each covariate coefficient when estimating from the true model for all of the three models are given in Table 5 of Appendix A. It is observed that the standard deviations and mean square errors are moderate and stable, and that the coverage probabilities are always around 0.95 under all three scenarios of (K₁, K₂).

Table 1.

Frequency of Ranking Each Model as Best under Different Scenarios

	DIC			LPML
(K1, K2)	FS Best	C Best	M Best	FS Best	C Best	M best
Data Simulated from FS Model
(5, 10)	0.626	0.002	0.372	0.608	0.000	0.392
(10, 20)	0.764	0.004	0.232	0.778	0.008	0.214
(15, 30)	0.892	0.006	0.102	0.918	0.006	0.076
Data Simulated from C Model
(5, 10)	0.194	0.524	0.282	0.190	0.482	0.328
(10, 20)	0.130	0.722	0.148	0.132	0.716	0.152
(15, 30)	0.156	0.732	0.112	0.158	0.726	0.116
Data Simulated from M Model
(5, 10)	0.096	0.044	0.860	0.100	0.072	0.828
(10, 20)	0.104	0.094	0.802	0.110	0.142	0.748
(15, 30)	0.098	0.154	0.748	0.120	0.192	0.688

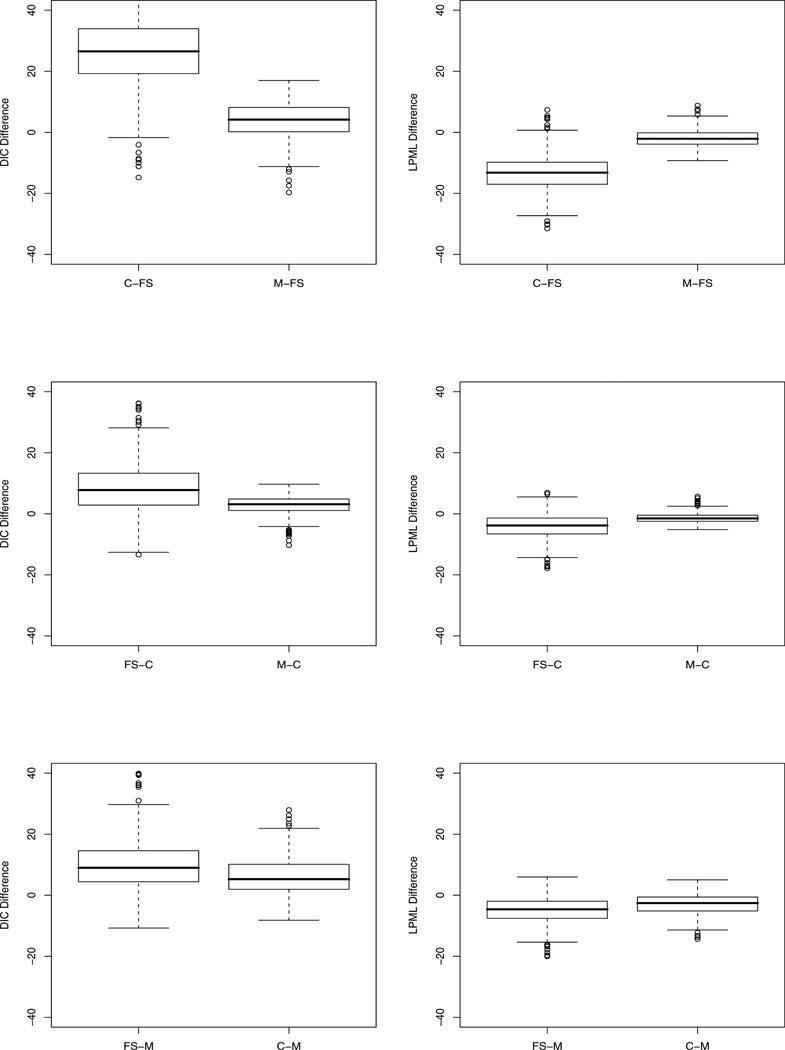
To further compare the models, the median and interquartile range (IQR) of the pairwise differences of DIC and LPML for two models under each scenario are calculated, and the corresponding boxplots are shown in Figure 1. When the data were simulated from another model, the mixture model and fully specified subdistribution model fit better than the cause-specific hazards model.

Fig. 1.

Box Plots of DIC and LPML Differences between Models

6 Analysis of the Prostate Cancer Data

A subset of data from the prostate cancer studies published in Choueiri et al. (2010) is analyzed using the three models. The response variable was the time from prostate-specific antigen (PSA) failure to death or to the last follow-up, whichever came first. The median follow-up time after PSA failure was 11.2 years with IQR=(5.8, 16.0). The sample size was 546, with 54 prostate cancer deaths and 151 other causes of deaths. Seven covariates were considered in the analysis, including patient’s age at the date of PSA failure, the natural logarithm of PSA (logpsa), prostatectomy Gleason score (7 (GS7= 1) or otherwise (GS7= 0)), prostatectomy Gleason score (8 to 10 (GS8H= 1) or otherwise (GS8H= 0)), prostatectomy T classification (T3 and higher (T3= 1) or otherwise (T3= 0)), surgical margin status (positive (margin= 1) or otherwise (margin= 0)), and PSA doubling time (DT) (less than 6 months (DT6= 1) or otherwise (DT6= 0)). In this analysis, the prostate cancer cause of death is the primary cause and the other cause of death is any causes of death other than prostate cancer. We let β₁ = (β₁₁, β₁₂, … , β₁₇) denote the vector of the corresponding regression coefficients for the prostate cancer cause of death.

Different values of K₁ and K₂ were tried out for optimizing the model fitting. In the mixture model, z is the vector of all covariates without preselecting for a fair comparison between the models. The values of DIC, p_D, and LPML for the 3 × 3 combinations of K₁ and K₂ under all three models are reported in Table 2. We see that (K₁, K₂) = (15, 20) is the optimum combination of (K₁, K₂) for almost all models, and that the fully specified subdistribution model always outperforms the other two models by achieving the smallest DIC and the largest LPML.

Table 2.

DIC, Dimension Penalty, and LPML of Three Models

		C Model			M Model			FS Model
K1	K2	DIC	pD	LPML	DIC	pD	LPML	DIC	pD	LPML
10	10	1586.5	34.3	−795.3	1580.0	42.5	−791.9	1565.3	34.4	−784.2
	20	1578.6	44.6	−792.5	1574.9	52.7	−791.2	1560.1	44.7	−782.9
	30	1600.8	55.0	−805.6	1596.0	63.0	−803.1	1581.5	55.1	−795.0
15	10	1584.2	39.9	−795.7	1576.4	48.3	−791.9	1564.4	39.8	−785.0
	20	1575.8	49.9	−792.7	1571.1	58.4	−790.3	1558.9	49.9	−783.5
	30	1598.0	60.3	−805.2	1592.1	68.8	−802.6	1580.1	60.5	−795.4
20	10	1599.8	45.1	−805.4	1592.6	53.6	−801.4	1579.4	45.2	−794.6
	20	1592.0	55.5	−802.6	1587.9	64.1	−800.3	1574.7	55.8	−793.4
	30	1614.1	65.9	−815.2	1609.6	74.7	−813.0	1595.4	65.9	−805.2

The subdistribution model of Fine and Gray (1999) was also fit the data. For the prostate cancer death, the estimates, standard errors (SEs) and 95% confidence intervals (CIs) of β₁ under the subdistribution model of Fine and Gray (1999) and the posterior means (estimates), posterior standard deviations (SDs), and 95% highest posterior density (HPD) intervals of β₁ under the FS model for the scenario of (K₁, K₂) = (15, 20) are shown in Table 3. We see, from Table 3, that all estimates were quite close and the two models gave consistent conclusions in terms of significance of covariates at a significance level of 0.05. Note that the estimates of β₁ under the subdistribution model of Fine and Gray (1999) were computed using the R-package cmprsk.

Table 3.

Estimates of β₁ under the Subdistribution Model and the Fully Specified Subdistribution Model

Variable	Subdistribution Model			Fully Specified Subdistribution Model
	Estimate	SE	95% CI	Estimate	SD	95% HPD Interval
age	0.017	0.022	(−0.026, 0.059)	0.020	0.020	(−0.017, 0.061)
logpsa	−0.057	0.143	(−0.337, 0.223)	0.036	0.139	(−0.225, 0.316)
GS7	−0.173	0.431	(−1.018, 0.672)	−0.123	0.411	(−0.935, 0.676)
GS8H	0.298	0.400	(−0.486, 1.082)	0.153	0.402	(−0.615, 0.951)
T3	0.453	0.409	(−0.348, 1.255)	0.598	0.417	(−0.195, 1.414)
margin	0.483	0.305	(−0.115, 1.080)	0.417	0.295	(−0.124, 1.035)
DT6	0.990	0.278	( 0.445, 1.535)	0.919	0.271	( 0.407, 1.467)

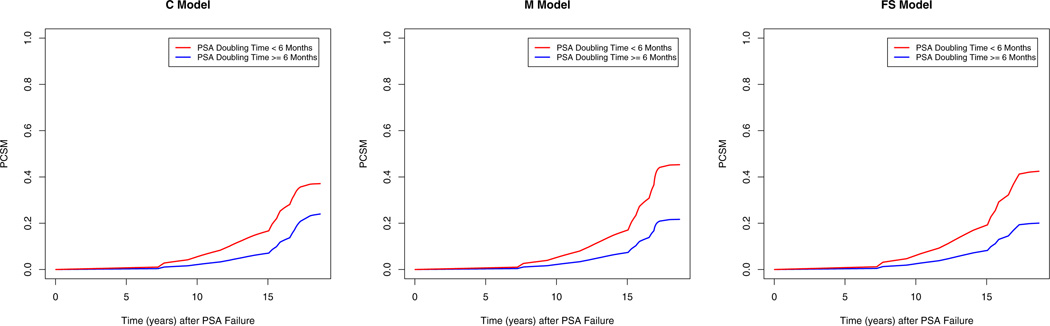
Let the prostate cancer specific mortality (PCSM) be the cumulative incident function corresponding to the primary cause of death due to prostate cancer. The covariate effect was further investigated by comparing the posterior means of the PCSM at different times stratified by PSA doubling time (DT6= 1 versus DT6= 0) under each of the three models, where the other covariates were fixed at age = mean age (66.5), logpsa = mean logpsa (2.5), GS7 = 1, GS8H = 0, T3 = 1, and margin = 1. The PCSM plots are shown in Figure 2. The shapes of the PCSM curves under the three models were similar except at the tail part and the difference between the two curves was slightly smaller under the cause-specific hazards model. For example, at the 10^th and 15^th year after PSA failure, the posterior means of PCSM under the cause-specific hazards model were 0.055 and 0.166 for patients with PSA doubling time less than 6 months and 0.021 and 0.071 for patients with PSA doubling time greater than or equal to 6 months; under the mixture model the posterior means of PCSM were 0.052 and 0.17 for patients with PSA doubling time less than 6 months and 0.022 and 0.073 for patients with PSA doubling time greater than or equal to 6 months; under the FS model the posterior means of PCSM were 0.061 and 0.192 for patients with PSA doubling time less than 6 months and 0.025 and 0.082 for patients with PSA doubling time greater than or equal to 6 months. Those PCSM plots indicate that the patients with PSA doubling time less than 6 months had worse PCSMs than those with PSA doubling time greater than or equal to 6 months. This covariate effect can directly be seen from Table 3 under the FS model as DT6 was significant at a significance level of 0.05. In addition, the proportional hazards structure of the FS model also allows us to compute the adjusted hazard ratio (AHR), which is defined as exp(β₁₇), of DT6 for the PCSM. Specifically, the posterior mean and 95% HPD interval of the AHR of DT6 were 2.601 and (1.369, 4.061), respectively. However, this covariate effect could not be directly assessed under the other two models. For example, under the mixture model with K₁ = 15,K₂ = 20, for the hazard regression sub-model corresponding to the prostate cancer death, the posterior mean, SD, and 95% HPD interval of β₁₇ for DT6 were 0.122, 0.384, and (−0.627, 0.865) while the posterior mean, SD, and 95% HPD interval of ϕ₇ for DT6 were 0.519, 0.168, and (0.187, 0.839) in the logistic regression sub-model for p₁, indicating that DT6 was significant.

Fig. 2.

Plots of the PCSMs under the Three Models

7 Discussion

In this paper, we have developed a fully specified subdistribution model of Fine and Gray (1999) and provided a justification of Fine and Gray’s partial likelihood via the profile likelihood approach and the Bayesian approach. Our Bayesian justification is the first such development in the context of competing risk models after the Bayesian justification of Cox’s partial likelihood (Kalbfleisch, 1978; Sinha et al., 2003) as the risk set at time t in Fine and Gray’s partial likelihood includes all patients who are still alive prior to t as well as the patients who were died from other causes of death up to t, which is quite different than the usual risk set in Cox’s partial likelihood (Cox, 1972, 1975). To fit the proposed FS model, a piecewise exponential model with Jeffreys-type priors, which is a special case of the gamma process prior when c₀ → 0+, is assumed for the baseline hazard function. Compared to the full gamma process priors, the gamma priors based on the piecewise exponential model relax the conditions for the posterior propriety and facilitate the development of an efficient Gibbs sampling algorithm for carrying out the posterior computation.

In Section 5, we conducted an extensive simulation study in examining the performance of DIC and LPML in identifying the model from which the data were generated. Our simulation results empirically showed that when the data are from one (the true model) of the three models (cause-specific hazards model, mixture model, and fully specified subdistribution model), it is unlikely that the other two models would have smaller DICs and larger LPMLs than the true model. This may be due to different proportional hazard functions assumed under these three models. For the prostate cancer data, the FS model had much smaller DIC and larger LPML than those under the cause-specific model and mixture model, implying that the FS model was much more appropriate for fitting this dataset than the other two models.

The fully specified subdistribution model can be further extended to the cases with more than 2 competing risks. Assume there are J competing risks with cause 1 as the cause of interest. Denote $T_j^{*}=T_j\times I(\delta =j)+\mathrm{\infty }\times I(\delta \ne j)$, j = 1, 2, … , J, and $T^{*}=\text{min}\{T_1^{*},T_2^{*},\dots ,T_J^{*}\}$. The cause-specific cumulative incidence functions can be constructed as follows: F₁(t) = Pr(T* ≤ t, δ = 1) = Pr(T₁ ≤ t, δ = 1), and F_j(t) = Pr(T* ≤ t, δ = j) = M_j(t)Pr(δ ≠ j − 1|δ ≠ 1, … , δ ≠ j − 2) … Pr(δ ≠ 2|δ ≠ 1)Pr(δ ≠ 1), j = 2, … , J, where M_j(t) is the probability of failure from cause j by time t conditional on not failing from causes 1, 2, … , j − 1.

In this paper, we only considered fixed covariates. Including time-dependent covariates in the FS model, as well as jointly modeling longitudinal measurements (e.g., a series of PSA measures over-time) and survival endpoints of cause-specific death times are important future research topics, which are under investigation currently. Models with frailty terms (Clayton, 1978; Vaupel et al., 1979) are commonly used for correlated survival data with multivariate risk factors. Dixon et al. (2011) introduced a multivariate subdistribution hazard model including frailty to induce correlations among clustered survival times. The FS model can be extended for correlated survival data in the presence of competing risks in the manner to include frailties. This is another interesting topic for future research.

In all the Bayesian computations, we used 10,000 Gibbs samples after a burn-in of 1000 iterations for each model to compute all the posterior estimates, including posterior means, posterior standard deviations, 95% HPD intervals, DICs and LPMLs. We also generated 50,000 Gibbs samples after a burn-in of 1000 to re-compute those posterior quantities and the results were very similar. The HPD intervals were computed via the Monte Carlo method developed by Chen and Shao (1999). Codes were written for FORTRAN 95 compiler, and we used IMSL subroutines with double precision accuracy. The fortran codes for the FS model are available upon request.

Appendix A: Additional Tables

Table 4.

Mean of DIC and LPML of the Three Models

	DIC			LPML
(K1, K2)	FS Model	C Model	M Model	FS Model	C Model	M Model
Data Simulated from FS Model
(5, 10)	2142.0	2167.1	2144.2	−1071.1	−1083.7	−1072.0
(10, 20)	2119.2	2145.6	2123.2	−1060.6	−1073.9	−1062.6
(15, 30)	2126.5	2153.9	2131.8	−1065.8	−1079.6	−1068.4
Data Simulated from C Model
(5, 10)	2064.8	2055.8	2056.6	−1032.5	−1028.0	−1028.2
(10, 20)	2039.0	2030.7	2033.4	−1020.5	−1016.4	−1017.8
(15, 30)	2044.6	2037.5	2040.8	−1024.9	−1021.4	−1023.0
Data Simulated from M Model
(5, 10)	2286.8	2283.7	2274.7	−1144.0	−1142.3	−1137.7
(10, 20)	2285.9	2282.3	2276.1	−1144.4	−1142.4	−1139.5
(15, 30)	2295.9	2291.8	2287.0	−1150.9	−1148.7	−1146.5

Table 5.

Posterior Estimates of β under the Three Models in Simulation Studies

		FS Model			C Model			M Model
(K1, K2) =		(5, 10)	(10, 20)	(15, 30)	(5, 10)	(10, 20)	(15, 30)	(5, 10)	(10, 20)	(15, 30)
β11	True	0.2			0.2			0.2
	Est	0.2	0.2	0.2	0.18	0.19	0.19	0.19	0.20	0.20
	SD	0.09	0.09	0.09	0.11	0.11	0.11	0.13	0.13	0.13
	MSE	0.01	0.01	0.01	0.01	0.01	0.01	0.02	0.02	0.02
	CP	0.94	0.94	0.94	0.95	0.95	0.95	0.94	0.94	0.94
β12	True	0.8			1.0			1.5
	Est	0.78	0.78	0.78	1.00	1.02	1.02	1.47	1.48	1.48
	SD	0.23	0.23	0.23	0.24	0.24	0.24	0.35	0.36	0.37
	MSE	0.05	0.05	0.06	0.06	0.06	0.06	0.14	0.15	0.16
	CP	0.95	0.95	0.95	0.95	0.95	0.95	0.95	0.94	0.94
β21	True	0.3			0.3			0.3
	Est	0.29	0.30	0.30	0.30	0.30	0.30	0.30	0.30	0.30
	SD	0.08	0.08	0.08	0.08	0.08	0.08	0.08	0.08	0.08
	MSE	0.01	0.01	0.01	0.01	0.01	0.01	0.01	0.01	0.01
	CP	0.97	0.96	0.96	0.95	0.95	0.95	0.95	0.95	0.95
β22	True	1.0			0.2			0.5
	Est	0.98	1.00	1.00	0.19	0.20	0.20	0.53	0.53	0.54
	SD	0.17	0.17	0.17	0.15	0.15	0.15	0.18	0.18	0.18
	MSE	0.03	0.03	0.03	0.02	0.02	0.02	0.03	0.03	0.03
	CP	0.94	0.95	0.95	0.96	0.95	0.96	0.96	0.96	0.96

Note that Est, SD, MSE, and CP denote the average of the posterior means, the average of the posterior standard deviations, and the mean square error, and the coverage probability of the 95% HPD intervals over 500 simulations.

Appendix B: Proofs of Theorems

Proof of Theorem 1 With the assumption that h₁₀ is zero after the last observation of failure due to cause 1, the likelihood function is now

$$L({\mathit{\beta }}_1,h_{10}|\mathit{y},X,\mathit{\delta })={\displaystyle \prod _{i=1}^{D_1}}[h_{10}(y_{(i)})\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)]\times \text{ exp }\{-{\displaystyle \sum _{i=1}^n}{H}_{10}(y_{(i)})\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\}.$$

The profile likelihood approach assumes that h₁₀ is zero except for the failure times due to cause 1. Then

$$L({\mathit{\beta }}_1,h_{10}|\mathit{y},X,\mathit{\delta })=[{\displaystyle \prod _{i=1}^{D_1}}{h}_{10}(y_{(i)})\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)]\times \text{ exp }\{-{\displaystyle \sum _{i=1}^{D_1}}{\displaystyle \sum _{k=1}^i}{h}_{10}(y_{(k)})\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)-{\displaystyle \sum _{i=D_1+1}^n}{\displaystyle \sum _{l=1}^{D_1}}{h}_{10}(y_{(l)})\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\}=[{\displaystyle \prod _{i=1}^{D_1}}{h}_{10}(y_{(i)})\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)]\times \text{ exp }\{-{\displaystyle \sum _{i-1}^{D_1}}{h}_{10}(y_{(i)}){\displaystyle \sum _{j\in R_i^{*}}}\text{exp}({\mathit{x}}_j^{\prime }{\mathit{\beta }}_1)\}.$$

Therefore, the profile maximum likelihood estimator of h₁₀ is given by

$${ĥ}_{10}(y_{(i)})=\frac{1}{{\displaystyle {\sum }_{j\in R_i^{*}}}\text{ exp}({\mathit{x}}_j^{\prime }{\mathit{\beta }}_1)}.$$

Plugging ĥ₁₀(y_(i)) in L(β₁, h₁₀|y, X, δ) results in the profile likelihood function given by

$$L_p^{*}({\mathit{\beta }}_1|\mathit{y},X,\mathit{\delta })\propto {\displaystyle \prod _{i=1}^{D_1}}\frac{\text{exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)}{{\displaystyle {\sum }_{j\in R_i^{*}}}\text{exp}\{{\mathit{x}}_j^{\prime }{\mathit{\beta }}_1\}},$$

which is (2.6).

Proof of Theorem 2 Assume the prior of h₁₀ only has value λ_i at times y_(i) such that δ_i = 1. Then λ_i = H₁₀(y_(i)) − H₁₀(y_(i−1)), and λ_D1+1 = ⋯ = λ_n = 0, i = 1, … , D₁. The survival function at time t is

$$\mathit{\text{Pr}}({\mathit{T}}_1^{*}>\mathit{t})={\displaystyle \prod _{i=1}^n}[1-F_1(y_{(i)})]=\text{exp }\{-{\displaystyle \sum _{i=1}^{D_1}}{H}_{10}(y_{(i)})\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)-{\displaystyle \sum _{i=D_1+1}^n}{H}_{10}(\mathrm{\infty })\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\}=\text{exp }\{-{\displaystyle \sum _{i=1}^{D_1}}{\displaystyle \sum _{k=1}^i}{\lambda }_k\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)-{\displaystyle \sum _{i=D_1+1}^n}{\displaystyle \sum _{l=1}^{D_1}}{\lambda }_l\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\}=\text{exp }\{-{\displaystyle \sum _{i=1}^{D_1}}{\lambda }_i{\displaystyle \sum _{j\in R_i^{*}}}\text{exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\}.$$ (B.1)

Then the likelihood function in (2.8) reduces to

$$L({\mathit{\beta }}_1,\mathbf{\lambda }|\mathit{y},X,\mathit{\delta })={\displaystyle \prod _{i=1}^{D_1}}[{\lambda }_i\text{ exp}(x_i^{\prime }{\mathit{\beta }}_1)]\times \text{ exp }\{-{\lambda }_i{\displaystyle \sum _{j\in R_i^{*}}}\text{exp}({\mathit{x}}_j^{\prime }{\mathit{\beta }}_1)\}={\displaystyle \prod _{i=1}^{D_1}}[\frac{\text{exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)}{{\displaystyle {\sum }_{j\in R_i^{*}}}\text{exp}(x_j^{\prime }{\mathit{\beta }}_1)}]\times [{\lambda }_i{\displaystyle \sum _{j\in R_i^{*}}}\text{exp}({\mathit{x}}_j^{\prime }{\mathit{\beta }}_1)]\times \text{ exp }\{-{\lambda }_i{\displaystyle \sum _{j\in R_i^{*}}}\text{exp}({\mathit{x}}_j^{\prime }{\mathit{\beta }}_1)\}.$$

Since $\pi (\mathit{\lambda })\propto {\displaystyle {\prod }_{i=1}^{D_1}}1/{\lambda }_i$, we have

$${\displaystyle \int }L({\mathit{\beta }}_1,\mathit{\lambda }|\mathit{y},X,\mathit{\delta })\pi (\mathit{\lambda })d\mathit{\lambda }={\displaystyle \int }{\displaystyle \prod _{i=1}^{D_1}}\frac{1}{{\lambda }_i}\times [\frac{\text{exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)}{{\displaystyle {\sum }_{j\in R_i^{*}}}\text{exp}({\mathit{x}}_j^{\prime }{\mathit{\beta }}_1)}]\times [{\lambda }_i{\displaystyle \sum _{j\in R_i^{*}}}\text{exp}({\mathit{x}}_j^{\prime }{\mathit{\beta }}_1)]\times \text{ exp }\{-{\lambda }_i{\displaystyle \sum _{j\in R_i^{*}}}\text{exp}({\mathit{x}}_j^{\prime }{\mathit{\beta }}_1)\}d\mathit{\lambda }={\displaystyle \prod _{i=1}^{D_1}}\frac{\text{exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)}{{\displaystyle {\sum }_{j\in R_i^{*}}}\text{exp}({\mathit{x}}_j^{\prime }{\mathit{\beta }}_1)}.$$

Proof of Theorem 3 Assume H₁₀ follows a gamma process prior. Let h_1i = H₁₀(y_(i)) − H₁₀(y_(i−1)), h_1i ~ G(c₀h₀i, c₀), i = 1, … , D₁. h_1i’s are independent of each other, and h_1,D1+1 = ⋯ = h_1n = 0. Similar to (B.1), we can show that the survival function at time t is given by

$$\mathit{\text{Pr}}({\mathit{T}}_1^{*}>\mathit{t})={\displaystyle \prod _{i=1}^n}[1-F_1(y_{(i)})]=\text{exp }\{-{\displaystyle \sum _{i=1}^{D_1}}{h}_{1i}{\displaystyle \sum _{j\in R_i^{*}}}\text{exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\}.$$

Taking expectation with respect to the gamma process prior gives

$$E^{h_{10}}[\mathit{\text{Pr}}({\mathit{T}}_1^{*}>\mathit{t})]={\displaystyle \prod _{i=1}^{D_1}}{\left[\frac{c_0}{c_0+{\displaystyle {\sum }_{j\in R_i^{*}}}\text{exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)}\right]}^{c_0{h}_{0i}}={\displaystyle \prod _{i=1}^{D_1}}\text{exp }\left\{c_0{\displaystyle \sum _{k=1}^i}{h}_{0k}\text{ log }\right(1-\frac{\text{exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)}{c_0+{\displaystyle {\sum }_{j\in R_i^{*}}}\text{exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)}\left)\right\}.$$

Now the expectation of the likelihood function in (2.8) with respect to the gamma process prior reduces to

$$E^{h_{10}}[L({\mathit{\beta }}_1,h_{10}|\mathit{y},X,\mathit{\delta })]={\displaystyle \prod _{i=1}^{D_1}}\text{exp }\{c_0{\displaystyle \sum _{k=1}^i}{h}_{0k}\text{ log }(1-\frac{\text{exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)}{c_0+{\displaystyle {\sum }_{j\in R_i^{*}}}\text{exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)})\}\times [-c_0{\displaystyle \sum _{k=1}^i}\frac{{\mathit{\text{dh}}}_{0k}}{{\mathit{\text{dy}}}_{(i)}}\text{ log }(1-\frac{\text{exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)}{c_0+{\displaystyle {\sum }_{j\in R_i^{*}}}\text{exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)})].$$

Since ${\text{lim}}_{c_0\downarrow 0}\text{exp }\{c_0{\displaystyle {\sum }_{k=1}^i}{h}_{0k}\text{ log }\left(1-\frac{\text{exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)}{c_0+{\displaystyle {\sum }_{j\in R_i^{*}}}\text{exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)}\right)\}=1$ and

$$\underset{c_0\downarrow 0}{\text{lim}}\text{ log }(1-\frac{\text{exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)}{c_0+{\displaystyle {\sum }_{j\in R_i^{*}}}\text{exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)})\approx -\frac{\text{exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)}{{\displaystyle {\sum }_{j\in R_i^{*}}}\text{exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)},$$

we have

$$\underset{c_0\downarrow 0}{\text{lim}}\frac{E^{h_{10}}[L({\mathit{\beta }}_1,h_{10}|\mathit{y},X,\mathit{\delta })]}{{\displaystyle {\prod }_{i=1}^{D_1}}[c_0+{\displaystyle {\sum }_{k=0}^i}\frac{{\mathit{\text{dh}}}_{0k}}{{\mathit{\text{dy}}}_{(i)}}]}\approx {\displaystyle \prod _{i=1}^{D_1}}\frac{\text{exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)}{{\displaystyle {\sum }_{j\in R_i^{*}}}\text{exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)}.$$

Proof of Theorem 4 To show that (3.3) is proper, it is needed to show that

$${\displaystyle \int }{\pi }^{*}({\mathit{\beta }}_1,{\mathit{\beta }}_2,{\mathit{\lambda }}_1,{\mathit{\lambda }}_2|\mathit{t},X,\mathit{\delta })d{\mathit{\beta }}_{1}d{\mathit{\beta }}_{2}d{\mathit{\lambda }}_{1}d{\mathit{\lambda }}_2<\mathrm{\infty },$$

where π*(β₁, β₂, λ₁, λ₂|t, X, δ) is the unnormalized joint posterior density defined in (3.3). After some algebra, we can show that

$${\pi }^{*}({\mathit{\beta }}_1,{\mathit{\beta }}_2,{\mathit{\lambda }}_1,{\mathit{\lambda }}_2|\mathit{t},X,\mathit{\delta })\le {\displaystyle \prod _{i=1}^n}{\displaystyle \prod _{k=1}^{K_1}}{[{\lambda }_{1k}\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\text{ exp }\{-\text{exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1){\lambda }_{1k}(t_i-s_{1,k-1})\left\}\right]}^{{\nu }_{1\mathit{\text{ik}}}I({\delta }_i=1)}\times {\lambda }_{1k}^{-1}{\lambda }_{1,K_1+1}^{a-1}\text{ exp}(-b{\lambda }_{1,K_1+1})\times {\displaystyle \prod _{i=1}^n}{\displaystyle \prod _{k=1}^{K_2}}[{\lambda }_{2k}\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_2)\text{ exp }{\{-\text{exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_2){\lambda }_{2k}(t_i-s_{2,k-1})]}^{{\nu }_{2\mathit{\text{ik}}}I({\delta }_i=2)}\times {\lambda }_{2k}^{-1}\equiv {\pi }^{**}({\mathit{\beta }}_1,{\mathit{\lambda }}_1|\mathit{t},X,\mathit{\delta })\times {\pi }^{**}({\mathit{\beta }}_2,{\mathit{\lambda }}_2|\mathit{t},X,\mathit{\delta }).$$

It suffices to show that

$${\displaystyle \int }{\pi }^{**}({\mathit{\beta }}_1,{\mathit{\lambda }}_1|\mathit{t},X,\mathit{\delta })d{\mathit{\beta }}_{1}d{\mathit{\lambda }}_1<\mathrm{\infty },$$

since ∫ π**(β₂, λ₂|t, X, δ)dβ₂dλ₂ < ∞ can be proved in a similar way.

Consider the transformation u_j = log(λ_1j), j = 1, 2, … , K₁, and let u = (u₁, u₂, … , u_K1)′. Then, we have

$${\displaystyle \int }{\pi }^{**}({\mathit{\beta }}_1,{\mathit{\lambda }}_1|\mathit{t},X,\mathit{\delta })d{\mathit{\beta }}_{1}d{\mathit{\lambda }}_1={\displaystyle \int }{\pi }^{**}({\mathit{\beta }}_1,\mathit{u}|\mathit{t},X,\mathit{\delta })d{\mathit{\beta }}_{1}d\mathit{u}\times {\displaystyle \int }{\lambda }_{1,K_1+1}^{a-1}\text{exp}(-b{\lambda }_{1,K_1+1})d{\lambda }_{1,K_1+1}\propto {\displaystyle \int }{\displaystyle \prod _{i=1}^n}{\displaystyle \prod _{k=1}^{K_1}}{[\text{exp}(u_k+{\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\times \text{exp}\{-\text{exp}(u_k+{\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)(t_i-s_{1,k-1})\left\}\right]}^{{\nu }_{1\mathit{\text{ik}}}I({\delta }_i=1)}d{\mathit{\beta }}_{1}d\mathit{u}.$$ (B.2)

It is easy to show that $\text{exp}(u_k+{\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\times \text{exp }\{-\text{exp}(u_k+{\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)(t_i-s_{1,k-1})\}\le M_1$, where M₁ > 0 is a constant. Under condition (ii), X₁ is of full rank. Thus, there exist distinct i₁, i₂, … , i_K1+p1, where p₁ = dim(β₁), such that the (K₁+p₁) × (K₁+p₁) matrix $X_1^{*}$, which has rows $({\mathit{x}}_{1\ell }^{*})\prime =({\nu }_{{\mathit{\text{ji}}}_{\ell }1},\dots ,{\nu }_{{\mathit{\text{ji}}}_{\ell }{K}_j},x_{i\ell }^{\prime })$ for ℓ = 1, … , K₁+p₁, is of full rank. Let k_iℓ be an integer such that t_iℓ ∈ (s_1,kiℓ−1, s_1kiℓ] for ℓ = 1, … , K₁+p₁. We take a one-to-one transformation ${\mathit{\xi }}_1=X_1^{*}(\mathit{u}\prime ,{\mathit{\beta }}_1^{\prime })\prime$. Using (B.2), we have

$${\displaystyle \int }{\pi }^{**}({\mathit{\beta }}_1,{\mathit{\lambda }}_1|t,X,\mathit{\delta })d{\mathit{\beta }}_{1}d{\mathit{\lambda }}_1\le M_2{\displaystyle \int }{\displaystyle \prod _{\ell =1}^{K_1+p_1}}(\text{exp}\{({\mathit{x}}_{1\ell }^{*})\prime (\mathit{u}\prime ,\mathit{\beta }\prime )\prime \}\text{ exp }[-\text{exp }\{({\mathit{x}}_{1\ell }^{*})\prime (\mathit{u}\prime ,\mathit{\beta }\prime )\prime (t_i-s_{1,k_{i_{\ell }}-1})\}])d\mathit{u}d\mathit{\beta }=M_3{\displaystyle \prod _{\ell =1}^{K_1+p_1}}{\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}}\text{exp }({\xi }_{1\ell })\text{ exp }\{-\text{exp }({\xi }_{1\ell })(t_i-s_{1,k_{i_{\ell }}-1})\}d{\xi }_{1\ell }=M_3{\displaystyle \prod _{\ell =1}^{K_1+p_1}}({(t_i-s_{1,k_{i_{\ell }}-1})}^{-1}<\mathrm{\infty },$$

where M₂ and M₃ are two positive constants. This completes the proof.

Appendix C: Generating η from [η|β₁, λ₁, β₂, λ₂, t,X, δ] and u from [u|β₁, λ₁, λ₂, η, t,X, δ]

Generating η from [η|β₁, λ₁, β₂, λ₂, t, X, δ] When δ_i = 0, we generate η_i by I(η_i = 1) ~ Bin(1, p_i1) and I(η_i = 2) = 1−I(η_i = 1), where $p_{i1}=\frac{a_i}{a_i+b_i},a_i=\text{exp }\{-H_{10}(t_i)\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\}-\text{exp }\{-H_{10}(\mathrm{\infty })\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\},\text{ and }{b}_i=\text{exp }\{-H_{20}(t_i)\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_2)-H_{10}(\mathrm{\infty })\text{ exp}({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\}$.

Generating u from [u|β₁, λ₁, λ₂, η, t, X, δ] When δ_i = 0 and η_i = 1, we generate u_i from a truncated piecewise exponential distribution f(u_i), where

$$f(u_i)\propto h_{10}(u_i)\text{ exp }({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\text{ exp }\{-H_{10}(u_i)\text{ exp }({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\},u_i\ge t_i.$$

Denote δ_ji as the index such that s_{j, δji−1} ≤ t_i < s_jδji. Let

$$\begin{array}{cc}\hfill a_{1i}& =\text{exp }\{-H_{10}(t_i)\text{exp }({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\}-\text{exp }\{-H_{10}(s_{1{\delta }_{1i}})\text{ exp }({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\},\hfill \\ \hfill a_{\mathit{\text{ki}}}& =\text{exp }\{-H_{10}(s_{1,{\delta }_{1i}+k-2})\text{ exp }({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\}-\text{exp }\{-H_{10}(s_{1,{\delta }_{1i}+k-1})\text{ exp }({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\},k=2,\dots ,K_1-{\delta }_{1i}+1.\hfill \\ \hfill a_{K_1-{\delta }_{1i}+2,i}& =\text{exp }\{-H_{10}(s_{1K_1})\text{ exp }({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\}-\text{ exp }\{-H_{10}(\mathrm{\infty })\text{ exp }({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\}.\hfill \end{array}$$

Generate v_i from a U(0, 1) distribution. If v_i falls into the $k_{{\upsilon }_i}^{\mathit{\text{th}}}$ interval such that

$$\frac{a_{1,i}+\cdots +a_{k_{\upsilon }-1,i}}{a_{1,i}+\cdots +a_{K_1-{\delta }_{1i}+2,i}}<{\upsilon }_i\le \frac{a_{1,i}+\cdots +a_{k_{\upsilon },i}}{a_{1,i}+\cdots +a_{K_1-{\delta }_{1i}+2,i}},$$

the inverse distribution function method is used to calculate u_i as

$${\upsilon }_i=\frac{a_{1,i}+\cdots +a_{k_{\upsilon }-1,i}+\text{exp }\{-H_{10}(s_{1,k_{\upsilon }-1})\text{ exp }({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\}-\text{exp }\{-H_{10}(u_i)\text{ exp }({\mathit{x}}_i^{\prime }{\mathit{\beta }}_1)\}}{a_{1,i}+\cdots +a_{K_1-{\delta }_{1i}+2,i}}.$$