Possible forcing of global temperature by the oceanic tides

Abstract

An approximately decadal periodicity in surface air temperature is discernable in global observations from A.D. 1855 to 1900 and since A.D. 1945, but with a periodicity of only about 6 years during the intervening period. Changes in solar irradiance related to the sunspot cycle have been proposed to account for the former, but cannot account for the latter. To explain both by a single mechanism, we propose that extreme oceanic tides may produce changes in sea surface temperature at repeat periods, which alternate between approximately one-third and one-half of the lunar nodal cycle of 18.6 years. These alternations, recurring at nearly 90-year intervals, reflect varying slight degrees of misalignment and departures from the closest approach of the Earth with the Moon and Sun at times of extreme tide raising forces. Strong forcing, consistent with observed temperature periodicities, occurred at 9-year intervals close to perihelion (solar perigee) for several decades centered on A.D. 1881 and 1974, but at 6-year intervals for several decades centered on A.D. 1923. As a physical explanation for tidal forcing of temperature we propose that the dissipation of extreme tides increases vertical mixing of sea water, thereby causing episodic cooling near the sea surface. If this mechanism correctly explains near-decadal temperature periodicities, it may also apply to variability in temperature and climate on other times-scales, even millennial and longer.

1. Introduction

The global record of atmospheric CO₂ since 1958 shows evidence of quasi-10-year periodicity nearly synchronous with variability in global surface temperature (1). We have explored whether the latter is exceptional or also found in earlier instrumental temperature records dating back to 1855 (2). Our quest has led us into a controversial subject area, with no clear consensus for or against the existence of periodic quasi-decadal variations in temperature, or what might cause such variations.

Claims of near 10-year periodicity in atmospheric temperature have often been linked with the sunspot cycle of approximately 11 years, but no consistent correlation has emerged (3). Changes in solar irradiance may explain solar forcing of temperature, but this mechanism seems negated by precise measurements of total irradiance that indicate only a very weak quasi-decadal variation (4). An association of temperature periodicity to the approximately 22-year solar magnetic “Hale” cycle has also been suggested (5), but without identification of a plausible temperature forcing mechanism.

Damaging to claims that the Sun causes periodicities in temperature, or other aspects of weather, are reported interruptions in solar–weather correlations, most conspicuous during the 1920s (3). These failures involved not only temperature, but also regional precipitation, movement of pressure centers, winds, and storm frequency. They occurred without any obvious interruptions in the sunspot cycle. Following some of these failures, solar correlations seem to have reappeared, but with unexplained reversals of phase (3), notably an association of high sunspot numbers with cool periods before 1920, but with warm periods after 1950.

Tidal action has also been suggested as a possible cause of periodicities in temperature and weather related either to the 18.6-year lunar nodical cycle or to its first harmonic. Many years ago (ref. 6, p. 222) it was proposed that abnormally great ocean tides modulate the amount of warm water entering the Arctic, Bering, and Baltic seas at 9-year intervals, perhaps by increasing the interchange of water across the sills separating these seas from the main oceans. Investigators more recently (7, 8) have proposed that weak but persistent north–south tidal currents, reversing over the 18.6-year nodical cycle, might periodically change sea surface temperature in the main oceans. Alternatively, it has been suggested (refs. 9 and 10, p. 41) that oceanic tides may affect sea surface temperature in shallow ocean waters by varying the intensity of vertical eddy diffusion there.

Two other possible causes of quasi-decadal variations in global temperature, which we can only briefly mention here, are volcanic eruptions and internal oscillations of the coupled atmosphere–ocean system. Volcanic eruptions, which have produced great dust veils (11) and hence substantial blocking of sunlight, have tended to occur close to times of quasi-decadal cooling since 1855. The picture is complicated, however, because the timing of eruptions with respect to cooling has varied from one century to the next. Internal oscillations of the earth climate system may cause quasi-decadal variability according to results of recent state-of-the-art coupled general circulation models (e.g., ref. 12), reinforcing a school of thought in meteorology (ref. 13, p. 72) that the circulation of the oceans and atmosphere can change on decadal time scales with no external cause. Whether this tenet is true or not, the possibility of periodic forcing of temperature externally for example, by variable solar irradiance, oceanic tides, or volcanic activity, is not precluded, because an unstable coupled system can respond to periodic external forcing as well as oscillate freely.

Here we present evidence that global temperature has fluctuated quasi-decadally since 1855, except for an interruption between about 1900 and 1945, thus supporting previous claims of failures of weather phenomena to maintain a correlation with the sunspot cycle near 1920. This interruption, although difficult to explain by a sunspot mechanism, does not rule out a tidal mechanism, because the astronomically driven tide raising forces since 1855 have exhibited strong 9-year periodicity only when quasi-decadal periodicity was evident in temperature data. Furthermore, unlike the perplexing shift in the phase of quasi-decadal temperature fluctuations with the sunspot cycle between the 19th and 20th centuries, there was no such shift in phase with respect to tidal forcing.

To investigate further a possible relationship between tidal forcing and temperature appears to us to be worthwhile, because the oceanic tide raising forces vary in strength predictably over a wide range of time scales. If they should be shown to influence temperature on any time scale, they may explain periodic changes in weather and climate on other time scales as short as fortnightly and as long as the Milankovitch cycles.

2. Air Temperature Analysis and Sunspots

To test the hypothesis of tidal forcing of temperature we have adopted a global compilation of temperature data over both land and in surface sea water (14), expressed as an anomaly beginning in 1855 and updated through mid-1995 (P. D. Jones, personal communication). We accept Jones’ premise that sea surface and marine air temperatures follow each other closely on interannual time scales, so that combined land and marine temperature data portray global average variations in surface air temperature.

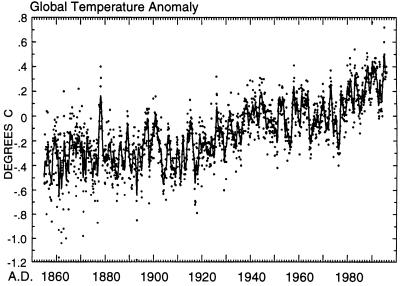
The large scatter in monthly averaged global temperature data (dots plotted in Fig. 1) is not a strong encouragement to look for cyclic phenomena. Nevertheless, if the data are fit to a flexible nodal spline (15, 16) (solid curve in Fig. 1) to suppress the high frequency scatter, periods of persistently warmer and cooler conditions are indicated. Many of the warmer periods occurred at times of El Niño events (ref. 17, p. 623), suggesting coherent interannual variability.

Figure 1.

Global surface temperature anomaly (combined land and marine) from 1855 through mid-1995 in degrees C (ref. 14 and P. D. Jones, personal communication). Monthly averages are shown as dots. The solid line is a spline fit (15) of these data with a standard error, σ, of 0.107°C.

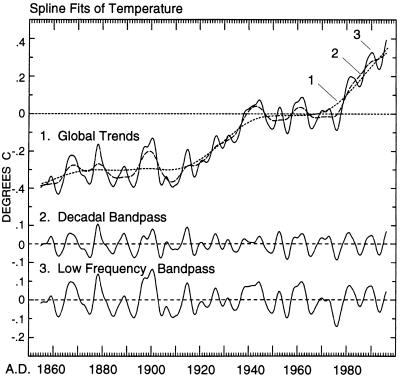
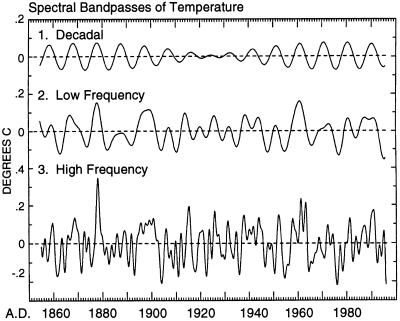
To detect possible fluctuations in global temperature on interannual time scales, we have fit monthly averages with nodal splines of successively greater stiffness (Fig. 2, Top), chosen to produce increasing degrees of low-pass filtering of the data. The choices were subjective, but are not critical to the outcome, because nearly the same distinct patterns are produced over a considerable range of stiffnesses. The stiffest spline (curve labeled 1) shows only a tendency for global air temperature to rise irregularly since 1855. The difference between the two looser splines produces an approximately decadal bandpass (Middle), whereas the difference between the stiffest and loosest curves shows a broad, low frequency bandpass (Bottom).

Figure 2.

Spline fits of the global temperature anomaly of Fig. 1 together with associated bandpasses. (Top) Global trends depicted by three superimposed spline fits (15), one consisting of a very stiff spline fit to yearly averages (dotted curve 1, σ of 0.106°C), and two consisting of splines of lesser stiffness fit to monthly averages (dashed curve 2 and solid curve 3, σs of 0.161 and 0.148°C, respectively). (Middle) Decadal bandpass (curve 3 minus curve 2). (Bottom) Low frequency bandpass (curve 3 minus curve 1).

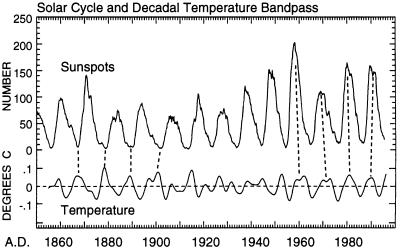
In Fig. 3, a record of sunspot numbers (18) is compared with the near-decadal bandpass of temperature of Fig. 2. As shown by broken lines, four near-decadal peak temperatures immediately before 1905 were close to sunspot minima, while four immediately after 1960 were close to sunspot maxima. For several decades near 1920, peak temperatures in the bandpass were only about 6 years apart and did not correlate with sunspots at all. These results are thus consistent with the earlier findings reported by Herman and Goldberg (3), of an intermittent correlation of temperature with sunspots and a reversal of phase.

Figure 3.

Comparison of mean sunspot number (ref. 18, 12-month running mean, upper curve) with the decadal bandpass of global surface temperature in degrees C, of Fig. 2 (Middle).

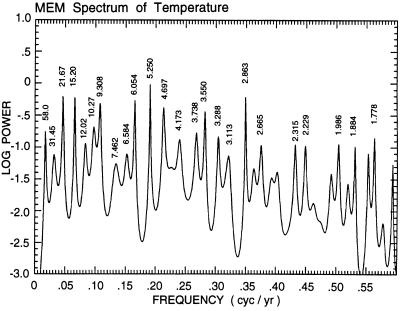
To examine further the oscillatory character of the global temperature record, we have computed its spectrum (Fig. 4) by the maximum entropy method (19), which is highly sensitive to spectral line detection. We have afterwards established the amplitudes and phases of 24 identified spectral peaks by least-squares fits, to avoid the problem that the maximum entropy method is not quantitatively reliable with respect to amplitudes and cannot establish phase relationships (20). Our method has been described in detail previously (21) and is applied here to an updated temperature record.

Figure 4.

Maximum entropy spectrum of the global surface temperature anomaly of Fig. 1. The logarithm of power is plotted versus frequency in cycles per year. Above the 24 most prominent spectral peaks are shown their periods, in years.

We reconstructed the time series of temperature by summing the resultant 24 computed sinusoidal spectral oscillations. Near the decadal time scale, a strong harmonic with a period of 9.3 years, when summed with a sideband at 10.3 years (Fig. 4) produces oscillations with an average period of 9.8 years and a maximum amplitude, peak-to-peak, of 0.14°C (Fig. 5 Top). The two harmonics, of nearly equal amplitude in the reconstruction, beat with a period of 100 years and exhibit interference near 1925. Inclusion of additional harmonics to form a low-frequency bandpass (Fig. 5 Middle) does not cancel out the stronger, near-decadal oscillations of Fig. 5 Top, but additionally produces near 6-year oscillations between approximately 1900–1945. The pattern of oscillations is essentially as seen in the similarly broad bandpass derived from spline fits (Fig. 2 Bottom). Also, a full reconstruction (24 harmonics summed, Fig. 5 Bottom) reproduces much of the higher frequency variability seen in Fig. 1. Thus, the amplitudes and phases obtained by spectral analysis do not appear to be falsified by the restricted number of degrees of freedom of the spectral compositing, (cf. ref. 21 and Fig. 7).

Figure 5.

Spectral bandpasses of the global temperature anomaly based on the maximum entropy spectrum of Fig. 4. (Top) Decadal (sum of two oscillations with periods of 9.31 and 10.27 years). (Middle) Low frequency (sum of nine oscillations with periods from 6.05 to 31.4 years, inclusive). (Bottom) Broad bandpass, including higher frequencies (sum of 24 spectral oscillations as described in text).

Figure 7.

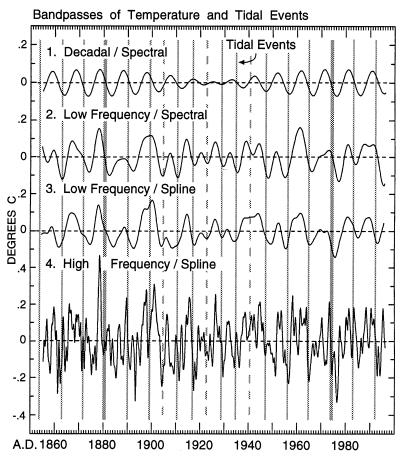
Comparison of prominent 6- and 9-year tidal events, shown by vertical hatched lines, as in Fig. 6, with fluctuations in temperature shown by time plots derived spectrally or from spline fits. (Curve 1, Decadal) Decadal spectral bandpass as in Fig. 5 (Top). (Curve 2, Low Frequency/Spectral) Low frequency spectral bandpass as in Fig. 5 (Middle). (Curve 3, Low Frequency/Spline) Low frequency spline plot as in Fig. 2 (Bottom). (Curve 4, High Frequency) High frequency spline plot derived by subtracting curve 1 of Fig. 2 (Top) from the spline of Fig. 1.

3. A Proposed Mechanism for Lunisolar Tidal Forcing

Our first objective in hypothesizing an oceanic tidal influence on global temperature is to propose a possibly plausible physical mechanism. We must bear in mind that the combined tide-raising forces of the Sun and Moon produce the same total tidal kinetic energy each year (D. E. Cartwright, personal communication). Nevertheless, the rate of production of kinetic energy varies for individual tidal events depending on the varying relative positions of the Earth, Moon, and Sun. We focus on oceanic tides, because the atmospheric tides are too small to be of practical importance in comparison (ref. 6, p. 218). The dominant constituents of oceanic tides are semi-diurnal and diurnal, but weaker, longer period elements also contribute to the tidal spectrum (ref. 22, p. 310). The strength of tides varies considerably with many cycles identified by Wood (ref. 23, pp. 201.42–201.60).

Tides might influence temperature and weather by direct transport of heat (8), although the very low amplitude of long-period tides (24) makes this seem unlikely. A mechanism more likely to be dominant on the global scale would appear to be vertical mixing caused by a modulation of the distribution of the tidal potential between semi-diurnal, diurnal, and long-period elements, as proposed by Loder and Garrett (9). Even this mechanism is not obviously adequate to explain near-decadal temperature variations. A small set of strong tides, occurring over only a few days, would seem unlikely to produce cooler sea surface temperatures lasting for months or years. Also, since the total tidal energy dissipated each year is the same, a tidal cooling process, to be effective in causing interannual oscillations, must be strongly nonlinear.

We propose that the dissipation of the strongest daily tides substantially increases vertical mixing in the oceans and thereby cools the overlying surface water, because the temperature of ocean water generally decreases with depth. This process is clearly nonlinear, because vertical eddy diffusivity depends quadratically on the tidal current velocity (9), and bottom friction dissipation on the third power of velocity (25). Also, prior mixing by only slightly weaker day-to-day tides in a series might reduce stratification and thereby promote greater impact of subsequent stronger events than otherwise. If tidally induced cooling should produce greater cloudiness or storminess, the attending lesser surface heating from the Sun or greater than average wind velocities should add even further to the nonlinearity. Finally, on longer time scales, greater ice formation and snow accumulation associated with cooling at high latitudes could provide additional positive feedback. These latter arguments are not dissimilar to those advanced to explain the ice ages, in which small changes in the latitudinal distribution of solar irradiance are believed to cause large climatic effects (26).

Some direct evidence of tidal forcing of temperature exists. A recent study (27) reports fortnightly and monthly variability in sea surface temperature at tidal frequencies throughout the seas of Indonesia, a region important to world climate because of its proximity to the pool of warm water that affects the El Niño cycle. These temperature variations appear to be due to nonlinear dynamics, which cause a redistribution of tidal energy from semi-diurnal and diurnal to fortnightly and longer periods. The resulting modulation of the heat flux between the atmosphere and the ocean is shown to be large enough (many tens of watts m⁻²) to affect weather and climate. Some support of tidal forcing is also found in claims of increased storminess and rainfall in the first and third quarter of the lunar cycle, i.e., subsequent to the strong tidal forcing that accompanies new Moon and full Moon (28–32).

For a tidal mechanism of sea surface temperature variability to be plausible, it must be shown that tide raising forces generate, and therefore dissipate, enough energy in mixing ocean water to compete with other mixing mechanisms. The nontidal kinetic energy of the oceans, arising from the drag of the wind on the ocean surface, and augmented by the work of pressure forces at the the ocean surface and by the conversion of potential energy, generates about 6 × 10⁻³ W m⁻² of kinetic energy (ref. 33, p. 7,683), therefore about 2 TW, integrated over the ice-free oceanic surface of 3.6 × 10¹⁴ m². In comparison, the oceanic tides generate approximately 4 TW (34, 35), adequate to cause significant mixing.

The mechanism of vertical mixing in the oceans is poorly understood, making it difficult to establish the importance of tidal mixing relative to other types of oceanic mixing. Nevertheless, recent studies suggest that the former may not be insignificant. Observations of sea water density (36) and a tracer experiment (37) indicate that mixing across density gradients (diapycnal mixing) is insufficient (about a factor 10 too small) to maintain the main thermocline of the open oceans. It is possible that vertical mixing occurs mainly at surface outcrops of density layers and in shallow areas where most tidal dissipation and consequent mixing takes place (27, 38–42). Tidal forcing may thus significantly influence the open ocean thermocline (35).

Tidal periodicities result from astronomical factors involving the rotation of the Moon and Earth in elliptical orbits about the Earth and Sun, respectively. The varying positions of the Earth, Moon, and Sun lead to global scale variations in the tide raising forces, but the distribution of tidal energy from these forces, and the fraction of the energy available to cause mixing, is unevenly distributed geographically. As a result, longer term tidal periodicities differ regionally (9). The quantitative prediction of possible tidal forcing of temperature therefore requires a detailed understanding of the actual tides not yet attained, but perhaps soon attainable (see e.g., ref. 35).

Notwithstanding these complications, the possibility should not be dismissed that changes in temperature, globally averaged, may show the effects of tidal forcing on a scale in which astronomical periodicities survive in the data. Extremes in tide-raising forces, which are those tidal phenomena likely to affect temperature globally, occur at predictable times as a result of nearly optimal alignment and proximities of the Earth, Moon, and Sun (43), irrespective of local tidal behavior. We therefore feel justified here to begin an appraisal of possible tidal influence on temperature simply by comparing astronomical properties of tides with global temperature records.

4. Periodicities of the Oceanic Tides

Our next objective is to describe the periodicities of extremely strong tidal events. In so doing we do not wish to imply that single tidal events are likely to be responsible for modulating sea surface temperature worldwide. They may be important, however, because they identify times of generally great tidal dissipation of kinetic energy, which could modulate temperature by means of an ensemble of events over days or even years.

The motions of the Earth and Moon, although periodic, do not produce truly periodic strong tidal events, because these events require the near coincidence of four incommensurate recurring astronomical relationships, namely syzygy, perigee, eclipse, and perihelion. This circumstance, although adding complexity to the analysis, may, however, be an asset in proving a connection between tides and temperature, because interrupted or transient tidal periodicities should produce characteristic signatures of tidal forcing in temperature records.

Eighteen-Year Repetitions of Strong Tides.

The times of strong lunisolar tidal forcing since 1850 are shown in Fig. 6 by thin vertical solid lines of irregular height plotted versus time. As an approximate relative measure of the global tide raising forces of individual strong tidal events we have adopted the factor, γ, of Wood (ref. 23, p. 201), defined as the angular velocity of orbital motion of the Moon with respect to the perturbed motion of perigee, in degrees of arc per day at the moment of maximum forcing. This velocity is shown above a threshold of 17.02° d⁻¹ by the length of each tidal line in Fig. 6. The tide raising forces define a hypothetical equilibrium tide (ref. 22, p. 316), which approximates the global average strength of the actual tides.

Figure 6.

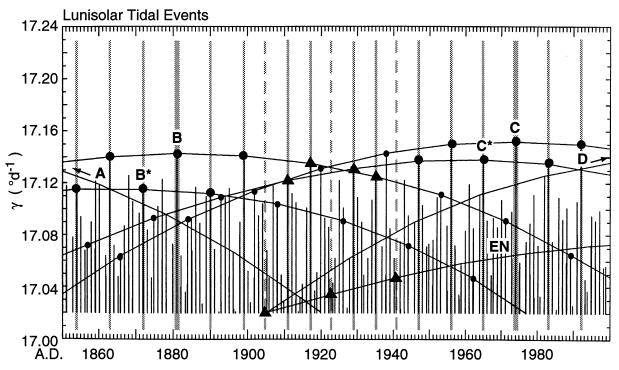
Timing of prominent lunisolar tide raising forces from A.D. 1850 to 2000 according to Wood (ref. 23, table 16). Each event is plotted as a vertical solid line whose length, above a threshold, is an approximate measure of the strength of forcing, expressed by the quantity γ, in degrees of arc per day, as described in the text. All events with γ greater than 17.02° d⁻¹ are shown, resulting in approximately one displayed event per year. Selected dominant sequences of 18.03-year events, labeled A-D, subdominant sequences, B* and C*, and an equinoctial sequence, EN, are identified by arcs connecting these tidal events and by dots or solid triangles (see text). Vertical hatched lines indicate times of events grouped 6 or 9 years apart, as described in the text.

Strong tide raising forces have occurred at very nearly 18-year intervals in staggered sequences, the most prominent of which are shown in Fig. 6 by arches of connecting lines and with black dots. The timing of several of these sequences is further indicated by vertical hatched lines. In the strongest dominant tidal sequence of the late 19th century, labeled B, forcing attained a maximum on December 31, 1880 (thick hatched line), and then declined. The subsequent dominant sequence of the 20th century, labeled C, reached a maximum 93.02 years later on January 8, 1974 (additional thick hatched line), and then similarly declined. Part of a dominant sequence before B, labeled A, and of one after C, labeled D, are also shown (without dots). All other tidal events depicted in Fig. 6 are also members of 18-year sequences. Also indicated in Fig. 6 by arches of connecting lines are two subdominant sequences, labeled B* and C*, which produced approximately 9-year events when combined, respectively, with Sequences B and C. Last, part of an equinoctial sequence, labeled EN, is shown (vertical broken lines). Between 1899 and 1947 this sequence produced 6-year events when combined with Sequences B and C* (vertical hatched lines and solid triangles).

Astronomical Basis for 18-Year Events.

Maximal tide raising forces occur only when the Sun and Moon are in direct mutual alignment. This occurs at syzygy (either full Moon or new Moon), provided also that the Moon or Sun be in eclipse with the Earth. The former two bodies must also be at the closest approach to the Earth, i.e., the Moon at perigee and the Sun at perihelion. Repetitions of syzygy, perigee, and eclipse are defined, respectively, by three lunar months (ref. 23, pp. 126–131): the synodic (29.5 days) representing every second recurrence of syzygy, the anomalistic (27.6 days) representing the recurrence of perigee, and the nodical (27.2 days) representing every second recurrence of the Moon positioned at its node, lying on the plane of the ecliptic, a requirement for an eclipse. The Earth and Sun attain closest approach (perihelion) once every anomalistic year. The anomalistic year is only slightly longer than the mean calendar year because perihelion advances very slowly, 1 day every 57 years (ref. 22, p. 304). Perihelion presently occurs on January 2 in the Christian calendar.

To assist in comprehending tidal periodicities we have listed selected periods of the near coincidence of two or more astronomical factors of tidal forcing in Table 1. As an exact, long-term measure of time we employ the “tropical year” of approximately 365.24 mean solar (calendar) days (ref. 22, p. 125), defined as the time between successive occurrences of the vernal equinox. (The tropical year, henceforth “year,” is essentially equal to the average calendar year. The anomalistic year is 1.00005 tropical years.)

Table 1.

Major lunisolar cycles

Period*	No. of lunar months†			Offset from synodic month‡
	Synodic	Anomalistic§	Nodical	Anomalistic	Nodical
0.080852	1.0	1	1.0	(−1.97)	(−2.32)
1.131929	14.0	15	15.0	−0.11	(−5.25)
2.263858	28.0	30	30.5	−0.22	(3.12)
2.789396	34.5	37	37.5	0.71	1.65
2.870249	35.5	38	38.5	−1.26	−0.67
3.314935	41.0	44	44.5	1.64	0.19
3.005052¶
5.659645	70.0	75	76.0	−0.55	0.99
6.185184	76.5	82	83.0	0.38	−1.48
6.010103‖
8.974580	111.0	119	120.5	1.10	1.18
9.055432	112.0	120	121.5	−0.88	−1.14
9.015154**
18.030012	223.0	239	242.0	0.22	0.04
93.020310	1115.0	1223	1248.5	−0.28	−0.48

^*Period, in tropical years (365.2421988 days), for the number of synodic months indicated. Important average periods in boldface. 

^†Synodic month, 29.53059 days; anomalistic month, 27.55455 days; nodical month, 27.21222 days. 

^‡In days. Parentheses indicate poor matching with the synodic month. 

^§Must be a whole number. 

^¶Equal to (2.789396 + 2.870249 × 3 + 3.314935 × 2)/6. 

^‖Equal to (5.659645 + 6.185184 × 2)/3. 

^**Equal to (8.974580 + 9.055432)/2. 

The shortest period in which syzygy, perigee, an eclipse, and perihelion nearly coincide is 18.030 tropical years (18.029 anomalistic years), consisting nominally of 223 synodic, 239 anomalistic, and 242 nodical months (see Table 1). Because even for these nearly commensurate periods there are offsets in timing (see Table 1), the maximal tidal-forcing event in any sequence of 18-year tides is preceded and succeeded by events having lesser tidal forcing. For Sequences A through D, shown in Fig. 6, the alignments of a given sequence are thus ever poorer, the greater the time interval from the climactic event of that sequence.

Longer Term Patterns of Strong Tides.

The interval between the climatic events of Sequences B and C is 93.02 years (compare with the thick hatched lines in Fig. 6), made up of five 18.03-year intervals and an additional interval of 2.87 years. The latter interval shows up as an offset of individual events of Sequence B from those of Sequence C. Because of this offset, there is no sustained periodicity related to dominant tidal events over more than about half a century (four 18-year cycles).

Decadal Repetitions of Strong Tides.

Subdominant tidal sequences, such as those labeled B* and C* in Fig. 6, have occurred almost midway between tidal events of dominant sequences. Each B* event occurred 8.97 years (111 synodic months) after a B event, the latter followed by another B* event 9.06 years (112 synodic months) later. The interval between individual B* and C* events, as between B and C events, was 2.87 years. In combination, the dominant and subdominant sequences, B, C, B*, and C*, have produced nearly decadal events, at times indicated in Fig. 6 by vertical hatched lines and large solid dots before 1900 and after 1945.

Perigean Eclipse Cycle.

The strength of strong tidal events, measured by the factor γ, is sensitive to their timing with respect to perihelion (ref. 23, p. 218). The climactic events of Sequence B in December 1880 and Sequence C in January 1974 both occurred within a week of the date of perihelion. Weaker events of these sequences occurred ever further from perihelion because of the 0.029-year (11 day) deviation in timing of these events from exactly 18 anomalistic years. Near 1920, the timing with respect to perihelion was poor for both dominant Sequences B and C. As a consequence, another tidal cycle came into prominence in which the average timing of strong tidal events involved only perigee and eclipses.

This cycle is characterized by two lunar orbital lines that rotate in opposite senses and at different rates. One, the line of apsides, is the major axis of the elliptical orbit of the Moon; rotating in the same sense as the Moon and Earth revolve around the Sun; it completes a revolution in 8.8475 tropical years on average (ref. 23, p. 179). The other is the line of nodes, defined as the intersection of the plane of the ecliptic with the plane of the Moon’s orbit, the latter inclined to the former by 5.15°; it rotates in the opposite sense to the line of apsides, completing the well-known lunar nodical cycle in 18.6134 tropical years (ref. 23, p. 189).

The line of apsides and line of nodes come into mutual alignment on average twice every 5.997 years. This time interval,

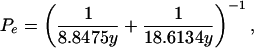1

the perigean eclipse cycle, is also the beat period between the anomalistic and nodical months. Because the timing of syzygy is not commensurate with P_e/2, one-half of the eclipse cycle expresses only the long-term average of the return period of perigean eclipses, the actual times varying from about 2.8 to 3.3 years (see Table 1).

Six-Year Repetitions of Strong Tides.

Prominent tidal events of the perigean eclipse cycle are shown in Fig. 6 between 1899 and 1947 as solid triangles. These events were associated with three sequences of 18-year tides, spaced approximately 6 years apart. Two of these sequences, B and C*, because they represent events occurring near the date of perihelion, also contributed to near-decadal periodicity, but the third sequence, EN, produced events near the autumnal equinox having little diurnal tidal contribution and relatively weak γ values (their semidiurnal tidal strength not well represented by γ values.) Of the three equinoctial tidal events, distinguished by broken lines, that of September 21, 1922, produced the greatest semidiurnal tide in an interval of 4 centuries (43). All three can be assumed to have caused remarkable tides in regions where the semi-diurnal component predominates, such as in the north Atlantic Ocean (35). Sequence C events during this same period contributed strong forcing nearly midway between several of these 6-year events, but this did not lead to a sustained 3-year periodicity at P_e/2 because the other two associated 18-year sequences were too weak.

Millennial Repetitions.

The perigean eclipse cycle also influences tidal events on the millennial time scale because the return time for near coincidence of events of this cycle with perihelion is approximately 1,800 years. We propose that the repeat time of millennial extremes in tide raising forces, discussed below, relates to this return time, although the actual timing of such millennial events must be irregular, being sensitive to the exact time of syzygy (ref. 23, pp. 201–249). The near coincidence of perihelion with this cycle in the present millennium occurred near the time of a climactic tidal event in A.D. 1433 (ref. 6, p. 220).

5. Lunisolar Tides as a Forcing Agent of Temperature

Our final objective is to demonstrate that the times of strong tidal forcing, based on astronomical factors, correlate with cool periods in the global temperature record at 6- to 10-year intervals. In Fig. 7 are shown four bandpasses of the global temperature anomaly obtained by either spectral analysis or spline fits. The upper three were shown previously; the lowest, including higher frequencies, is new. Also shown, by vertical hatched lines, are the times of selected tidal events as in Fig. 6. In referring to tidal events that occurred near the date of perihelion, we will cite the year of the event as though it occurred in January, unless we give the exact date.

We first draw attention to the climactic tidal events of December 31, 1880, and January 8, 1974 (thick vertical hatched lines). Close to these dates (hereafter referred to as 1881 and 1974), spectrally derived oscillations in temperature, found by maximum entropy spectral analysis on the decadal time scale (curve 1, Decadal), show maximum rates of cooling, as indicated by the curve descending across the zero anomaly line. Thus, unlike the comparison of near-decadal temperature variations with the sunspot cycle (see Fig. 3), there is no shift in phase with respect to tidal forcing between centuries.

Next, still on the decadal time scale (curve 1), we examine the phasing of temperature variations with the timing of other tidal events (vertical hatched lines). The near coincidence of the climactic tidal events of 1881 and 1974 with maximum cooling rates did not extend to other decades, because the nearly 10-year intervals between cool periods exceeded the 9-year intervals between tidal events. The near-decadal temperature variations, nevertheless, have characteristics suggestive of tidal forcing. They are expressed as the sum of two harmonics (9.31 years and 10.23 years, see Fig. 4), which are close to the 9th and 10th harmonics of the 93-year tidal cycle. Also, they reinforced each other maximally close to the climactic tidal events of 1881 and 1974, and interfered maximally in the 1920s when the succession of 9-year tidal events was interrupted by an offset of 2.87 years. These two harmonics thus match the 93-year tidal cycle with its staggered sequences of 9-year events as well as can be expected for a single pair of spectral harmonics.

A broader spectral bandpass including nine oscillations (Curve 2, Low Frequency/Spectral) shows additional relations of temperature to tidal events. This bandpass shows oscillations in phase with those of Curve 1, before 1900 and after 1945, when Curve 1 shows reinforcement, but 6-year oscillations between these dates, when Curve 1 shows interference. Except near the times of the climactic tidal events of 1881 and 1974, tidal events tended to coincide with temperature minima rather than maximum cooling rates. After the 9-year tidal event of 1863, as already noted above, these cool periods occurred approximately 1 year further apart than the tidal events. As a consequence, a decadal cool event, occurring in 1883, lagged the Sequence B tidal event of 1881, to the extent that the latter nearly coincided with the maximum decadal cooling rate. Moreover, the next such cool period, in 1893, lagged the Sequence B* tidal event by so much that it nearly coincided with a Sequence C* event, and was thus in phase with subsequent 6-year temperature oscillations.

That these relationships are not an artifact of spectral analysis is shown by a lowpass spline fit (Curve 3, Low Frequency/Spline), which typically shows cool periods at the same times as by spectral analysis. This analysis, however, also shows the hint of a cool period near 1899, reinforcing the possibility that 6-year oscillations extended back to 1893. Thus, the 10-year spacing of cool events from 1863 to 1893 suggest an association with tidal forcing related to the perigean eclipse cycle; this forcing perhaps hastened (see Fig. 6) by the lesser strengths of the Sequence B* tidal events compared with Sequence C* events after 1900. (The tidal events of 1890 and 1893 indeed were of nearly equal strength.) The phasing of the temperature record with tidal events after 1956 is similar to that after 1863, leaving open the further possibility of similar tidal forcing 93 years after the events described for the late 19th century. Cool periods in a high-pass spline fit of temperature (Curve 4, High Frequency) also tend to coincide with 6- and 9-year tidal events. The cooling events of 1893 and 1899, discussed above, are seen to have been quite intense, although brief.

In summary, since 1855, cool periods of global extent at near-decadal tidal intervals have typically occurred in episodes lasting about half a century, before, during, and after climactic tidal events spaced about a century apart. Between these episodes, also for about half a century, cool periods tended to occur synchronously with strong tidal events at 6-year intervals. Almost all of the associated near-decadal and 6-year tidal events occurred at times of close mutual alignments of the Sun, Moon, and Earth with the Moon near perigee, but the former occurred closer to the date of perihelion than the latter. The changing importance of perihelion thus defined a near centennial tidal cycle, alternating between predominantly 6- and 9-year tidal forcing, which may be reflected in global temperature variations.

6. Further Implications of the Tidal Hypothesis

Centennial Climatic Variability.

To probe possible influences occurring on long time scales, we show in Fig. 8 the times and strengths of extreme tidal forcing back to A.D. 1600 and forward until A.D. 2140, according to Wood (23). As can be seen, the climactic tidal events that occurred 93.02 years apart in December 1880 and January 1974, were preceded, and will be succeeded, by other such climactic events. If our tidal hypothesis is valid these events should have been associated with times of unusually cool temperatures.

Figure 8.

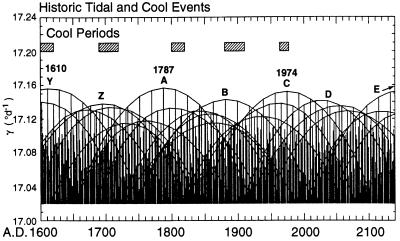
Timing of tidal forcing from A.D. 1600 to 2140, plotted with arcs connecting events of each prominent 18-year tidal sequence, as in Fig. 6. Also plotted are times of cool episodes seen in climate data identified by Jones and Bradley as of possibly global significance (ref. 44, pp. 658–659). A more recent global cool interval near 1970 is also shown, as discussed in the text. Dominant tidal Sequences A–D are labeled as in Fig. 6. Two earlier Sequences, Y and Z, and a later Sequence E are also labeled. Although climactic events of the dominant sequences from 1700 and 1974 are at 93-year intervals, there are irregularities in the time intervals between earlier and later climactic events, yielding an average near-centenniel interval of about 90 years.

A suggestion that this may have happened is indicated by the timing of cool episodes on a global scale identified by Jones and Bradley (ref. 44, pp. 658–659). These authors point out that the cool period that began near the end of the Middle Ages (the “Little Ice Age”) was not a monotonous period worldwide. Climactic evidence instead suggests several cool episodes, each lasting up to about 3 decades. These episodes, which appear to have been synchronous on the hemispheric and global scale, are shown as hatched rectangles in Fig. 8. As can be seen, they all occurred close to the times of near-centennial climactic tidal events, labeled Y, Z, A, and B. We have added an additional conforming cool period for the decades of the 1960s and 1970s, which would perhaps have been more pronounced in the absence of an anthropogenic warming component in recent years (45).

As mentioned above in Section 4, we do not wish to imply that each of these cool periods could have been caused by only one or a few individual climactic tidal events. A more likely hypothesis is that they may have been caused by clusters of strong tidal events. A clustering tendency over several decades is suggested in Fig. 8 by a pyramidal pattern of more densely spaced quasi-annual tidal events in phase with climactic events of the dominant sequences. We postulate that a strongly nonlinear temperature response to an ensemble of strong tidal events may explain the global cooling that evidently occurred for several decades near the times of these climactic events.

Longer-Term Climate Variability.

The climactic tidal events shown in Fig. 8 alternated between stronger events (labeled Y, A, and C) and weaker events, with the two greatest occurring in 1610 [or in 1619 according to Cartwright (43)] and in 1787. Also, tidal events, as strong or nearly as strong, evidently occurred in 1247 and 1433 (11), thus forming, with the events in 1610 and 1787, a series with a repeat period of approximately 180 years.

An even longer perspective of strong tidal forcing is gained from a study of the timing of astronomical alignments by Cartwright (43), who showed that the greatest tide raising forces in the past millennium occurred between A.D. 1340 and 1619, at 93-year intervals, when the perigean eclipse cycle was almost optimally timed with respect to perihelion. By his calculation, tides of such great magnitude will not occur again until A.D. 3182, an interval corresponding approximately to the near 1,800-year return period of optimal timing of perigean eclipses with perihelion discussed above in Section 4. According to the calculations of Otto Pettersson made many years ago, tides of great magnitude conforming roughly to this return period also occurred near 3500 B.C., 1900 B.C., and 200 B.C., as well as in A.D. 1433 (ref. 6, pp. 220–222).

Although records of weather before the late Middle Ages appear to be too sketchy to test convincingly for a millennial tidal influence on climate, we point out that the 1,800-year tidal cycle, outlined above, implies that the climactic tides of the millennium before A.D. 1200 were weaker than those of recent centuries and should have promoted a warmer climate. The “medieval warm period,” between about A.D. 800 and 1000, followed by a decline in weather in the 1200s (ref. 13, pp. 177–187), conforms to this expectation, especially when considered together with the severe weather of the succeeding Little Ice Age. Moreover, for still earlier times, there is at least a hint of more unsettled weather (13) near the centuries of great tidal forcing as calculated by Pettersson.

Over still longer times, the strength of tidal forcing must have changed in response to secular changes in the extreme distances of the Earth from the Moon and Sun, the inclination of the Earth’s rotational axis to the ecliptic, and the position of perihelion with respect to the vernal equinox. Three of these quantities, involving the Earth and Sun, also determine the Milankovitch cycles, which have been shown with considerable statistical reliability to explain the timing of the ice ages over the past million years (26). It is widely held that solar irradiance reaching the Earth, because it is modified cyclically as a function of latitude by these three factors, has been the driving force for the ice ages, but the mechanism is less certain than the cyclic correlation. Also, the mechanism of the Milankovitch cycles does not appear to explain shorter period fluctuations seen in glacial data of the most recent ice age and the interglacial period preceding it (46, 47). Perhaps tidal forcing was also involved (48).

7. Discussion and Conclusions

In our quest to understand quasi-decadal oscillations observed in atmospheric carbon dioxide, we have been led to investigate seemingly similar oscillations in global air temperature. Employing a much longer temperature record than that available for atmospheric CO₂, we have found that near-decadal variations in global air temperature are characteristic of the past 141 years, except for a roughly 45-year interruption centered near 1920. This pattern has also emerged using spectral analysis, specifically from the beating of two frequencies found to be close to the 9th and 10th harmonics of the lunisolar tidal cycle of 93 years. Furthermore, temperature oscillations with periods near 6 years were found in the temperature record by spectral analysis near the time of interference of the two near-decadal oscillations, and thus close in period to the 6-year repeat period of another prominent lunisolar tidal cycle.

Is it possible that the oceanic tides influence global temperature? Perceptions of cyclic behavior in the climatic record have in the past involved so many exceptions and inconsistencies that the subject does not have a good reputation among scientists. Compelling evidence that a recognized periodicity is actually caused by an identifiable extraterrestrial forcing agent is difficult to find. Our task is not made any easier by the nonstationarity of the lunisolar tidal cycles resulting from the incommensurability of the various astronomical periodicities. Although patterns in the strength of tidal forcing often recur, they don’t repeat identically even after hundreds of years. Evidence of a tidal connection therefore cannot rely solely on the usual past practice of looking for a correlation with temperature at a single tidal periodicity.

Although we have delved into properties of the tides in some detail to test whether a correlation of tidal strength with temperature exists, much more might be accomplished by a closer attention to the possible physical basis for the correlations found. Until now, to mount such an effort has not seemed worthwhile, given the small perceived likelihood that any lunisolar tidal connection to climate exists. We have only touched upon a possible cause by proposing that strong tides increase vertical mixing in the oceans and thereby episodically cool the sea surface. Also, we have explored in detail only 6- to 10-year periodicities seen in records of both temperature and tidal forcing. We propose, nevertheless, that the near synchronicities seen at these periodicities argue sufficiently in favor of a tidal-forcing hypothesis, to justify further investigation of a possible tidal mechanism of temperature and climate variability.