Abstract
Kinetic studies aimed at determining the most probable mechanism for the proton-dependent [FeII(SMe2N4(tren))]+ (1) promoted reduction of superoxide via a thiolate-ligated hydroperoxo intermediate [FeIII(SMe2N4(tren))(OOH)]+ (2) are described. Rate laws are derived for three proposed mechanisms, and it is shown that they should conceivably be distinguishable by kinetics. For weak proton donors with pKa(HA) >pKa(HO2) rates are shown to correlate with proton donor pKa, and display first-order dependence on iron, and half-order dependence on superoxide and proton donor HA. Proton donors acidic enough to convert O2− to HO2 (in tetrahydrofuran, THF), that is, those with pKa(HA) < pKa(HO2), are shown to display first-order dependence on both superoxide and iron, and rates which are independent of proton donor concentration. Relative pKa values were determined in THF by measuring equilibrium ion pair acidity constants using established methods. Rates of hydroperoxo 2 formation displays no apparent deuterium isotope effect, and bases, such as methoxide, are shown to inhibit the formation of 2. Rate constants for p-substituted phenols are shown to correlate linearly with the Hammett substituent constants σ−. Activation parameters ((ΔH‡ = 2.8 kcal/mol, ΔS‡ = −31 eu) are shown to be consistent with a low-barrier associative mechanism that does not involve extensive bond cleavage. Together, these data are shown to be most consistent with a mechanism involving the addition of HO2 to 1 with concomitant oxidation of the metal ion, and reduction of superoxide (an “oxidative addition” of sorts), in the rate-determining step. Activation parameters for MeOH- (ΔH‡ = 13.2 kcal/mol and ΔS‡ = −24.3 eu), and acetic acid- (ΔH‡ = 8.3 kcal/mol and ΔS‡ = −34 eu) promoted release of H2O2 to afford solvent-bound [FeIII(SMe2N4(tren))(OMe)]+ (3) and [FeIII(SMe2N4(tren))(O(H)Me)]+ (4), respectively, are shown to be more consistent with a reaction involving rate-limiting protonation of an Fe(III)–OOH, than with one involving rate-limiting O–O bond cleavage. The observed deuterium isotope effect (kH/kD = 3.1) is also consistent with this mechanism.
Introduction
Superoxide is a toxic radical, formed during the adventitious reduction of dioxygen, that has been implicated in a number of disease states, including Alzheimer’s, Parkinson’s, and cancer.1 The mechanism by which superoxide (O2−) is degraded depends on the organism. Aerobic organisms disproportionate superoxide (to O2 and H2O2), using Cu, Mn, Ni, or Fe–containing enzymes known as superoxide dismutases (SODs).2-4 Anaerobic organisms reduce superoxide (to H2O2, thereby avoiding O2 formation) using a trans cysteinate-ligated non-heme iron enzyme, known as superoxide reductase (SOR).5,6 The catalytically active form of SOR contains a redox active, high-spin (S = 2) FeII ion ligated by four equatorial histidines and one apical cysteinate trans to an open-site.6-9 The mechanism by which SOR reduces O2− is proposed to involve the oxidative addition of O2− to the ferrous ion, trans to the cysteinate, to afford two transient intermediates (T1, T2),10 observable by electronic absorption spectroscopy (Scheme 1).5,11-14 The first intermediate T1 forms at nearly diffusion controlled rates (kobs= 1.2×109 M−1 s−1),10,13 and is proposed to be an FeIII–peroxo species, although vibrational data to support this has yet to be reported. Density functional theory (DFT) calculations are consistent with the assignment of T1 as either a low-spin (S=1/2),15 or high-spin (S=5/2)16 end-on hydroperoxo FeIII-OOH. Rates for the first step in the SOR reaction mechanism (rxn (1), Scheme 1) are pH independent.1,10,11 The second intermediate T2, has an isotope-sensitive solvent-derived νFe–O stretch, and forms more slowly (kobs=3.8×102 s−1), at pH-dependent rates,10-12 with a noticeable deuterium isotope effect17 (kH/kD=2.1).11,18 This would be consistent with solvent H2O-induced protonation at the proximal peroxide oxygen in this second step (rxn (2); Scheme 1) to release H2O2 and afford an FeIII–OH species.13,18 The glutamate-bound resting state (R; Scheme 1) eventually forms (kobs=25 s−1) in the absence of additional substrate (O2−) or electrons. Well-documented cases of superoxide-promoted oxidation of small molecule Fe(II) complexes are rare, and include that of Fe(II)(EDTA),19 and Fe(II)(TPP),20 both of which have been shown to occur via an inner-sphere mechanism. Superoxide-promoted reduction of [Fe(III)(EDTA)-(H2O)]− has also been shown to occur via an inner-sphere mechanism.21 Biomimetic thiolate-ligated analogues synthesized in our lab (vide infra) provide support for the proposed Fe(III)-OOH SOR intermediate T1.22,23 X-ray structures are available for the catalytically active Fe(II) SOR enzyme,8 the Glu-bound resting state (R),7 and a H2O2-generated SOR mutant (Ala14Glu) end-on Fe(III)-OOH species.6
Scheme 1.
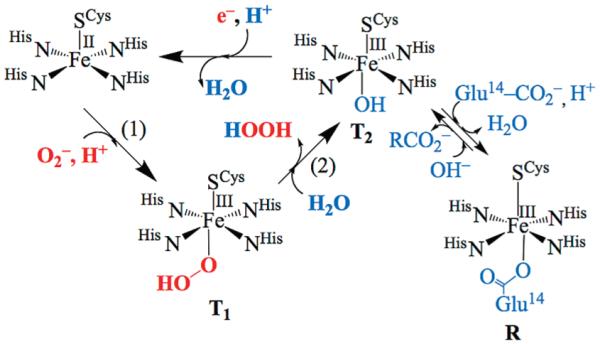
Proposed Mechanism for SOR-Catalyzed Reduction of Superoxide via Hydroperoxo (T1) and Solvent-Bound Intermediates (T2)a
a In the absence of substrate or reducing equivalents the active site converts to the glutamate-bound resting (R).
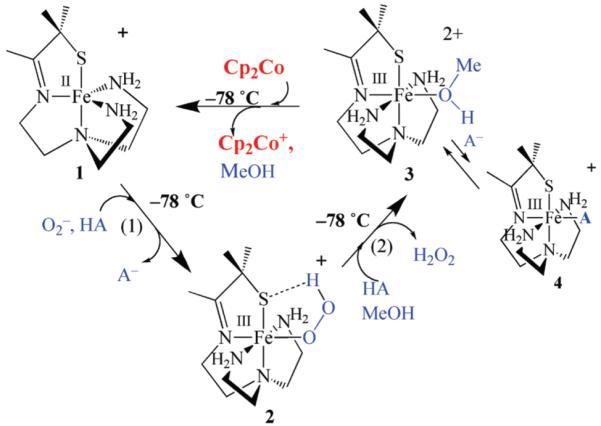
Our group has shown that despite having a cis-, as opposed to trans-thiolate, five-coordinate [FeII(SMe2N4(tren))]+ (1; Scheme 2) will reduce superoxide to afford H2O2 in a semi-catalytic manner.23-27 This reaction is proton-dependent and requires the addition of an external proton donor HA if it is carried out in rigorously dried THF.26 An intermediate, [FeIII(SMe2N4(tren))(OOH)]+ (2; Scheme 2), with properties consistent with an Fe(III)-OOH,23 is detected when this reaction is run at low-temperatures (−78 °C). The FeII “catalyst” 1 is regenerated via the addition of Cp2Co to the FeIII solvent-bound intermediate [FeIII(SMe2N4(tren)) (O(H)Me)]+ (3) generated via proton-induced release of H2O2 from 2 (rxn (2) of Scheme 2). To avoid H2 formation, or spontaneous disproportionation of superoxide,28 the proton donor, substrate, and reductant must be added separately to our biomimetic catalyst (at low temperatures), in a manner similar to that used by Schrock to reduce N2.29,30 In the absence of 1 at low-temperatures, superoxide is not reduced (via disproportionation) in dry THF using the weakly acidic proton donors used in this study. To understand the proton-dependence of peroxo 2 formation, and determine the mechanism of superoxide reduction by our synthetic SOR analogue 1, we herein examine the kinetics of reaction steps (1) and (2) outlined in Scheme 2.
Scheme 2.
Experimental Section
General Methods
All reactions were performed under an atmosphere of nitrogen in a Vacuum Atmospheres glovebox, or in a custom-made anaerobic two-necked solution cell equipped with a threaded glass connector sized to fit an ATR (attenuated total reflectance) dip probe. Unless otherwise stated, chemical reagents purchased from commercial vendors were of the highest purity available and used without further purification. Tetrahydrofuran (THF), Et2O, and CH3CN were rigorously degassed and purified using solvent purification columns housed in a custom stainless steel cabinet, dispensed via a stainless steel Schlenk-line (GlassContour). MeOH and MeOD were distilled from magnesium methoxide. All solvents were rigorously degassed prior to use. Ferrous [FeII(SMe2N4(tren))] (PF6)(1) was synthesized according to literature procedures.23
Kinetic Measurements
Kinetic measurements were performed on a Varian Cary 50 spectrophotometer equipped with a “C-technologies” fiber optic cable and remote-read dip probe which was inserted into a custom-made anerobic solution cell. Reactions were run under pseudo first order conditions, with at least a 10-fold excess of 1 and proton donor, relative to superoxide. The purity of 1 was checked prior to each run by forming the Fe(III)-OOH intermediate in MeOH at −78 °C, and comparing its extinction coefficient to previously published values.23
Probing the Proton Donor-, and Iron-Dependence of [FeIII (SMe2N4(tren))(OOH)](PF6)(2) Formation
Superoxide-induced formation of hydroperoxo [FeIII(SMe2N4(tren))(OOH)]+ (2) is most reproducibly monitored in THF, a solvent which can be rigorously dried to avoid spurious sources of protons (i.e., H2O), and which does not freeze at temperatures above −70 °C. Hydroperoxo 2 is less stable at temperatures above −70 °C, and once protonated, superoxide spontaneously disproportionates at ambient temperatures (to afford O2 + H2O2) via a bimolecular reaction dependent on HO2 and O2− concentrations.31 In the absence of protons, superoxide does not disproportionate since the peroxide dianion O22- is extremely unstable. In aprotic solvents even with mildly acidic proton donors such as H2O (or MeOH) at ambient temperatures superoxide disproportion is 8 orders of magnitude slower than in water (kdisp25 °C (DMF, HA=H2O)=1×10−3 M−1 s−1 versus kdisp25 °C (H2O, pH=7)=4.5×105 M−1 s−1), and protonation of O2− is rate-limiting.31 At temperatures below −70 °C with submilimolar superoxide concentrations the former (aprotic solvent) reaction is significantly slower as was determined by monitoring the superoxide absorbance band at 250(2690) nm.28 For all of the reasons outlined above, kinetic studies described herein were monitored at low temperatures (−78 °C) in THF with superoxide as the limiting reagent in low concentration (0.1–0.4 mM). The limited solubility of O2− in THF (2.0 mM), even when solubilized as the 18-crown-6-K+ salt, also governed its choice as the limiting reagent. Proton donors were only introduced at low temperatures (−78 °C), and in the presence of excess amounts of our Fe2+ complex 1, that is, conditions under which superoxide disproportionation would not compete with its reaction with 1. The selection of proton donors was based not only on their pKa but also on their solubility in THF and requisite freezing point below −78 °C.
In a typical experiment, 20 mL of a 6.7 mM stock solution of 1 in THF was injected, via a gastight syringe, into a custom-made anaerobic cell, which had been purged with Ar for a minimum of 30 min to avoid μ-oxo dimer {[FeIII(SMe2N4 (tren)]2 (μ-O)}2+ formation. Once formed, the metastable nature of hydroperoxo 2 was verified by warming the solution resulting in the rapid decay of the λmax=464 nm absorbance band. Once temperature equilibrated to −78 °C, a 250 μL aliquot of a rapidly stirring, extremely fine (opaque) 28 mM suspension of (18-crown-6-K+)O2— in rigorously dried THF was then injected into a cold (−78 °C) THF solution of 1, resulting in a final superoxide concentration of 0.35 mM. A more concentrated (18-crown-6-K+)O2– slurry, as opposed to more dilute (18-crown-6-K+)O2− solution, was used to minimize mixing times, the time required for temperature re-equilibrataion, and to avoid altering bulk solvent properties. The high reproducibility of results demonstrated that as long as aliquots were drawn in exactly the same manner, reproducible amounts of (18-crown-6-K+)O2− could be transferred. The accuracy of this method was verified by transferring aliquots drawn as described above, to 20 mL of MeCN, and measuring the superoxide absorbance band at 250(2690) nm28 to determine its concentration. Experiments involving large volumes of more dilute (<2 mM) homogeneous (18-crown-6-K+)O2− stock solutions were significantly less reproducible.
Following the low temperature (−78 °C) equilibration of clear colorless THF solutions containing 1 + 0.35 mM (18-crown-6-K+)O2−, the absorbance was then scanned from 800 to 200 nm to get a baseline reading prior to the addition of the proton donor. Upon injection of the proton the solution gradually (over the course of several minutes to hours, depending on the proton source and concentration) turned orange with a λmax=464 nm consistent with the formation of [FeIII(SMe2N4 (tren))(OOH)]+ (2). Both the proton donor concentration and acidity were varied, while maintaining constant iron and superoxide concentrations, to establish the order with respect to proton donor and reaction dependence on pKa. In a separate set of experiments, the superoxide concentration and proton donor source (MeOH) concentration were kept constant, and the iron concentration was varied to establish the order with respect to iron. Proton donors examined include MeOH, MeOD, NH4+, PhOH, and p-X-PhOH (X = Br, I, NO2, NH2, CF3). Final concentrations of the proton donors varied depending on the acidity of the proton source. The MeOH concentration was allowed to vary from 61 mM to 1060 mM, that of MeOD from 27 mM to 535 mM, that of NH4+ from 1.1 mM to 12.3 mM, that of PhOH from 3.5 mM to 35 mM, that of p-Br-PhOH from 3.1 mM to 8.0 mM, that of p-I-PhOH from 0.8 to 8.1 mM, that of p-NO 2 -PhOH from 1.1 to 22.4 mM, and that of p-CF3 -PhOH from 3.5 to 56.8 mM.
The rate of [FeIII(SMe2N4(tren))(OOH)]+ (2) formation was monitored by probing changes in absorbance (at λmax = 464 nm) versus time over the course of several hours. Scans were collected automatically every 1–5 min at a scan rate of 600–4800 nm/min (depending on the acid and its concentration) over the wave-length range of 200–800 nm. Reactions were allowed to proceed for at least three half-lives. Unless otherwise indicated, temperatures were maintained at −78 °C throughout the course of an experiment.
Kinetics Measurements Probing Methanol- and Acetic Acid-Induced Release of H2O2 from [FeIII(SMe2N4(tren))(OOH)]+ (2) to Afford [FeIII(SMe2N4(tren))(OMe)]+ (3) and [FeIII(SMe2N4 (tren))(O(H)Me)]+ (4), Respectively
Kinetic runs involving acetic acid-induced H2O2 release from hydroperoxo 2 were performed under pseudo first order conditions, with at least a 10-fold excess of acetic acid relative to [FeIII(SMe2N4(tren)) (OOH)]+ (2). In a typical experiment, 1 equiv of (18-crown-6-K+)O2− in THF was injected into a precooled (−78 °C) MeOH solution of [FeII(SMe2N4(tren))](BPh4) (1·BPh4) under argon resulting in the immediate formation of [FeIII(SMe2N4(tren)) (OOH)]+ (2). To this solution, varying amounts of HOAc (or DOAc) were then added. The solvent volumes of added reagents were varied such that the final concentration of iron was 0.3 mM in all cases. The HOAc concentration (in MeOH) was varied between 2.9 mM and 240 mM, and that of DOAc (in MeOD) between 2.9 mM and 850 mM. The disappearance of 2 was monitored at −78 °C over several hours at λmax = 464 nm and at a scan rate of 4800 nm/minute. The absorbance was measured until the reaction reached completion so that it could be corrected for absorbing species other than the one of interest. The reaction was considered complete when no further changes in absorbance occurred. Methanol-induced H2O2 release was monitored in the same manner (over a longer time period) in neat MeOH with no other added acid. Rate constants (kobs)were obtained from the slope of linear fits to ln(A464)t – ln(A464)∞ versus time plots, where (A464)t is the experimentally measured optical absorbance at 464 nm at time t, and (A464)∞ is the experimentally measured optical absorbance at 464 nm after the reaction had reached completion. Non-linear fits to the data over all wavelengths were best fit to a pseudo first order process, modeled using eq 1.
| (1) |
where α=constant. Temperature-dependent studies were performed using the following low-temperature baths: acetone/dry ice (−78 °C); acetonitrile/dry ice (−60 °C to −35 °C); methanol/ice (−20 °C); or salt/ice (−18 °C to −12 °C)).
Results and Discussion
Possible Mechanisms for Proton-Dependent FeIII-OOH Formation
In rigorously dried THF solutions, [FeII(SMe2N4− (tren))]+ (1)(λmax = 262(4700)) does not react with KO2 (solubilized by 18-crown-6) until an external proton donor is added.26 This rules out a mechanism involving H+ or H-atom abstraction from the ligand (e.g., an amine N–H).28,32 Addition of even mildly acidic proton donors (e.g., EtOH) to 1 + KO2 results in the formation of a tangerine orange metastable hydroperoxo intermediate [FeIII(SMe2N4(tren))(OOH)]+ (2)26 at low temperatures (−78 °C). Initial studies involved MeOH as proton donor since previous work had shown that MeOH was basic enough to allow the intermediate to fully form, at reasonable rates, without subsequent release of H2O2. If the added proton donor is too acidic, then intermediate 2, which has an associated low-spin electron paramagnetic resonance (EPR) signal (g⊥ = 2.14, g∥ = 1.97), νO–O− (ν18O–18O) = 784(753) cm−1, λmax = 464(2540) nm (in THF), and short EXAFS-determined Fe–O bond (1.86 Å),23 is not observed. With MeOH as the proton donor, warming causes the solution color to change to burgundy (λmax = 511(1765) nm), and the low-spin EPR signal to convert to an intermediate-spin S = 3/2 signal (g = 4.10, 3.53), both characteristic features of methoxide-bound [FeIII(SMe2N4(tren))(OMe)]+ (3).23
The proton-dependence of hydroperoxo intermediate 2 formation26 is consistent with three possible mechanisms that conceivably should be distinguishable based on kinetics. One possible mechanism (Scheme 3) would involve initial protonation of the superoxide anion prior to its coordination to the metal to afford HO2, a more potent oxidant than O2−. A similar mechanism involving protonated superoxide (HO2) has been implicated in SOD-promoted superoxide disproportionation.33 Aqueous redox potentials for the superoxide/peroxide couple are highly pH-dependent and shift in a more oxidizing direction as [H+] is increased (E1/2(pH=0) = +1.27 versus SCE; E1/2(pH=14) = −0.04 versus SCE).28 In aprotic solvents, in the absence of a proton donor, this potential shifts to a significantly more negative value (e.g., −1.75 V versus NHE in DMF).28 Although O2− is not very basic in H2O (pKa(HO2) = 4.7), it is reasonably basic in aprotic solvents (pKa(HO2) = 12 in DMF).31
Scheme 3.
A second mechanism (Scheme 4) would involve the initial protonation of the thiolate sulfur of complex 1, to afford a dicationic thiol intermediate [FeII(HSMe2N4 (tren))]2+ (5). Although the weak basicity of a metal coordinated thiolate makes protonation at this site less likely, the generation of even minor concentrations of such a species would be advantageous given that a dication would be generated that would likely have a higher affinity for O2− relative to monocationic 1. Given that superoxide is a relatively weak-field ligand (frequently referred to as a “pseudo halide”)28 this could be important in promoting reactivity. The other advantage of this mechanism is that the proton would be readily available for intramolecular transfer, with minimal reorganization, to the bound superoxide. A related mechanism, involving intramolecular proton transfer from a coordinated ligand (OH−), is involved in dioxygen binding to hemerythrin.34 Although one would not expect an Fe(II)–SR to have a high affinity for protons, a stable protonated iron-bound cysteine Fe(II)–S(H)R species (known as P420) has been shown to form preferentially in reduced FeII–P450.35 Spectroscopic evidence also suggests that a protonated Ni–S(H)Cys forms in Ni–SOD,36 and theoretical calculations by Siegbahn suggest that this Ni–S(H)Cys species transfers a proton to superoxide during the Ni–SOD catalytic cycle.37
Scheme 4.
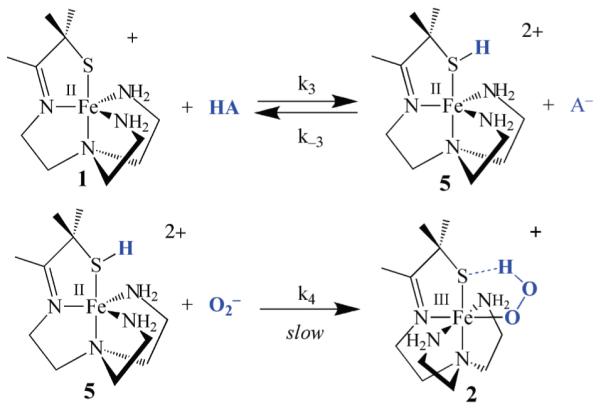
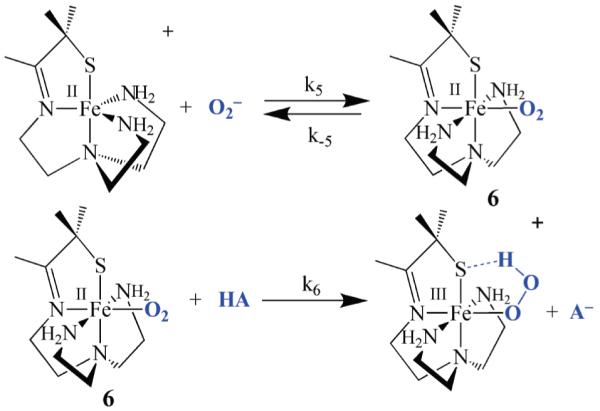
A third mechanism (Scheme 5) would involve the binding of O2− to the metal ion to form an FeII-superoxo intermediate, [FeII(SMe2N4(tren))(O2)] (6), which could then convert to a peroxo upon the addition of a proton. Protonation at the superoxo distal oxygen would be expected to shift electron density toward the dioxygen ligand, resulting in the oxidation of the metal ion in a proton-induced electron “transfer” reaction. Theoretical calculations suggest that a superoxo intermediate, analogous to 6, is involved in the SOR mechanism.16 However, we detect no intermediates, other than hydroperoxo 2, in our biomimetic reaction. Proposed intermediates 5 and 6 might be difficult to detect, especially if they form only in small concentrations, since they would be EPR silent (Fe2+) and colorless. Given its low dielectric constant, THF would favor the formation of neutral, as opposed to charged species, thus favoring the third (Scheme 5) mechanism over the first (Scheme 3) and second (Scheme 4), since it converts cationic 1 and anionic O2− to neutral [FeII(SMe2N4(tren))(O2)] (6) (Scheme 5).
Scheme 5.
Derivation of the Rate Expressions
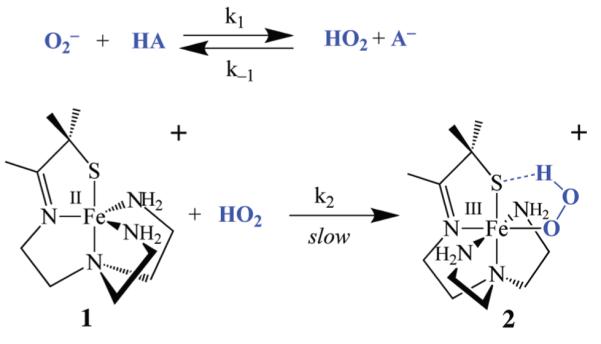
The three mechanisms outlined in Schemes 3–5 should be distinguishable by kinetics as shown by their distinct rate expressions, and corresponding reaction order with respect to iron and proton donor (Table 1). If the rate-limiting step involves oxidative addition of HO2 to the metal ion (Scheme 3), and superoxide is protonated in a rapid pre-equilibrium step, then reaction rates would be dependent on both iron [FeII(SMe2N4(tren))]+ (1; abbreviated in the equations below as “FeII”) and HO2 concentrations as shown in eq 2 below.
| (2) |
For acids appreciably more acidic than HO2 (i.e., those for which pKa(HA) < pKa(HO2), where pKa(HO2) is log of the equilibrium constant defined in eq 4, and pKa(HA) is log of the equilibrium constant defined in eq 5), the pre-equilibrium step shown in Scheme 3 would lie all the way to the right, and all of the superoxide anion added would be converted to HO2 (i.e., [HO2] = [O2−]). In these cases, the second order rate constant k2 could be obtained directly from a plot of kobs = k2[FeII] versus [FeII] under pseudo first order conditions ([Fe]0 ≥ 10[HO2]0), and rates (k2) would be independent of proton donor concentration (vide infra). For weaker acids, such as MeOH, on the other hand, the concentration of HO2 would be determined by the pre-equilibrium constant, Keq (eq 3), which would depend on the relative acidities of HO2 (eq 4) versus HA (eq 5).
| (3) |
| (4) |
| (5) |
In THF, Keq would also depend on the relative stability of ion pairs, (18-crown-6-K+)O2− versus (18-crown-6-K+)A−.38,39 If the reaction is carried out in the absence of added anion, then at equilibrium, [HO2] = [A−], and eq 3 becomes
| (6) |
Using eq 6, [HO2] can be expressed in terms of known concentrations, and the pre-equilibrium constant Keq
| (7) |
Substituting this into eq 2, the rate expression for the mechanism outlined in Scheme 3 (Table 1) becomes
| (8) |
where the rate constant k2 is defined in Scheme 3. On the basis of this rate expression, we expect half-order dependence on the proton donor and superoxide, and first-order dependence on iron, for a mechanism involving the initial protonation of superoxide (Scheme 3). Under limiting superoxide conditions, the rate expression becomes
| (9) |
where kobs is defined as
| (10) |
If, on the other hand, the mechanism involves initial protonation of the thiolate sulfur (Scheme 4), then the rate law can be derived in a similar manner to afford the rate expression shown in eq 11 (Table 1), where the rate constant k4 is defined in Scheme 4, Ka(HA) is defined
| (11) |
in eq 5, and Ka(FeSH) is the acid dissociation constant for the protonated thiol intermediate 5. On the basis of this rate expression, we expect half-order dependence on iron and the proton donor, and first-order dependence on superoxide. For the third mechanism involving an FeII-superoxo intermediate (Scheme 5), if we assume that a steady state concentration of this intermediate forms, then the rate law of eq 12 would hold, where the rates constants are defined in Scheme 5.
| (12) |
On the basis of this rate expression (Table 1), we expect first order dependence on [FeII] and [O2−], but a mixed-order dependence on [HA]. At high concentrations of [HA] saturation kinetics would be expected. If k−5 ⪢ k6[HA], then first order dependence on [HA] would be expected. If k6[HA] ⪢ k−5, then rates would be independent of [HA].
Table 1.
Rate Expressions for Three Proposed Mechanisms of Proton-Dependent Fe(III)-OOH (2) Formation via Superoxide Addition to Thiolate-Ligated Fe(II) (1)
Kinetics of Fe(III)–OOH Formation
To determine the most probable mechanism for hydroperoxo [FeIII-(SMe2N4(tren))(OOH)]+ (2) formation, kinetic studies were performed. The proposed mechanisms of Schemes 3–5 should be distinguishable based on the predicted reaction order with respect to [FeII(SMe2N4(tren))](PF6)(1), superoxide, and proton donor (HA). The intense absorption band associated with hydroperoxo 2 (λmax = 464(2540) nm in THF) provides a convenient means to monitor reaction rates using electronic absorption spectroscopy. Product growth, as opposed to reactant disappearance, was monitored because the reactants are all colorless and spectroscopically “silent” in the visible region. Kinetics experiments were carried out following the procedure outlined in the Experimental Section. Representative absorbance versus wavelength, and absorbance versus time plots for the reaction between 1 and O2− are shown in Figures 1a and 1b, respectively. Kinetic traces for all but the more acidic acids (NH4+ and p-NO2 -PhOH) were evaluated at 464 nm by plotting ([1 − ((A464)t ) − ((A464)0)/((A464)∞) − ((A464)0]1/2) versus time (see derivation Supporting Information), where (A464)t is the absorbance at 464 nm at time t, and (A464)0 is the initial, and (A464)∞ is the final absorbance at 464 nm. From each of these plots, a kobs value was obtained according to eq 13 below, 40 where
| (13) |
“slope” is the slope of the ([1 − ((A464)t ) − ((A464)0)/((A464)∞) − ((A464)0]1/2) versus time plot. Nonlinear fits to the data, using a program written for MATlab, verified the results obtained from the above linear plots. Data was fitted (over all wavelengths, 300–800) to eq 14 , 40 by finding the kobs, A0, and A∞ values that minimized the residual of eq 15 , while at the same time restricting kobs to be constant over all wave-lengths.
| (14) |
| (15) |
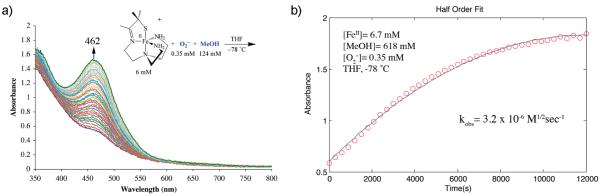
Figure 1.
(a) Absorbance versus wavelength plot for hydroperoxo [FeIII(SMe2N4(tren))(OOH)]+ (2) formation via FeII-promoted superoxide reduction in THF at −78 °C. [FeII]=6 mM, [O2−]=0.35 mM, [MeOH]=124 mM. Successive plots taken at regular intervals (one every 5 min) over the course of 3 h. (b) Non-linear half-order fit to absorbance versus time plot associated with hydroperoxo [FeIII(SMe2N4(tren))(OOH)]+ (2) formation in THF at −78 °C. [FeII]=6.7 mM, [O2−]=0.35 mM, [MeOH]=618 mM.
For the more acidic proton donors, NH4+ and p-NO2-PhOH (vide infra), kinetic traces were evaluated at 464 nm by plotting ln(A464)t – ln( A464)0 versus time and obtaining kobs from the slope. Second order rate constants for these acids were obtained from the slope of kobs versus [FeII] plots. All reactions were run under pseudo half order, or first order, conditions, depending on the acid, with the concentration of both 1 and HA in at least 10-fold excess of O2−. Over the concentration ranges examined (see Experimental Section) all reactions were well-behaved over at least three half-lives.
Both the proton donor concentration and acidity were varied, while maintaining constant iron and superoxide concentrations, in one set of experiments. This established the proton-dependent nature of the reaction, and the order with respect to proton donor. In a separate set of experiments, the superoxide and proton donor (MeOH) concentrations were kept constant, and the iron concentration was varied to establish the order with respect to iron. Rates were found to increase with increasing FeII concentration (Figure 2), and display first-order dependence on [FeII], as shown by the log(kobs) versus log[FeII] plot of Supporting Information, Figure S-1. First-order dependence on [FeII] would be consistent with the first and third mechanisms (Scheme 3 (eq 8) and Scheme 5 (eq 12), respectively) but inconsistent with the second mechanism (Scheme 4, eq 11).
Figure 2.
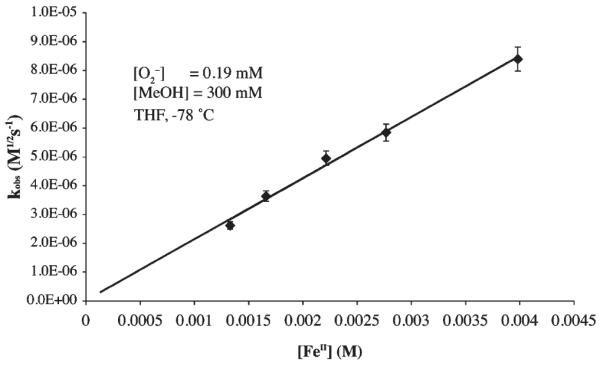
kobs versus [FeII] plot for MeOH-promoted hydroperoxo [FeIII(SMe2N4(tren))(OOH)]+ (2) formation in THF at −78 °C. [O2−]=0.19 mM, [MeOH] = 300 mM.
One could differentiate between the first (Scheme 3) and third (Scheme 5) mechanisms by determining the order with respect to proton donor, since half-order dependence would be expected for the former (eq 8), while more complex behavior involving saturation at high HA concentrations (eq 12) would expected with the latter. Initial results with MeOH did not provide evidence for saturation at high HA concentrations (up to 1720 mM). Thus the data was treated using the pseudo half-order expression shown in eq 9, and kobs values were determined according to eq 13. As shown by the kobs versus [HA]1/2 plot for mildly acidic proton donors in Figure 3 (and Supporting Information, Figures S-2 to S-8), the rate at which peroxo intermediate 2 forms displays a clear dependence on the concentration and pKa of the proton donor (Table 2 and Table 3). For these weaker proton donors (Table 2), log(kobs) versus log[HA] plots are roughly linear with slopes consistently closer to 1/2 than to 1.0 (Figures 4, and Supporting Information, Figures S-9 to S-14), indicative of half-order dependence on proton donor (HA). Half-order dependence on HA would be most consistent with mechanisms involving protonation of superoxide (Scheme 3, eq 8), or the coordinated thiolate (Scheme 4, eq 11) in a rapid-pre-equilibrium step. The latter is ruled out by the observed first order-dependence on iron. As shown in Figure 3, there does not appear to be a deuterium isotope effect, ruling out the mechanisms (Scheme 4 and 5) involving X–H bond cleavage (X = S, A) in the rate-determining step. Bases such as methoxide inhibit the reaction as shown in Figure 5. Thus it appears, based on kinetics, that the mechanism by which our biomimetic analogue reduces superoxide involves oxidative addition of HO2 to FeII in the rate-determining step. This conclusion is corroborated by the fact that initial rates roughly double, from 2.62 × 10−5 s−1 to 6.82 × 10−5 s−1, when the superoxide concentration is quadrupled (from 0.066 mM to 0.26 mM) and FeII (1) and HA = MeOH concentrations are held constant.
Figure 3.
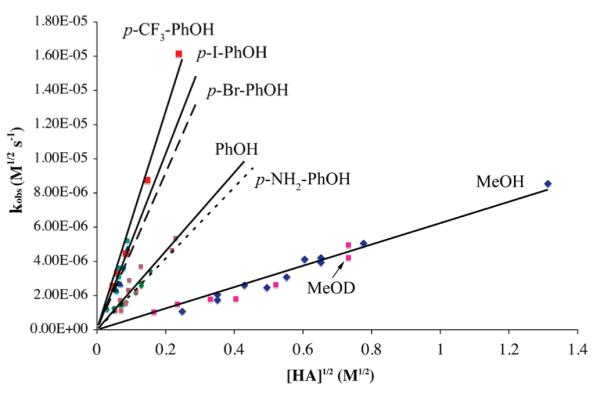
kobs versus [HA]1/2 plot for hydroperoxo [FeIII(SMe2N4-(tren))(OOH)]+ (2) formation in THF at −78 °C, showing rate dependence on proton donor concentration and pKa.
Table 2.
Slope of kobs versus [HA]1/2 Plotsa for Fe(III)-OOH Formation at −78 °C
| HA | Slope (sec−1) |
|---|---|
| p-CF3-PhOH | 6.4(1)×10−5 |
| p-I-PhOH | 5.1(1)×10−5 |
| p-Br-PhOH | 4.6(1)×10−5 |
| PhOH | 2.3(1) ×10−5 |
| p-NH2-PhOH | 2.1(1)×10−5 |
| MeOH | 6.2(1)×10−6 |
| MeOD | 5.8(1)×10−6 |
Table 3.
Solvent-Dependent pKa Data for HO2 versus Selected Acids Involved in This Study
| HA | pKa in H2O |
pKa in DMSO |
pKa in MeOHc |
pKa in THFd |
|---|---|---|---|---|
| MeOH | 15.5 | 29b | 30 | |
| PhOH | 9.95 | 18b | 14.33 | 21 |
| HO2 | 4.7 | 12a | NR | 19 |
| p-NO2-PhOH | 7.18 | 10.8b | 11.30 | 18 |
| NH4+ | 9.24 | 10.5b | 10.78 | 16 |
Measured in DMF. Chin, D.-H.; Chiericato, G., Jr.; Nanni, E. J., Jr.; Sawyer, D. T. J. Am. Chem. Soc. 1982, 104, 1296–1299.
Bordwell, F. G. Acc. Chem. Res. 1988, 21, 456–463.
Rived, F.; RosÈs, M.; Bosch, E. Anal. Chim. Acta 1998, 374, 309–324.
This work.
Figure 4.
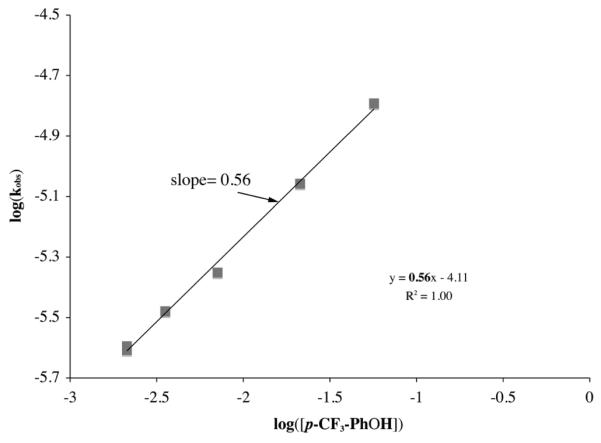
Determination of the reaction order (half) with respect to HA = p-CF3-PhOH, using a log(kobs) versus log([HA]) plot, for the proton-assisted formation of [FeIII(SMe2N4(tren))(OOH)]+ (2) in the reaction between [FeII(SMe2N4(tren))]+ (1) + (18-crown-6-K+)(O2−) in THF at −78 °C. [O2−] = 0.35 mM, [FeII] = 6.5 mM.
Figure 5.
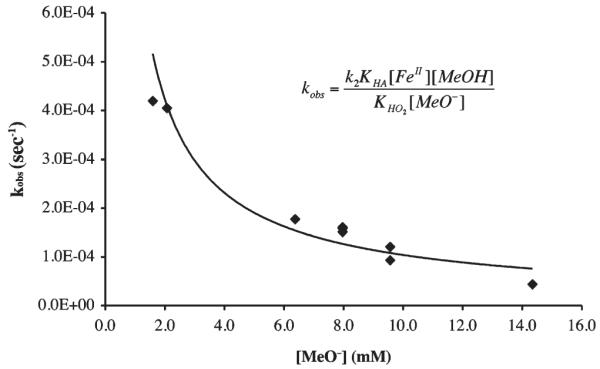
kobs versus [MeO−] plot for the MeOH-induced formation of [FeIII(SMe2N4(tren))(OOH)]+ (2) in THF at −78 °C. The curve represents a reciprocal fit (x−0.9) to the data consistent with methoxide inhibition.
As shown in Figure 6, rate constants for p-substituted phenols (Table 2) roughly correlate linearly with the Hammett substituent constants σ− (which take into account resonance stabilization).41 The slope of this Hammett plot (log(kx/kH) versus σ−) yields a reaction constant ρ = +0.64 ± 0.1, indicating that electron withdrawing substituents promote the reaction, as one would expect for a proton transfer reaction, and that is within error of the theoretically predicted value (ρ = +0.50) for a reaction involving half-order dependence on HA.42 There is no dramatic change in slope, indicating that, as the electronic nature of the proton donor is changed, the mechanism does not change.42 In THF, protons are most likely transferred directly between the proton donor HA, and proton acceptor, without the involvement of solvent.
Figure 6.
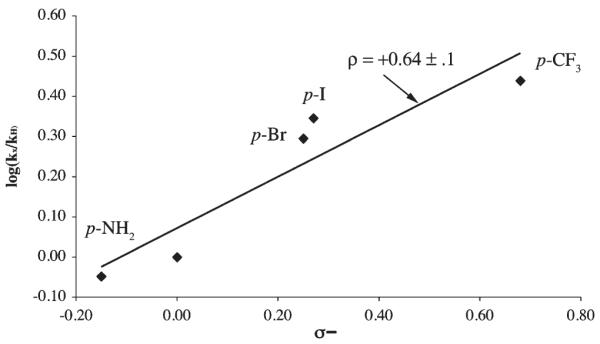
Hammett plot for p-X-PhOH–induced formation of [FeIII(SMe2N4(tren))(OOH)]+ (2) via the oxidative addition of superoxide to [FeII(SMe2N4(tren))]+ (1). Values shown are the mean of three independent experimental runs.
With more acidic acids, such as NH4+ and p-NO2-PhOH, rates are independent of pKa and HA concentration (Supporting Information, Figures S-15, S-17 to S-18) implying that the pre-equilibrium of Scheme 3 lies significantly to the right, (i.e., [HO2] = [O2−]). In these cases, the reaction is then pseudo first order with respect to HO2 (eq 1), and k2 can be obtained directly from the slope of a kobs versus [FeII] plot (Figure 7 and Supporting Information, Figure S-15), and the reaction order with respect to iron can be obtained from the slope of a log(kobs) versus log([FeII]) plot (Supporting Information, Figure S-16). The first order-dependence so determined is again consistent with a mechanism involving initial protonation of O2− in a rapid pre-equilibrium step.
Figure 7.
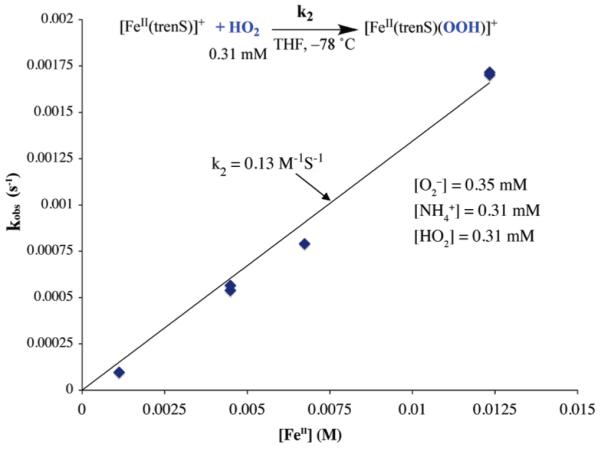
kobs versus [FeII] plot for a proton donor (HA = p-NO2-PhOH) strong enough to completely convert O2− to HO2 . Under these conditions, i.e., when [HO2] = [O2−], the rate constant k2 can be obtained directly from the slope.
The pKa dependence of peroxo intermediate [FeIII-(SMe2N4(tren))(OOH)]+ (2) formation differs notably from the pH-independent rate at which the SOR FeIII-OOH intermediate forms. Most likely this is a consequence of carrying out these reactions in different media, less polar, aprotic THF versus water. In H2O, one would expect proton transfer to be more facile (especially if the metal ion active site resides on the surface of the protein). The fact that the pKa of the proton donor influences rates with the more basic proton donors (HA = MeOH, PhOH, p-CF3-PhOH, p-I-PhOH, p-Br-PhOH, and p-NH2-PhOH) implies that the initial protonation site of our biomimetic reaction (Scheme 2) is more acidic than these proton donors. And, the proton-donor independent rates observed with more acidic proton-donors HA = p-NO2-PhOH and NH4+ implies that the initial protonation site is more basic than these proton donors. Although pKa data has been extensively tabulated in H2O as a solvent (in water (pKa(HO2) = 4.5), data is more limited for organic solvents (Table 3) DMF,31 DMSO,43 MeCN,44–46 and MeOH.47 In THF, the most comprehensive set of pKa’s has been assembled by Streitwieser and co-workers; this list does not, however, include the acids involved in the study herein.48
Using Streitwieser’s method,38,49 we determined the pKa’s of acids used in this study by measuring equilibrium ion pair acidity constants for the reaction between Li+ salts of highly colored carbanion indicator dyes (Ind−),48 and proton donors HA, in THF as described in the Supporting Information. The Li+ salts have been shown to form solvent separated ion pairs in the concentration range utilized in this investigation.38 The ion pair acidity constants were then converted to an absolute scale as described by Streitwieser to afford the pKa’s listed in Table 3.50 The relative ordering of HA pKa values relative to HO2 determined using this method (Table 3) would be consistent with a mechanism for [FeIII(SMe2N4(tren))-(OOH)]+ (2) formation (Scheme 3) that involves the initial protonation of O2− to afford HO2. This would explain the proton donor-dependent rates observed with MeOH and PhOH (i.e., those with pKa(HA)>pKa(HO2)), and proton-donor independent rates observed with p-NO2-PhOH and NH4+ (i.e., those with pKa(HA) < pKa(HO2)).
Activation parameters for MeOH-promoted [FeIII-(SMe2N4(tren))(OOH)]+ (2) formation were obtained by measuring T-dependent rates at constant O2−, MeOH, and FeII (1) concentrations. The observed rate constant for this reaction, kobs, is defined by eq 10, and from this the second order rate constant k2 associated with the rate-liming step (Scheme 3) can be determined using the experimentally determined Ka values for HO2 and MeOH in THF (vide supra, Table 3), and known (constant) O2− and MeOH concentrations. Although activation parameters for multistep reactions represent composite values that include contributions from all equilibrium constants and rate constants involved, and thus can not be interpreted in a straightforward manner, the enthalpy of activation, (ΔH‡ = 2.8 kcal/mol) obtained from the slope of the resulting Eyring plot (Figure 8) would be consistent with a low-barrier process (i.e., HO2 binding to 1) that does not involve extensive bond cleavage. The entropy of activation (ΔS‡ = −31 eu), obtained from the intercept, is consistent with an associative mechanism, and closely matches the theoretically calculated value for a bimolecular collision involving the loss of translational motion for two particles. Rybak-Akimova, Busch, and Schindler have observed similar enthalpies of activation for reactions involving dioxygen binding to Co(II) and Fe(II).51,52
Figure 8.
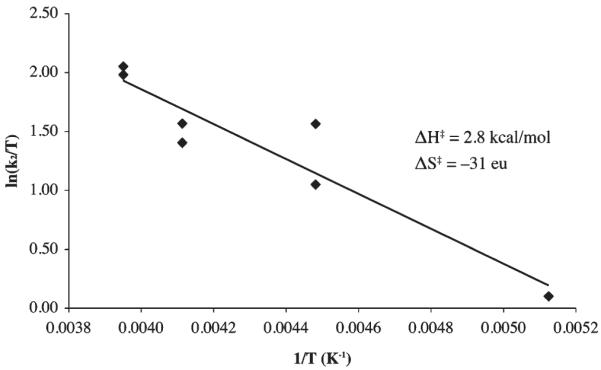
Eyring plot associated with the reaction between HO2 and [FeII(SMe2N4(tren))]+ (1) in THF, with MeOH as the proton donor, to afford hydroperoxo [FeIII(SMe2N4(tren))(OOH)]+ (2).
Acetic Acid- and MeOH-Induced H2O2 Release
Hydrogen peroxide is released from [FeIII(SMe2N4(tren)) (OOH)]+ (2) fairly rapidly upon the addition of more acidic proton donors (e.g., HOAc) to afford a stable solvent-coordinated species, presumably via protonation of the proximal peroxo oxygen.23,26 This reaction (Scheme 6) is best monitored in MeOH at −78 °C, conditions under which hydroperoxo-intermediate [FeIII(SMe2N4(tren))-(OOH)]+ (2)is relatively stable (t1/2 =69.2h;Supporting Information, Figure S-19). Weaker acids, such as MeOH afford burgundy methoxide-bound [FeIII(SMe2N4(tren))(OMe)]+ (3)(λmax= 511(1770) nm), whereas stronger acids such as HOAc, HCl, and HBF4, afford eggplant purple methanol-bound [FeIII(SMe2N4(tren))(O(H)Me)]+ (4, λmax =530 nm).26 Alternative protonation sites would include the thiolate sulfur or distal peroxo oxygen (Supporting Information, Figure S-20). However, the former is ruled out by the retention of the thiolate sulfur-to-Fe(III) charge transfer band, and the latter is ruled out by the observed Fe(III)-solvent and H2O2 products.23 Possible side-reactions involving O–O bond cleavage via protonation of the distal peroxo to afford an Fe(V)=O (Supporting Information, Figure S–20) would be energetically less feasible53 and inconsistent with the observed H2O2 product.23 The rate of H2O2 release (krelease) is dependent on the pKa of the proton donor. Methanol–induced H2O2 release occurs with a krelease (−60 °C) = 5.1×10−7 M−1 sec−1, and activation parameters of ΔH‡=13.2 kcal/mol and ΔS‡=−24.3 eu (Figure 9). This translates into a hydroperoxo intermediate 2 half-life of approximately 1 min at ambient temperature in neat MeOH. Acetic acid-induced H2O2 release (Supporting Information, Figure S-21) occurs, on the other hand, with krelease(−78 °C)=3.7 × 10−2 M−1 sec−1 (Figure 10), and activation parameters of ΔH‡ = 8.3 kcal/mol and ΔS‡ = −34 eu (Supporting Information, Figure S-22), with a deuterium isotope effect of kH/kD = 3.1 (Supporting Information, Figure S-23). The rate at which SOR intermediate T1 converts to intermediate T2 (Scheme 1) is also pH dependent, and displays a deuterium isotope effect of kobs,H2O/kobs,D2O ~ 2.11,17 The enthalpy of activation for our biomimetic reaction (HA=MeOH, Scheme 6, Figure 9) is comparable to that (ΔH‡=12 kcal/mol) of H2O-induced conversion of SOR intermediate T1 to SOR intermediate T2 (Scheme 1).17 The entropy of activation is consistent with a reaction involving the rate-limiting protonation of an Fe(III)–OOH ( Supporting Information, Figure S-20 , path a) via an associative mechanism. If O–O bond cleavage were rate-limiting, then one would expect ΔS‡ to be positive, and the enthalpy of activation to be significantly larger, and there would not be a significant primary deuterium isotope effect (Supporting Information, Figure S-23). The larger deuterium isotope effect observed with our biomimetic reaction relative to that of SOR could be attributed, in part, to the fact that kinetics were run at low temperatures (i.e., −78 °C). The influence of temperature on isotope effects have been noted previously for peroxo protonation reactions.54
Scheme 6.
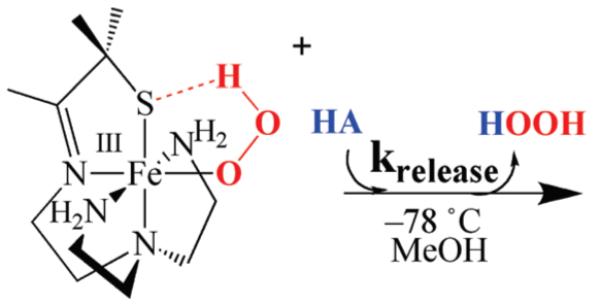
Figure 9.
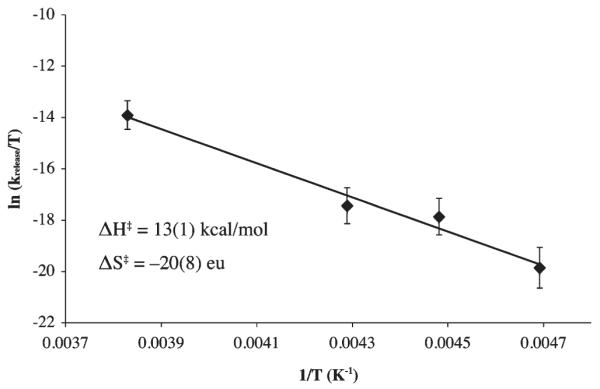
Eyring plot for MeOH-induced release of H2O2 from hydroperoxo [FeIII(SMe2N4(tren))(OOH)]+ (2) to afford methoxide-bound [FeIII(SMe2N4(tren))(OMe)]+ (3).
Figure 10.
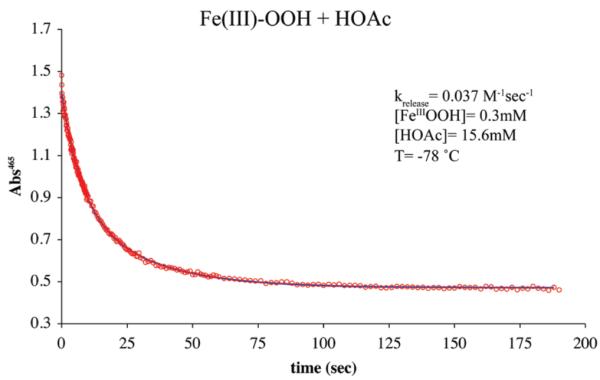
Non-linear second-order fit to absorbance versus time plot for acetic acid-induced release of H2O2 from [FeIII(SMe2N4(tren))(OOH)]+ (2) to afford [FeIII(SMe2N4(tren))(O(H)Me)]+ (4) in MeOH at −78 °C.
Summary and Conclusions
Three possible mechanisms are proposed to explain the proton-dependent formation of a synthetic thiolate-ligated Fe(III)–OOH intermediate [FeIII(SMe2N4(tren))-(OOH)]+ (2) via oxidative addition of superoxide to [FeII(SMe2N4(tren))]+ (1). The first mechanism involves the initial protonation of O2− prior to its coordination to the metal to afford HO2, a more potent oxidant. A second mechanism would involve the initial protonation of the Fe-(II)-coordinated thiolate sulfur of 1 to afford a dicationic thiol intermediate that has a higher affinity for O2−. And, a third mechanism involves the binding of O2− to the metal ion to form an FeII-superoxo intermediate, protonation of which induces electron transfer from the metal ion to superoxide. Derivation of the rate-laws shows that these mechanisms should conceivably be distinguishable based on kinetics, the reaction order with respect to iron, superoxide, and proton donor, and the dependence on proton donor pKa. Kinetic studies were performed in rigorously dried THF at low temperatures (−78 °C) using electronic absorption spectroscopy. Rates were shown to correlate with proton donor pKa, display first-order dependence on FeII, and half-order dependence on superoxide for mildly acidic proton donors with pKa(HA) >pKa(HO2). For proton donors acidic enough to convert O2− to HO2 (in THF), that is, those with pKa(HA)<pKa(HO2), the reaction displays first-order dependence on both superoxide and iron, with rates that are independent of HA. This strongly suggests that a mechanism involving oxidative addition of HO2 to FeII in the rate-determining step is involved. Relative pKa values in THF were established for the proton donors used in this study by measuring equilibrium ion pair acidity constants using Streitwieser’s method.48,55 There is no apparent deuterium isotope effect, and bases, such as methoxide, were shown to inhibit the reaction. Activation parameters for this reaction (ΔH‡ = 2.8 kcal/mol, ΔS‡=−31 eu) were shown to be consistent with a low-barrier associative mechanism that does not involve extensive bond cleavage. Rate constants for p-substituted phenols were shown to roughly correlate linearly with the Hammett substituent constants σ−. Acetic acid and MeOH convert hydroperoxo intermediate 2 to solvent-bound [FeIII(SMe2N4(tren))(O(H)Me)]+ (4) and [FeIII(SMe2N4(tren))(OMe)]+ (3), respectively.23,26 Activation parameters for these reactions (MeOH: ΔH‡=13.2 kcal/mol and ΔS‡=−24.3 eu, HOAc: ΔH‡ = 8.3 kcal/mol and ΔS‡ = −34 eu) were shown to be consistent with a reaction involving rate-limiting protonation of an Fe(III)–OOH. The observed deuterium isotope effect (kH/kD=3.1) is also consistent with this mechanism.
The strong correlation between rates of hydroperoxo intermediate 2 formation and proton donor pKa differs from the pH-independent rate at which the metalloenzyme superoxide reductase (SOR) FeIII–peroxo intermediate forms.11,13 This suggests that the mechanisms are different, most likely because of the different solvent media (less polar, aprotic THF versus water). It is also possible that the highly conserved Glu–CO2H near the active site facilitates proton transfer and rapid formation of HO2, making the reaction rates independent of pH.
Supplementary Material
Acknowledgment
We thank Elena Rybak-Akimova for helpful discussion.
Footnotes
Supporting Information Available: Contains experimental details regarding determination of pKa for proton donors HO2, MeOH, PhOH, p-NO2-PhOH, and NH4+ in THF. Residuals for the global non-linear fit to the kinetic data for MeOH-induced formation of hydroperoxo 2. Source code for the MATLAB program, “KinCalc”, which does global non-linear fits to kinetic data. Kinetics (kobs versus [HA]1/2 and log(kobs) versus log([FeII, HA])) plots for Fe(III)-OOH formation promoted by proton donors MeOH, MeOD, PhOH, and p-X-PhOH (X = Br, I, NH2, CF3). Kinetics plots (kobs versus [FeII, HA] and log(kobs) versus log([FeII ])) for stronger acids p-NO2 -PhOH and NH4+. Kinetics (ln(A460) versus time) plot for MeOH-induced conversion of Fe(III)-OOH to Fe(III)-OMe. Scheme outlining possible protonation pathways. Kinetics (absorbance versus λ, Eyring, non-linear fits to absorbance versus time) plots for H(D)OAc-induced conversion of Fe(III)-OOH to Fe(III)-O(H)Me. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- (1).Kurtz DM., Jr. Acc. Chem. Res. 2004;37:902–908. doi: 10.1021/ar0200091. [DOI] [PubMed] [Google Scholar]
- (2).Perry JJP, Hearn AS, Cabelli DE, Nick HS, Tainer JA, Silverman DN. Biochemistry. 2009;48:3417–3424. doi: 10.1021/bi8023288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (3).Miller AF. Acc. Chem. Res. 2008;41:501–510. doi: 10.1021/ar700237u. [DOI] [PubMed] [Google Scholar]
- (4).Neupane KP, Gearty AF, Shearer J. J. Am. Chem. Soc. 2007;129:14605–14618. doi: 10.1021/ja0731625. [DOI] [PubMed] [Google Scholar]
- (5).Mathé C, Weill CO, Mattioli TA, Berthomieu C, Houée-Levin C, Tremey E, Nivière V. J. Biol. Chem. 2007;282:22207–22216. doi: 10.1074/jbc.M700279200. [DOI] [PubMed] [Google Scholar]
- (6).Katona G, Carpentier P, Nivière V, Amara P, Adam V, Ohana J, Tsanov N, Bourgeois D. Science. 2007;316:449–453. doi: 10.1126/science.1138885. [DOI] [PubMed] [Google Scholar]
- (7).Yeh AP, Hu Y, Jenney FE, Jr., Adams MWW, Rees DC. Biochemistry. 2000;39:2499–2508. doi: 10.1021/bi992428k. [DOI] [PubMed] [Google Scholar]
- (8).Santos-Silva T, Trincão J, Carvalho AL, Bonifácio C, Auchère F, Raleiras P, Moura I, Moura JJ, Romão MJ. J Biol Inorg Chem. 2006;11:548–558. doi: 10.1007/s00775-006-0104-y. [DOI] [PubMed] [Google Scholar]
- (9).Adam V, Royant A, Niviere V, Molina-Heredia FP, Bourgeois D. Structure. 2004;12:1729–1740. doi: 10.1016/j.str.2004.07.013. [DOI] [PubMed] [Google Scholar]
- (10).Rodrigues JV, Abreu IA, Cabelli D, Teixeira M. Biochemistry. 2006;45:9266–9278. doi: 10.1021/bi052489k. [DOI] [PubMed] [Google Scholar]
- (11).Huang VW, Emerson JP, Kurtz DM. Biochemistry. 2007;46:11342–11351. doi: 10.1021/bi700450u. [DOI] [PubMed] [Google Scholar]
- (12).Niviere V, Asso M, Weill CO, Lombard M, Guigliarelli B, Favaudon V, Houe’e-Levin C. Biochemistry. 2004;43:808–818. doi: 10.1021/bi035698i. [DOI] [PubMed] [Google Scholar]
- (13).Rodrigues JV, Abreu IA, Cabelli D, Teixeira M. Biochemistry. 2006;45:9266–9278. doi: 10.1021/bi052489k. [DOI] [PubMed] [Google Scholar]
- (14).Kurtz DM., Jr. J. Inorg. Biochem. 2006;100:679–693. doi: 10.1016/j.jinorgbio.2005.12.017. [DOI] [PubMed] [Google Scholar]
- (15).Silaghi-Dumitrescu R, Silaghi-Dumitrescu I, Coulter ED, Kurtz DM., Jr. Inorg. Chem. 2003;42:446–456. doi: 10.1021/ic025684l. [DOI] [PubMed] [Google Scholar]
- (16).Dey A, Jenney FE, Adams MW, Johnson MK, Hodgson KO, Hedman B, Solomon EI. J. Am. Chem. Soc. 2007;129:12418–12431. doi: 10.1021/ja064167p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (17).Emerson JP, Coulter ED, Cabelli DE, Phillips RS, Kurtz DM., Jr. Biochemistry. 2002;41:4348–4357. doi: 10.1021/bi0119159. [DOI] [PubMed] [Google Scholar]
- (18).Mathé C, Nivière V, Mattioli TA. J. Am. Chem. Soc. 2005;127:16436–16441. doi: 10.1021/ja053808y. [DOI] [PubMed] [Google Scholar]
- (19).McClune GJ, Fee JA, McCluskey GA, Groves JT. J. Am. Chem. Soc. 1977;99:5220–5222. [Google Scholar]
- (20).McCandlish E, Miksztal AR, Nappa M, Sprenger AQ, Valentine JS, Stong JD, Spiro TG. J. Am. Chem. Soc. 1980;102:4268–4271. [Google Scholar]
- (21).Summers JS, Baker JB, Meyerstein D, Mizrahi A, Zilbermann I, Cohen H, Wilson CM, Jonmes JR. J. Am. Chem. Soc. 2008;130:1727–1734. doi: 10.1021/ja077193b. [DOI] [PubMed] [Google Scholar]
- (22).Kitagawa T, Dey A, Lugo-Mas P, Benedict J, Kaminsky W, Solomon E, Kovacs JA. J. Am. Chem. Soc. 2006;128:14448–14449. doi: 10.1021/ja064870d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Shearer J, Scarrow RC, Kovacs JA. J. Am. Chem. Soc. 2002;124:11709–11717. doi: 10.1021/ja012722b. [DOI] [PubMed] [Google Scholar]
- (24).Kovacs JA, Brines LM. Acc. Chem. Res. 2007;40:501–509. doi: 10.1021/ar600059h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).Brines LM, Kovacs JA. Eur. J. Inorg. Chem. 2007:29–38. [Google Scholar]
- (26).Theisen RM, Kovacs JA. Inorg. Chem. 2005;44:1169–1171. doi: 10.1021/ic048818z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (27).Shearer J, Nehring J, Kaminsky W, Kovacs JA. Inorg. Chem. 2001;40:5483–5484. doi: 10.1021/ic010221l. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (28).Sawyer DT, Valentine JS. Acc. Chem. Res. 1981;14:393–400. [Google Scholar]
- (29).Yandulov DV, Schrock RR. Science. 2003;301:76–78. doi: 10.1126/science.1085326. [DOI] [PubMed] [Google Scholar]
- (30).Yandulov DV, Schrock RR. J. Am. Chem. Soc. 2002;124:6252–6253. doi: 10.1021/ja020186x. [DOI] [PubMed] [Google Scholar]
- (31).Chin D-H, Chiericato G, Jr., Nanni EJ, Jr., Sawyer DT. J. Am. Chem. Soc. 1982;104:1296–1299. [Google Scholar]
- (32).Bernhard P, Anson FC. Inorg. Chem. 1988;27:4574–4577. [Google Scholar]
- (33).Smirnov VV, Roth JP. J. Am. Chem. Soc. 2006;128:16424–16425. doi: 10.1021/ja066369r. [DOI] [PubMed] [Google Scholar]
- (34).Brunold TC, Solomon EI. J. Am. Chem. Soc. 1999;121:8288–8295. [Google Scholar]
- (35).Perera R, Sono M, Sigman JA, Pfister TD, Lu Y, Dawson JH. Proc. Natl. Acad. Sci. U.S.A. 2003;100:3641–3646. doi: 10.1073/pnas.0737142100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (36).Szilagyi RK, Bryngelson PA, Maroney MJ, Hedman B, Hodgson KO, Solomon EI. J. Am. Chem. Soc. 2004;126:3018–3019. doi: 10.1021/ja039106v. [DOI] [PubMed] [Google Scholar]
- (37).Siegbahn PEM, Pelmenschikov V. J. Am. Chem. Soc. 2006;128:7466–7475. doi: 10.1021/ja053665f. [DOI] [PubMed] [Google Scholar]
- (38).Kaufman MJ, Gronert S, Streitwieser A. J. Am. Chem. Soc. 1988;110:2829–2835. [Google Scholar]
- (39).Fulton JR, Sklenak S, Bouwkamp MW, Bergman RG. J. Am. Chem. Soc. 2002;124:4722–4737. doi: 10.1021/ja011876o. [DOI] [PubMed] [Google Scholar]
- (40).Espenson JH. Chemical Kinetics and Reaction Mechanisms. McGraw-Hill; New York: 1981. [Google Scholar]
- (41).Jaffe HH. Chem. Rev. 1953;53:191–261. [Google Scholar]
- (42).Lowry TH, Richardson KS. Mechanism and Theory in Organic Chemistry. 2nd ed Harper and Row; New York: 1981. [Google Scholar]
- (43).Bordwell FG. Acc. Chem. Res. 1988;21:456–463. [Google Scholar]
- (44).Coetzee JF, Padmanabhan GR. J. Am. Chem. Soc. 1965;87:5005–5010. [Google Scholar]
- (45).Edidin RT, Sullivan JM, Norton JR. J. Am. Chem. Soc. 1987;109:3945–3953. [Google Scholar]
- (46).Kolthoff IM, Chantooni MK, Bhowmik S. J. Am. Chem. Soc. 1968;90:23–28. [Google Scholar]
- (47).Rived F, RosÈs M, Bosch E. Anal. Chim. Acta. 1998;374:309–324. [Google Scholar]
- (48).Streitwieser A, Wang DZ, Stratakis M, Facchetti A, Gareyev R, Abbotto A, Krom JA, Kilway KV. Can. J. Chem. 1998;76:765–769. [Google Scholar]
- (49).Streitwieser A. Acc. Chem. Res. 1984;17:353–357. [Google Scholar]
- (50).Facchetti A, Streitwieser A. J. Org. Chem. 1999;64:2281–2286. [Google Scholar]
- (51).Rybak-Akimova EV, Otton W, Deardorf P, Roesner R, Busch DH. Inorg. Chem. 1997;36:2746–2753. doi: 10.1021/ic961371c. [DOI] [PubMed] [Google Scholar]
- (52).Kryatov SV, Rybak-Akimova EV, Schindler S. Chem. Rev. 2005;105:2175–2226. doi: 10.1021/cr030709z. [DOI] [PubMed] [Google Scholar]
- (53).Solomon EI. Inorg. Chem. 2001;40:3656–3669. doi: 10.1021/ic010348a. [DOI] [PubMed] [Google Scholar]
- (54).Davydov R, Matsui T, Fujii H, Ikeda-Saito M, Hoffman BM. J. Am. Chem. Soc. 2003;125:16208–16209. doi: 10.1021/ja038923s. [DOI] [PubMed] [Google Scholar]
- (55).Streitwieser A, Kim YJ. J. Am. Chem. Soc. 2000;122:11783–11786. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.