The Fundamental Role of Flexibility on the Strength of Molecular Binding

Abstract

Non-covalent molecular association underlies a diverse set of biologically and technologically relevant phenomena, including the action of drugs on their biomolecular targets and self- and supra-molecular assembly processes. Computer models employed to model binding frequently use interaction potentials with atomistic detail while neglecting the thermal molecular motions of the binding species. However, errors introduced by this simplification and, more broadly, the thermodynamic consequences of molecular flexibility on binding, are little understood. Here, we isolate the fundamental relationship of molecular flexibility to binding thermodynamics via simulations of simplified molecules with a wide range of flexibilities but the same interaction potential. Disregarding molecular motion is found to generate large errors in binding entropy, enthalpy and free energy, even for molecules that are nearly rigid. Indeed, small decreases in rigidity markedly reduce affinity for highly rigid molecules. Remarkably, precisely the opposite occurs for more flexible molecules, for which increasing flexibility leads to stronger binding affinity. We also find that differences in flexibility suffice to generate binding specificity: for example, a planar surface selectively binds rigid over flexible molecules. Intriguingly, varying molecular flexibility while keeping interaction potentials constant leads to near-linear enthalpy-entropy compensation over a wide range of flexibilities, with the unexpected twist that increasing flexibility produces opposite changes in entropy and enthalpy for molecules in the flexible versus the rigid regime. Molecular flexibility is thus a crucial determinant of binding affinity and specificity and variations in flexibility can lead to strong yet non-intuitive consequences.

Introduction

Reversible molecular association, via the formation of thermally reversible noncovalent bonds, drives much of the highly complex behaviour in soft matter systems, from biomolecular recognition (enzyme/substrate, antibody/antigen, cell signalling) to self- and supra-molecular assembly. The ability to more accurately predict the strength of molecular association of a given pair of molecules would greatly facilitate advances in medicine, biotechnology, and materials science.

The pharmaceutical and biotechnology industries have invested heavily in ‘docking’-based computational approaches,^1–9 in which molecular mechanical force fields are used to evaluate the binding affinity of a given pairing of molecules. Docking calculations are widely employed to inform the drug discovery process, an approach referred to as structure-based drug design. However, docking approaches are still not consistently effective in predicting binding strength.^10–13 Clearly, their reliability is limited in part by force field accuracy, and a great deal of effort has, appropriately, been devoted to evaluating and improving the effectiveness of force fields, including adjustments to fit empirical data and the development of fully ‘knowledge-based’ force fields. The present article, however, addresses another issue: the role of molecular flexibility as a determinant of affinity.

Early docking approaches embodied the classic Fischer lock-and-key model of molecular association, as they treated molecules as rigid and sought highly shape-complementary bound conformations. Current methods go beyond the original lock-and-key picture by allowing the molecules to change shape and thus adapt to each other through changes in their rotatable torsions. This technique accounts for one aspect of molecular flexibility, as it can identify optimized rigid bound structures that would otherwise be sterically inaccessible.^{8, 14–18} However, it still does not address the full thermodynamic consequences of molecular flexibility; these are typically either neglected or treated through strongly simplifying approximations. One reason for this state of affairs is, presumably, the computational challenge associated with accounting for flexibility; but another is the paucity of basic information regarding how strongly and in what manner molecular flexibility influences binding.

Here, we look beyond the basic notion of induced fit, applying molecular dynamics simulations to systematically investigate how pure variations in molecular flexibility affect the thermodynamics of binding. A central finding is that molecular flexibility can strongly control affinity through influences on both entropy and energy, and that neglecting these consequences can be a major a source of error in silico. Thus, in stark contrast to the early lock-and-key model, modern insights based on statistical mechanics imply that molecules must be understood as inherently dynamic entities whose conformational fluctuations can greatly influence molecular binding.

Simulation Approach

Interacting entities were designed as generic representations, not of entire molecules, but rather of fragments of interacting molecules whose intimate contact contributes significantly to intermolecular cohesion. For highly structured molecules, interacting fragments possess complimentary shape-matching structures, in which favourable intermolecular contacts are realized by bringing together the fragments with the correct orientation. The binding of a given pair of molecules is ultimately attributable to the association of one or more of such intermolecular fragment pairs. We have devised a minimal model of chain fragments, composed of linear chains of coarse-grained beads, whose binding behaviour is consistent with this fundamental picture of binding. Minimum energy chain structures were chosen to be fully extended, a simple and arbitrary choice of chain architecture that ensures shape-matching between partners. The degree of chain flexibility was controlled by applying a harmonic bending energy potential, U = k_bend (θ−θ_o)², to each angle, θ, formed by consecutive triplets of beads along the chain. The extended configuration was set as the energy minimized structure by setting θ_o = 180°.

Fundamental insight into the role of flexibility on binding must be independent of specific choice of potential function and molecular architecture. For this reason, we have chosen to make non-bonded interactions between chains independent of flexibility and as generic as possible. Our intent here is not to model a specific binding complex, but rather to explore in a fundamental way the effect of chain flexibility on binding strength. Thus, non-bonded bead-bead interactions were provided by Lennard-Jones potentials and no distinction was made between the individual beads based upon either position along the chain or overall chain flexibility. As intermolecular interaction potentials are equivalent for all chain pairs, differences in binding strength for various chain pairs can be interpreted unambiguously as arising from differences in flexibility.

Our basic simulation procedure involves placing a pair of model chains into a periodic simulation box, such that repeated encounters occur with time. Binding state was periodically evaluated based on the number of intermolecular contacts present in a given instantaneous configuration, as described in Computational Methods and Electronic Supplementary Information (ESI).

We assume that our system is ergodic, implying that the association constant, K_a, can be calculated as K_a = V t_bound /t²_unbound, where t_bound and t_unbound are the fraction of simulation time that the system spends in the bound and unbound state, respectively. The free energy of binding can be determined as ΔG = −RTlnK_a; the enthalpy of binding, ΔH, as the difference of the average enthalpy of the bound and unbound state; and the entropy of binding as ΔS = (ΔG − ΔH)/T. The simulation procedure was repeated for numerous chain pairs for a range of flexibility values spanning three orders of magnitude.

All units presented are reduced by characteristic units of length (1 nm) and energy (k_BT₂₉₈). Bending energy coefficients considered span the range 0.3 < k_bend < 1000. Non-bonded bead-bead interactions were parameterized with Lennard-Jones parameters σ = 0.85 and ε = 1.0, independent of chain flexibility. Chain lengths of N = 20, 25, 30, 35 and 40 were used. Simulations of the adsorption of these chain-like molecules to a rigid, planar wall treated the bead-wall interactions as LJ potentials, with σ = 0.75 and ε = 1.15.

Computational Methods

All simulation runs were performed using the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS),¹⁹ available for download at http://lamps.sandia.gov. Simulations were run for 7 × 10⁸ molecular dynamics steps, with the binding state evaluated every 4000 steps based on the number of close contacts between beads on opposing chains. In particular, the bound state was structurally defined as a configuration with at least 10 inter-chain bead-bead contacts, each with a separation of less than 1.6 length units. Additional information on the determination of binding status and the number of binding transitions observed is provided in Electronic Supplementary Information (ESI).

Simulations were performed in the canonical ensemble using a Langevin thermostat with a coefficient of viscous drag, ζ, equal to 1.0. The simulation algorithm entails solving the Langevin equation of motion for each bead in the system,

$$m_i{\ddot{r}}_{ij}=-{\nabla }_j{U}_i-\zeta {\stackrel{.}{r}}_{ij}+f_{ij}^{\mathit{rand}}$$ (1)

where i is the bead index, j is the dimensional index, and U_i is the sum of the configuration–dependent bead-bead interactions described above. The second and third terms provide implicit treatment of solvent through viscous drag and random force, respectively. The random force depends on temperature and viscous coefficient, ζ, through the fluctuation-dissipation theorem,

$$\langle f_i(t)·f_j(t^{\prime })\rangle ={\delta }_{ij}6k_{B}T\zeta \delta (t-t^{\prime })$$ (2)

where t is time and δ is the Kronecker delta. A dimensionless timestep of 0.005 was used.

Results and Discussion

Bindng Affinity as a Function of Flexibility

Representative snapshots of associating chain pairs of various flexibilities are shown in Figure 1. The bound structures illustrate the broad flexibility range of model chains studied, from collapsed configurations typical of polymers (k_bend = 0.3, 5) to highly ordered structures displaying little variation from the minimum energy elongated structure (k_bend = 274, 1000). The nature of binding is seen to depend on flexibility. For the most rigid chain pair, k_bend = 1000, each bead on a given chain is in close contact with its corresponding bead on the partner chain. For chain pairs with more flexibility, i.e. k_bend = 274 and k_bend = 5, individual chain structures become notably decoupled from their partners. For the most flexible chain pairs (k_bend = 0.3, 5), individual beads make multiple contacts with beads on the partnering chain.

Fig. 1.

Snapshots of Associating Chain Pairs of Length N = 40.

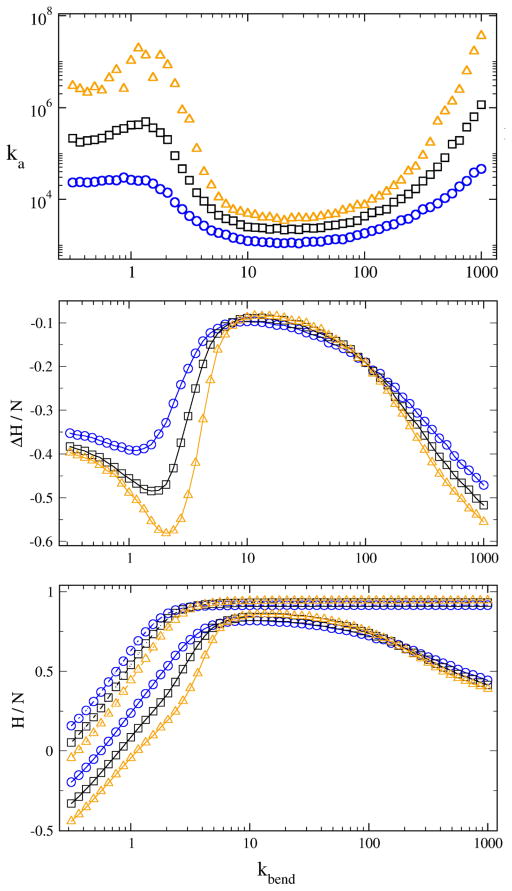
In Figure 2a, the association constant, K_a, is plotted as a function of k_bend for chains of length N = 20, 25, and 30. This computed binding affinity displays remarkably strong dependence on flexibility, with measured K_a values spanning orders of magnitude. The form of the flexibility dependence of binding is also remarkable, as binding is found to be particularly strong for both highly flexible chains and highly rigid chains. Consistent with intuition, binding is invariably stronger for longer chain fragments, for which additional inter-chain contacts are available.

Fig. 2.

Dependence of binding constant and enthalpy on chain flexibility. Flexibility decreases with k_bend (see text). Chain pairs of three lengths are shown: N = 20 (circles), N = 25 (squares), and N = 30 (triangles). (A) Association constant vs. k_bend; (B) Change in enthalpy on binding per bead, ΔH/N, vs. k_bend; (C) Enthalpy per bead, H/N, of unbound (upper curves) and bound (lower curves) state vs. k_bend.

We begin by discussing the physical basis for enhanced binding of highly rigid chains. Consider the difference between binding of a perfectly rigid pair of molecules and a pair of molecules with nonzero, but still minimal, flexibility. For chains with nonzero flexibility, conformational entropy, expressed as fluctuations of individual chain configurations, decouples individual bead-bead contacts in the bound state and thus increases the enthalpy of bound structures.²⁰ Thus, a balance exists between a gain of entropy and loss of favourable enthalpy of binding. As the rigid limit of molecular flexibility is approached, enthalpy can be expected to play an increasingly important role in binding, with bound structures characterized by progressively lower enthalpy. In Figure 2b, the per bead change in enthalpy of binding, ΔH, is plotted as a function of k_bend. In Figure 2c, the components of ΔH, i.e. enthalpy of the bound state (solid lines) and unbound state (dashed lines) are plotted as a function of k_bend. In the rigid regime (20 < k_bend < 1000), ΔH is indeed seen to decrease with increasing rigidity due to decrease in the enthalpy of the bound state (Figure 2c, solid lines).

Given the corresponding increase in association constant with k_bend in the rigid regime (Figure 2a), our results confirm that increasing flexibility in the rigid regime leads to decreasing binding affinity, as favorable enthalpy is sacrificed to accommodate a higher entropy bound state. The decrease in binding enthalpy and corresponding increase in binding affinity of highly rigid structures is consistent with experimental reports of exceptionally strong binding of ligands to unusually high rigidity molecules, such as the cucurbituril²¹ class of molecules. While it is somewhat intuitive that increasing flexibility should reduce association strength, it was surprising to note the degree to which the association constant of rigid molecules is sensitive to small changes in flexibility. In particular, Figure 2a suggests that employing a fully rigid model, even for molecules with little flexibility, can result in large errors in predicted affinity.

More unexpected is the observation that the affinity does not continue to decrease as flexibility increases. Rather, increasing flexibility in the flexible regime (k_bend < 20) leads to increasing binding affinity, to the point that the binding affinities attained by flexible chain pairs are comparable to those for highly rigid chain pairs (Figure 2a). In explaining this reversal of the trend of binding strength with flexibility, we begin by pointing out that, regardless of flexibility regime, individual pairwise contacts must continue to become progressively disfavoured with increasing flexibility. How then can the number of enthalpic contacts actually increase with flexibility? As chains become sufficiently flexible, bound structures become more compact, eventually to the extent that individual beads can make multiple contacts with beads on the partner chain, effectively discounting the entropic price per enthalpic contact (Figure 1). In Figure 2c, it can be seen that the region k_bend < 10 is characterized by a sharp decrease in the bound state enthalpy.

For the most flexible chains considered, i.e. k_bend < 3, favourable intra-chain interactions become accessible and the enthalpy of unbound chains (Fig. 2c, dashed lines) drops sharply due to single-chain collapse. The favourable enthalpy of the collapsed unbound state somewhat offsets the favourable enthalpy of the bound state, such that ΔH actually becomes slightly less favourable and plateaus for k_bend < 2 (Fig. 2b).

The present results suggest that applying the rigid approximation in docking simulations may lead to large errors in binding affinity predictions, even for highly structured biomolecules. The main rationale for treating proteins and other structured biomolecules as being rigid is their low flexibility in comparison to other polymeric molecules. However, we find that the dependence of K_a on flexibility is particularly strong in the rigid regime, so that even a small amount of flexibility can have considerable impact on binding affinity. This effect is not expected to be dependent upon any specific molecular structure or sequence.

The richness of the behaviour observed here for even a simple model system may pose a challenge to docking predictions. On the other hand, a fundamental appreciation of the role of flexibility in molecular interactions may provide a basis to adjust for errors in protein-ligand modelling studies and could lead to approximate methods of accounting for flexibility that are computationally tractable. Insight regarding the consequences of flexibility for binding are also highly relevant for our understanding of self-assembly processes in Nature and may further suggest novel approaches to manipulate soft matter systems. For example, there is evidence that chain flexibility effects on association are important for supra-molecular assembly and molecular switching processes for both synthetic and biological systems. Zhang et al.²² have shown that cation valency affects both chain flexibility and the structure and size of transient domains of polyelectrolytes in solution. Flexibility is also likely to play a role in nanoparticle/molecule interactions, where chain flexibility may affect both the number and type of molecules that attach themselves to nanoparticles, which in turn will affect important nanoparticle behaviours, such as aggregation and transport.

Antibody maturation provides a fascinating example of a process that is intimately related to changes in molecular flexibility. It has been shown that Nature employs a strategy of gradual progression from flexible non-specific binding to rigid specific binding during antibody maturation,^23–25 exploiting the full range of flexibility-dependent binding behaviour elucidated in our simulations.

The results presented above concern chain pairs with matched flexibility values. In Electronic Supplemental Information, we present results from similar simulations in which chain flexibility is varied independently for each member of the chain pair. The central observation is that a chain prefers to bind another chain of similar flexibility; i.e., rigid prefers rigid and flexible prefers flexible. This observation may have implications for the optimization of drug-like ligands targeting protein binding sites having various degrees of flexibility.

Enthalpy-Entropy Compensation

Recent studies of molecular association in diverse ligand-receptor pairs have indicated that changes in molecular structure that favour stronger enthalpic association tend to be counterbalanced by unfavourable changes in entropy.^26–32 Enthalpy-entropy compensation has also been observed in many molecular association and self-assembly processes,^33–40 including protein-protein and protein-nanoparticle associative binding.^{29, 41} While compensation is nearly ubiquitous in molecular binding processes, its molecular origin has not been elucidated. It has been suggested that compensation arises due to specific chemical interactions, most notably hydrogen bonding.⁴² It has also been suggested that compensation is independent of specific molecules, but rather arises due to the role of solvent,⁴³ or may simply arise due to measurement error.^{44, 45} We now consider whether the previously discussed trends of enthalpy and entropy of binding in our simulations constitute an expression of enthalpy-entropy compensation, which would suggest that molecular flexibility, a characteristic common in varying degrees to all molecules, may play a central role in this phenomenon.

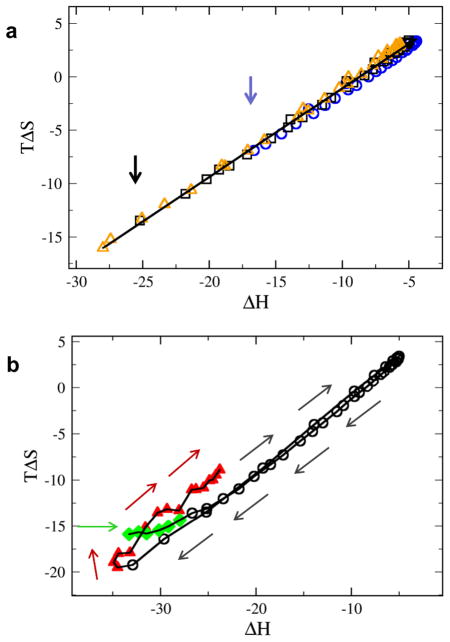
In Figure 3a, we plot TΔS vs. ΔH from simulations for chains of length N = 25 (circles), N = 30 (squares), and N = 35 (triangles) and flexibility values from the range 3 < k_bend < 1000. Our simulation model does indeed display compensation, as manifested by the degree to which the data is fitted by linear regression. The slope of the compensation line, known as the compensation temperature,⁴³ is equal to 0.84 in dimensionless temperature units. Chain pairs of progressively greater length conform to the same compensation line, with points along the compensation line simply extending further along the low enthalpy region for longer chains. The most favourable enthalpy values attained for N = 25 and N = 30 are indicated by coloured vertical arrows in Fig. 3a.

Fig. 3.

Enthalpy-entropy compensation plot. (A) TΔS vs. ΔH plot for N=25 (blue circles); N=30 (black squares); and N=35 (triangles). For each N, flexibility ranges from 3 < k_bend < 1000. (B) TΔS vs. ΔH for N=30 and 0.3 < k_bend < 5000. The progression of values with increasing flexibility is illustrated by arrows. Values deviate from the compensation line for molecular pairs with high rigidity (k_bend > 1000, diamonds) and high flexibility (k_bend < 3, triangles).

Further insight can be obtained by examining the progression of [ΔS,ΔH] points as a function of increasing flexibility, as plotted in Figure 3b for chains of length N = 30. The points on the compensation plot follow a well-behaved and informative trajectory as function of flexibility, as indicated by the sequence of arrows in Figure 3b. Regions of very high rigidity (k_bend > 1000, diamonds) and high flexibility (k_bend < 3, triangles) are distinguished by symbol type from the majority of the data (3 < k_bend < 1000, circles). In the rigid regime, binding is characterized by nearly perfect chain alignment, with bound chains translating and rotating in unison (see Figure 1, k_bend = 1000). Consequently, the high rigidity data points of the compensation plot reside within the region of favourable enthalpy and unfavourable entropy. Increasing flexibility of rigid chains results in an increasingly favourable entropy of binding and a decreasingly favourable enthalpy of binding, a trend that continues well into the region of intermediate flexibility. It should be pointed out that increased flexibility will increase the entropy of both the bound and unbound states and it is therefore not obvious that additional flexibility should have a net favourable effect on binding entropy. Not only is an increase in binding entropy observed with increased flexibility, but this increase is offset by a loss in binding enthalpy and the compensation occurs in a linear fashion for all but the most rigid chains. Our model suggests that such compensation is a fundamental characteristic of structured molecules with finite flexibility.

Maximum values of TΔS and ΔH are attained at k_bend = 11.55, corresponding roughly to the flexibility at which bound structures begin to collapse, as indicated by the drop in bound state enthalpy for k_bend < 11.55 (Figure 2c). In this regime, additional flexibility enables the formation of bound configurations in which individual beads attain multivalent contacts with beads on the partner chain, leading to progressively lower bound-state enthalpy and a corresponding loss of entropy on binding. Remarkably, although the physical origin of entropy-enthalpy compensation in this regime is entirely different from that in the rigid regime (above), the trajectory of the entropy-enthalpy points (Figure 3b) nonetheless exactly reverses the trajectory of the entropy-driven ascent along the compensation line in the rigid regime.

Finally, for the most flexible chain pairs, k_bend < 3, (Fig. 3b, triangles), additional flexibility once again leads to a more favourable entropy of binding. In this regime, bound structures are sufficiently collapsed that bead-bead pairings become increasingly decoupled. Individual beads on one chain can thus pair indiscriminately and dynamically with beads on the other chain. In this way, additional flexibility allows chains to express an increasing number of chain configurations in the bound state. While the resulting increase in favourable entropy of binding is offset by a corresponding increase in binding enthalpy, the compensation behaviour does not precisely retrace the trajectory along the compensation line. Rather, the mutual accommodation attainable by a pair of highly flexible chains is associated with more favourable ΔS for a given ΔH value (Figure 3b, triangles) than was found in other regimes.

Compensation, by definition, mitigates the variation in binding strength observed per unit change in binding enthalpy. Nonetheless, we report large variations in binding affinity for our system. These results illustrate that a linear correlation of enthalpy and entropy is zero-sum in terms of free energy only when the compensation temperature is unity (in reduced units). A compensation temperature less than unity, as observed here, means that enthalpy changes are incompletely offset by entropy changes, so that low-enthalpy bound structures are able to produce strong binding. The compensation temperature is likely a function of, among other factors, the degree to which binding partners are shape-matched, a topic we will explore in a future publication. It is also intriguing that deviations from the linear entropy-enthalpy correlation are observed for both highly rigid (diamonds) and highly flexible (triangles) chains, and that these deviations are all above the line and hence in the direction of greater affinity.

Flexibility and Self Assembly

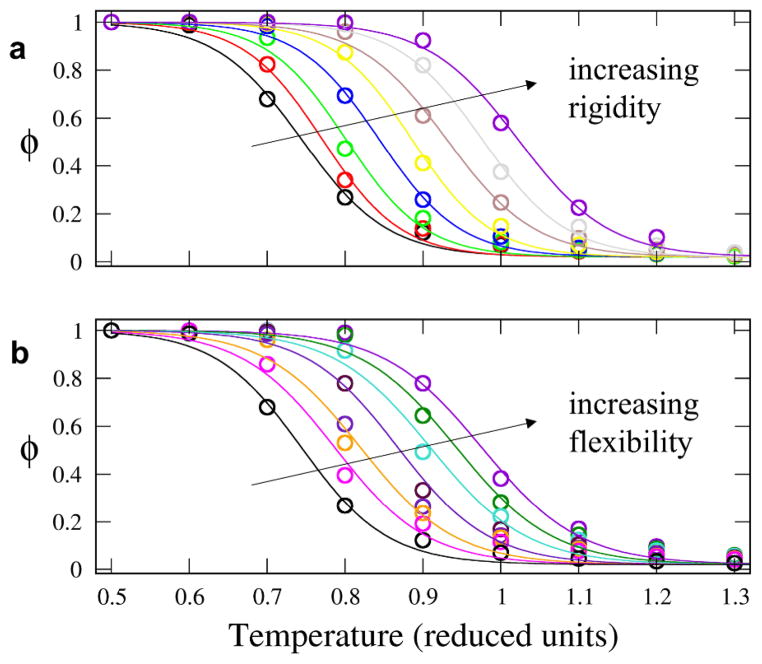
While we have thus far emphasized binding affinity predictions, it is interesting to consider how flexibility might affect the self-assembly behaviour of systems of associating polymers. In this context, it is useful to consider association strength in terms of the transition temperature between the assembled and disassembled states, i.e bound vs. unbound states. In Figure 4, the temperature dependence of the order parameter, φ = t_bound / t_total, is plotted for a number of k_bend values for N=20 chain pairs. The temperature dependence of φ is sigmoidal, with the inflexion point indicating the transition temperature. The transition temperature can be seen to depend on k_bend, with opposing trends observed depending on the flexibility regime: for rigid molecules, increasing rigidity increases the transition temperature, whereas for flexible molecules, increasing flexibility increases the transition temperature. Such behaviour suggests, for example, that networks of reversibly associated polymers can be tailored to undergo controlled switching of network properties by inducing changes in chain flexibility. Again, the consequences of a change in flexibility depend sharply upon whether the system is in the flexible versus rigid regime.

Fig. 4.

Order parameter, φ, vs. temperature. Open circles are simulation results and solid lines are sigmoidal fits to data. Trend in k_bend flexibility indicated by arrow direction. Data is presented separately for two regimes of k_bend: (A) “rigid regime”: k_bend = 17, 31, 56, 100, 177, 316, 562, and1000; (B) “flexible regime”: k_bend = 2.0, 3.0, 3.6, 4.2, 4.5, 5.3, and 17.8.

Flexibility and Adsorption to a Rigid Surface

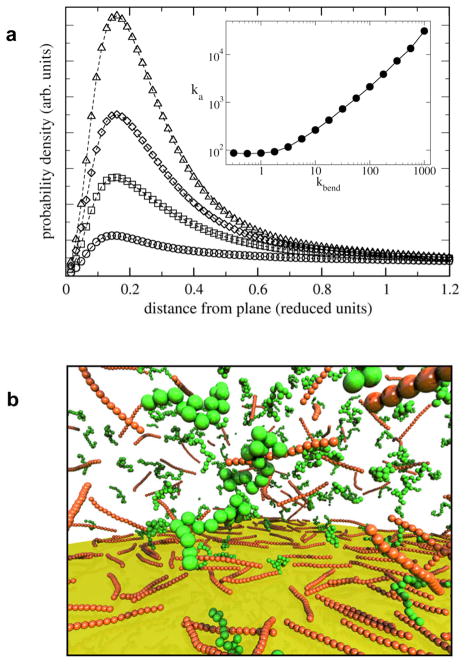
As touched on above and detailed in Electronic Supplementary Information (ESI), we find that rigid chains preferentially bind other rigid chains over flexible ones. This observation suggests that the flexibility of a molecule can also influence its adsorption to a rigid surface, or wall. We investigated this with simulations of chain-wall interactions as a function of chain flexibility, with a separate simulation performed for various k_bend values. As shown in Fig 4a (inset), K_a for chain-wall binding is greatly enhanced for rigid chains. In addition, there is no strong-binding regime at low flexibility, as the rigid wall is unable to provide the kind of mutual configurational accommodations afforded by a flexible partnering chain. This result suggests that flat, rigid surfaces might preferentially select the more rigid chains from a mixture of chains of varying flexibility. To explore this possibility, a simulation was performed in which 1500 chains, with k_bend values of 10, 50, 100, 200, were simultaneously placed into a simulation box, which was bounded on one face by a flat rigid wall. The probability distribution of each type of chain as a function of distance from the attractive wall clearly shows that the wall separates extremely rigid chains from highly flexible ones (Figure 5a). This separation is visualized in a snapshot from a simulation of a mixture of chains representing flexible and rigid extremes (k_bend = 0.3 and k_bend = 5000, respectively), in which only rigid chains are seen to bind to the wall (Figure 5b).

Fig. 5.

(A) (insert) K_a as a function of k_bend; (A) Bead probability density as a function of distance from the wall for k_bend = 10 (circles); k_bend = 50 (squares); k_bend = 100 (diamonds); and k_bend = 200 (triangles). (B) Snapshot of simulation of mixture of rigid and flexible chains, showing surface selection of rigid chains.

The selection of straight rigid chains at the surface brings to mind the case of nanotubes, which may undergo a similar preferential adhesion to flat surfaces. It would be interesting to consider whether the dynamics of more flexible surfaces, such as lipid membranes with undulations and dynamic protuberances, affect their binding specificities.

Flexibility Studies: Precedence in Polymer Physics and Relevance to Biomolecules

To our knowledge, the work presented in this manuscript represents the first systematic demonstration of flexibility as a fundamental determinant of intermolecular interaction strength, one that can dramatically impact the binding of a generic pair of molecules. This study was inspired in large part bythe findings of polymer physics and its statistical mechanical underpinnings. In particular, as further considered below, it is well known that phase transitions in polymer systems involve a competition between the configurational entropy of the polymer and enthalpic interactions favouring the ordering process. Consequently, chain flexibility can be expected to affect many thermodynamic transition processes involving polymeric materials in a manner consistent with our observations for chain binding. However, while appreciation for the significance of configurational entropy to polymer behaviour dates to the origins of polymer science itself,^{46, 47} its relevance to a broader range of molecules, in particular to biomolecules, has not been generally accepted.

Biomolecules are distinguished from typical synthetic polymers by their ability to fold into regular three-dimensional structures, often possessing discrete, saturable binding sites. While the ordering of biomolecules reduces configurational entropy in comparison to flexible polymers, internal degrees of freedom are not entirely eliminated, as evidenced by crystallographic temperature factors and NMR order parameters. Furthermore, some proteins possess substantial segments that are disordered under physiological conditions^48–52. Thus, a key question for relatively rigid biomolecules is to what extent the remaining flexibility can affect binding affinity^53–60. Our results suggest a conclusion quite contrary to current consensus: that changes in configurational entropy can strongly affect the binding affinities of even highly rigid molecules.

Although the model molecules studied here lack the complex three dimensional structures typical of biomolecules, they share an essential characteristic of structured biomolecules, namely, the existence of a dominant minimum-energy structure, about which fluctuations occur in proportion to molecular flexibility. The elongated chain structure considered here simply represents an arbitrary choice of minimum energy structure and as such should have little qualitative bearing on the present findings. Nonetheless, it will be great interest to study how the present results map to molecules with more complex architectures.

Finally, it is worth putting the present results into the context of relevant prior findings relating phase behaviour in polymer systems to chain flexibility. In particular, it has long been known that chain stiffness increases the polymer adsorption transition due to a corresponding reduction in the entropic cost of adsorption.^61–67 Similarly, increasing chain stiffness tends to increase the melting temperature of crystalline domains of polymers.⁶⁸ In some cases, increases in melting temperature have been reported to exceed the theta temperature of the polymer, where the second osmotic virial coefficient vanishes, such that the collapse transition becomes preempted by crystallization.⁶⁹ Binder and coworkers⁷⁰ have also found that the theta temperature can itself be shifted downward appreciably with increasing stiffness. Furthermore, the theta temperature shows a non-monotonic variation with chain stiffness in a fashion somewhat reminiscent of our work on molecular binding between chains.

Although these previous studies have not considered the entropy-enthalpy compensation revealed in our work, previous work on the self-assembly of micelles from polymeric surfactant species⁷¹ has demonstrated that increasing chain stiffness leads to both a general upward shift of the micellization temperature, associated with entropy-enthalpy compensation. Compensation has also been derived using analytic theories based on statistical mechanical models for solutions of self-assembling telechelic molecules⁷² and for systems undergoing crowding-induced self-assembly.⁷³ Based on such prior results and the new ones presented here, we expect the entropy-enthalpy compensation with variation of chain stiffness to be a widely occurring phenomenon in polymer binding and phase transition phenomena, with relevance as well to general molecular association.

Conclusions

We have employed a simple in silico model to isolate and study the role of molecular flexibility in noncovalent binding. It is perhaps unsurprising that the binding constant is found to depend strongly upon flexibility. More unexpected, however, is the identification of two regimes in which flexibility plays opposite roles: in the rigid regime, increased flexibility leads to lower affinity; in the flexible regime, increased flexibility leads to higher affinity. The latter phenomenon traces to the ability of highly flexible chains to collapse into bound structures with many energetically favourable interactions. The sensitivity of the binding constant to flexibility for chains well within the rigid regime—where simple lock-and-key binding might be expected, also is striking. We find, furthermore, that molecular flexibility can, on its own, provide a basis for specific binding and hence molecular recognition. Thus, molecules of like flexibility were found to bind preferentially to each other, and a rigid surface was found to selectively adsorb rigid molecules over flexible ones, despite identical an identical interaction potential.

Intriguingly clear-cut enthalpy-entropy compensation was observed over the full range of flexibilities considered, a remarkable finding, given the numerous disparate binding regimes observed for different regions of flexibility.

In summary, the present results demonstrate that an improved understanding of molecular binding demands a fuller consideration of the truly dynamic nature of molecular associations, in particular the manner in which molecular flexibility contributes to binding strength and specificity. Molecular flexibility will likely provide an essential variable for engineering molecular recognition systems and self-assembly processes for diverse technological and biological applications, and can play a key role in the ubiquitous and important phenomenon of enthalpy-entropy compensation.