Ecological inference

Abstract

Ecological inference is the process of drawing conclusions about individual-level behavior from aggregate-level data. Recent advances involve the combination of statistical and deterministic means to produce such inferences.

Ecological inference is the process of using aggregate (historically called “ecological”) data to draw conclusions about individual-level behavior when no individual-level data are available. The fundamental difficulty with such inferences is that many different possible relationships at the individual level can generate the same observation at the aggregate level. For example, there are a very large number of ways in which electoral support for a political candidate can break down among individual voters and still produce the same aggregate level of support. In the absence of individual-level measurement (for example in the form of surveys), such information needs to be inferred.

The ecological inference problem has been among the most persistent statistical problems in the social sciences. The need to draw microlevel conclusions from macrolevel data is faced by researchers in political science as well as in epidemiology, geography, sociology, economics, and history, among others. In a study of the voting behavior of newly enfranchised women in Oregon, almost eight decades ago, it was noted that “even though the method of voting makes it impossible to count women’s votes, one wonders if there is not some indirect method of solving the problem” (1). The proposed “indirect method” involved correlating aggregates: by observing that local voting districts (“precincts”) with higher proportions of women voters revealed higher proportions of negative votes on certain referenda, it could be reasoned that women, apparently, were casting votes against the referendum at a higher rate than men.

However, this conclusion drawn from aggregate quantities is valid only if the different ratios of men to women across different precincts are not in themselves correlated with their voting behavior. Correlating aggregates results in an “ecological fallacy” if men in heavily female precincts are more likely to vote against the referendum than they are in precincts with higher male representation. Indeed, one of the most influential contributions to the ecological-inference literature was the demonstration that true individual-level relationships often were the inverse of aggregate-level relationships (2). In the absence of data measuring voting behavior at the individual level, there was no way of knowing deterministically—that is, with certainty—how behavior at the ballot box broke down by gender.

Indeed, there can be no deterministic solution to the ecological inference problem: individual-level information is irrecoverably lost in the process of aggregation. This impossibility has led a number of researchers to seek out a statistical solution instead. Because microlevel information (for example, about the voting behavior of men and women in electoral precincts) could not be measured from aggregate data, attempts were made to estimate such information. Quite frequently, however, statistically derived results were unreliable, often falling outside of the range of what was even possible—for example estimating that more than 100% of a particular demographic group voted for a particular candidate. The most recent advance in ecological inference is to be found, not in a pure statistical, but in a deterministic–statistical method. This type of approach combines deterministic information—information that is known with certainty—with a method of statistical likelihood estimation.

Deterministic Information

As a running example, consider an electoral precinct with a population of black and white voters. Available to the researcher are both the precinct’s racial composition and precinct-level aggregate turnout rates in elections. Given the secret nature of voting, however, an unobservable quantity of interest is turnout among these racial groups. The question of how voter participation breaks down by race is identical to our initial question of how opposition to a referendum breaks down by gender.

Formally, for a specific precinct i with a total voting population N_i, aggregate numbers of blacks X_i and whites 1 − X_i are observed, as are the proportions of voting-age individuals who participate in the election T_i and of those who abstain 1 − T_i (see table in Box) (3). Not known are the numbers of black and white participating voters, respectively denoted by β_i^b and β_i^w.

Race of voting-age	Voting Decision
person	Vote	No vote
Black	βib	1 − βib	Xi
White	βiw	1 − βiw	1 − Xi
	Ti	1 − Ti

Notation for Precinct i. Ecological inference is to estimate the quantities of interest, β_i^b (the fraction of blacks who vote) and β_i^w (the fraction of whites who vote) from the aggregate variables X_i (the fraction of voting-age people who are black), T_i (the fraction of people who vote), and N_i (the known number of voting-age people).

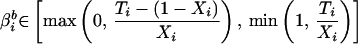1

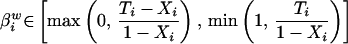2

Formal expression of the deterministic bounds on voter turnout among blacks, β_i^b (Eq. 1), and whites β_i^w (Eq. 2). T_i is voter turnout in Precinct i. X_i is the proportion of black voters among Precinct i’s voting-age population, with (1 − X_i) representing the complement white voters.

Of course, there are extreme instances where aggregate-level information provides a certain solution: if a precinct’s population is 100% white or black (if X_i = 0 or X_i = 1.0), the ratio of racial composition collapses into its extreme and a deterministic point estimate can be produced. While this case is statistically uninteresting, it is instructive. For even in more realistic instances where both racial groups are represented, deterministic information can still be derived. In this case, we can no longer derive unique individual-level point estimates but can derive ranges within which such values necessarily will reside.

This approach is known as the “method of bounds” (4). It tells us that there is both a minimum and a maximum possible value for the number of participating black voters. At a minimum, this value can be no lower than the total number of voters participating in the election, minus the number of whites in the voting-age population. If this number is smaller than zero (that is, if the number of voting-age whites is greater than the total number of participating voters), the minimum possible number of blacks voting in the population is zero. At a maximum, the number of participating black voters in the population can be no greater than either the number of voting-age blacks, or the total number of voters, whichever is smaller.

The level of deterministic information that can be derived for each quantity will vary by instance, as the extent of the restriction is a function of the data. In the type of example discussed here, the width of the bound typically is reduced to less than half the [0, 1] (or 0–100%) range. There is nothing questionable about results provided by the method of bounds, although it may at times be too unrestrictive to be of substantive value for the researcher. Controversy enters the scene when a statistical solution is introduced, either as an alternative to the method of bounds, or as a procedure to reduce its range further.

Statistical Solutions

A fundamental feature of any inference method is that assumptions are introduced. Researchers pursuing a statistical approach to ecological inference, consequently, need to address three questions.

First, and most obviously, are the assumptions correct for the given data? Second, what happens to the estimation procedure when the assumptions are incorrect, given its particular substantive application? Third, will the researcher know if the assumptions are incorrect? The first question concerns the specification of assumptions. The second concerns the estimation procedure’s robustness to a mis-specification of assumptions. And the third concerns the procedure’s diagnostic capacity of identifying a mis-specification of assumptions.

The original study of voting behavior among women in Oregon represents an early, crude, attempt at a statistical solution to the ecological inference problem. Correlating aggregates of precincts’ gender composition and support for a particular referendum yielded a point estimate for women’s opposition to a referendum. Yet this conclusion was entirely dependent on the assumption that men’s and women’s attitudes toward the referendum were not themselves affected by the relevant precinct’s gender composition. Furthermore, there were no diagnostic features in the estimation procedure that would indicate to researchers how much faith they could have in their estimates.

A more recent statistical approach is found in the “neighborhood model” (5). It, too, assumes that demographic composition will not determine voting behavior and simply projects the ratio of demographic composition within a precinct onto its voting behavior. For example, if 40% of a voting-age population is female, then 40% of that same precinct’s Democratic voters are estimated to be female.

The neighborhood model was formulated in response to an earlier statistical approach known as Goodman’s “ecological regression” (6). This method would estimate voter participation not at the local precinct level, but at the more aggregated district level. Each district contains several precincts. Unlike for the neighborhood model, precinct-level estimates in ecological regression can be inferred from the district-level only on the specific assumption that voter participation by race remains constant across precincts.

In terms of its diagnostic and robustness qualities, neither Goodman’s regression nor the neighborhood model fares well. In terms of diagnostics, neither approach will typically reveal information about the appropriateness of its statistical assumptions. In terms of robustness, the reliability of estimation is highly sensitive to the correctness of its underlying assumptions. In addition, because Goodman’s method utilizes linear regression, it quite frequently produces estimates outside of the [0, 1] interval, thus providing impossible microlevel estimates smaller than 0% or greater than 100%. As recently as 1990, in a federal trial in Ohio on the redrawing of electoral districts, an expert witness using Goodman’s regression was forced to state that 109.63% of blacks voted for the Democratic candidate in District 42. Despite these problems, Goodman’s method until recently has remained the only court-accepted method of ecological inference in legal testimony.

Deterministic–Statistical Solutions

There are crude ways in which deterministic information can be brought to bear on the statistical results obtained through ecological regression. At a minimum, all estimates outside of the [0, 1] interval can be capped at the interval’s limit. Adding information from the method of bounds, estimates can be narrowed further by drawing them into the limit of the deterministic ranges. Either method, however, generates an unreasonable number of “corner solutions,” in which a disproportionate number of observations reside at the limit of the range. Furthermore, it is unlikely that the remaining realistic-appearing estimates are reliable, if others become so only once they are reined in.

A more sophisticated combination of the deterministic method of bounds and a statistical approach is found in King’s procedure, EI (named after the software program that implements it) (3). EI begins with the method of bounds to establish a deterministic range within which true values must reside. The procedure subsequently utilizes a statistical method to further narrow these bounds: following a maximum likelihood approach, each possible value within the deterministic bounds is given a relative likelihood of being the true value. These likelihoods are generated through the addition to Goodman’s regression model of three statistical assumptions.

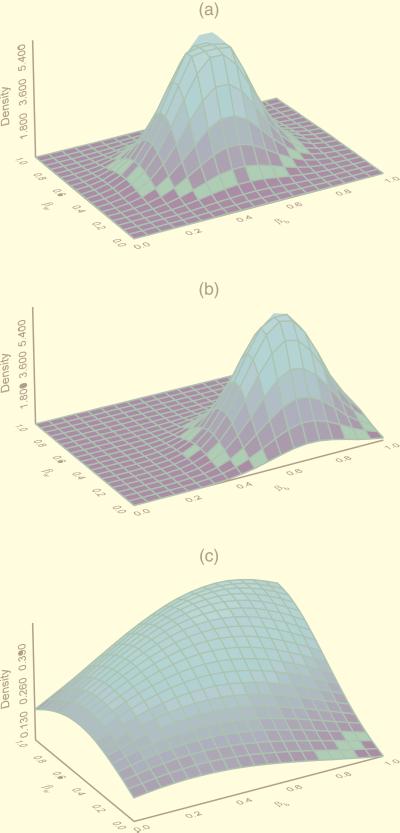
First, in contrast to Goodman’s method, which requires the assumption that voter participation by race remains constant across precincts, black and white turnout can now vary across different precincts, and will do so in a mutually dependent manner. The relationship between the two is defined by a (bivariate) normal distribution, with its tails truncated at the deterministic bounds. Fig. 1 shows this relationship graphically and also reveals how flexible the assumption of this type of mutually dependent variation is. As the figure shows, values for both black and white turnout (β_i^b and β_i^w) could be dispersed very narrowly around a particular point, or either one or both quantities could be dispersed more widely. One fundamental feature of the normality assumption is the presence of a single mode in the bivariate distribution of β_i^b and β_i^w.

Figure 1.

Three different truncated bivariate normal distributions for β_i^b and β_i^wbiw. Graphs b and c are more affected by the truncating bounds than is graph a.

The two remaining assumptions are, first, that voter turnout (T) in one precinct is independent of turnout in another—there is no “spatial correlation.” Second, in the basic EI model, the different turnouts among black and white voters are uncorrelated with the proportion of voter-age blacks (X_i) and whites (1 − X_i) in the precinct population. In an extended EI model, this latter assumption is relaxed, and the dependence of black and white turnout on the precinct’s racial composition itself can be assumed or estimated.

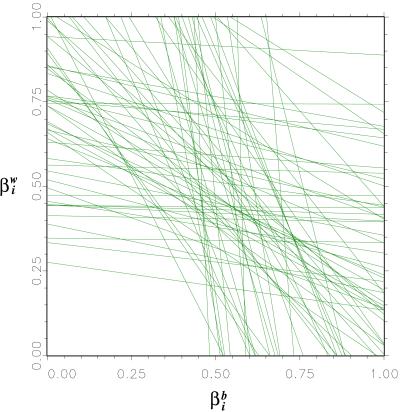
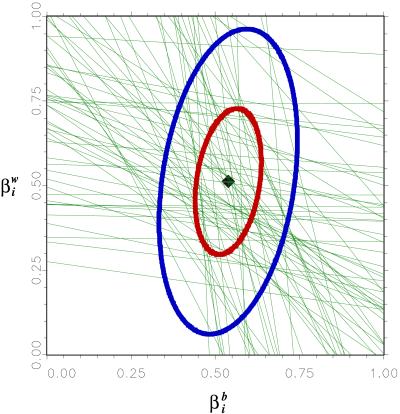
Fig. 2 provides a graphical representation of the deterministic information about β_i^b and β_i^w, given combinations of T_i and X_i in each precinct. Each line represents all possible values for black and white voter turnout for one precinct, given its voter turnout and its racial composition. The horizontal spread of a line across the [0, 1] interval provides that precinct’s deterministic bound on β_i^b, the percentage of blacks voting. The vertical spread of a line does the same for β_i^w. EI subsequently superimposes a probability density, as in Fig. 1, on the deterministic information of Fig. 2. The peak of the superimposed surface is anchored above the highest density of line intersections, as it is here that combinations of β_i^b and β_i^w are most likely. Fig. 3 shows the resultant probability contours corresponding to different heights of the probability surface.

Figure 2.

Tomography plot showing the deterministic information about β_i^b and β_i^w, given combinations of T_i and X_i in a precinct. The horizontal spread of a line across the [0, 1] interval provides a particular precinct’s deterministic bound on β_i^b. The vertical spread of a line does the same for β_i^w.

Figure 3.

Tomography plot with 95% (blue) and 50% (red) maximum likelihood contours superimposed on the deterministic information of Fig. 2. Each contour represents a constant height sliced out of the truncated bivariate normal distribution from which β_i^b and β_i^w are assumed to be drawn. The peak of the probability surface is anchored above the highest density of line intersections and represents the point estimate.

The procedure follows the logic of tomography in seismic or medical imaging: X-rays are sent through a human head, with each individual ray revealing information as to whether it has passed through a tumor. We know whether a tumor resides along the path of any one ray. We do not know, however, how far into that ray’s path the tumor was hit. Assembling information from several rays, shot at different angles, however, allows the researcher to infer a cluster of hits, resulting in a probabilistic estimate of the tumor’s location. The tumor most likely resides at the point at which most tumor-striking rays intersect. EI—in much the same way—borrows strength from the information of all other precinct-level lines by anchoring the peak of its probability surface above the highest density of line intersections, thus revealing probabilistically information about any one precinct’s black and white turnout values.

There is some controversy surrounding the reliability of EI’s estimation procedure. While several researchers have found EI to produce reliable point estimates and a trustworthy measure of confidence attached to each estimate, some have begun to identify conditions under which EI may produce misleading results, or its diagnostic capacity for detecting a violation of assumptions may fail (7, 8). An important consideration is the consequence of assumption violation. While here, too, no broad consensus exists, researchers have found that for at least some violations that occur in practice, EI’s estimation is remarkably robust (3, 9). More work remains to be done on uncovering the exact contours of EI’s performance under different conditions. However, it is not premature to note that this estimation procedure to date represents the most dramatic advance in researchers’ abilities to draw microlevel inferences from aggregate-level data. Perhaps more importantly still, its general approach—combining statistical and deterministic means—has set a new methodological direction for ecological inference.

The Future of Ecological Inference

Several EI-focused developments are currently underway. Researchers have begun to utilize alternative distributional specifications for instances in which diagnostic plots indicate that the assumption of a single mode in the probability surface is not appropriate (10). Others have developed an approach of ecological panel inference (EPI) which enables researchers to use independent surveys taken at different points in time, from different segments of the population, to infer how individuals’ behavior changed over time (9). Previously such information could be obtained only from rarely collected panel data which tracks individual-level behavior by repeatedly asking the same respondents the same questions on different occasions. In addition, researchers have begun to improve efficiency of computationally intensive EI procedures (10, †). They have also begun to establish simplified estimation procedures for cases where parameters of interest divide into more than two categories (for example, when voters break down into more than two demographic groups) (11).

These continued advances should not, however, deflect from our original emphasis: The ecological inference problem will never yield a deterministic solution. Recent advances in ecological inference do, however, strongly suggest two important characteristics for its future. First, further improvements most likely will continue to combine a deterministic and a statistical approach. Second, they will involve the development of new statistical methods of bringing external qualitative information (e.g., from ethnographic or journalistic accounts) to bear on the estimation procedure. There will always be instances where a statistical procedure will not improve—significantly, sufficiently, or at all—on deterministic ranges on the basis of aggregate data alone. This is not a weakness of the statistical method itself but a consequence of the irrecoverable loss of microlevel information as it is aggregated. Much of the future of ecological inference, therefore, paradoxically resides in the development of statistical–deterministic means of introducing into its inference what is known (or suspected) at the microlevel.