Abstract
This paper is aimed at exploring the effect of cortical brain atrophy on the currents induced by transcranial magnetic stimulation (TMS). We compared the currents induced by various TMS conditions on several different MRI derived finite element head models of brain atrophy, incorporating both decreasing cortical volume and widened sulci. The current densities induced in the cortex were dependent upon the degree and type of cortical atrophy and were altered in magnitude, location, and orientation when compared to healthy head models. Predictive models of the degree of current density attenuation as a function of the scalp-to-cortex distance were analyzed, concluding that those which ignore the electromagnetic field–tissue interactions lead to inaccurate conclusions. Ultimately, the precise site and population of neural elements stimulated by TMS in an atrophic brain cannot be predicted based on healthy head models which ignore the effects of the altered cortex on the stimulating currents. Clinical applications of TMS should be carefully considered in light of these findings.
Keywords: Cortical atrophy, Finite element model, Transcranial magnetic stimulation, Brain stimulation, Neuromodulation, Brain plasticity
Introduction
Transcranial magnetic stimulation (TMS) is a noninvasive procedure that utilizes pulsed magnetic fields to induce stimulating currents in cortical tissue (Barker et al. 1985). When this current is applied repetitively, repetitive transcranial magnetic stimulation (rTMS), it can modulate cortical excitability, decreasing or increasing it, depending on the parameters of stimulation. Since its inception, researchers have proposed the use of TMS and rTMS to study and treat neuropsychiatric diseases, such as major depression (Pascual-Leone et al. 1996; George et al. 2000; Martin et al. 2003; Holtzheimer et al. 2004; Rumi et al. 2005), schizophrenia (Hoffman et al. 2003; Lee et al. 2005), Parkinson’s disease (Mally and Stone 1999; de Groot et al. 2001; Khedr et al. 2003; Fregni et al. 2004; Lefaucheur et al. 2004), dystonia (Huang et al. 2004), epilepsy (Tergau et al. 1999; Menkes and Gruenthal 2000; Daniele et al. 2003; Fregni et al. 2005) and the acute or chronic sequels derived from stroke (Mansur et al. 2005). However, a fundamental question that needs to be addressed before the wide-spread use of TMS in clinical practice, is how the modification of brain anatomy and tissue properties caused by certain neuropsychiatric diseases can alter the effects of TMS.
With TMS, changes in the tissue anatomy and electromagnetic properties have been shown to alter the TMS induced stimulating currents in both phantom and modeling studies (Yunokuchi et al. 1998) (Liu and Ueno 2000; Wagner 2001; Miranda et al. 2003; Wagner et al. 2004). We have shown previously that the damaged areas in patients with stroke can perturb the location and magnitude of the stimulating cortical currents (Wagner et al. 2005). The main reason for this perturbation is that the altered distribution of cerebral spinal fluid (CSF) to brain tissue modifies the conductive tissue properties in the infarction region and effectively provides a path of lowered resistance for the stimulating currents to flow along. Several diseases explored or treated with TMS, such as depression (Pascual-Leone et al. 1996; George et al. 2000; Martin et al. 2003; Holtzheimer et al. 2004; Rumi et al. 2005), Alzheimer’s disease (Alagona et al. 2004; Pierantozzi et al. 2004), Huntington’s disease (Modugno et al. 2001), corticobasal degeneration (Kuhn et al. 2004) and Creutzfeldt–Jakob’s disease (Sakuishi et al. 2005), as well as normal aging (Sowell et al. 2003), show related anatomical changes that could have an impact on the TMS induced electric currents. All of these populations are characterized by varying degrees of cortical atrophy, where brain tissue is replaced by CSF, the CSF to cortical tissue volume ratios increase, and oftentimes the cerebral sulci widen. However to date, there has been no systematic study of the effects that cortical atrophy and the altered CSF to cortical tissue ratios can have on the currents induced by TMS in neural tissue.
Herein we systematically explored how the electrical and anatomical changes caused by cortical atrophy can perturb the TMS induced stimulating currents in the cortex through multiple MRI derived finite element TMS head models. We also discuss the potential clinical implications of current perturbations under TMS in patients with cortical atrophy.
Methods
Models
Multiple MRI based finite element head models were constructed and evaluated for different stimulation orientations to address the effects of cortical atrophy on the TMS induced stimulating current.
MRI guided finite element head model
An initial sinusoidal steady-state finite element model (FEM) was developed using the Ansoft 3D Field Simulator software package with eddy current solver (Ansoft 2002). We used an MRI-guided, three-dimensional CAD rendering of the human head to solve for the currents induced in the cortex during magnetic stimulation, described in detail in Wagner et al. (2004). We refer to this as the healthy head model (see Fig. 1a). This model was generated to include the skin, skull, CSF, gray matter, and white matter. The tissue conductivities in the model were assigned the mean value from multiple compiled references; skin at 0.465 S/m, bone at 0.010 S/m, CSF at 1.654 S/m, gray matter at 0.276 S/m, and white matter at 0.126 S/m (Crille et al. 1922; Oswald 1937; Lepeschkin 1951; Freygang and Landau 1955; Ranck 1963; Radvan-Ziemnowicz et al. 1964; Hasted 1973; Geddes 1987; De Mercato and Garcia Sanchez 1992; Gabriel and Gabriel 1996; Akhtari et al. 2002; Kammer et al. 2004); thus, each individual tetrahedron of the FEM was assigned the conductivity corresponding to its tissue type. Tissue permittivities were also assigned values reflective of trends in the literature (see Table 1) (Pethig and Kell 1987; Dissado 1990; Foster and Schwan 1996; Gabriel and Gabriel 1996; Hart et al. 1996). The source was modeled as a figure-of-eight copper coil with two 3.5 cm radius windings made of a single turn of 7 mm radius copper wire. The source current was set at 5 kHz with a 1.8 × 103 A peak (5.65 × 107 A/s, rate of change of the peak current with time). A more detailed discussion of the healthy head model generation, the FEM solution technique, the tissue values used, and the underlying physics are discussed in detail in an earlier paper (Wagner et al. 2004). The coordinate frame used in this paper is defined in Fig. 1a in mm units.
Fig. 1. Geometries.
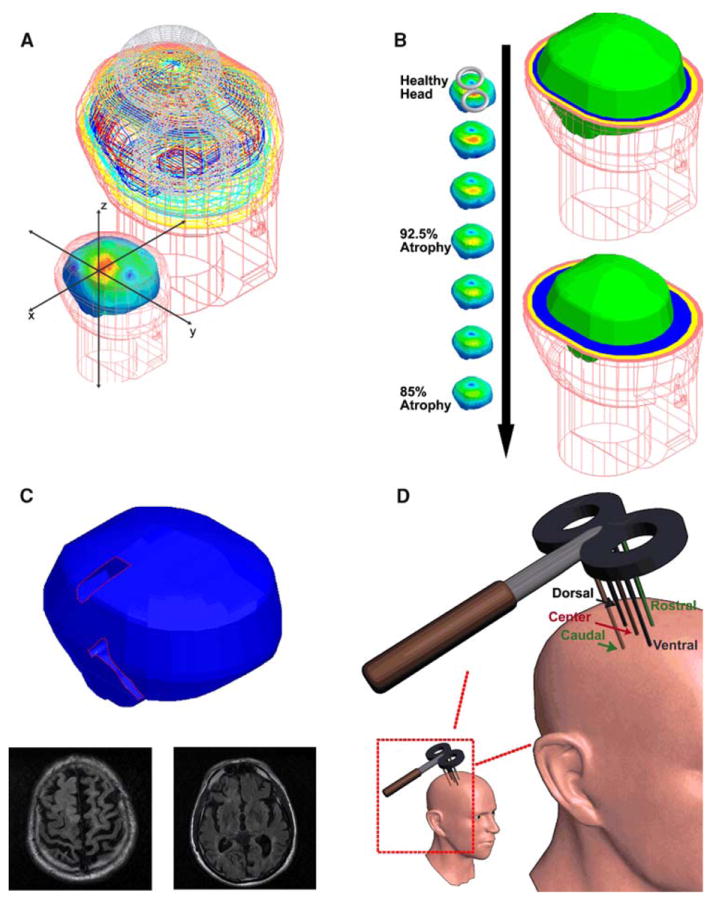
a Healthy head model and the model coordinate system: This image depicts the Wnite element mesh borders of the skin (flesh color), skull (yellow), CSF (light blue), gray matter (dark blue), and white matter (red). The coordinate system is shown in the foreground image and was used for all the models. b Increasing symmetric atrophy models: the models are displayed from the healthy head model to the 85% atrophy model. On the right side, the healthy head model (upper) and the 85% atrophy model (lower) are shown to highlight the increasing thickness of the CSF and the decreasing cortical thickness. The skin mesh is shown in the flesh color where the tissue thicknesses are highlighted in the transverse slices; scalp (flesh colored), skull (yellow), CSF (blue), brain (bright green). Notice the increasing CSF thickness and the decreased cortical size between the two models. c. Widened sulci model: the base sulci model is shown with the widened sulcal regions highlighted and sample MRI slices. d Evaluation line locations: the lines were located with the center line normal to the figure-of-eight coil center and the other lines 1 cm ventral, dorsal, anterior, and posterior to the center line (note that the figure is not drawn to scale but with the lines and the coil drawn to highlight their placement)
Table 1.
Mean conductivity values and relative permittivity schemes used
| Tissue | Mean conductivity (S/m) | Relative permittivity scheme (F/m) |
|---|---|---|
| Skin–scalp | 0.465 | 1.2 × 104ε0 |
| Bone–skull | 0.010 | 0.8 × 104ε0 |
| Cerebral spinal fluid | 1.654 | 0.60 × 104ε0 |
| Gray matter | 0.276 | 1.2 × 104ε0 |
| White matter | 0.126 | 1.2 × 104ε0 |
Atrophy models
We implemented ten different atrophy models of increasing severity and varied cortical modifications to compare to the healthy head model under different stimulation conditions.
Six of the models were constructed by decreasing the overall volume of the gray and white matter symmetrically by 2.5% steps, from 100 to 85%, and filling the area with CSF as seen in in-vivo imaging and postmortem histology studies (Silbert et al. 2003; Sowell et al. 2003). These models will be referred to by their percent of atrophy (i.e., the 97.5% atrophy model). See Fig. 1b for a graphical representation of the models.
Four additional models were constructed to explore the effects of expanded cerebral sulci. These models were constructed by altering the healthy head model’s cortical geometry based on the MRIs of patients treated at Beth Israel Deaconess Medical Center (with atrophic regions cut with straight edges along their borders and with tissue regions clearly demarcated for use in the FEM solver). One model was constructed by removing the cortical tissue in the areas of the central sulcus and the sylvian fissure from the healthy head model and replacing the gray matter with CSF. This model is referred to as the base sulci model. Three further models were constructed based on this base sulci model, with symmetrically decreased cortical volumes, with 95, 90, and 85% of the brain volume of the base sulci model. See Fig. 1c for the base sulci model and its MRI basis.
Analyses
The following specific tests were conducted to explore the effects of atrophy on the TMS induced stimulating currents:
Effects of the degree of atrophy on the induced stimulating currents
In order to investigate the effects that increasing atrophy can have on the induced stimulating currents, solutions were obtained and contrasted for both the healthy head model and the six symmetric atrophy models with the coil placed over the right dorsal lateral prefrontal (DLPF) cortex and the right primary (M1) motor cortex (with the coil center located at (43.8, 51.0, 48.0) and (43.1, 7.5, 51.0) respectively).
For each model and coil position, the magnitude and location of the maximum cortical current density were evaluated along with the surface area on the cortex where the current density was greater than 90% of its maximum value. We will refer to this as the maximum cortical current surface area. To examine the current behavior in the region of the expected current density maximum, the current density magnitude was determined along evaluation lines perpendicular to the coil at its center and at locations 10 mm anterior, posterior, rostral, and caudal to the center line (as defined in Fig. 1d). The distance from the skin surface to the cortical surface along each of these lines was determined for each model. Finally, the induced current density vector behavior was also analyzed in all the tissues.
Once the magnitude of the current density at the cortical interface and the distance from the scalp to the interface were determined for each model, plots were generated of the maximum magnitude on the surface of the cortex of each model relative to the healthy head model as a function of distance into the brain model along the aforementioned evaluation lines. We constructed a set of stochastic models of the relative magnitude of the cortical current density as a function of distance from the coil. In one embodiment, the current magnitude was modeled using a single decaying exponential function with independent identically distributed Gaussian noise (i.e., this model accounted for scalp to cortex distance alone and was represented by a single exponential function). An alternative model postulated that the current magnitude was described by separate distributions for each coil location, each with distinct exponential decay functions and noise variance parameters (i.e., this model accounted for both scalp-to-cortex distance and the coil position and was represented by two separate exponential functions, one for the DLPC and one for the motor strip coil locations—note that the coil position relative to the underlying electrical/anatomical distribution were constant for each line in this model embodiment). The exponential and variance parameters for the above models were fit with maximum likelihood methods. Using these models, we constructed a likelihood ratio test for the null hypothesis that the data from both coil positions was captured by the single exponential function versus the alternative hypothesis that the data was better explained by a distinct exponential function for each position. For this test, the loglikelihood ratio statistic should approximately follow a χ2 distribution with 3 degrees of freedom (Pawitan 2001).
Effects of widened sulci on the induced stimulating currents
Solutions were obtained with the coil placed above the dorsal lateral prefrontal cortex for the four widened sulci models and compared to the heterogeneous healthy head model and the analogous atrophy models with the coil in the same position. The analysis of the magnitude and location of the maximum cortical current density, the maximum cortical current surface area, the current density magnitude behavior along the evaluation lines, and the induced current density vector behavior detailed in the section above was completed for these models.
Results
Effects of the degree of atrophy on the induced stimulating currents
Every model converged below the 1.0% energy error stopping criteria defined in Wagner et al. (2004). With the coil placed over the motor strip (and the dorsal lateral prefrontal cortex), the maximum cortical current densities decayed by approximately 33.9% (33.3%) at a vertical distance of 12.4 mm (14.5 mm) from the scalp (see Fig. 2). The maximum cortical current surface areas showed no consistent trend in area relative to the degree of atrophy. Over the motor cortex, the location of the maximum cortical current density was found at increasingly anterior and medial positions relative to the coil with increasingly severe atrophy, while over prefrontal cortex it was found at the CSF-gray matter interface with little variation in the degree of atrophy. The magnitude, location (and vertical distance from the scalp), and area of the maximum cortical current densities are tabulated for the various models in Table 2.
Fig. 2. Current density magnitudes.
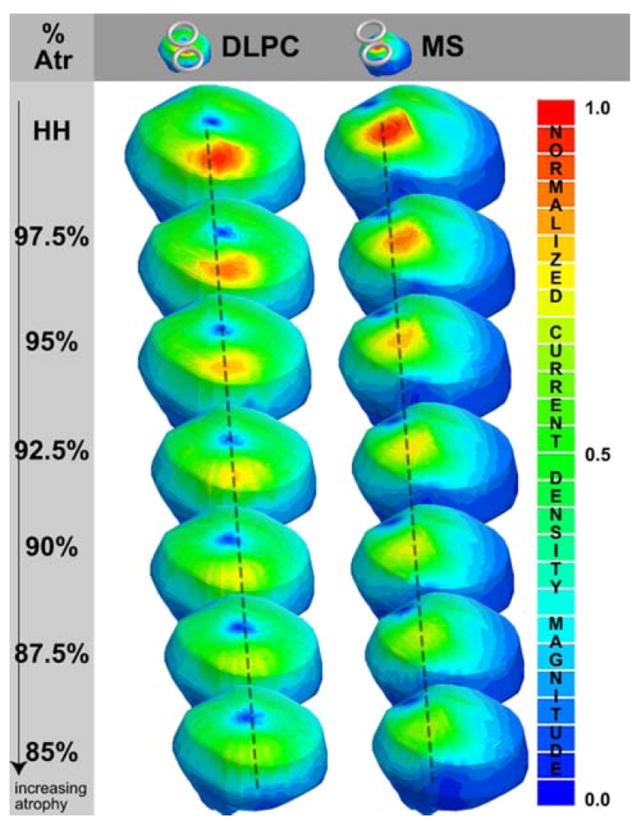
the current density magnitudes are plotted for the dorsal lateral prefrontal cortex (DLPC) and the motor strip (MS) coil position the healthy head model (HH) to the 85% atrophy model. Note that the normalized current density magnitude is relative to the maximum current density magnitude for the healthy head model for each coil position (i.e., the DLPC scale ranges from 0 to 2.82 A/m2 and the MS scale ranges from 0 to 3.57 A/m2)
Table 2.
Data for the maximum current density on the cortical surface
| Model and position | MCDCS | % HH CDMax | MCDCS location | MCDCS relative to coil | VerD scalp | Area |
|---|---|---|---|---|---|---|
| HHms | 3.57 (12.93) | 100.0 | (29.8, 7.2, 35.3) | (−13.3, −0.3, −15.7) | 5.7 | 218.0 |
| 975ms | 3.20 (11.59) | 89.6 | (30.5, 9.9, 33.9) | (−12.6, 2.4, −17.1) | 6.9 | 228.0 |
| 95ms | 2.98 (10.80) | 83.5 | (29.7, 7.6, 33) | (−13.4, 0.1, −18.0) | 8.3 | 221.2 |
| 925ms | 2.78 (10.07) | 77.9 | (31.6, 7.4, 31) | (−11.5, −0.1, −20.0) | 9.3 | 238.0 |
| 90ms | 2.59 (9.38) | 72.5 | (28.5, 7.9, 31.1) | (−14.6, 0.4, −19.9) | 10.4 | 217.1 |
| 875ms | 2.45 (8.88) | 68.6 | (25.9, 12.2, 31) | (−17.2, 4.7, −20.0) | 11.4 | 191.2 |
| 85ms | 2.36 (8.55) | 66.1 | (22.4, 12.9, 31.1) | (−20.7, 5.4, −19.9) | 12.4 | 209.0 |
| HHdlpc | 2.82 (10.21) | 100.0 | (34.5, 45, 29.6) | (−9.3, −6, −18.4) | 6.5 | 224.0 |
| 975dlpc | 2.58 (9.34) | 91.5 | (34.5, 42.3, 28.86) | (−9.3, −8.7, −19.14) | 7.7 | 176.0 |
| 95dlpc | 2.37 (8.59) | 84.0 | (33.7, 41.1, 28.1) | (−10.1, −9.9, −19.9) | 8.9 | 218.0 |
| 925dlpc | 2.32 (8.41) | 82.3 | (33, 43.7, 26.5) | (−10.8, −7.3, −21.5) | 10.3 | 170.3 |
| 90dlpc | 2.27 (8.22) | 80.5 | (32, 42.7, 25.8) | (−11.8, −8.3, −22.2) | 11.5 | 143.0 |
| 875dlpc | 2.08 (7.53) | 73.8 | (31.1, 41.8, 24.9) | (−12.7, −9.2, −23.1) | 12.7 | 149.0 |
| 85dlpc | 1.88 (6.81) | 66.7 | (32.4, 42.9, 22.7) | (−11.4, −8.1, −25.3) | 14.5 | 192.4 |
The first column indicates the model and coil position; where HH stands for healthy head model, ms for the motor strip coil position, dlpc for the dorsal lateral prefrontal cortex coil position, and the number corresponds to the degree of atrophy (i.e., 925ms indicates the 92.5 atrophy model with the coil in motor strip position. The second column indicates the maximum current density on the cortical surface (MCDCS), in A/m2 (and the electric field strength in V/m). The third column indicates the magnitude of the current density on the cortical surface relative to the healthy head model for the coil in the same position. The fourth column provides the MCDCS location in the absolute coordinate system, while the fifth column provides the location relative to the coil center point, and the sixth indicates the vertical distance from the scalp to the MCDCS location. And the final column reports the maximum cortical current surface area
The current density magnitude was calculated along the evaluation lines that were defined in Fig. 1d. The current density showed stair step jumps in magnitude at the tissue boundary interfaces in every solution, which correlated to the conductivity of the tissues (see Fig. 3a for graphical examples of the cortical current density behavior along the center evaluation line for the healthy head model). Similar trends were calculated along the other lines for both the motor strip and dorsal lateral prefrontal cortex coil positions; with a greater decay where the lines ran proximal to the lateral cortical face such that they intersected at deeper points (for example see Table 3 for the DLPC).
Fig. 3. Current density behavior with distance.
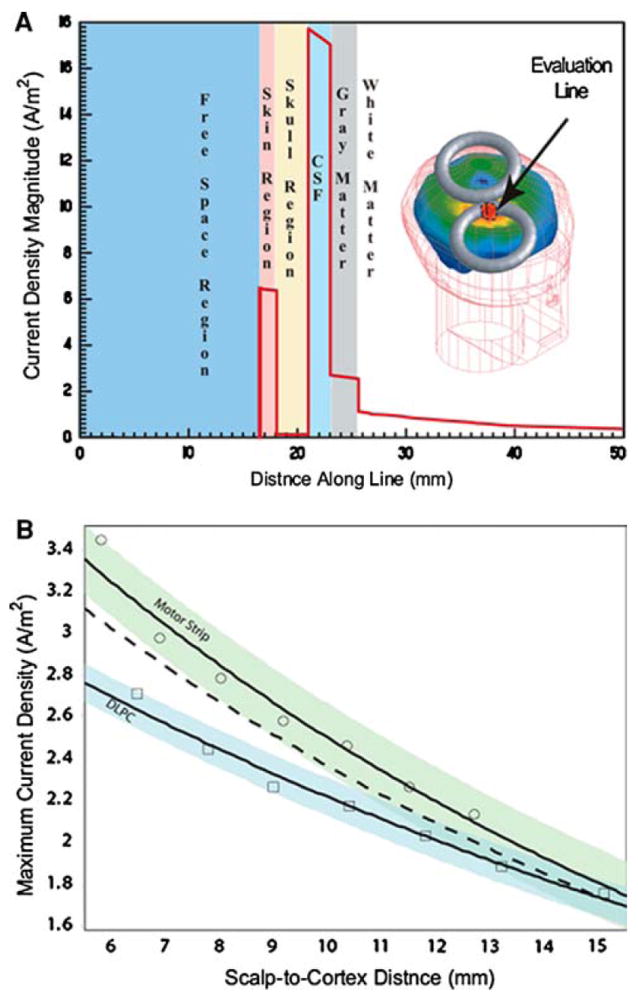
a Current density magnitude evaluated along the center evaluation line in the healthy head model with the coil in the dorsal lateral prefrontal cortex coil location. Note that the current density magnitude varies with the conductivity of the tissues. b Exponential models for maximum current density: exponential models for maximum cortical current density as a function of distance for position dependent and independent models. Circles and squares represent simulated current density values from the motor strip and the dorsal lateral prefrontal cortex coil positions respectively. The dashed line represents the mean exponential trend for the position independent model. The light green and light blue areas represent a 95% confidence region for the position dependent models
Table 3.
Data for the maximum current density on center evaluation line
| Model and position | CLine CSCD | % HH CDMAx | LineDis from scalp |
|---|---|---|---|
| HHms | 3.43 (12.43) | 100.00 | 5.8 |
| 975ms | 2.96 (10.72) | 86.30 | 6.9 |
| 95ms | 2.77 (10.03) | 80.76 | 8.0 |
| 925ms | 2.57 (9.31) | 74.93 | 9.2 |
| 90ms | 2.45 (8.87) | 71.43 | 10.4 |
| 875ms | 2.25 (8.15) | 65.60 | 11.5 |
| 85ms | 2.12 (7.68) | 61.81 | 12.7 |
| HHdlpc | 2.70 (9.78) | 100.00 | 6.5 |
| 975dlpc | 2.43 (8.80) | 90.00 | 7.8 |
| 95dlpc | 2.25 (8.15) | 83.33 | 9.0 |
| 925dlpc | 2.16 (7.82) | 80.00 | 10.4 |
| 90dlpc | 2.02 (7.31) | 74.81 | 11.8 |
| 875dlpc | 1.87 (6.78) | 69.26 | 13.2 |
| 85dlpc | 1.74 (6.30) | 64.44 | 15.1 |
The first column indicates the model and coil position. The second column indicates the maximum current density on the cortical surface where the center line intersects the cortex, in A/m2 (and the electric field strength in V/m). The third column indicates the magnitude of the current density at the cortical surface intersection relative to the healthy head model for the coil in the same position. The fourth column indicates the distance from the scalp to the cortical intersection along the evaluation line
Once the magnitude of the current density at the cortical interface and the distance from the scalp to the interface were determined for each model, plots of the maximum magnitude on the surface of the cortex were generated for each model relative to the healthy head model as a function of distance along each evaluation line. Exponential models were fit to the data series as a function of either scalp to cortex distance alone or for both scalp to cortex distance and coil position using maximum likelihood. The expected values of these models for the center evaluation line are shown as trend lines in Fig. 3b for both models. If the relationship between distance and current magnitude were independent of coil position we would expect the exponential curves to approximately coincide. However, the parameters of these exponential models were found to be significantly different, suggesting that distance alone does not predict current magnitude as well as distance and coil position considered together. We tested the null hypothesis that the data from both coil locations came from the model of distance alone against the alternative hypothesis of the expanded model using a log likelihood test, and found that the data strongly rejected the null hypothesis (P < 1e–15). The alternative model with separate distributions for the two coil positions explains over 97% of the variance in the cortical current density. Similar results were found for analysis along the different lines and at different locations in the model (e.g., 1 mm below the CSF-gray matter interface, at the gray matter–white matter interface, 1 mm below the gray matterwhite matter interface, etc.) (Table 4).
Table 4.
Exponential functions of the percentage of the maximum current density magnitude on the surface of the cortex of each model, relative to the healthy head model, as a function of distance into the brain model for each evaluation line
| Evaluation line-coil position | Exponential trend line |
|---|---|
| Center line-MS | y = 139.54e−0.0655x |
| Caudal line-MS | y = 138.74e−0.0628x |
| Rostral line-MS | y = 128.1e−0.0458x |
| Dorsal line-MS | y = 137.42e−0.0631x |
| Ventral line- MS | y = 112.07e−0.0225x |
| Center line -DLPC | y = 133.5e−0.0492x |
| Caudal line-DLPC | y = 140.92e−0.0584x |
| Rostral line-DLPC | y = 131.87e−0.0531x |
| Dorsal line-DLPC | y = 135.69e−0.054x |
| Ventral line- DLPC | y = 145.73e−0.0542x |
Note that cortex starts at approximately 6 mm, dependent upon evaluation line
Effects of widened sulci on the induced stimulating currents
In the widened sulci models, the behavior in the location of the current density maxima was less consistent. The behavior of the current density distribution directly under the coil center was very similar to the analogous atrophy models, but far less predictable along the widened sulci borders, similar to the results seen in stroke (Wagner 2001; Wagner et al. 2005) and heterogeneity studies (Wagner 2001; Miranda et al. 2003). There were locations directly below the most posterior portion of the figure-of-eight coil, along the widened central sulci border, where current density magnitudes were within ±15% of the maximums found under the coil center (3.59, −0.85, 6.61, and 14.35%, respectively for the base, 95, 90, and 85% widened sulci models).
In general the current density was increased in regions proximal to the widened sulci (within approximately 1 cm), most particularly in the region of the central sulcus. The differences in magnitude were generally unchanged at a distance greater than a centimeter away from the borders, but increased with decreasing distances from the border (see Fig. 4a). There was less of a change in the current densities along the widened Sylvian fissure, where the differences in current density magnitudes were generally less than ±10% of the magnitude of the current density at the same location in the analogous models without the widened sulci. These results are tabulated in Table 5.
Fig. 4. Widened sulci current density variations.
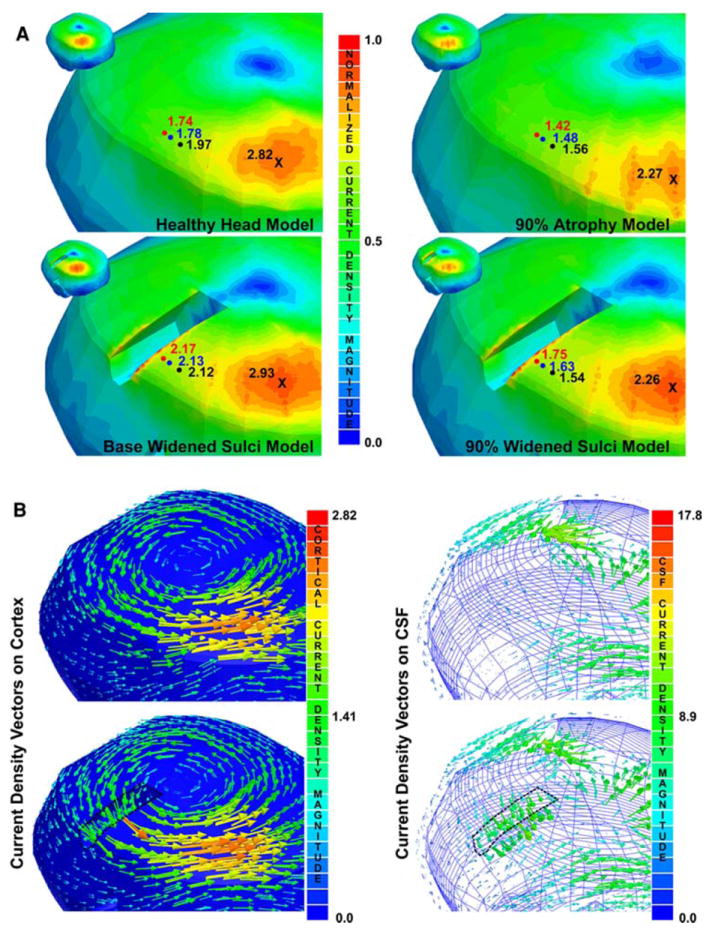
a Current density magnitudes: the current density magnitudes are shown for the base and 90% widened sulci models focused on the region near the central sulcus and in the same locations for the analogous models without the widened sulci in the cortex (i.e., healthy head and 90% atrophy models). Note that the current density magnitudes in the region of the figure-of-eight coil center’s, indicated by the X’s, are consistent for the models with the same % of atrophy. However, the current density magnitudes increase as one gets closer to the widened central sulcus; the black, blue, and red circles indicate analogous points in the models with consistent % atrophies at points 10, 5, and 2.5 mm, respectively. b Current density vector distribution: the left most image shows the vector density distribution on the surface of the cortex for the healthy head and base widened sulci model highlighting the behavior in the central sulcus region. The right most image shows the vector behavior on the surface of the CSF for the healthy head and base widened sulci model. Note that the current density scale is normalized to the maximum current densities for the widened sulci models (i.e., the models on the left are normalized to the maximum cortical current density in the base widened sulci models, 3.06 A/m2, and for the 90% widened sulci model, 2.42 A/m2)
Table 5.
Data for the maximum current density on the cortical surface for the widened sulci models
| Model and position | MCDCS under coil | MCDCS location under coil | VerD scalp | Area |
|---|---|---|---|---|
| Bws | 2.93 (10.61) | (32.9, 43.9, 28.1) | 6.9 | 168.0 |
| 95ws | 2.38 (8.62) | (34, 41.2, 28.0) | 8.9 | 272.0 |
| 90ws | 2.26 (8.19) | (37.9, 34.6, 25.3) | 11.5 | 111.0 |
| 85ws | 1.97 (7.14) | (37.8, 35.6, 22.1) | 14.6 | 78.0 |
| MCDCS on sulcal edges | MCDCS location on sulcal edges | |||
| Bws | 3.06 (11.09) | (45.2, 4.1, 28.1) | 6.8 | 5.1 |
| 95ws | 2.44 (8.84) | (25.3, −2.2, 34.6) | 7.9 | 4.5 |
| 90ws | 2.42 (8.77) | (24.2, −3.8, 32.6) | 10.2 | 2.2 |
| Note: two other locations were within ±15% of the under the coil max: at (41.4, 1.83, 24.7) with 2.37 (8.59) magnitude and 3 mm2 area and at (45.2, −0.1, 20.4) with a 2.38 (8.62) magnitude and 4 mm2 area | ||||
| 85ws | 2.30 (8.33) | (36.4, 2.06, 24.17) | 12.5 | 9 |
| Note: three other locations were within ±15% of the under the coil max: at (24.3, −5.3, 30.2) with a 2.05 (7.43) magnitude and 4 mm2 area, at (30.4, −7.2, 20.7) with a 2.21 (8.00) magnitude and 6 mm2 area and at (42.5, −0.4, 19.2) with a 2.09 (7.57) magnitude and a 4 mm2 area | ||||
The first column indicates the model and coil position, where Bws stands for base widened sulci model, ws for widened sulci, and the number corresponds to the degree of atrophy (i.e., 85ws indicates the 85% widened sulci model. The second column indicates the maximum current density on the cortical surface (MCDCS), in A/m2 both under the coil and along the sulcal border (and the electric field strength in V/m). The third column provides the MCDCS location under the coil and along the sulcal border, while the fourth column indicates the vertical distance from the scalp to the MCDCS location. And the final column reports the maximum cortical current surface area. Note that for the 90ws and 85ws models, there were multiple regions along the border where the current density was with ±15% of the maximum current density under the coil, these are reported in the adjacent row in the table
The current density distribution directly under the coil center was very similar to the analogous atrophy models, and thus the behavior of the current densities along the evaluation lines were largely similar to those in the nonwidened sulci models. Similarly, the current density vector behavior was consistent in the area under the figure-eight-center with the other atrophy models. However, the current density vector distributions deviated from predictable figure-of-eight distributions that were seen in the cortices of the models without the widened sulci to conform to the sulcal boundaries, such that the current vectors became more perpendicular to the borders. Additionally, in the CSF the current density vectors were directed into the widened sulci in the CSF surrounding the sulci (see Fig. 4b). Similar effects were seen in the current density behavior within the white matter along the widened sulcal boundaries.
Discussion
This paper explores the effect that electrical and anatomical changes caused by cortical atrophy have on TMS induced electrical currents in the brain. The healthy head model was discussed in an earlier publication (Wagner et al. 2004), and herein we focus on the difference between healthy and atrophy head models. The results show that the alterations derived from cortical atrophy can modify the effect of TMS in several ways. As expected, the magnitude of the current densities induced on the cortex was dependent upon the degree of cortical atrophy and decreased in magnitude as the distance from the scalp to the cortex increased. However, the degree of attenuation did not solely depend on the distance, but also on the relative coil position and anatomical and electrical features of the tissues. The location of the maximum cortical current density varied with the degree and type of atrophy, whereas current density vectors were altered in the widened sulci models, conforming to the altered tissue geometries. In addition to analyzing the current density results for the individual models, exponential trend lines were fit to the data to predict how the current densities would decay at different locations in the models. Along the individual evaluation lines, the models that accounted for position and distance fit the data very well, but no single exponential model successfully captured the relation between cortical current density and the distance between the scalp and cortex. The clinical implications of some of our observations for TMS based tests and therapies are discussed.
Symmetric atrophy models
The magnitude of the maximum cortical current density decreased with increasing scalp to cortex distances in each of the models. While maintaining the coil location at a constant position and evaluating the current density as a function of the distance, the degree of attenuation could be well predicted by exponential functions, with the appropriate decay rate for a given coil position and evaluation line. Along a single evaluation line, these exponential models of distance alone explained over 97% of the variability in the cortical current density magnitude, suggesting that the distance between the scalp and cortex is an important predictor of the expected degree of attenuation when TMS is used in the settings of cortical atrophy. However, no one single function based on the distance alone could predict the degree of attenuation for the coil placed at different locations on the scalp (or for a single coil position at different locations). Our data strongly indicate that the functional form of the current magnitude attenuation differs between the two coil positions studied, suggesting that other factors such as the relative coil to scalp location and the electrical properties of the tissues significantly affect the final current density distribution.
In light of these findings, we conclude that the value of functions, based solely on static magnetic field measurements or simplified models as those adjusting the source magnetic field strength based on the scalp to cortex distance (Bohning 2000; Nahas et al. 2004; Knecht et al. 2005; Stokes et al. 2005) are insufficient and the implications of their clinical use need to be critically reevaluated.
Widened sulci models
For the TMS frequency spectrum and given tissue resistive values implemented in the model, the current density vector distribution is governed by the condition that the normal current density vector components must be continuous across boundaries of media with differing conductivities (Zahn 2003; Wagner et al. 2005). Thus, when one goes from the highly conductive CSF to the less conductive cerebral tissue at the widened sulci borders (or from the more conductive gray matter to the less conductive white matter), a jump in the normal component of the electrical field dictating final current density direction and magnitude along sulcal borders is expected. Thus, new small areas—less than 10 mm2—of maximum cortical current density magnitude found along the sulcal borders, are areas of least resistance indicative of these changes in current density distribution.
The extremes described in these widened sulci models (where current densities were seen in excess of 150% as compared to identical regions in the analogous atrophy models without altered sulci features) will most likely be rare in clinical cases of atrophy, since the linear edges will be more curvilinear in human brains. However, in large areas of perturbation surrounding these regions of extreme perturbation there was a consistent increase in the current density (see Fig. 4a). These current amplifications were dependent upon the geometry of the widened sulci and are basically indicative of regions with lowered resistance. In addition to the changes in magnitude, the current density vector orientation was altered along the sulcal borders. As stated above, the normal components of the current density must be continuous across tissue boundaries (CSF, white matter, gray matter) at sulcal borders, resulting in the alteration of the current density vector orientations (see Fig. 4b for an example).
It is important to note that many of those effects could also theoretically occur in normal sulcal regions to varying degrees. These will obviously depend on the geometry and electrical tissue distributions in the regions of the sulci, but earlier studies have clearly shown the effects of heterogeneities, as those operating at sulcal borders, can be extremely significant (Wagner 2001: Wagner et al. 2004, 2005; Miranda et al. 2003). As is supported by studies examining corner points in other electromagnetic models (Deeley 1990), we hypothesize that the effects will be most extensive at regions where the border geometries result in corner regions, such as could be seen along irregular edges of scar tissue along an infarction border. However, future studies need to be conducted to explore the subject since many other variables likely to have an influence (such as the effects of very tight sulcal folds) need further exploration (see Miranda et al. 2003 for further discussion).
Clinical implications
In this study we examined the alterations in the pattern of TMS induced current density distributions in both symmetric atrophy and widened sulci models. In the clinical setting, such clear demarcation of both types of structural abnormalities is unlikely and to some degree, a combination of both will be always present. According to our predictions, under conditions of increasing atrophy or sulcal width alterations, current density distributions will be altered in magnitude, orientation, and location; all of which might significantly alter the location and manner by which a core population of neural elements will be practically affected by TMS-induced currents, in spite of the initial targeting and intended plan. Even though the scalp-brain distance alone is not the only variable accounting for the final current density distributions, it is clear that the use of TMS under conditions of increasing scalp to cortical distances requires special precautions. In particular, one should not make use of varied scalp to cortex distance to infer a single, general stimulus intensity versus depth relationship. In vitro experimental and modeling data suggests that the site of activation is predicted by the peak electric field magnitude (Amassian et al. 1992; Maccabee et al. 1993; Nagarajan et al. 1993; Nagarajan and Durand 1995). Moreover, in vivo TMS experiments in both the motor and visual cortex have provided evidence that stimulation occurs at the location of the peak electric field (Wassermann et al. 1996; Krings et al. 1997; Boroojerdi et al. 1999). Thus, even with minimal changes in the neural architecture (i.e., relative neural cell to current density orientations) current density magnitude attenuation seen with increasing atrophy should lead to an expected alteration in physiological (e.g., MEP, phosphene values) or behavioral (recovery from a given cognitive sequel) outputs in atrophic regions as compared to nonatrophic areas (see Fig. 3b). This effect is nonlinear and brain location dependent; and as such, it cannot be captured by a single function as the current modifications will be patient specific and dependent upon the coil position relative to a the specific tissue distribution.
In spite of the demonstrated decay of the current density magnitude at increasing scalp-to-coil distances, simple linear increases in the applied TMS intensity should not be pursued in the clinical setting, even if there is no perturbation in the current location. Oftentimes brain atrophy is also associated with a change in brain activity and therefore the remaining active neurons in the atrophic brain might have an altered excitability, as proven for example in patients with Alzheimer’s and Parkinson’s disease displaying motor cortex hyperexcitability (Ridding et al. 1995; de Carvalho et al. 1997; Liepert et al. 2001; Bhatia et al. 2003; Di Lazzaro et al. 2004; Lefaucheur 2005), and thus respond differently to the same patterns of induced electric current.
In addition to the magnitude changes, the vector current density orientation in the cortex was altered proximal to the widened sulci. With such changes, different neural elements as those initially targeted could also be activated proximal to the sulci as it is clear that the directionality of the induced currents plays a clear role in which neurons are stimulated (Chiappa 1994). Finally, this study also provides evidence that the focus of induced current from TMS can be appreciably diminished in the region of widened sulci with multiple disjoint areas, around the sulcal borders, where the current density is near its maximum or greatly increased as compared to the corresponding atrophy models without the widened sulci. In cases where the coil is placed more proximal or overlying the widened sulci, the current density distributions will be even less predictable than those accounted for with the coil positions that were implemented (dependent upon the individual geometry and electrical makeup of the sulci) as has been seen in the case of stroke (Wagner et al. 2005).
Many of these problems could be addressed by combining electromagnetic field solvers, based on individualized MRI based solutions, with stereotactic tracking technology to provide the clinician with a tool to predict the location, orientation, and magnitude of stimulation based on the patients unique electromagnetic tissue interactions which constrain the final stimulating currents. In the meantime, until such a solution is implemented, care must be taken, particularly in regions of pathologies, to not make oversimplifications based on distance alone.
Study limitations and areas of future research
Some limitations of this study suggest areas of possible future research. First, the resolution of the model is constrained by the CAD rendering of the human head, which unfortunately does not share the same resolution as the MRI that was used to derive it. The shape of the widened sulci was similarly limited in detail because of the same resolution restrictions. In order to cope with these limitations, the field solver must be modified to work on structural high spatial resolution MRI data sets directly. Additionally, further research needs to be completed on the low frequency tissue electrical properties to account for their dispersive properties, anisotropies, and heterogeneities. The model should be expanded in the future to account for these tissue properties as data becomes available. Finally, we limited our discussion to the cortical current densities and their perturbation by structural alterations during the “on line” local effects of TMS and in the future the models could be extended to address “off line” effects through the integration of physiological models of stimulation derived from human or animal studies (Valero-Cabre et al. 2005, 2006, 2007; Wagner et al. 2007).
Conclusions
We demonstrate that TMS induced currents in the cortex can be modified in magnitude, location, and orientation under conditions of brain atrophy and/or sulcus widening. These cortical current density perturbations could prove to be dangerous or at the very least lead to unreliable results as those initially intended if guided by computational TMS neuronavigation and current distribution models that neglect the crucial role of structural and tissue electromagnetic alterations induced by the underlying conditions of the treated patients. Future efforts and model refinements will help to further increase our understanding of the effects of atrophy on TMS.
Acknowledgments
We acknowledge the contribution of the Maxwell software from the Ansoft Corporation, Pittsburgh, PA that was used in this study. This work was supported in part by Center for Integration of Medicine and Innovative Technology (CIMIT) under Grant numbers 45335 and 20736, and by grants from the National Institutes of Health (K24 RR018875, RO1 EY12091, R01 EB005047, RO1 DC05672, RO1 NS47754, RO1 NS20068). F.F. received support under a grant from the Harvard Medical School Scholars in Clinical Science Program (NIH K30 HL04095-03). AV-C was supported in part by the National Institutes of Health (NS32137 and NS33975 to BP/MM-AVC, and grants from ‘La Caixa’ (Spain) and the Spanish Ministry of Education Culture and Sports, EX2002-041).
Contributor Information
Tim Wagner, Email: twagner@alum.mit.edu, Division of Health Sciences and Technology, Harvard Medical School/Massachusetts Institute of Technology, Boston, MA, USA; Harvard Center for Non-Invasive Brain Stimulation, Beth Israel Deaconess Medical Center, 330 Brookline Ave # KS452, Boston, MA 02215, USA; Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA, USA.
Uri Eden, Division of Health Sciences and Technology, Harvard Medical School/Massachusetts Institute of Technology, Boston, MA, USA; Department of Mathematics and Statistics, Boston University, Boston, MA, USA.
Felipe Fregni, Harvard Center for Non-Invasive Brain Stimulation, Beth Israel Deaconess Medical Center, 330 Brookline Ave # KS452, Boston, MA 02215, USA.
Antoni Valero-Cabre, Harvard Center for Non-Invasive Brain Stimulation, Beth Israel Deaconess Medical Center, 330 Brookline Ave # KS452, Boston, MA 02215, USA; Boston University School of Medicine, Boston, MA, USA; CNRS UMR 5105, Grenoble, ERT TREAT Vision and Department of Neurology, Fondation Ophtalmologique Rothschild, Paris, France.
Ciro Ramos-Estebanez, Harvard Center for Non-Invasive Brain Stimulation, Beth Israel Deaconess Medical Center, 330 Brookline Ave # KS452, Boston, MA 02215, USA.
Valerie Pronio-Stelluto, Division of Health Sciences and Technology, Harvard Medical School/Massachusetts Institute of Technology, Boston, MA, USA.
Alan Grodzinsky, Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA, USA; Center for Biomedical Engineering, Massachusetts Institute of Technology, Cambridge, MA, USA.
Markus Zahn, Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA, USA.
Alvaro Pascual-Leone, Harvard Center for Non-Invasive Brain Stimulation, Beth Israel Deaconess Medical Center, 330 Brookline Ave # KS452, Boston, MA 02215, USA.
References
- Akhtari M, Bryant HC, Mamelak AN, Flynn ER, Heller L, Shih JJ, Mandelkern M, Matlachov A, Ranken DM, Best ED, DiMauro MA, Lee RR, Sutherling WW. Conductivities of three-layer live human skull. Brain Topogr. 2002;14:151–167. doi: 10.1023/a:1014590923185. [DOI] [PubMed] [Google Scholar]
- Alagona G, Ferri R, Pennisi G, Carnemolla A, Maci T, Domina E, Maertens de Noordhout A, Bella R. Motor cortex excitability in Alzheimer’s disease and in subcortical ischemic vascular dementia. Neurosci Lett. 2004;362:95–98. doi: 10.1016/j.neulet.2004.03.006. [DOI] [PubMed] [Google Scholar]
- Amassian V, Eberle L, Maccabee P, Cracco R. Modeling magnetic coil excitation of human cerebral cortex with a peripheral nerve immersed in a brain-shape volume conductor: the signicance of fiber bending in excitation. Electroenceph clin Neurophysiol. 1992;85:291–301. doi: 10.1016/0168-5597(92)90105-k. [DOI] [PubMed] [Google Scholar]
- Ansoft. Maxwell 3D. Ansoft; Pittsburgh: 2002. [Google Scholar]
- Barker AT, Freeston IL, Jalinous R, Merton PA, Morton HB. Magnetic stimulation of the human brain. J Physiol (Lond) 1985;369:3. abstract. [Google Scholar]
- Bhatia M, Johri S, Behari M. Increased cortical excitability with longer duration of Parkinson’s disease as evaluated by transcranial magnetic stimulation. Neurol India. 2003;51:13–15. [PubMed] [Google Scholar]
- Bohning D. Introduction and overview of TMS physics. In: George MS, Belmaker B, editors. Transcranial magnetic stimulation in neuropsychiatry. American Psychiatric Press; Washington DC: 2000. [Google Scholar]
- Boroojerdi B, Foltys H, Krings T, Spetzger U, Thron A, Topper R. Localization of the motor hand area using transcranial magnetic stimulation and functional magnetic resonance imaging. Clin Neurophysiol. 1999;110:699–704. doi: 10.1016/s1388-2457(98)00027-3. [DOI] [PubMed] [Google Scholar]
- Chiappa KH. Transcranial motor evoked potentials. Electromyogr Clin Neurophysiol. 1994;34:15–21. [PubMed] [Google Scholar]
- Crille GW, Hosmer HR, Rowland AF. The electrical conductivity of animal tissues under normal and pathological conditions. Am J Physiol. 1922;60:59–106. [Google Scholar]
- Daniele O, Brighina F, Piazza A, Giglia G, Scalia S, Fierro B. Low-frequency transcranial magnetic stimulation in patients with cortical dysplasia—a preliminary study. J Neurol. 2003;250:761–762. doi: 10.1007/s00415-003-1080-6. [DOI] [PubMed] [Google Scholar]
- de Carvalho M, de Mendonca A, Miranda PC, Garcia C, Luis ML. Magnetic stimulation in Alzheimer’s disease. J Neurol. 1997;244:304–307. doi: 10.1007/s004150050091. [DOI] [PubMed] [Google Scholar]
- de Groot M, Hermann W, Steffen J, Wagner A, Grahmann F. Contralateral and ipsilateral repetitive transcranial magnetic stimulation in Parkinson patients. Nervenarzt. 2001;72:932–938. doi: 10.1007/s001150170006. [DOI] [PubMed] [Google Scholar]
- De Mercato G, Garcia Sanchez FJ. Correlation between low-frequency electric conductivity and permittivity in the diaphysis of bovine femoral bone. IEEE Trans Biomed Eng. 1992;39(5):523–526. doi: 10.1109/10.135546. [DOI] [PubMed] [Google Scholar]
- Deeley EM. Surface impedance near edges and corners in three-dimensional media. IEEE Trans Magn. 1990;26:712–714. [Google Scholar]
- Di Lazzaro V, Oliviero A, Pilato F, Saturno E, Dileone M, Marra C, Daniele A, Ghirlanda S, Gainotti G, Tonali PA. Motor cortex hyperexcitability to transcranial magnetic stimulation in Alzheimer’s disease. J Neurol Neurosurg Psychiatry. 2004;75:555–559. doi: 10.1136/jnnp.2003.018127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dissado LA. A fractal interpertation of the dielectric response of animal tissues. Phys Med Biol. 1990;35:1487–1503. doi: 10.1088/0031-9155/35/11/005. [DOI] [PubMed] [Google Scholar]
- Foster KR, Schwan HP. Dielectric properties of tissues. In: Polk C, Postow E, editors. Biological effects of electromagnetic fields. CRC Press; New York: 1996. pp. 25–102. [Google Scholar]
- Fregni F, Santos CM, Myczkowski ML, Rigolino R, Gallucci-Neto J, Barbosa ER, Valente KD, Pascual-Leone A, Marcolin MA. Repetitive transcranial magnetic stimulation is as effective as fluoxetine in the treatment of depression in patients with Parkinson’s disease. J Neurol Neurosurg Psychiatry. 2004;75:1171–1174. doi: 10.1136/jnnp.2003.027060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fregni F, Thome-Souza S, Bermpohl F, Marcolin MA, Herzog A, Pascual-Leone A, Valente KD. Antiepileptic effects of repetitive transcranial magnetic stimulation in patients with Cortical malformations: an EEG and clinical study. Stereotact Funct Neurosurg. 2005;83:57–62. doi: 10.1159/000086674. [DOI] [PubMed] [Google Scholar]
- Freygang WH, Landau WM. Some relations between resistivity and electrical activity in the cerebral cortex of the cat. J Cell Comp Physiol. 1955;45:377–392. doi: 10.1002/jcp.1030450305. [DOI] [PubMed] [Google Scholar]
- Gabriel C, Gabriel S. Air Force Material Command. Brooks Air Force Base; San Antonio: 1996. Compilation of the dielectric properties of body tissues at RF and microwave frequencies. [Google Scholar]
- Geddes LA. Optimal stimulus duration for extracranial cortical stimulation. Neurosurgery. 1987;20:94–99. doi: 10.1097/00006123-198701000-00023. [DOI] [PubMed] [Google Scholar]
- George MS, Nahas Z, Molloy M, Speer AM, Oliver NC, Li XB, Arana GW, Risch SC, Ballenger JC. A controlled trial of daily left prefrontal cortex TMS for treating depression. Biol Psychiatry. 2000;48:962–970. doi: 10.1016/s0006-3223(00)01048-9. [DOI] [PubMed] [Google Scholar]
- Hart FX, Toll RB, Berner NJ, Bennett NH. The low frequency dielectric properties of octopus arm muscle measured in vivo. Phys Med Biol. 1996;41:2043–2052. doi: 10.1088/0031-9155/41/10/013. [DOI] [PubMed] [Google Scholar]
- Hasted JB. Aqueous dielectrics. Halsted Press; New York: 1973. [Google Scholar]
- Hoffman RE, Hawkins KA, Gueorguieva R, Boutros NN, Rachid F, Carroll K, Krystal JH. Transcranial magnetic stimulation of left temporoparietal cortex and medication-resistant auditory hallucinations. Arch Gen Psychiatry. 2003;60:49–56. doi: 10.1001/archpsyc.60.1.49. [DOI] [PubMed] [Google Scholar]
- Holtzheimer PE, Avery D, Schlaepfer TE. Antidepressant effects of repetitive transcranial magnetic stimulation. Br J Psychiatry. 2004;184:541–542. doi: 10.1192/bjp.184.6.541-a. [DOI] [PubMed] [Google Scholar]
- Huang YZ, Edwards MJ, Bhatia KP, Rothwell JC. One-Hz repetitive transcranial magnetic stimulation of the premotor cortex alters reciprocal inhibition in DYT1 dystonia. Mov Disord. 2004;19:54–59. doi: 10.1002/mds.10627. [DOI] [PubMed] [Google Scholar]
- Kammer T, Puls K, Strasburger H, Hill NJ, Wichmann FA. Transcranial magnetic stimulation in the visual system I. The psychophysics of visual suppression. Exp Brain Res. 2004;160(1):118–128. doi: 10.1007/s00221-004-1991-1. [DOI] [PubMed] [Google Scholar]
- Khedr EM, Farweez HM, Islam H. Therapeutic effect of repetitive transcranial magnetic stimulation on motor function in Parkinson’s disease patients. Eur J Neurol. 2003;10:567–572. doi: 10.1046/j.1468-1331.2003.00649.x. [DOI] [PubMed] [Google Scholar]
- Knecht S, Sommer J, Deppe M, Steinstrater O. Scalp position and efficacy of transcranial magnetic stimulation. Clin Neurophysiol. 2005;116:1988–1993. doi: 10.1016/j.clinph.2005.04.016. [DOI] [PubMed] [Google Scholar]
- Krings T, Buchbinder BR, Butler WE, Chiappa KH, Jiang HJ, Cosgrove GR, Rosen BR. Functional magnetic resonance imaging and transcranial magnetic stimulation: complementary approaches in the evaluation of cortical motor function. Neurology. 1997;48:1406–1416. doi: 10.1212/wnl.48.5.1406. [DOI] [PubMed] [Google Scholar]
- Kuhn AA, Grosse P, Holtz K, Brown P, Meyer BU, Kupsch A. Patterns of abnormal motor cortex excitability in atypical parkinsonian syndromes. Clin Neurophysiol. 2004;115:1786–1795. doi: 10.1016/j.clinph.2004.03.020. [DOI] [PubMed] [Google Scholar]
- Lee SH, Kim W, Chung YC, Jung KH, Bahk WM, Jun TY, Kim KS, George MS, Chae JH. A double blind study showing that two weeks of daily repetitive TMS over the left or right temporoparietal cortex reduces symptoms in patients with schizophrenia who are having treatment-refractory auditory hallucinations. Neurosci Lett. 2005;376:177–181. doi: 10.1016/j.neulet.2004.11.048. [DOI] [PubMed] [Google Scholar]
- Lefaucheur JP. Motor cortex dysfunction revealed by cortical excitability studies in Parkinson’s disease: influence of antiparkinsonian treatment and cortical stimulation. Clin Neurophysiol. 2005;116:244–253. doi: 10.1016/j.clinph.2004.11.017. [DOI] [PubMed] [Google Scholar]
- Lefaucheur JP, Drouot X, Von Raison F, Menard-Lefaucheur I, Cesaro P, Nguyen JP. Improvement of motor performance and modulation of cortical excitability by repetitive transcranial magnetic stimulation of the motor cortex in Parkinson’s disease. Clin Neurophysiol. 2004;115:2530–2541. doi: 10.1016/j.clinph.2004.05.025. [DOI] [PubMed] [Google Scholar]
- Lepeschkin E. Modern electrophysiology. Williams and Wilkins; Baltimore: 1951. [Google Scholar]
- Liepert J, Bar KJ, Meske U, Weiller C. Motor cortex disinhibition in Alzheimer’s disease. Clin Neurophysiol. 2001;112:1436–1441. doi: 10.1016/s1388-2457(01)00554-5. [DOI] [PubMed] [Google Scholar]
- Liu R, Ueno S. Calculating the activating function of nerve excitation in inhomogeneous volume conductor during magnetic stimulation using the finite element method. IEEE Trans Magn. 2000;36:1796–1799. [Google Scholar]
- Maccabee P, Amassian V, Eberle L, Cracco R. Magnetic coil stimulation of straight and bent amphibian and mammallian peripheral nerve in vitro: locus of excitation. J Physiol. 1993;460:201–219. doi: 10.1113/jphysiol.1993.sp019467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mally J, Stone TW. Improvement in Parkinsonian symptoms after repetitive transcranial magnetic stimulation. J Neurol Sci. 1999;162:179–184. doi: 10.1016/s0022-510x(98)00318-9. [DOI] [PubMed] [Google Scholar]
- Mansur CG, Fregni F, Boggio PS, Riberto M, Gallucci-Neto J, Santos CM, Wagner T, Rigonatti SP, Marcolin MA, Pascual-Leone A. A sham stimulation-controlled trial of rTMS of the unaffected hemisphere in stroke patients. Neurology. 2005;64:1802–1804. doi: 10.1212/01.WNL.0000161839.38079.92. [DOI] [PubMed] [Google Scholar]
- Martin JL, Barbanoj MJ, Schlaepfer TE, Thompson E, Perez V, Kulisevsky J. Repetitive transcranial magnetic stimulation for the treatment of depression. Systematic review and meta-analysis. Br J Psychiatry. 2003;182:480–491. doi: 10.1192/bjp.182.6.480. [DOI] [PubMed] [Google Scholar]
- Menkes DL, Gruenthal M. Slow-frequency repetitive transcranial magnetic stimulation in a patient with focal cortical dysplasia. Epilepsia. 2000;41:240–242. doi: 10.1111/j.1528-1157.2000.tb00146.x. [DOI] [PubMed] [Google Scholar]
- Miranda PC, Hallett M, Basser PJ. The electric field induced in the brain by magnetic stimulation: a 3-D finite-element analysis of the effect of tissue heterogeneity and anisotropy. IEEE Trans Biomed Eng. 2003;50:1074–1085. doi: 10.1109/TBME.2003.816079. [DOI] [PubMed] [Google Scholar]
- Modugno N, Curra A, Giovannelli M, Priori A, Squitieri F, Ruggieri S, Manfredi M, Berardelli A. The prolonged cortical silent period in patients with Huntington’s disease. Clin Neurophysiol. 2001;112:1470–1474. doi: 10.1016/s1388-2457(01)00599-5. [DOI] [PubMed] [Google Scholar]
- Nagarajan S, Durand DM. Analysis of magnetic stimulation of a concentric axon in a nerve bundle. IEEE Trans Biomed Eng. 1995;42:926–933. doi: 10.1109/10.412659. [DOI] [PubMed] [Google Scholar]
- Nagarajan S, Durand DM, Warman EN. Effects of induced electric fields on finite neuronal structures: a simulation study. IEEE Trans Biomed Eng. 1993;40:1175–1188. doi: 10.1109/10.245636. [DOI] [PubMed] [Google Scholar]
- Nahas Z, Li X, Kozel FA, Mirzki D, Memon M, Miller K, Yamanaka K, Anderson B, Chae JH, Bohning DE, Mintzer J, George MS. Safety and benefits of distance-adjusted prefrontal transcranial magnetic stimulation in depressed patients 55–75 years of age: a pilot study. Depress Anxiety. 2004;19:249–256. doi: 10.1002/da.20015. [DOI] [PubMed] [Google Scholar]
- Oswald K. Messung der leitfahigkeit und Dielektrizitatkonstante biologischer Gewebe un Flussigkeiten bei kurzen Wellen. Hochfreq Tech Elektroakust. 1937;49:40–49. [Google Scholar]
- Pascual-Leone A, Rubio B, Pallardo F, Catala MD. Rapid-rate transcranial magnetic stimulation of left dorsolateral prefrontal cortex in drug-resistant depression. Lancet. 1996;348:233–237. doi: 10.1016/s0140-6736(96)01219-6. [DOI] [PubMed] [Google Scholar]
- Pawitan Y. In all likelihood: statistical modelling and inference using likelihood. Oxford University Press; New York: 2001. [Google Scholar]
- Pethig R, Kell DB. The passive electrical propeties of biological systems: their signicance in physiology, biophysics, and biotechnology. Phys Med Biol. 1987;32:933–970. doi: 10.1088/0031-9155/32/8/001. [DOI] [PubMed] [Google Scholar]
- Pierantozzi M, Panella M, Palmieri MG, Koch G, Giordano A, Marciani MG, Bernardi G, Stanzione P, Stefani A. Different TMS patterns of intracortical inhibition in early onset Alzheimer dementia and frontotemporal dementia. Clin Neurophysiol. 2004;115:2410–2418. doi: 10.1016/j.clinph.2004.04.022. [DOI] [PubMed] [Google Scholar]
- Radvan-Ziemnowicz JC, McWilliams JC, Kucharski WE. Conductivity versus frequency in human and feline cerebrospinal fluid. In: Werner Ma., editor. Proceedings of 17th annual conference in medicine and Biology. Washington 12, DC: 1964. [Google Scholar]
- Ranck JB., Jr Analysis of specific impedance of rabbit cerebral cortex. Exp Neurol. 1963;7:153–174. doi: 10.1016/s0014-4886(63)80006-0. [DOI] [PubMed] [Google Scholar]
- Ridding MC, Inzelberg R, Rothwell JC. Changes in excitability of motor cortical circuitry in patients with Parkinson’s disease. Ann Neurol. 1995;37:181–188. doi: 10.1002/ana.410370208. [DOI] [PubMed] [Google Scholar]
- Rumi DO, Gattaz WF, Rigonatti SP, Rosa MA, Fregni F, Rosa MO, Mansur C, Myczkowski ML, Moreno RA, Marcolin MA. Transcranial magnetic stimulation accelerates the antidepressant effect of amitriptyline in severe depression: a double-blind placebo-controlled study. Biol Psychiatry. 2005;57:162–166. doi: 10.1016/j.biopsych.2004.10.029. [DOI] [PubMed] [Google Scholar]
- Sakuishi K, Hanajima R, Kanazawa I, Ugawa Y. Periodic motor cortical excitability changes associated with PSDs of EEG in Creutzfeldt–Jakob disease (CJD) Clin Neurophysiol. 2005;116:1222–1226. doi: 10.1016/j.clinph.2005.01.004. [DOI] [PubMed] [Google Scholar]
- Silbert LC, Quinn JF, Moore MM, Corbridge E, Ball MJ, Murdoch G, Sexton G, Kaye JA. Changes in premorbid brain volume predict Alzheimer’s disease pathology. Neurology. 2003;61:487–492. doi: 10.1212/01.wnl.0000079053.77227.14. [DOI] [PubMed] [Google Scholar]
- Sowell ER, Peterson BS, Thompson PM, Welcome SE, Henkenius AL, Toga AW. Mapping cortical change across the human life span. Nat Neurosci. 2003;6:309–315. doi: 10.1038/nn1008. [DOI] [PubMed] [Google Scholar]
- Stokes MG, Chambers CD, Gould IC, Henderson TR, Janko NE, Allen NB, Mattingley JB. A simple metric for scaling motor threshold based on scalp-cortex distance: application to studies using transcranial magnetic stimulation. J Neurophysiol. 2005;94(6):4520–4527. doi: 10.1152/jn.00067.2005. [DOI] [PubMed] [Google Scholar]
- Tergau F, Naumann U, Paulus W, Steinhoff BJ. Low-frequency repetitive transcranial magnetic stimulation improves intractable epilepsy. Lancet. 1999;353:2209. doi: 10.1016/S0140-6736(99)01301-X. [DOI] [PubMed] [Google Scholar]
- Valero-Cabre A, Rushmore R, Lomber SG, Payne BR, Pascual-Leone A. Impact of repetitive transcranial magnetic stimulation of the parietal cortex on metabolic brain activity: a 14C-2DG tracing study in the cat. Exp Brain Res. 2005;163:1–12. doi: 10.1007/s00221-004-2140-6. [DOI] [PubMed] [Google Scholar]
- Valero-Cabre A, Rushmore RJ, Payne BR. Low frequency transcranial magnetic stimulation on the posterior parietal cortex induces visuotopically specific neglect-like syndrome. Exp Brain Res. 2006;172:14–21. doi: 10.1007/s00221-005-0307-4. [DOI] [PubMed] [Google Scholar]
- Valero-Cabre A, Payne BR, Pascual-Leone A. Opposite impact on (14)C-2-deoxyglucose brain metabolism following patterns of high and low frequency repetitive transcranial magnetic stimulation in the posterior parietal cortex. Exp Brain Res. 2007;176:603–615. doi: 10.1007/s00221-006-0639-8. [DOI] [PubMed] [Google Scholar]
- Wagner T. EECS. Massachusetts Institute of Technology; Cambridge: 2001. Field distributions within the human cortex induced by transcranial magnetic stimulation; p. 186. [Google Scholar]
- Wagner TA, Zahn M, Grodzinsky AJ, Pascual-Leone A. Three-dimensional head model simulation of transcranial magnetic stimulation. IEEE Trans Biomed Eng. 2004;51:1586–1598. doi: 10.1109/TBME.2004.827925. [DOI] [PubMed] [Google Scholar]
- Wagner T, Fregni F, Eden U, Ramos-Estebanez C, Grodzinsky A, Zahn M, Pascual AP. Transcranial magnetic stimulation and stroke: a computer based human model study. Neuroimage. 2005;30(3):857–870. doi: 10.1016/j.neuroimage.2005.04.046. [DOI] [PubMed] [Google Scholar]
- Wagner T, Valero-Cabre A, Pascual-Leone A. Noninvasive human brain stimulation. Annu Rev Biomed Eng. 2007;9:527–565. doi: 10.1146/annurev.bioeng.9.061206.133100. [DOI] [PubMed] [Google Scholar]
- Wassermann EM, Wang B, Zeffiro TA, Sadato N, Pascual-Leone A, Toro C, Hallett M. Locating the motor cortex on the MRI with transcranial magnetic stimulation and PET. Neuroimage. 1996;3:1–9. doi: 10.1006/nimg.1996.0001. [DOI] [PubMed] [Google Scholar]
- Yunokuchi K, Kato R, Yoshida H, Tamari Y, Saito M. Study on the distributions of induced electric field in an inhomogeneous medium exposed a pulsed magnetic field. Annual international conference of the IEEE of the engineering in medicine and biology society. 1998;6:3294–3297. [Google Scholar]
- Zahn M. Electromagnetic field theory: a problem solving approach. Krieger Publishing Company; Melbourne: 2003. [Google Scholar]


