Abstract
Purpose
3,3′-Diindolylmethane (DIM) is the major in vivo product of the acid-catalyzed oligomerization of indole-3-carbinol present in cruciferous vegetables. 1, 1-bis (3′-indolyl)-1-(p-substituted phenyl) methanes [C-substituted diindolylmethanes (C-DIMs)] are a new class of anticancer compounds derived from indole 3-carbinol. Despite rapidly increasing knowledge regarding mechanisms responsible for the chemopreventive properties of DIM-C-pPhC6H5, there have been relatively few studies determining the absorption and pharmacokinetic properties of DIM-C-pPhC6H5 to explore its clinical utility.
Methods
In this study, we assessed the solubility, lipophilicity and Caco-2 cell permeability of methylene-substituted DIM. Pharmacokinetic properties in rats were determined following i.v. and oral administration of a novel analog of DIM. Pharmacokinetic parameters were determined using noncompartmental and compartmental techniques with WinNonlin® 5.0 software. To explore potential In Vitro–In Vivo Correlation (IVIVC) between the in vitro permeability values, and the oral absorption pharmacokinetics, we employed deconvolution of i.v. and oral data using a three compartment Exact Loo–Riegelman method.
Results
The oral absorption and disposition were described by a three compartment model with combined zero-order/Michaelis–Menten limited systemic uptake using differential equations, at physiologically relevant doses. The saturation model obtained accounts for a nonlinear change in Cmax/Dose, and the absolute bioavailability (0.13 ± 0.06) was also dose dependent. The absorption rate profile of DIMC-pPhC6H5 across Caco-2 cells was significantly different than in vivo. Conclusions: The pharmacokinetic absorption model presented represents a useful basis for obtaining plasma level predictability for poorly bioavailable, highly lipophilic drugs, such as the DIM analog DIM-C-pPhC6H5.
Keywords: Anticancer, Pharmacokinetic model, Chemoprevention, DIM, Anticarcinogen
1. Introduction
Bis(3′-indolyl)methane (or 3,3′-diindolylmethane (DIM)) is an active metabolite of indole-3-carbinol (I3C) (Fig. 1A) derived from cruciferous vegetables and this compound exhibits a broad spectrum of anticancer activities including its antiestrogenic and antiandrogenic effects(Chang et al., 2005; Nachshon-Kedmi et al., 2004). DIM has poor oral bioavailability due to its low solubility/high lipophilicity (Lipinski et al., 2001) and it is very well known that compounds such as DIM with Log K0/w values greater than four have limited absorption from intestinal lumen. Administration of DIM by intraperitoneal injection to rats induces CYP-450 to a greater extent than observed after oral administration, indicative of impaired systemic absorption from the GI tract (Jellinck et al., 1993). Studies on DIM pharmacokinetics reveal dose-dependent absorption and nonlinear increases in Cmax, indicative of systemic absorption saturation (Reed et al., 2006, 2008). However, solubility-enhancing microencapsulated formulations of DIM with extended-release provide increased bioavailability suggestive of solubility-limited absorption (Anderton et al., 2004; Reed et al., 2008).
Fig. 1.
Structures of (A) indole-3-carbinol (I3C); (B) 3,3′ diindolylmethane (DIM); (C) DIM-C-pPhC6H5 (DIM-P).
Methylene-substituted 3,3′-diindolylmethanes (C-DIMs) are a new class of synthetic analogs of DIM which show structure dependent peroxisome proliferator-activated receptor-γ (PPARγ) agonist activity. These compounds are triarylmethane derivatives which differ from DIM (a diarylmethane) (Fig 1B), and C-DIMs activate unique growth inhibitory and proapoptotic pathways compared to DIM (Ichite et al., 2009; Safe et al., 2008). Studies on the activity of a series of 1, 1-bis(3′-indolyl)-1-(p-substituted phenyl)methane analogs showed that the p-phenyl derivative, DIM-C-pPhC6H5 (DIM-P) is a highly active PPARγ agonist (Qin et al., 2004). DIM-P is prepared by condensing indole with p-biphenyl carboxyaldehyde to give the triaryl methane compound containing two indole and one biphenyl ring (see Fig. 1C). The rationale behind the development of DIM-P was to retain and enhance the chemoprotective and chemotherapeutic properties of DIM, and shows cell context-dependent PPARγ dependent and independent mechanisms of action with potential for clinical applications (Ichite et al., 2009; Lei et al., 2008, 2006; Vanderlaag et al., 2008). Research in our laboratory has shown that DIM-P has promising activity against lung cancer in animal models via oral (Ichite et al., 2009) and inhalational delivery (Ichite et al., 2010). However, the overall ‘clinical utility’ of these lipophilic methylene-substituted DIMs, their pharmacokinetics and (oral) absolute bioavailability, have yet to be studied.
The current work evaluates whether the lipophilic DIM-P confers sufficient oral absorption and pharmacokinetic properties for clinical development. The role of drug lipophilicity in pharmacokinetics has been well established, and although larger, more lipophilic derivatives often confer high affinity binding to active sites, there is a concomitant increased risk of ‘developability’ – including oral absorption, permeation and solubility (Testa et al., 2000). The lipophilicity of a drug provides an indication of its ability to transfer to and from aqueous phases (such as the apical unstirred water layer) (Leeson and Springthorpe, 2007). If the lipophilicity of DIM analog and other novel compounds are too low/high, the compound loses “ADME druggability” which is a qualitative concept used to predict whether a chemical compound will be pharmacologically and biopharmaceutically viable as an orally administered drug in humans (Panchagnula and Thomas, 2000). Additionally, permeability studies are also essential and several correlations have been established between permeability coefficients determined in Caco-2 cells (Polli and Ginski, 1998) and artificial membrane based (PAMPA) (Sugano et al., 2003) models, and intestinal absorption rate constants.
In this study, we have developed a pharmacokinetic model that describes the absorption and disposition of this highly lipophilic DIM analog, and provide important insight on the mechanism of absorption of DIM-P from a vitamin E-TPGS formulation. In addition, we used the permeation properties of DIM-P in vitro (using Caco-2 monolayers and PAMPA) to understand the in vivo absorption rate profile which was constructed using Loo–Riegelman deconvolution. This work demonstrates predictability in the drug exposure metrics (i.e., absolute bioavailability and Cmax) of a highly lipophilic compound, while providing a potential framework for the mechanism of absorption of DIM-P from a vitamin E-TPGS formulation.
2. Materials and methods
2.1. Materials
DIM-P was prepared as described (Qin et al., 2004). Caco-2 cells were obtained from American Type Culture Collection (Rockville, MD, USA). Dulbecco’s modified Eagle’s medium with 20% fetal bovine serum, 1% nonessential amino acids and 0.25% trypsin–EDTA were obtained from Invitrogen (Grand Island, NY, USA). All culture media contained antibiotic–antimycotic solution of penicillin (5000 U/mL), streptomycin (0.1 mg/mL), and neomycin (0.2 mg/mL). Hank’s balanced salt solution (HBSS) and N-hydroxyethylpiperazine-N′-2-ethanesulfonate buffer solution (HEPES, pH 7.4) were obtained from Invitrogen. All other chemicals used were of analytical grade.
2.2. Animals
Male Sprague–Dawley rats weighing 240–350 g (Charles River Laboratories, Wilmington, MA, USA) were utilized for the studies. The protocol was approved by the Animal Care and Use Committee, Florida A & M University. Animals were maintained on standard animal chow and water ad libitum, in a climate controlled room (22 ± 1 °C @ 35–50% relative humidity) for one week prior to experiments.
2.3. Maintenance of cell cultures
Caco-2 cells (passage #29) were cultured at 37 °C with culture medium replaced every 2 days in an atmosphere of 5% CO2 and 95% relative humidity. Cells were harvested upon reaching approximately 80–90% confluence with 0.25% trypsin–EDTA. Cells were grown on 1.12 cm2 0.4 μm pore polycarbonate membrane inserts in 12 mm × 12 transwell permeable support plates (Corning, NY, USA). Caco-2 cells were seeded onto membranes at 100,000 cells/well. Individual wells received 1.5 mL of culture medium which was changed on alternate days. Confluent monolayers were used for experimentation ~21 days post seeding.
2.4. Experimental solubility and lipophilicity
Saturation solubility measurements were carried-out using shake-flask techniques, followed by reverse-phase HPLC (C-18) in 90% acetonitrile and 10% water at the λmax of 242 nm. Briefly, an excess amount of DIM-P was suspended in 1.0 mL of different buffers (citrate, HEPES, and phosphate) at GI relevant pH values of 2.0, 4.0, 5.0, 6.0, 7.0 and 8.0 in centrifuge tubes. The tubes were placed in a shaker at 25.0 ± 0.1 °C @ 1500 rpm for 24 h. Drug suspensions were left unshaken for overnight before centrifuged and supernatants passed through 0.1 μm filters prior to HPLC analysis. The lipophilicity was measured by determining the partition coefficient of DIM-P in an octanol:water system at pH 7.0. Octanol and water were mixed in 1:1 concentrations, and 1.0 mg of DIM-P was added to 4.0 mL of the binary mixture followed by vigorous shaking for 30 min. Mixtures were separated by centrifugation and filtered through 0.1 μm filters prior to HPLC analysis.
2.5. Bidirectional permeability in Caco-2 monolayers
Transepithelial electrical resistance (TEER) of Caco-2 monolayers was measured prior to all experiments using the EVOM volt-ohm-meter (Millicell-ERS; Millipore, USA) to ensure monolayer integrity. The TEER (Ω cm2) values of the cell monolayers were determined by the resistance (Ω) × effective membrane area (cm2). TEER values were measured across each cell monolayer prior to beginning the experimentation and at the last sample collection time point (Konsoula and Barile, 2007). Transport studies were initiated by removing culture medium from the apical (A) and basolateral (B) sides of the cell monolayer. Cells were washed once with HBSS (37 °C), and replaced with fresh 10 mM 2-(N-morpholino) ethanesulfonic acid (pH 5.0–5.8) or HEPES (pH 6.8–7.8) in HBSS, and equilibrated for 30 min. The volumes of A and B compartments were 0.5 and 1.5 mL, respectively. The monolayers were placed onto a plate shaker set at 30 rpm throughout the experiment to minimize the influence of the aqueous boundary layer. Cell monolayers were incubated for 120 min with continuous agitation at 37 °C with 100 μL of DIM-P solution (0.5 mg/mL) in the donor compartment at pH 5.0, 5.8 and 6.8. All samples were withdrawn from the receiver compartment, and replaced with fresh buffer at 15, 30, 45, 60, 90 and 120 min for HPLC analysis. The paracellular integrity of monolayers was ensured based on low permeability of Lucifer yellow (a passive diffusional marker) and TEER consistently above 400 Ω cm2. The effective permeability (Peff) (cm/s) was determined using Eq. (1):
| (1) |
where, VR is the volume of the receptor chamber, A is the surface area of the filter, C0 is the initial donor concentration, and dC/dt is the slope of the cumulative concentration in the receiver chamber with time.
2.6. Parallel artificial membrane permeability assay (PAMPA)
PAMPA is a non-cell-based permeability model (Kansy et al., 1998) which provides an estimate of a passive transcellular intrinsic permeability coefficient because it lacks transporter- and pore-mediated permeability (Chen et al., 2008). The PAMPA is a useful permeation model because it is robust, reproducible, relatively fast (2–16 h) and inexpensive. The PAMPA procedure was conducted according to the manufacturer’s protocol (pION Inc., Woburn, MA, USA). The PAMPA kit includes 96-well filter plates used as the permeation receptor and 96-well receiver plates used as the permeation donor. Phosphate buffered saline (PBS) (pH 7.4) was used both as donor and receptor buffer throughout the study. Immediately after the application of the artificial membrane, 150 μL of drug solution (equivalent to 100 μg/mL of DIM-P in donor compartment) was added to each well of the donor plate and PBS (250 μL) was added to each well of the receptor plate. The filter plate was then coupled with the receiver plate making sure the underside of the membrane was in contact with the buffer. The μION Gut-BoxTM (P/N 110205) was used to affect stirring (180 rpm) and enable environmental control. The PAMPA sandwich was formed when not stirred, and allowed to incubate in the Gut-Box at 23 ± 1 °C for 4 h in an atmosphere saturated in humidity and scrubbed free of oxygen and carbon dioxide. After the permeation time in the environmental box was reached, the PAMPA plate sandwich was separated, and both the donor and acceptor compartments were assayed for DIM-P concentrations by a UV microplate reader. The donor-to-receptor apparent permeability (Papp) was calculated using PAMPA Explorer™ software.
2.7. Pharmacokinetic studies
Pharmacokinetic properties of DIM-P in Sprague–Dawley rats were determined following i.v. and oral administration. Animals were randomly distributed into four experimental groups (n = 5). DIM-P was formulated by partly dissolving crystalline compound in 0.5 mL of ethanol and 500 mg of α-tocopherol polyethylene glycol succinate (TPGS), and diluted to 10 mL with distilled water slowly (≈over 2 min) to achieve a 2% (w/v) solution. The oral groups were given 20, 40, or 60 mg/kg of DIM-P by gastric gavage. The fourth group was dosed by injection into the tail vein (5.0 mg/kg). All animals were fasted overnight prior to drug administration with free access to water. Blood samples (250 μL) were withdrawn from the tail vein predose, and at the following time points after dosing: 0.017 (only following i.v. dosing), 0.25, 0.5, 0.75, 1, 3, 6, 8 and 24 h. After each blood sampling, an equal volume of sterile 0.9% sodium chloride solution containing heparin (100 U/mL) was injected via tail vein to maintain the blood volume. Samples were immediately centrifuged at approximately 1500g for 10 min at 4 °C and the plasma stored at −80 °C until HPLC analysis.
2.8. Bioanalytical method for plasma analysis
A bioanalytical method was developed and validated for accuracy, precision, linearity and limit of quantification for DIM-P. 100 μL of plasma samples were spiked with 50 μL of internal standard solution (100 μg/mL nimesulide in acetonitrile) and vortexed well. Drug was separated from plasma by protein precipitation using acetonitrile, and samples were vortexed and then subjected to centrifugation (15 min at 10,000g). Supernatant was resolved on a mobile phase consisting of acetonitrile and water (90:10% v/v) pumped through a Waters Symmetry® C18 guard column (5 μm, 3.9 × 20 mm) (Milford, MA, USA) and a Waters Symmetry® C18 column (5 μm, 4.6 × 250 mm) (Milford, MA, USA) at a flow rate of 1.0 mL/min and the eluent monitored at 242 nm. DIM-P in acetonitrile stock solution was used to prepare serial working standards in mobile phase. Quantification of DIM-P was accomplished by a linear calibration curve (R2 = 0.996) between 0.05 and 8.00 μg/mL using nimesulide as the internal standard. The recovery efficiency of DIM-P from plasma was greater than 90%. The validation parameters for accuracy ranged from 98.7% to 100.8%, and precision expressed as the relative standard deviation (RSD) and limit of quantification were 1.27% and 0.05 μg/mL, respectively.
2.9. Pharmacokinetic data analysis
Pharmacokinetic parameters were determined using non-compartmental and compartmental techniques with WinNonlin® 5.0 software (Pharsight Corporation, Mountain View, CA, USA). SHAM analysis (i.e., Slope, Height, Area, and Moment) (Jusko, 1980) utilized plasma concentration–time data to estimate the area under the curve (AUC), apparent terminal elimination rate constant (λz), terminal elimination half-life (t1/2), and the area under the first moment of the plasma concentration–time curve (AUMC). The AUC was calculated for each rat using the piecewise log trapezoidal areas and extrapolated to infinity by dividing λz into the last measured plasma concentration (i.e., Clast/λz). From the values of AUC0–∞ and AUMC0–∞, the clearance (CL), mean residence time (MRT) and volume of distribution at tissue equilibrium (Vss) were calculated based on noncompartmental monoexponential assumptions as: CL = Dose/AUC, MRT ≃ AUMC/AUC and Vss = CL × MRT. The noncompartmental parameters were calculated for each rat before averaging parameters in each dose group.
Compartmental modeling techniques were employed post hoc when absorption nonlinearity was detected as described in the following subsection. Data at each dose were pooled and simultaneously fitted into projected models via generalized least squares using WinNonlin® with appropriate variance error models, and non-compartmental estimates of parameters used as initial fitting parameters. Model discrimination was achieved via a series of goodness-of-fit criteria as described in this section.
2.10. Statistical analysis
Pooled data are expressed as mean ± standard deviations (SD) and model parameters as estimates with ± standard errors (SE). Means were compared between two groups by student’s t test and between three dose groups by one-way variance analysis (ANOVA); data were explored for two-way ANOVA analyses where applicable. Correlations between doses and parameters were sought by use of the linear regression coefficient (r) and the coefficient of determination (R2). Probability (p) values <0.05 were considered significant. Model discrimination was achieved by visual evaluation of goodness-of-fit, residual plots, standard errors, coefficient of variation (CV%), the planar and univariate CI95% of the parameter estimates and the smallest Akaike Information Criterion (AIC) of the objective function. Dose-proportionality was evaluated on PK metrics (e.g. AUC and Cmax) by fitting to the power model equation Metric = α × Doseβ. β was estimated with a 95% confidence interval from linear regression of log (AUC and Cmax) data against log (Dose) according to: log (Metric) = log α + β × log(Dose), where a perfectly dose proportional relationship exists if β = 1. All statistical analyses were performed using GraphPad Prism® 5.0 software (San Diego, CA).
3. Results
3.1. Solubility and lipophilicity of DIM-P
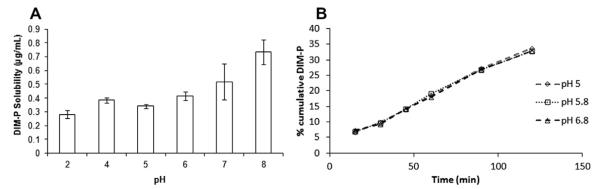
The maximum aqueous solubility of DIM-P was 0.73 ± 0.09 μg/mL (Log S = −6.03) at pH 8.0 which was significantly different than the observed aqueous solubility of 0.28 ± 0.03 μg/mL (Log S = −5.57) at pH 2.0 (p < 0.01) (Fig. 2). Although the aqueous solubility was pH sensitive across GI relevant pH values, overall solubility of DIM-P at pH range 2–8 remained less than 1.0 μg/mL. The experimental Log K0/w value was 6.79 ± 0.12. These experimentally determined values were similar to in silico values of −5.6 and 7.14 for Log S and Log K0/w respectively using the ALOGPs and ALOGpS algorithms (Tetko and Bruneau, 2004).
Fig. 2.
(A) pH-solubility profile of DIM-P (μg/mL vs pH), (B) cumulative amount of DIM-P absorbed through caco-2 monolayers at different apical pH.
3.2. Bidirectional permeability of DIM-P
The TEER values and mean permeability values of paracellular control Lucifer Yellow were >400 Ω cm2 and <0.15 × 10−6 cm/s, respectively which was within normal limits, thus confirming paracellular integrity of monolayers. The average Peff, A–B of DIM-P across Caco-2 cell monolayers (Table 1) was approximately 0.34 ± 0.08 × 10−6 cm/s, and B–A was 0.51 ± 0.09 × 10−6 cm/s. The TEER values of monolayers were indicative of tight junction integrity, and did not show any significant changes of TEER value throughout the experiment. The donor-to-receptor apparent permeability (Papp) values using the PAMPA assay for DIM-P was 0.58 ± 0.07 × 10−6 cm/s and 2.69 ± 0.08 × 10−6 cm/s, respectively for unstirred and stirred water layers, respectively.
Table 1.
Bidirectional permeability [apical to basolateral (A–B) and basolateral to apical (B–A)] of DIM-P across caco-2 monolayers at different apical pH.
| Permeation direction |
Peff × 10−6 cm/s |
||
|---|---|---|---|
| pH 5 | pH 5.8 | pH 6.8 | |
| A–B | 0.34 ± 0.06 | 0.33 ± 0.07 | 0.35 ± 0.06 |
| B–A | 0.53 ± 0.08 | 0.50 ± 0.06 | 0.52 ± 0.07 |
3.3. Noncompartmental pharmacokinetic characterization of DIM-P
The plasma concentration–time profiles of DIM-P following oral doses of 20, 40 and 60 mg/kg are shown in Fig. 3. The maximum plasma levels after administration of 20 and 40 mg/kg were observed after 2 h whereas at 60 mg/kg dose the maximum plasma level was observed at 3 h. SHAM analysis revealed an apparent nonlinear (i.e., sub proportional) increase in Cmax with increasing doses. After the peak plasma concentration was observed, DIM-P plasma concentrations declined in a biphasic manner. Noncompartmental pharmacokinetic parameters are shown in Table 2.
Fig. 3.
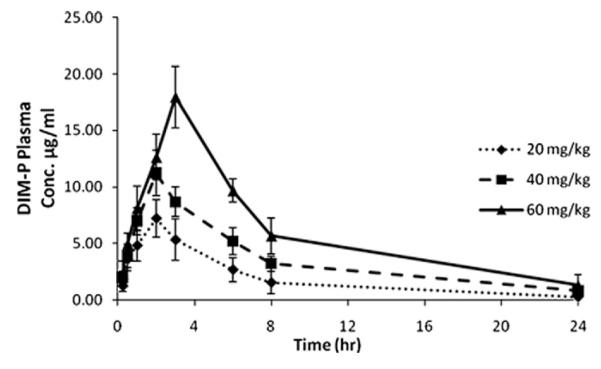
Plasma profile of DIM-P (μg/mL) in rats following 20, 40, and 60 mg/kg oral doses in vitamin E-TPGS solution.
Table 2.
Noncompartmental pharmacokinetic parameters for DIM-P in rats following oral administration.
| Parameter | DOSE (mg/kg) |
||
|---|---|---|---|
| 20 | 40 | 60 | |
| Cmax(μg/mL) | 7.21 ± 1.19 | 11.27 ± 1.04 | 17.86 ± 1.62 |
| Cmax/dose | 0.36 ± 0.06 | 0.28 ± 0.03* | 0.30 ± 0.03* |
| AUC0–24h (μg × min/mL) | 45.60 ± 9.23 | 84.41 ± 19.81 | 138.99 ± 28.01 |
| AUC0–24h /Dose (min/L) *10−3 | 2.28 ± 0.46 | 2.21 ± 0.50 | 2.32 ± 0.46 |
| AUMC0–24h (μg × min2/mL) | 250.45 ± 62.42 | 548.85 ± 207.09 | 912.16 ± 299.02 |
| AUMC0–24h/Dose (min2/mL) | 0.012 ± 0.003 | 0.014 ± 0.005 | 0.015 ± 0.005 |
| Terminal t1/2 (hr) | 6.91 ± 3.84 | 7.86 ± 3.12 | 7.60 ± 2.34 |
| Vss (mL/kg) | 499.79 ± 223.605 | 548.61 ± 164.78 | 542.39 ± 128.04 |
| CL (mL/kg/hr) | 51.91 ± 3.89 | 49.89 ± 4.52 | 50.38 ± 3.49 |
| MRT (hr) | 5.47 ± 0.64 | 6.29 ± 1.14 | 6.43 ± 0.81 |
| FBIO | 0.13 ± 0.03 | 0.12 ± 0.03 | 0.13 ± 0.03 |
p < 0.05
Dose proportionality analysis based on AUC0–24h (instead of AUC0–∞ due to larger than 10% total area from Clast to infinity) was suggestive of dose-independent kinetics. However the observed “less-than-proportional” increase in Cmax at higher doses relative to 20 mg/kg (p < 0.05) indicated a potential nonlinear process and therefore results for oral DIM-P were subjected to compartmental modeling.
3.4. Compartmental pharmacokinetic modeling
The plasma drug-concentration profile following i.v. administration of DIM-P showed a rapid decline (i.e., <2 h apparent distributional phase) followed by prolonged disposition through the sampling times. Thus, intravenous DIM-P was first investigated as a two compartment model compound. The two compartment linear model revealed a poor structural fit with the data (not shown), irrespective of the error model and was a strong indicator that another kinetic process may be involved. We proposed a third exponential in the model based on graphical observation of the data to account for the lack-of-fit.
To arrive at confident estimates, the rate of change of DIM-P concentrations in the plasma and tissue compartments for the 5.0 mg/kg group was fitted (see Fig. 4) to the following mass–balance differential equations for a three-compartment model:
| (2) |
| (3) |
| (4) |
where, Cp, C1 and C2 are the plasma and tissue concentrations of DIM-P; CL, CLd1, and CLd2 refer to the central and peripheral compartmental distributional clearances; and Vc, V1 and V2 are the apparent central and tissue compartmental distributional volumes of DIM-P. The initial conditions for Eqs. (3) and (4) were set to zero.
Fig. 4.
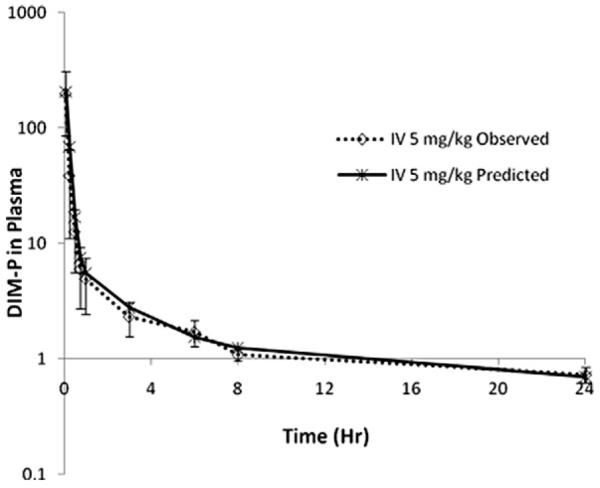
Three-compartment model fit following i.v. administration of DIM-P (5.0 mg/kg).
The primary and secondary parameters estimated from curve fitting following i.v. administration of 5.0 mg/kg are shown in Table 3. AUC calculated by the pharmacokinetic model (AUC0–∞ =(A/α)+(B/β)+(C/ξ)) was not significantly different from trapezoidal methods (p < 0.05), and secondary parameters were calculated according to:
| (5) |
| (6) |
Table 3.
Pharmacokinetic parameters for DIM-P estimated from three compartment model fitting following i.v. administration (5.0 mg/kg) in rats.
| Parameter | Estimate | CV% | |
|---|---|---|---|
| Primary | CLC (mL min−1 kg−1) | 0.74 | 20.9 |
| CLd1 (mL min−1 kg−1) | 0.56 | 23.03 | |
| CLd2 (mL min−1 kg−1) | 0.29 | 42.91 | |
| VC (mL kg−1) | 13.65 | 20.9 | |
| V1 (mL kg−1) | 640.98 | 75.01 | |
| V2 (mL kg−1) | 28.22 | 83.11 | |
| Secondary | VSS (mL kg−1) | 682.85 | – |
| t1/2 (min) | 639.18 | – |
The oral plasma-concentration profiles were then subjected to simultaneous model fitting with i.v. data, and we observed neither pure first order nor zero order input into the plasma. To probe the mechanism of drug input, we explored the use of zero order liberation of drug combined with an Input function for absorption saturation (as suggested by the nonlinear change in Cmax) which resulted in the following equations:
| (7) |
| (8) |
| (9) |
where, Tsite is the time required for drug to reach absorption site, SD50 is amount of drug at the absorption site at 50% saturation, Massgut is the amount of drug in gut available for absorption, FBIO is the absolute bioavailability and Abmax is the maximum absorption rate at saturation. The results from plasma concentration–time modeling of DIM-P following i.v. (5.0 mg/kg) and oral doses of 20, 40 and 60 mg/kg are shown in Fig. 5 with simultaneous fitting curves for oral and i.v. data. The absorption and disposition parameters estimated from simultaneous curve fitting following i.v. and oral administration are shown in Table 4.
Fig. 5.
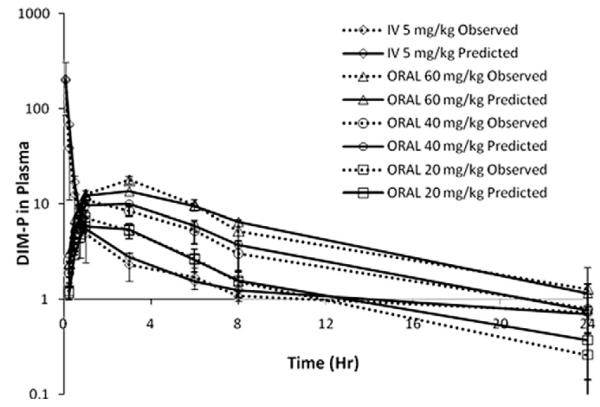
Simultaneous model fit following i.v. (5.0 mg/kg) and oral (20 mg/kg, 40 mg/kg and 60 mg/kg) administration of DIM-P in rats.
Table 4.
Pharmacokinetic parameters for DIM-P in rats following simultaneous three compartment model fit for i.v. and oral administration.
| Parameter | Estimate | CV% | |
|---|---|---|---|
| Disposition | CLC (mL min−1 kg−1) | 0.77 | 13.81 |
| CLd1 (mL min−1 kg−1) | 0.606 | 13.04 | |
| CLd2 (mL min−1 kg−1) | 0.319 | 24.86 | |
| VC (mL kg−1) | 13.9 | 16.04 | |
| V1 (mL kg−1) | 646.06 | 42.43 | |
| V2 (mL kg−1) | 28.50 | 47.17 | |
| Absorption | FBIO | 0.126 | 7.93 |
| Tsite (min) | 85.20 | 18.22 | |
| Abmax (μg min−1 kg−1) | 60.65 | 37.15 | |
| SD50 (μg kg−1) | 8679.7 | 55.76 |
4. Discussion
The objective of this work was to evaluate the biopharmaceutical and pharmacokinetic behavior of DIM-P. Pursuant to successful evaluation of the efficacy of DIM-P, a novel anticancer drug (Abdelrahim et al., 2006; Ichite et al., 2009; Lei et al., 2008, 2006), the clinical applications of DIM-P will be dependent on favorable pharmacokinetic properties. Addition of biphenyl ring on the DIM structure was critical for PPARγ activity; however this results in a very large increase in lipophilicity (Log K0/w ≈ 7.0 compared to ≈4.0 for DIM). The solubility of DIM-P was sensitive to pH but solubility remained less than 1.0 μg/mL from pH 2 to 8.
PAMPA and Caco-2 cells in combination can be effectively used to determine maximum permeability/absorption profile (Balimane et al., 2006) and the A–B effective permeability of 0.34 ± 0.08 × 10−6 cm/s for DIM-P was indicative of “low permeability”. As such DIM-P can be categorized as a Class IV drug substance according to the Biopharmaceutics Classification System (BCS), and the absorption characteristics would be expected to show strong formulation dependence. Additionally, there was no significant effect (p > 0.05) of pH on the apparent permeability, suggesting that the intra-duodenal pH gradient relative to the stomach would not impact the absorption or absolute bioavailability of DIM-P in the apical layer microenvironment at the concentrations investigated in this study. Likewise, the permeability at pH 5.0, 5.8 and 6.8 indicated that transcellular transport of DIM-P is likely to be independent of intestinal pH variations (Table 1). However, the unstirred water layer and mucous layers may be formidable barriers, as indicated by significant changes in donor-to-receptor apparent permeability (Papp) values of unstirred and stirred water layers (p < 0.05) observed in the PAMPA study. Our Caco-2 experiments employed a shaking technique to potentially mitigate the effect of unstirred layers; however the in vitro permeability remained poor. In contrast, the effect of an unstirred water layer on permeability was fairly dramatic in the PAMPA experiments (data not shown). The apparent permeability from PAMPA was slightly higher than the effective permeability in Caco-2 cells, and could suggest active efflux processes in Caco-2 cells. However, bidirectional Caco-2 studies showed no active efflux in comparing the absorptive (A–B) versus secretive (B–A) transport, which was nearly unity. The lack of an active efflux process coupled with the molecular size of DIM-P (M.W. ≈ 302 g/mol), and the unstirred water layer effect in the PAMPA experiment suggested a passive transcellular diffusion pathway with the unstirred water layer creating a rate-limiting barrier. As such, the absorption of DIM-P in vivo is expected to be dependent on limited solubility and slow transport across intestinal epithelial cells.
Noncompartmental analysis after oral administration of DIM-P (20, 40 and 60 mg/kg) suggested that the disposition kinetics was dose proportional and linear as indicated by an insignificant difference in dose-normalized AUC0–24h (Table 2), and hence the clearance. The oral profiles through 24 h consistently showed poor absolute bioavailability. The higher variability in Clast time points prevented us from relying on AUC0–∞, to evaluate the linearity, due to a large percent of total AUC extrapolation. It was noted in the results, that there was a nonlinear increase in Cmax and a longer Tmax with higher doses of DIM-P. The sub-proportional increase in observed Cmax suggested the presence of absorption saturation. Reed et al. reported similar results with DIM, where single 100, 200, and 300 mg doses of DIM resulted in Cmax values of 32, 104, and 108 ng/mL, respectively (Reed et al., 2008). This apparent nonlinear kinetic absorption process suggested that more information could be extracted from the data via compartment modeling.
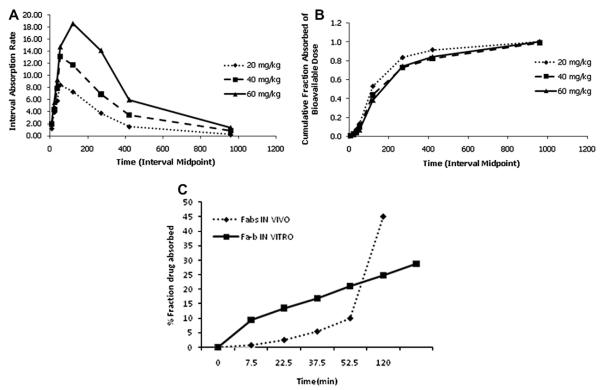
Due to the high lipophilicity of DIM-P and likely passive transcellular mechanism of absorption, we attempted to derive a potential In Vitro–In Vivo Correlation (IVIVC) between the in vitro permeability, and the oral absorption pharmacokinetics (Davis et al., 2006). We employed deconvolution of i.v. and oral data using a three compartment Loo–Riegelman method (Wagner, 1983)to determine the fraction absorbed (FA) with time in vivo (Fig. 6B), and compared this to our FA in Caco-2 cells (Karlsson, 1991). There was no correlation found between in vitro permeability values and the oral absorption pharmacokinetics (Fig. 6C). We observed an initial phase of reduced DIM-P absorption rates over 50 min following oral administration (Fig. 6A and C), which may have led to a lack of correlation with in vitro permeability assays. Generally, mechanisms which cause a delay in maximum absorption rates are slow physiological (e.g., gastric emptying) or physicochemical (e.g., dissolution) processes, and were explored via compartment modeling.
Fig. 6.
(A) DIM-P absorption rate vs time (in vivo deconvolution); (B) fraction of bioavailable dose absorbed vs time and (C) correlation comparison between fraction drug absorbed in vivo (Fabs) and in vitro (Fab).
We performed compartment modeling for i.v. administration at 5.0 mg/kg to obtain the characteristic impulse response of the system. The data was fit to a conventional bi-exponential relationship with various error models, however the structural fit was poor based on an array of goodness-of-fit measures and therefore the data was further investigated in a three compartment model. The results revealed a proper structural fit, with peripheral and deep tissue clearances lacking any overlap in the confidence interval of their estimates. Since Dim-P is highly lipophilic, it was very likely that the terminal phase or distribution equilibrium into deep compartments had not been reached at the end of the sampling period. As such, more extensive sampling and time-points beyond 24 h would be expected to more fully characterize the parameters in a three compartment model (Gustafson et al., 2003). It should be noted that confidently estimating six pharmacokinetic parameters in a three compartment model using 8 or 9 data points (i.e., low degrees of freedom) would require a selection of sampling times that minimize the determinant of the variance–covariance matrix, a D-optimal design, for precise parameter estimates. In this case, the model was not known a priori, and the ad hoc sampling schedule used in this study provides tissue distribution and terminal clearance parameters that should be viewed with caution. This Therefore, although the model was apparently consistent with the data, it was also potentially “ill-conditioned”. A three compartment model has been successfully utilized to explain the pharmacokinetic profile of other drug molecules, such as was used by Koolen et al. to describe pharmacokinetic data for docetaxel following intravenous and oral administration (Koolen et al., 2010). Similarly, propofol (Yamashita et al., 2010), a nonpolar compound, and troxacitabine (Ng et al., 2010), a polar compound, have been best described by three compartment model.
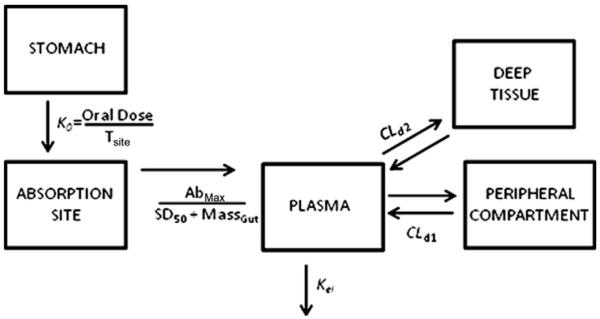
The lack of a data points for a three compartment model also likely contributed to high CV% for volume of distribution estimates (Table 2), and were expected to show more confidence following simultaneous oral fitting. To probe the mechanism of absorption, the oral datasets across three doses were pooled and fitted simultaneously with the i.v. data to obtain one set of pharmacokinetic parameters for DIM-P. We observed no modeling fits across three doses with simple zero-order input functions to potentially account for a completely saturated absorption site. Likewise, any attempts to fit first-order input functions (with or without lagtime), were met with very rapid absorption phases during simulations, which were poorly fit by the data. These approaches were followed by attempts to fit Michaelis–Menten absorption saturation expressions, assuming the data was approaching saturation at the higher doses used in our experiment. Again, we noticed no obtainable fits for the data. It was observed during our experiments that DIM-P precipitates if gastric stimulus fluid is added suddenly in the TPGS solution of DIM-P (data not shown). It was believed that the formulation in vivo may have resulted in (a) GI precipitation followed by a slow re-dissolution phase, or (b) oil–water partitioning release before absorption. This would result in a dramatically reduced initial absorption rate or dissolution/partitioning-controlled absorption. Analytical deconvolution of the absorption data using the Loo–Riegelman relationship (Wagner, 1983), revealed a low initial rate of absorption prior to absorption rate declines. Therefore a more detailed model was developed to combine zero-order release to a theoretical absorption site (as caused from re-dissolution, oil–water partitioning, or gastric emptying), and Michaelis–Menten absorption saturation processes in order to describe the data (see Fig. 7). The combined zero-order/Michaelis–Menten limited absorption, three compartment disposition model was observed to fit quite well (Fig. 5). The results suggest that the dose to cause 50% saturation of the absorption process was 8.7 mg/kg with a maximum absorption rate of 3.6 mg/hr/kg and zero-order absorption site access rates of 14, 28 and 42 mg/hr/kg for 20, 40 and 60 mg/kg doses respectively. We therefore hypothesized that the low solubility and high lipophilicity of DIM-P may cause constant rate access or appearance of soluble drug to the absorption site prior to a saturable uptake process. It should be noted that the available data and modeling however do not discern the mechanism of the apparent zero-order process, i.e., whether drug precipitation and zero-order re-dissolution or delayed zero-order gastric emptying is involved. This is because it was unknown if a low calorie oral gavage administered to the rats would induce a fed state sufficient for constant gastric emptying, thus the precise mechanism involved remained unknown. Lastly, low permeability, as observed in Caco-2 and PAMPA experiments, supported a hypothesis of transport resistance and absorption saturation potentially due to low solubility in an unstirred aqueous layer at the intestinal absorption sites.
Fig. 7.
Model diagram for DIM-P oral absorption three compartment kinetics.
5. Conclusion
DIM-P is potent anticarcinogenic compound but due to its low solubility, low permeability and poor absorption the clinical application of this compound are of concern. This work however shows that DIM-P can be administered in a routine vitamin ETPGS formulation and yield predictable plasma concentration levels using the absorption model presented. The results suggest that the use of novel formulations will also improve the uptake and absorption of DIM-P. These studies are currently ongoing in our laboratory in order to further increase the potential and clinical application of DIM-P alone and in combination with other anticancer agents.
Abbreviations
- DIM
3,3′-diindolylmethane
- C-DIMs
C-substituted diindolylmethanes
- IVIVC
In Vitro–In Vivo Correlation
- i.v.
intravenous
- PPARγ
peroxisome proliferator-activated receptor-γ
- HBSS
Hank’s balanced salt solution
- HEPES
N-hydroxyethylpiperazine-N′-2-ethanesulfonate buffer solution
- DIM-P
DIM-C-pPhC6H5
- TEER
transepithelial electrical resistance
- Ω
ohm
- PAMPA
parallel artificial membrane permeability assay
- TPGS
α-tocopherol polyethylene glycol succinate
- AUC
area under the curve
- λz
apparent terminal elimination rate constant
- t1/2
terminal elimination half-life
- AUMC
area under the first moment of the plasma concentration-time curve
- CL
clearance
- MRT
mean residence time
- Vss
volume of distribution at tissue equilibrium
Footnotes
Funding Funded by NIH Grant No. G12RR03020.
References
- Abdelrahim M, Newman K, Vanderlaag K, Samudio I, Safe S. 3,3′-Diindolylmethane (DIM) and its derivatives induce apoptosis in pancreatic cancer cells through endoplasmic reticulum stress-dependent upregulation of DR5. Carcinogenesis. 2006;27:717–728. doi: 10.1093/carcin/bgi270. [DOI] [PubMed] [Google Scholar]
- Anderton MJ, Manson MM, Verschoyle R, Gescher A, Steward WP, Williams ML, Mager DE. Physiological modeling of formulated and crystalline 3,3′-diindolylmethane pharmacokinetics following oral administration in mice. Drug Metab. Dispos. 2004;32:632–638. doi: 10.1124/dmd.32.6.632. [DOI] [PubMed] [Google Scholar]
- Balimane PV, Han YH, Chong S. Current industrial practices of assessing permeability and P-glycoprotein interaction. AAPS J. 2006;8:E1–E13. doi: 10.1208/aapsj080101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang X, Tou JC, Hong C, Kim HA, Riby JE, Firestone GL, Bjeldanes LF. 3,3′-Diindolylmethane inhibits angiogenesis and the growth of transplantable human breast carcinoma in athymic mice. Carcinogenesis. 2005;26:771–778. doi: 10.1093/carcin/bgi018. [DOI] [PubMed] [Google Scholar]
- Chen X, Murawski A, Patel K, Crespi CL, Balimane PV. A novel design of artificial membrane for improving the PAMPA model. Pharm. Res. 2008;25:1511–1520. doi: 10.1007/s11095-007-9517-8. [DOI] [PubMed] [Google Scholar]
- Davis JL, Little D, Blikslager AT, Papich MG. Mucosal permeability of water-soluble drugs in the equine jejunum: a preliminary investigation. J. Veterinary Pharmacol. Ther. 2006;29:379–385. doi: 10.1111/j.1365-2885.2006.00757.x. [DOI] [PubMed] [Google Scholar]
- Gustafson DL, Long ME, Zirrolli JA, Duncan MW, Holden SN, Pierson AS, Eckhardt SG. Analysis of docetaxel pharmacokinetics in humans with the inclusion of later sampling time-points afforded by the use of a sensitive tandem LCMS assay. Cancer Chemother. Pharmacol. 2003;52:159–166. doi: 10.1007/s00280-003-0622-z. [DOI] [PubMed] [Google Scholar]
- Ichite N, Chougule MB, Jackson T, Fulzele SV, Safe S, Singh M. Enhancement of docetaxel anticancer activity by a novel diindolylmethane compound in human non-small cell lung cancer. Clin. Cancer Res. 2009;15:543–552. doi: 10.1158/1078-0432.CCR-08-1558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ichite N, Chougule MB, Patel AR, Jackson T, Safe S, Singh M. Inhalation delivery of a novel diindolylmethane derivative for the treatment of lung cancer. Mol. Cancer Ther. 2010;9:3003–3014. doi: 10.1158/1535-7163.MCT-09-1104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jellinck PH, Forkert PG, Riddick DS, Okey AB, Michnovicz JJ, Bradlow HL. Ah receptor binding properties of indole carbinols and induction of hepatic estradiol hydroxylation. Biochem. Pharmacol. 1993;45:1129–1136. doi: 10.1016/0006-2952(93)90258-x. [DOI] [PubMed] [Google Scholar]
- Jusko WJ. Guidelines for collection and pharmacokinetic analysis of drug disposition data. In: Evans WE, S. JJ, Jusko WJ, editors. Applied Pharmacokinetics. Applied Therapeutics, Inc.; San Francisco: 1980. [Google Scholar]
- Kansy M, Senner F, Gubernator K. Physicochemical high throughput screening: parallel artificial membrane permeation assay in the description of passive absorption processes. J. Med. Chem. 1998;41:1007–1010. doi: 10.1021/jm970530e. [DOI] [PubMed] [Google Scholar]
- Karlsson P.A.a.J. Correlation between oral drug absorption in humans and apparent drug permeability coefficients in human intestinal epithelial (Caco-2) cells. Biochem. Biophys. Res. Commun. 1991;175:880–885. doi: 10.1016/0006-291x(91)91647-u. [DOI] [PubMed] [Google Scholar]
- Konsoula R, Barile FA. Correlation of in vitro cytotoxicity with paracellular permeability in mortal rat intestinal cells. J. Pharmacol. Toxicol. Methods. 2007;55:176–183. doi: 10.1016/j.vascn.2006.06.001. [DOI] [PubMed] [Google Scholar]
- Koolen SL, Oostendorp RL, Beijnen JH, Schellens JH, Huitema AD. Population pharmacokinetics of intravenously and orally administered docetaxel with or without co-administration of ritonavir in patients with advanced cancer. Br. J. Clin. Pharmacol. 2010;69:465–474. doi: 10.1111/j.1365-2125.2010.03621.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leeson PD, Springthorpe B. The influence of drug-like concepts on decision-making in medicinal chemistry. Nat. Rev. Drug Discov. 2007;6:881–890. doi: 10.1038/nrd2445. [DOI] [PubMed] [Google Scholar]
- Lei P, Abdelrahim M, Cho SD, Liu S, Chintharlapalli S, Safe S. 1,1-Bis(3′-indolyl)-1-(p-substituted phenyl)methanes inhibit colon cancer cell and tumor growth through activation of c-jun N-terminal kinase. Carcinogenesis. 2008;29:1139–1147. doi: 10.1093/carcin/bgn103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lei P, Abdelrahim M, Safe S. 1,1-Bis(3′-indolyl)-1-(p-substituted phenyl)methanes inhibit ovarian cancer cell growth through peroxisome proliferator-activated receptor-dependent and independent pathways. Mol. Cancer Ther. 2006;5:2324–2336. doi: 10.1158/1535-7163.MCT-06-0184. [DOI] [PubMed] [Google Scholar]
- Lipinski CA, Lombardo F, Dominy BW, Feeney PJ. Experimental and computational approaches to estimate solubility and permeability in drug discovery and development settings. Adv. Drug Deliv. Rev. 2001;46:3–26. doi: 10.1016/s0169-409x(00)00129-0. [DOI] [PubMed] [Google Scholar]
- Nachshon-Kedmi M, Fares FA, Yannai S. Therapeutic activity of 3,3′-diindolylmethane on prostate cancer in an in vivo model. Prostate. 2004;61:153–160. doi: 10.1002/pros.20092. [DOI] [PubMed] [Google Scholar]
- Ng CM, Patnaik A, Beeram M, Lin CC, Takimoto CH. Mechanism-based pharmacokinetic/pharmacodynamic model for troxacitabine-induced neutropenia in cancer patients. Cancer Chemother. Pharmacol. 2010;67(5):985–994. doi: 10.1007/s00280-010-1393-y. [DOI] [PubMed] [Google Scholar]
- Panchagnula R, Thomas NS. Biopharmaceutics and pharmacokinetics in drug research. Int. J. Pharm. 2000;201:131–150. doi: 10.1016/s0378-5173(00)00344-6. [DOI] [PubMed] [Google Scholar]
- Polli JE, Ginski MJ. Human drug absorption kinetics and comparison to Caco-2 monolayer permeabilities. Pharm. Res. 1998;15:47–52. doi: 10.1023/a:1011992518592. [DOI] [PubMed] [Google Scholar]
- Qin C, Morrow D, Stewart J, Spencer K, Porter W, Smith R, 3rd, Phillips T, Abdelrahim M, Samudio I, Safe S. A new class of peroxisome proliferator-activated receptor gamma (PPARgamma) agonists that inhibit growth of breast cancer cells: 1,1-Bis(3′-indolyl)-1-(p-substituted phenyl)methanes. Mol. Cancer Ther. 2004;3:247–260. [PubMed] [Google Scholar]
- Reed GA, Arneson DW, Putnam WC, Smith HJ, Gray JC, Sullivan DK, Mayo MS, Crowell JA, Hurwitz A. Single-dose and multiple-dose administration of indole-3-carbinol to women: pharmacokinetics based on 3,3′-diindolylmethane. Cancer Epidemiol. Biomarkers Prev. 2006;15:2477–2481. doi: 10.1158/1055-9965.EPI-06-0396. [DOI] [PubMed] [Google Scholar]
- Reed GA, Sunega JM, Sullivan DK, Gray JC, Mayo MS, Crowell JA, Hurwitz A. Single-dose pharmacokinetics and tolerability of absorption-enhanced 3,3′-diindolylmethane in healthy subjects. Cancer Epidemiol. Biomarkers Prev. 2008;17:2619–2624. doi: 10.1158/1055-9965.EPI-08-0520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Safe S, Papineni S, Chintharlapalli S. Cancer chemotherapy with indole-3-carbinol, bis(3′-indolyl)methane and synthetic analogs. Cancer Lett. 2008;269:326–338. doi: 10.1016/j.canlet.2008.04.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sugano K, Nabuchi Y, Machida M, Aso Y. Prediction of human intestinal permeability using artificial membrane permeability. Int. J. Pharm. 2003;257:245–251. doi: 10.1016/s0378-5173(03)00161-3. [DOI] [PubMed] [Google Scholar]
- Testa B, Crivori P, Reist M, Carrupt PA. The influence of lipophilicity on the pharmacokinetic behavior of drugs: Concepts and examples. Perspect. Drug Discovery Des. 2000;19 [Google Scholar]
- Tetko IV, Bruneau P. Application of ALOGPS to predict 1-octanol/water distribution coefficients, logP, and logD, of AstraZeneca in-house database. J. Pharm. Sci. 2004;93:3103–3110. doi: 10.1002/jps.20217. [DOI] [PubMed] [Google Scholar]
- Vanderlaag K, Su Y, Frankel AE, Grage H, Smith R, 3rd, Khan S, Safe S. 1,1-Bis(3′-indolyl)-1-(p-substituted phenyl)methanes inhibit proliferation of estrogen receptor-negative breast cancer cells by activation of multiple pathways. Breast Cancer Res. Treat. 2008;109:273–283. doi: 10.1007/s10549-007-9648-y. [DOI] [PubMed] [Google Scholar]
- Wagner JG. Pharmacokinetic absorption plots from oral data alone or oral/intravenous data and an exact Loo–Riegelman equation. J. Pharm. Sci. 1983;72:838–842. doi: 10.1002/jps.2600720738. [DOI] [PubMed] [Google Scholar]
- Yamashita S, Kaneda K, Han TH. Population pharmacokinetics of a propofol bolus administered in patients with major burns. Burns. 2010;36(8):1215–1221. doi: 10.1016/j.burns.2010.03.003. [DOI] [PubMed] [Google Scholar]