Detecting multiple change points in piecewise constant hazard functions

Abstract

The National Cancer Institute (NCI) suggests a sudden reduction in prostate cancer mortality rates, likely due to highly successful treatments and screening methods for early diagnosis. We are interested in understanding the impact of medical breakthroughs, treatments, or interventions, on the survival experience for a population. For this purpose, estimating the underlying hazard function, with possible time change points, would be of substantial interest, as it will provide a general picture of the survival trend and when this trend is disrupted. Increasing attention has been given to testing the assumption of a constant failure rate against a failure rate that changes at a single point in time. We expand the set of alternatives to allow for the consideration of multiple change-points, and propose a model selection algorithm using sequential testing for the piecewise constant hazard model. These methods are data driven and allow us to estimate not only the number of change points in the hazard function but where those changes occur. Such an analysis allows for better understanding of how changing medical practice affects the survival experience for a patient population. We test for change points in prostate cancer mortality rates using the NCI Surveillance, Epidemiology, and End Results dataset.

1. Introduction

According to the National Cancer Institute, there has been a sudden reduction in mortality rates for prostate cancer, likely due to highly successful treatments, screening methods for early diagnosis, and public health programs [1]. This reduction in mortality rates has sparked interest towards a better understanding of the impact of medical breakthroughs, treatments, and interventions, on the survival experience for a population. We are interested in estimating the underlying hazard function, with possible time change points, as it will provide a general picture of the survival trend and when this trend is disrupted.

An estimate of the overall survival trend for an entire patient population can provide a better understanding of how changing medical practice, health policy, the role of the health care system, and public health services, affect the population survival experience. Furthermore, from an individual perspective, understanding the hazard function including how and when changes in the risk for mortality occur, allows for a life course view.

Several authors (see, for example, [2,10,11]) have proposed methods for detecting a single change point in a piecewise constant hazard function. However, with advances in biomedical research and increasing survival rates of patients we believe there may be some cases where a model with two or more change points is more appropriate [8]. We consider the situation where there are multiple changes in the piecewise constant hazard function at a few unknown time points, often referred to as the change points. We propose a data-driven approach for detecting the number of change points in the hazard function, and estimating all of the unknown parameters in the model, including the change points. An alpha-spending scheme [9] is developed such that the maximum number of change points, K, does not need to be prespecified. We propose a Wald-type test statistic based on the theoretical results of Yao [17], as the likelihood ratio test is controversial in a change-point setting due to the irregularity of models and issues of singularity [4,11,12,15]; simulation studies confirm the validity of our proposed test.

The rest of this article is structured as follows. We define the piecewise constant model with multiple change points and develop a Wald-type test statistic in Section 2. We discuss the issue of sequential testing and model selection using an alpha-spending type function in Section 3. For methodology assessment, simulation studies to investigate the overall Type I error, power, and estimation of parameters are presented in Section 4. We apply our proposed methods to test for change points in the mortality rates of prostate cancer patients in the NCI Surveillance, Epidemiology, and End Results (SEER) Program in Section 5. We conclude with a general discussion in Section 6.

2. Piecewise constant multiple change point model

Let X₁, …, X_n denote independent identically distributed survival times, and C₁, …, C_n be the censoring times which are assumed to be independent of X. We only observe the pairs (T_i, δ_i), i = 1, 2, …, n, where T_i = min(X_i, C_i) and δ_i = 1 if X_i ≤ C_i and zero otherwise. Consider the following change point model:

$$\mathrm{\lambda }(t)=\{\begin{array}{cc}{\alpha }_1,\hfill & 0\le t\le {\tau }_1,\hfill \\ {\alpha }_2,\hfill & {\tau }_1<t\le {\tau }_2,\hfill \\ ⋮\hfill & \hfill \\ {\alpha }_{k+1,}\hfill & t>{\tau }_k,\hfill \end{array}$$ (1)

where 0 = τ₀ < τ₁ < ⋯ < τ_k = ∞ are the change points, k the number of change points in the model, and α_j the value of the hazard function between the time points τ_j−1 and τ_j.

We propose a maximum (profile) likelihood estimation to estimate the unknown parameters of α and τ. Based on Equation (1), the log-likelihood function is

$$\text{log }L({\alpha }_1,\dots ,{\alpha }_{k+1},{\tau }_1,\dots ,{\tau }_k)={\displaystyle \sum _{j=1}^{k+1}}[X({\tau }_j)-X({\tau }_{j-1})]\text{ log }{\alpha }_j-{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^{k+1}}{\alpha }_j(T_i\wedge {\tau }_j-T_i\wedge {\tau }_{j-1}),$$

where $X(t)={\displaystyle {\sum }_{i=1}^n}I(T_i\le t,{\delta }_i=1)$ is the number of deaths observed up to time t. With τ_j, j = 1, …, k, fixed, some algebra yields that the maximizers of α_j,j = 1, …, k + 1 are given by ${\mathrm{\alpha ̂}}_j=(X({\tau }_j)-X({\tau }_{j-1}))/{\displaystyle {\sum }_{i=1}^n}(T_i\wedge {\tau }_j-{\tau }_{j-1})I(T_i>{\tau }_{j-1})$. Substituting these values into log L gives the profile likelihood for τ_j’s, which can be expressed as

$$\ell ({\tau }_1,\dots ,{\tau }_k)={\displaystyle \sum _{j=1}^{k+1}}\{X({\tau }_j)-X({\tau }_{j-1})\}\text{ log }\left\{\frac{X({\tau }_j)-X({\tau }_{j-1})}{{\displaystyle {\sum }_{i=1}^n}(T_i\wedge {\tau }_j-{\tau }_{j-1})I(T_i>{\tau }_{j-1})}\right\}.$$

We then maximize ℓ(τ₁, …, τ_k) with respect to τ_j, j = 1, …, k and insert the obtained values back to α̂_j, j = 1, …, k + 1 for the MLEs of α_j.

Our primary interest is to test for the existence of change points in the hazard function; or equivalently, to test whether the hazard before and after such points are different. To test the null hypothesis of no change points against the alternative of one change point, we develop a hypothesis test based on the hazard parameters (H₀ : α₁ − α₂ = 0). Yao [17] showed that the estimates of the α_j and τ_j are independent. Based on this, we formulate the Wald-type test statistic solely on the hazard rate (α_j) parameters while treating the change point (τ_j) parameters as fixed.

Hence, to test H₀ : α_k−1 − α_k = 0 versus H₁ : α_k−1 − α_k ≠ 0, we use a Wald-type test statistic of the form,

$$X_{\mathrm{W}}=\frac{{({\mathrm{\alpha ̂}}_{k-1}-{\mathrm{\alpha ̂}}_k)}^2}{\text{Var}({\mathrm{\alpha ̂}}_{k-1}-{\mathrm{\alpha ̂}}_k)},$$ (2)

which asymptotically follows a Chi-squared distribution with one degree of freedom under the null hypothesis.

3. Sequential testing and model selection

We assume that the maximum number of change points in the model is some finite number K. Our aim is to find the model, with the number of change points k (k = 0, …, K) that best fits our data. We frame our model selection process as a sequential testing problem. We start with the model with no change points and perform a hypothesis test to compare it with the model with one change point. If we fail to reject the null hypothesis, then we stop and conclude that the final model has no change points. However, if we reject the null hypothesis, then we will continue on to the next hypothesis test; compare the model with one change point, to the model with two change points. If the null hypothesis is rejected we test the subsequent hypothesis. That is, we will test for the existence of τ_k only after verifying the existence of τ_k−1. The algorithm is continued until we fail to reject a hypothesis.

We are cautious of choosing an over-fitted model with a large number of change points. The issue of selecting the appropriate number of change points is similar in spirit to the issue of selecting bin width in a smoothing problem. To address this issue, we borrow methodology from the group sequential analysis literature. Lan and DeMets [9] proposed an alpha spending technique in which the nominal significance level needed to reject the null hypothesis at each analysis is ≤ α and increases as the study progresses. Thus, for the test, it is more difficult to reject the null at the earliest analysis but easier later on. They proposed

$${\alpha }^{*}(k)=\alpha s^{*}(k),$$

where α^*(k) is the significance level for the kth hypothesis and s^*(k) = k/K is the spending function. Here, α^*(1) < α^*(2) < ⋯ < α^*(K); an increasing alpha spending function.

In order to find a parsimonious model, we want strong evidence for choosing a more complicated model, a model with more change points, over a simpler one. Therefore, we are interested in a decreasing alpha spending function, where α^*(1) > α^*(2) > ⋯ > α^*(K); the test for each additional change point will be conducted at a more conservative α level than the one before it.

If the overall significance level is α, we propose α^*(k) = α/2^k−1, where α^*(k) is the significance level for the kth hypothesis test. An advantage of this alpha spending function is that it does not depend on the overall number of hypothesis tests being conducted. Therefore, one does not need to specify K, the maximum number of change-points, which is ideal for flexibility in model selection.

In this setting, Type I error is the probability of incorrectly choosing a model that has more change points than the true model. We show that the type I error rate will not exceed α by calculating three probabilities (i) choosing a model with one or more change points given the true model has no change points, (ii) choosing a model with k change points given the true model has no change points, and (iii) choosing a model with more than k change points given the true model has k change points, are all at most α.

Let M_i be the event that the model has i change points. Then

$$P(M_{i\ge 1}|M_0)=1-P(M_0|M_0)=1-(1-\alpha )=\alpha ,$$ (3)

$$P(M_k|M_0)=(1-\frac{\alpha }{2^k}){\displaystyle \prod _{i=1}^k}\frac{\alpha }{2^{i-1}}<\frac{{\alpha }^k}{{\displaystyle {\prod }_{i=1}^k}{2}^{i-1}}<\alpha ,$$ (4)

and for k ≥ 1

$$P(M_{i>k}|M_k)={\displaystyle \sum _{j=1}^{\mathrm{\infty }}}[(1-\frac{\alpha }{2^{k+j}}){\displaystyle \prod _{i=k+1}^{k+j}}\frac{\alpha }{2^{i-1}}]<\alpha .$$ (5)

The derivations of Equations (4) and (5) can be found in Appendix 1.

4. Simulation

In order to test our proposed methodology, we conducted simulation studies on models with two, three, and four change points. In this paper we discuss and present results for the model with two change points as this is the simplest multiple change point case and simulation studies for models with a greater number of change points are easily extrapolated from those of two change point model. We conducted simulation studies to investigate the estimation of model parameters, the power of our proposed test, and the overall Type I error rate.

Survival times for a piecewise constant hazard model with two change points were generated by inverting the cumulative distribution function and using the probability integral transformation. In this case, three different distributions have to be generated: (1) survival times before the first change point; (2) survival times between the first change point and the second change point and (3) survival times after the second change point. Censoring times were generated from three corresponding uniform distributions. Five parameters need to be specified a priori: the value of the hazard function for the three distributions and the two change points. We developed simulation scenarios that closely approximated those of the SEER data from the application in Section 5 and simulated models under the following conditions 0 < α_k < 1, 0 < τ₁ < 5, and τ₁ < τ₂ < 10. Censoring percentages were calculated for each simulated data set. We manipulated the amount of censoring by changing the ranges on the censoring distributions. We tested a variety of model scenarios and compared the average of each simulated data set to the theoretical average of the specified model.

We start by using the Wald-type test statistic (see Equation (2)) to compare the null model with no change points to an alternative model with one change point. If we reject the null model we continue to the next hypothesis and test the null model of one change point to the alternative model of two change points. We continue this algorithm until we are unable to reject a hypothesis. The α level for each test was determined using the decreasing alpha spending function proposed in Section 3. We simulated 5000 datasets; for each dataset a final model was chosen and the parameters were estimated by maximizing the likelihood function for the final model using the Nelder–Mead Simplex algorithm, a reliable procedure to carry out such optimization (available in common statistical software). Table 1 displays the results of our simulations for n = 500, under 7 different model scenarios:

1. α₁ = 0.95, α₂ = 0.55, α₃ = 0.15, τ₁ = 2.0, τ₂ = 4.0, and 0% censoring;

2. α₁ = 0.15, α₂ = 0.55, α₃ = 0.35, τ₁ = 2.0, τ₂ = 4.0, and 5% censoring;

3. α₁ = 0.15, α₂ = 0.35, α₃ = 0.55, τ₁ = 1.0, τ₂ = 3.5, and 20% censoring;

4. α₁ = 0.65, α₂ = 0.35, α₃ = 0.15, τ₁ = 1.5, τ₂ = 3.5, and 25% censoring;

5. α₁ = 0.15, α₂ = 0.35, α₃ = 0.55, τ₁ = 1.0, τ₂ = 2.5, and 30% censoring;

6. α₁ = 0.15, α₂ = 0.55, α₃ = 0.95, τ₁ = 2.0, τ₂ = 4.0, and 35% censoring;

7. α₁ = 0.15, α₂ = 0.95, α₃ = 0.45, τ₁ = 2.0, τ₂ = 4.0, and 50% censoring.

Table 1.

Estimation for piecewise constant model with two change points based on 5000 simulations (n = 500).

Censor (%)	Parameters	Parameter value	Mean estimated value	Std. error estimated value	Model based std. dev.	Coverage probability
0	α1	0.95	0.953	0.053	0.046	0.949
	α2	0.55	0.545	0.077	0.076	0.941
	α3	0.15	0.145	0.032	0.034	0.923
	τ1	2.0	1.992	0.118
	τ2	4.0	3.968	0.182
5	α1	0.15	0.149	0.014	0.013	0.940
	α2	0.55	0.558	0.039	0.035	0.947
	α3	0.35	0.342	0.032	0.036	0.937
	τ1	2.0	2.009	0.176
	τ2	4.0	4.018	0.170
20	α1	0.15	0.148	0.021	0.017	0.933
	α2	0.35	0.352	0.030	0.023	0.934
	α3	0.55	0.579	0.059	0.060	0.951
	τ1	1.0	1.023	0.218
	τ2	3.5	3.556	0.243
25	α1	0.65	0.655	0.040	0.038	0.946
	α2	0.35	0.346	0.048	0.048	0.937
	α3	0.15	0.133	0.035	0.045	0.896
	τ1	1.5	1.502	0.140
	τ2	3.5	3.486	0.208
30	α1	0.15	0.148	0.019	0.019	0.935
	α2	0.35	0.352	0.033	0.028	0.942
	α3	0.55	0.569	0.048	0.045	0.946
	τ1	1.0	1.012	0.092
	τ2	2.5	2.535	0.144
35	α1	0.15	0.158	0.015	0.013	0.945
	α2	0.55	0.550	0.051	0.046	0.943
	α3	0.95	1.065	0.158	0.128	0.942
	τ1	2.0	2.009	0.059
	τ2	4.0	4.055	0.169
50	α1	0.15	0.126	0.014	0.017	0.558
	α2	0.95	0.821	0.087	0.074	0.512
	α3	0.45	0.387	0.071	0.084	0.874
	τ1	2.0	2.005	0.017
	τ2	4.0	3.761	0.392

The mean estimated value is the average estimated parameter value from all 5000 simulation runs, and the standard error is the standard deviation of these estimates. Based on simulation studies our method estimates the change points and the value of the hazard quite well even with a moderate amount of censoring. In most cases, the coverage probability is close to the nominal level of 95%. However, for n = 500 as the percentage of censoring increases above 40% the coverage probability decreases significantly (see Table 1).

We examined the power of the test under the two change points alternative. The power is essentially a measure of the accuracy of our algorithm in choosing the final model. Table 2 displays the results of the power analysis for samples of size 500 under 10 different model scenarios:

1. α₁ = 0.15, α₂ = 0.55, α₃ = 0.95, τ₁ = 2.0, τ₂ = 4.0, and 1% censoring;

2. α₁ = 0.15, α₂ = 0.55, α₃ = 0.35, τ₁ = 2.0, τ₂ = 4.0, and 3% censoring;

3. α₁ = 0.95, α₂ = 0.55, α₃ = 0.15, τ₁ = 2.0, τ₂ = 4.0, and 16% censoring;

4. α₁ = 0.15, α₂ = 0.35, α₃ = 0.55, τ₁ = 1.0, τ₂ = 3.5, and 23% censoring;

5. α₁ = 0.95, α₂ = 0.35, α₃ = 0.75, τ₁ = 1.5, τ₂ = 3.5, and 26% censoring;

6. α₁ = 0.95, α₂ = 0.65, α₃ = 0.45, τ₁ = 1.0, τ₂ = 3.5, and 27% censoring;

7. α₁ = 0.15, α₂ = 0.35, α₃ = 0.55, τ₁ = 1.0, τ₂ = 3.5, and 27% censoring;

8. α₁ = 0.15, α₂ = 0.55, α₃ = 0.95, τ₁ = 2.0, τ₂ = 4.0, and 36% censoring;

9. α₁ = 0.15, α₂ = 0.95, α₃ = 0.45, τ₁ = 2.0, τ₂ = 4.0, and 49% censoring;

10. α₁ = 0.15, α₂ = 0.95, α₃ = 0.45, τ₁ = 2.0, τ₂ = 4.0, and 57% censoring.

Power was most affected by sample size, the difference between α_k−1 and α_k, and the difference between τ_k−1 and τ_k. With samples of size 500, |α_k−1 − α_k| > 0.2, |τ_k−1 − τ_k| > 1.5, and < 30% censoring, we observed power of at least 90%, however as the censoring percentage increase above 30% the power decreases (see Table 2).

Table 2.

Power analysis for the piecewise constant model with two change points based on 5000 simulations (n = 500).

α2 − α1	α3 − α2	τ2 − τ1	% Censoring	Power
0.4	0.4	2	1	0.98
0.4	−0.2	2	3	0.98
−0.4	−0.4	2	16	0.95
0.2	0.2	1.5	23	0.93
−0.6	0.4	2	26	0.92
−0.3	−0.2	1.5	27	0.93
0.2	0.2	1.5	27	0.96
0.4	0.4	2	36	0.81
0.8	−0.5	2	49	0.90
0.8	−0.5	2	57	0.69

To test the overall Type I error rate, we simulated data with two change points (α₁ = 0.95, α₂ = 0.55, α₃ = 0.25, τ₁ = 2, and τ₂ = 4) and implemented our stepwise model selection algorithm. We developed a censoring distribution using three uniform distributions, zero to the first change point, from the first change point to the second change point, and from the second change point to the largest survival time. On average, this distribution produces a 35% censoring percentage; we decrease the censoring percentage by increasing the upper limits on the censoring distributions and increase the censoring percentage by decreasing the upper limits on the censoring distributions. Table 3 displays a sample of our results for samples of size 500. The Type I error is the number of times our algorithm chooses a final model with three or more change points over the null model of two change points. The observed overall Type I error rate is similar to the nominal significance level of the test (see Equation (5)).

Table 3.

Type I error analysis for the piece-wise constant change-point model based on 5000 simulations (n = 500).

% Censoring	Type I error
0	0.048
5	0.048
10	0.046
15	0.044
20	0.050
25	0.052
30	0.048
40	0.049
45	0.053
50	0.052
60	0.047
80	0.053

5. Prostate cancer mortality

To examine prostate cancer mortality, we analyze the Surveillance, Epidemiology, and End Results (SEER) Program (www.seer.cancer.gov) Public-Use Data (1973–2007), National Cancer Institute, DCCPS, Surveillance Research Program, Cancer Statistics Branch. This data set contains cancer incidence and survival for cases diagnosed from 1973 to 2007, follow-up continued until 31 December 2007. We are interested in finding: (i) if there are change points in the hazard function, (ii) the number of change points and (iii) estimating the location of the change points and all other model parameters.

We define an event as death from prostate cancer. Subjects who died from another cause are censored at the time of death. We restrict our analysis to men who were diagnosed with prostate cancer between 1973 and 2002 to allow for at least five years of follow-up. For the purpose of analysis, we excluded subjects with unknown follow-up time. To avoid singularity, we restrict the change points to be larger than the first survival time and smaller than the second to last survival time, assuming these are non-censored time points, T₍₁₎ < τ₁ < ⋯ < τ_k < T_(n−1) [13,17].

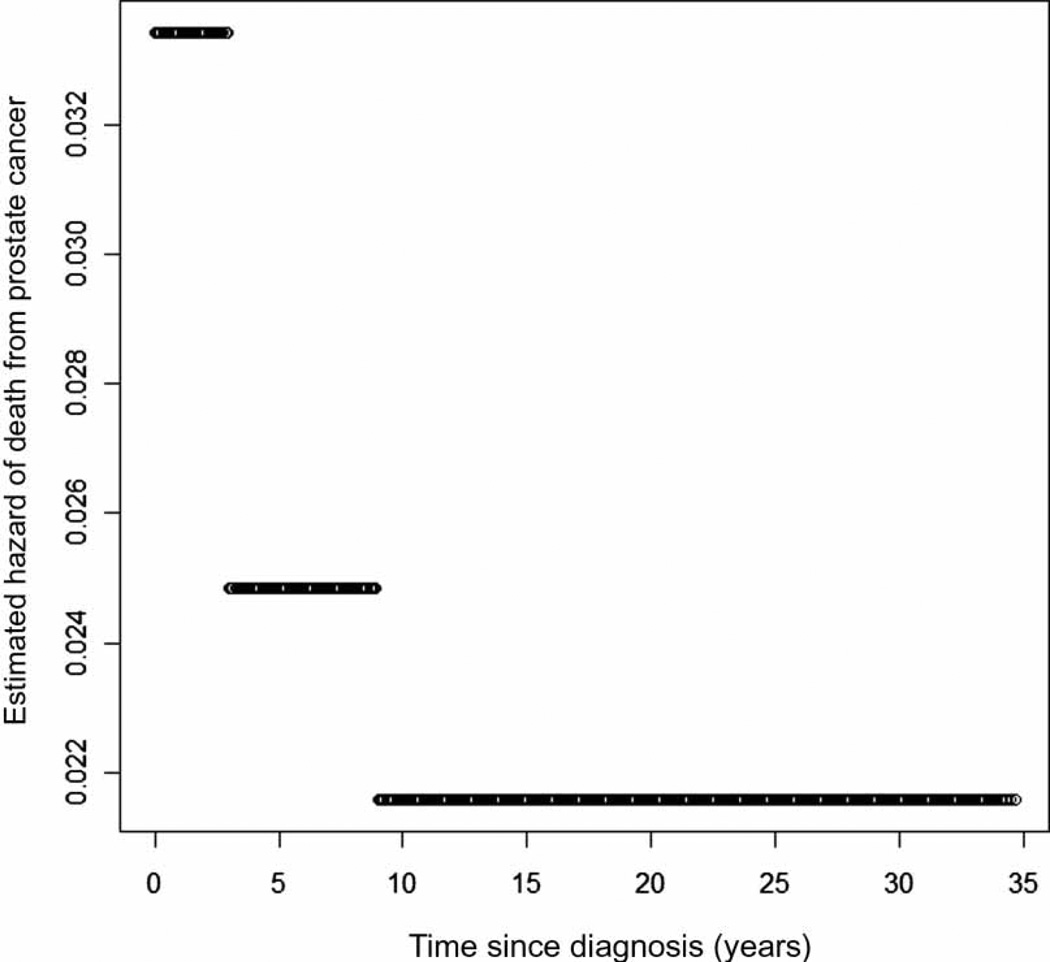
There were 378,095 men who fit our restriction criteria in the SEER data set with 75,343 events and 80.1% of the observations being censored. The average age of men in the sample is 84 with an average age at diagnosis of 71. In our sample population 84% of the men are non-Hispanic white, 11% are non-Hispanic Black and approximately 5% are another race/ethnicity (i.e. Hispanic, American Indian/Alaska Native or Asian). The estimated hazard function has two change points (namely at 3.0 and 5.4) and is defined by Equation (6).

$$\mathrm{\lambda }(t)=\{\begin{array}{cc}0.0334,\hfill & 0\le t\le 3.0,\hfill \\ 0.0249,\hfill & 3.0<t\le 5.4,\hfill \\ 0.0216,\hfill & t>5.4.\hfill \end{array}$$ (6)

Before the first change point there are 32,247 events and 63% censoring, between the first change point and the second change point there are 16,140 events and 71% censoring and after the second change point there are 26,956 events and 89% censoring. Figure 1 displays the estimated hazard function. The hazard function for men diagnosed with prostate cancer between 1973 and 2002 starts at 33.4 per 1000 population until 3 years after diagnosis, it decreases to 24.9 per 1000 population until 5.4 years after diagnosis and then decreases to 21.6 per 1000 population until the end of the follow-up period. When a one change point model is fit to this data the change point is estimated at 2.8 very close to the first estimated change point (3.0) in the two change point model.

Figure 1.

Estimated prostate cancer mortality hazard function for men diagnosed 1973–2002.

6. Discussion

Inference about the change-point in the piecewise constant model is a nontrivial issue previously discussed in the literature (see, for example, [5–7]). We developed a Wald-type test statistic employing the statistical independence of the estimates of the hazard rates and the change point parameters [17]. The Wald test has a known asymptotic Chi-squared distribution, facilitating drawing inference. Our methodology requires use of the Nelder–Mead Simplex optimization algorithm [14], this algorithm uses only function values and is robust but can be relatively slow. It will work reasonably well for non-differentiable functions and requires the user to provide initial starting values for the parameter estimates. From our simulation studies we found these values need to be reasonable but not precise. There are other optimization methods available (e.g. quasi-Newton variable metric algorithm, conjugate gradients method, box constraints) and easily implemented in most software packages each with their own set of advantages and disadvantages [16].

An advantage of our method is its ability to appropriately handle sequential testing with careful selection of a parsimonious model over an over fitted model. Although traditional smoothing techniques (see, for example [3]) can be applied to estimate the hazard function. When using these methods the knots and the number of knots are to be pre-specified by the data analyst. Our approach uses the data to determine the number and value of the change points. In settings where there is an interest in not only knowing the trend of the hazard function but when the changes in trend occur, our proposed methodology has several advantages when compared to existing approaches.

The methods we propose are easily implemented, using maximum likelihood estimation and Wald-type test statistics, and can be applied to other important applications. The resulting estimate of the hazard function can also be used for predictive purposes and allows for non-parametric extrapolation of very long term survival by extrapolating the trend from the last change point. Change-point hazard functions may have implications in health care policy decisions. With an enhanced understanding of the changes in population mortality rates we can identify gaps, seek solutions, improve performance, and ultimately, better the public’s health.

Appendix. Proofs of Inequalities (4) and (5)

Proof of Inequality (4): Note that

$$P(M_k|M_0)=(1-\frac{\alpha }{2^k}){\displaystyle \prod _{i=1}^k}\frac{\alpha }{2^{i-1}}<\frac{{\alpha }^k}{{\displaystyle {\prod }_{i=1}^k}{2}^{i-1}}<\frac{\alpha }{{\displaystyle {\prod }_{i=1}^k}{2}^{i-1}}<\alpha ,$$

where the first equality follows from the fact that (1 − α/2^k) < 1, the second follows from the fact that 0 < α < 1, α^k < α, and the last equality follows from the fact that ${\displaystyle {\prod }_{i=1}^k}{2}^{i-1}>1$.

Proof of Inequality (5): Note that

$$P(M_{i>k}|M_k)={\displaystyle \sum _{j=1}^{\mathrm{\infty }}}[(1-\frac{\alpha }{2^{k+j}}){\displaystyle \prod _{i=k+1}^{k+j}}\frac{\alpha }{2^{i-1}}]<{\displaystyle \sum _{j=1}^{\mathrm{\infty }}}{\displaystyle \prod _{i=k+1}^{k+j}}\frac{\alpha }{2^{i-1}}<{\displaystyle \sum _{j=1}^{\mathrm{\infty }}}\frac{\alpha }{2^j}=\alpha .$$