Multi-Label Multi-Kernel Transfer Learning for Human Protein Subcellular Localization

Abstract

Recent years have witnessed much progress in computational modelling for protein subcellular localization. However, the existing sequence-based predictive models demonstrate moderate or unsatisfactory performance, and the gene ontology (GO) based models may take the risk of performance overestimation for novel proteins. Furthermore, many human proteins have multiple subcellular locations, which renders the computational modelling more complicated. Up to the present, there are far few researches specialized for predicting the subcellular localization of human proteins that may reside in multiple cellular compartments. In this paper, we propose a multi-label multi-kernel transfer learning model for human protein subcellular localization (MLMK-TLM). MLMK-TLM proposes a multi-label confusion matrix, formally formulates three multi-labelling performance measures and adapts one-against-all multi-class probabilistic outputs to multi-label learning scenario, based on which to further extends our published work GO-TLM (gene ontology based transfer learning model for protein subcellular localization) and MK-TLM (multi-kernel transfer learning based on Chou's PseAAC formulation for protein submitochondria localization) for multiplex human protein subcellular localization. With the advantages of proper homolog knowledge transfer, comprehensive survey of model performance for novel protein and multi-labelling capability, MLMK-TLM will gain more practical applicability. The experiments on human protein benchmark dataset show that MLMK-TLM significantly outperforms the baseline model and demonstrates good multi-labelling ability for novel human proteins. Some findings (predictions) are validated by the latest Swiss-Prot database. The software can be freely downloaded at http://soft.synu.edu.cn/upload/msy.rar.

Introduction

Recent years have witnessed much progress in computational modelling for protein subcellular localization [1]. However, researches on human genome and proteomics seem more urgent and important for human disease diagnosis and drug development. Unfortunately, there are far few specialized predictive models for human protein subcellular localization thus far [2], [3], [4], [5]. Furthermore, many human proteins have multiple subcellular locations, which renders the computational modelling more complicated. Up to the present, there are only two models (Hum-mPLoc [4] and Hum-mPLoc 2.0 [5]) that can be applicable to multiple subcellular localization of human proteins.

Although many protein sequence feature extraction methods have been successfully developed for protein subcellular localization, such as signal peptide [6], sequence domain [7], PSSM [8], [9], k-mer [10], [11] etc., the accuracy of the models is still moderate or unsatisfactory, most of which average about 70% [6], [7], [9], [10], [11]. Garg A et al (2005) [3] used sequence features only (amino acid composition and its order information) for human protein subcellular localization, and the result is satisfactory (84.9%), but it covers only 4 subcellular locations. The Gene Ontology (GO) project has developed three structured controlled vocabularies (ontologies) that describe gene products in terms of their associated biological processes, cellular components and molecular functions in a species-independent manner, and the GOA database [12] provides high-quality electronic and manual associations (annotations) of GO terms to UniProt Knowledgebase (UniProtKB) entries [13]. Because the three aspects of gene ontology are closely related and the GO terms of cellular component contains direct indicative information about protein subcellular location, GO has become a generally effective feature for the prediction of protein subcellular localization [2], [4], [5], [14], [15], [16], [17], [18], [19], [20], [21], [22], [23], [24], [25], [26], [27], [28], [29]. Chou K.C. et al [2] proposed an ensemble leaning model called Hum-PLoc for human protein subcellular localization. The model consists of two parts: GO-based kNN and PseAAC-based kNN, and the latter part was designed to compensate for the model performance in the case of GO unavailability. To cover multiplex human proteins that reside in or transport across multiple subcellular locations, Shen HB et al [4] further proposed an improved model called Hum-mPLoc, which extended the number of subcellular locations from 12 to 14 and formally formulated the concept of locative protein and the success rate for multiplex protein subcellular localization. Hum-PLoc, Hum-mPLoc and the work [2], [15], [16], [17], [18], [19], [20], [21], [22] used the target protein's own GO information to train model, thus inapplicable to novel protein prediction. Many recent GO-based methods generally exploit the homolog GO information for novel protein subcellular localization [5], [23], [24], [25], [26], [27], [28], [29], [30]. Based on Hum-mPLoc, Shen HB et al [5] further proposed Hum-mPLoc2.0 for multiplex and novel human protein subcellular localization, where a more stringent human dataset with 25% sequence similarity threshold is constructed to train a kNN ensemble classifier. Hum-mPLoc2.0 incorporated those homologs with sequence similarity 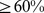, but achieved relatively low accuracy (62.7%). However, the method of setting threshold for homolog incorporation has the following disadvantages: (1) significant homolog (high sequence identity, assuming 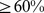) may potentially be divergent from the target protein in terms of protein subcellular localization, for instance, the target protein P21291 resides in subcellular locations: Nucleus, while its significant homolog P67966 (sequence identity: 90.16%; PSI-Blast E-value: 13e-174072, obtained by Blast default options) resides in subcellular locations: Cytoplasm and Cytoskeleton. High threshold of sequence identity, e.g. 60%, can not guarantee that no noise would be introduced to the target protein; (2) remote homolog (low sequence identity, assuming 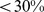) may be convergent to the target protein in terms of protein subcellular localization, for instance, the target protein P21291 resides in subcellular locations: Endoplasmic reticulum, Membrane and Microsome, while its first 7 significant remote homologs queried against SwissProt 57.3 database [13] with default Blast option: O75881(26.82%,4e-041),O02766(25.05%,4e-028), Q63688 (25.66%,2e-027),P22680(23.68%,4e-026),Q16850(23.92%,4e-025),O88962 (25.05%, 4e-025), Q64505 (23.13%, 1e-024) (the first number in parenthesis denotes sequence identity and the second number denotes PSI-Blast E-value), also reside in the subcellular locations: Endoplasmic reticulum, Membrane and Microsome. High threshold of sequence identity (60%) would filter out all the convergent remote homologs that are informative to protein subcellular localization, and thus no homolog knowledge would be transferred to the target protein P21291. We can see that both significant homolog and remote homolog can be convergent homolog, or divergent homolog in terms of protein subcellular localization, thus we should conduct homolog knowledge transfer in a proper way, so that the noise from divergent homolog can be effectively depressed. Mei S et al [25] proposed a transfer learning model (gene ontology based transfer learning for protein subcellular localization, GO-TLM) to measure the individual contribution of GO three aspects to the model performance, where the kernel weights are evaluated by simple nonparametric cross validation. Mei S [26] further proposed an improved transfer learning model (MK-TLM), which conducted improvements on GO-TLM from the two major concerns: (1) more rational noise control over divergent homolog knowledge transfer; (2) comprehensive survey of model performance, especially for novel protein prediction. However, many human proteins reside in or transport across multiple cellular compartments, and the proteins with multiple locations may help reveal special biological implications to basic research and drug discovery [30], [31]. Neither GO-TLM nor MK-TLM is applicable to multiple protein subcellular localization prediction.

In this paper, we propose a multi-label multi-kernel transfer learning model for large-scale human protein subcellular localization (MLMK-TLM). Based on the work [25], [26], MLMK-TLM proposes a multi-label confusion matrix and adapts one-against-all multi-class probabilistic outputs to multi-label learning scenario. With the advantages of proper homolog knowledge transfer, comprehensive survey of model performance for novel protein and multi-labelling capability, MLMK-TLM gains more practical applicability. To validate MLMK-TLM's effectiveness, we conduct a comprehensive model evaluation on the latest human protein dataset Hum-mPLoc 2.0 [5].

Methods

1. Transfer learning

As a research field of machine learning community, transfer learning has attracted more and more attentions in recent years [32]. Traditional supervised learning generally assumes that all the data, including training data and unseen test data, are subjected to independent and identical distribution (iid), which doesn't hold true under many practical circumstances, especially in the field of biological data analysis. For example, the microarray gene expression data from different experimental platforms would be subjected to different level of experimental noise [33]. Transfer learning can be viewed as a bridge to transfer useful knowledge across two related domains with heterogeneous feature representations and different distributions. Pan S et al [32] reviewed the recent progress of transfer learning modelling and classified transfer learning into three categories based on the way of knowledge transfer: instance-based knowledge transfer [34], feature-based knowledge transfer [35] and parameter-based knowledge transfer [36].

Transfer learning modelling is generally conducted around three central dogmas: (1) how to define the relatedness between domains; (2) what to transfer; (3) how to transfer. In our work, we explicitly define the relatedness between protein sub-families and super-families by protein sequence evolution, i.e. protein homolog. Evolutionally closely-related proteins share similar subcellular localization patterns with high probability. Correspondingly, what to transfer is naturally the homolog GO term. Such a way of transfer learning modelling is computationally simple and biologically interpretable. In order to reduce the risk of negative transfer, GO-TLM [25] and MK-TLM [26] proposed a non-parametric multiple kernel learning method to measure the contribution of GO three aspects, target GO information and homolog GO information to the model performance. In this paper, we redefine confusion matrix, so that the GO kernel weights can be derived by cross validation for multi-label learning scenario.

2. GO feature construction

All the proteins are represented with both the target GO terms and the homolog GO terms, which are extracted from GOA database [12] (77 Release, as of 30 November, 2009), and the homologs are extracted from SwissProt 57.3 database [13] using PSI-Blast [37]. Assume there are u GO terms x_i (i = 1, 2,…, u), then protein 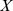can be represented as follows:

(1)

If GO term x_i is assigned to the protein x in GOA database, then x_i = 1; Otherwise, x_i = 0. To expressly estimate the individual contribution of the three GO aspects, GO-TLM [25] decomposed the feature vector (1) into the following three binary feature vectors:

(2)

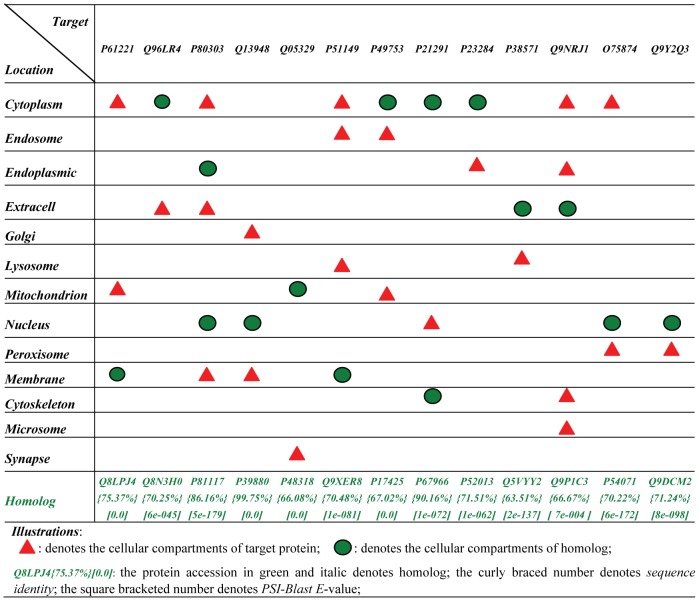
However, GO-TLM aggregated the target GO information and the homolog GO information into one single feature vector, such that the two kinds of GO information are treated equally. We know that such a way of feature construction is not rational because divergent homolog GO information carries much noise. Figure 1 shows the difference of subcellular localization patterns between target human protein (P61221 thru. Q9Y2Q3) and its homolog protein. The homologs are queried against SwissProt 57.3 database [13] with default Blast options (E-value: 10; substitution matrix: BLOSUM62). E-value is relaxed to 10 to obtain remote homologs for those proteins that have no significant homologs. For a target protein, we may encounter three cases for the selected homologs: (1) all homologs are significant homologs; (2) one part of homologs is significant homolog and the other part of homologs is remote homolog; (3) all homologs are remote homologs. Some remote homologs are convergent to the target protein in terms of protein subcellular localization (e.g. remote homologs O75881, O02766, Q63688, P22680, Q16850, O88962 and Q64505 to target protein P21291), thus we should exploit the useful information from remote homologs; meanwhile, some remote homologs are divergent to the target protein, thus we should prevent negative knowledge transfer from the remote homolog. As compared to remote homolog, significant homolog is more likely to be convergent in terms of protein subcellular localization, but in some case, significant homolog is also likely to be divergent. Figure 1 lists one divergent homolog for each target protein. The illustrated divergent homolog has the highest sequence identity and PSI-Blast E-value among the target protein's divergent homologs. From Figure 1, we can see that the significant homologs reside in definitely distinct subcellular locations from the target protein, which implies that we should also depress noise from the significant homologs even though we encounter the above case (1). Similar to MK-TLM [26], we also separate the target GO information from its homolog GO information for the convenience of noise control. Here, we use T to denote the target protein and H to denote its homolog, thus the target GO feature vector is expressed as formula (3), and the homolog GO terms are aggregated into one homolog feature vector as formula (4):

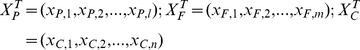(3)

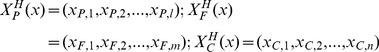(4)

Thus, each protein is represented by six binary feature vectors: .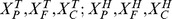

Figure 1. Illustration of divergent homolog in terms of subcellular localization.

3. Non-parametric multiple kernel learning

The six binary GO feature vectors {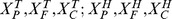} are used to derive six GO k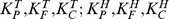ernels {}, and the GO kernels are further combined in the way that MK-TLM does [26]. In such a setting, higher homolog GO kernel weight implies more positive knowledge transfer, and lower homolog GO kernel weight can depress the potential noise by divergent homolog. Different to MK-TLM, MLMK-TLM adapts confusion matrix to multi-label learning scenario based on the concept of locative protein [4], [5]. For self-contained description and integrity, we give the full description of non-parametric kernel weight estimation in multi-label learning scenario as below, though some part of which is identical to MK-TLM [26]. Similar to GO-TLM and MK-TLM, the final kernel is defined as the following linear combination of sub-kernels:

(5)

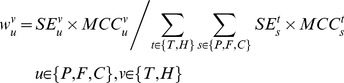(6)

Where SE denotes recall rate or sensitivity and MCC denotes Matthew's correlation coefficient. The kernel weights 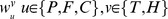are derived by cross validation. Given a training dataset, we divide the training set into k-fold disjoint parts. For each fold cross validation, one part is used as validation set and the other parts are merged as training set to train the combined-kernel SVM. Thus, we can derive a confusion matrix M by evaluating the trained SVM against the test set. From the confusion matrix M, we can derive the kernel's SE and MCC measure as follows:

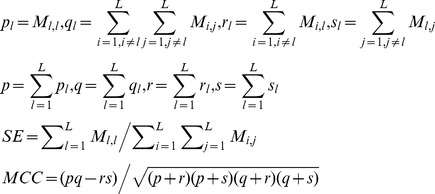(7)

Where, 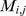records the counts that class are classified to class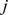; superscript 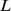denotes subcellular locations; and all the other variables are intermediate variables that can be derived from the confusion matrix .

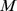In single-label learning scenario, 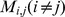records the counts that class are misclassified to class 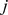, which is not applicable to multi-label learning scenario. Let's borrow the notion of locative protein [4], [5] to describe the multi-label confusion matrix. Assume that a protein p is located at two subcellular locations 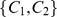, i.e., 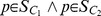( 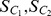denote the set of proteins that reside in 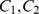, respectively), the notion of locative protein means that protein p can be viewed as two different proteins 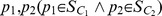. Now take 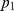protein as test protein and the trained SVM labels 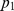as follows:

(8)

Where, 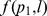denotes the probability that protein 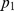is assigned the label 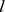(see Section 4 of Methods for how to derive probability outputs). Thus, the multi-label confusion matrix can be defined as follows:

(9)

Formula (9) shows that only if the predicted label of locative protein 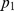hits its true label 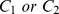, the prediction is deemed as correct; otherwise, the prediction would be deemed as incorrect.

As regards with kernel 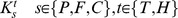, Gaussian kernel is used here:

(10)

4. Multi-label learning

In our work, we extend MK-TLM [26] to multi-learning scenario based on one-against-all multi-class learning and binary SVM probability outputs [38]. Probability outputs tell us the confidence level that a query protein belong to each subcellular location, thus more intuitive and reasonable than ensemble voting [4], [5], [39] and label transfer of kNN nearest neighbour protein [27], [28], [30].

Assuming there are K subcellular locations, for each subcellular location k, we view the proteins that belong to k as positive examples and the proteins that belong to other subcellular locations except k as negative examples, based on which to train one binary SVM. Thus, we have K trained binary SVMs. If each binary SVM outputs {−1, +1} labels, multiple {+1} outputs can be viewed as multiple protein subcellular locations [40]. Because the {−1, +1} labels can not tell us the confidence level that a query protein belongs to each subcellular location, we don't adopt the method. If each binary SVM yields probability output, we can choose the label with the highest probability as the protein subcellular location, which is s-called one-against-all multi-class learning [38], [41]; if we set some probability threshold, the labels with probability over the threshold can be viewed as multiple protein subcellular locations, thus intuitively applicable to multi-label learning scenario. Platt J [41] proposed a method to adapt binary SVM {−1, +1} labels to posterior class probability as defined below:

(11)

Where the coefficient A and B can be derived from data by cross validation, and f(x) is uncalibrated decision value of binary SVM.

Actually, the one-against-all multi-class SVM with probability output has been implemented into the LIBSVM tool (http://www.csie.ntu.edu.tw/~cjlin/libsvm/), which can be easily used for multi-label learning. Only if we set LIBSVM prediction option “-b 1” (LIBSVM command option –b 1 means probability rather than {−1, +1} output), we can obtain the probability vector that a query protein is predicted to each subcellular location. By setting optimal probability threshold, we can determine the optimal multiple labelling for the query protein based on the predicted probability vector.

5. Model evaluation and model selection

The existing GO-based models only reported the optimistic performance by evaluating the proposed model against information-rich (GO, PPI, image) test proteins, and seldom reported the performance for novel proteins [4], [5], [14], [15], [16], [17], [18], [19], [20], [21], [22], [23], [24], [25], [27], [28], [29], [30]. Apparently, the optimistic performance is not enough to be a comprehensive survey of the model's true predictive ability, especially for novel protein prediction. MK-TLM [26] attempted to conduct a comprehensive survey of the model performance in optimistic, moderate and pessimistic cases, and demonstrated good performance for novel proteins and those proteins that belong to the protein family we know little about. In this paper, the proposed MLMK-TLM inherits all MK-TLM's advantages. The Optimistic case means the training set and the test set both abound in GO information; the Moderate case means that the test set contains no GO information at all, which can be simulated by removing the test kernels 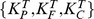; the Pessimistic case means that both the training set and the test set contains no GO information at all where the target GO information is removed from both the training set and the test set, which can be simulated by removing the training kernels 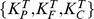and test kernels .

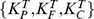The performance evaluation under multi-label learning scenario seems more complicated as compared to single-label learning scenario. Because the model performance estimation involves both singlex protein (only one subcellular location) and multiplex protein (multiple subcellular locations), we should conduct two performance estimation experiments: one experiment is overall performance estimation on locative dataset, where multiplex protein is viewed as multiple singlex proteins as Hum-mPLoc 2.0 [4], Virus-mPLoc [15], iLoc-Euk [27], iLoc-Virus [28] and Plant-mPLoc [30] did; the other experiment is multi-labelling estimation for multiplex proteins. The first experiment is similar to traditional supervised learning estimation except that multi-label confusion matrix is adopted instead (see formula 8 & 9); in the second experiment, cross validation is conducted on multiplex proteins only and the singlex proteins are always treated as training data. Thus, the whole training set is composed of two parts: fixed part from the singlex proteins and the variable part from the multiplex proteins. In addition, the model performance estimation in the second experiment is much more complicated. To simplify the formulation, lets' first give several symbol annotations: (1) 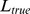denotes the true label set of a multiplex protein p; (2) 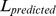denotes the predicted label set of a multiplex protein p; (3) 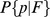denotes the protein set P whose protein p satisfies the condition F; (4) denotes set cardinal; (5) minus symbol denotes set difference; (6) 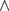denotes logic AND. Based on the symbols, we can formally define Label Hit Rate (LHR), Perfect Label Match Rate (PLMR) and Non-target Label Hit Rate (NT-LHR) as follows:

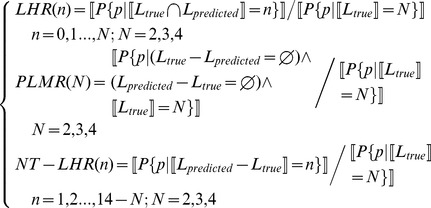(12)

where N denotes the number of subcellular locations a protein may reside in, with maximum value 4 here; n denotes the number of correct HITs or wrong HITS, with maximum value 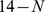here (we assume the total number of subcellular locations is 14). The multiplex proteins in Hum-mPLoc 2.0 [5] can be divided into 3 subsets that possesses 2, 3 and 4 labels (subcellular locations), respectively. We will report LHR, PLMR and NT-LHR on each subset. Take 2-label subset as example, the prediction may hit 0, 1 or 2 true labels. Low 0-label hit rate and high 1- and/or 2-label hit rate imply good model performance. However, the prediction may also hit 1∼12 non-target labels (excluding 2 true labels from total 14 subcellular locations). High NT-LHR implies high misleading tendency, which should be as low as possible. The existing multi-label learning model for protein subcellular localization [4], [5], [15], [19], [27], [28], [29], [30] seldom reported NT-LHR. If the prediction hits the true labels and yields no other misleading labels, we call the case perfect label match; otherwise, we call the case non-perfect label match. High Perfect Label Match Rate (PLMR) implies good predictive ability and low misleading tendency.

MLMK-TLM is a relatively complex model that requires time-consuming computation for model comparison and model selection. Apart from SVM regularization parameter C and kernel parameter , MLMK-TLM introduces a hyper-parameter 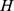that denotes the number of homologs for knowledge transfer. Assume there are N proteins in the dataset and the hyper-parameter sets are 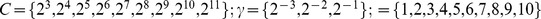, MLMK-TLM has to fix one hyper-parameter to optimize the other hyper-parameters, and in each iteration has to compute kernel matrices, thus the computational complexity is 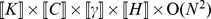, where denotes set cardinal, 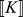denotes the number of kernel matrices and O 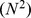denotes the computational complexity for kernel computing. For large-scale human protein dataset Hum-mPLoc 2.0 [5], the model selection is rather time-consuming. Hence, we adopt 5-fold cross validation instead of leave-one-out cross validation (LOOCV) (Jackknife) as GO-TLM [25] and MK-TLM [26] did. For multi-labelling estimation, the multiplex proteins are divided into 5 nearly-even parts, one part as test set, and the other parts are merged with the singlex proteins into training set, thus iterates for 5 times until all the multiplex proteins participate in the performance estimation process (see Section 6 of Results).

For performance estimation on locative proteins, we adopt the performance measures: Sensitivity (SE), Specificity (SP), Matthew's correlation coefficient (MCC), Overall MCC, and Overall Accuracy. For multi-labelling estimation, we adopt LHR, PLMR and NT-LHR.

Results

1. Dataset

Shen HB et al [5] constructed a large-scale human protein dataset. The dataset covers 14 subcellular locations and contains 3106 distinct human proteins, where 2580 proteins belong to one subcellular location, 480 to two locations, 43 to three locations, and 3 to four locations. The protein with multiple subcellular locations should be treated as one training example of each subcellular location it belongs to, thus the same protein should be viewed as different protein within different subcellular location, referred to as locative protein in the literatures [4], [5], [15], [19], [27], [28], [29], [30]. Thus, there are 3681 locative proteins in the dataset [5]. The dataset is a good benchmark for model performance comparison, because none of the proteins has ≥25% sequence identity to any other proteins in the same subcellular location. Accordingly, we choose Hum-mPLoc 2.0 [5] as the baseline models for performance comparison. Although the dataset [40] collected much more multiplex human proteins, we don't use it to evaluate the multi-labelling, because the sequence similarity reaches 80%, so high as to yield performance overestimation.

2. Model performance evaluation

2.1 Optimistic case: both training set and test set abound in target GO information

The optimistic case assumes that both the training set and the test set abound in target GO information, that's, the training proteins and the test protein by themselves contain rich GO information before incorporating the homolog GO information. We call this case MLMK-TLM-I. As shown in MLMK-TLM-I section of Table 1, MLMK-TLM achieves 87.04% accuracy and 0.8606 MCC on Hum-mPLoc 2.0 human protein data, significantly outperforming the baseline Hum-mPLoc 2.0 62.7% [5]. Actually, Hum-mPLoc 2.0 aggregated the target protein's GO information together with the homolog GO information to train classifier, thus the overall accuracy 62.7% is the model's optimistic performance. The optimal hyper-parameter setting is 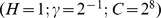, where 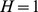means that only one homolog GO information is transferred to the target protein. The high MCC value (0.8606) implies that MLMK-TLM achieves good predictive balance among the 14 human protein subcellular locations. We can see from MLMK-TLM-I section of Table 1 that MLMK-TLM achieves good model performance one most subcellular locations, even the small Peroxisome (SP = 0.9750; SE = 0.8298; MCC = 0.8983) and Microsome (SP = 0.9500; SE = 0.7917; MCC = 0.8665). MLMK-TLM relatively underperforms on the small subcellular locations: Endosome (SP = 0.9167; SE = 0.4583; MCC = 0.6467) and Synapse (SP = 1.0000; SE = 0.5455; MCC = 0.7375). The poor performance may result from the sources: (1) small number of training proteins; (2) the target GO information is not as rich as the other subcellular locations; (3) the homolog GO information may be more divergent.

Table 1. Optimal performance on 3681 human locative protein dataset.

Subcellular location	Size	MLMK-TLM-I (optimistic)			MLMK-TLM-II (moderate)			MLMK-TLM-III (pessimistic)
		SP	SE	MCC	SP	SE	MCC	SP	SE	MCC
Centrosome	77	0.9063	0.7532	0.8229	0.8772	0.6494	0.7504	0.8235	0.7273	0.7694
Cytoplasm	817	0.7845	0.8556	0.7704	0.8061	0.8042	0.7552	0.7380	0.8446	0.7322
Cytoskeleton	79	0.9123	0.6582	0.7710	0.7910	0.6709	0.7231	0.8333	0.6329	0.7212
Endosome	24	0.9167	0.4583	0.6467	0.8000	0.5000	0.6306	0.9167	0.4583	0.6467
Endoplasmic reticulum	229	0.9302	0.8734	0.8951	0.9151	0.8472	0.8730	0.8818	0.8472	0.8557
Extracell	385	0.9525	0.8857	0.9096	0.9284	0.8753	0.8906	0.9413	0.8753	0.8977
Golgi apparatus	161	0.9214	0.8012	0.8534	0.9161	0.8137	0.8576	0.8705	0.7516	0.8010
Lysosome	77	1.0000	0.7143	0.8426	0.9828	0.7403	0.8504	0.9825	0.7273	0.8426
Microsome	24	0.9500	0.7917	0.8665	0.8947	0.7083	0.7949	0.8947	0.7083	0.7949
Mitochondrion	364	0.9620	0.9038	0.9255	0.9477	0.8956	0.9131	0.9339	0.8544	0.8825
Nucleus	1021	0.8479	0.9334	0.8486	0.8156	0.9314	0.8238	0.8287	0.8815	0.8028
Peroxisome	47	0.9750	0.8298	0.8983	0.9318	0.8723	0.9004	0.9762	0.8723	0.9219
Plasma membrane	354	0.8746	0.8672	0.8576	0.8169	0.8446	0.8130	0.8680	0.8362	0.8370
Synapse	22	1.0000	0.5455	0.7375	1.0000	0.5455	0.7375	1.0000	0.5000	0.7060
Overall Accuracy/MCC		87.04%/0.8606			85.22%/0.8411			83.97%/0.8277

2.2 Moderate case: training set abounds in target GO information while test set contains no target GO information

The most common scenario we encounter may be that we have a plenty of well-annotated training proteins and need to label some novel proteins at hand. We call the scenario as moderate case, referred to as MLMK-TLM-II. Novel proteins generally have no GO information at all. Most of the existing GO-based models except the work [26] ignored performance estimation in this case. Once the proposed models work in such a scenario, the performance may not be as optimistic as reported. Therefore, experiments should be expressly designed for the moderate case to test MLMK-TLM's applicability to novel proteins.

The test procedure for moderate case seems more complicated than that for optimistic case, because the proteins in the test set have no target GO information. Thus, the three target test kernels 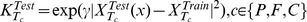can not be derived, because 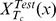is null (superscript Test denotes test set and Train denotes training set). For the reason, we substitute the homolog GO feature vector of test protein for its target GO feature vector to calculate the test kernel as follows:

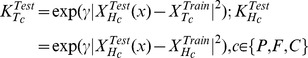(13)

As shown in MLMK-TLM-II section of Table 1, MLMK-TLM achieves 85.22% accuracy and 0.8411 MCC on the benchmark data, still significantly outperforming the baseline Hum-mPLoc 2.0 62.7% [5] and nearly 2% lower than the optimistic case (87.04% accuracy; 0.8606 MCC). Except for small performance decrease, MLMK-TLM-II demonstrates similar behaviour to MLMK-TLM-I (predictive balance and relative poor performance on Endosome & Synapse, see the underscored SE measures). The results show that MLMK-TLM is convincingly applicable to novel protein prediction, and the performance decrease shows that it is necessary to expressly report the model performance in moderate case.

2.3 Pessimistic case: both training set and test set contain no target GO information

In this section, we study an extreme case, called pessimistic case, where a protein subfamily or species is not GO-annotated at all, that's, we know nothing about the protein subfamily or species but the protein sequence information. The key point is whether the homolog GO information is informative enough to train an effective prediction model for the protein subfamily or species we know little about. To validate the point, we assume that at least one GO-annotated homolog can be queried for the target protein, which is not restrictive with the rapid progress of GOA database [12]. If experimental results support the idea, MLMK-TLM will gain much wider application. Different from the optimistic case and the moderate case, the pessimistic test procedure contains only three homolog GO kernels with target GO kernels missing.

As shown in MLMK-TLM-III section of Table 1, MLMK-TLM achieves 83.97% accuracy and 0.8277 MCC on the benchmark data, significantly outperforming the baseline Hum-mPLoc 2.0 62.7% [5], nearly 3% lower than the optimistic case (87.04% accuracy; 0.8606 MCC) and nearly 1.5% lower than the moderate case (85.22% accuracy; 0.8411 MCC). Similarly, MLMK-TLM-II demonstrates similar behaviour to MLMK-TLM-I & MLMK-TLM-I (predictive balance and relative poor performance on Endosome & Synapse, see the underscored SE measures). The results show that MLMK-TLM is applicable to novel protein prediction for the protein subfamily or species that we know little about.

3. Optimal number of homologs

Homolog is a good bridge for knowledge transfer between two evolutionarily- related protein subfamilies, super-families or species. However, biological evidences demonstrate that divergent homologs are subjected to different subcellular localization patterns from the target protein (see Figure 1), thus incorporating divergent homologs would leads to negative transfer and do harm to model performance. Thus, it is highly required to quantitatively study how much homolog GO information should be transferred to the target protein. Most of the existing Homolog-GO-based models except the work [26] seldom conducted the quantitative analysis. Because the homolog space is generally quite huge, the model selection is unendurably long if the hyper-parameter H is large, so we empirically define the homolog search space as 7 homologs with the most significant E-value.

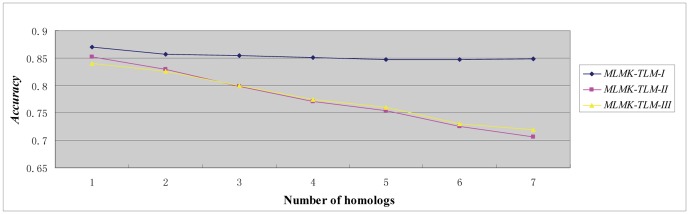
As shown in Figure 2, the optimal number of homologs is 1 for optimistic case (MLMK-TLM-I), moderate case (MLMK-TLM-II), and pessimistic case (MLMK-TLM-III). The model performance slightly decreases for the optimistic case (MLMK-TLM-I) with the incorporation of more homologs, while the model performance decreases sharply for the moderate (MLMK-TLM-II) & pessimistic case (MLMK-TLM-III). When the number of homologs reaches 7, the accuracy sharply drops about 15% for moderate & pessimistic case. We can see that divergent homologs adversely contribute little to the optimistic case, partly because the target protein's own GO information can counteract the unfavourable impact of the divergent homolog GO information. For the moderate & pessimistic case, the unfavourable divergent homolog GO information greatly deteriorates the model performance. From the results, we can safely conclude that it is highly necessary to quantitatively study how much homolog GO information should be transferred to the target protein.

Figure 2. Performance on 3681 human protein dataset with varying homologs.

It is worthy noting that the pessimistic case contains no target GO information but slightly outperforms the moderate case beyond our expectation (except at the first & second points of the curve in Figure 2). The reason may be that the substitution of the homolog GO feature vector for the target GO feature vector results in the slight performance deterioration (see Formula 13).

4. Kernel weight distribution

The GO kernel weights are evaluated using 3-fold cross validation as described in Section 3 of Methods, rather than 5-fold cross validation as GO-TLM [25] conducted, because the additional hyper-parameter H makes the model selection more time-consuming. Actually, to evaluate the model performance, we conduct two-level cross validation: the outer 5-fold cross validation uses the whole dataset to evaluate performance, and the inner 3-fold cross validation uses the training set from the outer cross validation to estimate the kernel weights. Similar to GO-TLM [25] and MK-TLM [26], the kernel weight distributions yielded from the outer 5-fold cross validation is quite similar, so we choose one typical kernel weight distribution to illustrate the GO kernels' contribution to the model performance.

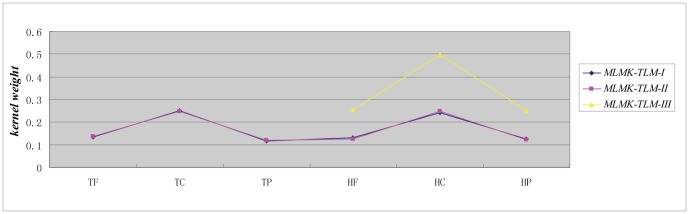
As shown in Figure 3, the x axis denotes the six GO kernels, where T denotes target, H denotes homolog, F, C and P denote the three aspects of gene ontology (molecular function, cellular compartment and biological process), respectively. We can see that both the optimistic case and the moderate case have similar kernel weight distributions on the benchmark dataset, while the pessimistic case is similar to the homolog GO kernel weight distribution of the optimistic case and the moderate case (see the latter part of curve in Figure 3) (the pessimistic case contains only three homology GO kernels in that the target protein's GO information is missing). No matter the target GO kernels or the homolog GO kernels, C (cellular component) demonstrates much higher kernel weight. For optimistic case and moderate case, both the target GO kernels and the homolog GO kernels make equivalent contribution to the model performance (compare the former half part and the latter half part of the curve in Figure 3). From the results, we can conclude that the homolog knowledge transfer is instrumental to novel target protein research.

Figure 3. Kernel weight estimation on 3681 human locative protein dataset.

5. Multi-labelling estimation

As stated in Section 4 of Methods, MLMK-TLM can yield the probability outputs from Formula 11. We can assign to the test protein the subcellular locations whose predicted probability is greater than the optimal probability threshold. The threshold setting should achieve rational balance between higher LHR (Label Hit Rate) & PLMR (Perfect Label Match Rate) and lower NT-LHR (Non-target Label Hit Rate) defined by Formula 12 in Section 5 of Methods. Generally, higher LHR & PLMR also implies higher NT-LHR. In the work, the optimal probability threshold is selected from 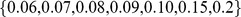. Besides LHR, PLMR and NT-LHR (Table 2 thru. Table 4), we also list some proteins of perfect label match (Table 5) and non-perfect label match (Table 6) to demonstrate MLMK-TLM's multi-labelling ability. Interestingly, some non-target label hits in terms of the original Hum-mPLoc 2.0 dataset (GOA database version 70.0 released March 10 2008) are validated as TRUE LABEL (Correct Prediction) by the latest Swiss-Prot database (UniProt release 2011_11 Nov 16, 2011, http://www.uniprot.org/) (see Table 6).

Table 2. Multi-labelling evaluation for optimistic case.

Multiplex Locations	Size	Label Hit Rate					PLMR	Non-target Label Hit Rate
		0	1	2	3	4		1	2	3	4
2	480	3.33%	38.12%	58.54%	0	0	42.92%	18.96%	8.54%	2.92%	0.42%
3	43	2.33%	25.58%	44.19%	27.91%	0	13.95%	25.58%	16.28%	2.33%	0
4	3	0	33.33%	0	33.33%	33.33%	33.33%	0	0	33.33%	0

Table 4. Multi-labelling evaluation for pessimistic case.

Multiplex Locations	Size	Label Hit Rate					PLMR	Non-target Label Hit Rate
		0	1	2	3	4		1	2	3	4
2	480	3.75%	38.12%	58.13%	0	0	34.58%	24.58%	11.67%	4.79%	2.50%
3	43	0	25.58%	41.86%	32.56%	0	9.30%	25.58%	18.60%	11.63%	0
4	3	0	33.33%	0	66.67%	33.33%	0	0	33.33%	0	33.33%

Table 5. Multi-labelling evaluation—perfect label match.

	Protein Accessions
Optimistic case [> = 0.09]	Q9UHB9;Q9UBQ5;Q9BT78;Q6SJ96;Q86W56;Q14145;Q9GZM5;Q9ULJ6;Q96Q15;Q15025;P06734;Q9NTJ3;O95391;Q92973;Q9UNS2;Q53HL2;Q9BZZ5;O43592;Q13352;Q9UHD9;Q9UHB6;Q9UQ80;P61221;Q9C0E2;P61011;P35520;O43324;Q9UI26;Q14738;P04792;Q9NYL5;Q7L7V1;Q86VP3;Q15392;Q7Z699;Q07954;Q13421;P11532;Q15004;Q12794;Q9P1T7;Q96QU8;Q9GZU1;Q9UKA2;O95070;P00488;O95153;Q12830;P16989;Q9Y6A2;Q92934;O60869;Q8N2I9;Q8N488;P38936;P16442;Q14493;Q9Y282;Q9HAP2;Q92551;Q9Y3C4;Q9NS86;Q96DU7;Q14978;P07954;Q9NXE4;P37840;Q9NRA8;P15907;Q08211;O76054;Q02880;O95997;Q8TEM1;P24071;Q969M3;Q9Y251;O95406;Q8NFM7;Q8WXI7;P14060;Q92820;P30519;Q96S99;Q7Z417;O95163;P23490;Q9BUP3;Q96Q89;Q96FX2;Q9Y6K9;O43157;O75533;Q49AN0;O75312;P56693;O60921;O95456;Q9Y6Q9;Q9BZG8;Q8N668;Q86X55;P35052;Q86UB2;Q99436;P29728;Q96PL5;Q9NY26;O14492;O15360;O75419;Q15020;P31512;O95273;Q8TEQ6;Q96PM5;Q9UNY4;O14980;Q9BV57;Q92681;Q6AZY7;O95479;Q9NZ42;O43174;Q93084;P20309;Q71F23;Q08J23;Q99519;Q86UW9;Q49MI3;P52630;P62826;Q00597;P61457;O00628;P60900;Q9H8E8;Q96C86;Q9BZJ0;Q9H8T0;Q9UKT4;Q12934;Q06787;Q13485;Q8IVL5;Q6RW13;Q8IWL8;Q13363;Q9Y314;P55060;Q9GZY1;O95453;Q07955;Q8WXG1;Q9C000;Q6IMN6;Q13765;O94829;Q9BRS8;O75365;P13987;O15354;Q9NSB8;Q14512;Q8TC92;Q96BI3;Q9NPH3;Q14703;P78329;Q04656;P58340;Q15276;O75884;Q7L5N1;Q969Q6;Q96KS0;Q86UA6;Q9NQW1;Q13098;Q7Z4G1;Q9BWU0;Q9BWS9;P21580;Q9UN88;Q13868;Q9NPD3;O14929;O15304;P61960;Q15650;Q13231;Q9NXR7;Q86YF9;P08684;Q9NWZ8;Q9BPZ7;P50748;Q03933;Q9NYF8;Q9Y397;Q96FF9;Q14534;P50542;Q00978;Q9H9T3;Q11203;O75881;Q9Y6K0;Q9P212;P43681;O43493;Q9UM00;
Moderate case [> = 0.08]	Q9UHB9;Q9UBQ5;Q9BT78;Q6SJ96;Q86W56;Q9GZM5;Q9ULJ6;O43663;Q96Q15;Q15025;Q9NTJ3;O95391;Q92973;Q9UNS2;Q53HL2;Q8IZY2;Q9BZZ5;O43592;Q13352;Q9UHB6;Q9UQ80;Q9C0E2;P22059;P61011;P35520;O43324;Q9UI26;Q14738;P04792;Q9NYL5;Q7L7V1;Q86VP3;Q15392;Q9UHK6;Q7Z699;P08962;Q15004;Q12794;Q9P1T7;Q96QU8;Q9GZU1;Q9UKA2;O95070;P00488;O95153;Q12830;P16989;Q13316;Q9Y6A2;Q92934;O60869;Q8N2I9;Q8N488;P38936;P16442;Q14493;Q9Y282;Q9HAP2;Q92551;Q9Y3C4;Q9NS86;Q96DU7;Q14978;P07954;Q9NXE4;Q9Y5Z9;P37840;Q9NRA8;P15907;Q08211;O76054;Q02880;O95997;Q8TEM1;Q969M3;Q9Y251;O95406;Q8WXI7;P14060;Q92820;P30519;Q96S99;Q7Z417;O95163;Q9BUP3;Q96Q89;Q96FX2;Q9Y6K9;O75533;Q49AN0;O75312;P56693;O60921;O95456;Q9Y6Q9;Q9BZG8;Q8N668;Q86X55;P35052;Q86UB2;Q99436;Q96PL5;O15360;O75419;Q15020;O95273;Q8TEQ6;Q96PM5;Q9UNY4;O14980;Q9BV57;Q92681;O95479;Q9NZ42;O43174;Q8ND25;P20309;Q71F23;Q08J23;Q99519;Q86UW9;P52630;P62826;Q00597;P61457;O00628;Q9H8E8;Q96C86;Q9BZJ0;Q9UKT4;Q12934;Q06787;Q13485;Q6RW13;Q8IWL8;Q13363;Q9Y314;P55060;Q9GZY1;O95453;Q07955;Q9C000;Q13765;O94829;Q9BRS8;O15354;Q9NSB8;Q14512;Q8TC92;Q96BI3;Q9NPH3;Q14703;P78329;P58340;Q15276;O75884;Q7L5N1;Q969Q6;Q96KS0;Q86UA6;Q92624;Q13098;Q7Z4G1;Q9BWU0;Q9BWS9;P21580;Q13868;Q9NPD3;O14929;P61960;Q15650;Q13231;Q9NXR7;Q86YF9;P08684;Q03135;Q9NWZ8;Q9BPZ7;P50748;Q03933;Q9NYF8;Q9Y397;Q96FF9;Q14534;P50542;Q00978;Q11203;O75881;Q9Y6K0;Q9P212;
Pessimistic case [> = 0.07]	Q9UBQ5;Q9BT78;Q6SJ96;Q86W56;Q9ULJ6;O43663;Q96Q15;Q15025;P06734;Q9NTJ3;O95391;Q92973;Q9UNS2;Q53HL2;Q9BZZ5;O43592;Q13352;Q9UHB6;Q9UQ80;Q9C0E2;P61011;P35520;O43324;Q9UI26;Q14738;P04792;Q9NYL5;Q7L7V1;Q15392;Q9UHK6;Q7Z699;P11532;Q15004;Q12794;Q9P1T7;Q96QU8;Q9UKA2;A5X5Y0;P00488;O95153;Q12830;P16989;Q9Y6A2;Q92934;O60869;Q8N488;P38936;P16442;Q14493;Q9HAP2;Q92551;Q9Y3C4;Q9NS86;Q96DU7;Q14978;P07954;Q9NXE4;Q9Y5Z9;P37840;Q9NRA8;P15907;Q08211;O76054;Q02880;O95997;Q9UKL3;P24071;Q969M3;Q9Y251;O95406;Q92820;P30519;Q96S99;Q7Z417;O95163;Q9BUP3;Q96Q89;Q96FX2;O75533;Q49AN0;P56693;O60921;O95456;Q9Y6Q9;Q9BZG8;Q86X55;P35052;P58335;Q86UB2;Q99436;Q96PL5;O15360;O75419;Q15020;O95273;Q8TEQ6;Q96PM5;Q9UNY4;O14980;Q9BV57;Q92681;Q9NZ42;O43174;P20309;Q71F23;Q08J23;Q86UW9;P52630;P62826;Q00597;P61457;Q9H8E8;Q96C86;Q9BZJ0;Q08378;Q9UKT4;Q06787;Q13485;Q8IWL8;Q13363;Q9Y314;P55060;O95453;Q07955;Q9C000;Q6IMN6;Q13765;O94829;Q9BRS8;Q9UKT7;P49721;Q14512;Q8TC92;Q96BI3;Q9NPH3;Q14703;P8329;Q04656;P58340;O75884;Q7L5N1;Q969Q6;Q96KS0;Q86UA6;Q92624;Q13439;Q13098;Q7Z4G1;Q9BWU0;Q9BWS9;P21580;Q13868;Q9NPD3;O14929;P61960;Q13231;Q9NXR7;P08684;Q9NWZ8;P50748;Q03933;Q9NYF8;Q9Y397;Q96FF9;Q14534;Q00978;Q53QV2;Q9H9T3;Q11203;O75881;

Table 6. Multi-labelling evaluation—non-perfect label match.

		True Subcellular Locations	Predicted Subcellular Locations
Optimistic Case [> = 0.09]	O43663	Cytoplasm; Nucleus	Nucleus[0.471]; Cytoplasm[0.365]; Cytoskeleton[0.136]
	Q92797	Cytoskeleton; Nucleus	Nucleus[0.470]; Cytoplasm[0.257]; Plasma membrane[0.129]
	Q92597	Cytoplasm; Nucleus; Plasma membrane	Nucleus[0.588]; Cytoplasm[0.333]
	P30533	Cytoplasm; Endoplasmic reticulum	Endoplasmic reticulum[0.237]; Cytoplasm[0.229] Nucleus[0.115]; Plasma membrane[0.181]
	Q9HD36	Mitochondrion; Nucleus	Nucleus[0.562];Mitochondrion[0.160];Cytoplasm[0.156]
	P22059	Cytoplasm; Golgi apparatus	Golgi apparatus[0.837]
	Q86YR5	Endoplasmic reticulum; Golgi apparatus	Golgi apparatus[0.454]; Endoplasmic reticulum[0.316]; Cytoplasm[0.091]
	P41222	Endoplasmic reticulum; Golgi apparatus; Nucleus	Endoplasmic reticulum[0.237]; Nucleus[0.207] Extracell[0.146]; Cytoplasm[0.143]; Golgi apparatus[0.107];
Moderate Case [> = 0.08]	P15941	Cytoplasm; Nucleus	Plasma membrane[0.467]; Nucleus[0.178]; Cytoplasm[0.145]
	Q14145	Cytoplasm; Nucleus	Cytoplasm[0.520]; Nucleus[0.292]; Endoplasmic reticulum[0.089]
	Q86YR5	Endoplasmic reticulum; Golgi apparatus	Golgi apparatus[0.371]; Endoplasmic reticulum[0.272]; Cytoplasm[0.129];Plasma membrane[0.124]
	P41222	Endoplasmic reticulum;Golgi apparatus Nucleus	Nucleus[0.257];Endoplasmic reticulum[0.214]; Cytoplasm[0.166]; Extracell[0.103]; Golgi apparatus[0.098]
	Q96JC1	Cytoplasm; Lysosome	Lysosome[0.676]; Endosome[0.208]
	Q96EY5	Cytoplasm; Nucleus	Nucleus[0.223]; Endosome[0.202]; Golgi apparatus[0.121] Cytoskeleton[0.092]
	Q86WA9	Endoplasmic reticulum;Golgi apparatus Plasma membrane	Lysosome[0.642]; Endoplasmic reticulum[0.136] Plasma membrane[0.101]
	Q9NWZ5	Cytoplasm; Nucleus	Endoplasmic reticulum[0.459]; nucleus[0.320]; Cytoplasm[0.133]
Pessimistic Case [> = 0.07]	Q9UHD9	Cytoplasm; Nucleus	Endoplasmic reticulum[0.315]; Nucleus[0.284]; Cytoplasm[0.202]
	P30533	Cytoplasm; Endoplasmic reticulum	Endoplasmic reticulum[0.250]; Cytoplasm[0.237] Nucleus[0.151]; Plasma membrane[0.139]
	Q86YR5	Endoplasmic reticulum;Golgi apparatus	Golgi apparatus[0.421]; Endoplasmic reticulum[0.202] Cytoplasm[0.136]; Plasma membrane[0.106]
	Q9NX74	Cytoplasm; Endoplasmic reticulum	Endoplasmic reticulum[0.273]; Cytoplasm[0.271] Mitochondrion[0.247]
	P41222	Endoplasmic reticulum;Golgi apparatus Nucleus	Nucleus[0.224]; Endoplasmic reticulum[0.197]; Cytoplasm[0.184]; Extracell[0.126];Golgi apparatus[0.077]
	Q96EY5	Cytoplasm; Nucleus	Nucleus[0.246]; Endosome[0.154]; Cytoskeleton[0.095]; Golgi apparatus[0.119];Plasma membrane[0.094]; Endoplasmic reticulum[0.075]
	P42858	Cytoplasm; Nucleus	Nucleus[0.285]; Cytoplasm[0.216]; Endoplasmic reticulum[0.071] Golgi apparatus[0.074]; Plasma membrane[0.096]
	Q9Y613	Cytoplasm; Cytoskeleton	Cytoskeleton[0.530]; Cytoplasm[0.146]; Nucleus[0.111]

Illustrations:

[1] True Subcellular Locations : denotes the labels from Hum-mPLoc 2.0 dataset (GOA database version 70.0 released March 10 2008);

[2] Cytoskeleton[0.136]:the label NOT included in the original Hum-mPLoc 2.0 dataset, but validated TRUE by the latest Swiss-Prot database ( http://www.uniprot.org/uniprot/ UniProt release 2011_11 Nov 16, 2011), where [0.136] denotes the probability that the protein is assigned to the label Cytoskeleton;

[3] Nucleus[0.115]: Non-target Label Hit (wrong prediction), NOT validated by the latest Swiss-Prot database ( http://www.uniprot.org/uniprot/ UniProt release 2011_11 Nov 16, 2011), where [0.115] denotes the probability that the protein is assigned to the label Nucleus;

As shown in Table 2 thru. Table 4, MLMK-TLM achieves 58.54%, 27.19% and 0 LHR (called complete label hit rate CLHR, in bold font) for 2, 3 and 4 multiple subcellular locations (optimistic case), respectively (see Table 2); 56.87%, 25.58%% and 0 LHR (CLHR, in bold font) for moderate case (see Table 3); and 58.13%, 32.56% and 33.33% LHR (CLHR, in bold font) for pessimistic case (see Table 4). The results seem much more promising than 24.3% for 2-label hit rate, 3.6% for 3-label hit rate and 6.7% for 4-label hit rate, reported in the work [40]. The complete label hit rate (CLHR) for pessimistic case seems better than the optimistic& moderate case, because of the probability thresholds: 0.09 for optimistic case, 0.08 for moderate case and 0.07 for pessimistic case. Relax probability threshold would yields higher Label Hit Rate (LHR), but would yields higher Non-target Label Hit Rate (NT-LHR) at the same time. From Table 2 to Table 4, we can see that the pessimistic case shows higher NT-LHR than the optimistic& moderate case. The complete label hit means that all the true labels are correctly hit by the prediction, but it can not measure the model's misleading tendency, because the prediction is still likely to hit non-target labels. Perfect Label Match Rate (PLMR) is the perfect measure that demonstrates the model's multi-labelling ability with zero misleading tendency. As shown thru. Table 2 to Table 4, we can see from PLMR measure that the optimistic case is the best (42.92%, 13.95%, 33.33%), the moderate case the second (38.75%, 9.30%, 0) and the pessimistic case the third (34.58%, 9.30%, 0). We can see that even MLMK-TLM's Perfect Label Match Rate is much better than the Partial Label Match Rate that was reported in the work [40]. Table 5 lists all the proteins of perfect label match in optimistic, moderate and pessimistic case, and the detailed probability outputs for the perfect label match proteins see Supporting Information (File S1 for optimistic case, File S2 for moderate case and File S3 for pessimistic case).

Table 3. Multi-labelling evaluation for moderate case.

Multiplex Locations	Size	Label Hit Rate					PLMR	Non-target Label Hit Rate
		0	1	2	3	4		1	2	3	4
2	480	4.37%	38.75%	56.87%	0	0	38.75%	22.29%	9.38%	3.96%	0.63%
3	43	0	25.58%	48.84%	25.58%	0	9.30%	20.93%	25.58%	2.33%	0
4	3	0	33.33%	33.33%	33.33%	0	0	33.33%	33.33%	0	0

To further demonstrate MLMK-TLM's multi-labelling ability, we list some proteins of non-perfect label match in Table 6 to show how the prediction varies from the true labels. Table 6 takes only 8 proteins for example and the full list of non-perfect label match proteins see Supporting Information (File N S1 for optimistic case, File N S2 for moderate case and File N S3 for pessimistic case). Take protein O43663 in the optimistic case as an example, O43663 is labelled Cytoplasm & Nucleus in the original Hum-mPLoc 2.0 dataset [5] (GOA database version 70.0 released March 10 2008), and the prediction not only hits the two true labels but also hit a non-target label Cytoskeleton with probability 0.136. From the latest Swiss-Prot database (UniProt release 2011_11 Nov 16, 2011, http://www.uniprot.org/), we can see that Cytoskeleton is truly assigned to protein O43663. The non-target labels validated as TRUE Label are underlined in Table 6. We can see that there are many underlined TRUE Labels in Table 6 for optimistic, moderate and pessimistic case. For example, Cytoplasm [0.166] & Extracell [0.103] for P41222 in the moderate case; Endoplasmic reticulum [0.071], Golgi apparatus [0.074] & Plasma membrane [0.096] for P42858 in the pessimistic case, etc., where the square bracketed number denotes probability. The underlined TRUE Labels demonstrates MLMK-TLM's generalization ability rather than misleading tendency. Actually, MLMK-TLM's misleading tendency is lower than the NT-LHR measures in Table 2 to Table 4 according to the latest Swiss-Prot database. No training proteins in Hum-mPLoc 2.0 dataset [5] are subjected to the subcellular localization pattern (Nucleus, Cytoplasm, Endoplasmic reticulum, Golgi apparatus, Plasma membrane) as P42858, whereas MLMK-TLM can correctly hit the five labels with different confidence levels, which is hard to achieve by the nearest neighbour based multi-label classifiers [19], [28], [29], [30], because the classifiers assigned to the query protein the labels that belong to the nearest training protein(s). Hum-mPLoc 2.0 web server (http://www.csbio.sjtu.edu.cn/bioinf/hum-multi-2/) labels O43663, P41222 and P42858 as follows: (1) O43663: Nucleus, without hitting Cytoplasm & Cytoskeleton; (2) P41222: Endoplasmic reticulum, Golgi apparatus and Nucleus, without hitting Cytoplasm & Extracell; (3) P42858: Cytoplasm, Golgi apparatus and Nucleus, without hitting Endoplasmic reticulum & Plasma membrane.

For both the moderate and the pessimistic case, the test proteins' own GO information is removed for the simulation of novel proteins, whereas MLMK-TLM can correctly predicts the test proteins' true labels and underlined TRUE Labels as illustrated in Table 2 to Table 6. The results show that MLMK-TLM has a good multi-labelling ability for novel multiplex human proteins. From Table 6, we also can see MLMK-TLM shows a certain misleading tendency, for example, Nucleus [0.115] & Plasma membrane [0.181] for P30533 in the optimistic case; Endoplasmic reticulum [0.089] for Q14145 in the moderate case; and Endoplasmic reticulum [0.315] for Q9UHD9 in the pessimistic case, etc. Hum-mPLoc 2.0 web server (http://www.csbio.sjtu.edu.cn/bioinf/hum-multi-2/) labels P30533, Q14145 and Q9UHD9 as follows: (1) P30533: Plasma membrane, Endoplasmic reticulum and Extracells, hitting non-target labels Plasma membrane & Extracells; (2) Q14145: Cytoplasm and Endoplasmic reticulum, hitting non-target label Endoplasmic reticulum; (3) Q9UHD9: Cytoplasm, Endoplasmic reticulum and Nucleus, hitting non-target label Endoplasmic reticulum. Misleading tendency is an important factor that should be given attention for multi-label learning scenario. The advantage of probability outputs is to inform the biologists of the confidence level of each subcellular location, and thus help biologists make a rational decision.

Discussion

In this paper, we propose a multi-label multi-kernel transfer learning model for human protein subcellular localization (MLMK-TLM), which o further extends our published work GO-TLM and MK-TLM to multi-label learning scenario, such that MLMK-TLM has the following advantages over the existing GO-based models [2], [4], [5], [14], [15], [16], [17], [18], [19], [20], [21], [22], [23], [24], [25], [26]: (1) proper homolog knowledge transfer with rational control over noise from divergent homologs; (2) comprehensive survey of model performance for novel protein; (3) multi-labelling capability with probability interpretation. As compared to single-label learning, multi-label learning is more complicated. In our work, we propose a multi-label confusion matrix and adapt one-against-all multi-class probabilistic outputs to multi-label learning scenario; meanwhile, we formally propose three multi-label learning performance measures: LHR (Label Hit Rate), PLMR (Perfect Label Match Rate) and NT-LHR (Non-target Label Hit Rate). NT-LHR is formally formulated to measure the model's misleading tendency. The experiments show that MLMK-TLM significantly outperforms the baseline model and demonstrates good multi-labelling ability for novel human proteins. Some findings (predictions) are validated by the latest Swiss-Prot database.

Supporting Information

File S1

Full list of perfect label match proteins in the optimistic case. For each multiplex protein in the supplementary documents, there are three lines of description. The first line describes the protein accession; the second line describes the true label(s) of the proteins; and the third line gives the predicted label(s) of the protein. Each predicted label is followed by a squared bracketed number that denotes the probability the protein is predicted to the label.

(DOC)

File S2

Full list of perfect label match proteins in the modest case. The file format dittos.

(DOC)

File S3

Full list of perfect label match proteins in the pessimistic case. The file format dittos.

(DOC)

File N S1

Full list of non perfect label match proteins in the optimistic case. The file format dittos.

(DOC)

File N S2

Full list of non perfect label match proteins in the modest case. The file format dittos.

(DOC)

File N S3

Full list of non perfect label match proteins in the pessimistic case. The file format dittos.

(DOC)