SNPs as Supplements in Simple Kinship Analysis or as Core Markers in Distant Pairwise Relationship Tests: When Do SNPs Add Value or Replace Well-Established and Powerful STR Tests?

Abstract

Background

Genetic tests for kinship testing routinely reach likelihoods that provide virtual proof of the claimed relationship by typing microsatellites-commonly consisting of 12–15 standard forensic short tandem repeats (STRs). Single nucleotide polymorphisms (SNPs) have also been applied to kinship testing but these binary markers are required in greater numbers than multiple-allele STRs. However SNPs offer certain advantageous characteristics not found in STRs, including, much higher mutational stability, good performance typing highly degraded DNA, and the ability to be readily up-scaled to very high marker numbers reaching over a million loci. This article outlines kinship testing applications where SNPs markedly improve the genetic data obtained. In particular we explore the minimum number of SNPs that will be required to confirm pairwise relationship claims in deficient pedigrees that typify missing persons’ identification or war grave investigations where commonly few surviving relatives are available for comparison and the DNA is highly degraded.

Methods

We describe the application of SNPs alongside STRs when incomplete profiles or allelic instability in STRs create ambiguous results, we review the use of high density SNP arrays when the relationship claim is very distant, and we outline simulations of kinship analyses with STRs supplemented with SNPs in order to estimate the practical limit of pairwise relationships that can be differentiated from random unrelated pairs from the same population.

Results

The minimum number of SNPs for robust statistical inference of parent-offspring relationships through to those of second cousins (S-3–3) is estimated for both simple, single multiplex SNP sets and for subsets of million-SNP arrays.

Conclusions

There is considerable scope for resolving ambiguous STR results and for improving the statistical power of kinship analysis by adding small-scale SNP sets but where the pedigree is deficient the pairwise relationships must be relatively close. For more distant relationships it is possible to reduce chip-based SNP arrays from the million+ markers down to ∼7,000. However, such numbers indicate that current genotyping approaches will not be able to deliver sufficient data to resolve distant pairwise relationships from the limited DNA typical of the most challenging identification cases.

Introduction

Currently the great majority of relationship testing is accomplished by typing standard forensic microsatellites or short tandem repeats (STRs). This approach provides the considerable advantages of using STRs: simple but very powerful statistics, straightforward kit-based chemistry; an extensive repository of allele frequency data, and community-wide consensus on dealing with interpretation issues such as inconsistent genotypes, difficult pedigree structures, and linkage. STRs resolve nearly all kinship cases to extremely high likelihood levels that support or exclude the claimed relationship, but their statistical power as a set of markers can be reduced in certain circumstances. Such situations include: partial profiles arising from highly degraded DNA, unknowingly testing a first-degree relative of the true father (such as a brother or father), ambiguous genotype patterns created by the relatively high mutational instability of STRs compared to other polymorphic markers, and relationship analyses where most or all other kinship members are unavailable for testing. Currently there are two choices available to practitioners to help overcome the above kinship testing challenges, adding supplementary STRs or combining the core STRs used with short-amplicon binary marker sets previously developed for forensic analysis of degraded DNA [1, 2, 3, 4]. Two kinds of short-amplicon markers are available: single nucleotide polymorphisms (SNPs) and insertion/deletion polymorphisms (indels). Their characteristics are well covered in companion papers in this issue. Herein, we use the term ‘SNPs’ to describe both types of binary marker as they have nearly identical qualities although indels enjoy the additional benefit of a typing system that uses a system of PCR amplification products put directly into capillary electrophoresis detection (PCR-to-CE), thus reducing tube transfers to one, bringing the same ease-of-use as STR kits and restoring the direct relationship between signal strength and input DNA (forensic SNP typing with SNaPshot primer extension employs two reactions, thus doubling the chance of stochastic effects).

In the first type of pedigree testing problems, where a close relative of the true father is unknowingly tested or a partial profile occurs due to highly degraded DNA, STR genotypes can produce low likelihoods that do not provide sufficient statistical support for a reliable relationship inference. In these cases SNPs offer supplementary data and better profile completeness from challenging DNA sources such as dentine or bone extracts. We describe examples of each scenario and show how SNPs can bring STR likelihoods up to levels of virtual proof.

Secondly, we give examples of the problem of interpreting inconsistent STR genotype patterns that give ambiguous results such that an exclusion of a first degree relative of the true father or one- or two-step repeat addition/diminution mutations are equally likely explanations of the data.

Lastly, we outline the problem of analyzing the most distant pairwise relationships, notably when the individuals tested come from a deficient pedigree, i.e. lacking any other immediate kinship members to help identify shared alleles. For sufficient statistical power, in these situations pairwise comparisons are dependent on the pair being reasonably closely related within the pedigree. When the examined relationship is distanced by several degrees of separation across multiple generations and pedigree branches much more genetic information must be obtained from the tested individuals. We outline computer simulations that seek to find the limits of pairwise relatedness beyond which STRs supplemented by an equal number of supplementary STRs and/or twice as many SNPs will not resolve the claim satisfactorily in a significant proportion of cases. From the data presented we suggest that pairwise comparisons of second cousins (described as an S-3–3 relationship as the subjects are separated by three generations on two pedigree branches, or, more specifically, siblings with a distance three generations from the root) will not be resolved in the majority of cases by use of small-scale marker sets alone. In fact, large-scale SNP genotyping arrays comprising over 1 million loci are the necessary step for such distant paired relationships, utilizing allele-sharing metrics compared to those of unrelated controls from the same population [5]. However, we also indicate that significantly reduced subsets of less than 10,000 markers can be sufficient to resolve S-3–3 pairs. We describe the analysis of a second cousin claim resolved using SNP array data and show that it is possible to reduce SNP data over 60-fold (<1.8% of data density) and properly differentiate the S-3–3 pair from random pairs of the same population.

Material and Methods

Small-Scale Genotyping: Single Multiplexes of STRs and SNPs

All STR genotyping followed manufacturer's recommended guidelines. We used Applied Biosystems (AB) AmpFlSTR Identifiler (Carlsbad, CA, USA) and Promega ESX-17 multiplex kits (Madison, WI, USA) providing 22 unique autosomal STRs of which 9 loci overlap between kits but have different primer sets allowing extended analysis of kit discordancies (see: www.cstl.nist.gov/strbase/NullAlleles.htm). We also use AB AmpFlSTR NGM+ multiplex STR kits instead of Identifiler. SNP typing uses the SNPforID Auto-1 and Auto-2 52-plex PCR and tandem 23-plex and 29-plex primer extension reactions, following previously described protocols throughout [6, 7]. Population frequencies for STRs and SNPs were obtained from pop. STR [8] and the SNP for ID frequency browser of SPSmart [9].

The alternative approach of adding extra STRs to the first-strike STR sets has become more straightforward recently by the addition of two commercial kits of supplementary STRs designed for this purpose: typing five novel markers in the 7-plex Promega CS7 and nine novel markers in the 12-plex of Qiagen Investigator HD-plex (Hilden, Germany) (details of the novel STRs of both kits are listed in table 1 of [10]). For simulation studies comparing SNP and STR supplementary sets we also examined the power of adding an inhouse 12-plex of novel STRs that have equivalent power to the components of Identifiler and ESX-17. These loci have not yet been published but we have observed that they are generally more informative than most of the composite loci of Promega CS-7 and broadly equivalent to those of Qiagen HD-plex. Therefore it is likely that addition of the 12-plex plus the nine novel Qiagen HD-plex markers represents the limit of STR data that can realistically be added to a first strike STR set of 15–22 markers. Simulations examined the power to infer a range of pairwise relationships [11] as summarized by the example pedigrees shown in figure 1, applying a core STR set of up to 21 loci, this core set plus 21 additional STRs (HD-plex + 12-plex), and then these two options plus 52 SNPs.

Table 1.

Percentage proportions of relationship inferences made for simulated true related pairs and unrelated random pairs (same allele frequencies) for four degrees of relatedness: 1/4–1/32^a

Pairwise relationship	No relationship	Doubtful relationship	Proven relationship
33 STRs
1/4: Grandfather-grandson
Related	16.13	47.59	36.28
Unrelated	99.03	0.95	0.01
1/8: First cousins
Related	64.9	34.34	0.76
Unrelated	98.55	1.45	0.002
1/16: S-3-2
Related	94.77	5.23	0.003
Unrelated	99.49	0.32	0
1/32: Second cousins
Related	99.72	0.28	0
Unrelated	99.98	0,024	0
42 STRs
1/4: Grandfather-grandson
Related	8.01	29.4	62.59
Unrelated	99.52	0.47	0.01
1/8: First cousins
Related	51.99	44.71	3.3
Unrelated	98.57	1.43	0.001
1/16: S-3-2
Related	90.69	9.3	0.01
Unrelated	99.49	0.51	0
1/32: Second cousins
Related	99.48	0.52	0
Unrelated	99.97	0.03	0
42 STRs + 52 SNPs
1/4: Grandfather-grandson
Related	4.82	20.53	74.65
Unrelated	99.68	0.31	0.004
1/4: Uncle-nephew
Related	4.85	20.99	74.65
Unrelated	99.68	0.3	0.012
1/8: First cousins
Related	45.39	49.24	5.37
Unrelated	98.59	1.41	0.002
1/8: Great grandfather-great grandson
Related	45.13	49.24	5.37
Unrelated	98.59	1.41	0.002
1/16: S-3-2
Related	88.4	11.58	0.02
Unrelated	99.37	0.63	0
1/32: Second cousins
Related	99.4	0.6	0
Unrelated	99.96	0.04	0

^aValues given for three supplce:italicented marker sets beyond standard paternity testing STR sets of 15–21: adding 12-plex (33); 12-plex plus Qiagen HD-plex 9; and these plus 52 SNPs. Bold values indicate erroneous inferences – i.e. no relationship inferred in the related pairs and proven relationships inferred in the Unrelated pairs. The full 42+52 marker set analyses show parallel 1/4 and 1/8 related pairs (includes uncle-nephew and great grandfather-great grandson respectively) that were run to assess consistency.

Fig. 1.

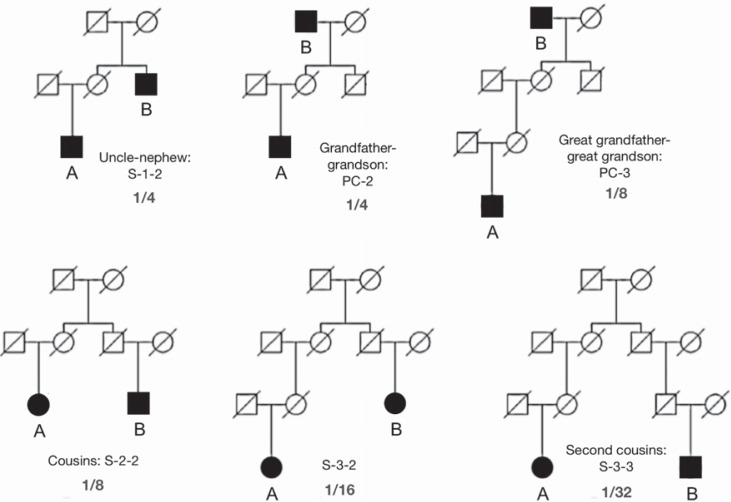
Six pairwise relationships (individuals A and B) of increasing distance typical of simple (1/4 genetic variation shared) through to challenging (1/32 shared) deficient kinship analyses.

Large-Scale Genotyping: High Density SNP Arrays

We routinely use the Affymetrix 6.0 genome-wide SNP array (Santa Clara, CA, USA) for association studies in the same laboratory as relationship testing and applied this technology to resolve a second cousin claim with a data-parsing regime that reduced data density into a viable format for allele-sharing calculations by removing non-informative, non-autosomal, and redundant genetic variability.

The 6.0 array comprises 1.8 million markers (946,000 copy number variants or CNVs (mostly short indels) plus 906,600 single nucleotide polymorphisms). DNA samples were processed following the Affymetrix Nsp/Sty assay protocol. An additional ten control samples from the same population (Northwest Spain) were typed to provide allele-sharing reference data representative of unrelated individuals with the same allele frequencies as the tested pair. Redundant and non-informative SNPs, sites on both X- and Y-chromosomes, plus mitochondrial DNA data were removed, and remaining SNP genotypes were parsed with centiMorgan (cM) chromosomal location and minor allele frequency (MAF) data obtained from HapMap Europeans (CEU: http://hapmap.ncbi.nlm.nih.gov/). The reduced SNP data was then thinned by applying 0.1 cM and 0.1 MAF filters to create a dataset of 30,564 loci. We used three other cM filters to explore effects of SNP density on informativeness of the data, these comprised 0.001 cM (318,977 SNPs), 0.01 cM (156,201 SNPs), and 0.5 cM (6,908 SNPs). The FEST R library was used to estimate allele-sharing proportions (alternatively termed proportion of identity-by-descent alleles or IBD) and convert these into relationship index (RI) likelihoods [12, 13, 14]. The RI is a simple likelihood ratio based on a posterior probability for a hypothesis test where H1 is unrelated (calculated from the control IBD values) and H2 the claimed relationship prescribed a priori from the claim (plus H3 if there is a competing claim). The use of a priori information to arrange hypotheses is important-even very high-density SNP data will not guarantee to differentiate the alternative relationships of a pairwise comparison in a complex pedigree. For example, uncle-nephew and grandparent-grandson show identical allele-sharing distributions (median of 1 in 4) and are clearly indistinguishable as hypotheses, but a small proportion of IBD values at the lowest end of the distribution will overlap with those of, say, great grandparent-great grandson relationships (median of 1 in 8).

Simulation Frameworks

Additional 12-plex STR data for a series of small-scale relationship testing simulations was based on inhouse data for European samples of the CEPH (Centre d'Etude du Polymorphisme Humain) human genome diversity panel. Additional frequency data for the large-scale relationship testing simulations of SNP arrays was obtained from the HapMap database accessed using the SPSmart frequency browser [15] or are available from Affymetrix for the Indel loci of the 6.0 array. No significant differences were found in the allele frequency distributions of HapMap CEU versus those of Northwest Spain obtained from the control samples.

Simulations for simple pairwise relationship inferences with various small-scale marker set combinations were made by modeling 100,000 relationships and random pairs in each relationship scenario using European allele frequencies. The simulations established density distributions of RIs obtained for six degrees of relatedness: grandfather-grandson (PC-2); uncle-nephew (S-1-2); great grandfather-great grandson (PC-3), first cousins (S-2-2); first cousins, once removed (S-3-2, i.e. the relationship between an individual and their cousin's offspring); and second cousins (S-3-3). Bracketed codes refer to the suggested shorthand descriptions of various relationships outlined by Skare et al., [12]. The RI values were classified into three possible categories based on the following probability threshold ranges: i) no relationship: RI = 0–10, ii) doubtful: RI = 10–1,000, iii) proven relationship: RI > 1,000. As a crosscheck of the simulation accuracy, two pedigree relationships with identical allele sharing to PC-2 and S-2-2 were run in tandem: uncle-nephew and great grandfather-great grandson, i.e. with 1 in 4 and 1 in 8 shared variation matching PC-2 and S-2-2 respectively (fig. 1).

Simulations for the second cousin analysis consisted of modeling 600 unrelated pairs and 600 S-3-3 relatives from CEU frequencies for the 30,564 SNP data set. Onto these distributions the actual IBD values could be overlaid and compared. Identical simulations were made for the other three SNP subsets of 0.001 cM, 0.01 cM, and 0.5 cM in order to gauge to what extent recorded IBD values matched simulated IBD distributions at different marker densities. It should be noted that the effect of linkage between markers in the lower cM value subsets was considered too difficult to model accurately, and this will skew the simulated IBDs obtained towards smaller values than those found in real related pairs.

Results and Discussion

Using SNPs to Improve the Relationship Likelihood Values Obtained from STRs

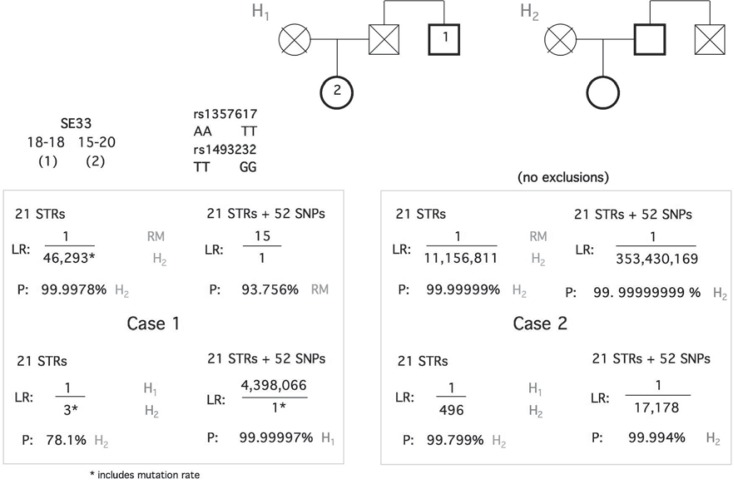
We describe two identical deficient kinship analyses with different outcomes obtained from the initial analysis of STRs and the subsequent addition of 52 SNPs. Both pedigrees involved a paternity claim made against the brother of the originally supposed father. In both cases the brother was tested along with the daughter, but with both the mother and supposed father deceased, without interred remains available for testing, and with Y chromosome marker typing not being possible. Figure 2 gives the alternative pedigrees and their hypotheses of H1 (the man and offspring were uncle and niece) or H2 (paternity of the tested man).

Fig. 2.

Identical pedigrees analyzed in two cases with different outcomes. The first case results support the hypothesis H1 - that the tested man was the uncle of the child due to the presence of multiple incompatible genotypes. The second case results supports hypothesis H2 - that the tested man is the father, based on a likelihood that brought a request for extended testing from the court.

In case 1, a single second-order exclusion of incompatible genotypes, SE33 18–18 (man) and 15–20, was obtained from typing 21 STRs. SE33 has the highest mutation rate of any STR but is a common additional system used for analyzing deficient pedigrees or indeed is frequently added when a single second-order exclusion such as that described above is found with first-strike STRs. SE33 has a 5-fold higher mutation rate of 0.0065 compared to an STR-wide average of 0.0013, while this is more than four orders of magnitude higher than the ∼2.5 × 10^–8 average mutation rate of SNPs. Therefore, this represents an ambiguous result; it is not possible to say whether the man is the father and a two repeat-addition mutation has occurred or if he is the brother of the true father and the ability to detect exclusions is compromised by his close relationship to the father plus the deficient pedigree. This is reflected in the likelihood ratios obtained strongly favoring H2 against a random man when the SE33 mutation rates are factored into the equation, but not strongly favoring either H1 or H2. SNP testing produces two additional exclusions and even when allowing for three independent mutations favors H2 very strongly and resolves the case.

In contrast, case 2 did not detect exclusions between tested individuals and gave a reasonable likelihood of paternity for the tested man. However, the court requested higher statistical support for H1 against H2 - so SNPs were added to increase the likelihood value 35-fold.

Figure 3 shows examples of pedigree analyses based on challenging DNA extracted from three femurs in progressively worse states of degradation: 1 year internment, 19 years internment, and 10 years post-mortem followed by further destruction of the remains by a forest fire [16]. Across this series, the STR profiles decreased in completeness from full to 53% to zero results. All SNP profiles were complete, and the relationship likelihoods they produced in the three cases, though less than those that can be expected from full STR profiles, strongly endorse the use of SNPs or indels as supplementary marker sets when the DNA is likely to be highly degraded.

Fig. 3.

Three simple pairwise relationship tests where the state of the DNA created incomplete STR profiles that required supplementary SNP tests. Cases are ordered from best at the top to worst condition (1 year, 19 and 10 years internment indicated).

Resolving Ambiguous Results from Inconsistent STR Genotypes between Pedigree Members

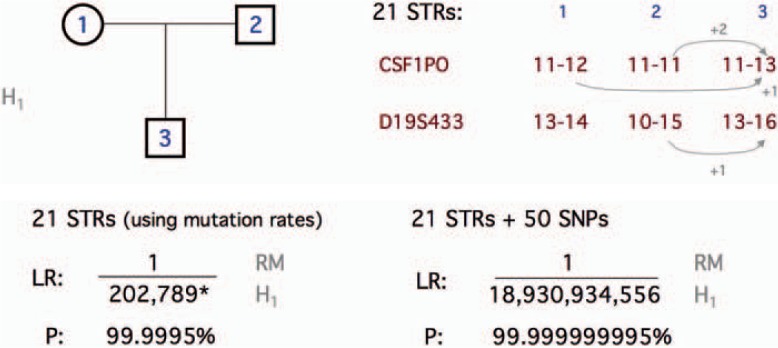
The case described in figure 4 is a simple trio that gave two independent incompatible genotypes between father and child from STR analysis. Even with the comparatively high mutation rates found with STRs the probability of two separate mutation rates is low. However the genotypes shown in the figure reveal that a single-step mutation in the father and in the mother can explain the detected incompatibilities. When 50 SNPs are added (2 of 52 SNPs were inconclusive), the final likelihood ratio strongly favors paternity, and the occurrence of two independent mutations becomes much more likely than non-paternity. This case is typical of the type of kinship analyses where a simple additional marker set of SNPs avoids the trap of including extra STRs and expanding the probability of finding more incompatible results which can create a scenario where the real source of the incompatibilities, mutations or exclusions (i.e. unknowingly testing a close relative of the true father), cannot be differentiated.

Fig. 4.

Simple trio kinship analysis with two independent STR incompatibilities (possible step mutations shown). In this case the absence of exclusions in SNPs added to a likelihood ratio that included the STR mutation rates that led to virtual proof of paternity.

Simulations of Pairwise Relationship Testing in Deficient Pedigrees: STRs Supplemented with STRs and SNPs

It is important to know the limitations of core and supplementary markers when analyzing distant relationships in deficient pedigrees, which are known to be the most challenging scenario for routine kinship analysis [17]. Therefore, we examined the effect of adding extra STRs and SNPs to 21 core STR markers. Since all indications show that 21 STRs do not provide sufficient statistical power for pairwise relationships beyond grandfather-grandson, we only made simulations for three stages: 21 STRs plus 12 inhouse STRs; these 33 plus 9 Qiagen HD-plex STRs, and these 42 STRs plus 52 SNPs. There are two sources of erroneous inference in pairwise kinship analysis: commonly that the RI value is so low that ‘no relationship’ is concluded, and much more rarely that unrelated pairs by chance share sufficient alleles to show an RI value suggesting a proven relationship. In table 1 we show the RI values obtained from the simulations put into three categories: no relationship; doubtful and proven, for four increasingly distant relative pairs compared to random pairs for three marker sets: 33 STRs, 42 STRs, and 42 STRs plus 52 SNPs. The full 94 marker set data of table 1 includes parallel analyses of equivalent 1/4 and 1/8 relationships comprising uncle-nephew and great grandfather-great grandson, respectively. These show consistent results compared to grandfather-grandson and cousins, based on independent simulations in each case. The distribution of log RI values obtained from the full 94 markers is also shown in figure 5 relative to the doubtful and proven log RI limits of 9 and 999. The choice of the 12-plex as the first supplementary set to apply was based on assessments of these STRs in comparison with core STR sets of Identifiler and NGM, in which simulated pairwise analyses indicated near identical power to differentiate each relationship. This suggests the 12 additional STRs of our inhouse set to be equivalent to those of the routine marker sets used for most relationship testing. We include these comparative simulation results in the supplementary data figure S1 (available online at http://content.karger.com/ProdukteDB/produkte.asp?doi=338857).

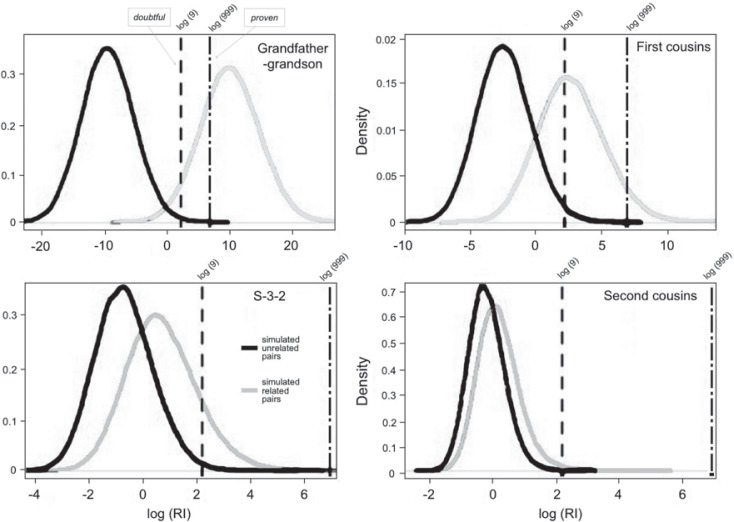
Fig. 5.

Density distributions of log RI values obtained from 100,000 simulations each of unrelated (black distributions) and related pairs (grey), for four different pairwise relationships. Reference lines of log 9 and log 999 represent doubtful and proven relationship likelihood thresholds respectively. The closest related pairs of grandfather-grandson show almost fully separated distributions with nearly all unrelated pairs less than doubtful and a large majority of related pairs more than proven. This pattern is progressively eroded as the related pairs become more distant, till the second cousin pairs’ distributions are near identical to unrelated pairs showing almost no pairs higher than doubtful.

Both table 1 and figure 5 suggest that when testing close pairwise relationships (such as grandfather-grandson) the addition of extra STRs and SNPs brings down the risk of assigning a no-relationship inference from 16% of cases to ∼5%. The probability of failing to infer no relationship in unrelated pairs drops marginally from about 1% of cases to one in 250 cases. However much more distant pairwise relationships do not improve sufficiently well with extra markers-indicated by increasing overlap between unrelated and related pairs, reaching near-complete overlap of log RI distributions for simulated second cousins and unrelated pairs.

These simulations led us to recommend that analysis beyond cousin pairs in a deficient pedigree would not be sufficiently resolved by any of the small-scale marker sets available to our laboratory. However, simulations also became important in deciding to assign an RI value in the form of an IBD metric compared to random pairs after exploring data generated from the much more extensive sets of SNP markers from arrays.

High-Density SNP Array Data: A Second Cousin Claim Resolved and Exploration of the Minimum SNP Numbers Required to Differentiate Distant Relatives from Random Pairs

High-density SNP arrays require a slightly different approach to normal relationship testing dictated by the volume of data and the fact that the more distant the related pairs in question the more they will resemble random pairs from the same population. Therefore, both reduction of the data density and exploration of the base level of relatedness amongst random pairs in the population were important steps towards data management for analysis of a second cousin claim we were asked to accomplish.

Data reduction achieved through applying minimum allele frequency and cM spacing filters preserved the maximum information content but significantly reduced the complexity of simulated pairwise comparisons required to gauge random pair relatedness as well as that of the claimants. So we were able to run simulations and IBD calculations on a subset of 30,564 SNPs - a 60-fold reduction that we expected to be powerful enough to differentiate related and random pairs. The first set of simulations using 30,564 SNPs provided distributions of allele sharing amongst random pairs and second cousins that had almost no overlap-these distributions are shown in the supplementary data figure S1 (available online at http://content.karger.com/ProdukteDB/produkte.asp?doi=338857). The distributions centered on 42,418 or 42,850 shared alleles. These median values for each distribution might appear to be very similar but when we overlaid three population control pairs and the tested pair these showed greater separation with the tested pair having 43,101 shared alleles compared to 42,300–42,600 in the control pairs. In fact only 0.68% of the simulated second cousins had greater allele sharing than the tested pair which we interpreted to indicate that the effects of linkage between component markers (which cannot be properly simulated) suggests that the actual separation of IBD comparing second cousins to random pairs will be greater. Therefore, we concluded that the tested pair were second cousins as claimed. To begin exploring the lower limits of power of more reduced subsets, we performed identical simulations comprising 6,908 SNPs (0.5 cM), and to confirm our findings with the computationally efficient set of 30,564 SNPs, we altered the cM filter to analyze 0.01 cM (156,201) and 0.001 cM (318,977) intervals. We modeled 600 random and second cousin pairs and used the kinship co-efficient metric better suited to intensive simulations. Figure 5 shows the distributions obtained and positions of the tested pair. In each case the random pairs center on zero and the second cousin pairs center on 0.015626 - the expected kinship co-efficient for this relationship. Again in each case the actual values obtained from the tested pair are well above the simulation distributions, and we interpret this to indicate the effect of linkage when comparing real allele distributions amongst related individuals with modeled distributions where linkage cannot be factored adequately. Finally when using 6,908 SNPs, the very small amount of kinship coefficient overlap between second cousins and random pairs and well separated distributions confirms that much smaller subsets of markers well below 10,000 are a realistic option for analyzing this degree of relatedness. This finding has prompted us to begin exploring the effect of further reductions in marker density down to levels that might provide realistic approaches for genotyping highly degraded DNA typical of missing person identification.

Concluding Remarks

In the current period of DNA analysis, the choice of markers available for relationship testing has expanded markedly, namely by short binary polymorphisms such as SNPs and indels being applied and by new STR sets becoming commercially available specifically for the purpose of supplemented kinship analyses. Therefore, it is more important than ever to properly gauge the limitations of pairwise relationship analysis in deficient pedigrees that can help define the likelihoods that can be expected from analyzing varying degrees of relatedness and marker densities. It is clear that pairwise relationships in deficient pedigrees cannot be adequately differentiated from random unrelated pairs with small-scale multiplexes when the relationships go beyond 1 in 4 to 1 in 8 shared variation. However, it is equally evident that the 1.8 million markers typical of high-density SNP arrays are far more than is necessary to differentiate second cousins from unrelated pairs, in fact numbers as low as 7,000 SNPs are able to make this differentiation with little overlap of likelihoods. This suggests that it will be possible to develop dedicated marker sets with medium-scale multiplexing (256–1,000) that could provide suitable tools for challenging kinship analyses applied to degraded DNA typical of missing persons investigations.

Disclosure Statement

The authors declare no conflict of interest.