Abstract
Tetratricopeptide repeats (TPRs) are a class of all alpha-helical repeat proteins that are comprised of 34-aa helix-turn-helix motifs. These stack together to form nonglobular structures that are stabilized by short-range interactions from residues close in primary sequence. Unlike globular proteins, they have few, if any, long-range nonlocal stabilizing interactions. Several studies on designed TPR proteins have shown that this modular structure is reflected in their folding, that is, modular multistate folding is observed as opposed to two-state folding. Here we show that TPR multistate folding can be suppressed to approximate two-state folding through modulation of intrinsic stability or extrinsic environmental variables. This modulation was investigated by comparing the thermodynamic unfolding under differing buffer regimes of two distinct series of consensus-designed TPR proteins, which possess different intrinsic stabilities. A total of nine proteins of differing sizes and differing consensus TPR motifs were each thermally and chemically denatured and their unfolding monitored using differential scanning calorimetry (DSC) and CD/fluorescence, respectively. Analyses of both the DSC and chemical denaturation data show that reducing the total stability of each protein and repeat units leads to observable two-state unfolding. These data highlight the intimate link between global and intrinsic repeat stability that governs whether folding proceeds by an observably two-state mechanism, or whether partial unfolding yields stable intermediate structures which retain sufficient stability to be populated at equilibrium.
Keywords: protein folding, repeat protein, energy landscape, TPR
Introduction
The linear repeat proteins are a diverse collection of superfamilies that are all comprised of small modules (20–40 amino acids), which are stacked together to form stable nonglobular domains.1–3 After immunoglobulins, linear repeat proteins constitute the second most abundant group of proteins whose primary function is ligand-binding. For example, the TPR superfamily, identified in 1990, is ubiquitous throughout nature and currently numbers over 119,000 entries in the PFAM database.4–6 They are used by a diverse set of proteins for roles in eukaryotic cell-signalling (protein phosphatase 5), chaperone-assisted protein folding (Hop), regulation of cell-division (anaphase promoting complex) and mitochondrial fission in the budding yeast Saccharomyces cerevisiae (Fis1), amongst others.7, 8
There are many other families of linear repeat proteins which include proline-rich repeats (PRR), leucine-rich repeats (LRR) and ankyrins.1–3 Unlike globular proteins, these repeat proteins do not rely on complex long-range stabilizing interactions. Instead, their modular nonglobular structures are dominated by regularized short-range interactions (both inter- and intra-repeat). This distinctive feature, which results in a quasi one-dimensional structure, has made them extremely attractive targets as models for protein folding and design studies.3, 9–11
Recently, the literature has shown great interest in the folding kinetics, cooperativity and equilibrium stability of repeat proteins.12–20 In particular, studies have primarily focused on natural ankyrin repeat proteins and, to a lesser extent, TPR repeat proteins. These have investigated whether the modular nonglobular structures of repeat proteins inherently influence their folding and stability. Significantly, this has been shown to be the case, with both their kinetic and equilibrium folding being prone to the population of partially folded intermediate states. However, whether such intermediates are populated seems to be linked to the competing factors of the intrinsic stability of helices/repeats and the generation of favorable interfaces between helices/repeats.
Designed consensus repeat proteins provide an excellent system for further investigation into the fundamental properties of repeat proteins, as each repeat has identical intra- and intra-repeat interactions.3, 21 Thus, designed repeat proteins are more structurally symmetrical than natural repeat proteins and can easily be extended or shortened by adding or removing whole repeats. This tolerance to sequence splicing is remarkable, compared to globular proteins and is exquisitely tuneable, thus forming a powerful sandbox for exploring the effects of their modular design on their biophysical characteristics. A prime example of such a system of designed consensus proteins is one based on the tetratricopeptide repeat family.11
We and the Regan laboratory have engineered two series of designed consensus TPR proteins (in which the repeating unit is a stacking helix-turn-helix motif, 34 residues in length), called CTPR and CTPRa proteins. These proteins represent a highly tunable system that has allowed investigation of the dependence of folding kinetics, thermodynamic characteristics, and the denatured state upon increasing repeat number (Fig. 1; the two series only differ by a 2-aa substitution per repeat).11, 12, 17 NMR and equilibrium chemical denaturation studies on the CTPR2 and CTPR3 proteins suggest that, despite the apparent cooperative equilibrium unfolding, intermediate states with frayed terminal helices are populated through the denaturation transition.23, 24 Further, Regan and coworkers have used DSC to show that all the CTPRa proteins undergo multistate equilibrium folding under their conditions.20 This multistate folding was elegantly described by fitting and modeling the thermodynamic unfolding transition of chemical denaturations to these repeat proteins using a homozipper Ising model.12 The model was defined as a series of coupled folding units (individual helices) via nearest-neighbor interactions within a one-dimensional lattice.
Figure 1.
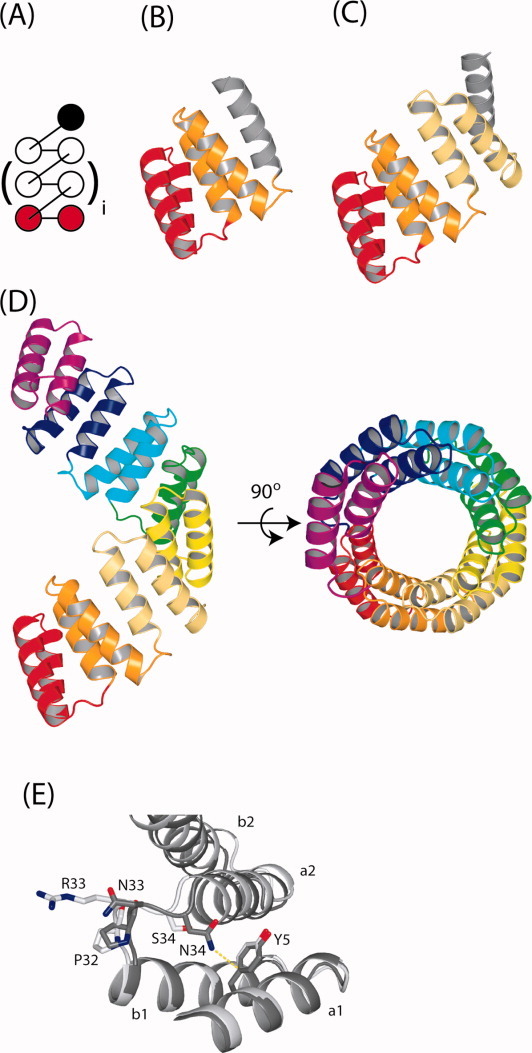
Topological and ribbon representations of CTPR/CTPRa proteins. (A) Topological map of a native CTPR/CTPRa proteins. The brackets around the central TPR motif indicate that the CTPR/CTPRa proteins can be increased or decreased in size whilst retaining the same topology. For example, for CTPR3, i = 1. (B–D) The crystal structures of CTPR2 (PDB entry: 1NA3), CTPR3 (PDB entry: 1NA0) and CTPRa8 (PDB entry: 2FO7), respectively. In A–D the consecutive repeat units are colored from red (N-terminus) to magenta (C-terminus), with the solvating helix (S) in gray (absent from the crystal structure of CTPRa8). (E) shows detail of the different interactions that the -PNN- of CTPR3 and the -PRS- of the CTPRa8 make in their respective crystal structures. It can be seen that the double mutation (N33R and N34S) changes the interactions present within the interrepeat loops. The N34 sidechain of CTPR3 is optimally aligned for making an amide–pi bond with Y5 of the A-helix from the preceding repeat (a1): the δ-nitrogen of the amide is positioned 3.66 Å from the phenolic ring pi system in the crystal structure of CTPR3.22 N33 is oriented toward solvent. The R33 and S34 sidechains of CTPRa8 have no opportunity to make stabilizing interactions in the crystal form of CTPRa8 and are oriented toward solvent. These structural features result in the -PNN- loop of the CTPR conferring greater stability than the -PRS- loop of the CTPRa protein counterparts. These figures were prepared using PYMOL. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]
These biophysical studies provide a strong foundation for understanding the thermodynamic behavior (stability, energetics, and equilibrium two to multistate folding) of repeat proteins and, specifically, designed TPR proteins. Such investigations are essential as repeat proteins begin to be used as biomaterials25 (Phillips et al. manuscript in preparation), antibody substitutes26, 27 and disease diagnostics/drugs.28 However, such uses will involve changes in protein sequence and chemical environment. Therefore in this study, we have investigated how changing environmental conditions and intrinsic stability of constructs effect the equilibrium unfolding energy landscape of the CTPR proteins. To do so, we probe the equilibrium thermal and chemical unfolding of two series of CTPR proteins of differing intrinsic stabilities (CTPRa2 to CTPRa10 and CTPR2 to CTPR3) and compare them to studies conducted in different pH and salt regimes. The data illustrate the subtlety of the equilibrium energy landscape of the designed TPRs by showing how destabilizing these normally multistate folding proteins can induce observably two-state folding. Importantly, they also show that observable multistate folding can be tuned by changing the intrinsic stability of the repeat modules through mutation and by altering the cumulative stability of the entire protein.
Results
Consensus TPR proteins (CTPRs) were built from arraying multiple copies (n) of a 34-aa idealized sequence with a C-terminal single “solvating” (S) helix. The CTPR and CTPRa series differ in the loop region between the B-helix of one TPR and the A-helix of the next (AEAWYNLGNAYYKQGDYDEAIEYYQKALEL DPXX). The CTPR series loop encodes PNN and the CTPRa series loop encodes PRS (amino acid positions 33 and 34 in the TPR repeat). Both CTPR and CTPRa series have the same sequence for the C-terminal, solvating S-helix (AEAKQNLGNAKQKQG). All proteins adopt the distinctive alpha helical TPR fold with the unique feature of possessing identical modular structures, although the two series differ slightly in structure around the two different residues described above (Fig. 1). Here we have studied and compared the chemical and thermal denaturations of seven proteins from the CTPRa series (CTPRa2 to CTPRa10) and two from the CTPR series (CTPR2 and CTPR3).
Thermal denaturation of CTPRa and CTPR proteins
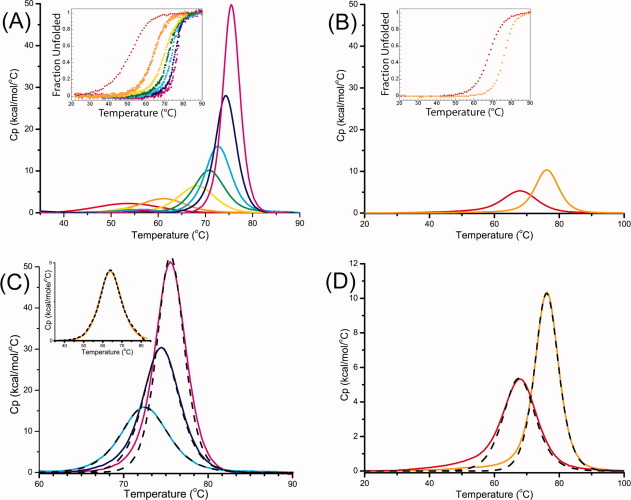
Thermal unfolding of the two series of consensus linear repeat proteins (CTPRa2 to CTPRa10 and CTPR2 to CTPR3) were performed at pH 7 (50 mM phosphate) by differential scanning calorimetry (DSC) and by thermal melting monitored by circular dichroism (CD) ellipticity at 222 nm (Fig. 2; Table I; Supporting Information Fig. 1). All of the CTPRa and CTPR proteins underwent a single reversible transition as the increase in temperature caused unfolding of their native structure to yield a denatured polypeptide. This is evident as there is only a single transitional peak by DSC and a single unfolding transition by CD (midpoints of unfolding, Tm, are consistent between both experimental methods—Fig. 2; Table I).
Figure 2.
DSC Thermograms of CTPRan and CTPRn protein series. DSC thermograms for the series of (A) CTPRan (2 ≤ n ≤ 10) and (B) CTPRn (for n = 2,3) at protein concentrations between 20 and 100 μM. Inset in both (A) and (B) are the thermal denaturation traces of the CTPRa and CTPR proteins, respectively, followed by ellipticity at 222 nm shown as a fraction of unfolded protein. The denaturation midpoint (Tm) from DSC and CD were in good agreement. (C) and (D) illustrate the limits of a two-state model (black dashed line) to fit the DSC thermograms of CTPRan and CTPRn proteins. Data are shown as solid lines. For both series of CTPRan/CTPRn: n = 2 (red), 3 (orange), 4 (yellow), 5 (green), 6 (cyan), 8 (blue), and 10 (magenta). The fits to the data in (C) and (D) are shown in dashed lines. The two-state model, in which ΔHvH = ΔHcal, reasonably fits CTPRan for n ≤ 6, but does not adequately fit the data for CTPRa proteins with eight or ten repeat units (C). Neither of the CTPRn proteins studied could be fit to a two-state model (D). [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]
Table I.
Thermodynamic Measurements from DSC and CD Monitored Thermal Melts
| Differential scanning calorimetry (DSC)a | ||||||||
|---|---|---|---|---|---|---|---|---|
| Model independent fit (numerically integrated) | Model dependent fit (two state) | C.D. thermal meltbc | ||||||
| Protein | Tm (°C) | ΔHcal (kcal mol−1) |
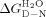 (10°C), (kcal mol−1) (10°C), (kcal mol−1) |
Tm (°C) | ΔHvH (kcal mol−1) | β (°C)d | Tm | ΔHvH (kcal mol−1)e |
| CTPRa2 | 53 ± 0.3 | 44 ± 4 | 3.2 ± 0.6 | 55 ±1.2 | 48 ± 4 | 0.9 ± 0.1 | 51 ± 0.2 | 37 ± 4 |
| CTPRa3 | 63 ± 0.6 | 65 ± 3 | 4.8 ± 0.4 | 62 ±1.1 | 59 ± 1 | 1.1 ± 0.1 | 62 ± 0.04 | 60 ± 6 |
| CTPRa4 | 68 ± 0.1f | 73 ± 7 | 4.2 ±1.1 | 68 ±0.7 | 88 ± 1 | 0.8 ± 0.1 | 67 ± 0.03 | 67 ± 7 |
| CTPRa5 | 71 ± 0.1 | 95 ± 5 | 6.0 ± 0.8 | 71 ±0.5 | 101 ± 5 | 1.0 ± 0.1 | 70 ± 0.03 | 84 ± 8 |
| CTPRa6 | 71 ± 1.0 | 116 ± 2 | 7.7 ± 0.2 | 73 ±0.3 | 112 ± 15 | 1.0 ± 0.1 | 71 ± 0.03 | 99 ± 10 |
| CTPRa8 | 74 ± 0.5 | 178 ± 8 | 14.3 ± 1.5 | g | g | g | g | g |
| CTPRa10 | 74 ± 1.3 | 250 ± 11 | 23.4 ± 2.1 | g | g | g | g | g |
| CTPR2 | 68 ± 0.04f | 73 ± 0.4 | 7.6 ± 1.1 | g | g | g | g | g |
| CTPR3 | 76 ± 0.1f | 108 ± 1 | 12.0 ± 0.7 | g | g | g | g | g |
The thermodynamic data have been calculated from the DSC thermograms using a model free analysis in MicroCal Origin. Values are the mean of at least two independents experiments. Errors, unless otherwise stated, are the mean spread of at least two experiments. In most cases the error in the fit was smaller than the mean spread between experiments.
Values were obtained from singly fitted datasets to a two state folding model with errors given as the fit of the data. CTPRa3 and CTPRa4 were repeated twice and produced Tm and ΔHvH that were within the error of the data fitting.
Values obtained are estimated using ΔCp calculated from a value of 10 cal/mol/residue/deg (7).
β is the ratio of ΔHCal/ΔHvH. For a two-state, fully co-operative unfolding transition the calorimetric enthalpy should be identical to the van't Hoff enthalpy, i.e., β = 1.
Errors stated are ±10% owing to fitting constraints.
Errors stated are from the fit of individual experiments as this was greater than the mean spread between experiments.
Not calculated as endotherms/melts are not two state transitions.
Differential scanning calorimetry
All CTPRa and CTPR proteins unfolded reversibly under the conditions studied. This was confirmed by subjecting samples to multiple cycles in the calorimeter cell and through repeating experiments at differing protein concentrations. These showed that the Tm did not significantly alter, with a variance of only ±0.4 K (Supporting Information Fig. 1). To analyze each DSC endotherm, Origin software modified by MicroCal Software was used to convert each trace to excess heat capacity, it was then buffer reference subtracted, normalized for protein concentration and then progress baselines subtracted—Material and Methods. Each trace was numerically integrated to obtain the area under the heat capacity endotherm and a Tm (using previously published values of ΔCp assumed to be invariant with temperature.20). After correcting for concentration, the area beneath a DSC endotherm is equal to ΔHcal (the enthalpy change of unfolding per mole of the protein). In both series of proteins, as the number of arrayed repeat units increased, so did the Tm and also ΔHcal, indicating that the proteins were growing in stability (Table I).
The ΔHcal obtained for each protein was then used together with their Tm and ΔCp20 to calculate a model-independent free energy of unfolding (ΔGD-N) using the Gibbs–Helmholtz equation [Eq. (1) and Table I]. This calculation was performed for each of the CTPRa/CTPR proteins and extrapolated to 10°C (temperature at which our previous study of chemical denaturations were performed17—Table I and Figures 2 and 3. When these stabilities for both CTPRa and CTPR proteins are compared, they show that the CTPR proteins are of greater stability than the CTPRa proteins of the same size (due their different sequences, wherein CTPR proteins make an amide–pi interaction between the interrepeat loop and the preceding A-helix, which is abrogated by the N to S mutation in CTPRa—Fig. 1). They also show, in line with published data that as each series increases in repeat number, stability is also increased. Interestingly, when the proteins in the more extensive CTPRa series are compared, their stability increases relatively linearly from CTPRa2 to CTPRa6, corresponding to an addition of ≍1 kcal mol−1 per repeat, but this deviates and the increase in stability becomes nonlinear from CTPRa8 onward (Table I; Fig. 3). Taken together, this suggests a switch from an apparent cooperative two-state folding to less cooperative multisate folding. As, if the folding switches to multistate, the intermediates populated would require additional energy to unfold. This is also consistent with the changing shape of the DSC endotherms. These reduce in symmetry upon increasing repeat number, also suggesting a switch from two to multistate folding (Fig. 2).
Figure 3.
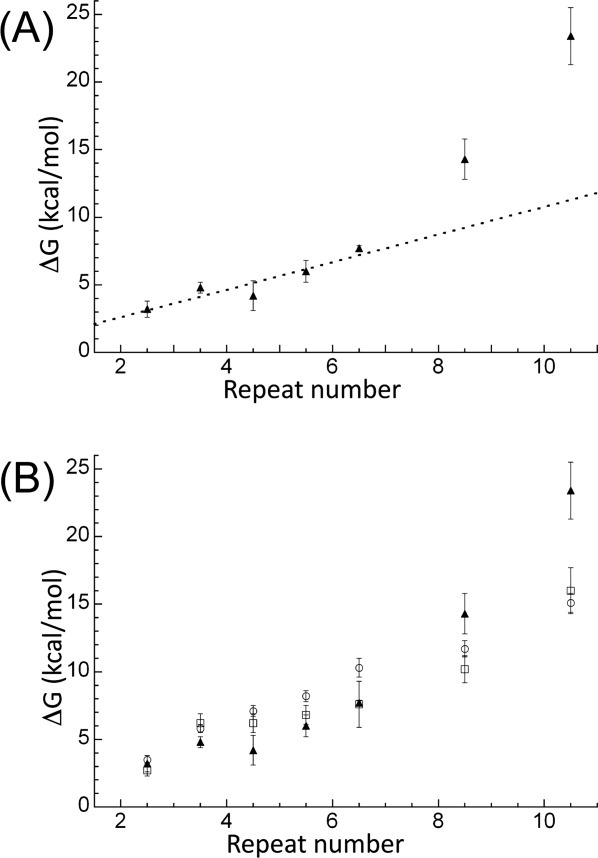
The stability at 10°C of each CTPRan protein versus number of linearly arrayed repeat units (C-terminal capping helix represented here as half a repeat) calculated using three different experiments. (A) ΔG values were calculated from model-free analysis of DSC data (filled triangles). The dashed line shows the linear best fit to CTPRa2 to CTPRa6 (a gradient of ≍1.0 kcal/TPR). (B) ΔG values shown were calculated from two-state fit to urea denaturation CD data (open squares) and two-state analysis of GuHCl denaturation CD data (open circles) and model-free analysis of DSC data (filled triangles). All chemical denaturation stabilities were obtained from Javadi and Main.17 Error bars represent the propagation of error from data fitting for chemical denaturation and mean spread of at least two experiments for DSC. For chemical denaturations analyzed by a two-state model free energy was calculated as the product of the denaturant midpoint and the m-value, whereas for DSC experiments the ΔG was calculated at 10°C by extrapolation using the Gibbs–Helmholtz equation [Eq. (1)].
Equilibrium folding cooperativity—from two to multistate equilibrium unfolding
Importantly, in addition to a model-free enthalpy and stability, DSC provides a definitive means to assess the cooperativity of a protein's equilibrium folding, that is, whether a protein unfolds in a simple two state manner where only the denatured and native state are populated or in a multistate manner where intermediate states are also populated. This is because, in addition to a model independent fit, DSC endotherm traces can also be fitted to a specific folding model to give an ΔHvH (enthalpy change of unfolding per mole of cooperative folding unit). In the case of a two-state folding process, endotherms are fit to the van't Hoff equation that assumes a single two-state transition [ΔHvH(T) = -R(dlnK/dT−1)]. If a protein folds via a cooperative two-state equilibrium process: (i) the DSC endotherm will fit well to this two state model (single cooperative folding unit29–31) and (ii) the ΔHvH produced from the model-dependent equation will equal the model-independent ΔHcal (as shown by many studies on small globular proteins).32, 33
When the CTPRa protein endotherms were fit to the two-state model it was found that qualitatively between two and six repeats fit well (CTPRa2-CTPRa6). In contrast, CTPRa8, CTPRa10 and the CTPR proteins did not produce satisfactory fits [Fig. 2(c,d)]. This discrepancy was quantified by comparing the χ2/DoF values and the residuals of the two state fit to those of the numerically integrated model-independent fit (Supporting Information Fig. 2). For CTPRa2 to CTPRa6, the residuals to the different model fits overlapped with an amplitude <1 kcal mol−1 deg−1 and both produced similar χ2/DoF values. In contrast, χ2/DoF for the two-state fit to CTPRa8 thermal unfolding data were two orders of magnitude greater than for the multistate fit. This difference increased to more than three orders of magnitude when fit to CTPRa10 data. Applying this same index to the more stable CTPRn series, the χ2/DoF for a two-state fit to CTPR2 was two times that of the multistate fit and this increased to a fivefold difference for CTPR3. This shows that the CTPR proteins and the largest two CTPRa proteins in this study cannot be adequately fit to a two state model, giving a clear indication of multistate folding. In contrast, CTPRa2 to CTPRa6 fit equally well to the simpler, two-state model which supports the interpretation that they fold in an observable two state manner under the conditions studied. To confirm, the ΔHcal and ΔHvH values for CTPRa2 to CTPRa6 were compared as a ratio, β, in Table I. For a two-state, fully cooperative unfolding transition one would expect the calorimetric enthalpy to be identical to the van't Hoff enthalpy, that is, β = 1. This is precisely what is observed (Table I). These data show that total stability of the CTPR/CTPRa protein constructs (as a result of the differing loop sequences and of the number of arrayed repeat units) is correlated with their ability to form stable intermediate species, that is, observable multistate folding can be tuned by changing the intrinsic stability of the constructs through mutation and by altering the cumulative stability through the number of arrayed repeat modules.
Modulation of observable equilibrium multistate folding of CTPRa proteins through extrinsic influences on global stability
When our DSC melts of the CTPRa series are compared to those recently published by Cortajarena and Regan in different buffer conditions (with NaCl and at lower pH) we find that for all proteins our Tm values are lower and the areas beneath the endotherms are smaller, Table II.20 For example, the ΔHcal and Tm for CTPRa4 in Cortajarena and Regan's work are 103 kcal mol−1 and 73°C, respectively, whereas we observed values of 73 ± 7 kcal mol−1 and 68°C. These data show that by changing buffer conditions we are changing the absolute stability of the CTPRa proteins. This was confirmed by performing thermal denaturations monitored by CD for CTPRa3 and CTPRa4 between pH 5 and pH 8 (Supporting Information Fig. 3 and Supporting Information Table I). In both cases the Tms of the curves significantly increased as pH decreased. This behavior can be rationalized as the CTPRan and CTPRn proteins have a predicted isoelectric point of 4.2 and 4.0, respectively. These changes in stability (Supporting Information Fig. 3 and Supporting Information Table I) can again be correlated with a switch from simple two-state to multistate folding of the TPRs: the more stable conditions of Regan and coworkers resulted in observably multistate folding for almost all lengths of arrayed CTPRan, whereas under our conditions (at higher pH and without NaCl) we observed two-state folding up until six arrayed repeat modules (CTPRa6), with CTPRa8 and CTPRa10 being multistate.
Table II.
Thermodynamic Measurements from Our DSC Study in Comparison to Published Cortajarena and Regan Study
| DSC—this studya | DSC—Cortajarena and Reganb | |||||
|---|---|---|---|---|---|---|
| Tm (°C) | ΔT1/2 | ΔHcal (kcal mol−1) | Tm (°C) | ΔT1/2 | ΔHcal (kcal mol−1) | |
| CTPRa2 | 53 ± 0.3 | 17 | 44 ± 4 | 58 | 16 | 47 |
| CTPRa3 | 63 ± 0.6 | 11 | 65 ± 3 | 68 | 11 | 78 |
| CTPRa4 | 68 ± 0.1c | 9 | 73 ± 7 | 73 | 9 | 103 |
| CTPRa6 | 71 ± 1.0 | 6.5 | 116 ± 2 | 77 | 6 | 192 |
| CTPRa8 | 74 ± 0.5 | 5 | 178 ± 8 | 79 | 5 | 257 |
| CTPRa10 | 74 ± 1.3 | 4 | 250 ± 11 | 80 | 4 | 335 |
The thermodynamic data have been calculated from the DSC thermograms using a model-free analysis in MicroCal Origin. Values are the mean of at least two independents experiments. Errors, unless otherwise stated, are the mean spread of at least two experiments. In most cases the error in the fit was smaller than the mean spread between experiments.
Duplicated from Table 1 of Cortajarena and Regan 2011 (7).
Errors stated are from the fit of individual experiments as this was greater than the mean spread between experiments.
Equilibrium chemical denaturation
Comparison with DSC ΔGD-N values
Chemical denaturations performed previously at 10°C with the same buffer conditions and analyzed with a two-state and Ising model analysis17 were compared with the (model free fit) DSC presented here (Fig. 3). Significantly, they show that, for those proteins that have been shown here to be observably two-state (CTPRa2 to CTPRa6), there is a broad agreement between the DSC model free ΔGD-N and ΔGD-N from the two state fit of the chemical denaturation. For those shown to be observably multistate by DSC (CTPRa8, CTPRa10, and the CTPR series), the ΔGD-N was larger by DSC than by two-state analysis of chemical denaturation (as one would expect from multistate folding proteins). This reaffirms the two-state to multistate equilibrium unfolding spectrum with respect to the length, thus total stability, of the CTPRa array, as highlighted by the DSC analysis.
Comparison of chemical denaturation upon changing buffer conditions
To confirm the differing trends in multistate behavior observed by DSC upon changing buffer conditions, chemical denaturations using Guanidine hydrochloride (GuHCl) were performed at 25°C under our buffer conditions and were compared with published results acquired at lower pH and with the addition of NaCl (Fig. 4, Supporting Information Fig. 4).12 There are six CTPRa proteins (CTPRa2, 3, 4, 6, 8, 10)12 and both CTPRn proteins.23 for which published reciprocal data exists under alternative buffer conditions. When these are compared there is a clear difference in the unfolding equilibria for the CTPRan proteins [Fig. 4(B) and Supporting Information Fig. 4]. All denaturations still have a single reversible transition; however, both the midpoint and the gradient of the transition, therefore stability, increase in those experiments conducted at a more acidic pH and in the presence of NaCl. Both of these effects are most pronounced for the CTPRa proteins (concomitant with both a lower stability and also a greater change in pH between experimental conditions).
Figure 4.
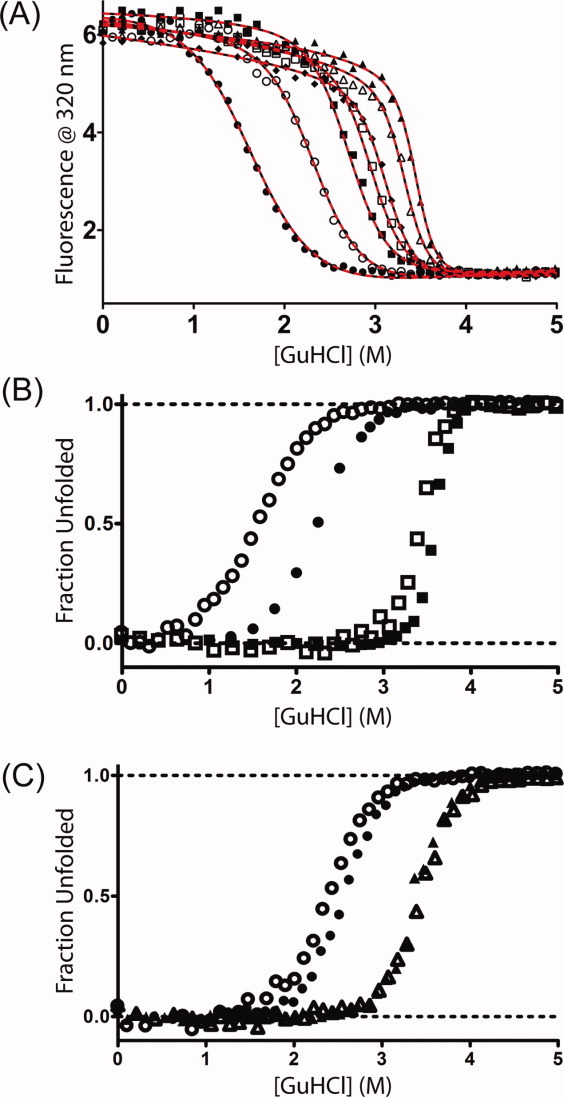
Denaturation of consensus TPR proteins in GuHCl at 25°C. (A) Fluorescence at 320 nm for CTPRan constructs with protein concentrations between 1 and 4 μM in 50 mM phosphate at pH 7.0—CTPRa2 (filled circles), CTPRa3 (open circles), CTPRa4 (filled squares), CTPRa5 (open squares), CTPRa6 (filled diamonds), CTPRa8 (open triangles), CTPRa10 (filled triangles). Lines correspond to the global best fits to a description based on the Regan-derived (solid black) or Barrick-derived (dashed red) one-dimensional Ising model—Materials and Methods. (B) Comparison of fraction unfolded versus [GuHCl] for CTPRa2 (circles) and CTPRa10 (squares) under differing buffer conditions: open symbols—50 mM phosphate, pH 7.0; filled symbols—50 mM phosphate, pH 6.5 + 150 mM NaCl (filled symbols—data obtained from Kajander et al.12 with the program Un-SCAN-IT [Silk Scientific]). (C) Comparison of fraction unfolded versus [GuHCl] for CTPR2 (circles) and CTPR3 (triangles) under differing buffer conditions: open symbols—50 mM phosphate, pH 7.0; filled symbols—pH 6.8 phosphate buffer + 150 mM NaCl (filled symbols—data were obtained from Main et al.23
Homozipper Ising model analysis
Recently, we and other groups have analyzed linear repeat protein equilibrium unfolding using a 1D homozipper Ising model.12, 17, 19, 34, 35 This model treats each arrayed element of a repeat protein as an equivalent independently folding unit with nearest-neighbor pairwise interactions between those units. Thus, it breaks down the folding of a linear repeat protein into a linear series of interacting units. By globally fitting a homozipper Ising model to chemical denaturations for a whole series of repeat proteins that differ only by their number of identical repeats, the intrinsic energy of a repeated unit and the interaction energy between the folded units can be delineated.12, 17, 19, 35 These values can then be summed to obtain the total stability of each protein within the series. We analyzed our denaturation data obtained at 25°C and compared it to previously published values under differing buffer conditions, but at the same temperature. Both the Regan-derived 1D Ising model12 and an alternative formulation used by Barrick and coworkers35 was used to fit the data—Material and Methods [Fig. 4(A)].
All datasets fit well to these models and gave the following parameters for the Regan-derived Ising: xc (midpoint of unfolding of a single α-helix in the protein), m1 (denaturant dependence of a single α-helix in the protein), J (the coupling energy between α-helices) from which H (half of the difference in free energy between the folded and denatured states of a single helix in the absence of coupling to its neighbors; Supporting Information Table II). From these data a 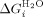 (intrinsic helix energy in water),
(intrinsic helix energy in water), 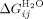 (Interface interaction energy between folded helices in water; Table III) and
(Interface interaction energy between folded helices in water; Table III) and 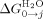 (the free energy of folding in water for a protein with j α-helices) can be calculated (Table III, Supporting Information Table III). In a similar manner, data fit to the Barrick-derived Ising model directly produces
(the free energy of folding in water for a protein with j α-helices) can be calculated (Table III, Supporting Information Table III). In a similar manner, data fit to the Barrick-derived Ising model directly produces 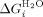 , m1 (denaturant dependence of a single α-helix in the protein) and
, m1 (denaturant dependence of a single α-helix in the protein) and 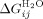 . From these,
. From these, 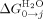 can also be calculated. Both formulations of the Ising model give values for the stability of a helix and interface interaction energy between helices that were essentially the same (Supporting Information Table III). They show, as expected and previously reported, that in water individual helices and single repeat units are not stable, but 1.5 repeats are marginally stable with all larger constructs being stably folded. This is achieved through the additive positive effects of the stronger favorable interaction energy between folded helices that overcomes their unfavorable intrinsic stability.
can also be calculated. Both formulations of the Ising model give values for the stability of a helix and interface interaction energy between helices that were essentially the same (Supporting Information Table III). They show, as expected and previously reported, that in water individual helices and single repeat units are not stable, but 1.5 repeats are marginally stable with all larger constructs being stably folded. This is achieved through the additive positive effects of the stronger favorable interaction energy between folded helices that overcomes their unfavorable intrinsic stability.
Table III.
Intrinisic Stability of a Helix and the Interface Energy Between Helices Obtained from Fitting Chemical Denaturations Conducted at 25°C for the CTPRan and CTPRn Series of Proteins to the Regan-Derived Homozipper Ising Model Under Different Buffer Conditions
| Protein series | Study | Temp. (°C) | pH | Salt (mM) | mia |
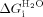 (kcal mol−1)b (Intrinsic helix energy) (kcal mol−1)b (Intrinsic helix energy) |
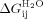 (kcal mol−1)c (interface interaction energy) (kcal mol−1)c (interface interaction energy) |
|---|---|---|---|---|---|---|---|
| CTPRan | This studyd | 25°C | 7.0 | 0 | 0.7 ± 0.02 | 3.0 ± 0.2 | −4.5 ± 0.2 |
| Kajander et al.e | 25°C | 6.5 | 150 | 0.96 ± 0.01 | 2.3 ± 0.1 | −4.5 ± 0.1 | |
| CTPRn | This studyd | 25°C | 7.0 | 0 | 0.8 ± 0.03 | 4.4 ± 0.6 | −7.0 ± 0.6 |
| Main et al.d,f | 25°C | 6.8 | 150 | 0.9 ± 0.02 | 4.1 ± 0.3 | −6.9 ± 0.3 |
Obtained from global fit of equilibrium data using Eq. (5).
Obtained using Eq. (6).
Obtained using Eq. (7).
Errors are the propagated errors from the fit of the data and are quoted to a 95% confidence interval (twice the standard error of the fit).
Experimental results and errors obtained from Kajander et al. (17) and propagated.
Data obtained from Main et al.(26) and reanalyzed with regan-derived ising model. Values are the average of those obtained from fitting CTPRn series of GuHCl denaturations followed by CD and fluorescence.
Interestingly, it has been suggested that the propensity of a repeat protein to exhibit multistate or two state folding can be resolved by examining the mismatch between these intrinsic and interfacial energies.19 For example, a repeat protein that has a large mismatch from a high magnitude of favorable interfacial energies and unfavorable intrinsic repeat stabilities is more likely to cooperatively fold/unfold in a two state manner. When previous studies on CTPRn/CTPRans proteins are compared to other repeat proteins like ankyrins, they have a much lower mismatch and are therefore proposed to be more likely multistate. Here we can compare the differences in interface and intrinsic stabilities when changing the total stabilities of the proteins through buffer conditions and mutation (Table III).
Change in buffer
For the CTPRan protein series, the switch in buffer composition gives the same interface energy between folded repeat units, but under the more stabilizing conditions causes the intrinsic stability of a folded repeat to be less unfavorable (by 0.7 kcal mol−1). This change slightly increases the mismatch energy and, when combined to give the total energy of the protein, the small differences stack quickly to produce proteins of far greater stability. For the CTPRn constructs the conditions are not changed sufficiently to change the stability substantially (all values are within error).
Change in sequence
In comparison to the change in buffer, the mutation of -PRS- (CTPRan) to -PNN- (CTPRn) destabilizes the intrinsic stability of the helices but also greatly increases the stabilizing interaction energy between helices. The greater of the two effects resides with the increase of the interface interaction energy; which leads to an increase in mismatch energy for the more stable CTPRn over the CTPRan constructs and thus a greater total protein stability. This change can be rationalized as the crystal structures show that the change from -PRS- to -PNN- causes the gain of the stabilizing amide–pi bond with the preceding A-helix (Fig. 1).
In both cases, highlighted above, increasing total stability through changes in sequence or buffer causes slight increases in the mismatch between interface and intrinsic stabilities. The additive effect of these quickly produces large increases in total protein stability. This would therefore suggest that although mismatch of the energies is an important factor in determining the propensity for a repeat protein to be two- or multistate folding; here, the total stability of the native protein and minimally stable species, under the unfolding conditions present, is of more importance.
Discussion
The modulation of cooperative equilibrium folding in designed TPRs
The calorimetric and equilibrium chemical denaturation data presented here highlight three features of the designed CTPRan and CTPRn series: (i) for the CTPRa series the absolute stability of the proteins and, consequently, the stability of the minimally folded unit are influenced by changing the buffer conditions; (ii) the stability of the proteins is increased in positive correlation with the number of TPR units, but the relationship is not linear by DSC using a model free analysis; (iii) the stabilizing interrepeat loop mutations from -PRS- (in CTPRan) to -PNN- (in CTPRn) significantly increase ΔGD-N, facilitating the emergence of stable intermediate states with a smaller number of repeats. In contrast, the absolute stability of the CTPRan is reduced in our buffer conditions, to the extent that the size of the minimally stable species is necessarily larger. Where they occur as partially folded states of larger structures, these species constitute the intermediate states. Consequently, intermediates and multistate behavior are only observed in the larger CTPRan proteins.
Thus, although it has been shown that at equilibrium CTPRan and CTPRn proteins have the propensity for multistate folding and the population of stable intermediates,23, 24, 36 our data show that this observable multistate folding can be modulated and is determined by the total stability of the protein and, consequently, the stability of the remaining partially folded species under the unfolding conditions. If they are unstable the protein acts as an observably two-state unfolding system (e.g., CTPRa2 and CTPRa3), with intermediates being high-energy and not populated. However, as the number of repeats (n) is increased, the stability of the whole protein and partially unfolded intermediates increases. Under our conditions the switch in behavior from observable two-state equilibrium unfolding to a situation where partially folded states are populated under the unfolding conditions, occurs between CTPRa6 to CTPRa8 for the CTPRan series and CTPR2 onward for the CTPR series. Interestingly, the total stability of the whole protein at which intermediates are populated at equilibrium is around the same stability in both the CTPRn and CTPRan series (above 7.5 kcal mol−1). After this stability is reached, either through a greater number of arrayed repeat units or with stabilizing mutations (i.e., PRS in CTPRan to PNN in CTPRn), multistate folding is observable.
Importantly, these results show that observable multistate folding can be tuned by changing the intrinsic stability of the repeat modules through mutation and by altering the cumulative stability of the entire protein, either through changes to the environment or to the number of linearly arrayed repeat modules. The generality of such an approach leads to exciting possibilities. For example, one can envisage a designed repeat protein that could be triggered to specifically partially unfold in response to environmental stimuli, thus exposing a cryptic interface. Such behavior represents an exciting opportunity, as it would be the first step in designing new types of biosensors/switches as synthetic components.
Materials and Methods
Cloning, protein production, and purification
The two differing series of designed CTPR/CTPRa proteins were expressed, and purified as previously described.11, 12 As stated at the beginning of the results section, the CTPR and CTPRa series differ in the loop region between the B-helix of one TPR and the A-helix of the next (AEAWYNLGNAYYKQGDY DEAIEYYQKALELDPXX). The CTPR series loop encodes PNN and the CTPRa series loop encodes PRS (amino acid positions 33 and 34 in the TPR repeat). This difference arose from the need for an effective and simple cloning strategy when making the larger series of consensus repeat proteins (CTPRan series). As such it was not easily feasible to construct synthetic genes for CTPR proteins of greater repeat number. These considerations meant that the CTPRan series of proteins were extended to 10 repeats, whereas the CTPR series only contained CTPR1 to CTPR3. Earlier publications describe both the synthesis and cloning rationale in detail.11, 12
Biophysical studies
All biophysical measurements were performed at 10°C in 50 mM phosphate pH 7.0 buffer (phosphate buffer), unless otherwise stated.
Differential scanning calorimetry
DSC was performed from 20 to 90°C, at a rate of 1°C min−1 with a MicroCal VP-DSC. Protein samples were dialyzed into phosphate buffer and were scanned against this dialysis buffer at concentrations of 30–150 μM. The thermograms generated with the protein samples were analyzed using Origin software (MicroCal Software). Data were converted to excess heat capacity, reference trace-subtracted, normalized for concentration and then progress baselines were subtracted. The processed data were then fitted to a model free analysis in the MicroCal Origin software to obtain the midpoint of unfolding (Tm), calorimetric enthalpy (ΔHcal) and width at half height of denaturation peak (ΔT1/2). To obtain the van't Hoff enthalpy (ΔHvH), the processed data were also fitted to a model-dependent two-state folding analysis and a non-two-state analysis fitted with one transition (MicroCal Origin software).
Using the Gibbs–Helmholtz equation [Eq. (1)], the free energy of unfolding, ΔGD-N, was calculated for each protein at 10°C (283 K):
| (1) |
where ΔHD-N (the enthalpy term) is substituted with either ΔHcal or ΔHvH, Tm is the midpoint of unfolding, ΔCp is the change in heat capacity (assumed to be invariant with temperature over the range studied37) obtained from Regan and co-workers20 and T is temperature at which you wish to calculate ΔGD-N (10°C).
Although the errors in enthalpy at the Tm are large (≤17 kcal mol−1) with respect to the free energy of folding, which for most proteins lies around 5–15 kcal mol−1, the extrapolation to a common temperature (283 K) from the Tm serves to reduce the error since:
| (2) |
where δΔGD-N(T), δΔHD-N(Tm), δTm, and δΔCp are the errors in the free energy of unfolding at temperature T, in the enthalpy of unfolding at the melting temperature, in the calculation of the melting temperature and in the change in absolute specific heat capacity of the protein with temperature respectively.38
Thermally induced unfolding monitored by far-UV CD
Reversible thermal unfolding of all protein samples (1–4 μM) were monitored by far-UV CD at 222 nm from 20 to 90 or 95°C. The temperature was ramped at a rate of 1°C min−1 with data points taken every degree. Data were fitted to a two-state folding model (using KaleidaGraph™ software—Synergy Software, PCS), represented by Eq. (3):
 |
(3) |
where αN and αU are the intercepts, and βN and βD are the slopes of the baselines at the low (N) and high (D) denaturant concentrations, ΔHD-N is the enthalpy of unfolding, Tm is the midpoint of unfolding, ΔCp is the change in heat capacity (assumed to be invariant with temperature over the range studied37) obtained from Regan and co-workers20 and T is temperature.
Once values for ΔHD-N and Tm are known, together with ΔCp, Eq. (1) was used to give the free energy of unfolding at temperature T.
Equilibrium chemical denaturation experiments
Fluorescence and far-UV circular dichroism equilibrium unfolding measurements were performed as described previously.17
Equilibrium data analysis
Data were analyzed in two specific ways. They were either analyzed with a two-state model17 or with a homozipper Ising model12, 17, 35 Analysis of the data with the homoziper Ising model is described below. In the case of two-state model analysis, free energy of unfolding in water was calculated from the relationship:
1D Ising model
We fitted the data to two formulations of one-dimensional homozipper Ising model. One was that defined by the Regan Laboratory12 and the other was that of the Barrick Laboratory.35 In both cases GraphPad Prism (using a Marquardt algorithm nonlinear least-mean-squares fitting routine) was used to globally fit each series of CTPRan proteins equilibrium data simultaneously (either CD or Fluorescence).
Regan Laboratory homozipper Ising model
The partition function for a CTPRn/CTPRan protein of N-helices was taken as:
| (4) |
where N is the number of helices within a CTPRn/CTPRan protein, J is the interaction between lattice sites (α-helices), 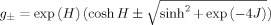 and H is the internal energy of a single lattice site (each α-helix).
and H is the internal energy of a single lattice site (each α-helix).
The global fitting of equilibrium curves was achieved by numerically calculating the magnetization, m = dlogZ/dH, and thus the fraction folded, f = (1 + m)/2, as a function of J and H = 1/2m1([D] - [D]c). Where m1 is denaturant dependence of a single α-helix in the protein, [D] is the concentration of denaturant and [D]c is the value at which H = 0. To numerically calculate the magnetization a step size of 0.001M was used. The global fitting produced values for J, m1 and [D]c that were the same for all of the series of proteins fitted.
The equilibrium curves could also be globally fitted, in the same manner as above, without converting the observed signal to fraction folded by using Eq. (5):
| (5) |
where  is the observed signal (fluorescence or CD), αN and αD are the intercepts, and βN and βD are the slopes of the baselines at the low (N) and high (D) denaturant concentrations, [D] is the concentration of denaturant and f = f(H,J) is the fraction of the protein that is folded according to the Ising Model. Here, J, m1 and [D]c were globally fitted to obtain values that were the same for all CTPRan proteins. Whereas, αN, αD, βN, and βD were not globally fit, but were specific for each CTPRan protein's equilibrium unfolding curve. Equation (5) assumes that λobs of each proteins native state, λN, and each proteins denatured state, λD, are linearly dependent on the denaturant concentration (λN = αN + βN[D], λD = αD + βD[D]).
is the observed signal (fluorescence or CD), αN and αD are the intercepts, and βN and βD are the slopes of the baselines at the low (N) and high (D) denaturant concentrations, [D] is the concentration of denaturant and f = f(H,J) is the fraction of the protein that is folded according to the Ising Model. Here, J, m1 and [D]c were globally fitted to obtain values that were the same for all CTPRan proteins. Whereas, αN, αD, βN, and βD were not globally fit, but were specific for each CTPRan protein's equilibrium unfolding curve. Equation (5) assumes that λobs of each proteins native state, λN, and each proteins denatured state, λD, are linearly dependent on the denaturant concentration (λN = αN + βN[D], λD = αD + βD[D]).
Free energies for folding were then calculated using Eqs. (6)–(9):
| (6) |
| (7) |
| (8) |
| (9) |
where, 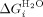 is the intrinsic helix energy in water,
is the intrinsic helix energy in water, 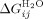 is the interface interaction energy between folded helices in water),
is the interface interaction energy between folded helices in water), 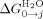 is the free energy of folding in water for a protein with j α-helices, n is the number of folded α-helices in each protein, R is the gas constant, T the temperature at which the experiment was calculated, H is the internal energy of a single lattice site (α-helices) and is calculated from H = 1/2 m1([D] - [D]c) and J is the interaction between the lattice site (α-helices).
is the free energy of folding in water for a protein with j α-helices, n is the number of folded α-helices in each protein, R is the gas constant, T the temperature at which the experiment was calculated, H is the internal energy of a single lattice site (α-helices) and is calculated from H = 1/2 m1([D] - [D]c) and J is the interaction between the lattice site (α-helices).
Barrick laboratory homozipper Ising model
We constructed a one-dimensional homozipper Ising model essentially as was previously described.35, 39 This takes two equilibrium constants, κ and τ, for the unfolding of an arrayed unit (helix) and dissociation of folded units, respectively:
| (10) |
| (11) |
The partition function, Z, and thus the fraction of folded protein, Θ, for a protein of n arrayed repeat units (helices) are given by Eqs. (12) and (13):
| (12) |
| (13) |
The experimental data were globally fitted to the Ising model using Eq. (5), where f=Θ [Eq. (13)]. Gi, Gij, and m were reproducibly convergent to shared values for all members of CTPRan and for all members of CTPRn. Baseline interpolation parameters αN, αD, βN, and βD were specific for each protein's equilibrium unfolding curve.
Acknowledgments
The authors thank Dr. R. Rose and Dr. A.R. Lowe for critical reading of the manuscript and insightful discussions.
Supplementary material
Additional Supporting Information may be found in the online version of this article.
References
- 1.Groves MR, Barford D. Topological characteristics of helical repeat proteins. Curr Opin Struct Biol. 1999;9:383–389. doi: 10.1016/s0959-440x(99)80052-9. [DOI] [PubMed] [Google Scholar]
- 2.Kobe B, Kajava AV. When protein folding is simplified to protein coiling: the continuum of solenoid protein structures. Trends Biochem Sci. 2000;25:509–515. doi: 10.1016/s0968-0004(00)01667-4. [DOI] [PubMed] [Google Scholar]
- 3.Main ERG, Jackson SE, Regan L. The folding and design of repeat proteins: reaching a consensus. Curr Opin Struct Biol. 2003;13:482–489. doi: 10.1016/s0959-440x(03)00105-2. [DOI] [PubMed] [Google Scholar]
- 4.Hirano T, Kinoshita N, Morikawa K, Yanagida M. Snap helix with knob and hole: essential repeats in S. pombe nuclear protein nuc2+ Cell. 1990;60:319–328. doi: 10.1016/0092-8674(90)90746-2. [DOI] [PubMed] [Google Scholar]
- 5.Sikorski RS, Boguski MS, Goebl M, Hieter P. A repeating amino acid motif in CDC23 defines a family of proteins and a new relationship among genes required for mitosis and RNA synthesis. Cell. 1990;60:307–317. doi: 10.1016/0092-8674(90)90745-z. [DOI] [PubMed] [Google Scholar]
- 6.Finn RD, Mistry J, Tate J, Coggill P, Heger A, Pollington JE, Gavin OL, Gunasekaran P, Ceric G, Forslund K, Holm L, Sonnhammer EL, Eddy SR, Bateman A. The Pfam protein families database. Nucleic Acids Res. 2010;38:D211–222. doi: 10.1093/nar/gkp985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Blatch GL, Lassle M. The tetratricopeptide repeat: a structural motif mediating protein–protein interactions. Bioessays. 1999;21:932–939. doi: 10.1002/(SICI)1521-1878(199911)21:11<932::AID-BIES5>3.0.CO;2-N. [DOI] [PubMed] [Google Scholar]
- 8.D'Andrea LD, Regan L. TPR proteins: the versatile helix. Trends Biochem Sci. 2003;28:655–662. doi: 10.1016/j.tibs.2003.10.007. [DOI] [PubMed] [Google Scholar]
- 9.Mosavi LK, Minor DL, Peng ZY. Consensus-derived structural determinants of the ankyrin repeat motif. Proc Natl Acad Sci USA. 2002;99:16029–16034. doi: 10.1073/pnas.252537899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kohl A, Binz HK, Forrer P, Stumpp MT, Pluckthun A, Grutter MG. Designed to be stable: crystal structure of a consensus ankyrin repeat protein. Proc Natl Acad Sci USA. 2003;100:1700–1705. doi: 10.1073/pnas.0337680100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Main ERG, Xiong Y, Cocco MJ, D'Andrea L, Regan L. Design of stable alpha-helical arrays from an idealized TPR motif. Structure. 2003;11:497–508. doi: 10.1016/s0969-2126(03)00076-5. [DOI] [PubMed] [Google Scholar]
- 12.Kajander T, Cortajarena AL, Main ERG, Mochrie SGJ, Regan L. A new folding paradigm for repeat proteins. J Am Chem Soc. 2005;127:10188–10190. doi: 10.1021/ja0524494. [DOI] [PubMed] [Google Scholar]
- 13.Lowe AR, Itzhaki LS. Rational redesign of the folding pathway of a modular protein. Proc Natl Acad Sci USA. 2007;104:2679–2684. doi: 10.1073/pnas.0604653104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Werbeck ND, Itzhaki LS. Probing a moving target with a plastic unfolding intermediate of an ankyrin-repeat protein. Proc Natl Acad Sci USA. 2007;104:7863–7868. doi: 10.1073/pnas.0610315104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hagai T, Levy Y. Folding of elongated proteins: conventional or anomalous? J Am Chem Soc. 2008;130:14253–14262. doi: 10.1021/ja804280p. [DOI] [PubMed] [Google Scholar]
- 16.Low C, Weininger U, Neumann P, Klepsch M, Lilie H, Stubbs MT, Balbach J. Structural insights into an equilibrium folding intermediate of an archaeal ankyrin repeat protein. Proc Natl Acad Sci USA. 2008;105:3779–3784. doi: 10.1073/pnas.0710657105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Javadi Y, Main ER. Exploring the folding energy landscape of a series of designed consensus tetratricopeptide repeat proteins. Proc Natl Acad Sci USA. 2009;106:17383–17388. doi: 10.1073/pnas.0907455106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wetzel SK, Ewald C, Settanni G, Jurt S, Pluckthun A, Zerbe O. Residue-resolved stability of full-consensus ankyrin repeat proteins probed by NMR. J Mol Biol. 2010;402:241–258. doi: 10.1016/j.jmb.2010.07.031. [DOI] [PubMed] [Google Scholar]
- 19.Aksel T, Majumdar A, Barrick D. The contribution of entropy, enthalpy, and hydrophobic desolvation to cooperativity in repeat-protein folding. Structure. 2011;19:349–360. doi: 10.1016/j.str.2010.12.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Cortajarena AL, Regan L. Calorimetric study of a series of designed repeat proteins: modular structure and modular folding. Protein Sci. 2011;20:336–340. doi: 10.1002/pro.564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Main ERG, Lowe AR, Mochrie SGJ, Jackson SE, Regan L. A recurring theme in protein engineering: the design, stability and folding of repeat proteins. Curr Opin Struct Biol. 2005;15:464–471. doi: 10.1016/j.sbi.2005.07.003. [DOI] [PubMed] [Google Scholar]
- 22.Imai YN, Inoue Y, Nakanishi I, Kitaura K. Amide-pi interactions between formamide and benzene. J Comput Chem. 2009;30:2267–2276. doi: 10.1002/jcc.21212. [DOI] [PubMed] [Google Scholar]
- 23.Main ERG, Stott K, Jackson SE, Regan L. Local and long-range stability in tandemly arrayed tetratricopeptide repeats. Proc Natl Acad Sci USA. 2005;102:5721–5726. doi: 10.1073/pnas.0404530102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Cortajarena AL, Mochrie SGJ, Regan L. Mapping the energy landscape of repeat proteins using NMR-detected hydrogen exchange. J Mol Biol. 2008;379:617–626. doi: 10.1016/j.jmb.2008.02.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Galler KM, Aulisa L, Regan KR, D'Souza RN, Hartgerink JD. Self-assembling multidomain peptide hydrogels: designed susceptibility to enzymatic cleavage allows enhanced cell migration and spreading. J Am Chem Soc. 2010;132:3217–3223. doi: 10.1021/ja910481t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zahnd C, Kawe M, Stumpp MT, de Pasquale C, Tamaskovic R, Nagy-Davidescu G, Dreier B, Schibli R, Binz HK, Waibel R, Pluckthun A. Efficient tumor targeting with high-affinity designed ankyrin repeat proteins: effects of affinity and molecular size. Cancer Res. 2010;70:1595–1605. doi: 10.1158/0008-5472.CAN-09-2724. [DOI] [PubMed] [Google Scholar]
- 27.Patricia MK, Stefan N, Rothschild S, Pluckthun A, Zangemeister-Wittke U. A novel fusion toxin derived from an EpCAM-specific designed ankyrin repeat protein has potent antitumor activity. Clin Cancer Res. 2011;17:100–110. doi: 10.1158/1078-0432.CCR-10-1303. [DOI] [PubMed] [Google Scholar]
- 28.Cortajarena AL, Liu TY, Hochstrasser M, Regan L. Designed proteins to modulate cellular networks. Acs Chem Biol. 2010;5:545–552. doi: 10.1021/cb9002464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Jackson WM, Brandts JF. Thermodynamics of protein denaturation—a calorimetric study of reversible denaturation of chymotrypsinogen and conclusions regarding accuracy of 2-state approximation. Biochemistry. 1970;9:2294–2301. doi: 10.1021/bi00813a011. [DOI] [PubMed] [Google Scholar]
- 30.Sturtevant JM. Some applications of calorimetry in biochemistry and biology. Annu Rev Biophys Bio. 1974;3:35–51. doi: 10.1146/annurev.bb.03.060174.000343. [DOI] [PubMed] [Google Scholar]
- 31.Cooper A, Nutley MA, Wadood A. Differential scanning microcalorimetry in Harding SE. Protein-Ligand Interactions: hydrodynamics and calorimetry. In: Chowdhry BZ, editor. Oxford New York: Oxford University Press; 2000. pp. 287–318. [Google Scholar]
- 32.Nowak UK, Cooper A, Saunders D, Smith RA, Dobson CM. Unfolding studies of the protease domain of urokinase-type plasminogen activator: the existence of partly folded states and stable subdomains. Biochemistry. 1994;33:2951–2960. doi: 10.1021/bi00176a027. [DOI] [PubMed] [Google Scholar]
- 33.McCrary BS, Edmondson SP, Shriver JW. Hyperthermophile protein folding thermodynamics: differential scanning calorimetry and chemical denaturation of Sac7d. J Mol Biol. 1996;264:784–805. doi: 10.1006/jmbi.1996.0677. [DOI] [PubMed] [Google Scholar]
- 34.Kloss E, Courtemanche N, Barrick D. Repeat-protein folding: new insights into origins of cooperativity, stability, and topology. Arch Biochem Biophys. 2008;469:83–99. doi: 10.1016/j.abb.2007.08.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Aksel T, Barrick D. Analysis of repeat-protein folding using nearest-neighbor statistical mechanical models. Methods Enzymol Biothermodyn A. 2009;455:95–125. doi: 10.1016/S0076-6879(08)04204-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kajander T, Cortajarena AL, Mochrie S, Regan L. Structure and stability of designed TPR protein superhelices: unusual crystal packing and implications for natural TPR proteins. Acta Cryst D. 2007;63:800–811. doi: 10.1107/S0907444907024353. [DOI] [PubMed] [Google Scholar]
- 37.Privalov PL, Gill SJ. Stability of protein structure and hydrophobic interaction. Adv Protein Chem. 1988;39:191–234. doi: 10.1016/s0065-3233(08)60377-0. [DOI] [PubMed] [Google Scholar]
- 38.Matouschek A, Matthews JM, Johnson CM, Fersht AR. Extrapolation to water of kinetic and equilibrium data for the unfolding of barnase in urea solutions. Protein Eng. 1994;7:1089–1095. doi: 10.1093/protein/7.9.1089. [DOI] [PubMed] [Google Scholar]
- 39.Mello CC, Barrick D. An experimentally determined protein folding energy landscape. Proc Natl Acad Sci USA. 2004;101:14102–14107. doi: 10.1073/pnas.0403386101. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.