Abstract
The wide applications of next-generation sequencing (NGS) technologies in metagenomics have raised many computational challenges. One of the essential problems in metagenomics is to estimate the taxonomic composition of a microbial community, which can be approached by mapping shotgun reads acquired from the community to previously characterized microbial genomes followed by quantity profiling of these species based on the number of mapped reads. This procedure, however, is not as trivial as it appears at first glance. A shotgun metagenomic dataset often contains DNA sequences from many closely-related microbial species (e.g., within the same genus) or strains (e.g., within the same species), thus it is often difficult to determine which species/strain a specific read is sampled from when it can be mapped to a common region shared by multiple genomes at high similarity. Furthermore, high genomic variations are observed among individual genomes within the same species, which are difficult to be differentiated from the inter-species variations during reads mapping. To address these issues, a commonly used approach is to quantify taxonomic distribution only at the genus level, based on the reads mapped to all species belonging to the same genus; alternatively, reads are mapped to a set of representative genomes, each selected to represent a different genus. Here, we introduce a novel approach to the quantity estimation of closely-related species within the same genus by mapping the reads to their genomes represented by a de Bruijn graph, in which the common genomic regions among them are collapsed. Using simulated and real metagenomic datasets, we show the de Bruijn graph approach has several advantages over existing methods, including (1) it avoids redundant mapping of shotgun reads to multiple copies of the common regions in different genomes, and (2) it leads to more accurate quantification for the closely-related species (and even for strains within the same species).
Key words: closely-related genomes, de Bruijn graph, metagenomics, quantification
1. Introduction
With the recent cost reduction, next generation sequencing (NGS) techniques have been applied to a broad range of biological problems, including metagenomics, which aims to characterize the microbial composition and diversity in an environmental microbial community (Venter et al., 2004). To achieve this primary goal, two approaches are often taken. The first approach, referred to as the 16S rRNA profiling, amplifies variable regions in 16S rRNA genes (i.e., the amplicon) from an environmental DNA sample by PCR, which are subsequently sequenced using NGS techniques (i.e., 454 pyrosequencing). The resulting sequences can be used as markers to characterize the taxonomic composition within the community by comparing their divergences with the 16S rRNA sequences from cultured species, and to estimate the taxonomic distribution within the sample based on the relative abundances of 16S rRNA sequence markers (Hamady et al., 2008). Although this approach has been commonly used in profiling microbial communities, the resolution of this method is limited at the genus level owing to the relatively low resolution of amplicon sequences, e.g., the microbial 16S rRNA sequences from different species of the same genus can be very similar, and therefore are indistinguishable. The second approach utilizes the shotgun metagenome sequencing of a microbial community (Wooley and Ye, 2009), which represents the DNA sequences randomly sampled from a mixture of many various microbial genomes. The resulting sequences can then be mapped to previously sequenced microbial genomes to estimate the relative abundances of these microbial species. However, reads mapping of a shotgun metagenomic dataset is not trivial. First, repetitive sequences make up a significant fraction of almost all microbial genomes. Second, for closely-related genomes (e.g., genomes of the species within the same genus or genomes of the strains within the same species), there are a significant portion of homologous sequences that can be very similar or almost identical from each other (Kumar and Filipski, 2007). Consequently, many reads can be mapped to either multiple locations of the same genome or multiple different genomes, and are classified as the multiply mapped reads. Because it is difficult to know which genome these reads are actually sampled from, they are usually not considered in the characterization of taxonomic diversity. As a result, it is a common practice to limit the quantification of the taxonomic distribution within a shotgun metagenomic dataset only at the genus level (Arumugam et al., 2011), based on the reads mapped to all species in the same genus or alternatively to a set of representative genomes, each selected for a different genus.
Here we introduce a novel approach to quantitatively estimating closely-related genomes (e.g., from the species within the same genus or the strains within the same species). Instead of mapping each read to multiple genomes individually, we first represent multiple closely-related genomes by a de Bruijn graph, in which the common genomic regions among them are collapsed. De Bruijn graph is employed as an efficient data structure for most short read assemblers (e.g., Velvet [Zerbino and Birney, 2008], ALLPATHS-LG [Gnerre et al., 2011], and SOAPdenovo [Li et al., 2010]). It was originally proposed to replace the traversal of Hamiltonian paths in the overlap graph by the traversal of Eulerian paths (Pevzner et al., 2001). Utilizing this data structure, we aim to convert the problem of mapping short reads to multiple related genomes to the problem of mapping reads to a de Bruijn graph of these genomes, in which each edge represents either an unique segment in a single genome (i.e., the unique edges), or a common segment shared by more than one genome (i.e., the degenerate edges), and each genome is then represented by a path in the graph (Fig. 1). To map short reads to the de Bruijn graph, we concatenate the edges in the graph, and map the reads against the concatenated sequences. In this way, we can utilize the existing reads mapping algorithms, such as BWA (Li and Durbin, 2009), mrFAST (Alkan et al., 2009), or Bowtie (Langmead et al., 2009). We note that a few reads mapping algorithms supporting simultaneous mapping of reads to multiple genomes, including GenomeMapper (Schneeberger et al., 2009) and DynMap (Flouri et al., 2011). But these methods only handle small genomic variations, such as single nucleotide substitutions, insertions or deletions. For example, GenomeMapper was developed to take into consideration the polymorphisms found in plant genomes; and the performance of DynMap was demonstrated on the genomes of multiple E. coli strains, among which, however, only single nucleotide polymorphisms were present. In comparison, by using the de Bruijn graph representation, in addition to single nucleotide variations, we are able to handle large-scale variations (such as long insertions/deletions, inversions and duplications) among the genomes of closely-related species.
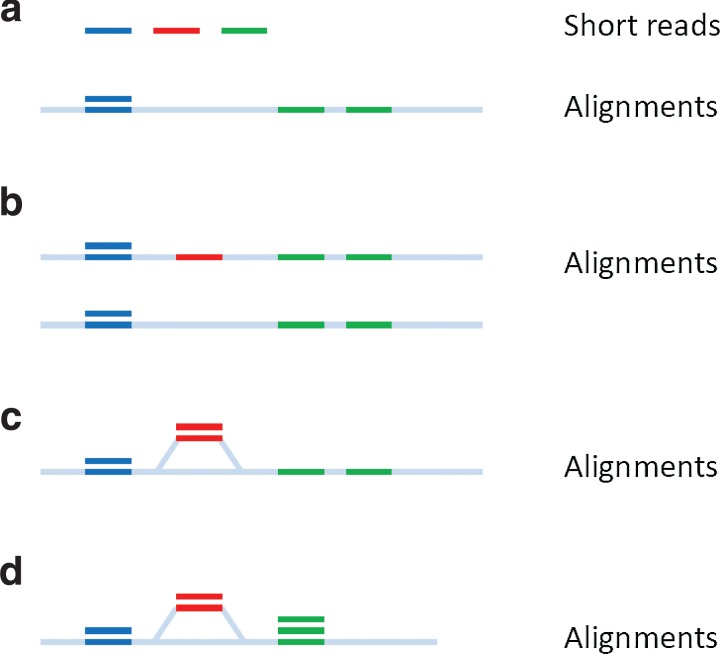
FIG. 1.
Reads mapping to multiple closely-related genomes. (a) Short reads aligned to individual reference genomes. Only sufficiently similar reads can be recruited. (b) Short reads aligned to both closely related genomes separately. Reads from divergent region can be mapped to one of the two reference genomes, but reads from common regions will be mapped to both genomes. (c) Short reads aligned to a graph incorporating known polymorphisms. Reads from divergent regions will be recruited, but reads from repeats still result in redundant alignment. (d) Short reads aligned to a de Bruijn graph. Not only it considered divergence between the two genomes, but also it glues all similar repeats, further reducing the size of the reference.
Based on the reads mapping on the de Bruijn graph, we are able to improve the abundance estimation for each of the closely-related genomes. We tested two methods for this purpose. In the first method, we estimate the abundance of each genome based on the normalized number of reads that can be mapped to the unique edges from this genome (referred to as the unique region approach). In the second method, we use a Poisson distribution model that utilizes the reads mapped to both the unique and degenerate edges (referred to as the redundant approach). We tested our methods on both simulated and real metagenomic datasets, and the results show that our methods provide fast reads mapping onto a group of closely-related genomes by avoiding redundant mapping of short reads to the shared genomic segments, and accurate estimates of the quantitative distribution of closely-related species (or different strains in the same species) within a community.
2. Methods
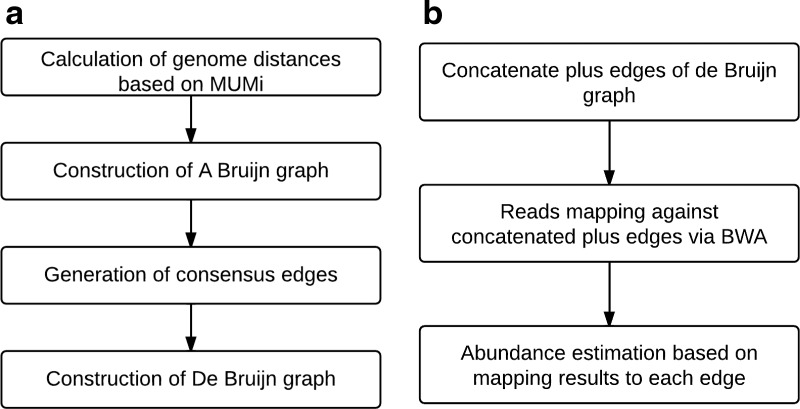
Given a collection of reference genomes, our pipeline for the species quantification consists of two steps: (1) the construction of a de Bruijn graph, based on all-against-all pairwise alignments of the genomic sequences (by using BLASTN [Altschul et al., 1997]); and (2) the estimation of relative abundances of the genomes based on the number of mapped reads on unique or degenerate edges in the de Bruijn graph, as illustrated in Figure 2.
FIG. 2.
The de Bruijn graph approach to estimating the relative abundances of closely-related species in a microbial community. (a) Construction of de Bruijn graph from a collection of genomic sequences. (b) Reads mapping by BWA (Li and Durbin, 2009) and species quantification based on the number of reads mapped to unique and degenerate edges.
2.1. Construction of the de Bruijn graph from genomic sequences
2.1.1. Grouping reference genomes based on MUMi distances
In order to collapse similar genomic segments (e.g., the repeats) in the same genome as well as homologous regions among multiple genomes, we first need to cluster closely-related genomes into groups so that the genomes in the same group tend to share highly homologous (and even nearly identical) sequences, and hence the de Bruijn graph built from them will be more compact than individual genomes. Furthermore, we need to choose the parameters for building the de Bruijn graph of each group based on the overall similarity among these genomes. We calculate the similarity between genomic sequences using the maximal unique matches index (MUMi) distance, which was devised to measure the similarity level between two microbial genomes from closely-related species (e.g., within a genus) or strains of the same species (Deloger et al., 2009). For two genomes to be compared, MUMi can be calculated as
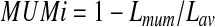 |
(1) |
where Lmum represents the sum of the lengths of all non-overlapping MUMs between two genomes, and Lav is the average length of the two genomes.
2.1.2. Construction of an A-Bruijn graph
As closely related species often do not share identical genomic sequences, the de Bruijn graph directly built from these genomes may contain many detailed structures (like bulges and cycles) introduced by the non-identical sequences even within the nearly identical genomic segments. To address this issue, we use the A-Bruijn graph approach (Pevzner et al., 2004), in which nearly identical sequences, defined by a similarity threshold in the pairwise alignment, are all collapsed into a single edge. Subsequently, we use the consensus sequences derived from all the sequences collapsed into the same edge to represent the edge, and then the reads are mapped to the consensus sequences in the graph. In the end, we can obtain a compact de Bruijn graph representation of a collection of genomes. Specifically, the procedure consists of two steps: (1) BLASTN [Altschul et al., 1997] is used to identify similar subsequences between every pair of genomes in input set of selected genomes; and (2) a A-Bruijn graph is built by gluing all pair of positions in the input genomes that are aligned together for the alignments longer than a threshold (default 100 nts) and with similarity higher than a threshold (default 97%) (Pevzner et al., 2004).
2.1.3. Generation of consensus edges of the A-Bruijn graph
After the construction of an A-Bruijn graph, the segments collapsed into the same edge should be represented by the same sequence, i.e., the consensus sequence of all these segments. The Consensus Alignment (CA) algorithm (Ye, 2010) was used in this step for each edge in which multiple genomic segments are collapsed (i.e., the multiplicity of the edge ≥ 1). According to our experiment, using consensus sequences to represent edges improves the downstream reads mapping, because this reduces the average distance between the representative sequence of the edge and each genomic segment.
2.1.4. Construction of the de Bruijn graph
After obtaining the consensus edges from A-Bruijn graph, we can “reconstruct” the sequence of each input genome by traversing the A-Bruijn graph and concatenating the consensus sequence of each edge in the path. We then use the reconstructed genome sequences as input to build a de Bruijn graph. We set k-mer size for the de Bruijn graph equal to or greater than the length of short reads (e.g., l = 100 for Illumina reads) to be mapped onto the graph: k ≥ l. By setting a large k, we can then simply use the sequences of all edges in a de Bruijn graph for downstream reads mapping without explicitly considering the junctions of the genomic segments in the graph.
2.2. Reads mapping and relative-abundance estimation
2.2.1. Reads mapping via BWA
As we mentioned above, we can collect the edges from the de Brujin graph for reads mapping (there is no need to explicitly consider the edge junctions in the graph). The advantage of this approach is that we can then utilize the best mapping tools available (which are typically developed for mapping reads onto linear sequences). After experimenting with different available mapping algorithms, we chose BWA (Li and Durbin, 2009) for our purpose, because it provided an accurate mapping results in a way that can be used in our downstream analyses. As BWA reports mapping positions for both strands of input reads, we use only the the edges from one (i.e., the plus) strand as the reference.
2.2.2. Abundance estimation based on reads mapping
In theory, if the genomes are divergent enough from each other, reads mapping is independent from one genome to another and abundance estimation becomes trivial. However, multiple closely-related genomes are often present in a metagenomic dataset. Hereby we propose two quantification approaches to address this issue: the unique region approach, and the redundant approach. The unique region approach utilizes only the reads mapped to the unique edges in the de Bruijn graph. And the relative abundance of each genome in the sample is inferred by computing the total number of mapped reads to the genome per kilobase of the genome length per million mapped reads (RPKM), a commonly used quantitative measure. The redundant approach utilizes the reads mapped to both the unique and degenerate edges. For this approach, we adopt a Poission model and use hill climbing method to make point estimation of the relative abundances of each genome, similar to the method used for the inference of the abundance of splicing isoforms from RNA-seq data (Jiang and Wong, 2009). Our experiments show that both methods work well for simple cases, whereas the redundant approach has superior statistical power over the simpler unique region approach for complex cases.
In the redundant approach, a Poisson model is used to model the random sequence. Let G be a set of groups of closely-related genomes. For a group of closely-related genomes (i.e., from species within the same genus or strains within the same species), let 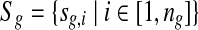 be the genomes in the group, where ng is a positive integer. Also, let
be the genomes in the group, where ng is a positive integer. Also, let 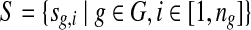 be the set of all genomes in the sample being sequenced. For any genome
be the set of all genomes in the sample being sequenced. For any genome 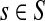 , let ls be its genome length, and let ks be the abundance (copy number) of s in the sample. Based on the above notation, the total length of the genomes in the sample is
, let ls be its genome length, and let ks be the abundance (copy number) of s in the sample. Based on the above notation, the total length of the genomes in the sample is 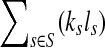 . The sequencing process can be modeled as a simple random sampling, in which every read is sampled independently and uniformly from every possible nucleotide in the sample. Therefore, the probability that a read comes from the genome s is
. The sequencing process can be modeled as a simple random sampling, in which every read is sampled independently and uniformly from every possible nucleotide in the sample. Therefore, the probability that a read comes from the genome s is 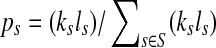 . By defining
. By defining 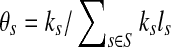 (representing the relative abundance of the genome s), we can rewrite ps as ps = θsls, with
(representing the relative abundance of the genome s), we can rewrite ps as ps = θsls, with 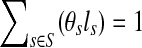 .
.
Let r be the total number of mapped reads. Given a genome s, and a genomic segment of length l in s, the number of reads sampled from this segment, denoted by some random variable X, follows a binomial distribution with parameters r and p = θsl. Since usually r is very large and p is small, the binomial distribution here can be approximated well by a Poisson distribution with parameter λ = rθsl. Given all the groups of genomes (and the genomes in each group), and the sequencing reads, i.e., G, S, l, r are all known, the problem is to estimate θs for all 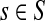 . Given a group, suppose the relative abundances of the genomes in a sample are
. Given a group, suppose the relative abundances of the genomes in a sample are 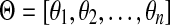 , and the genomes in the group are represented as a de Bruijn graph of m edges with lengths
, and the genomes in the group are represented as a de Bruijn graph of m edges with lengths 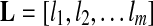 . Let
. Let 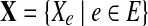 be the set of observations, where E is an index set of all the de Bruijn graph edges, and
be the set of observations, where E is an index set of all the de Bruijn graph edges, and 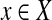 is a random variable representing the number of reads mapped onto a particular edge. For every
is a random variable representing the number of reads mapped onto a particular edge. For every 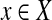 , it follows a Poisson distribution with parameter λ. For each edge,
, it follows a Poisson distribution with parameter λ. For each edge, 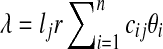 , where cij = 1 if the genome of strain i contains edge j and 0 otherwise. From the probability mass function of the Poisson distribution, the likelihood of having Θ given an observation x is
, where cij = 1 if the genome of strain i contains edge j and 0 otherwise. From the probability mass function of the Poisson distribution, the likelihood of having Θ given an observation x is
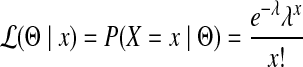 |
(2) |
Assuming the samplings of reads from each edge (and junction) are independent from each other, the joint log-likelihood over the whole set of observations 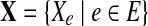 can then be computed as,
can then be computed as,
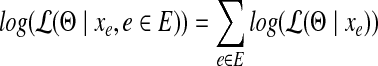 |
(3) |
and the maximum likelihood estimation (MLE) can be obtained by
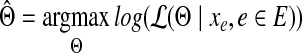 |
(4) |
Note that Jiang and Wong (2009) proved that the joint log-likelihood function (equation 3) is concave. As a result, one can use any optimization method to compute the parameters Θ, as any local maximum is guaranteed to reach the global maximum. In our case, coordinate-wise hill climbing was used for solving this optimization problem, and individual parameters are optimized in turn until convergence.
3. Results
We tested our methods using both simulated and real metagenomic datasets. The results show that our methods provide both fast mapping of reads to a collection of closely-related genomes, and accurate quantification of the underlining species, in comparison to existing methods such as GenomeMapper and DynMap.
3.1. A simulated microbial community with five E. coli strains
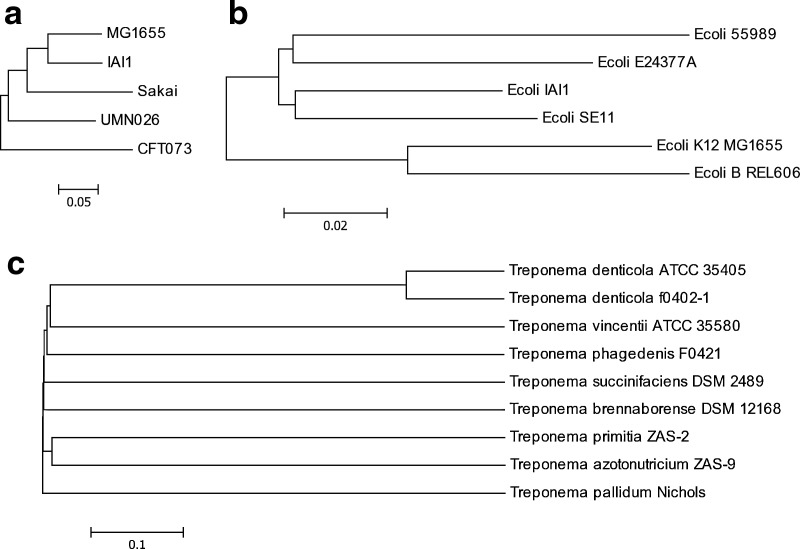
E. coli is a well studied model prokaryotic organism and high variations among different E. coli strains were observed. Considering that some of the reference E. coli genomes are extremely similar to each other (and thus indistinguishable based on reads mapping), we first selected 5 most divergent E. coli genomes based on their MUMi measures, and simulated reads from these genomes to create a simulated dataset to test our method (Touzain et al., 2010) (Fig. 3a).
FIG. 3.
Neighbor-joining trees based on MUMi measures for three microbial communities: five most divergent E. coli genomes (a), six closely related E. coli genomes (b) and nine Treponema genomes (c).
The de Bruijn graph. We used 97% and 100 nts as the identity and length thresholds, respectively, for constructing the de Bruijn graph of the five genomes. The resulting de Bruijn graph is composed of 30,324 edges of average length 698 bp, the longest of which is 70,418 bp and the shortest 101 bp. The total base of the edges is 10,823,143 bp, 57% shorter than the total length of all 5 E. coli genomes. As a result, the de Bruijn graph representation reduces over half of the total length of the reference sequences for reads mapping.
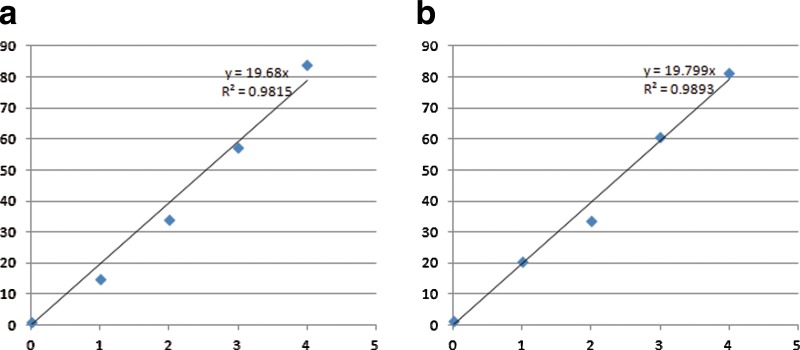
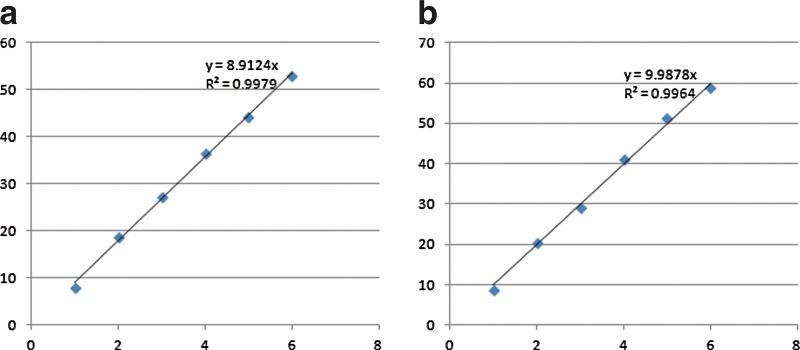
Reads mapping and abundance estimation. We randomly sampled 260,000 reads of 100 bps at a 1.5% substitution error rate using MetaSim (Richter et al., 2008), with 0% reads from MG1655, 10% from IAI1, 20% from Sakai, 30% from UMN026, and 40% from CFT073 (i.e., the average coverages are 0, 0.5, 1, 1.5, and 2 in these genomes, respectively). For this simulation, 188,373 out of 260,000 reads were uniquely mapped to the de Bruijn graph at a maximum edit distance of 3 by BWA. We also aligned the simulated reads to individual genomes (Table 1). In total, 260,000 reads can be mapped onto the five E. coli genomes at 391,238 locations, indicating that many reads are mapped to the non-unique regions in these genomes. As a result, the quantification of the five genomes based on the reads mapping on individual genomes will lead to incorrect estimation of the species (for example, there are no reads sampled from MG1655 in the simulation, but still this genome recruited 112,455 reads as it shares a large fraction of genomic sequences with other E. coli strains). Moreover, if we simply assume that reads mapping are independent using each individual genome as the reference (Naive method), the computed RPKM will be inconsistent with the expected values (Table 1). On the other hand, both the unique region approach and the redundant approach can successfully estimate the relative abundance of each genome (Fig. 4). Similar performance was observed when we simulated short reads from the 5 E. coli genomes using different coverages ranging from 0 to 40×.
Table 1.
Comparison of Quantifying Five E. coli Genomes Using Different Approaches
| Strain | MG1655 | IAI1 | Sakai | UMN026 | CFT073 |
|---|---|---|---|---|---|
| Relative abundance | 0 | 1 | 2 | 3 | 4 |
| Reads uniquely mapped to individuals | 156,429 | 160,321 | 172,985 | 185,128 | 188,202 |
| Naive method | 39.06 | 39.52 | 36.45 | 41.23 | 41.68 |
| Estimated abundance (unique region approach) | 1.19 | 20.46 | 33.59 | 60.49 | 81.21 |
| Estimated abundance (redundant approach) | 0.81 | 14.90 | 34.13 | 57.17 | 83.93 |
FIG. 4.
Scatter plots of the expected (x-axis) and estimated abundance (y-axis) of the species in the simulated community of five divergent E. coli strains using the unique region approach (a) and the redundant approach (b).
Comparison between BWA and BLAST in reads mapping. Throughout this article, we used BWA, a fast read alignment algorithm for mapping short reads onto the reference microbial genomes. To study the impact of the read alignment algorithm in the species quantification, we compared the results of BWA with the conventional alignment tool BLAST, in terms of the number of mapped reads and the quantification results. We simulated 2,500,000 short reads with an error rate of 0.01 and 0.03, respectively. To mimic the error model in Illumina sequencing that is commonly used in metagenomics, we set the ratio of indel and substitution errors at 2:3. Table 2 shows the comparison results. As we expected, BLAST can map more reads when the error rate is high (0.03), whereas BWA and BLAST perform similarly when the error rate is low (0.01). However, the quantification results are almost the same in both cases, indicating BWA can achieve accurate quantification results even when the difference between the reads and the reference genome is high. Therefore, we employed BWA in our analytical pipeline because it runs much (1–2 magnitudes) faster than BLAST.
Table 2.
Comparison Between BWA and BLAST in Short Reads Mapping
| |
Error rate: 0.03 |
Error rate: 0.01 |
||
|---|---|---|---|---|
| BWA | BLAST | BWA | BLAST | |
| No. reads recruited (%) | 60.06 | 82.39 | 89.22 | 86.35 |
| Quantification (R2) | 0.9884 | 0.9924 | 0.9923 | 0.99 |
3.2. A simulated community with six closely-related E. coli strains
We further tested the methods on a simulated dataset sampled from 6 relatively more closely-related E. coli strains (Fig. 3b, Table 3).
Table 3.
Comparison of Quantifying Six E. oli Genomes Using Different Approaches
| Strain | 55989 | REL606 | E24377A | IAI1 | MG1655 | SE11 |
|---|---|---|---|---|---|---|
| Relative abundance | 1 | 2 | 3 | 4 | 5 | 6 |
| Reads uniquely mapped to individuals | 84,143 | 80,382 | 86,051 | 85,774 | 82,876 | 87,745 |
| Naive method | 32.2 | 34.25 | 34.09 | 35.99 | 35.23 | 35.41 |
| Estimated abundance (unique region approach) | 7.96 | 18.57 | 27.12 | 36.53 | 44.16 | 52.94 |
| Estimated abundance (redundant approach) | 8.51 | 20.21 | 29.02 | 40.90 | 51.15 | 58.92 |
The de Bruijn graph. Using 97% and 100 nts as the identity and length thresholds, we built the de Bruijn graph of these 6 E. coli strains, which has 9,578 edges of average length of 1,448 bp, with the longest edge of 81,443 bp, and the shortest 101 bp. The concatenated edges are 67.8% shorter than the total length of the individual genomes.
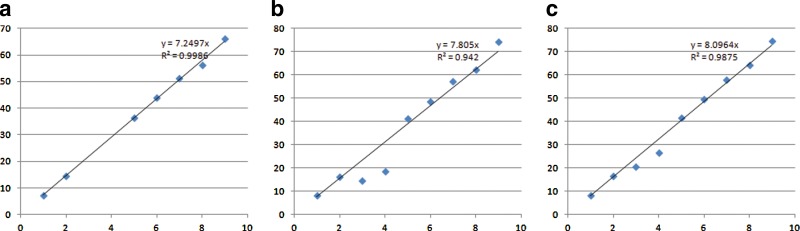
Reads mapping and abundance estimation. The 6 E. coli genomes in this experiment are more similar to each other as compared to the previous simulation study (so they share more common regions in their genomic sequences). Although we expected that the quantification of these E. coli genomes would be even more difficult, our methods still give satisfactory results as shown in Figure 5.
FIG. 5.
Scatter plots of the expected (x-axis) and estimated abundance (y-axis) of the species in the simulated community of six closely related E. coli strains using unique region approach (a) and redundant approach (b).
3.3. Quantification of Treponema species in real human microbiome datasets
The NIH Human Microbiome Project (HMP) has resulted in several hundred metagenomic datasets, enabling the studies of many functional elements in human-associated microbial communities (Peterson et al., 2009). Here, we present the identification of oral spirochetes, some of which are implicated in periodontal disease (Seshadri et al., 2004), in normal human individuals using the mapping of short reads onto the reference Trepnoma genomes that are available. We collected 9 Treponema genomes: 6 have complete genomic sequences whereas the other 3 only have draft sequences (contigs/scaffolds). We included the draft genome sequences as they appear to have good coverages (as compared to complete Treponema genomes) (Table 4). The selected Treponema strains are isolated from various environments, and we expect they are present at different abundances in human microbiome samples.
Table 4.
Nine Selected Treponema Genomes
| Strain | Living/sampling Site | Sequencing Status | Genome size (bp) |
|---|---|---|---|
| Azotonutricium ZAS-9 | Termite gut | Complete | 3,855,671 |
| Primitia ZAS-2 | Termite gut | Complete | 4,059,867 |
| Denticola ATCC 35405 | Homo sapiens oral cavity | Complete | 2,843,201 |
| Denticola f0402-1 | Homo sapiens oral cavity | Contigs | 2,734,980 |
| Vincentii ATCC 35580 | Homo sapiens oral cavity | Contigs | 2,514,590 |
| Phagedenis F0421 | Homo sapiens urogenital tract | Scaffolds | 2,830,421 |
| Brennaborense DSM 12168 | Bovine foot | Complete | 3,055,580 |
| Pallidum Nichols | Homo sapiens | Complete | 1,138,011 |
| Succinifaciens | Swine intestine | Complete | 2,731,853 |
The de Bruijn graph. Using 0.97 and 100 nt as the identity and length thresholds, we built a de Bruijn graph for the 9 Treponema genomes. The resulted de Bruijn graph has 30,592 edges in total, with an average length of 1,693 bp. The genomes are so divergent that the concatenated edges are only 4.3% shorter than the total length of the reference genomes.
Reads mapping and abundance estimation. Before employing our methods to the real metagenomic sequences, we tested it on simulated datasets with reads sampled from the Treponema genomes. We simulated 1.25 millon error-free reads from the 9 genomes (Table 5), with coverage ranging from 1 to 9. Over 96% of reads are uniquely mapped to the de Bruijn graph at a maximum edit distance of 3 (which is expected, as these 9 Treponema genomes are rather divergent, except the two denticola genomes). If we do not try to distinguish the reads mapped to the two denticola genomes (MUMi = 0.21), we achieved almost perfect quantification of the Treponema genomes with reference to each individual genome for this simulated dataset (Fig. 6a). However, as shown in Figure 6b,c, our methods can even distinguish the two denticola genomes, with the redundant method showing superior statistical power over the simpler unique region method (Table 5).
Table 5.
Comparison of Quantification of Nine Treponema Genomes Using Different Approaches
| Strain | Expected | Mapped reads | Naive method | Unique-region | Poisson-model |
|---|---|---|---|---|---|
| Azotonutricium ZAS-9 | 1 | 37,964 | 7.24 | 8.10 | 8.20 |
| Brennaborense DSM 12168 | 2 | 60,255 | 14.50 | 16.19 | 16.41 |
| Denticola ATCC 35405 | 3 | 155,749 | 40.28 | 14.50 | 20.52 |
| Denticola f0402-1 | 4 | 163,131 | 43.85 | 18.56 | 26.67 |
| Pallidum Nichols | 5 | 56,087 | 36.24 | 41.27 | 41.62 |
| Phagedenis F0421 | 6 | 168,700 | 43.82 | 48.62 | 49.49 |
| Primitia ZAS-2 | 7 | 282,497 | 51.16 | 57.40 | 57.93 |
| Succinifaciens DSM 2489 | 8 | 209,265 | 56.32 | 62.21 | 64.37 |
| Vincentii ATCC 35580 | 9 | 226,432 | 66.21 | 74.29 | 74.74 |
FIG. 6.
Scatter plots of the expected (x-axis) and estimated abundances (y-axis) of the species in the simulated community of nine Treponema species using the naive mapping method (excluding the two denticola genomes) (a), using the unique region approach (b), and the redundant approach (c).
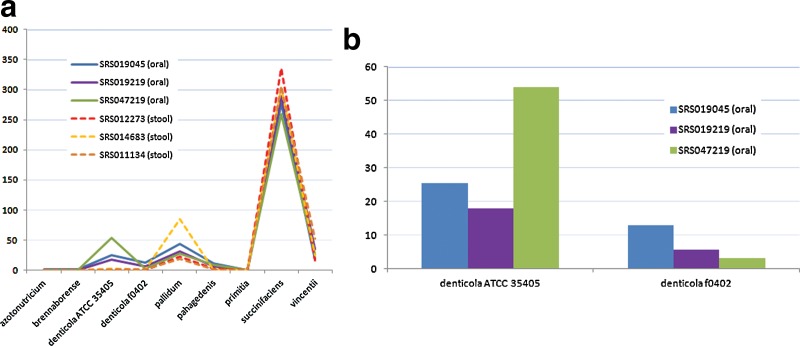
Estimation of the abundances of Treponema species in human microbiomes. We tested 6 datasets from the Human Microbiome Project: Human Microbiome Illumina WGS Reads (HMIGWS) Build 1.0 (available at http://hmpdacc.org/HMIWGS). Three of the samples were collected from tongue dorsum and the other three were collected from stool. From the plot, it is obvious that all six samples have extremely low abundances of azotonutricium ZAS-9 and primitia ZAS-2 (Fig. 7). This result is expected as it has been reported that the termite-derived strains are not closely related to other known treponema strains in terms of their 16S rRNA sequences (Graber et al., 2004). Also, all three oral samples have high abundances of denticola while the three stool samples nearly have no denticola species (Fig. 7). Furthermore, we can observe a relatively high abundance of pallidum and succinifaciens in all six samples—this may be due to the presence of closely-related genomes to pallidum or succinifaciens in the datasets (Treponema succinifaciens was found in swine intestine and is involved in carbohydrates oxidization [Han et al., 2011]). In addition, we observed that the three oral HMP samples that we tested have different proportions of the two Tremnoma denticola strains (Fig. 7b), with sample SRS047219 having the highest denticola ATCC 35405 and lowest denticola f0402. This indicates that it is important to have a mapping/quantification method that can distinguish different strains in the same species, which shows strain variations among multiple samples.
FIG. 7.
The estimation of the relative abundances of Treponema species in six HMP datasets: SRS019045, SRS019219, and SRS047219 are datasets from tongue dorsum, while the remaining three datasets are stool samples (a) and the estimated abundances of two denticola genomes in oral samples (b).
3.4. Comparison with GenomeMapper and DynMap
We only compared our methods with GeomeMapper and DynMap in terms of mapping results, as they do not offer the functionality of quantification. We used the two E. coli genomes (one is K-12 MG1655 and the other is simulated with only very minor differences from K-12) that are used for comparison between GenomeMapper and DynMap in the DynMap paper (Flouri et al., 2011). We simulated 5,000,000 reads of 36bp using MetaSim at 1% deletion rate, 1% insertion rate and 2% substitution rate. Our method is comparable or better than the other two methods in terms of mapping results (Table 6), although its running time was longer than DynMap. Note that DynMap was specifically designed for the reads mapping onto multiple genomes with only small differences, and thus runs faster than our method in these cases.
Table 6.
Comparison Between Our Method with Genomemapper and Dynmap on Reads Mapping
| Program | Alignment | Total time |
|---|---|---|
| GenomeMapper | 77.3% | 5m26s |
| DynMap | 95.71% | 44s |
| DBGraph + BWA | 97.6% | 2m47s |
Both GenomeMapper and DynMap require predefined list of polymorphisms as input, whereas our method offers the option to directly take genomic sequences (and their pairwise alignments) as input to construct a de Bruijn graph, which has advantages of presenting the similarity and dissimilarity of a group of genomes as compared to the data structures used in the other two tools.
4. Discussion
Using de Bruijn graph allows for efficient mapping of short reads to multiple closely-related genomes simultaneously. Based on the accurate and sensitive alignment of short reads, we can estimate the relative abundance of each of the closely-related genomes in a microbial community. Currently, we used BWA to map the reads onto a single sequence from the concatenation of sequences of all edges in the de Bruijn graph. We plan to develop a tool allowing the direct mapping of the reads to the de Bruijn graph, which may make the mapping process even more efficient.
Due to the limitation of memory requirement, our current tool can only handle a limited number of closely-related genomes. Therefore, it is important to select representative genomes and to set appropriate parameters for constructing the de Bruijn graph. We are currently constructing a library of de Bruijn graphs, each for a selected set of representative genomes from a genus, and then we can quantify the species (of sequenced genomes) by directly mapping reads from a metagenomic dataset to these graphs.
When genomes are divergent, accurate abundance estimation for the genomes can be reached even based on reads mapped to individual genomes, e.g., for the divergent Treponema species. Thus, it is accurate to compute the abundance of each genus by summing up the abundance of each species in the genus, as commonly used in current metagenomic analysis (Arumugam et al., 2011). However, our method extended the capability of quantification to more closely-related genomes, as shown in the two highly similar Treponema species. It is anticipated that the unique region approach works well if the unique edges for each genome are sufficiently long, while the redundant method works better for the genomes that have fewer unique edges.
Our method has limitations. Based on our experience, genomes from different substrains within the same strain are often indistinguishable because they are almost identical to each other. For example, Treponema pallidum pallidum SS14 and Treponema pallidum pallidum Nichols both belong to the subspecies T. pallidum subsp. pallidum with a MUMi distance of merely 0.02. In practice, it is almost impossible to quantify each of those two genomes in the community. However, in reality, we may not need to distinguish them, and it should be sufficient to quantify them together by selecting one of them as a representative for reads mapping. Also, our quantification method is reference-based and relies on the available genomic sequences. In principle, we can use our method to quantify each genome in the sample and therefore can estimate the abundance at different taxonomic levels (strain, species, genus, etc.), if the existing genomes represent all major taxonomic groups. In this case, because the representative genomic sequences may be deviated from the sequences from the sample (as we can select a representative genome from each strain or substrain), we may have to use rigorous but slower alignment tools like BLAST for reads mapping to achieve more accurate quantification of species. Nevertheless, we believe our method is ready for the quantification of known genomes, even if they are closely-related and their sequences are similar.
Acknowledgments
We are grateful to the editors of the Journal of Computational Biology special issue for inviting us to submit this manuscript in honor of Michael Waterman's 70th and Simon Tavarés 60th birthday. This work was partially supported by the National Institutes of Health (grants 1R01HG004908 and 1U01HL098960).
Disclosure Statement
No competing financial interests exist.
References
- Alkan C. Kidd J.M. Marques-Bonet T., et al. Personalized copy number and segmental duplication maps using next-generation sequencing. Nat. Genet. 2009;41:1061–1067. doi: 10.1038/ng.437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Altschul S.F. Madden T.L. Schaffer A.A., et al. Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res. 1997;25:3389–3402. doi: 10.1093/nar/25.17.3389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arumugam M. Raes J. Pelletier E., et al. Enterotypes of the human gut microbiome. Nature. 2011;473:174–180. doi: 10.1038/nature09944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deloger M. El Karoui M. Petit M.A. A genomic distance based on MUM indicates discontinuity between most bacterial species and genera. J. Bacteriol. 2009;191:91–99. doi: 10.1128/JB.01202-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flouri T. Iliopoulos C.S. Pissis S.P. DynMap: mapping short reads to multiple related genomes. Proceeding of the 2nd Conference on Bioinformatics, Computational Biology, and Biomedicine (ACMBCB, '11); 2011. pp. 330–334. [Google Scholar]
- Gnerre S. Maccallum I. Przybylski D., et al. High-quality draft assemblies of mammalian genomes from massively parallel sequence data. Proc. Natl. Acad. Sci. U.S.A. 2011;108:1513–1518. doi: 10.1073/pnas.1017351108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graber J.R. Leadbetter J.R. Breznak J.A. Description of Treponema azotonutricium sp. nov. and Treponema primitia sp. nov., the first spirochetes isolated from termite guts. Appl. Environ. Microbiol. 2004;70:1315–1320. doi: 10.1128/AEM.70.3.1315-1320.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamady M. Walker J.J. Harris J.K., et al. Error-correcting barcoded primers for pyrosequencing hundreds of samples in multiplex. Nat. Methods. 2008;5:235–237. doi: 10.1038/nmeth.1184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han C. Gronow S. Teshima H., et al. Complete genome sequence of Treponema succinifaciens type strain (6091) Stand. Genomic Sci. 2011;4:361–370. doi: 10.4056/sigs.1984594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang H. Wong W.H. Statistical inferences for isoform expression in RNA-Seq. Bioinformatics. 2009;25:1026–1032. doi: 10.1093/bioinformatics/btp113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar S. Filipski A. Multiple sequence alignment: in pursuit of homologous DNA positions. Genome Res. 2007;17:127–135. doi: 10.1101/gr.5232407. [DOI] [PubMed] [Google Scholar]
- Langmead B. Trapnell C. Pop M., et al. Ultrafast and memory-efficient alignment of short DNA sequences to the human genome. Genome Biol. 2009;10:R25. doi: 10.1186/gb-2009-10-3-r25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H. Durbin R. Fast and accurate short read alignment with Burrows-Wheeler transform. Bioinformatics. 2009;25:1754–1760. doi: 10.1093/bioinformatics/btp324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li R. Zhu H. Ruan J., et al. De novo assembly of human genomes with massively parallel short read sequencing. Genome Res. 2010;20:265–272. doi: 10.1101/gr.097261.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peterson J. Garges S. Giovanni M., et al. The NIH Human Microbiome Project. Genome Res. 2009;19:2317–2323. doi: 10.1101/gr.096651.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pevzner P.A. Pevzner P.A. Tang H., et al. De novo repeat classification and fragment assembly. Genome Res. 2004;14:1786–1796. doi: 10.1101/gr.2395204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pevzner P.A. Tang H. Waterman M.S. An Eulerian path approach to DNA fragment assembly. Proc. Natl. Acad. Sci. U.S.A. 2001;98:9748–9753. doi: 10.1073/pnas.171285098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richter D.C. Ott F. Auch A.F., et al. MetaSim: a sequencing simulator for genomics and metagenomics. PLoS ONE. 2008;3:e3373. doi: 10.1371/journal.pone.0003373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneeberger K. Hagmann J. Ossowski S., et al. Simultaneous alignment of short reads against multiple genomes. Genome Biol. 2009;10:R98. doi: 10.1186/gb-2009-10-9-r98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seshadri R. Myers G.S. Tettelin H., et al. Comparison of the genome of the oral pathogen Treponema denticola with other spirochete genomes. Proc. Natl. Acad. Sci. U.S.A. 2004;101:5646–5651. doi: 10.1073/pnas.0307639101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Touzain F. Denamur E. Medigue C., et al. Small variable segments constitute a major type of diversity of bacterial genomes at the species level. Genome Biol. 2010;11:R45. doi: 10.1186/gb-2010-11-4-r45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Venter J.C. Remington K. Heidelberg J.F., et al. Environmental genome shotgun sequencing of the Sargasso Sea. Science. 2004;304:66–74. doi: 10.1126/science.1093857. [DOI] [PubMed] [Google Scholar]
- Wooley J.C. Ye Y. Metagenomics: facts and artifacts, and computational challenges. J. Comput. Sci. Technol. 2009;25:71–81. doi: 10.1007/s11390-010-9306-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ye Y. Identification and quantification of abundant species from pyrosequencing of 16S rRNA by consensus alignment. Proc. Bioinform. Biomed. (BIBM) 2010 IEEE Int. Conf. 2010:153–157. doi: 10.1109/BIBM.2010.5706555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zerbino D.R. Birney E. Velvet: algorithms for de novo short read assembly using de Bruijn graphs. Genome Res. 2008;18:821–829. doi: 10.1101/gr.074492.107. [DOI] [PMC free article] [PubMed] [Google Scholar]