Efficient Simulation and Likelihood Methods for Non-Neutral Multi-Allele Models

Abstract

Throughout the 1980s, Simon Tavaré made numerous significant contributions to population genetics theory. As genetic data, in particular DNA sequence, became more readily available, a need to connect population-genetic models to data became the central issue. The seminal work of Griffiths and Tavaré (1994a, 1994b, 1994c) was among the first to develop a likelihood method to estimate the population-genetic parameters using full DNA sequences. Now, we are in the genomics era where methods need to scale-up to handle massive data sets, and Tavaré has led the way to new approaches. However, performing statistical inference under non-neutral models has proved elusive. In tribute to Simon Tavaré, we present an article in spirit of his work that provides a computationally tractable method for simulating and analyzing data under a class of non-neutral population-genetic models. Computational methods for approximating likelihood functions and generating samples under a class of allele-frequency based non-neutral parent-independent mutation models were proposed by Donnelly, Nordborg, and Joyce (DNJ) (Donnelly et al., 2001). DNJ (2001) simulated samples of allele frequencies from non-neutral models using neutral models as auxiliary distribution in a rejection algorithm. However, patterns of allele frequencies produced by neutral models are dissimilar to patterns of allele frequencies produced by non-neutral models, making the rejection method inefficient. For example, in some cases the methods in DNJ (2001) require 10⁹ rejections before a sample from the non-neutral model is accepted. Our method simulates samples directly from the distribution of non-neutral models, making simulation methods a practical tool to study the behavior of the likelihood and to perform inference on the strength of selection.

1. Introduction

While genetic variation is ultimately resolved by DNA sequencing, much of our understanding of natural populations continues to be based on the results of allele-frequency analysis. Therefore, developing likelihood-based methods to assess the strength of selection using allele-frequency data is of interest. However, evaluating likelihood functions and simulating samples under non-neutral models is computationally difficult, posing challenges in developing likelihood-based inference methods.

In this article, we present computationally efficient methods for approximating likelihood functions and generating samples under a class of non-neutral models. We consider models that describe the distribution of allele frequencies in a sample of chromosomes from diploid organisms at a single non-recombining region of the genome in the following setup. We assume a fixed number of allelic types at a region of the genome. The frequency of a particular allele is defined as the ratio of the number of chromosomes that are identical to the given allele over this region to the total number of chromosomes in the population. Alleles are subject to a random parent-independent mutation process, in which, the type of the new allele from a mutation event is chosen from the types existing in the population, independently of the type of the parent. Selection acts on a diploid genotype of two alleles and each genotype in the population is assigned a selection coefficient representing the relative advantage of that genotype with respect to a fixed arbitrary genotype in the population. Under these asumptions, the distribution of allele frequencies in a population evolving for a long time can be obtained as the stationary distribution in the diffusion limit, which is governed by a mutation parameter and a matrix of selection parameters. Ultimately, we are interested in performing likelihood-based inference on the strength of selection, given a sample of allele frequencies from the population.

Likelihoods arising from the distribution of the allele frequencies in the class of non-neutral models described in the previous paragraph have an unknown normalizing constant that depends on the parameters of the model. Evaluation of likelihood functions and generating samples under the non-neutral models require approximating this unkown constant, either by direct computation or by a stochastic simulation approach that bypassess its direct computation. Before describing our method, we briefly discuss the disadvantages associated with stochastic simulation approaches available to evaluate likelihoods and to generate samples for the class of non-neutral models we study.

In principle, rejection sampling, importance sampling, and Markov chain Monte Carlo (MCMC) methods can be used to simulate allele-frequency data from non-neutral models and to approximate the normalizing constants in non-neutral models. These Monte Carlo methods use an auxiliary distribution under which simulating the allele frequencies is easy and their computational efficiency increase when the auxiliary distribution mimics the target non-neutral model closely. However, designing a good auxiliary distribution for non-neutral models is difficult in practice because of high-dimensional data and potentially high-dimensional parameter space. When a distribution based on a neutral model is used as the auxiliary distribution to generate a sample from a non-neutral model by rejection sampling, the acceptance rate remains low. For example, under the model presented in DNJ (2001), the rejection method with an auxiliary distribution based on the neutral model in some cases requires 10⁹ trials before a sample from the distribution under the non-neutral model is accepted. Approximating normalizing constants by importance sampling, by first expressing them as expectations of neutral distributions and using samples generated from neutral models, suffers from the same inefficieny. Distributions based on neutral models make poor auxiliary distributions in stochastic simulation methods targeting non-neutral models, because under appreciable selection, the allele-frequency patterns produced by neutral models differ substantially from the allele-frequency patterns produced by non-neutral models.

MCMC methods have also been used to simulate samples under a variety of non-neutral models. For example, Fearnhead (2001, 2003), developed methods based on perfect simulation (Propp and Wilson, 1996). MCMC methods based on perfect simulation have the advantage to be applicable to parent-dependent mutation schemes, in which, the type of a mutant allele may depend on the type of its parent. Murray et al. (2006) developed a similar approach to sample the posterior distribution of parameters when the model has an unknown normalizing constant dependent on the parameters (Møller et al., 2006). However, perfect simulation is computationally feasible only for small values of the selection parameter and for haploid populations. As the strength of selection increases, one has to look further back in time in the history of the sample and deeper on the genealogical tree to capture the branches on which selection events occur on the genealogical tree. Further, MCMC methods produce correlated samples from the target distribution, which is a disadvantage when independent samples are required. In summary, there is a lack of efficient computational methods that can operate under a wide range of parameter values and high-dimensional data and parameter spaces.

We present numerical analysis methods to compute the parameter-dependent unknown constant efficiently and accurately for a sub-class of non-neutral models in which the matrix of selection parameters is diagonal. In our numerical analysis approach, we break the high-dimensional integral in the normalizing constant into a series of one-dimensional iteratively defined integrals. In the end, we compute these integrals to produce a series of numerical approximations to a sequence of conditional cumulative distribution functions. Using these cumulative distribution functions, we simulate independent samples directly from distributions of non-neutral models. To simulate samples from non-neutral models with a non-diagonal matrix of selection parameters, our numerical analysis methods allow the use of distributions in non-neutral models with a diagonal matrix of selection parameters as auxiliary distributions in a rejection sampling setup, improving the efficiency of the rejection sampling.

Our method combines the advantages of stochastic approaches with the advantages of numerical approaches. By taking a numerical analysis approach to compute the normalizing constant, we avoid stochastic error. Yet, because we can produce a series of conditional cumulative distribution functions, simulating independent samples directly from the distribution of interest is feasible. Combined with stochastic samplers such as rejection algorithm or MCMC, our numerical methods provide an efficient algorithm to sample the joint posterior distribution of the mutation and selection parameters under non-neutral models.

We demonstrate the application of our methods with two examples using a symmetric balancing selection model, which corresponds to the special case where the matrix of selection parameters is diagonal with equal elements. Balancing selection is a diversity-promoting mode of selection, resulting from a variety of mechanisms, such as heterozygote advantage and negative-frequency-dependence. Applications of balancing selection arise in many areas, from plant genetics to environmental genomics. Estimating the strength of balancing selection and determining whether balancing selection is a prevalent force are key to understanding evolution in these contexts.

In the first example, we investigate the performance of our inferences on the strength of balancing selection using our methods in conjunction with approximate Bayesian computation, based on rejection sampling (Tavaré et al. 1997; Pritchard et al., 1999; Beaumont et al., 2002). Approximate Bayesian computation performs inference on the posterior distribution of the parameters utilizing the data sets simulated under a model. In the second example, we focus on the stationary distribution of the r largest allele frequencies in a population with K total allelic types (Watterson, 1977). Based on this distribution, we investigate the effect of using an incorrect K-allele model in which small-frequency alleles are missing in the sample, on the posterior distribution of the selection parameter, using an MCMC approach.

2. Models

2.1. Neutral K-allele model

In a population with K allelic types, evolving for a long time under the neutral model with parent-independent mutation, the stationary distribution of allele frequencies (), where x_i denotes the frequency of the ith allelic type, is given by the Dirichlet distribution (Wright, 1949):

(1)

Here, θ = 4Nμ is the population-scaled mutation parameter, where N is the effective population size, μ is the mutation rate per gene per generation, is the fraction of the mutation rate corresponding to allele i, and I{A} is the indicator function taking a value of 1 on set A and 0 otherwise. The normalizing constant b(θν) is a well-known ratio of gamma functions and is given by

The sampling distribution L_N(n) of a sample of size n under the multinomial sampling from distribution given in equation (1) is given by

where, , n_i is the number of copies of ith allele in the sample, is the sample size, and is the rising factorial. The multinomial sampling probabilities in this case are also given by b(θν + n)/b(θν). The Dirichlet distribution is conjugate under multinomial sampling (Kotz, 2000), meaning that if the prior probabilities on the population frequencies is Dirichlet distributed, then the posterior probabilities of the population frequencies given a sample is also Dirichlet distributed. The conditional distribution of the population frequencies given a sample from the distribution in equation (1) is Dirichlet with

(2)

2.2. K-allele model with selection

The stationary distribution of allele frequencies in the presence of selection is related to the stationary distribution under neutrality given in equation (1) in the following way. For a population with allele frequencies x, we define the mean fitness by

where σ(A_i, A_j) denotes the parameter for the strength of selection of a genotype with allelic types A_i and A_j. We let Σ be the symmetric matrix whose (i, j)th element is σ(A_i, A_j) = σ_ij. Then, the stationary distribution of allele frequencies in the K-allele model with selection (Wright, 1949) can be expressed as

(3)

where c(Σ, θν) is the normalizing constant and x′ denotes the transpose of the vector x. The normalizing constant is given by

subject to , where we used the integral sign for multiple integration over the allele-frequency space. An argument in Joyce (1994) uses equation (2) to show that the relationship between the sampling distribution of a sample of size n under selection, L_S(n), and under neutrality, L_N(n), is given by

(4)

where E_N(·) is the expectation with respect to the distribution under neutrality given by equation (1) and the last equality follows by the fact that L_N(n) = b(θν + n)/b(θν).

Under non-neutral models we describe, the likelihoods are intractable because the normalizing constants c(Σ, θν) and c(Σ, θν + n) in equation (4) are difficult to compute. Monte Carlo integration, based on generating many independent copies of x_i under the neutral model and approximating the expectation in equation (4) by the average

(5)

is inefficient when selection is strong, because the allele-frequency patterns under the non-neutral model are substantially different than the allele-frequency patterns under the neutral model. Importance sampling improves the estimation of to some extent, although obtaining many such estimates remains computationally infeasible.

3. Computing Likelihoods and Simulating Data

In the last section, we argued that the intractability of likelihoods under non-neutral models is due to difficulties in obtaining the normalizing constants, which appear as high-dimensional integrals in the form c(Σ, θν) and c(Σ, θν + n). In this section, we present a numerical analysis approach to compute these constants in the special case where Σ is a diagonal matrix. The method extends the results presented in Genz and Joyce (2003) and has some similarities to a method reported by Fearnhead and Meligkotsidou (2004). Below, we give a brief description of how we implement the numerical methods of Joyce and Genz, and focus in detail on how these methods can be utilized in performing statistical inference on the strength of selection. The mathematical properties of the numerical methods we use, such as computational efficiency, algorithmic complexity, accuracy of approximations, and handling of the end-point singularities in the integrals are described in detail in Joyce and Genz (2003).

The main idea behind our numerical analysis approach is to break the K dimensional integral in the normalizing constant into K one dimensional iteratively defined integrals. Each one-dimensional integral is calculated by numerical integration methods, producing an approximation to the value of the normalizing constant and a series of numerical approximations to a sequence of conditional cumulative distribution functions. On one hand, computing the constant with this method allows the evaluation of likelihood functions. On the other hand, using the cumulative distribution functions produced in the process of computing the normalizing constant, allele frequencies can be simulated directly from the non-neutral model. Thus, using efficient numerical methods, we approximate the intractable likelihoods under non-neutral models with a diagonal matrix of selection parameters.

3.1. Computation of the normalizing constant when Σ is diagonal

We let Σ be a diagonal matrix with elements , in the diagonal and 0 elsewhere. We implement the numerical methods with σ_i <  0 because this type of selection matrix characterizes balancing selection, a selection scheme of biological importance as we discuss in our examples in Section 3.2. The normalizing constant for the stationary distribution of allele frequencies under the non-neutral model under this parameterization is given by

The special structure of the integrand allow computing c(σ, θν) as a sequence of one-dimensional integrals. In order to demonstrate this, we first separate the inner exponential term into factors which are distributed to the respective outer integrals, and we rewrite c(σ, θν) as

(6)

where and α_i ≡ θν_i − 1. We note that the constant c(σ, θν) is expressed as a (K − 1)-dimensional integral in equation (6). This is possible since the frequency of the Kth allele given the frequencies , can be determined using the constraint on the allele frequencies, which allows us to write . Now we consider the integral with respect to x_K−1 on the right side of equation (6) which we rewrite as

and we note that this last expression depends on the variables only through the term . We define and denote the last integral by the function g_K−1(y_K−1). We have

(7)

Substituting the right hand side of equation 7 into equation (6), we get

Continuing in this manner, we define the successive integrals by

(8)

for , and i = K − 1, . The required normalizing constant c(σ, θν) is given by g₁(1).

For numerical computations, we introduce the same mesh k/m, for , for each of the y_i variables. Then the g_i(y_i) values on this mesh are approximated using a trapezoidal integration rule, and g₁(1) is approximated by computing g_i(y_i) mesh approximations for i = K − 1, . The resulting g₁(1) approximation can be accurately and efficiently computed in O(m²) time (Genz and Joyce, 2003), except in some cases, where the α_i values produce end-point singularities for the g_i(y_i) integrals. In those cases, we use standard numerical methods for “subtracting out the singularities” (David and Rabinowitz, 1984), to eliminate the singular integrand behaviors and produce rapidly converging approximations to g₁(1).

3.2. Generating samples when Σ is a diagonal matrix

We define the cumulative distribution functions F_i(·; z) with parameter z, for as

where g_i(y) is defined by equation (8). We note that . Since F_i(·;z) is a strictly increasing function for 0 < y < z, it has a well-defined inverse that we denote by . Given these definitions, we now generate a sequence of random variables with joint probability density function given by equation (3) when the matrix of selection parameters is diagonal. The method, which is an application of inversion sampling (i.e., “the CDF method”) is as follows. We let U₁ be a uniformly distributed random number on [0, 1]. That is, U₁ ∼UNIF[0, 1]. We define . Now we define iteratively

• 1. Generate U_i ∼ UNIF ,

• 2. Define .

If the normalizing constant is calculated using the method described in Section 3.1, then approximations for the g_i(y) functions have also been computed, and we can generate independent random vectors of allele frequencies using the above algorithm. Each vector X is a realization of the (random) population allele frequencies under selection. To simulate a sample of size n with allele counts given by n and distribution given by equation (3), it is sufficient to draw a multinomial sample conditional on the given population frequencies X.

4. Applications of the Numerical Method for Inference Under Non-Neutral Models

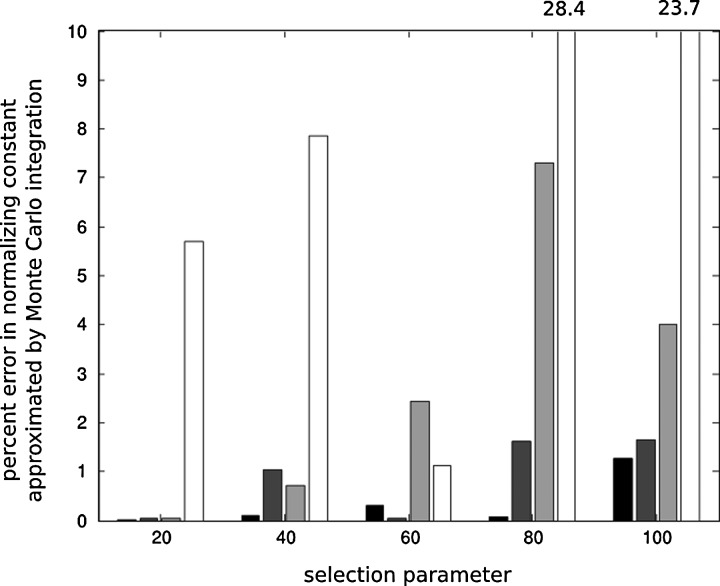
Computation of the normalizing constant c(σ, θν) by methods of Section 4.1 allows us to approximate the intractable likelihoods and to perform inference on the strength of selection under non-neutral models. For comparison purposes, we provide percent error estimates when the normalizing constant c(σ, θν) is obtained by naive Monte Carlo integration using equation (5), with a diagonal matrix of selection parameters, where we assume that c(σ, θν) computed using our numerical methods is the true value (Fig. 1). Accuracy of our numerical methods has been studied in Genz and Joyce (2003). In practice, the normalizing constants can be computed only once on a grid and stored in a lookup table for repeated use. In our tests, computing an approximate likelihood surface with 1000 × 1000 evaluations for a non-neutral model with K = 10 alleles and a diagonal matrix of selection parameters took on average less than minute on a decent desktop computer.

FIG. 1.

Percent error in normalizing constant c(Σ, θν) obtained by Monte Carlo integration using samples simulated under the neutral model when the selection matrix in the non-neutral model is diagonal and all values of selection parameters are equal. Monte Carlo averages in calculating the normalizing constants are based on 10³,10⁴,10⁵, and 10⁶ samples drawn from the neutral model, illustrated from dark to light color respectively. The true value of c(Σ, θν) is assumed to be the value computed by numerical analysis methods. As the strength of selection (given by parameter σ = (20, 40, 60, 80, 100)) increases, the relative error in c(Σ, θν) obtained by Monte Carlo integration increases on average because of substantial difference between allele frequency patterns in the non-neutral model and allele frequency patterns in the neutral model. Percent error values larger than 10% are given at the top of the corresponding bar numerically.

The maximum likelihood estimates for the strength of selection can be obtained by standard maximization methods of likelihood surfaces, computed by our numerical methods. Alternatively, the joint posterior distribution of selection and mutation parameters can be sampled combining our numerical methods with MCMC (Buzbas et al., 2009, 2011).

4.1. Bayesian inference under non-neutral models

By Bayes' Theorem, under the non-neutral model with diagonal matrix of selection parameters, , the joint posterior distribution of selection and mutation parameters can be written as

(9)

where f (x|σ, θν) is the likelihood and π(σ, θν) is the joint prior. For simplicity, we assume that mutation is non-preferential among the K alleles and we fix although use of other schemes does not add difficulty to the analysis. Further, we assume the prior independence of selection and mutation parameters and write π(σ, θν) = π(σ)π(θν). When sampling the joint posterior distribution in equation (9), the normalizing constant in the denominator need not be computed, since most stochastic samplers require the posterior distribution to be known up to a constant free of parameters. However, this is not the normalizing constant computed by our methods in Section 3.1. In equation (9), the parameter-dependent normalizing constant computed by our methods is hidden in the likelihood f (x|σ, θν). We let, and n_o to denote the observed population frequencies and sample frequencies respectively. If the sample frequencies are taken as proxy to population frequencies and the population distribution is used, the likelihood f (x_o|σ, θν) can be explicitly written as

(10)

and if the sampling distribution is used, it can be written as

(11)

We now define the statistics

(12)

and express the density of the non-neutral model with diagonal matrix of selection parameters as

The right-hand side of the last equality depends on the allele frequencies x only through the functions of F and G, and the Fisher-Neyman factorization theorem implies that F and G are jointly sufficient for the parameters σ and θ. To sample the joint posterior distribution of the selection and mutation parameters we use an approximate Bayesian computation algorithm with the likelihood based on equation (10):

Algorithm–ABC (with rejection):

• 1. Simulate a value θ* from the prior distribution π(θ) and a value σ* from the prior distribution π(σ)

• 2. Simulate a vector of population allele-frequencies x* from the non-neutral model with parameters θ*, σ* using the numerical methods of Section 4.

• 3. Compute the statistics F*, G* by equation (12) using x*.

• 4. Accept θ*, σ* as a sample from the posterior distribution if

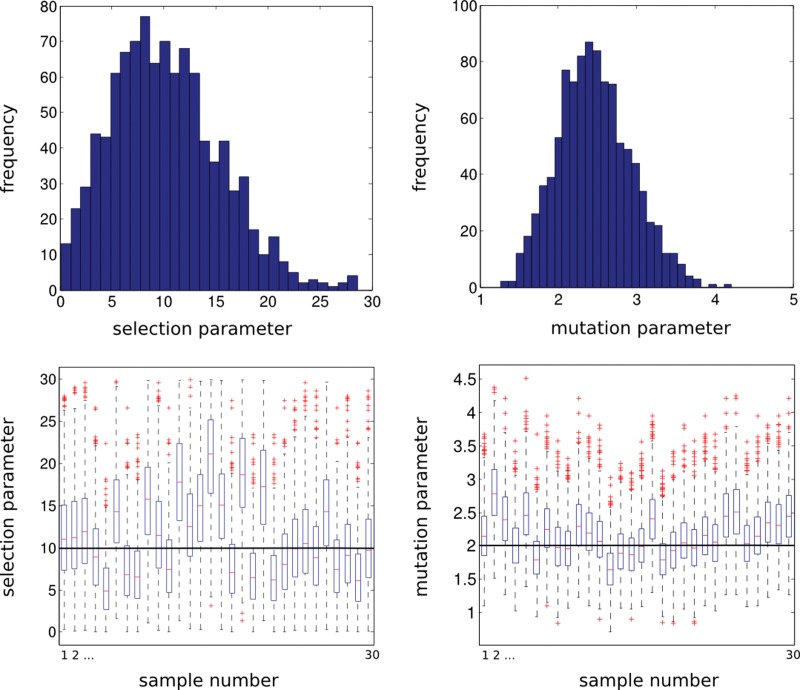
where F_o and G_o are the statistics computed from the observed data, || · || is the Euclidean distance, and δ is a suitable tolerance parameter. The posterior sample obtained by Algorithm–ABC is from the correct posterior distribution as δ approaches zero. We also note that, since the summary statistics are sufficient for the parameters under this non-neutral model, there is no approximation associated with reducing the full-data likelihood to a likelihood based on the summary statistics. An example for the performance of inference on the joint distribution of the parameters is given in Figure 2, using the likelihood based on the population frequencies (i.e., equation (10)). We simulated the “true” population frequencies used as test data, from a model with 10 replications, from a locus with K = 10 alleles, under a selection parameter σ = 10 and a mutation parameter θ = 2. We generated 10⁵ data sets under the model with 10⁵ parameter values (σ, θ), drawn from their prior distribution (Step 2 in Algorithm-ABC above), and 1% of the parameters which generated the summary statistics (F*, G*) closest to the observed summary statistics (F_o, G_o) in the Euclidean sense, are taken as a sample from the posterior distribution.

FIG. 2.

Posterior distributions (top) and boxplots (bottom) of selection and mutation parameters. The “true” population frequencies are simulated under a K = 10 allele model with 10 replicates (e.g., 10 loci) and a diagonal selection matrix where all elements are equal (i.e., symmetric balancing selection model). The “true” selection parameter is σ = 10 and the mutation parameter is θ = 2. Top left and right histograms are posterior samples of selection and mutation parameters respectively, both obtained by approximate Bayesian computation as explained in Algorithm-ABC in the text. Bottom left and right series of box plots are from posterior samples for 30 independent runs of “true” population frequencies, obtained by the same procedure as above.

4.2. The distribution of the r-largest allele frequencies

In models considered thus far, we assumed that all the allelic types present in the population are observed in the sample, treating K as fixed and known. In many practical problems, this assumption might not be reasonable. For example, in highly-polymorphic immune system genes in humans such as Human Leukocyte Antigen (HLA), some of the low-frequency alleles in the population will likely be missing in the sample. The stationary distribution of allele frequencies for a diagonal matrix of selection parameters for various cases of missing data and when K is unkown is studied in detail by Watterson (1977). Here, we consider the distribution of the r-largest allele frequencies in a population with K total alleles (r < K), to investigate the effect of missing low-frequency alleles in the sample when performing inference on the strength of balancing selection.

The distribution of the r-largest allele frequencies , in a population of K total types can be written as (Watterson, 1977),

(13)

where

(14)

(15)

(16)

The distribution of the r-largest allele frequencies has a normalizing constant that is a ratio of two integrals. The first integral, which appears in the denominator of equation (13) is the normalizing constant of the full model with K-alleles. The second integral, which appears in the numerator of equation (13) is a (K − r)-dimensional integral and is a sum over the frequencies of unobserved alleles. The methods of Section 3.1 can be modified to compute the integral in the numerator and hence the normalizing constant in equation (13). Application of our numerical methods, once for the integral in the numerator and once for the integral in the denominator, allows us to evaluate likelihoods in r-largest allele frequencies based on equation (13).

To demonstrate the use of the distribution of r-largest allele frequencies, we consider the following idealized example, where sample frequencies are reasonable proxy for population frequencies. We simulate a vector of population frequencies under the model with K = 10, σ = 100, and θ = 5 to represent the “true” state of the population at a locus. We now consider three analyses. First, we assume that r = 7 largest-frequency alleles are observed in a sample with the true frequencies as in the population and analyze these frequencies using a K = 7 allele model. This is a case where three alleles are missing in the data set, since the true K is 10, and we are unaware that we are missing the three smallest-frequency alleles, using a model with K = 7 to analyze the data. Second, we assume that r = 7 largest-frequency alleles are observed in a sample with the true frequencies as in the population and analyze these data using equation (13) where K = 10. This is a case where again three alleles are missing in the data set, since the true K is 10, but this time we know that we are missing the three smallest-frequency alleles and use a model with K = 10 to analyze the data. Third, we assume all K = 10 alleles are observed in a sample with the true frequencies as in the population and analyze these data with a model with K = 10 alleles. The posterior distribution obtained from the third analysis represents the ideal situation, in which there are no missing alleles in the sample and the sample frequencies are proxy for the population frequencies. Therefore, the posterior distribution obtained from the third procedure is the gold standard for the posterior distributions obtained from the first and second analyses. We obtain posterior samples for all three scenarios using an MCMC approach with 100,000 iterations and 10,000 burn in steps.

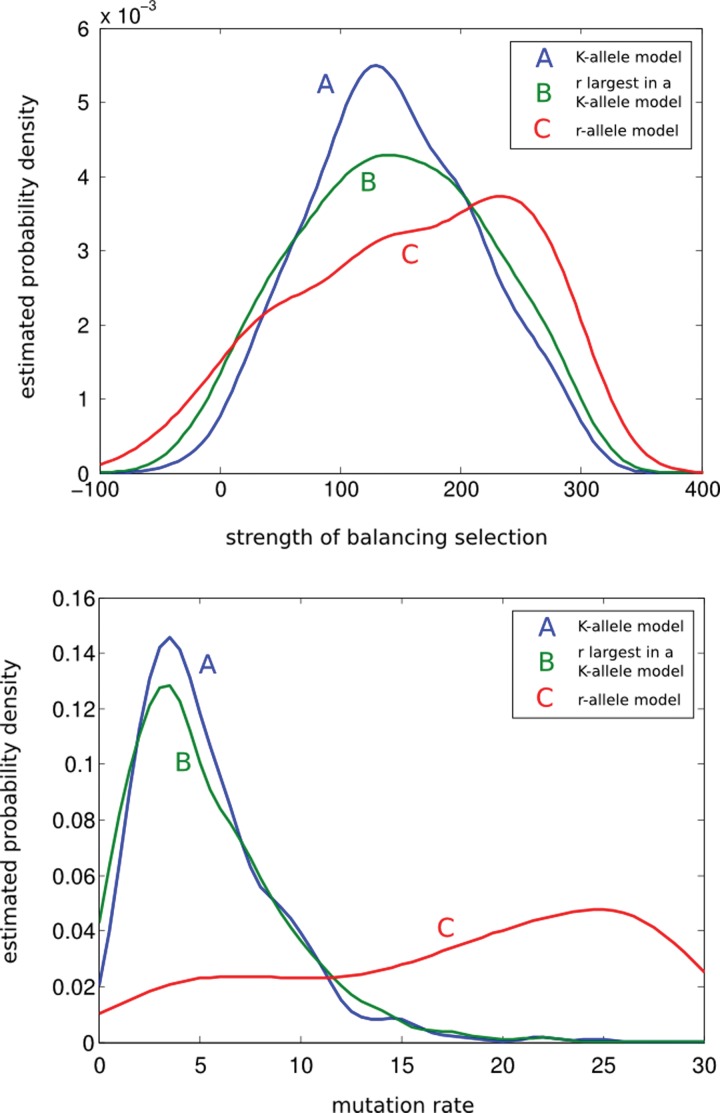
The posterior distribution of the selection and mutation parameters obtained using the first analysis results in biased estimates for selection and mutation parameters (Fig. 3). Low-frequency alleles carry valuable information on mutation and consequently the posterior distribution of the mutation parameter is substantially affected. Using the distribution of the r-largest allele frequencies results in improved estimation, as the model compensates the missing alleles. However, a good estimate of K is required in this case, close to its true value. These results suggest that in a K-allele balancing selection model, it might be important to capture the low-frequency alleles in the sample to obtain good estimates of the strength of selection, especially when K is unknown and no good estimates for K exist.

FIG. 3.

Kernel density estimates of posterior distributions of selection (top) and mutation (bottom) parameters obtained analyzing allele-frequencies under three non-neutral models. The models differ in their assumptions on the number of allelic types in the population, K. The “true” population has K = 10 alleles but only 7 largest-frequency alleles are observed in the sample. Green plots are obtained by analyzing these 7 frequencies under the assumption that r = 7 largest-frequency alleles out of K = 10 total alleles are observed in the data. Red plots are obtained by analyzing the 7 frequencies under the assumption that these are all the existing allelic types in the population. Hence, the second model corresponds to using a K = 7 allele model, whereas the frequencies are actually generated under a model with K = 10. Using the second model, the mutation parameter is overestimated (bottom, red plot) because of missing three small-frequency alleles. Consequently, estimates for the selection parameter are not accurate. Blue plots are obtained by assuming ideal conditions where all 10 allelic types are observed and the sample frequencies are proxy for the population frequencies. Hence, the blue plots are obtained under the correct model when there is no missing data and inference in this case is the gold standard for the other two models.

5. Conclusion

Both likelihood and Bayesian statistical approaches provide powerful tools for modeling and analyzing genetic polymorphism. However, as we are now well into the genomics era, the argument for or against statistical methods is now more practical than philosophical. The central question is whether statistical methods, especially those that involve averaging over a large amount of missing data, scale appropriately to handle large genomic data sets. Some have argued that the exponential increase in computing power, that we have enjoyed over the past two decades, will continue and effectively solve the problem of scalability of statistical methods for genomic data sets. We now know that increased computing power per se is not enough to provide methods that scale up to handle immense amount of data pouring out of tech-powered wet labs. Therefore, modelers and statisticians have taken two conceptual approaches to address the problem of scalability, both of which aim to maintain benefits of statistical modeling while keeping the methods practical for genomic data sets. The first approach is to abandon the likelihood analysis based on the full-data and settle for an approximate method. Examples include composite likelihood methods and likelihood methods based on summary statistics (Hudson, 2001; Marchini, 2004). While these approaches are suboptimal from a statistical perspective, the increase in algorithmic speed often more than makes up for the slight loss of information. The second approach is to settle for an approximate mechanistic description of the natural system and build a statistical model on which an analysis based on full-data likelihood can be performed (Li and Stephens, 2003). Thus, the first approach uses a simplified statistical method whereas the second approach uses a simplified statistical model. For example, our assumption of using a parent-independent mutation scheme in non-neutral models used in this paper, is a simplification of a more realistic mutation model and therefore an example to the second approach. On the other hand, in our first application in Section 5, we performed inference using an approximate Bayesian computation approach based on the likelihood of summary statistics and not the likelihood of the full-data. Hence, our analysis in that application is in principle an example to the first approach, although in our case summary statistics were sufficient and there was no information loss.

Using a parent-independent mutation model may limit the application of non-neutral models considered in this article when a more realistic mutation model is desired. However, when our numerical methods are embedded in likelihood-based statistical methods, they are scalable to genomic data sets and may provide a reasonable approximate method for detecting selection when the parent-independent mutation assumption is violated.

Acknowledgments

Funding for this work was provided by NSF EPSCoR, EPS-0132626, NSF Population Biology Panel DEB-0089756, and NIH NCRR grant NIH NCRR 1P20RR016448-01. The research of P.J. is supported in part by the Initiative in Bioinformatics and Evolutionary Studies (IBEST) at the University of Idaho. The research of E.B. is supported in part by NIH R01 GM081441, NIH P20 RR016454 from the INBRE Program of the National Center for Research Resources.

Disclosure Statement

No competing financial interests exist.