Likelihood functions for the analysis of single-molecule binned photon sequences

Abstract

We consider the analysis of a class of experiments in which the number of photons in consecutive time intervals is recorded. Sequence of photon counts or, alternatively, of FRET efficiencies can be studied using likelihood-based methods. For a kinetic model of the conformational dynamics and state-dependent Poisson photon statistics, the formalism to calculate the exact likelihood that this model describes such sequences of photons or FRET efficiencies is developed. Explicit analytic expressions for the likelihood function for a two-state kinetic model are provided. The important special case when conformational dynamics are so slow that at most a single transition occurs in a time bin is considered. By making a series of approximations, we eventually recover the likelihood function used in hidden Markov models. In this way, not only is insight gained into the range of validity of this procedure, but also an improved likelihood function can be obtained.

1. Introduction

Conformational dynamics of a single molecule can be studied by analyzing fluorescence emission from dyes attached to the molecule [1–4]. Photophysical properties of the dyes depend on the distance to a quencher or, in the case of Förster resonance energy transfer (FRET), on the distance between donor and acceptor dyes. Conformational changes lead to changes in these distances, which are reflected in the fluctuations of fluorescence emission. The problem is how to extract the information about the conformational dynamics.

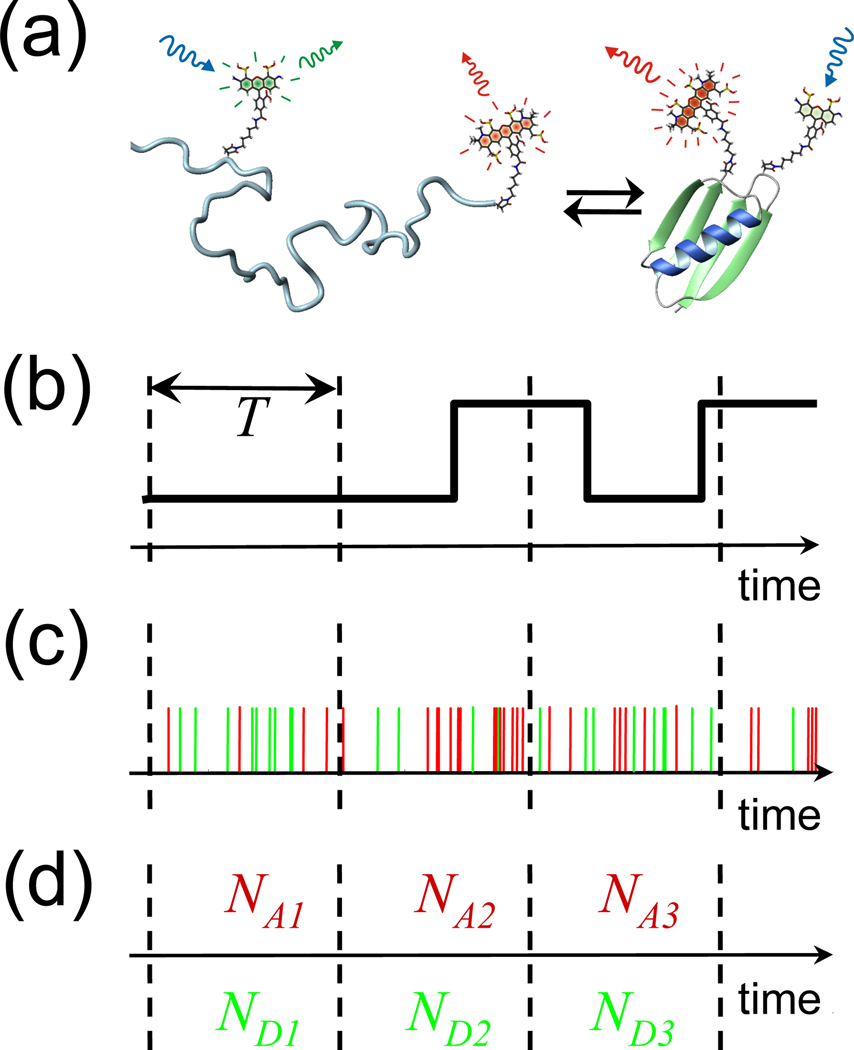
Figure 1 schematically illustrates a simple example of the problem considered here. Suppose that a protein can exist in only folded and unfolded state (see Fig. 1(a)). Figure 1(b) shows a conformational trajectory as the system jumps between the two states. However, this trajectory is not observed directly. What can be observed are photons emitted by the donor and acceptor fluorescent dyes attached to the molecule (see Fig. 1(c)). Since the average distance between the dyes is different in the two states, the corresponding donor and acceptor fluorescence intensity will also differ. Time resolution is not always sufficient to measure photon arrival times, in which case only numbers of photons during observation (bin) time are monitored. Figure 1(d) shows a time-binned photon trajectory where the numbers of acceptor (N_A) and donor (N_D) photons in time bins of the same duration T are determined. In this paper, we consider only this type of measurements. The sequence of photon counts can be converted into a sequence of FRET efficiencies defined in each bin as the fraction of acceptor photons, i.e., E = N_A/(N_A + N_D).

Figure 1.

FRET and two-state protein folding. (a) Kinetic scheme that describes the folding and unfolding of a protein with attached donor and acceptor dyes. (b) The conformational trajectory which is of interest but invisible. (c) The observed photon trajectory when the arrival time of each detected photon is recorded. (d) A photon trajectory when only the numbers of acceptor and donor photons in a time bin of duration T is recorded.

A widely used method of analyzing photon counts is to construct histograms of photon counts or, more commonly, the histograms of FRET efficiencies. In such a procedure, the correlation between successive bins resulting from conformational dynamics is apparently lost. A different approach involves the analysis of the whole sequence of photon counts using a likelihood function. The starting point is the probability distribution of observing the sequence of photon counts given a model of conformational dynamics. This distribution is considered as the likelihood that the model of conformational dynamics describes the observed ordered sequence of photons. The likelihood function is then analyzed to solve various inference problems. These include finding optimal model parameters (by using gradient methods, or expectation-maximization, or Monte-Carlo methods), establishing the most likely conformational state trajectory (e.g., using the Viterbi algorithm), identification of the number of conformations, and model comparison among others. During the last decade, likelihood-based methods have been used to analyze many different biophysical experiments, including those dealing with ion channels [5, 6], molecular motors [7], protein dynamics [8], and unzipping of DNA by nanopores [9]. Even in the specialized area of single-molecule photon counting, there is now a rather extensive literature [10–21].

Finding the likelihood function that corresponds to a specific physical problem is the first and most crucial step in all likelihood-based methods. We recently presented such a study for the sequences of photons with observed arrival times and photon colors [15]. In this paper, we will consider the likelihood function to handle single-molecule experiments where only the numbers of photons in time bins are recorded.

Sequences of photon counts and FRET efficiencies have been previously analyzed in the framework of hidden Markov models (HMM) [14, 16, 19]. In this technique, a molecule can change its state only at regularly spaced discrete times [22]. Being in a particular state, the molecule “emits a signal” (e.g., a number of photons or FRET efficiency) with an “emission” probability distribution associated with that state. Lee [16] pointed out to the fundamental limitation in the application of HMM to single-molecule data since transitions between conformational states in HMM are synchronized with the beginning of the time bin. Liu et al. [19] found that the parameters of the model of conformational dynamics determined using HMM are sensitive to the choice of the “emission” distribution.

In this paper, we focus on the study of the likelihood function for the sequence of photons detected in consecutive time bins. Other inference problems such as methods of optimization are outside the scope of the present paper. Our approach is based on the exact likelihood function corresponding to the model of photon statistics and conformational dynamics described below in Section 2. Although we are primarily interested in FRET, in the next section we will assume that all detected photons have the same color. The reason is that the mathematical formalism is more transparent in this case and can readily be generalized to FRET with two- and even three-color photons [2], as will be shown below in Section 4. The exact likelihood function is rather complicated. Therefore, we make a series of controlled approximations to derive likelihood functions that are practically useful, rather then simply postulating them. The relationship of these likelihood functions with those used in HMM will be established. In addition to the sequence of photon counts, the sequence of FRET efficiencies and corresponding likelihood functions are considered in Section 5. The last section summarizes results and gives concluding remarks.

2. The model

The model of conformational and photophysical dynamics adopted here is as follows. The molecule has M discrete conformational states. Being in a particular state, the molecule emits photons whose statistics are Poissonian (shot noise). This means that when the system is in state i, the distribution of the number of photons, N, detected in a time bin of duration T is (n_iT)^N exp(−n_iT)/N!, where n_i is the average number of photons that are detected per unit time (i.e., the photon count rate of state i). The mean number of photons in a bin is 〈N〉 = n_iT. For the photons of two colors, statistics of photons depend on two parameters, i.e., acceptor, n_Ai, and donor, n_Di, photon count rates.

The interconversion among conformations is described by a set of rate equations for the population of state i at time t, p_i(t). In matrix notation, these equations are written as dp/dt = Kp. The ijth off-diagonal element of the rate matrix K, K_ij, is the rate constant that describes the transition from state j to i. The diagonal element, K_ii, describes escape from state i and is equal to the negative of the sum of all rates that deplete state i, K_ii = −Σ_j≠i K_ji. The vector of normalized equilibrium populations, p_eq, is obtained by solving Kp_eq = 0. Detailed balance imposes the constraints on the matrix elements, K_ijp_eq(j) = K_jip_eq(i).

The above model of photon statistics is based on the separation of all processes that influence fluorescence emission into fast and slow compared to the average time between detected photons, which is usually on the microsecond time scale. When all fluctuations are fast, the photon statistics are Poissonian. A detection device such as CCD camera may distort this distribution. Here we follow Liu et al. [19] and assume that, after appropriate scaling, the resulting fluorescence intensity is still Poissonian. The Poisson distribution depends on the count rate that involves the parameters of fast processes. The count rates are determined by many factors such as dye excitation, energy transfer, decay of the donor and acceptor excited states, spectral crosstalk, linker and dye orientation dynamics on submicrosecond time scale, as well as the detection efficiency and Poissonian background noise [23]. Fortunately, all these complications should be considered only if one wishes to interpret the extracted count rates in structural terms (e.g., to get the interdye distance). They do not affect the parameters of conformational dynamics.

Dynamical processes that are comparable or slower than the mean interphoton time modulate photon count rates and alter the statistics of photon counts. We define a “conformation” in a broad sense as any state of the molecule that has different photon count rates. This may be due to a different interdye distance that changes on a microsecond time scale and slower. This may be also due to “long-lived” photophysical states of the fluorophores [20, 24], labeling permutations [3, 25], etc.

The kinetic model of conformational dynamics is not restrictive as may appear at first sight. If conformational space is continuous (e.g., diffusion on a free energy surface), we can discretize it and construct the rate matrix from the finite difference approximation of the appropriate differential evolution operator. To describe conformational states whose lifetime distribution is multiexponential, we can introduce several, appropriately connected, Markovian states that have identical photon count rates.

It is interesting to note that the model adopted in this paper is a special case of what is called a Markov Modulated Poisson Process in the statistics literature [26]. This model has been applied to treat photon sequences in time-resolved experiments with recorded interphoton times [13, 15, 17, 20, 21].

3. Photons of the same color

We start by considering photons of one color. First, we obtain the exact likelihood function for a sequence of photon counts assuming that conformational dynamics are described by conventional rate equations and statistics of photons in each conformational state are Poissonian (see Section 2). Then we discuss various approximations that eventually lead to the likelihood function used in the standard HMM.

The likelihood function is equal to the probability distribution of observing a sequence of photon counts in consecutive time bins (i.e., N₁, N₂, N₃, …). This distribution is related to the probability to detect N photons during the time interval of duration T and to be in conformational state i at the end of the time interval, given the molecule was in state j at the beginning. We denote this probability by P_ij (N). In general, this is a complex object because the system can visit many states during the time interval and the number of photon counts is correlated with the visited states.

Let assume for simplicity that the observed sequence of photons consists of three time bins with recorded numbers of one-color photons N₁, N₂, and N₃. The probability to observe such sequence (the likelihood function) is

$$\begin{array}{cc}L\hfill & ={\displaystyle \sum _{i,j,k,l=1}^M}{P}_{\mathit{\text{lk}}}(N_3)P_{\mathit{\text{kj}}}(N_2)P_{\mathit{\text{ji}}}(N_1)p_{\mathit{\text{eq}}}(i)\hfill \\ \hfill & ={\mathbf{1}}^{\top }\mathit{P}(N_3)\mathit{P}(N_2)\mathit{P}(N_1){\mathit{p}}_{\mathit{\text{eq}}}\hfill \end{array}$$ (1)

where P(N) is the matrix with elements P_ij (N) and 1^⊤ is the transpose of a column vector with every element equal to unity. This probability has a transparent interpretation. Reading from right to left, the first term, p_eq(i), is the probability that the system is in state i at the beginning of the first time interval. Since i can be any state, we sum over i. The next term P_ji(N₁) is the probability that the system starts in the state i at the beginning of the interval and is in state j at the end and N₁ photons have been detected. The next term, P_kj (N₂), corresponds to the second bin, in which N₂ photons have been detected, and so on.

The generalization to a larger number of time bins (J) is:

$$L={\mathbf{1}}^{\top }\mathit{P}(N_J)\dots \mathit{P}(N_3)\mathit{P}(N_2)\mathit{P}(N_1){\mathit{p}}_{\mathit{\text{eq}}}$$ (2)

The above expression is the likelihood that the parameters of the kinetic model (i.e., the rates K_ij and photon count rates n_i) describe the observed sequence of photon counts. The likelihood function is presented as a product of matrices. Note this formally exact likelihood function involves the probabilities P_ij (N) that depend on the initial (j) and final (i) states in the bin interval.

In order to be able to estimate the model parameters, we need to specify the matrix P(N). This matrix can be found analytically only for a two-state system. The two states (e.g., unfolded and folded states in Fig. 1(a)) are characterized by the photon count rates n₁ and n₂. The transitions between the states are described by the rates k₁ (1 → 2) and k₂ (2 → 1). The exact expressions for the matrix elements P_ij(N) can be obtained by averaging the Poissonian distribution of photon counts over the distribution of the time spent in one of the two interconverting states. This distribution can be found by generalizing the distribution in Ref. [27]. For n₂ > n₁, it can be shown that the diagonal (ii = 11, 22) and off-diagonal (ij = 12, 21) matrix elements are

$$\begin{array}{c}{P}_{\mathit{\text{ii}}}=\frac{{(n_{i}T)}^N}{N!}{e}^{-{(n_i+k_i)}^T}+k_i{\displaystyle {\int }_0^T}\frac{{[n_{1}t+n_2(T-t)]}^N}{N!}{e}^{-(n_1+k_1)t-(n_2+k_2)(T-t)}\times {(k_1(T-t)/(k_{2}t))}^{i-3/2}{I}_1(\sqrt{4k_1{k}_{2}t(T-t)})\mathit{\text{dt}}\hfill \\ P_{\mathit{\text{ij}}}=k_j{\displaystyle {\int }_0^T}\frac{{[n_{1}t+n_2(T-t)]}^N}{N!}{e}^{-(n_1+k_1)t-(n_2+k_2)(T-t)}{I}_0(\sqrt{4k_1{k}_{2}t(T-t)})\mathit{\text{dt}}\hfill \end{array}$$ (3)

where I₀(x) and I₁(x) are the modified Bessel functions. Equations (2) and (3) provide an exact analytical expression for the likelihood function in the case of two-state conformational dynamics. This result can be readily generalized to photons of two and three photon colors.

Even in the case of the two-state model, the exact likelihood function is rather complicated. To simplify it and to treat more than two states, we start with the generating function of the matrix P(N), for which a compact expression was previously obtained [23, 28]

$${\displaystyle \sum _{N=0}^{\mathrm{\infty }}}{\mathrm{\lambda }}^N\mathit{P}(N)=e^{(\mathit{K}-(1-\mathrm{\lambda })\mathit{𝒩})T}$$ (4)

Here 𝒩 is a diagonal matrix with the photon count rates of each conformation on the diagonal (𝒩_ij = n_iδ_ij, where δ_ij is the Kronecker delta defined so that it is unity when i = j and zero otherwise). This relation means that P(N) is the coefficient of λ^N in the expansion of the matrix exponential, exp((K −(1−λ)𝒩)T), in powers of λ.

To make progress, we consider the important special case when conformational dynamics is so slow that at most a single transition can occur during the bin time. In this limit, the transition rates are small, K_ijT ≪ 1, and one can expand the generating function in Eq. (4) to linear order in K [29]

$${\displaystyle \sum _{N=0}^{\mathrm{\infty }}}{\lambda }^N\mathit{P}(N)\approx e^{-(1-\lambda )\mathit{𝒩}T}+{\displaystyle {\int }_0^T}{e}^{-(1-\lambda )\mathit{𝒩}(T-t)}\mathit{K}{e}^{-(1-\lambda )\mathit{𝒩}t}\mathit{\text{dt}}$$ (5)

Expanding the right hand side in a power series in λ and equating the coefficients of λ^N, we find

$$P_{\mathit{\text{ii}}}(N)\approx (1+K_{\mathit{\text{ii}}}T)\frac{{(n_{i}T)}^N}{N!}{e}^{-n_{i}T}=(1-{\displaystyle \sum _{j\ne i}}{K}_{\mathit{\text{ji}}}T)\frac{{(n_{i}T)}^N}{N!}{e}^{-n_{i}T}$$ (6)

When i ≠ j,

$$P_{\mathit{\text{ij}}}(N)\approx K_{\mathit{\text{ij}}}T{\displaystyle {\int }_0^T}\frac{{[n_{j}t+n_i(T-t)]}^N}{N!}{e}^{-n_{j}t-n_i(T-t)}\mathit{\text{dt}}/T$$ (7)

Both of these equations have a simple physical interpretation. P_ii(N) corresponds to the molecule that has the same state i in the beginning and in the end of the bin time. In the limit of slow conformational dynamics, this means that no transition has occurred during the bin time. Therefore, the probability P_ii(N) is the product of the Poisson distribution of photon counts in state i (with count rate n_i) and the probability to have no transitions, which we denote by A_ii. This probability is A_ii = 1 − Σ_j≠i K_jiT. The above expansion is valid only if Σ_j≠i K_jiT < 1; therefore, A_ii is positive.

Now consider P_ij (N) with different initial and final states, i ≠ j. In the limit of slow conformational dynamics, this means that a transition from j to i must have occurred at some moment t in the time interval 0 ≤ t ≤ T. The probability that this happened is approximately A_ij = K_ijT. Note that the probabilities A_ij are normalized, ${\displaystyle {\sum }_{i=1}^M}{A}_{\mathit{\text{ij}}}=1$ (which means that the molecule either stays in state i or jumps to some other state). If the transition from j to i occurred at time t, then the mean number of photons is n_jt + n_i(T − t) and the distribution of photons in such bins is Poissonian with the corresponding mean. Since the transition can occur anywhere in the interval with equal probability, one must average over t, as done in Eq. (7).

Equations 6 and 7 can be be combined into a single expression valid for i = j and i ≠ j:

$$P_{\mathit{\text{ij}}}(N)\approx A_{\mathit{\text{ij}}}{B}_{\mathit{\text{ij}}}(N)$$ (8)

where A_ij = δ_ij + K_ijT and

$$B_{\mathit{\text{ij}}}(N)={\displaystyle {\int }_0^T}\frac{{[n_{i}t+n_j(T-t)]}^N}{N!}{e}^{-n_{i}t-n_j(T-t)}\mathit{\text{dt}}/T$$ (9)

The integral in the above equation can be evaluated analytically and B_ij (N) can be expressed in terms of the incomplete gamma-function, Γ(N, nT):

$$B_{\mathit{\text{ij}}}(N)=\frac{\mathrm{\Gamma }(N+1,n_{i}T)-\mathrm{\Gamma }(N+1,n_{j}T)}{(n_j-n_i)\mathit{\text{TN}}!}$$ (10)

Note that B_ij(N) is normalized as ${\displaystyle {\sum }_{N=0}^{\mathrm{\infty }}}{B}_{\mathit{\text{ij}}}(N)=1$ . The diagonal term is just a Poisson distribution, B_ii(N) = (n_iT)^N exp(−n_iT)/N!.

The likelihood function for three bins of photons in Eq. (1) can be written in terms of A_ij and B_ij (N) as

$$L={\displaystyle \sum _{i,j,k,l=1}^M}{A}_{\mathit{\text{lk}}}{B}_{\mathit{\text{lk}}}(N_3)A_{\mathit{\text{kj}}}{B}_{\mathit{\text{kj}}}(N_2)A_{\mathit{\text{ji}}}{B}_{\mathit{\text{ji}}}(N_1)p_{\mathit{\text{eq}}}(i)$$ (11)

The above equations present the likelihood function that can be applied to study conformational dynamics at times long compared to the bin time. It is assumed that no more than one transition can occur during the bin time. The structure of this likelihood function is similar to that in HMM [22] if A_ij are identified with the transition probabilities from j to i and B_ij(N) with the “emission” probabilities. However, B_ij (N) depends on both initial and final conformational states, unlike HMM where it is implied that a transition can occur only between two bins (which we refer here to as the standard HMM) and, therefore, the “emission” probability depends only on the initial state. Note that our likelihood function is to be read from right to left and the matrix of transition probabilities is the transpose of that used in statistical literature [22].

Now we turn to the consideration of the “emission” distribution B_ij (N). The diagonal term, B_ii(N), is just a Poisson distribution. Hence we focus on the distribution with nonequal initial and final states, i ≠ j. The analytical expression for this distribution, although it is available for one-color photons, cannot be extended to photons of two and three colors in general. Therefore, we proceed to various approximations, which will be also employed later in Section 4. These approximations are based on the mean μ_ij and variance ${\sigma }_{\mathit{\text{ij}}}^2$ of the number of photons N in the bins that have a transition from j to i during the bin time. They are defined as μ_ij = 〈N〉_ij and ${\sigma }_{\mathit{\text{ij}}}^2={\langle N^2\rangle }_{\mathit{\text{ij}}}-{\langle N\rangle }_{\mathit{\text{ij}}}^2$ , where 〈…〉_ij means averaging with distribution B_ij(N), Eq. (9). Evaluating the averages, we have:

$$\begin{array}{c}{\mu }_{\mathit{\text{ij}}}=(n_i+n_j)T/2\hfill \\ {\sigma }_{\mathit{\text{ij}}}^2={\mu }_{\mathit{\text{ij}}}+{(n_i-n_j)}^2{T}^2/12\hfill \end{array}$$ (12)

An approximation of B_ij(N) that gives the correct mean and variance can be obtained using a negative binomial distribution:

$$B_{\mathit{\text{ij}}}(N)\approx \frac{\mathrm{\Gamma }(N+r_{\mathit{\text{ij}}})}{N!\mathrm{\Gamma }(r_{\mathit{\text{ij}}})}{\left(\frac{{\mu }_{\mathit{\text{ij}}}}{{\sigma }_{\mathit{\text{ij}}}^2}\right)}^{r_{\mathit{\text{ij}}}}{(1-\frac{{\mu }_{\mathit{\text{ij}}}}{{\sigma }_{\mathit{\text{ij}}}^2})}^N$$ (13)

where $r_{\mathit{\text{ij}}}={\mu }_{\mathit{\text{ij}}}^2/({\sigma }_{\mathit{\text{ij}}}^2-{\mu }_{\mathit{\text{ij}}})$ . This distribution can be considered as the Poisson distribution with a random count rate distributed according to a gamma distribution. The negative binomial distribution reduces to the Poisson distribution when n_i = n_j.

When N is sufficiently large, we can use a Gaussian distribution with the correct mean and variance, Eq. (12):

$$B_{\mathit{\text{ij}}}(N)\approx {(2\pi {\sigma }_{\mathit{\text{ij}}}^2)}^{-1/2}\text{ exp }(-\frac{{(N-{\mu }_{\mathit{\text{ij}}})}^2}{2{\sigma }_{\mathit{\text{ij}}}^2})$$ (14)

Another approximation of B_ij(N) is to use the midpoint rule to evaluate the integral in Eq. (9) (i.e., set t = T/2). In this way, we find

$$B_{\mathit{\text{ij}}}(N)\approx \frac{{((n_i+n_j)T/2)}^N}{N!}{e}^{-(n_i+n_j)T/2}$$ (15)

This approximation is the Poisson distribution with a count rate in between n_i and n_j. This gives the correct mean number of photons averaged over all bins that have a transition from j to i. However, the approximation results in the incorrect variance, which is equal to the mean in this case.

The crudest approximation is to evaluate the integral in Eq. (9) by setting t = 0:

$$B_{\mathit{\text{ij}}}(N)\approx \frac{{(n_{j}T)}^N}{N!}{e}^{-n_{j}T}$$ (16)

This is the Poisson distribution with the count rate of the initial state. Substituting Eq. (16) into Eq. (11), we get the likelihood function for a three-bin sequence of photons that corresponds to this approximation

$$L={\displaystyle \sum _{i,j,k=1}^M}\frac{{(n_{k}T)}^{N_3}}{N_3!}{e}^{-n_{k}T}{A}_{\mathit{\text{kj}}}\frac{{(n_{j}T)}^{N_2}}{N_2!}{e}^{-n_{j}T}{A}_{\mathit{\text{ji}}}\frac{{(n_{i}T)}^{N_1}}{N_1!}{e}^{-n_{i}T}{p}_{\mathit{\text{eq}}}(i)$$ (17)

Here we used Σ_l A_lk = 1. This is the likelihood functions that one would use when applying the standard HMM to binned trajectories with photons of one color.

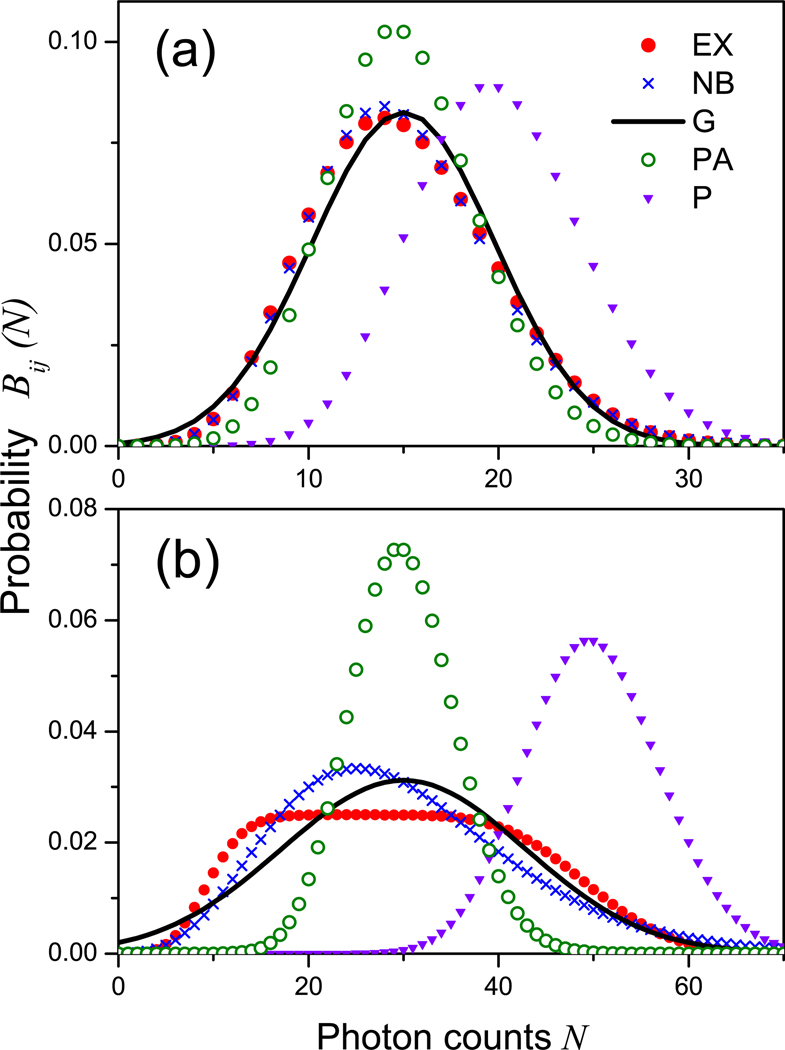
In Figure 2, we compare various approximation for B_ij(N), Eqs. (13)–(16), with the exact result in Eq. (10). It can be seen that even the simplest approximation (a Poisson distribution with the average count rate, Eq. (15), labeled as PA in Fig. 2) improves the “emission” probability associated with the initial state, Eq. (16). This is the simplest way of improving the likelihood function in Eq. (17). The Gaussian approximation in Eq. (14) or more sophisticated negative binomial distribution in Eq. (13) are preferable when the fluorescence intensity of the initial and final states differ considerably. Note that the figure refers to the bins that have a transition during the bin time. The number of such bins is small when the conformational dynamics are slow. The majority of the bins is described by the Poisson “emission” probability, B_ii(N) = (n_iT)^N/N! exp(−n_iT), which is the same for all approximations.

Figure 2.

Comparison of various approximations for the probability B_ij(N) of detecting N photons in the bins that undergo a single j → i transition. The exact (EX) distribution (dots, Eq. (10)) is compared with the negative binomial (NB) distribution (open circles, Eqs. (13) and (12)), the Gaussian (G) distribution (solid line, Eqs. (12) and (14)), the Poisson (PA) distribution with the average count rate (crosses, Eq. (15)), and the Poisson distribution (P) with the photon count rate of the initial state (triangles, Eq. (16)), which is implicit in the standard Hidden Markov Models. Mean numbers of photons in a bin in states i and j are (a) n_iT = 10, n_jT = 20; (b) n_iT = 10, n_jT = 50.

4. Two and three color FRET

In this section we extend the previous ideas and approximations to FRET where photons of two or more colors are observed. We start with the likelihood function for a sequence of donor and acceptor photon counts (see Fig. 1(d)). The molecule in conformational state i now emits acceptor and donor photons distributed according to a Poisson distribution with count rates n_Ai and n_Di. The likelihood function for a sequence containing both donor and acceptor photons is the generalization of Eq. (2). This can be written in terms of the probability P_ij(N_A,N_D) to detect N_A acceptor and N_D donor photons and to be in state i at the end of the bin time, given that the molecule is in state j at the beginning. All these probabilities are considered as elements of matrix P(N_A,N_D). ¹ The generating function for P(N) discussed in the previous section (see Eq. (4)) can be readily generalized to account for two photon colors[23, 28]:

$${\displaystyle \sum _{N_A,N_D=0}^{\mathrm{\infty }}}{\lambda }_A^{N_A}{\lambda }_D^{N_D}\mathit{P}(N_A,N_D)=e^{(\mathit{K}-(1-{\lambda }_A){\mathit{𝒩}}_A-(1-{\lambda }_D){\mathit{𝒩}}_D)T}$$ (18)

where [𝒩_A]_ij = n_Aiδ_ij and [𝒩_D]_ij = n_Diδ_ij. The likelihood function for a sequence of J bins with two-color photons is (c.f. Eq. (2))

$$L={\mathbf{1}}^{\top }\mathit{P}(N_{\mathit{\text{AJ}}},N_{\mathit{\text{DJ}}})\dots \mathit{P}(N_{A3},N_{D3})\mathit{P}(N_{A2},N_{D2})\mathit{P}(N_{A1},N_{D1}){\mathit{p}}_{\mathit{\text{eq}}}$$ (19)

These expressions provide an exact likelihood function for a time-binned sequence of donor and acceptor photons.

As before, we are interested in the case when conformational dynamics is so slow that at most one transition occurs during the bin time. In this case the generating function can be expanded to linear order in K (see Eq. (5)), resulting in the probability that generalizes Eq. (8):

$$P_{\mathit{\text{ij}}}(N_A,N_D)\approx A_{\mathit{\text{ij}}}{B}_{\mathit{\text{ij}}}(N_A,N_D)$$ (20)

Here the transition probability A_ij is the same as before, A_ij = δ_ij + K_ijT. The “emission” probability is

$$B_{\mathit{\text{ij}}}(N_A,N_D)={\displaystyle {\int }_0^T}\frac{{[n_{\mathit{\text{Ai}}}t+n_{\mathit{\text{Aj}}}(T-t)]}^{N_A}}{N_A!}\frac{{[n_{\mathit{\text{Di}}}t+n_{\mathit{\text{Dj}}}(T-t)]}^{N_D}}{N_D!}{e}^{-n_{i}t-n_j(T-t)}\mathit{\text{dt}}/T$$ (21)

where n_i = n_Ai+n_Di. This is just what one would expect from the extension of the expression in Eq. (9) for one-color photons to donor and acceptor photons. However, there is no closed form expression for this integral in general. When i = j, B_ij(N_A,N_D) in Eq. (21) is the product of two Poisson distributions with the acceptor and donor count rates n_Ai and n_Di. As in the case of one-color photons, B_ij(N_A,N_D) (i ≠ j) depends on both initial and final states in the bin, unlike the “emission” probability in the standard HMM.

To simplify the “emission” probability, we can make the same series of approximations for the off-diagonal B_ij(N_A,N_D), i ≠ j, as before. First, we find the mean (μ_Aij and μ_Dij), variance $({\sigma }_{\mathit{\text{Aij}}}^2\text{ and }{\sigma }_{\mathit{\text{Dij}}}^2)$ , and the correlation (ρ_ij) of acceptor and donor photon counts in the bins that have a single j → i transition. They are defined as μ_Fij = 〈N_F〉_ij, ${\sigma }_{\mathit{\text{Fij}}}^2={\langle {(N_F-{\mu }_{\mathit{\text{Fij}}})}^2\rangle }_{\mathit{\text{ij}}},\text{ and }{\rho }_{\mathit{\text{ij}}}^2={\langle (N_A-{\mu }_{\mathit{\text{Aij}}})(N_D-{\mu }_{\mathit{\text{Dij}}})\rangle }_{\mathit{\text{ij}}}/{\sigma }_{\mathit{\text{Aij}}}{\sigma }_{\mathit{\text{Dij}}}$ , where index F = A,D denotes acceptor or donor, 〈…〉_ij means averaging using the distribution B_ij(N_A,N_D) in Eq. (21). Evaluating the averages, we find

$$\begin{array}{cc}\hfill {\mu }_{\mathit{\text{Fij}}}& =(n_{\mathit{\text{Fi}}}+n_{\mathit{\text{Fj}}})T/2\hfill \\ \hfill {\sigma }_{\mathit{\text{Fij}}}^2& ={\mu }_{\mathit{\text{Fij}}}+{(n_{\mathit{\text{Fi}}}-n_{\mathit{\text{Fj}}})}^2{T}^2/12\hfill \\ \hfill {\rho }_{\mathit{\text{ij}}}{\sigma }_{\mathit{\text{Aij}}}{\sigma }_{\mathit{\text{Dij}}}& =(n_{\mathit{\text{Ai}}}-n_{\mathit{\text{Aj}}})(n_{\mathit{\text{Di}}}-n_{\mathit{\text{Dj}}})T^2/12\hfill \end{array}$$ (22)

Previously we presented two approximations that have the correct mean and variance, namely, a discrete negative binomial and a continuous Gaussian distributions. While it appears possible to generalize the former using negative multinomial distributions, for the sake of simplicity we present only the generalization of Eq. (14), which is a bivariate Gaussian distribution:

$$B_{\mathit{\text{ij}}}(N_A,N_D)\approx {\left(2\pi {\sigma }_{\mathit{\text{Aij}}}{\sigma }_{\mathit{\text{Dij}}}\sqrt{1-{\rho }_{\mathit{\text{ij}}}^2}\right)}^{-1}\times \text{ exp }(-\frac{{(N_A-{\mu }_{\mathit{\text{Aij}}})}^2}{2{\sigma }_{\mathit{\text{Aij}}}^2(1-{\rho }_{\mathit{\text{ij}}}^2)}-\frac{{(N_D-{\mu }_{\mathit{\text{Dij}}})}^2}{2{\sigma }_{\mathit{\text{Dij}}}^2(1-{\rho }_{\mathit{\text{ij}}}^2)}+\frac{{\rho }_{\mathit{\text{ij}}}(N_A-{\mu }_{\mathit{\text{Dij}}})(N_D-{\mu }_{\mathit{\text{Dij}}})}{{\sigma }_{\mathit{\text{Aij}}}{\sigma }_{\mathit{\text{Dij}}}(1-{\rho }_{\mathit{\text{ij}}}^2)})$$ (23)

where the parameters of the Gaussian are given by Eq. (22). As before, this approximation is applied only when i ≠ j.

The approximation that generalizes Eq. (15) is the product of the Poisson distributions for acceptor and donor photons with the count rates in between those in state i and j

$$B_{\mathit{\text{ij}}}(N_A,N_D)\approx \frac{{((n_{\mathit{\text{Ai}}}+n_{\mathit{\text{Aj}}})T/2)}^{N_A}}{N_A!}\frac{{((n_{\mathit{\text{Di}}}+n_{\mathit{\text{Dj}}})T/2)}^{N_D}}{N_D!}{e}^{-(n_i+n_j)T/2}$$ (24)

where n_i = n_Ai + n_Di is the total count rate in state i. This distribution has the correct mean but incorrect variance and correlation.

Finally, the approximation in the spirit of HMM that involves only the parameters of the state in the beginning of the bin (j) is

$$B_{\mathit{\text{ij}}}(N_A,N_D)\approx \frac{{(N_{\mathit{\text{Aj}}}T)}^{N_A}}{N_A!}\frac{{(n_{\mathit{\text{Dj}}}T)}^{N_D}}{N_D!}{e}^{-n_{j}T}$$ (25)

This is a generalization of Eq. (16) for one-color photons.

The distribution in the above equation is one of the “emission” probabilities used in the framework of HMM [19] in the analysis of binned sequences of acceptor and donor photon counts. It follows from our derivation that the likelihood function presented as the product of the transition and “emission” probabilities (as implied in the standard HMM) can be used only when conformational dynamics are slow on the time scale of the bin time. Even in this case, the “emission” probability can be improved by using the approximations in Eq. (23) or Eq. (24) instead of the simple Poisson distribution as in Eq. (25).

Three-color FRET

The likelihood function and its approximations for one- and two-color photons can be readily extended to three-color FRET. Consider a molecule with three labels attaches, namely, one donor, D, and two acceptors, A and B. The molecule in conformational state i can emit three kinds of photons with count rates n_Ai, n_Bi, and n_Di. As in the case of two-color FRET, it is not necessary to have a microscopic theory for these quantities in order to be able to extract the rates of conformational changes from photon trajectories. Instead of presenting the straightforward generalization of the previous theory, we right away consider the case of slow conformational dynamics so that only none or one transition occurs during a bin. In this case the likelihood function for three bins can be written as

$$L={\mathbf{1}}^{\top }\mathit{P}(N_{A3},N_{B3},N_{D3})\mathit{P}(N_{A2},N_{B2},N_{D2})\mathit{P}(N_{A1},N_{B1},N_{D1}){\mathit{p}}_{\mathit{\text{eq}}}$$ (26)

where

$$P_{\mathit{\text{ij}}}(N_A,N_B,N_D)\approx A_{\mathit{\text{ij}}}{B}_{\mathit{\text{ij}}}(N_A,N_B,N_D)$$ (27)

with the transition probability A_ij = δ_ij + K_ijT and the “emission” probability

$$B_{\mathit{\text{ij}}}(N_A,N_B,N_D)={\displaystyle {\int }_0^T}\frac{{[n_{\mathit{\text{Ai}}}t+n_{\mathit{\text{Aj}}}(T-t)]}^{N_A}}{N_A!}\frac{{[n_{\mathit{\text{Bi}}}t+n_{\mathit{\text{Bj}}}(T-t)]}^{N_B}}{N_B!}\times \frac{{[n_{\mathit{\text{Di}}}t+n_{\mathit{\text{Dj}}}(T-t)]}^{N_D}}{N_D!}{e}^{-n_{i}t-n_j(T-t)}\mathit{\text{dt}}/T$$ (28)

where n_i = n_Ai + n_Bi + n_Di. As before, this can be evaluated numerically or various approximations can be made.

The approximations for the “emission” probability for two-color FRET considered before can be readily extended to three colors. The approximation in the spirit of HMM [19], which generalizes Eq. (25), is the product of three Poisson distributions that involve only the parameters of the state at the beginning of the bin (j). The approximation that generalizes Eq. (24) is the product of three Poisson distributions with the count rates in between those in states i and j:

$$B_{\mathit{\text{ij}}}(N_A,N_B,N_D)\approx \frac{{\mu }_{\mathit{\text{Aij}}}^{N_A}}{N_A!}\frac{{\mu }_{\mathit{\text{Bij}}}^{N_B}}{N_B!}\frac{{\mu }_{\mathit{\text{Dij}}}^{N_D}}{N_D!}{e}^{-{\mu }_{\mathit{\text{Aij}}}-{\mu }_{\mathit{\text{Bij}}}-{\mu }_{\mathit{\text{Dij}}}}$$ (29)

where μ_Fij = (n_Fi + n_Fj)T/2 and index F now stands for A, B, and D.

The generalization of the Gaussian approximation in Eq. (23) involves three variables:

$$B_{\mathit{\text{ij}}}(N_A,N_B,N_D)\approx \frac{1}{\sqrt{{(2\pi )}^3\text{ det }\mathbf{\Sigma }}}{e}^{-\frac{1}{2}{\displaystyle {\sum }_{F,F\prime }}(N_F-{\mu }_{\mathit{\text{Fij}}})(N_{F\prime }-{\mu }_{F\prime \mathit{\text{ij}}}){[{\mathbf{\Sigma }}^{-1}]}_{\mathit{\text{FF}}\prime }}$$ (30)

where Σ is the covariance matrix with elements [Σ]_FF′ = μ_Fijδ_FF′ + (n_Fi − n_Fj)(n_F′i − n_F′j)T²/12 (cf. Eq. (22)). In the above equation, the summation is over all F and F′, which take values A, B, and D.

5. FRET efficiencies

Instead of studying sequences of donor and acceptor photon counts, one can construct and then analyze sequences of FRET efficiencies. They are particularly advantageous for the single-molecule measurements of the molecules diffusing through a laser spot because FRET efficiencies are less influenced by the fluctuations of the laser intensity inside the spot [31]. FRET efficiencies are calculated from photon counts in a bin as E_i = N_Ai/(N_Ai + N_Di). For example, the sequence of photons shown in Fig. 1(d) can be converted to the sequence of FRET efficiencies, E₁ = N_A1/(N_A1 + N_D1), E₂ = N_A2/(N_A2 + N_D2), E₃ = N_A3/(N_A3 + N_D3). The likelihood that parameters of the model are consistent with such a trajectory now depends on one variable (FRET efficiency), not two as in Eq. (19). The likelihood function for the sequence of J bins can be expressed in terms of matrix P(E), similar to Eq. 2:

$$L={\mathbf{1}}^{\top }\mathit{P}(E_J)\dots \mathit{P}(E_3)\mathit{P}(E_2)\mathit{P}(E_1){\mathit{p}}_{\mathit{\text{eq}}}$$ (31)

The matrix element P_ij(E) is the probability that FRET efficiency falls into an interval E ± h of size h for the bins in which the molecule is in state i at the end of the bin interval and in state j at the beginning. ² This probability is related to P_ij (N_A,N_D) and can be obtained from the latter by summing over N_A and N_D such that N_A/(N_A + N_D) = E ± h.

Now we proceed directly to the limit of slow conformational transitions, in which case P_ij (E) can be presented as the product of the transition probabilities, A_ij = δ_ij + K_ijT, and the “emission” probabilities, B_ij(E), similarly to Eqs. 8 and 20:

$$P_{\mathit{\text{ij}}}(E)\approx A_{\mathit{\text{ij}}}{B}_{\mathit{\text{ij}}}(E)$$ (32)

The “emission” probability B_ij(E) is the probability of E when at most a single transition occurs in a bin. This can be obtained only numerically from B_ij(N_A,N_D), Eq. (21), by summing over N_A and N_D. So the strategy we adopt here to simplify B_ij(E) is to find the mean and variance of B_ij(E) and then to use them to construct either a Beta or a Gaussian distribution.

The mean FRET efficiency of all bins in which the molecule is in state j and i at the beginning and end of the bin time is complicated unless the count rates are independent of conformation. Since the idea of using FRET efficiency rather than the number of acceptor and donor photons is only a good one when the total count rate does not depend on conformation, we shall now assume that this is the case here, i.e., n_Ai + n_Di = n is independent of i. Then, evaluating the average 〈E〉_ij ≡ 〈N_A/(N_A + N_D)〉_ij using the distribution B_ij(N_A,N_D) in Eq. (21), we have

$${ℰ}_{\mathit{\text{ij}}}\equiv {\langle E\rangle }_{\mathit{\text{ij}}}=\frac{1}{2}({ℰ}_i+{ℰ}_j)$$ (33)

where ℰ_i = n_Ai/(n_Ai + n_Di) = n_Ai/n is the average apparent FRET efficiency of conformation i.

Similarly, one can show that the variance ${\sigma }_{\mathit{\text{ij}}}^2\equiv {\langle E^2\rangle }_{\mathit{\text{ij}}}-{\langle E\rangle }_{\mathit{\text{ij}}}^2$ is

$${\sigma }_{\mathit{\text{ij}}}^2={ℰ}_{\mathit{\text{ij}}}(1-{ℰ}_{\mathit{\text{ij}}})\langle N^{-1}\rangle +\frac{1}{12}{({ℰ}_j-{ℰ}_i)}^2(1-\langle N^{-1}\rangle )$$ (34)

where 〈N⁻¹〉 is the mean of the reciprocal of the sum of acceptor and donor counts in a bin. Since the total count rate does not depend on the conformational state, 〈N⁻¹〉 is also state-independent.

Using the mean and variance in the above equations, B_ij(E) can be approximated as a continuous Gaussian distribution:

$$B_{\mathit{\text{ij}}}(E)\approx {(2\pi {\sigma }_{\mathit{\text{ij}}}^2)}^{-1/2}\text{ exp }(-\frac{{(E-{ℰ}_{\mathit{\text{ij}}})}^2}{2{\sigma }_{\mathit{\text{ij}}}^2})$$ (35)

Alternatively, one can use a Beta distribution

$$B_{\mathit{\text{ij}}}(E)\approx \frac{\mathrm{\Gamma }({\alpha }_{\mathit{\text{ij}}}+{\beta }_{\mathit{\text{ij}}})}{\mathrm{\Gamma }({\alpha }_{\mathit{\text{ij}}})\mathrm{\Gamma }({\beta }_{\mathit{\text{ij}}})}{E}^{{\alpha }_{\mathit{\text{ij}}}-1}{(1-E)}^{{\beta }_{\mathit{\text{ij}}}-1}$$ (36)

with the parameters chosen such that the mean and the variance are exact:

$$\begin{array}{c}{\alpha }_{\mathit{\text{ij}}}={ℰ}_{\mathit{\text{ij}}}^2(1-{ℰ}_{\mathit{\text{ij}}})/{\sigma }_{\mathit{\text{ij}}}^2-{ℰ}_{\mathit{\text{ij}}}\hfill \\ {\beta }_{\mathit{\text{ij}}}={ℰ}_{\mathit{\text{ij}}}{(1-{ℰ}_{\mathit{\text{ij}}})}^2/{\sigma }_{\mathit{\text{ij}}}^2-1+{ℰ}_{\mathit{\text{ij}}}\hfill \end{array}$$ (37)

Note that the “emission” probabilities in Eqs. (35) and (36) are applied for both i = j and i ≠ j.

Both Beta and Gaussian distributions were used to describe sequences of FRET efficiencies in the framework of HMM [14, 19]. However, the distributions used in these works differ from our approximations in two ways. First, our distributions depend on the initial and final states, which accounts for the fact that transitions between the conformational states can occur at any time during the bin, not just at the beginning. Second, the parameters of our Beta and Gaussian distributions are not free but related to the model parameters (i.e., FRET efficiencies of the states) via Eq. (34). The additional parameter 〈N⁻¹〉 can be obtained from the experimentally measured distribution of the total number of photons.

In addition to the the Beta distribution with parameters in Eq. (37), we consider a simpler set of parameters. Replacing ${\sigma }_{\mathit{\text{ij}}}^2\to {ℰ}_{\mathit{\text{ij}}}(1-{ℰ}_{\mathit{\text{ij}}})/[(n_{\mathit{\text{Aj}}}+n_{\mathit{\text{Dj}}})T]$ in Eq. (37) and using ℰ_ij in Eq. (33), we get at (n_Aj + n_Dj)T ≫ 1:

$$\begin{array}{c}{\alpha }_{\mathit{\text{ij}}}=(n_{\mathit{\text{Ai}}}+n_{\mathit{\text{Aj}}})T/2\hfill \\ {\beta }_{\mathit{\text{ij}}}=(n_{\mathit{\text{Di}}}+n_{\mathit{\text{Dj}}})T/2\hfill \end{array}$$ (38)

These parameters involve the average count rates, by analogy with Eq. (15) and (24).

Finally, we consider a third set of parameters for the Beta distribution, which depend only on the state of the molecule at the beginning of the bin:

$$\begin{array}{c}{\alpha }_{\mathit{\text{ij}}}=n_{\mathit{\text{Aj}}}T\hfill \\ {\beta }_{\mathit{\text{ij}}}=n_{\mathit{\text{Dj}}}T\hfill \end{array}$$ (39)

These are equal the mean numbers of acceptor and donor photons detected during bin time T when the molecule is in state j.

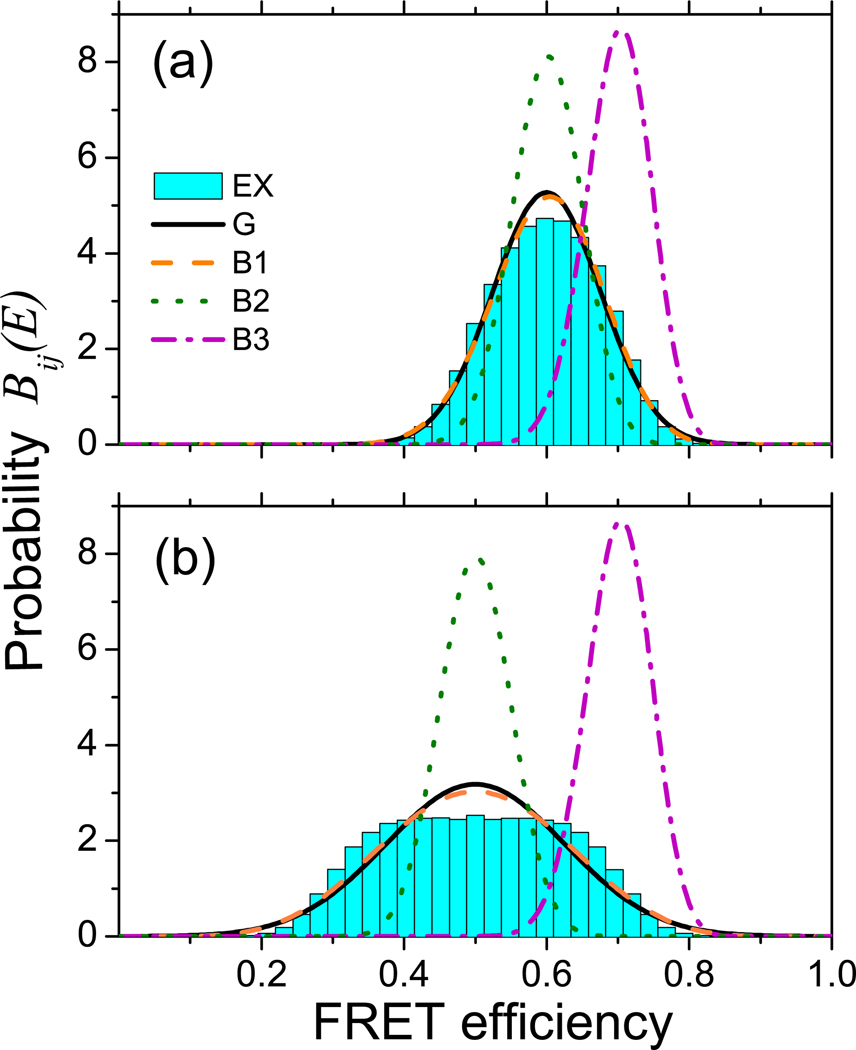
Figure 3 shows various approximations of the “emission” probability B_ij(E) are tested against exact histograms of the FRET efficiency for the bins in which the molecule has a j → i transition during the bin. The exact histograms are calculated by summing B_ij(N_A,N_D), Eq. (21), over N_A and N_D under the constraint that N_A/(N_A + N_D) is within E ± h, where h is the histogram step. The Gaussian distribution, Eqs. (33)–(35), and the Beta distribution, Eq. (36), with parameters in Eq. (37) (labeled as B1) are almost identical and are the best in describing the exact histogram. These distributions depend on both initial and final conformational states and results in the correct mean and variance. The Beta distribution with the parameters in Eq. (39) that depend only on the initial conformational state (labeled as B3) deviates significantly from the exact distribution. Using this “emission” probability in the likelihood function might lead to the loss of accuracy in determining the model parameters. Finally, the Beta distribution with average count rates in Eq. (38) (B2) has the correct mean but wrong variance of the distribution. This might be considered as the simplest (but not the best) way of correcting the parameters of the Beta distribution.

Figure 3.

Comparison of various approximations for the probability of FRET efficiency, B_ij(E), in the bins that undergo a single j → i transition. The exact (EX) histograms (bars) are calculated using Eq. (21). They are compared with the Gaussian (G) distribution (solid line, Eqs. (33)–(35)) and with Beta distributions, Eq. (36), with three different sets of parameters: parameters B1 result in the correct mean and variance (dashed line, Eq. (37)), B2 are determined by the average count rates (dotted, Eq. (38)), and B3 by the count rates of the initial state (dashed-dotted, Eq. (39)). Mean number of donor and acceptor photons in a bin is nT = 100, FRET efficiencies of the states are (a) ℰ_i = 0.5, ℰ_j = 0.7; (b) ℰ_i = 0.3, ℰ_j = 0.7

6. Concluding remarks

In this paper we considered how to construct the likelihood functions required to analyze a time-binned photon trajectory. The likelihood function can be presented in terms of the distribution of photon counts during the bin time. This distribution depends on whether a transition between conformational states has occurred during the bin time. For a two-state model, we have obtained the exact analytical expression for this distribution and, therefore, for the likelihood function. This result is valid for both long and short bin times that might be comparable to the time between state transitions. In general case, the likelihood function is more complex, and we have presented approximations starting from rigorous description of photon statistics.

In the case of slow conformational dynamics, the distribution of photons during the bin time can be presented as a product of the transition and “emission” probabilities. However, the “emission” probability depends on the molecule’s initial and final states, since a transition between conformational states can occur at any time during the bin time. When there are no transitions between the states, the “emission” distribution is Poissonian. When the conformational state changes during the bin time, the distribution is more complex. When no more than one transition during the bin time can occur, several approximations for the “emission” distribution have been suggested. The simplest and most evident (however, not necessarily most accurate) approximation is the Poisson distribution with a count rate in between of the initial and final count rates. More accurate approximations of the “emission” probability have been constructed using the exact mean and variance of the “emission” distribution. The approximate likelihood functions are valid for slow conformational dynamics compared to the bin time, as in the case of the standard HMM, but the restriction is less stringent. The approximations modify the “emission” probability for the bins with transitions between the states. Despite the fact that the number of such bins is small in the case of slow dynamics, we hope that these corrections to the “emission” probability will help to reduce bias in estimating model parameters.

Similar ideas have been employed to treat two-photon trajectories converted into sequences of FRET efficiencies. The “emission” distributions for the bins with and without transitions during the bin have been determined. It should be noted that apparent FRET efficiencies depend only on the conformational state, whereas photon count rates depend on both conformational state and location in the laser spot. This opens the possibility of using the likelihood function for the binned trajectories of FRET efficiencies presented above to analyze molecules diffusing through a laser spot. When a molecule diffuses through the laser spot, the only parameter that depends on the location in the spot is the reciprocal of the sum of acceptor and donor photons in the variance, Eq. 34.

The likelihood function can be either directly optimized with respect to the model parameters or used as the starting point of more sophisticated Bayesian procedures. Since likelihood-based methods depend on using the correct likelihood function, we hope that our work provides a sound foundation to build upon. One way to check the consistency of the observed photon trajectories with the model is to generate photon sequences according to the model, construct a FRET efficiency histogram (or the distribution of photon counts in the case of photons of one color) and compare this with the observed one [15]. The FRET efficiency distribution obtained from the simulated data constructed using HMM contains only peaks corresponding to the conformational states. However, real data may contain additional peaks due to exchange between the states [20, 32–34], which can be misinterpreted as an additional conformational state. The improved likelihood function presented in this paper should help to avoid such problems when analyzing photon trajectories, i.e., detection of false states that arise due to incorrect treatment of bins with transitions between states.

Research Highlights.

A sequence of photon counts can be analyzed using a likelihood function. An exact likelihood function for a two-state kinetic model is provided. Several approximations are considered for an arbitrary kinetic model. Improved likelihood functions are obtained to treat sequences of FRET efficiencies.